Different Formulations to Solve the Giesekus Model for Flow between Two Parallel Plates
Abstract
:1. Introduction
2. Mathematical Formulation
3. Different Formulations to Obtain the Fully Developed Laminar Flow with the Giesekus Model
3.1. Schleiniger and Weinacht Formulation
3.2. Independent Variable Change
- From Equation (28), it is possible to obtain the max, used to start the simulation and the recursive process;
- Equation (26) allows one to obtain the step size required to find the point distribution to increase , to obtain the coordinate y, respectively;
- Find by the Equation (29);
- Integrate numerically to obtain the velocity u. It is important to emphasize that, to calculate the integral numerically, an interpolation for new values of y equally spaced is adopted, since the analytical y obtained from is not equally spaced. A high-order finite difference approximation was adopted for this calculation;
- After the integral calculation, it is verified if the value of this integration is . This is the value obtained for Newtonian fluid in a Poiseuille flow with a maximum streamwise velocity equal to 1. If the value of the integral is different from , the Newton–Raphson method is used to obtain a pressure gradient where the flow resulting from this gradient has numerical integration of the velocity equal ;
3.3. High-Order Simulation (HOS)
- Apply a time integration for the vorticity and the extra-stress tensors (Runge–Kutta method);
- Calculate the extra-stress tensor components through the log-conformation method;
- Calculate the right-hand side of the Poisson equation given by Equation (35);
- Calculate the velocity v by solving the Poisson equation—Equation (35);
- Calculate the velocity u using the continuity equation—Equation (34);
- Update the vorticity at the walls;
- Apply a filter after the last step of the time integrator.
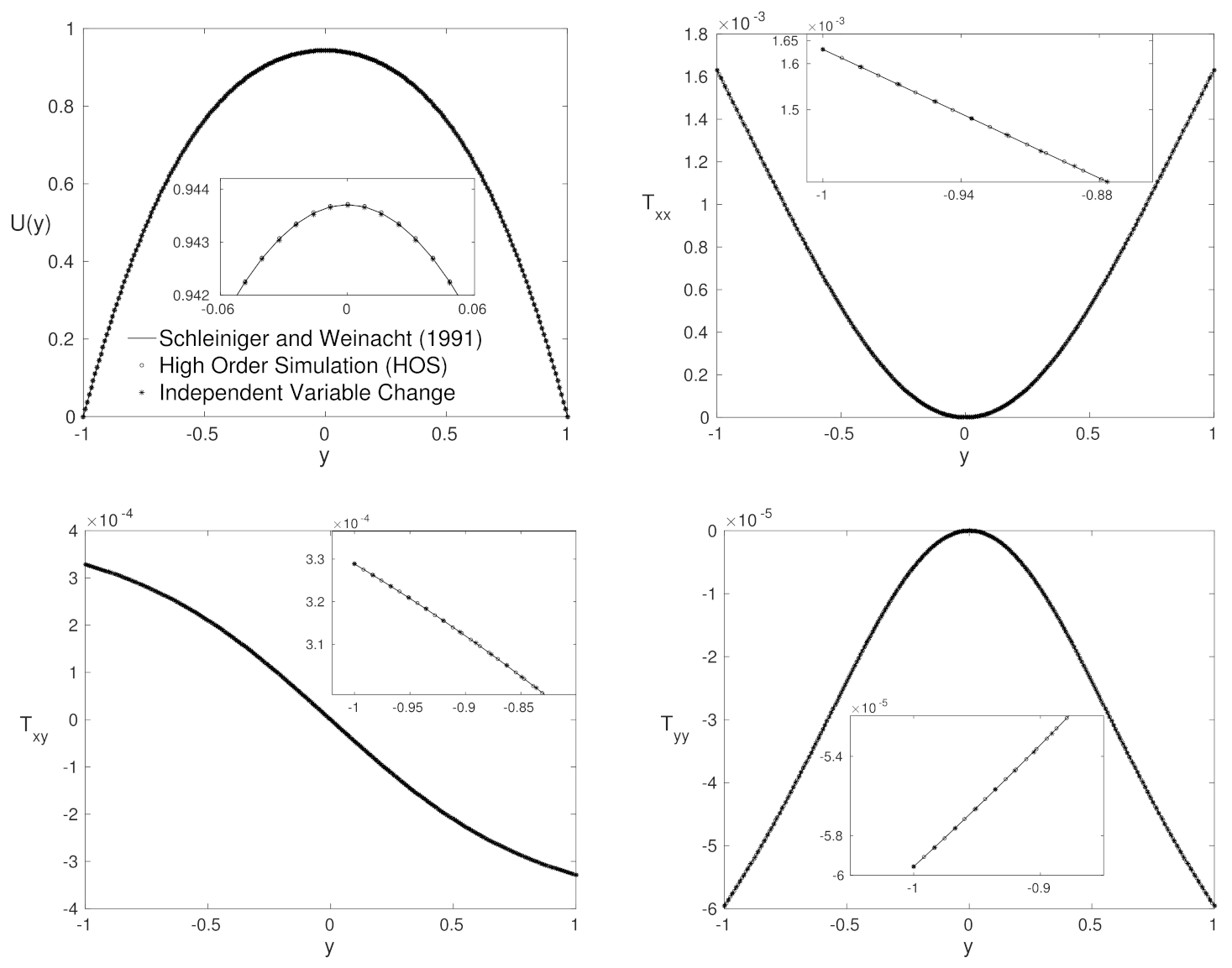
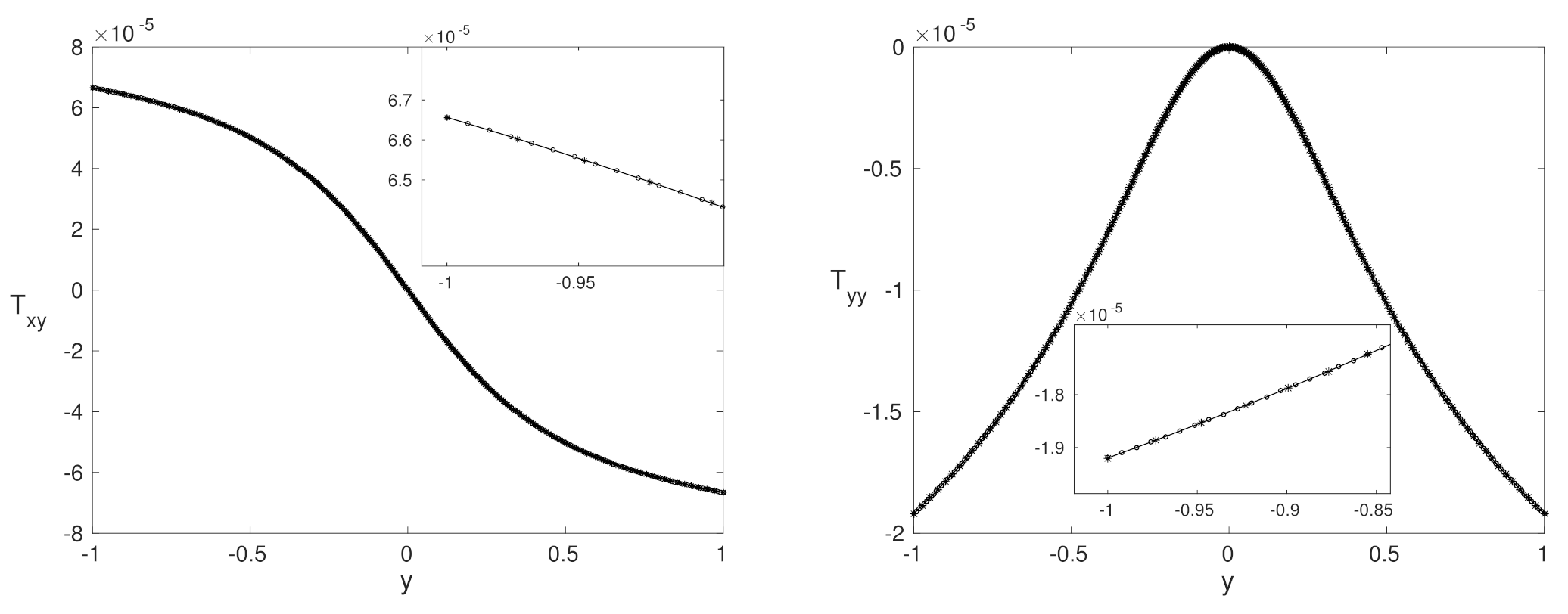
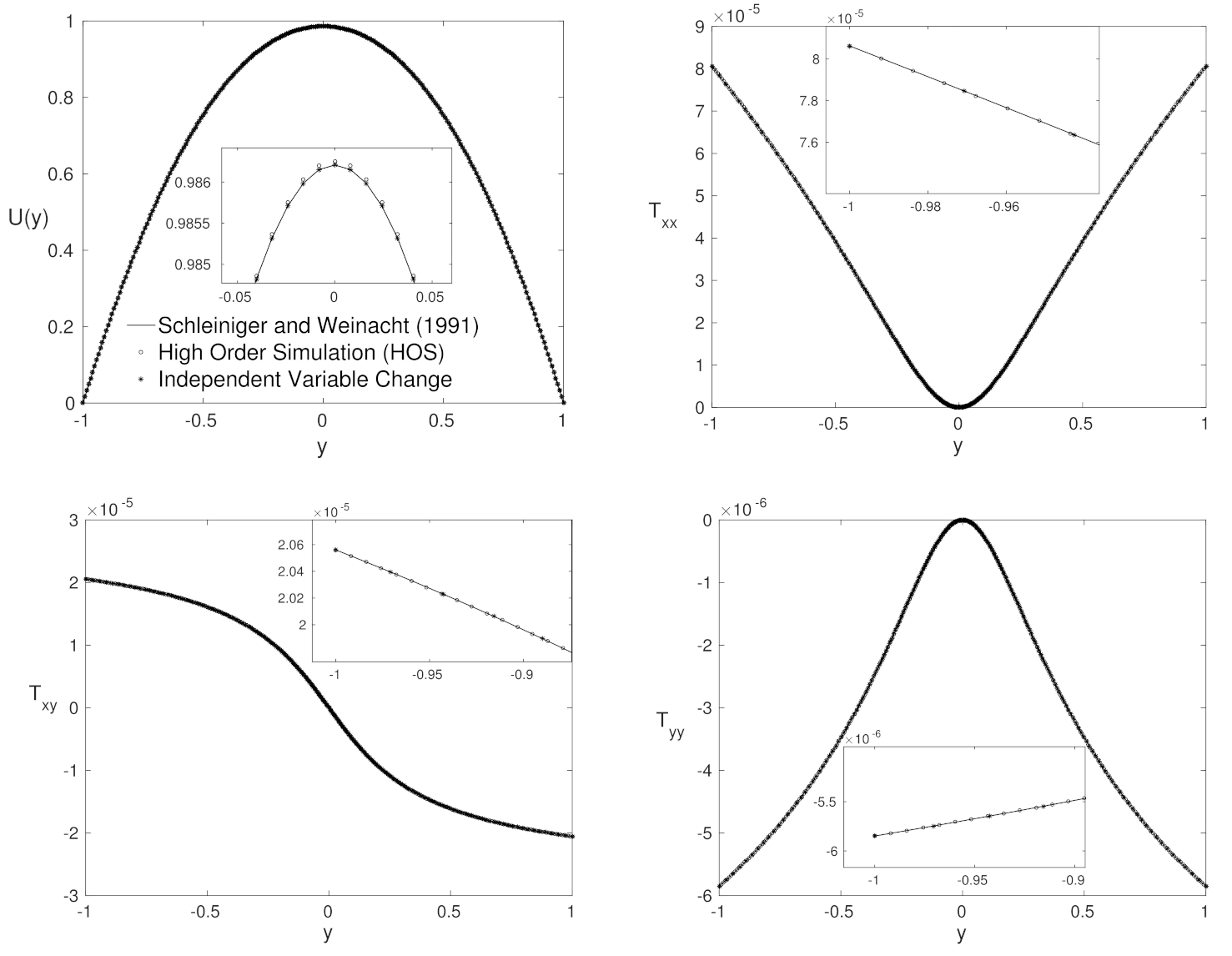
4. Results
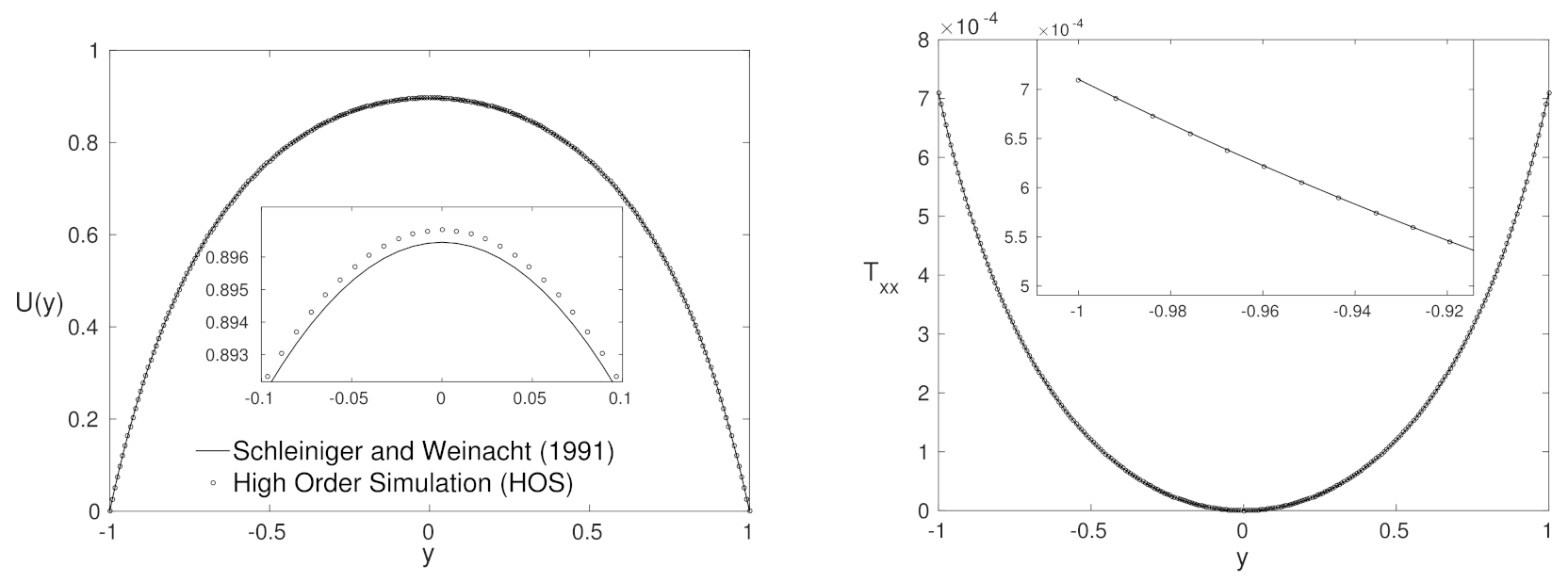
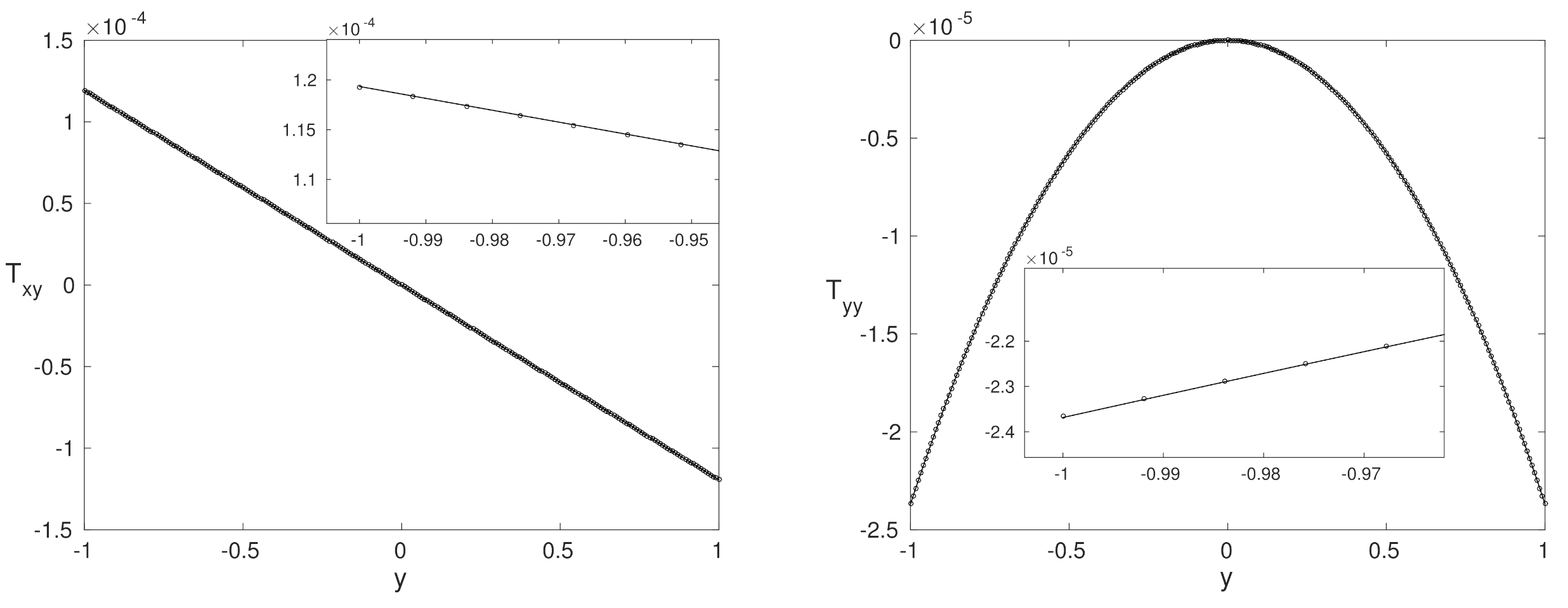
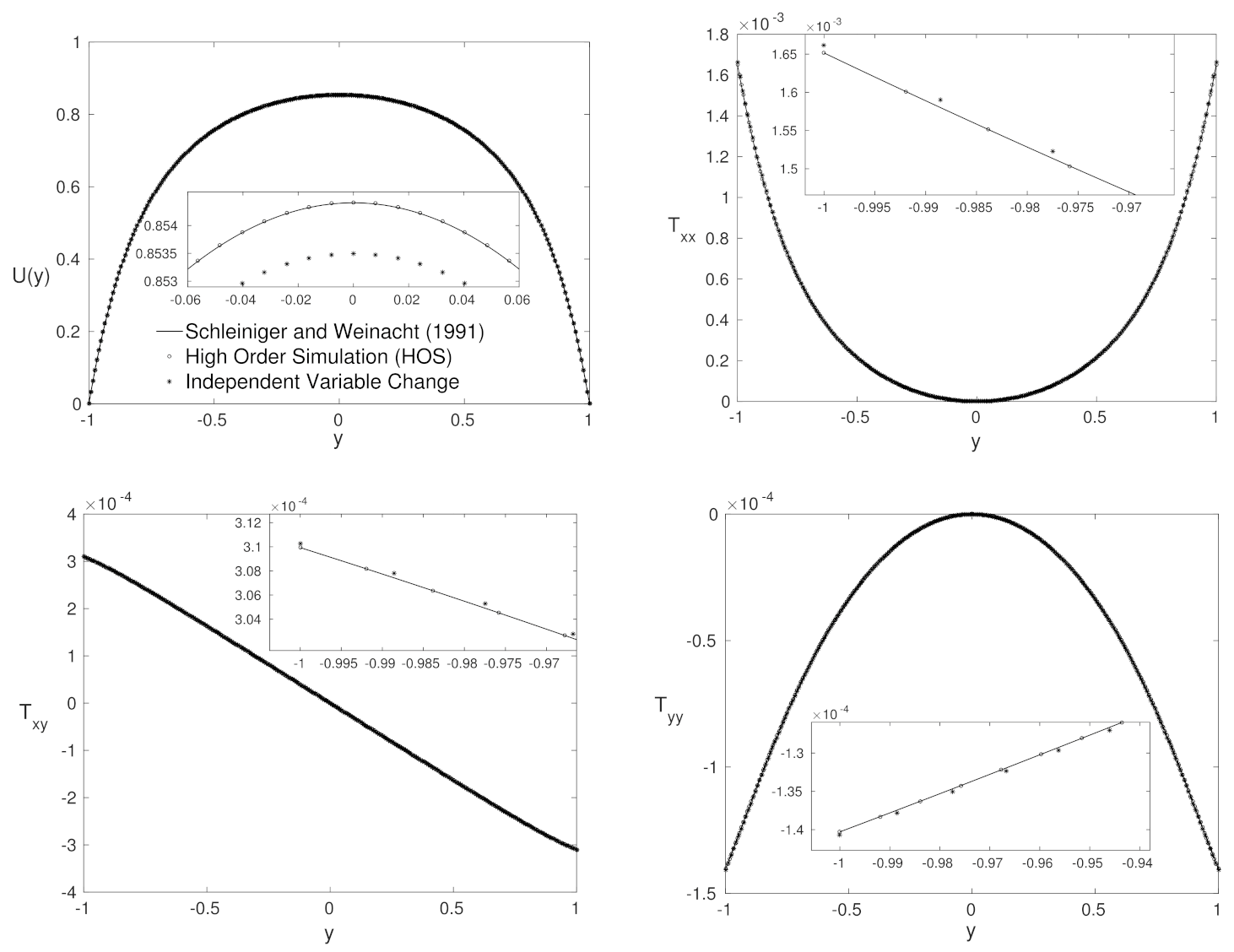
4.1. Agreement Region
- Reynolds number— 10,000;
- Weissenberg number—;
- parameter—;
- parameter—.
4.2. Purely Polymeric Flows
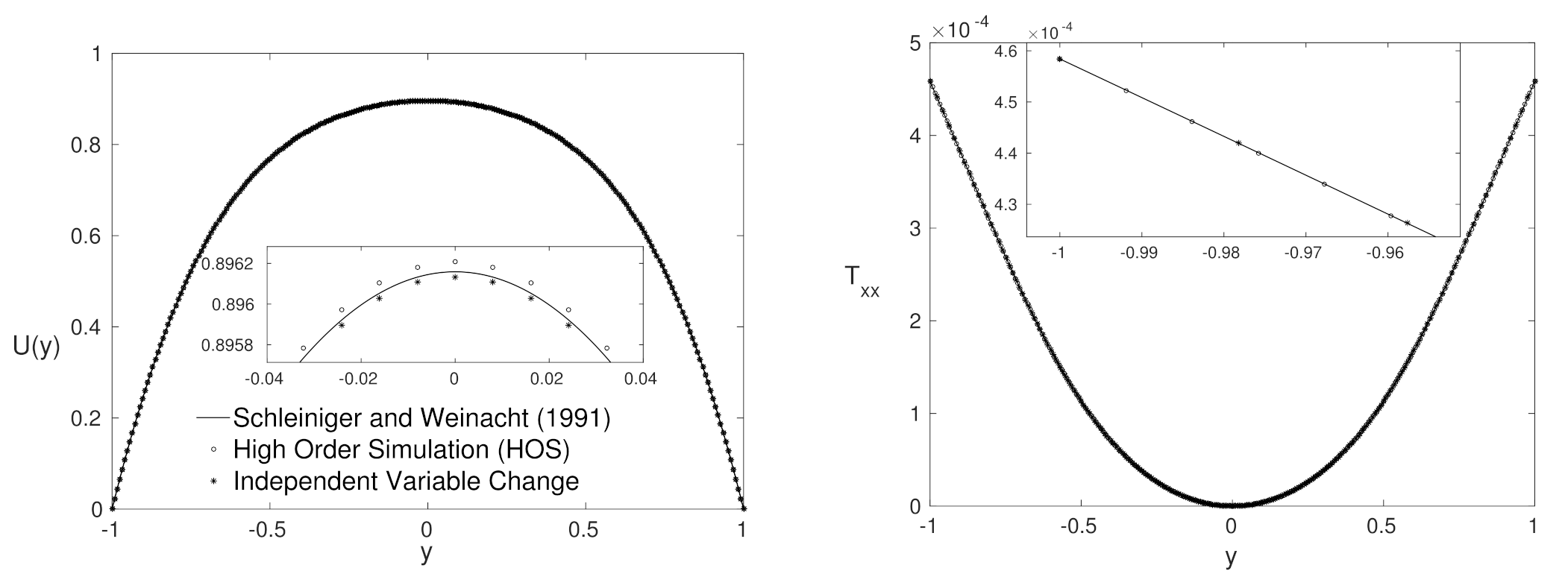
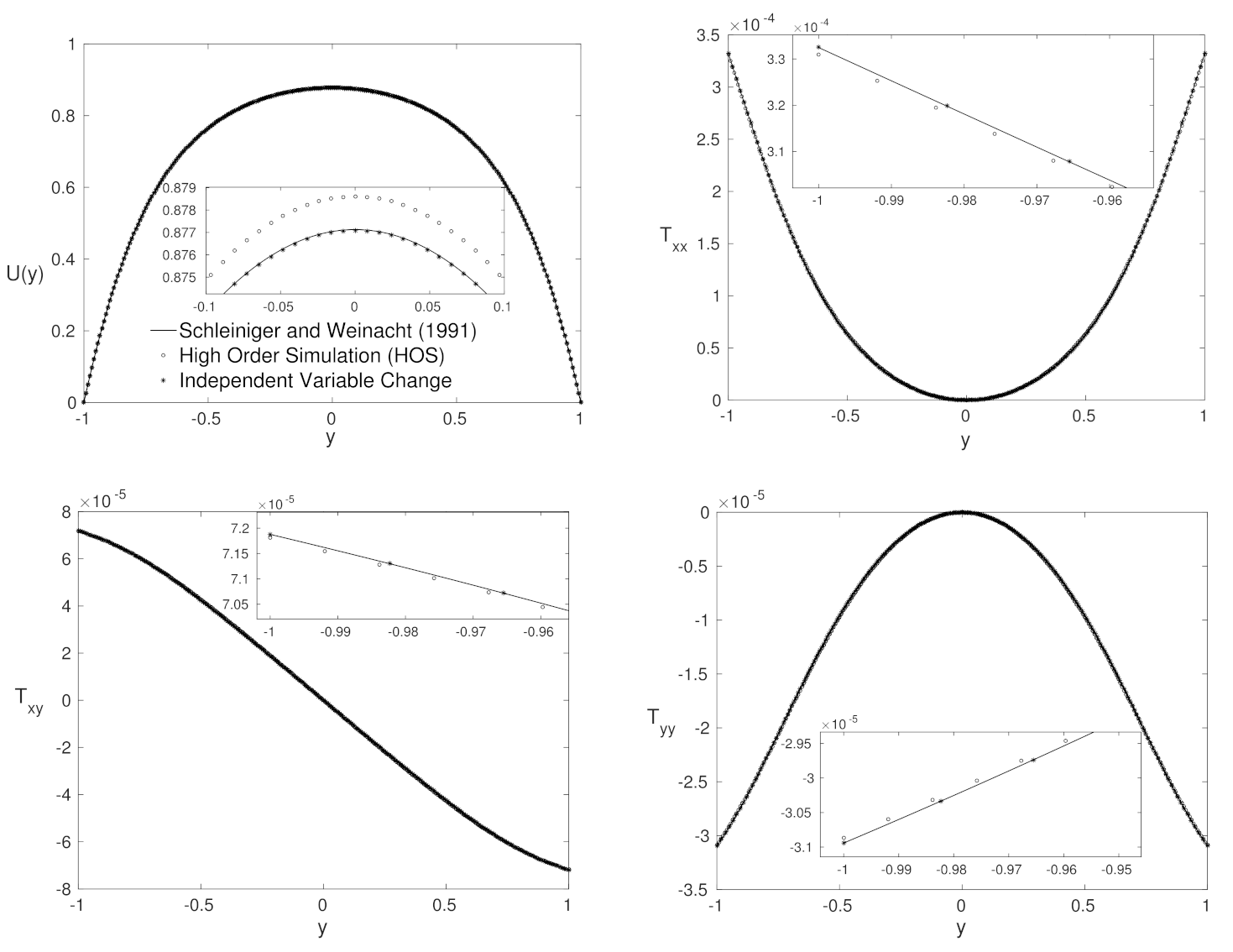
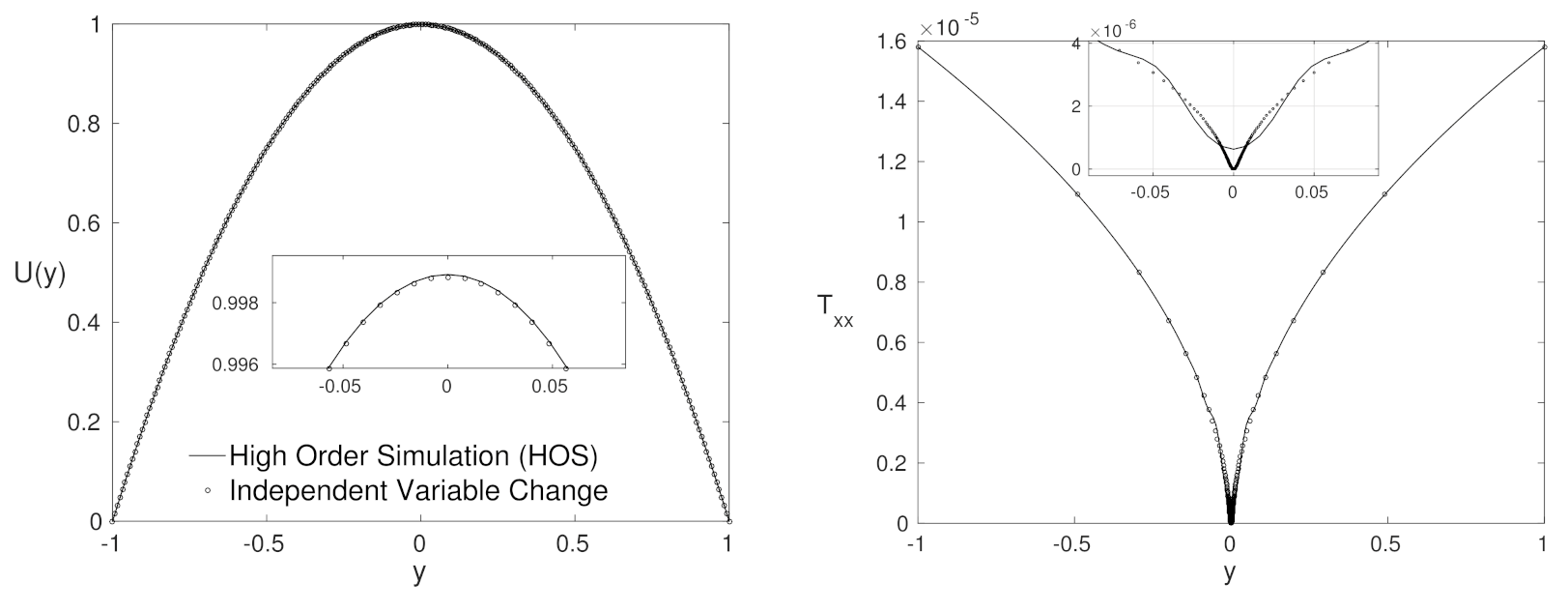
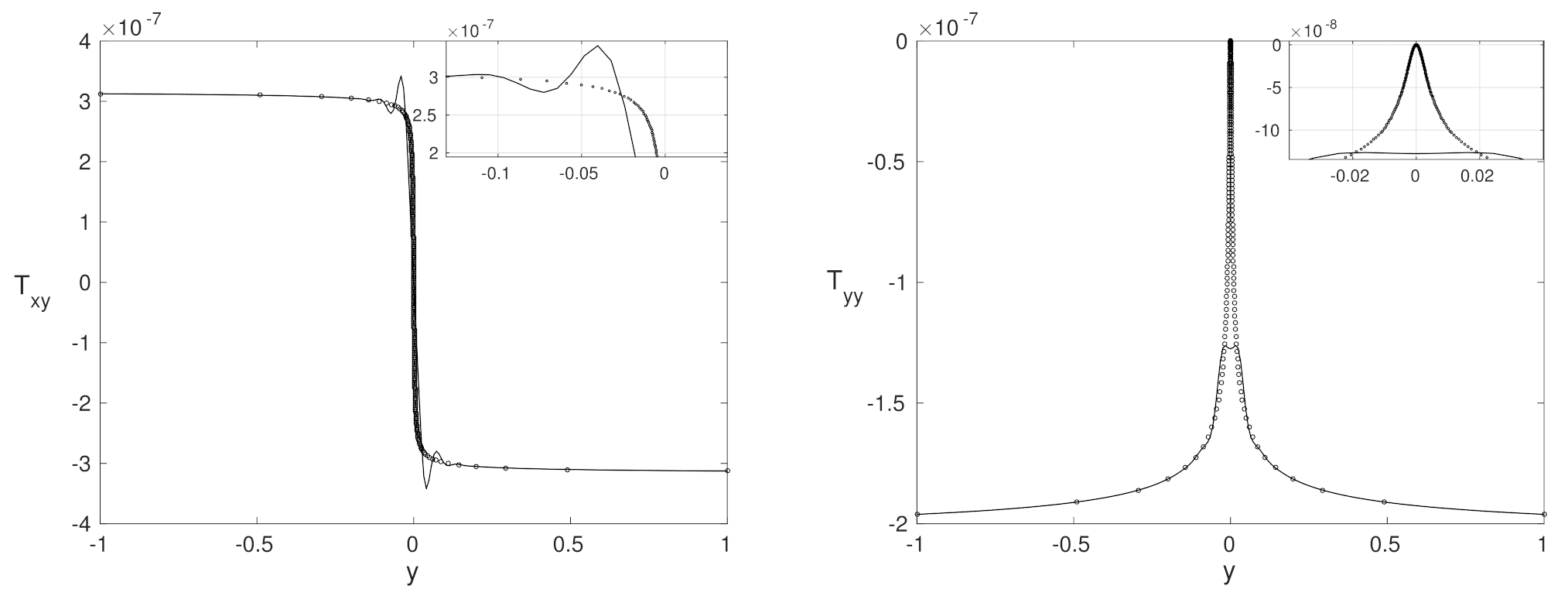
4.3. Low Number—Close to Purely Polymeric Flows
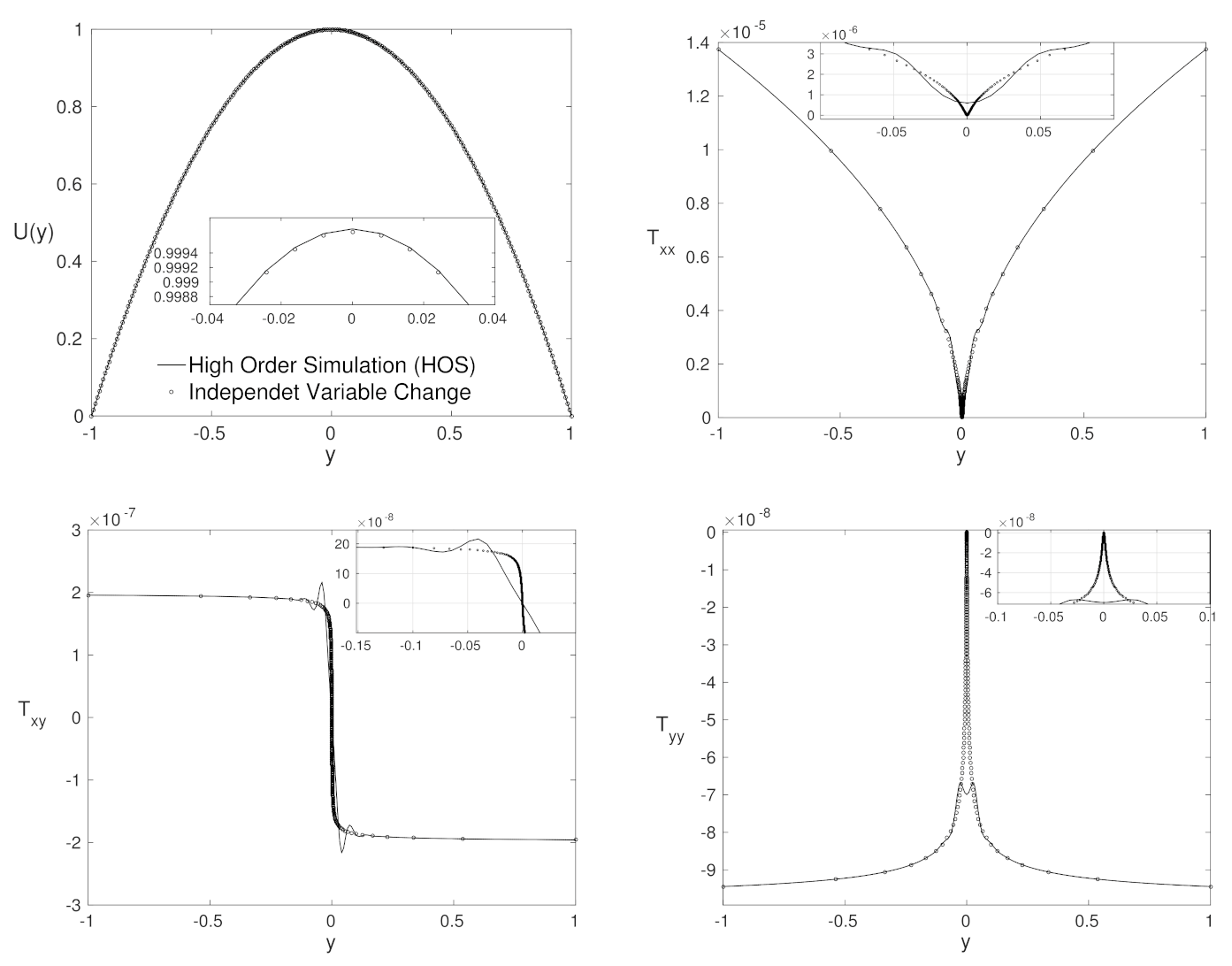
4.4. High Weissenberg Number
4.5. Advantages and Disadvantages for Each Formulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hayat, T.; Khan, M.; Ayub, M. Some simple flows of an Oldroyd-B fluid. Int. J. Eng. Sci. 2001, 39, 135–147. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.; Ayub, M. Exact solutions of flow problems of an Oldroyd-B fluid. Appl. Math. Comput. 2004, 151, 105–119. [Google Scholar] [CrossRef]
- Oliveira, P.J. An exact solution for tube and slit flow of a FENE-P fluid. Acta Mech. 2002, 158, 157–167. [Google Scholar] [CrossRef] [Green Version]
- Cruz, D.; Pinho, F.; Oliveira, P. Analytical solutions for fully developed laminar flow of some viscoelastic liquids with a Newtonian solvent contribution. J. Non-Newton. Fluid Mech. 2005, 132, 28–35. [Google Scholar] [CrossRef] [Green Version]
- Duarte, A.; Miranda, A.; Oliveira, P. Numerical and analytical modeling of unsteady viscoelastic flows: The start-up and pulsating test case problems. J. Non-Newton. Fluid Mech. 2008, 154, 153–169. [Google Scholar] [CrossRef] [Green Version]
- Paulo, G.; Oishi, C.; Tomé, M.; Alves, M.; Pinho, F. Numerical solution of the FENE-CR model in complex flows. J. Non-Newton. Fluid Mech. 2014, 204, 50–61. [Google Scholar] [CrossRef]
- Pinho, F.T.; Oliveira, P.J. Axial annular flow of a nonlinear viscoelastic fluid—An analytical solution. J. Non-Newton. Fluid Mech. 2000, 93, 325–337. [Google Scholar] [CrossRef]
- Ferrás, L.L.; Nóbrega, J.M.; Pinho, F.T. Analytical solutions for channel flows of Phan-Thien-Tanner and Giesekus fluids under slip. J. Non-Newton. Fluid Mech. 2012, 171–172, 97–105. [Google Scholar] [CrossRef]
- Yoo, J.Y.; Choi, H.C. On the steady simple shear flows of the one-mode Giesekus fluid. Rheol. Acta 1989, 28, 13–24. [Google Scholar] [CrossRef]
- Schleiniger, G.; Weinacht, R.J. Steady Poiseuille flows for a Giesekus fluid. J. Non-Newton. Fluid Mech. 1991, 40, 79–102. [Google Scholar] [CrossRef]
- James, D.F. Boger Fluids. Annu. Rev. Fluid Mech. 2009, 41, 129–142. [Google Scholar] [CrossRef]
- Giesekus, H. Elasto-viskose Flüssigkeiten, für die in stationären Schichtströmungen sämtliche Normalspannungskomponenten verschieden gross sind. Rheol. Acta 1962, 2, 50–62. [Google Scholar] [CrossRef]
- Raisi, A.; Mirzazadeh, M.; Dehnavi, A.; Rashidi, F. An approximate solution for the Couette–Poiseuille flow of the Giesekus model between parallel plates. Rheol. Acta 2008, 47, 75–80. [Google Scholar] [CrossRef]
- Tomé, M.; Araujo, M.; Evans, J.; McKee, S. Numerical solution of the Giesekus model for incompressible free surface flows without solvent viscosity. J. Non-Newton. Fluid Mech. 2019, 263, 104–119. [Google Scholar] [CrossRef]
- Giesekus, H. A simple constitutive equation for polymer fluids based on the concept of deformation-dependent tensorial mobility. J. Non-Newton. Fluid Mech. 1982, 11, 69–109. [Google Scholar] [CrossRef]
- Giesekus, H. Constitutive equations for polymer fluids based on the concept of configuration-dependent molecular mobility: A generalized mean-configuration model. J. Non-Newton. Fluid Mech. 1985, 17, 349–372. [Google Scholar] [CrossRef]
- Fattal, R.; Kupferman, R. Constitutive laws for the matrix-logarithm of the conformation tensor. J. Non-Newton. Fluid Mech. 2004, 123, 281–285. [Google Scholar] [CrossRef]
- Fattal, R.; Kupferman, R. Time-dependent simulation of viscoelastic flows at high Weissenberg number using the log-conformation representation. J. Non-Newton. Fluid Mech. 2005, 126, 23–37. [Google Scholar] [CrossRef]
- Souza, L.F.; Mendonça, M.T.; Medeiros, M.A.F. The advantages of using high-order finite differences schemes in laminar-turbulent transition studies. Int. J. Numer. Methods Fluids 2005, 48, 565–592. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1997. [Google Scholar]
- Stüben, K.; Trottenberg, U. Nonlinear Multigrid Methods, The Full Approximation Scheme; Springer: Koln-Porz, Germany, 1981; Chapter 5; pp. 58–71. [Google Scholar]
- Souza, L.F. Instabilidade Centrífuga e Transição Para Turbulência em Escoamentos Laminares Sobre Superfícies Côncavas. Ph.D. Thesis, Instituto Tecnológico de Aeronáutica, Sao Jose dos Campos, Brazil, 2003. [Google Scholar]
- Lele, S. Compact Finite Difference Schemes with Spectral-Like Resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]

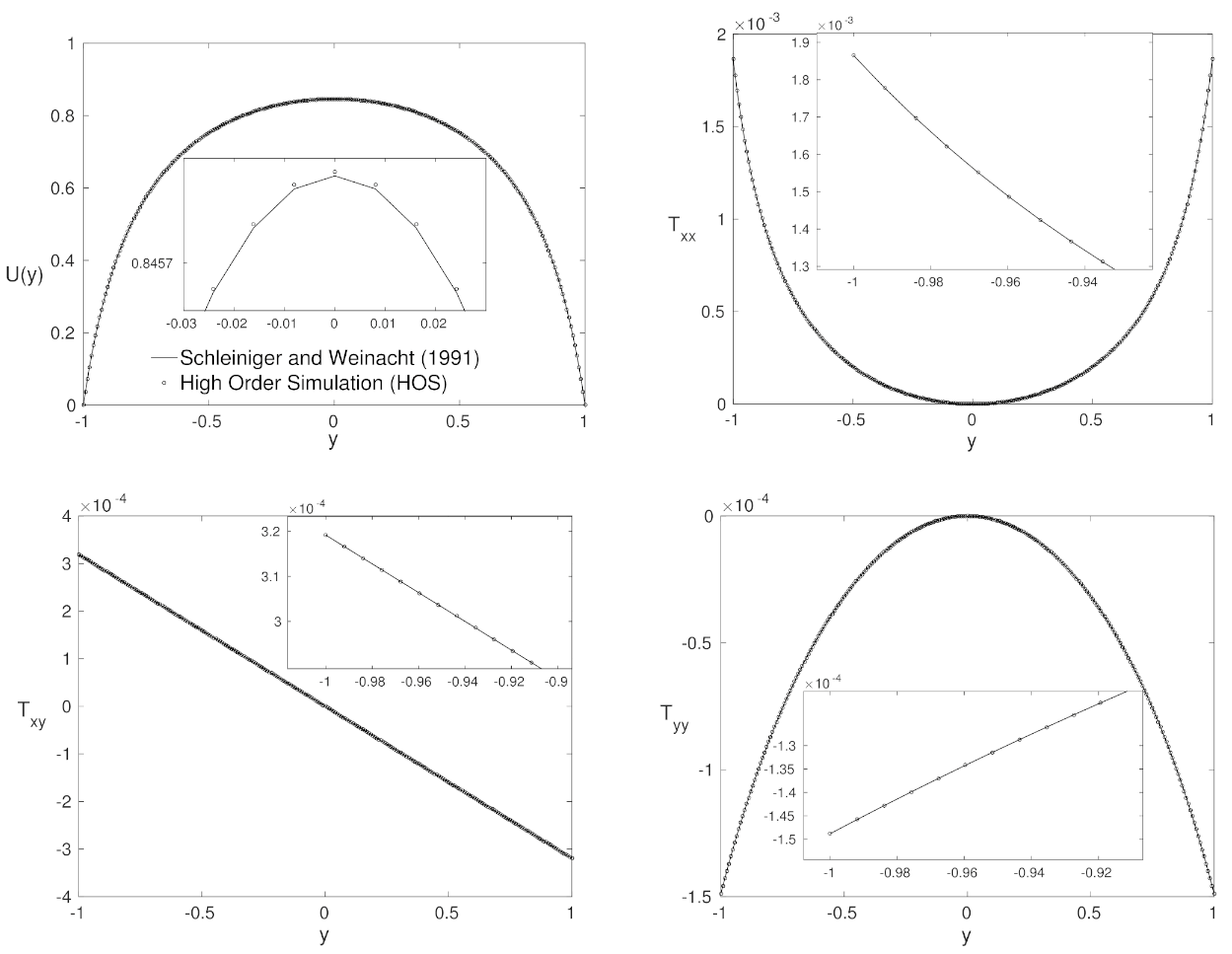



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva Furlan, L.J.; de Araujo, M.T.; Brandi, A.C.; de Almeida Cruz, D.O.; de Souza, L.F. Different Formulations to Solve the Giesekus Model for Flow between Two Parallel Plates. Appl. Sci. 2021, 11, 10115. https://doi.org/10.3390/app112110115
da Silva Furlan LJ, de Araujo MT, Brandi AC, de Almeida Cruz DO, de Souza LF. Different Formulations to Solve the Giesekus Model for Flow between Two Parallel Plates. Applied Sciences. 2021; 11(21):10115. https://doi.org/10.3390/app112110115
Chicago/Turabian Styleda Silva Furlan, Laison Junio, Matheus Tozo de Araujo, Analice Costacurta Brandi, Daniel Onofre de Almeida Cruz, and Leandro Franco de Souza. 2021. "Different Formulations to Solve the Giesekus Model for Flow between Two Parallel Plates" Applied Sciences 11, no. 21: 10115. https://doi.org/10.3390/app112110115
APA Styleda Silva Furlan, L. J., de Araujo, M. T., Brandi, A. C., de Almeida Cruz, D. O., & de Souza, L. F. (2021). Different Formulations to Solve the Giesekus Model for Flow between Two Parallel Plates. Applied Sciences, 11(21), 10115. https://doi.org/10.3390/app112110115






