Assignments as Influential Factor to Improve the Prediction of Student Performance in Online Courses
Abstract
:1. Introduction
- 1.
- How should the information about assignments be represented? Previous works in distance learning use a classical representation based on single instances. However, each course has different type and number of assignments, and these are submitted by few students, which suggests a high sparsity in the data. Representation should be adapted to this environment so that machine learning algorithms can perform well. We propose to use an optimized representation based on MIL able to adapt to the specific information available for each student.
- 2.
- Are machine learning algorithms affected by the way that assignments are represented? It is analyzed a wide set of machine learning algorithms using two different representations of assignments information: representation based on single instances (it is used in previous studies) and based on MIL (the representation that it has been proposed in the previous step). A significant performance difference between the same algorithms using both representations shows the relevance of an appropriate representation so that assignments can be considered a very influential factor for predicting students’ performance.
- 3.
- Is information about assignments a relevant feature to predict the student performance? The accuracy in predicting student performance using MIL is compared with previous studies that use different factors such as demographic features and interactions on VLEs to address the same problem. Algorithms using only information about submitted assignments reach competitive results achieving better accuracy in relation to the previous works that predict academic performance using other factors provided in the same dataset. This justifies the relevance of assignments to predict students’ performance, if it is represented appropriately.
2. Background
2.1. Multiple Instance Learning
2.2. Supervised Data Mining Techniques for Predicting Students’ Performance
3. Related Work
3.1. Predicting Student Success in Distance Higher Education
3.2. MIL in Educational Data Mining
4. Materials and Methods
4.1. Information Analysis of OULAD
4.2. Problem Representation Based on Assignment Information
4.2.1. Representation Based on Single Instance Learning
4.2.2. Representation Based on Multiple Instance Learning
5. Experimentation and Results
5.1. Configuration of Classification Algorithms
5.2. Configuration of Wrappers for MIL
- SimpleMI [67]: this wrapper makes a summary of all the instances of a bag in order to build a unique instance that can be processed by a simple instance algorithm.
- MIWrapper [68]: this wrapper assumes that all instances contribute equally and independently to the bag’s label. Thus, the method breaks up the bag into its individual instances labeling each one with the bag label and assigning weights proportional to the number of instances in a bag. At evaluation time, the final class of the bag is derived from the classes assigned to its instances.
- Configuration 1: computing arithmetic mean of each attribute using all instances of the bag and using it in the summarized instance.
- Configuration 2: computing geometric mean of each attribute using all instances of the bag and using it in the summarized instance.
- Configuration 1: computing the arithmetic average of the class probabilities of all the individual instances of the bag.
- Configuration 2: computing the geometric average of the class probabilities of all the individual instances of the bag.
- Configuration 3: checking the maximum probability of single positive instances. If there is at least one instance with its positive probability greater than 0.5, the entire bag is positive.
5.3. Evaluation Metrics
- is the number of students correctly identified to pass the course.
- is the number of students correctly identified to fail the course.
- is the number of students do not correctly identified to pass the course (it is predicted that students pass the course, but they really do not pass).
- is the number of students do not correctly identified to fail the course (it is predicted that students do pass the course, but they really pass).
- Accuracy is the proportion of correctly classified students, i.e., identifying if they pass or not the course.
- Sensitivity is the proportion of students correctly classified that pass the course.
- Specificity is the proportion of students correctly classified that do not pass the course.
5.4. Comparative Study
5.4.1. Comparative Analysis between Different Representations
5.4.2. Comparative Analysis with Previous Works
5.5. Discussion of Results
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yunusa, A.A.; Umar, I.N. A scoping review of Critical Predictive Factors (CPFs) of satisfaction and perceived learning outcomes in E-learning environments. Educ. Inf. Technol. 2021, 26, 1223–1270. [Google Scholar] [CrossRef]
- Romero, C.; Ventura, S. Data mining in education. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2013, 3, 12–27. [Google Scholar] [CrossRef]
- Tomasevic, N.; Gvozdenovic, N.; Vranes, S. An overview and comparison of supervised data mining techniques for student exam performance prediction. Comput. Educ. 2020, 143, 103676. [Google Scholar] [CrossRef]
- Gardner, J.; Brooks, C. Student success prediction in MOOCs. User Model. User Adapt. Interact. 2018, 28, 127–203. [Google Scholar] [CrossRef] [Green Version]
- Panagiotakopoulos, T.; Kotsiantis, S.; Kostopoulos, G.; Iatrellis, O.; Kameas, A. Early Dropout Prediction in MOOCs through Supervised Learning and Hyperparameter Optimization. Electronics 2021, 10, 1701. [Google Scholar] [CrossRef]
- Gong, J.W.; Liu, H.C.; You, X.Y.; Yin, L. An integrated multi-criteria decision making approach with linguistic hesitant fuzzy sets for E-learning website evaluation and selection. Appl. Soft Comput. 2021, 102, 107118. [Google Scholar] [CrossRef]
- Yang, Q.; Lee, Y.C. The Critical Factors of Student Performance in MOOCs for Sustainable Education: A Case of Chinese Universities. Sustainability 2021, 13, 8089. [Google Scholar] [CrossRef]
- Jaggars, S.S.; Xu, D. How do online course design features influence student performance? Comput. Educ. 2016, 95, 270–284. [Google Scholar] [CrossRef] [Green Version]
- Muñoz-Merino, P.J.; González Novillo, R.; Delgado Kloos, C. Assessment of skills and adaptive learning for parametric exercises combining knowledge spaces and item response theory. Appl. Soft Comput. J. 2018, 68, 110–124. [Google Scholar] [CrossRef]
- Birjali, M.; Beni-Hssane, A.; Erritali, M. A novel adaptive e-learning model based on Big Data by using competence-based knowledge and social learner activities. Appl. Soft Comput. J. 2018, 69, 14–32. [Google Scholar] [CrossRef]
- Abu Saa, A.; Al-Emran, M.; Shaalan, K. Factors Affecting Students’ Performance in Higher Education: A Systematic Review of Predictive Data Mining Techniques. Technol. Knowl. Learn. 2019, 24, 567–598. [Google Scholar] [CrossRef]
- Dietterich, T.G.; Lathrop, R.H.; Lozano-Pérez, T. Solving the multiple instance problem with axis-parallel rectangles. Artif. Intell. 1997, 89, 31–71. [Google Scholar] [CrossRef] [Green Version]
- Kuzilek, J.; Hlosta, M.; Zdrahal, Z. Data Descriptor: Open University Learning Analytics dataset. Sci. Data 2017, 4, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carbonneau, M.A.; Cheplygina, V.; Granger, E.; Gagnon, G. Multiple instance learning: A survey of problem characteristics and applications. Pattern Recognit. 2018, 77, 329–353. [Google Scholar] [CrossRef] [Green Version]
- Sudharshan, P.J.; Petitjean, C.; Spanhol, F.; Oliveira, L.E.; Heutte, L.; Honeine, P. Multiple instance learning for histopathological breast cancer image classification. Expert Syst. Appl. 2019, 117, 103–111. [Google Scholar] [CrossRef]
- Zafra, A.; Romero, C.; Ventura, S. Multiple instance learning for classifying students in learning management systems. Expert Syst. Appl. 2011, 38, 15020–15031. [Google Scholar] [CrossRef]
- Kotsiantis, S.; Kanellopoulos, D.; Tampakas, V. Financial application of multi-instance learning: Two Greek case studies. J. Converg. Inf. Technol. 2010, 5, 42–53. [Google Scholar]
- Foulds, J.; Frank, E. A review of multi-instance learning assumptions. Knowl. Eng. Rev. 2010, 25, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Alyahyan, E.; Düştegör, D. Predicting academic success in higher education: Literature review and best practices. Int. J. Educ. Technol. High. Educ. 2020, 17, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Hasan, R.; Palaniappan, S.; Mahmood, S.; Abbas, A.; Sarker, K.U.; Sattar, M.U. Predicting student performance in higher educational institutions using video learning analytics and data mining techniques. Appl. Sci. 2020, 10, 3894. [Google Scholar] [CrossRef]
- Hung, H.C.; Liu, I.F.; Liang, C.T.; Su, Y.S. Applying educational data mining to explore students’ learning patterns in the flipped learning approach for coding education. Symmetry 2020, 12, 213. [Google Scholar] [CrossRef] [Green Version]
- Shelton, B.E.; Hung, J.L.; Lowenthal, P.R. Predicting student success by modeling student interaction in asynchronous online courses. Distance Educ. 2017, 38, 59–69. [Google Scholar] [CrossRef]
- Coussement, K.; Phan, M.; De Caigny, A.; Benoit, D.F.; Raes, A. Predicting student dropout in subscription-based online learning environments: The beneficial impact of the logit leaf model. Decis. Support Syst. 2020, 135, 113325. [Google Scholar] [CrossRef]
- Kostopoulos, G.; Lipitakis, A.D.; Kotsiantis, S.; Gravvanis, G. Predicting student performance in distance higher education using active learning. Commun. Comput. Inf. Sci. 2017, 744, 75–86. [Google Scholar]
- Kostopoulos, G.; Kotsiantis, S.; Fazakis, N.; Koutsonikos, G.; Pierrakeas, C. A Semi-Supervised Regression Algorithm for Grade Prediction of Students in Distance Learning Courses. Int. J. Artif. Intell. Tools 2019, 28, 1940001. [Google Scholar] [CrossRef]
- Haiyang, L.; Wang, Z.; Benachour, P.; Tubman, P. A time series classification method for behaviour-based dropout prediction. In Proceedings of the 18th IEEE International Conference on Advanced Learning Technologies, Mumbai, India, 9–13 July 2018; pp. 191–195. [Google Scholar]
- Heuer, H.; Breiter, A. Student Success Prediction and the Trade-Off between Big Data and Data Minimization. In Die 16. E-Learning Fachtagung Informatik; Krömker, D., Schroeder, U., Eds.; Gesellschaft für Informatik e.V.: Bonn, Germany, 2018; pp. 219–230. [Google Scholar]
- Doijode, V.; Singh, N. Predicting student success based on interaction with virtual learning environment. In Proceedings of the SouthEast SAS Users Group Conference, Bethesda, MD, USA, 16–18 October 2016; p. 10. [Google Scholar]
- Alshabandar, R.; Hussain, A.; Keight, R.; Laws, A.; Baker, T. The Application of Gaussian Mixture Models for the Identification of At-Risk Learners in Massive Open Online Courses. In Proceedings of the IEEE Congress on Evolutionary Computation, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Netto Silveira, P.D.; Lube Dos Santos, O. A predictive model of academic failure or success for institutional and trace data. In Proceedings of the 14th Latin American Conference on Learning Technologies, San Jose Del Cabo, Mexico, 30 October–1 November 2019; pp. 162–165. [Google Scholar]
- Netto Silveira, P.D.; Cury, D.; Menezes, C.; Dos Santos, O.L. Analysis of classifiers in a predictive model of academic success or failure for institutional and trace data. In Proceedings of the IEEE Frontiers in Education Conference, Covington, KY, USA, 16–19 October 2019; pp. 1–8. [Google Scholar]
- Kuzilek, J.; Vaclavek, J.; Fuglik, V.; Zdrahal, Z. Student Drop-out Modelling Using Virtual Learning Environment Behaviour Data. In European Conference on Technology Enhanced Learning; Springer: Cham, Switzerland, 2018; pp. 166–171. [Google Scholar]
- Hussain, M.; Zhu, W.; Zhang, W.; Abidi, S.M.R. Student Engagement Predictions in an e-Learning System and Their Impact on Student Course Assessment Scores. Comput. Intell. Neurosci. 2018, 2018, 6347186. [Google Scholar] [CrossRef] [Green Version]
- Hassan, S.U.; Waheed, H.; Aljohani, N.R.; Ali, M.; Ventura, S.; Herrera, F. Virtual learning environment to predict withdrawal by leveraging deep learning. Int. J. Intell. Syst. 2019, 34, 1935–1952. [Google Scholar] [CrossRef]
- Aljohani, N.R.; Fayoumi, A.; Hassan, S.U. Predicting at-risk students using clickstream data in the virtual learning environment. Sustainability 2019, 11, 7238. [Google Scholar] [CrossRef] [Green Version]
- Hlosta, M.; Zdrahal, Z.; Zendulka, J. Ouroboros: Early identification of at-risk students without models based on legacy data. In Proceedings of the 7th International Learning Analytics &Knowledge Conference, Vancouver, BC, Canada, 13–17 March 2017; pp. 6–15. [Google Scholar]
- Casalino, G.; Castellano, G.; Mencar, C. Incremental and Adaptive Fuzzy Clustering for Virtual Learning Environments Data Analysis. In Proceedings of the International Conference on Information Visualisation, Paris, France, 2–5 July 2019; pp. 382–387. [Google Scholar]
- Azizah, E.N.; Pujianto, U.; Nugraha, E. Comparative performance between C4.5 and Naive Bayes classifiers in predicting student academic performance in a Virtual Learning Environment. In Proceedings of the 4th International Conference on Education and Technology, Malang, Indonesia, 26–28 October 2018; pp. 18–22. [Google Scholar]
- He, Y.; Chen, R.; Li, X.; Hao, C.; Liu, S.; Zhang, G.; Jiang, B. Online at-risk student identification using RNN-GRU joint neural networks. Information 2020, 11, 474. [Google Scholar] [CrossRef]
- Ho, L.C.; Jin Shim, K. Data Mining Approach to the Identification of At-Risk Students. In Proceedings of the IEEE International Conference on Big Data, Seattle, WA, USA, 10–13 December 2018; pp. 5333–5335. [Google Scholar]
- Waheed, H.; Hassan, S.U.; Aljohani, N.R.; Hardman, J.; Alelyani, S.; Nawaz, R. Predicting academic performance of students from VLE big data using deep learning models. Comput. Hum. Behav. 2020, 104, 106189. [Google Scholar] [CrossRef] [Green Version]
- Qiao, C.; Hu, X. A Joint Neural Network Model for Combining Heterogeneous User Data Sources: An Example of At-Risk Student Prediction. J. Assoc. Inf. Sci. Technol. 2019, 71, 1192–1204. [Google Scholar] [CrossRef]
- Song, X.; Li, J.; Sun, S.; Yin, H.; Dawson, P.; Doss, R.R.M. SEPN: A Sequential Engagement Based Academic Performance Prediction Model. IEEE Intell. Syst. 2021, 36, 46–53. [Google Scholar] [CrossRef]
- Rizvi, S.; Rienties, B.; Khoja, S.A. The role of demographics in online learning; A decision tree based approach. Comput. Educ. 2019, 137, 32–47. [Google Scholar] [CrossRef]
- Waheed, H.; Anas, M.; Hassan, S.U.; Aljohani, N.R.; Alelyani, S.; Edifor, E.E.; Nawaz, R. Balancing sequential data to predict students at-risk using adversarial networks. Comput. Electr. Eng. 2021, 93, 107274. [Google Scholar] [CrossRef]
- Hlosta, M.; Zdrahal, Z.; Zendulka, J. Are we meeting a deadline? classification goal achievement in time in the presence of imbalanced data. Knowl.-Based Syst. 2018, 160, 278–295. [Google Scholar] [CrossRef] [Green Version]
- Adnan, M.; Habib, A.; Ashraf, J.; Mussadiq, S.; Raza, A.A.; Abid, M.; Bashir, M.; Khan, S.U. Predicting at-Risk Students at Different Percentages of Course Length for Early Intervention Using Machine Learning Models. IEEE Access 2021, 9, 7519–7539. [Google Scholar] [CrossRef]
- Zafra, A.; Romero, C.; Ventura, S. DRAL: A tool for discovering relevant e-activities for learners. Knowl. Inf. Syst. 2013, 36, 211–250. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques, 4th ed.; Elsevier: Saint Louis, MO, USA, 2016; pp. 1–621. [Google Scholar]
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef] [Green Version]
- Salzberg, S.L. C4.5: Programs for Machine Learning by J. Ross Quinlan. Morgan Kaufmann Publishers, Inc., 1993. Mach. Learn. 1994, 16, 235–240. [Google Scholar] [CrossRef] [Green Version]
- Drmota, M. Random Trees: An Interplay between Combinatorics and Probability; Springer: New York, NY, USA, 2009; pp. 1–458. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Holte, R.C. Very Simple Classification Rules Perform Well on Most Commonly Used Datasets. Mach. Learn. 1993, 11, 63–90. [Google Scholar] [CrossRef]
- Martin, B. Instance-Based Learning: Nearest Neighbor with Generalization. Master’s Thesis, University of Waikato, Hamilton, New Zealand, 1995. [Google Scholar]
- Frank, E.; Witten, I.H. Generating accurate rule sets without global optimization. In Proceedings of the Fifteenth International Conference on Machine Learning, Hamilton, New Zealand, 24–27 July 1998; pp. 144–151. [Google Scholar]
- Gaines, B.R.; Compton, P. Induction of ripple-down rules applied to modeling large databases. J. Intell. Inf. Syst. 1995, 5, 211–228. [Google Scholar] [CrossRef]
- John, G.H.; Langley, P. Estimating Continuous Distributions in Bayesian Classifiers. In Proceedings of the 11th Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–20 August 2013; pp. 338–345. [Google Scholar]
- Cessie, S.L.; Houwelingen, J.C.V. Ridge Estimators in Logistic Regression. Appl. Stat. 1992, 41, 191. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Zhang, T. Solving large scale linear prediction problems using stochastic gradient descent algorithms. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; pp. 919–926. [Google Scholar]
- Meng, L.; Wu, Q.H. Fast training of Support Vector Machines using error-center-based optimization. Int. J. Autom. Comput. 2005, 2, 6–12. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Singer, Y.; Srebro, N.; Cotter, A. Pegasos: Primal estimated sub-gradient solver for SVM. Math. Program. 2011, 127, 3–30. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction; Springer: New York, NY, USA, 2009; p. 744. [Google Scholar]
- Freund, Y.; Schapire, R.E. Experiments with a New Boosting Algorithm. In Proceedings of the 13th International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Dong, L. A Comparison of Multi-Instance Learning Algorithms. Master’s Thesis, University of Waikato, Hamilton, New Zealand, 2006. [Google Scholar]
- Frank, E.; Xu, X.; Zealand, N. Applying propositional Learning Algorithms to Multi-Instance Data; Computer Science Working Papers; University of Waikato: Hamilton, New Zealand, 2003. [Google Scholar]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Sammut, C.; Webb, G.I. Encyclopedia of Machine Learning; Springer: Boston, MA, USA, 2010; p. 892. [Google Scholar]

| Work | Algorithm | Criteria | Prediction |
|---|---|---|---|
| [28] | Decision Tree | Demographic data. Number of clicks per day. Assignments data. | Final outcome. All courses together. |
| [40] | Decision Tree | Assignments data. | Final outcome: Fail vs. all. In courses CCC and FFF. |
| [44] | Decision Tree | Demographic data. | Final outcome, excluding Withdraw. In course AAA, per presentation. |
| [30,31] | J48 | Number of clicks per resource. | Final outcome binarized in Pass+Distinction/Fail+Withdraw. All courses separately. |
| [33] | J48 | Number of clicks per resource. | Engagement to the course: a combination of the first assignment score, course final result and total number of clicks. |
| [47] | Random Forest | Demographic data. Number of clicks per day. Assignments score. | Final outcome binarized in Pass+Distinction/Fail+Withdraw. All courses together. At different percentages of course length |
| [36,46] | XGBoost | Demographic data. Statistics over of clicks until the first assignment of the course. | Deadline compliance. In courses BBB, DDD, EEE, FFF, only last presentation |
| [38] | Naive Bayes | Demographic data. Total number of clicks, only in web page resource. | Final outcome, only Pass or Fail. All courses together. |
| [27] | Support Vector Machine | Demographic data. Number of clicks per day. | Final outcome binarized in Pass+Distinction/Fail+Withdraw. All courses together. |
| [29] | Gaussian Mixture Model | Number of clicks and number of sessions per resource and time-interval. | Final outcome: Withdraw vs. all. Course BBB. At different intervals of the course. |
| [37] | Dynamic Incremental Semi-Supervised Fuzzy C-Means | Demographic data. Number of clicks per resource. Assignments average score and number of submissions. | Final outcome binarized in Pass+Distinction/Fail+Withdraw. Course DDD. |
| [26] | Time Series Forest | Number of clicks per resource and day, only in 3 resources. | Final outcome: Withdraw vs. all. All courses and presentations separately. |
| [32] | Markov Chains | Number of clicks per week in planned and non-planned activities. | Final outcome: Withdraw vs. all. Course FFF, one presentation. |
| [3] | Artificial Neural Network (ANN) | Demographic data. Number of clicks per assignment. Assignment score. | Regression of final score. Course DDD, by presentations. |
| [41] | Deep Artificial Neural Network | Demographic data. Number of clicks. Assignments data. | Final outcome: Fail vs. all. In all courses. At different quarties of course. |
| [42] | Joint Neural Network Model | Demographic data. Number of clicks per resource and day. | Final outcome, only Pass or Fail. Courses BBB, CCC, FFF, one presentation. |
| [39] | Recurrent Neural Network | Demographic data. Number of clicks per week and resource. Assignment data. | Final outcome binarized in Pass+Distinction/Fail+Withdraw. All courses together. At different weeks. |
| [43] | Convolutional and recurrent deep model | Demographic data. Number of clicks. Assignment score. | Final score discretized in six ranges. Course AAA. |
| [45] | Up-sampling based on Adversarial Network + ANN | Number of clicks per resource and course quartiles. | Final outcome, only Pass or Fail. All courses together. |
| [34] | LSTM | Number of clicks per week of 25 first weeks. | Final outcome: Withdraw vs. all. |
| [35] | LSTM | Number of clicks per week. | Final outcome, only Pass or Fail. All courses together. |
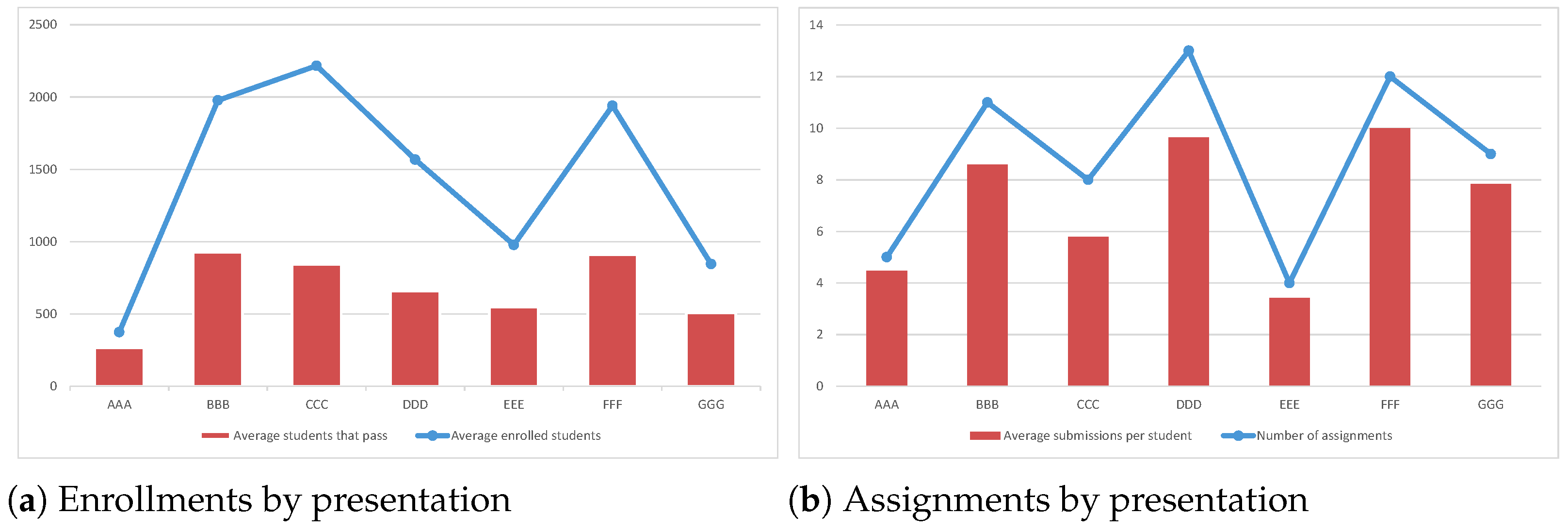
| Course | Calls | Enrollments | Assignments | Submissions | No-Pass Rate | |||
|---|---|---|---|---|---|---|---|---|
| Avg | SD | TMA | CMA | TMA | CMA | |||
| AAA | 2 | 374.00 | 12.73 | 5 | 0 | 4.47 | – | 29% |
| BBB | 4 | 1977.25 | 338.34 | 6 | 5 | 4.47 | 4.12 | 53% |
| CCC | 2 | 2217.00 | 397.39 | 4 | 4 | 2.89 | 2.91 | 62% |
| DDD | 4 | 1568.00 | 354.18 | 6 | 7 | 4.63 | 5.02 | 58% |
| EEE | 3 | 978.00 | 255.18 | 4 | 0 | 3.43 | – | 44% |
| FFF | 4 | 1940.50 | 446.52 | 5 | 7 | 3.96 | 6.04 | 53% |
| GGG | 3 | 844.67 | 102.00 | 3 | 6 | 2.69 | 5.15 | 40% |
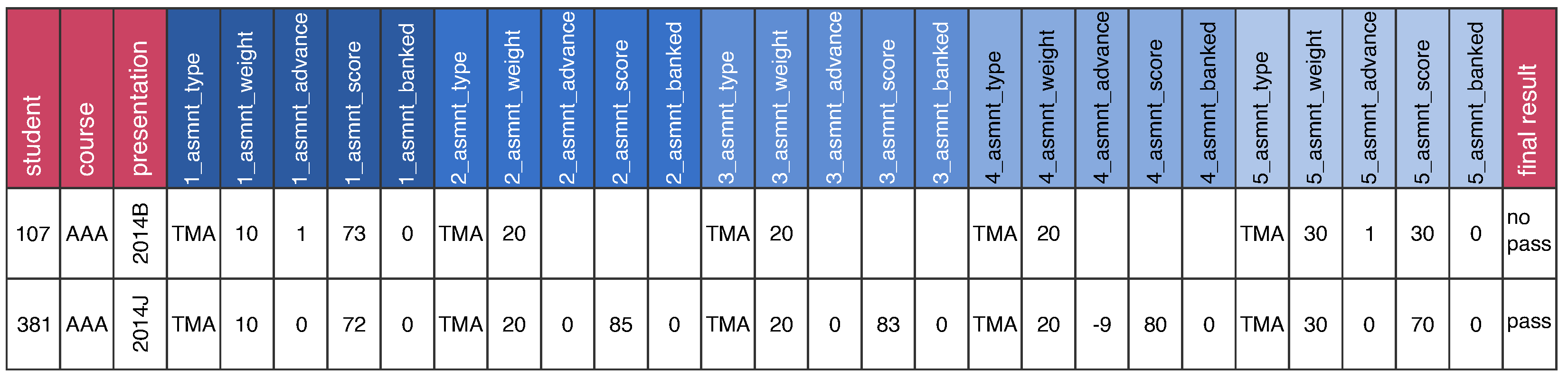
| Attribute | Description |
|---|---|
| assignment_type | Type of assignment: TMA or CMA. |
| assignment_weight | A number in range that represents the weight of the assignment in the course. |
| assignment_advance | The number of days in advance with which the student submitted the assignment. |
| assignment_score | The score of the student in the assignment in range . |
| assignment_banked | A boolean flag that indicates if the assignment has been transferred from a previous presentation. |
| Code | Attributes |
|---|---|
|
@relation assignments-course-AAA @attribute 1-assignment_type { TMA, CMA } @attribute 1-assignment_weight numeric ☐ @attribute 5-assignment_score numeric @attribute 5-assignment_banked numeric @attribute final_result { pass, no_pass } @data | 5 × assignment_type 5 × assignment_weight 5 × assignment_advance 5 × assignment_score 5 × assignment_banked Total: 25 attributes |
| Code | Attributes |
|---|---|
|
@relation assignments-course-DDD @attribute 1-assignment_type { TMA, CMA } @attribute 1-assignment_weight numeric ☐ @attribute 7-assignment_type { TMA, CMA } @attribute 7-assignment_weight numeric ☐ @attribute 13-assignment_score numeric @attribute 13-assignment_banked numeric @attribute final_result { pass, no_pass } @data | 13 × assignment_type 13 × assignment_weight 13 × assignment_advance 13 × assignment_score 13 × assignment_banked Total: 65 attributes |
| Code | Attributes |
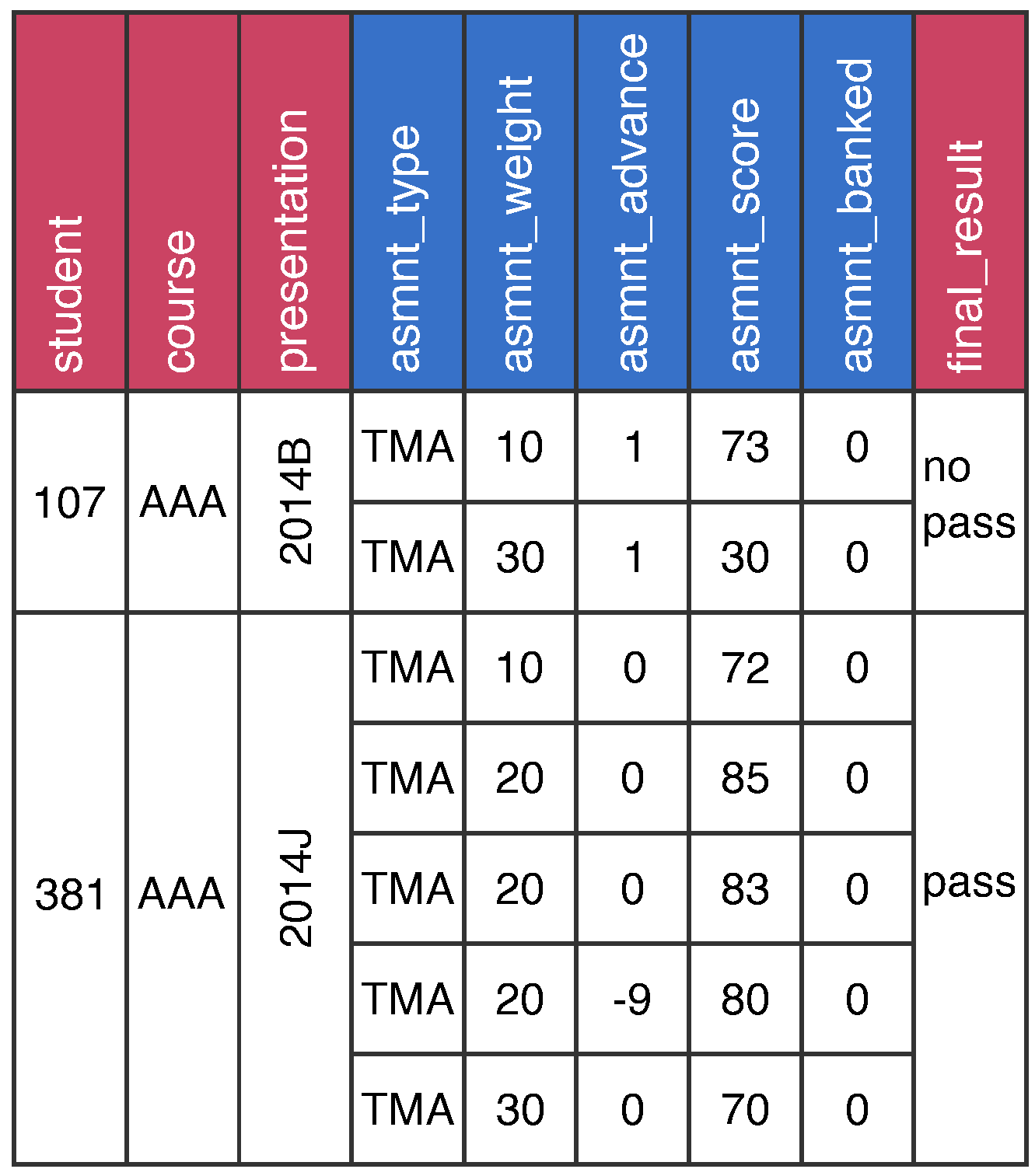
|---|---|
|
@relation assignments-course @attribute id_student-code_course-code_presentation {...} @attribute bag relational @attribute assignment_type { TMA, CMA } @attribute assignment_weight numeric @attribute assignment_advance numeric @attribute assignment_score numeric @attribute assignment_banked numeric @end bag @attribute final_result { pass, no_pass } @data | 1 × assignment_type 1 × assignment_weight 1 × assignment_advance 1 × assignment_score 1 × assignment_banked Total: 5 attributes |
| Algorithm | Parameter | Value | Algorithm | Parameter | Value |
|---|---|---|---|---|---|
| Decision Stump | - | - | ZeroR | - | - |
| J48 | binarySplits | False | OneR | minBucketSize | 6 |
| collapseTree | True | NNge | numAttemptsOf | ||
| GeneOption | 5 | ||||
| confidenceFactor | 0.25 | numFolderMIOption | 5 | ||
| doNotMakeSplit PointActualValue | False | PART | binarySplits | False | |
| minNumObj | 2 | confidenceFactor | 0.25 | ||
| numFolds | 3 | doNotMakeSplit PointActualValue | False | ||
| reduceErrorPruning | False | minNumObj | 2 | ||
| useLaplace | False | numFolds 3 | |||
| useMDLcorrection | True | reduceErrorPruning | False | ||
| Random Tree | allowUnclassified Instances | False | useMDLcorrection | True | |
| breakTiesRandomly | False | Ridor | folds | 3 | |
| maxDepth | 0 | majorityClass | False | ||
| minNum | 1.0 | minNo | 2.0 | ||
| minVarianceProp | 0.001 | shuffle | 1 | ||
| Random Forest | bagSizePercent | 100 | wholeDataErr | False | |
| breakTiesRandomly | False | Naive Bayes | useKernelEstimator | False | |
| computeAttribute Importance | False | useSupervised Discretization | False | ||
| maxDepth | 0 | Logistic | maxIts | −1 | |
| numFeatures | 0 | ridge | |||
| numIterations | 100 | useConjugate GradientDescent | False |
| Algorithm | Parameter | Value | Algorithm | Parameter | Value |
|---|---|---|---|---|---|
| LibSVM | SVMType | C-SVC | Multilayer Perceptron | decay | False |
| coef0 | 0 | hiddenLayers | a | ||
| cost | 1.0 | learningRate | 0.3 | ||
| degree | 3 | momentum | 0.2 | ||
| doNotReplace MissingValues | False | normalize Attributes | True | ||
| eps | 0.001 | reset | True | ||
| gamma | 0.0 | trainingTime | 500 | ||
| kernelType | radial | validationThreshold | 20 | ||
| normalize | False | RBF Network | maxIts | −1 | |
| probability Estimates | False | minStdDev | 0.1 | ||
| shrinking | True | numClusters | 2 | ||
| SGD | dontNormalize | False | ridge | ||
| dontReplace Missing | False | AdaBoost-Random Forest | numIterations | 10 | |
| epochs | 500 | useResampling | False | ||
| lambda | weightThreshold | 100 | |||
| learningRate | 0.01 | AdaBoost-PART | numIterations | 10 | |
| lossFunction | SVM | useResampling | False | ||
| SMO | buildCalibration Models | False | weightThreshold | 100 | |
| c | 1.0 | AdaBoost-Naive Bayes | numIterations | 10 | |
| epsilon | useResampling | False | |||
| filterType | Normalizetraining | weightThreshold | 100 | ||
| kernel | PolyKernel | Bagging—Random Forest | bagSizePercent | 100 | |
| toleranceParameter | 0.001 | numIterations | 10 | ||
| SPegasos | dontNormalize | False | Bagging—PART | bagSizePercent | 100 |
| dontReplace Missing | False | numIterations | 10 | ||
| epochs | 500 | Bagging—Naive Bayes | bagSizePercent | 100 | |
| lambda | numIterations | 10 | |||
| lossFunction | SVM |
| Wrapper | Comparison | p-Value | ||
|---|---|---|---|---|
| SimpleMI | Conf. 1 vs. Conf. 2 | 12,740.5 | 300.5 | |
| MIWrapper | Conf. 1 vs. Conf. 2 | 8274.0 | 4606.0 | |
| Conf. 1 vs. Conf. 3 | 12,846.0 | 195.0 | ||
| Conf. 2 vs. Conf. 3 | 12,847.0 | 194.0 |
| AAA | BBB | CCC | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Traditional | SimpleMI | WrapperMI | Traditional | SimpleMI | WrapperMI | Traditional | SimpleMI | WrapperMI | ||
| Trees methods | DecisionStump | 0.710 | 0.918 | 0.789 | 0.655 | 0.823 | 0.627 | 0.794 | 0.788 | 0.740 |
| J48 | 0.705 | 0.919 | 0.809 | 0.569 | 0.901 | 0.770 | 0.622 | 0.899 | 0.845 | |
| RandomTree | 0.693 | 0.868 | 0.796 | 0.624 | 0.853 | 0.750 | 0.701 | 0.860 | 0.832 | |
| RandomForest | 0.727 | 0.904 | 0.818 | 0.619 | 0.886 | 0.754 | 0.691 | 0.887 | 0.843 | |
| Rules methods | ZeroR | 0.710 | 0.752 | 0.752 | 0.525 | 0.618 | 0.618 | 0.622 | 0.509 | 0.509 |
| OneR | 0.710 | 0.918 | 0.775 | 0.653 | 0.902 | 0.627 | 0.800 | 0.889 | 0.712 | |
| NNge | 0.909 | 0.898 | 0.779 | 0.501 | 0.877 | 0.657 | 0.415 | 0.868 | 0.578 | |
| PART | 0.709 | 0.920 | 0.812 | 0.569 | 0.899 | 0.779 | 0.630 | 0.900 | 0.846 | |
| Ridor | 0.899 | 0.902 | 0.744 | 0.915 | 0.859 | 0.569 | 0.901 | 0.850 | 0.655 | |
| NaiveBayes | 0.730 | 0.921 | 0.810 | 0.785 | 0.735 | 0.706 | 0.823 | 0.779 | 0.807 | |
| Logistic | 0.722 | 0.925 | 0.788 | 0.797 | 0.807 | 0.740 | 0.904 | 0.837 | 0.822 | |
| SVM methods | LibSVM | 0.806 | 0.916 | 0.759 | 0.851 | 0.832 | 0.658 | 0.830 | 0.861 | 0.752 |
| SPegasos | 0.301 | 0.913 | 0.759 | 0.489 | 0.795 | 0.627 | 0.454 | 0.824 | 0.662 | |
| SGD | 0.733 | 0.915 | 0.755 | 0.755 | 0.805 | 0.627 | 0.815 | 0.836 | 0.729 | |
| SMO | 0.721 | 0.918 | 0.759 | 0.741 | 0.808 | 0.735 | 0.806 | 0.837 | 0.815 | |
| ANN methods | RBFNetwork | 0.758 | 0.859 | 0.813 | 0.856 | 0.907 | 0.687 | 0.882 | 0.873 | 0.829 |
| MultilayerPerceptron | 0.879 | 0.919 | 0.808 | 0.911 | 0.939 | 0.760 | 0.918 | 0.907 | 0.837 | |
| Ensembles methods | AdaBoost&RandomForest | 0.656 | 0.905 | 0.813 | 0.743 | 0.885 | 0.754 | 0.689 | 0.884 | 0.838 |
| AdaBoost&PART | 0.738 | 0.918 | 0.811 | 0.699 | 0.894 | 0.778 | 0.715 | 0.894 | 0.847 | |
| AdaBoost&NaiveBayes | 0.730 | 0.921 | 0.809 | 0.790 | 0.805 | 0.753 | 0.836 | 0.788 | 0.830 | |
| Bagging&RandomForest | 0.726 | 0.919 | 0.820 | 0.625 | 0.905 | 0.760 | 0.690 | 0.903 | 0.845 | |
| Bagging&PART | 0.715 | 0.915 | 0.811 | 0.562 | 0.895 | 0.778 | 0.629 | 0.892 | 0.848 | |
| Bagging&NaiveBayes | 0.732 | 0.920 | 0.809 | 0.785 | 0.699 | 0.683 | 0.826 | 0.777 | 0.795 | |
| DDD | EEE | FFF | GGG | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Traditional | SimpleMI | WrapperMI | Traditional | SimpleMI | WrapperMI | Traditional | SimpleMI | WrapperMI | Traditional | SimpleMI | WrapperMI | ||
| Trees methods | DecisionStump | 0.667 | 0.775 | 0.724 | 0.646 | 0.903 | 0.718 | 0.661 | 0.906 | 0.797 | 0.607 | 0.907 | 0.717 |
| J48 | 0.584 | 0.863 | 0.809 | 0.593 | 0.898 | 0.816 | 0.530 | 0.931 | 0.868 | 0.597 | 0.908 | 0.784 | |
| RandomTree | 0.584 | 0.828 | 0.776 | 0.596 | 0.872 | 0.789 | 0.667 | 0.909 | 0.830 | 0.590 | 0.862 | 0.771 | |
| RandomForest | 0.584 | 0.855 | 0.797 | 0.603 | 0.888 | 0.799 | 0.659 | 0.929 | 0.848 | 0.600 | 0.900 | 0.771 | |
| Rules methods | ZeroR | 0.584 | 0.528 | 0.528 | 0.562 | 0.718 | 0.718 | 0.530 | 0.580 | 0.580 | 0.598 | 0.717 | 0.717 |
| OneR | 0.665 | 0.844 | 0.668 | 0.646 | 0.904 | 0.729 | 0.656 | 0.924 | 0.611 | 0.603 | 0.907 | 0.720 | |
| NNge | 0.863 | 0.830 | 0.695 | 0.911 | 0.871 | 0.722 | 0.506 | 0.918 | 0.637 | 0.612 | 0.887 | 0.635 | |
| PART | 0.584 | 0.862 | 0.812 | 0.588 | 0.900 | 0.805 | 0.578 | 0.931 | 0.874 | 0.593 | 0.908 | 0.791 | |
| Ridor | 0.876 | 0.833 | 0.618 | 0.907 | 0.892 | 0.739 | 0.941 | 0.915 | 0.670 | 0.905 | 0.868 | 0.697 | |
| NaiveBayes | 0.817 | 0.765 | 0.742 | 0.602 | 0.900 | 0.773 | 0.789 | 0.910 | 0.832 | 0.588 | 0.902 | 0.814 | |
| Logistic | 0.833 | 0.842 | 0.780 | 0.802 | 0.899 | 0.794 | 0.917 | 0.915 | 0.826 | 0.610 | 0.907 | 0.743 | |
| SVM methods | LibSVM | 0.814 | 0.843 | 0.724 | 0.884 | 0.896 | 0.761 | 0.845 | 0.909 | 0.662 | 0.854 | 0.846 | 0.7232 |
| SPegasos | 0.583 | 0.840 | 0.767 | 0.443 | 0.902 | 0.748 | 0.495 | 0.911 | 0.601 | 0.598 | 0.907 | 0.717 | |
| SGD | 0.796 | 0.847 | 0.688 | 0.607 | 0.895 | 0.722 | 0.719 | 0.911 | 0.594 | 0.604 | 0.907 | 0.717 | |
| SMO | 0.787 | 0.845 | 0.771 | 0.592 | 0.895 | 0.781 | 0.786 | 0.906 | 0.793 | 0.600 | 0.907 | 0.717 | |
| RBFNetwork | 0.758 | 0.799 | 0.768 | 0.856 | 0.902 | 0.793 | 0.882 | 0.909 | 0.837 | 0.694 | 0.904 | 0.790 | |
| ANN methods | MultilayerPerceptron | 0.879 | 0.855 | 0.787 | 0.911 | 0.903 | 0.807 | 0.918 | 0.930 | 0.870 | 0.881 | 0.907 | 0.784 |
| Ensembles methods | AdaBoost&RandomForest | 0.761 | 0.857 | 0.786 | 0.679 | 0.889 | 0.792 | 0.805 | 0.926 | 0.838 | 0.728 | 0.898 | 0.769 |
| AdaBoost&PART | 0.623 | 0.859 | 0.808 | 0.721 | 0.894 | 0.799 | 0.701 | 0.929 | 0.873 | 0.677 | 0.904 | 0.793 | |
| AdaBoost&NaiveBayes | 0.820 | 0.814 | 0.767 | 0.818 | 0.900 | 0.779 | 0.838 | 0.910 | 0.855 | 0.588 | 0.902 | 0.809 | |
| Bagging&RandomForest | 0.584 | 0.868 | 0.798 | 0.602 | 0.901 | 0.803 | 0.667 | 0.935 | 0.854 | 0.602 | 0.912 | 0.775 | |
| Bagging&PART | 0.584 | 0.861 | 0.817 | 0.597 | 0.896 | 0.812 | 0.585 | 0.931 | 0.876 | 0.598 | 0.905 | 0.790 | |
| Bagging&NaiveBayes | 0.818 | 0.743 | 0.730 | 0.601 | 0.900 | 0.771 | 0.789 | 0.911 | 0.820 | 0.593 | 0.902 | 0.816 | |
| Accuracy | Sensitivity | Specificity | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Traditional | SimpleMI | WrapperMI | Traditional | SimpleMI | WrapperMI | Traditional | SimpleMI | WrapperMI | ||
| Trees methods | DecisionStump | 0.677 | 0.860 | 0.730 | 0.458 | 0.949 | 0935 | 0.822 | 0.703 | 0.300 |
| J48 | 0.600 | 0.903 | 0.814 | 0.434 | 0.953 | 0.959 | 0.592 | 0.802 | 0.505 | |
| RandomTree | 0636 | 0.865 | 0.792 | 0.504 | 0.889 | 0.951 | 0.616 | 0.807 | 0.463 | |
| RandomForest | 0640 | 0.893 | 0.804 | 0.510 | 0.931 | 0.957 | 0.610 | 0.810 | 0.485 | |
| Rules methods | ZeroR | 0.590 | 0.631 | 0.631 | 0.429 | 0.857 | 0.857 | 0.571 | 0.143 | 0.143 |
| OneR | 0.676 | 0.898 | 0.692 | 0.458 | 0.966 | 0.985 | 0.818 | 0.770 | 0.156 | |
| NNge | 0.674 | 0.878 | 0.672 | 0.954 | 0.905 | 0.891 | 0.397 | 0.814 | 0.298 | |
| PART | 0.607 | 0.903 | 0.817 | 0.443 | 0.949 | 0.957 | 0.604 | 0.806 | 0.515 | |
| Ridor | 0.906 | 0.874 | 0.670 | 0.948 | 0.949 | 0.871 | 0.732 | 0.720 | 0.291 | |
| NaiveBayes | 0.733 | 0.844 | 0.783 | 0.851 | 0.938 | 0.955 | 0.560 | 0.676 | 0.440 | |
| Logistic | 0.798 | 0.876 | 0.785 | 0.822 | 0.945 | 0.962 | 0.716 | 0.738 | 0.417 | |
| SVM methods | LibSVM | 0.841 | 0.872 | 0.720 | 0.978 | 0.920 | 0.989 | 0.667 | 0.769 | 0.218 |
| SPegasos | 0.480 | 0.870 | 0.697 | 0.548 | 0.948 | 0.964 | 0.483 | 0.717 | 0.193 | |
| SGD | 0.718 | 0.874 | 0.690 | 0.728 | 0.950 | 0.968 | 0.587 | 0.720 | 0.142 | |
| SMO | 0.719 | 0.874 | 0.767 | 0.722 | 0.953 | 0.965 | 0.585 | 0.716 | 0.354 | |
| ANN methods | RBFNetwork | 0.812 | 0.879 | 0.788 | 0.861 | 0.947 | 0.954 | 0.647 | 0.727 | 0.433 |
| MultilayerPerceptron | 0.899 | 0.909 | 0.808 | 0.919 | 0.943 | 0.954 | 0.757 | 0.788 | 0.498 | |
| Ensembles methods | AdaBoost&RandomForest | 0.723 | 0.892 | 0.798 | 0.607 | 0.930 | 0.953 | 0.719 | 0.810 | 0.478 |
| AdaBoost&PART | 0.696 | 0.899 | 0.816 | 0.684 | 0.946 | 0.956 | 0.617 | 0.799 | 0.514 | |
| AdaBoost&NaiveBayes | 0.774 | 0.863 | 0.800 | 0.843 | 0.925 | 0.949 | 0.617 | 0.738 | 0.488 | |
| Bagging&RandomForest | 0.642 | 0.906 | 0.808 | 0.513 | 0.958 | 0.957 | 0.610 | 0.799 | 0.495 | |
| Bagging&PART | 0.610 | 0.899 | 0.819 | 0.444 | 0.940 | 0.959 | 0.603 | 0.811 | 0.518 | |
| Bagging&NaiveBayes | 0.735 | 0.836 | 0.775 | 0.849 | 0.945 | 0.958 | 0.525 | 0.648 | 0.416 | |
| Comparison | p-Value | ||
|---|---|---|---|
| SimpleMI vs. Traditional | 273 | 3 | |
| MIWrapper vs. Traditional | 212 | 62 | 0.02332 |
| SimpleMI vs. MIWrapper | 275 | 0 |
| Comparison | p-Value | ||
|---|---|---|---|
| SimpleMI vs. Traditional | 269 | 7 | |
| MIWrapper vs. Traditional | 269 | 7 | |
| SimpleMI vs. MIWrapper | 44 | 231 | 0.003252 |
| Comparison | p-Value | ||
|---|---|---|---|
| SimpleMI vs. Traditional | 239 | 37 | 0.001279 |
| MIWrapper vs. Traditional | 0 | 276 | |
| SimpleMI vs. MIWrapper | 275 | 0 |
| Algorithm | Course | Previous Work | Proposed MIL Approach | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ref. | Assign. | Clicks | Demog. | Acc. | Assign. | Clicks | Demog. | Acc. | ||
| Decision tree | CCC | [40] | X | 86.6% | X | 89.9% | ||||
| FFF | 79.4% | X | 93.1% | |||||||
| AAA | [44] | X | 83.1% | X | 91.9% | |||||
| J48 | All courses | [30] | X | 86.7% | X | 90.3% | ||||
| [33] | X | 88.5% | ||||||||
| RandomForest | All courses | [47] | X | X | X | 81.8% | X | 89.3% | ||
| [26] | X | 86.2% | ||||||||
| NaiveBayes | All courses | [38] | X | X | 63.8% | X | 84.4% | |||
| SVM | All courses | [27] | X | X | 88.0% | X | 87.2% | |||
| ANN | All courses | [45] | X | 89.0% | X | 90.9% | ||||
| Course | Previous Work | Proposed MIL Approach | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ref. | Algorithm | Assign. | Clicks | Demog. | Acc. | Algorithm | Assign. | Clicks | Demog. | Acc. | |
| BBB | [29] | Gaussian Mixture | X | 85.5% | Multilayer Perceptron | X | 93.9% | ||||
| DDD | [37] | Dynamic Incremental Semi-supervised Fuzzy C-means | X | X | X | 89.3% | Bagging & RandomForest | X | 86.8% | ||
| AAA | [43] | Convolutional and Recurrent Deep Model | X | X | X | 61.0% | PART | X | 92.0% | ||
| All courses | [41] [39] [45] | Deep ANN Recurrent Neural Network Adversarial Network + ANN | X | X X X | X X | 84.5% 75.0% 89.0% | Multilayer Perceptron | X | | | 90.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esteban, A.; Romero, C.; Zafra, A. Assignments as Influential Factor to Improve the Prediction of Student Performance in Online Courses. Appl. Sci. 2021, 11, 10145. https://doi.org/10.3390/app112110145
Esteban A, Romero C, Zafra A. Assignments as Influential Factor to Improve the Prediction of Student Performance in Online Courses. Applied Sciences. 2021; 11(21):10145. https://doi.org/10.3390/app112110145
Chicago/Turabian StyleEsteban, Aurora, Cristóbal Romero, and Amelia Zafra. 2021. "Assignments as Influential Factor to Improve the Prediction of Student Performance in Online Courses" Applied Sciences 11, no. 21: 10145. https://doi.org/10.3390/app112110145
APA StyleEsteban, A., Romero, C., & Zafra, A. (2021). Assignments as Influential Factor to Improve the Prediction of Student Performance in Online Courses. Applied Sciences, 11(21), 10145. https://doi.org/10.3390/app112110145








