Damage Identification Method Using Additional Virtual Mass Based on Damage Sparsity
Abstract
:1. Introduction
2. Damage Identification Method Based on Additional Virtual Mass and Damage Sparsity
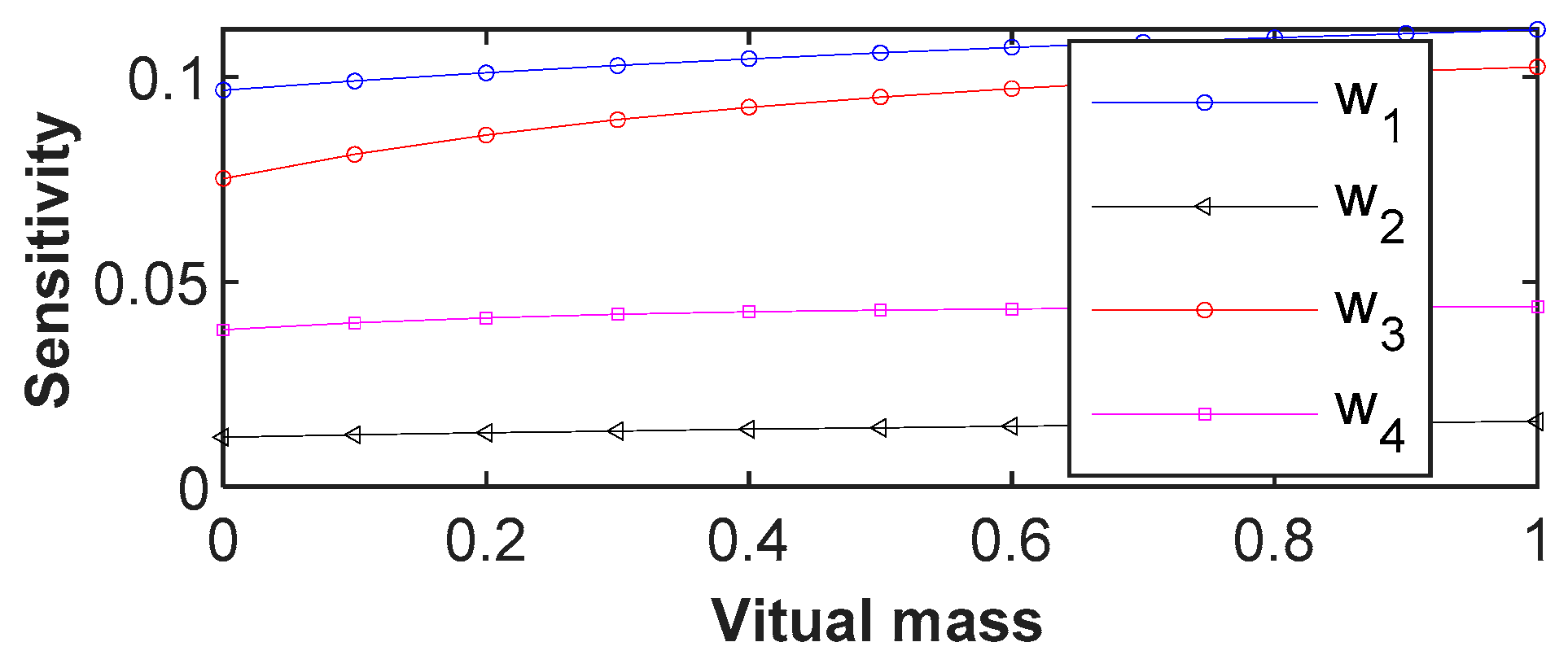
2.1. Additional Virtual Mass Method
2.2. Damage Identification Method Based on Sparsity
2.2.1. Basic Theory and Regression Model
- Traditional regression model
- 2.
- Non-parameter Gaussian kernel regression model
2.2.2. OMP Method
3. Improved OMP Damage Identification Method Based on Sparsity
3.1. Residual Vector Variance Criterion
3.2. Sensitivity Correlation Criterion
- The mean value of each row of the residual matrix was determined, and all elements were subtracted from their rows mean value to form matrix .
- The covariance matrix of was calculated, and the eigenvalues of this covariance matrix were determined and arranged in descending order to form .
- The ratio, , of the first i substructures eigenvalues to all eigenvalues was calculated. When reached a particular threshold, it was assumed that the first i substructures were damaged while the other parts of the structures were undamaged.
4. Numerical Simulation of Simply Supported Beam and Space Truss
4.1. Simply Supported Beam Model
4.1.1. Model and Damage Scenario
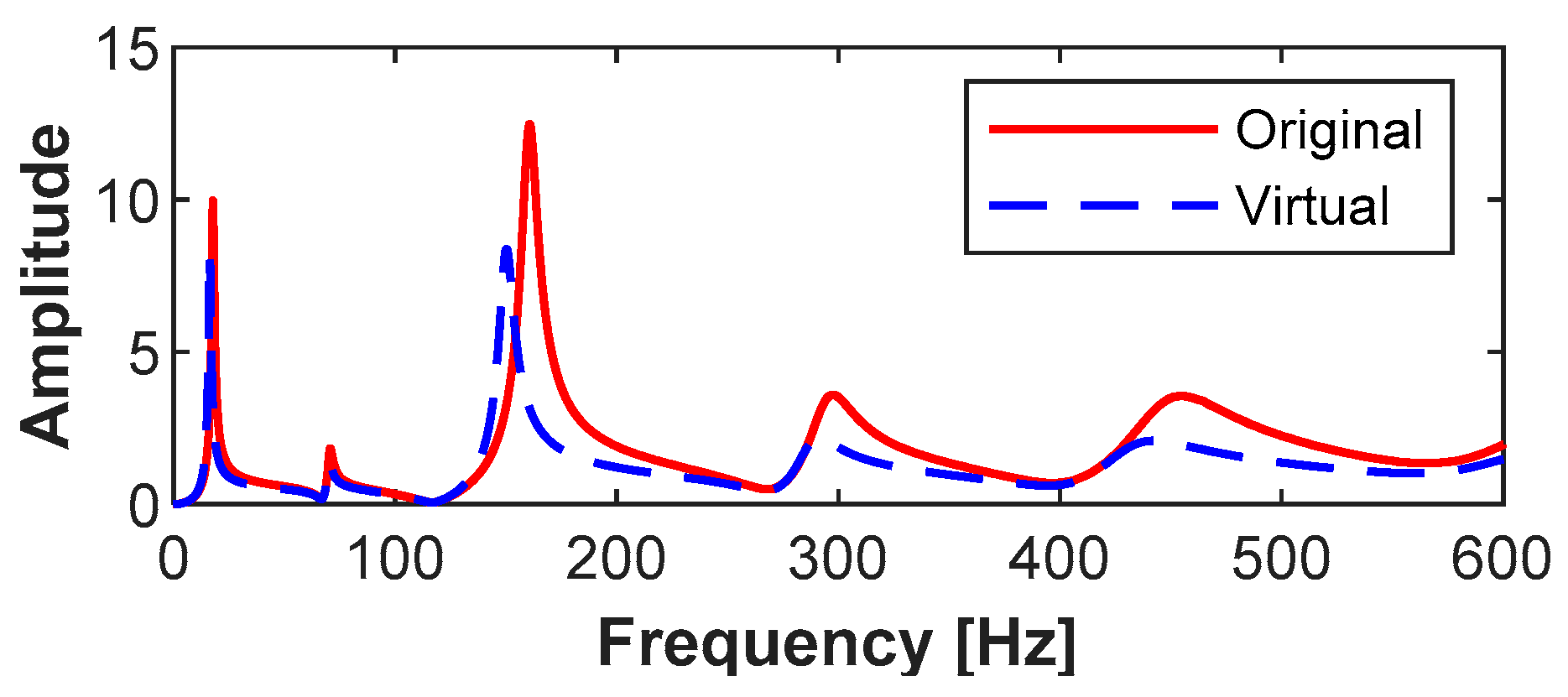
4.1.2. Virtual Mass Addition and Response Construction
4.1.3. Damage Identification
4.1.4. Susceptibility to Noise
4.2. Space Truss Model
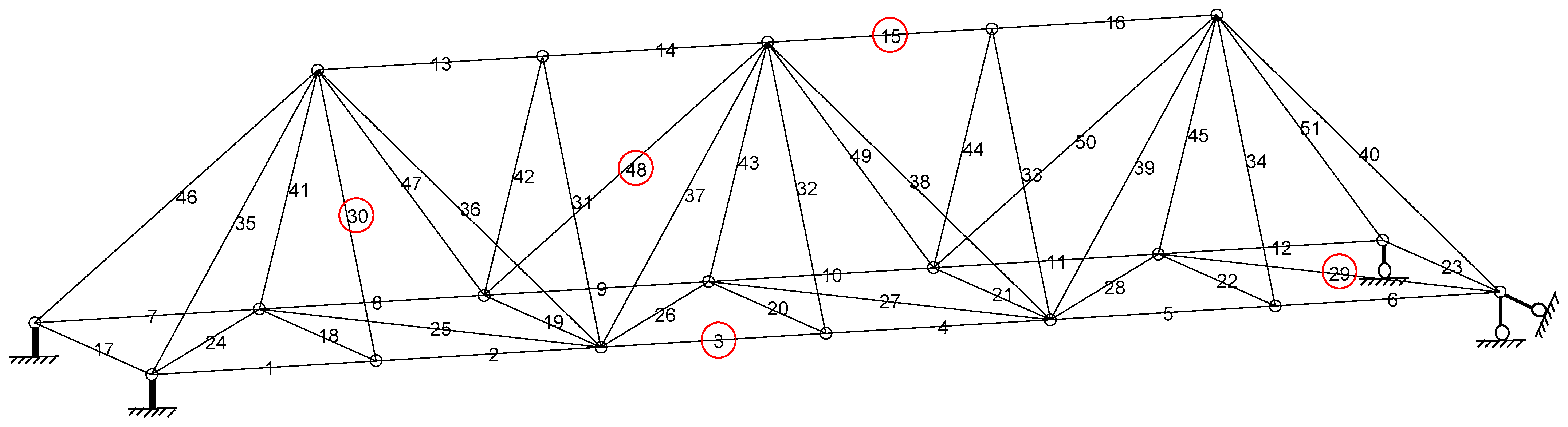
4.2.1. Model and Damage Scenario
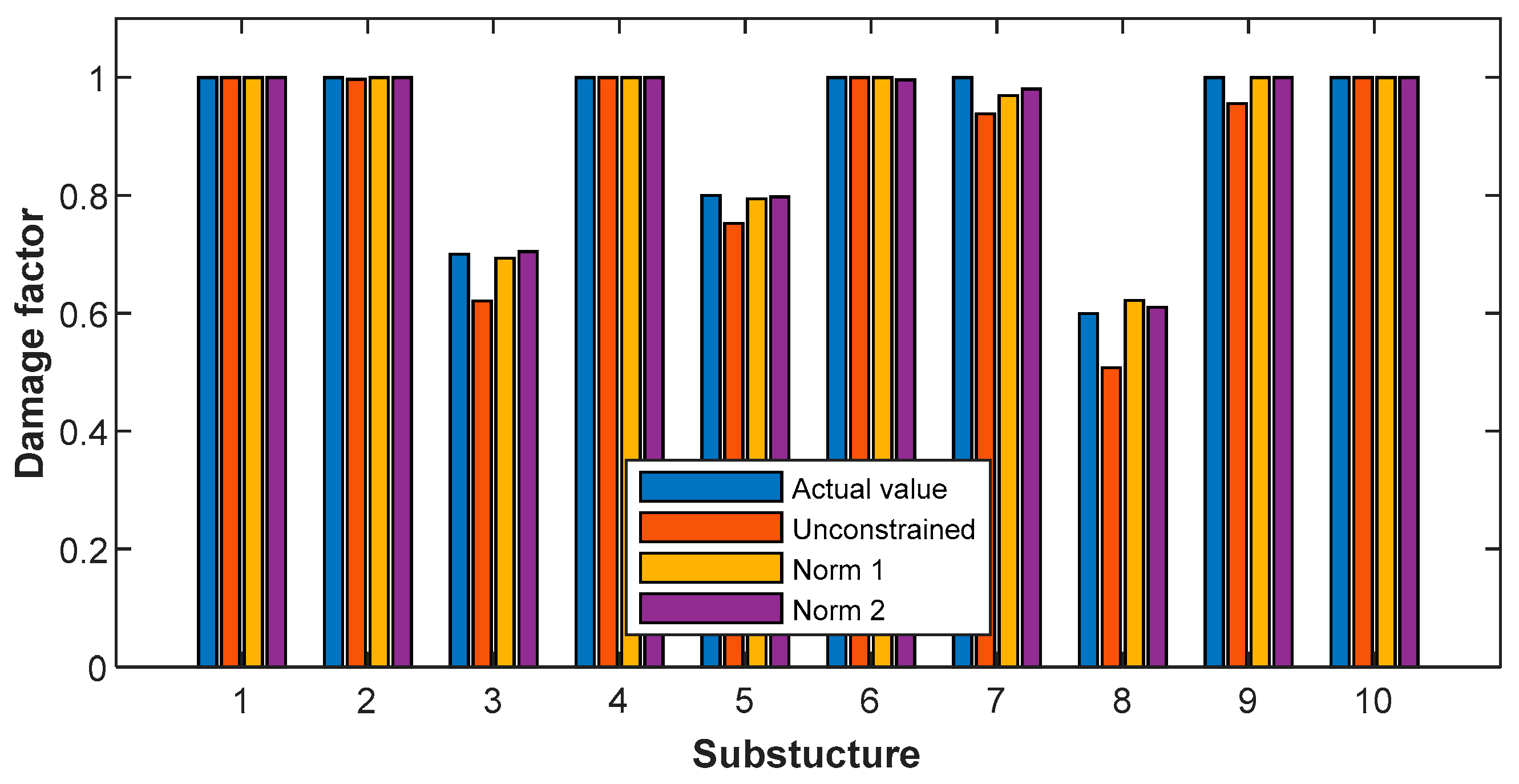
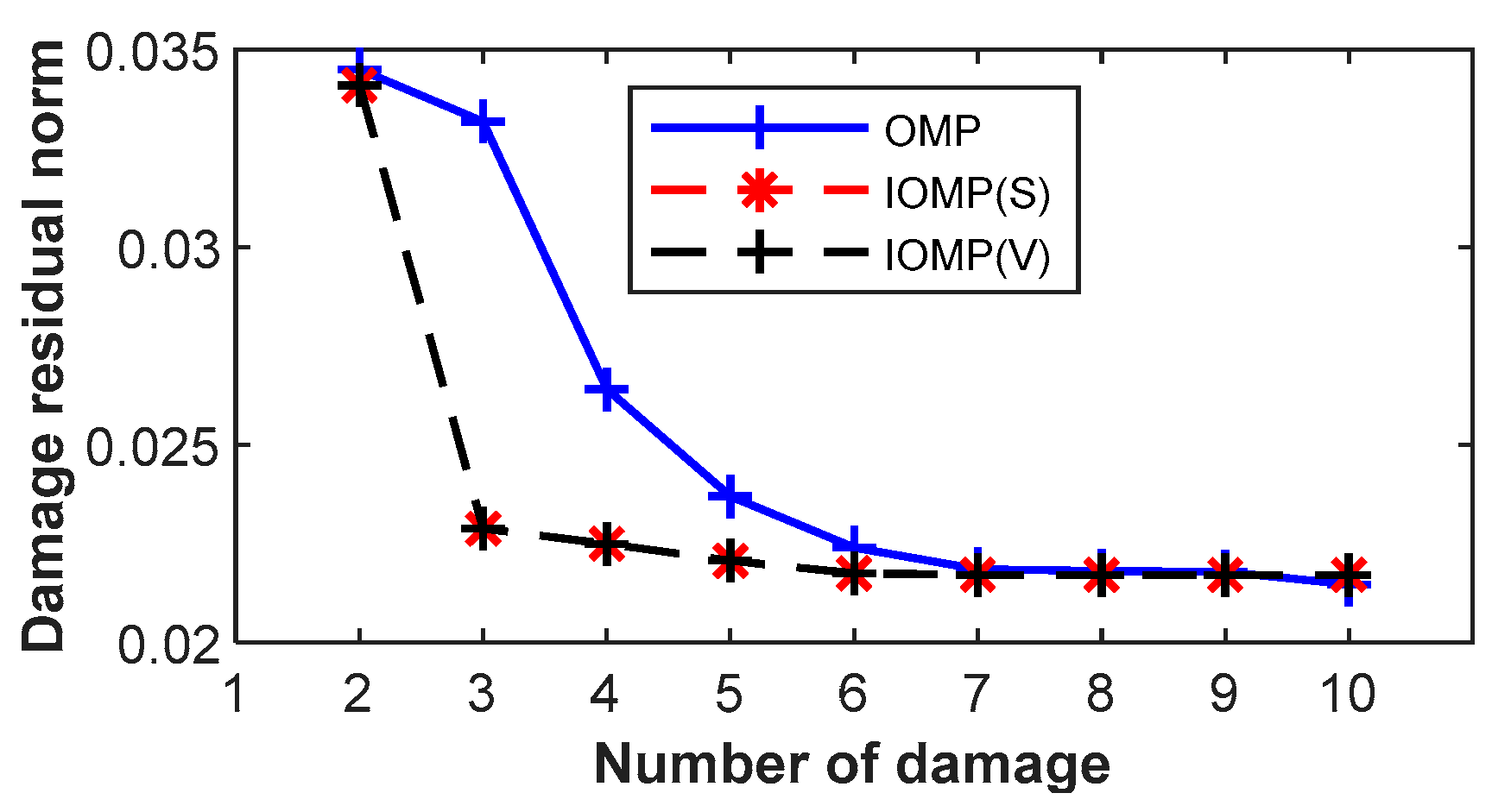
4.2.2. Damage Identification
5. Verification of Frame Experiment
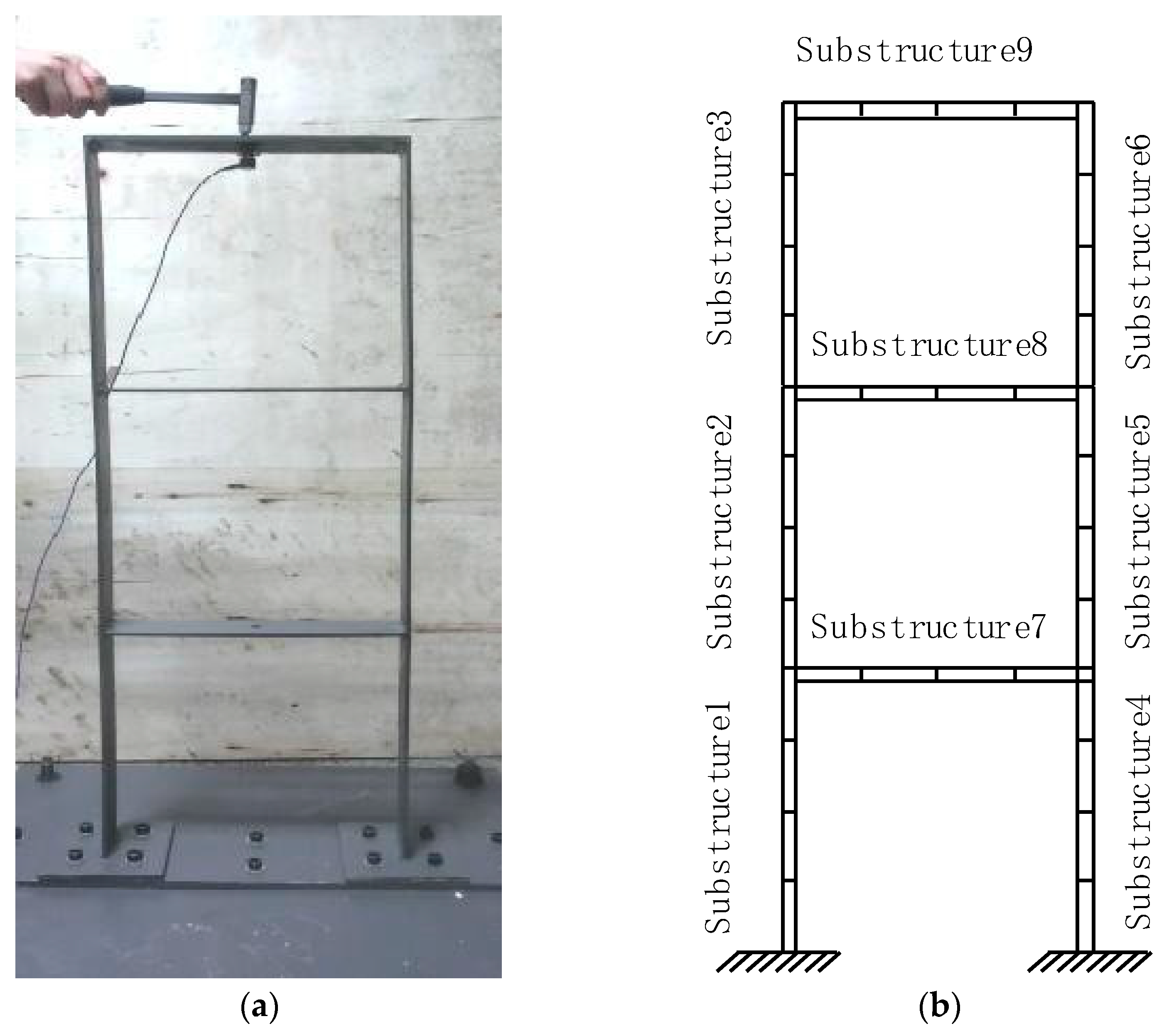
5.1. Model and Damage Scenario
5.2. Framework Dynamic Testing and Response Construction with Additional Virtual Mass
- Dynamic testing of undamaged structure: An acceleration sensor was installed in the middle position of substructures, and the other side was hit with a modal force hammer several times to obtain multiple sets of loads and acceleration response data. The measured data were processed to determine the experimental frequencies of the undamaged structures.
- Dynamic testing of damaged structure: The sensor was installed in the middle position of the substructures, and the structure was hit with a modal force hammer on the other side to obtain multiple sets of loads and acceleration data.
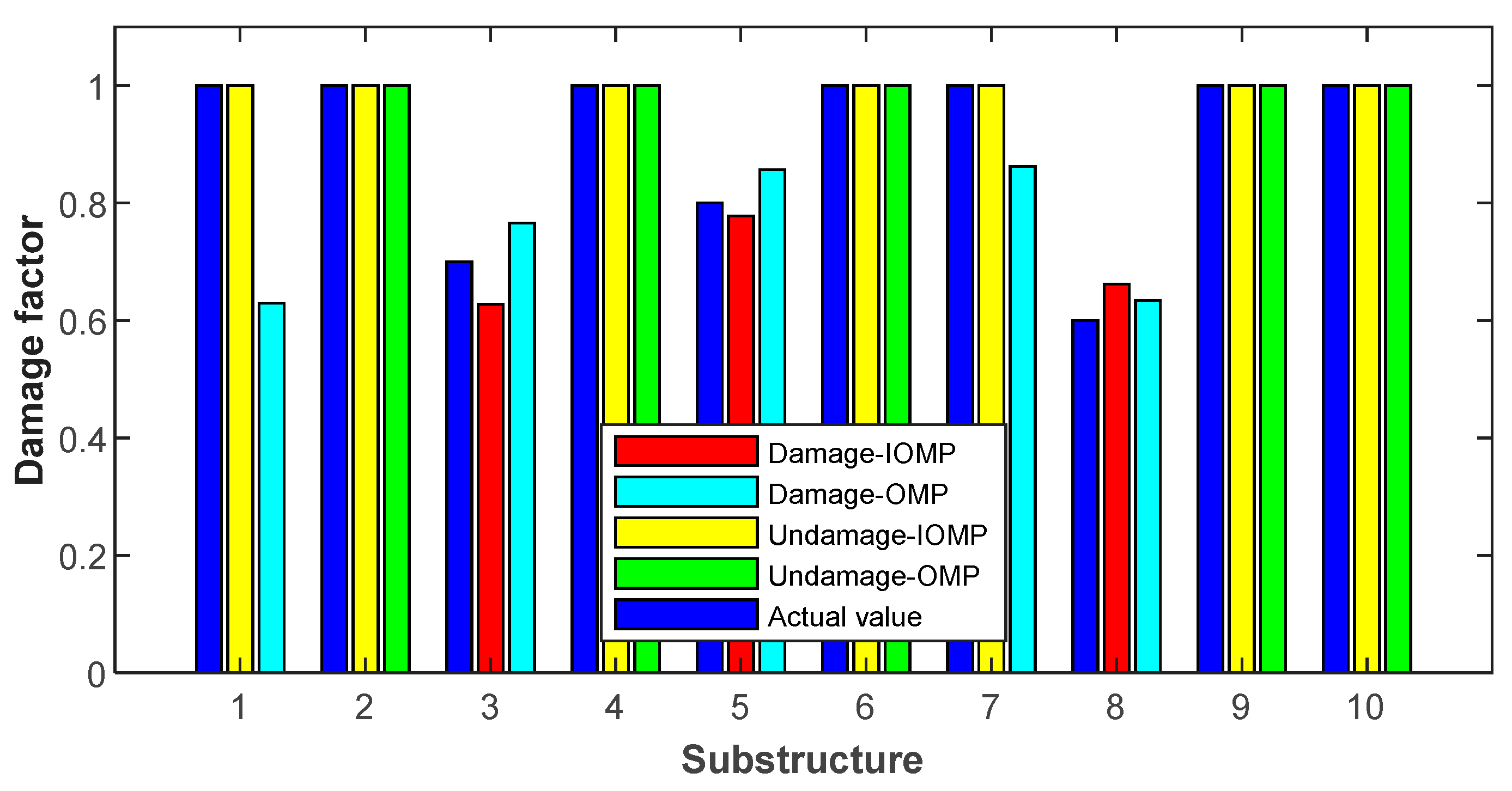
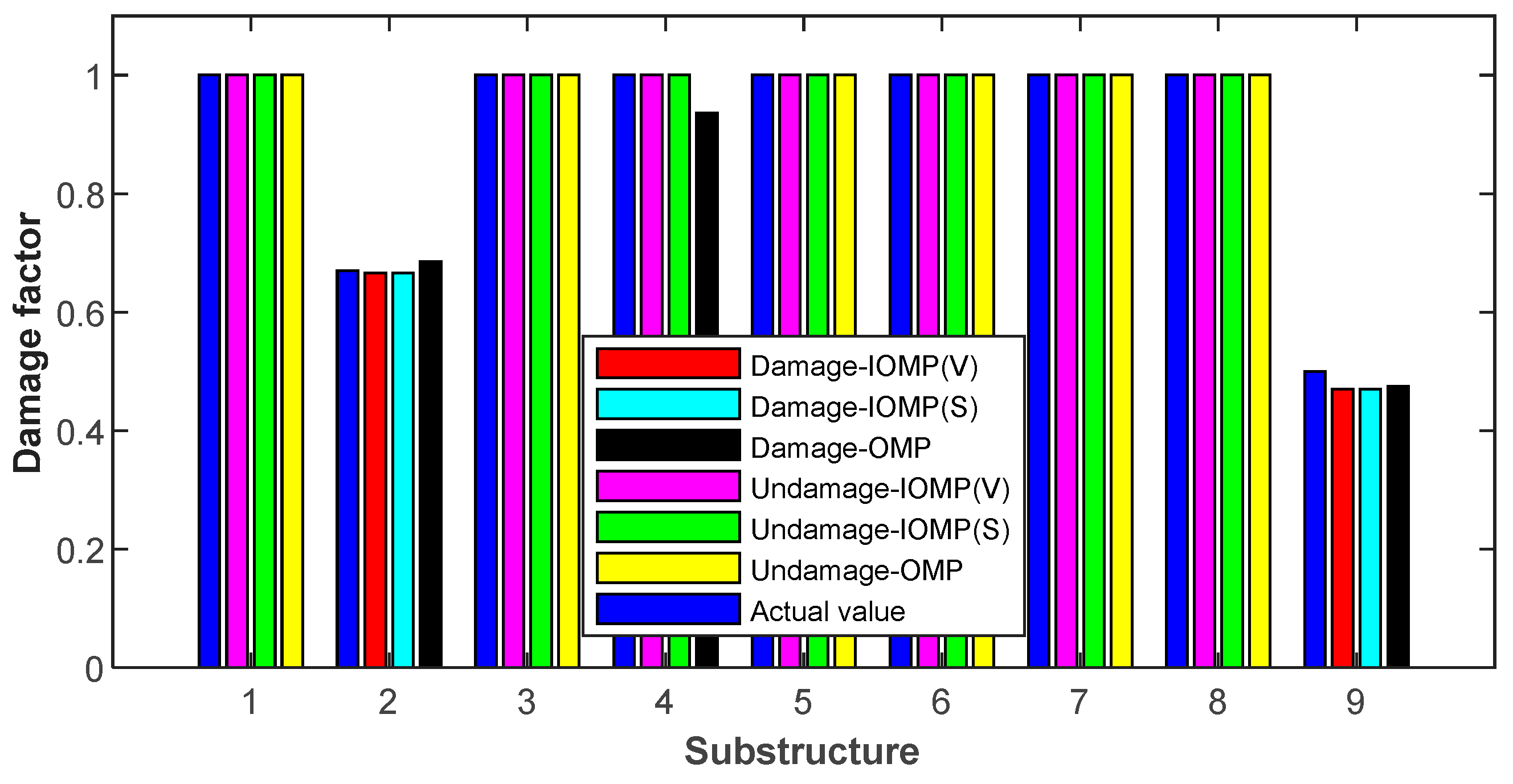
5.3. Damage Identification
6. Conclusions
- The IOMP method combined with the additional virtual mass method can effectively expand structural modal information to improve the accuracy of structural damage identification while constraining the optimization results to obtain sparse optimization results consistent with the actual local damage.
- Compared to the Lasso regression model with the norm and the ridge regression model with the norm, the IOMP method selects independently damage substructures, which satisfies the initial condition that structural damage is sparse. In addition, the IOMP method does not need to select the regularization coefficient , and thus, eliminates its direct influence on the optimization results to obtain more accurate damage identification results.
- The IOMP method improves the deficiency of the OMP method in that the recognition result is a local optimal solution when combined with the additional virtual mass method, which integrates the recognition result better. Furthermore, it improves the logical defects of the OMP method effectively in predicting damage sparsity. The IOMP method is also accurate for selecting damaged substructures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Toh, G.; Park, J. Review of Vibration-Based Structural Health Monitoring Using Deep Learning. Appl. Sci. 2020, 10, 1680. [Google Scholar] [CrossRef]
- Annamdas, V.G.M.; Bhalla, S.; Soh, C.K. Applications of structural health monitoring technology in Asia. Struct. Health Monit. 2017, 16, 324–346. [Google Scholar] [CrossRef]
- Hou, J.L.; Wang, S.J.; Zhang, Q.X.; Jankowski, L. An Improved Objective Function for Modal-Based Damage Identification Using Substructural Virtual Distortion Method. Appl. Sci. 2019, 9, 971. [Google Scholar] [CrossRef] [Green Version]
- Fan, W.; Qiao, P.Z. Vibration-based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Seo, J.; Hu, J.W.; Lee, J. Summary Review of Structural Health Monitoring Applications for Highway Bridges. J. Perform. Constr. Facil. 2016, 30, 9. [Google Scholar] [CrossRef]
- Weng, S.; Zhu, H.P.; Xia, Y.; Li, J.J.; Tian, W. A review on dynamic substructuring methods for model updating and damage detection of large-scale structures. Adv. Struct. Eng. 2020, 23, 584–600. [Google Scholar] [CrossRef]
- Cao, M.S.; Ding, Y.J.; Ren, W.X.; Wang, Q.; Ragulskis, M.; Ding, Z.C. HierarchicalWavelet-Aided Neural Intelligent Identification of Structural Damage in Noisy Conditions. Appl. Sci. 2017, 7, 391. [Google Scholar] [CrossRef] [Green Version]
- Chang, M.; Kim, J.K.; Lee, J. Hierarchical neural network for damage detection using modal parameters. Struct. Eng. Mech. 2019, 70, 457–466. [Google Scholar]
- Maia, N.M.M.; Silva, J.M.M.; Almas, E.A.M.; Sampaio, R.P.C. Damage detection in structures: From mode shape to frequency response function methods. Mech. Syst. Signal Proc. 2003, 17, 489–498. [Google Scholar] [CrossRef]
- Huang, Q.; Xu, Y.L.; Li, J.C.; Su, Z.Q.; Liu, H.J. Structural damage detection of controlled building structures using frequency response functions. J. Sound Vib. 2012, 331, 3476–3492. [Google Scholar] [CrossRef]
- Xie, L.Y.; Zhou, Z.W.; Zhao, L.; Wan, C.F.; Tang, H.S.; Xue, S.T. Parameter Identification for Structural Health Monitoring with Extended Kalman Filter Considering Integration and Noise Effect. Appl. Sci. 2018, 8, 2480. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.Y.; Law, S.S.; Zhang, L.M. Damage localization by directly using incomplete mode shapes. J. Eng. Mech. ASCE 2000, 126, 656–660. [Google Scholar] [CrossRef]
- Sinha, U.; Chakraborty, S. Detection of Damages in Structures Using Changes in Stiffness and Damping. In Recent Advances in Computational Mechanics and Simulations; Volume-I: Materials to Structures.Lecture Notes in Civil Engineering (LNCE 103); Springer: Singapore, 2021; pp. 259–271. [Google Scholar]
- Rao, P.S.; Ramakrishna, V.; Mahendra, N.V.D. Experimental and Analytical Modal Analysis of Cantilever Beam for Vibration Based Damage Identification Using Artificial Neural Network. J. Test. Eval. 2018, 46, 656–665. [Google Scholar] [CrossRef]
- Ali, J.; Bandyopadhyay, D. Experimental validation of the proposed technique for condition monitoring of structure using limited noisy modal data. Int. J. Struct. Integr. 2020, 11, 45–59. [Google Scholar] [CrossRef]
- Wu, Q.; Guo, S.; Li, X.; Gao, G. Crack diagnosis method for a cantilevered beam structure based on modal parameters. Meas. Sci. Technol. 2020, 31, 035001. [Google Scholar] [CrossRef]
- Chang, K.-C.; Kim, C.-W. Modal-parameter identification and vibration-based damage detection of a damaged steel truss bridge. Eng. Struct. 2016, 122, 156–173. [Google Scholar] [CrossRef]
- Bhowmik, B.; Tripura, T.; Hazra, B.; Pakrashi, V. Real time structural modal identification using recursive canonical correlation analysis and application towards online structural damage detection. J. Sound Vib. 2020, 468, 115101. [Google Scholar] [CrossRef]
- Ghahremani, B.; Bitaraf, M.; Rahami, H. A fast-convergent approach for damage assessment using CMA-ES optimization algorithm and modal parameters. J. Civ. Struct. Health Monit. 2020, 10, 497–511. [Google Scholar] [CrossRef]
- Rainieri, C.; Gargaro, D.; Reynders, E.; Fabbrocino, G. A study on the concurrent influence of liquid content and damage on the dynamic properties of a tank for the development of a modal-based SHM system. J. Civ. Struct. Health Monit. 2020, 10, 57–68. [Google Scholar] [CrossRef]
- Dinh, H.M.; Nagayama, T.; Fujino, Y. Structural parameter identification by use of additional known masses and its experimental application. Struct. Control Health Monit. 2012, 19, 436–450. [Google Scholar] [CrossRef]
- Rajendran, P.; Srinivasan, S.M. Performance of rotational mode based indices in identification of added mass in beams. Struct. Eng. Mech. 2015, 54, 711–723. [Google Scholar] [CrossRef]
- Dems, K.; Mroz, Z. Damage identification using modal, static and thermographic analysis with additional control parameters. Comput. Struct. 2010, 88, 1254–1264. [Google Scholar] [CrossRef]
- Hou, J.L.; Jankowski, L.; Ou, J.P. Structural damage identification by adding virtual masses. Struct. Multidiscip. Optim. 2013, 48, 59–72. [Google Scholar] [CrossRef]
- Knitter-Piatkowska, A.; Dobrzycki, A. Application of Wavelet Transform to Damage Identification in the Steel Structure Elements. Appl. Sci. 2020, 10, 8198. [Google Scholar] [CrossRef]
- Wang, S.; Xu, M.; Xia, Z.; Li, Y. A novel Tikhonov regularization-based iterative method for structural damage identification of offshore platforms. J. Mar. Sci. Technol. 2019, 24, 575–592. [Google Scholar] [CrossRef]
- Wu, Y.-H.; Zhou, X.-Q. L-1 Regularized Model Updating for Structural Damage Detection. Int. J. Struct. Stab. Dyn. 2018, 18, 1850157. [Google Scholar] [CrossRef]
- Weber, B.; Paultre, P. Damage Identification in a Truss Tower by Regularized Model Updating. J. Struct. Eng. 2010, 136, 307–316. [Google Scholar] [CrossRef]
- Hou, R.; Xia, Y.; Bao, Y.; Zhou, X. Selection of regularization parameter for l(1)-regularized damage detection. J. Sound Vib. 2018, 423, 141–160. [Google Scholar] [CrossRef]
- Racine, J.S. Foundations and Trends: Nonparametric Econometrics: A primer; Now Publishers Inc.: Boston, MA, USA, 2008; Volume 3, pp. 1–88. [Google Scholar]
- Dhulipala, S.J.S. Gaussian Kernel Methods for Seismic Fragility and Risk Assessment of Mid-Rise Buildings. Sustainability 2021, 13, 2973. [Google Scholar] [CrossRef]



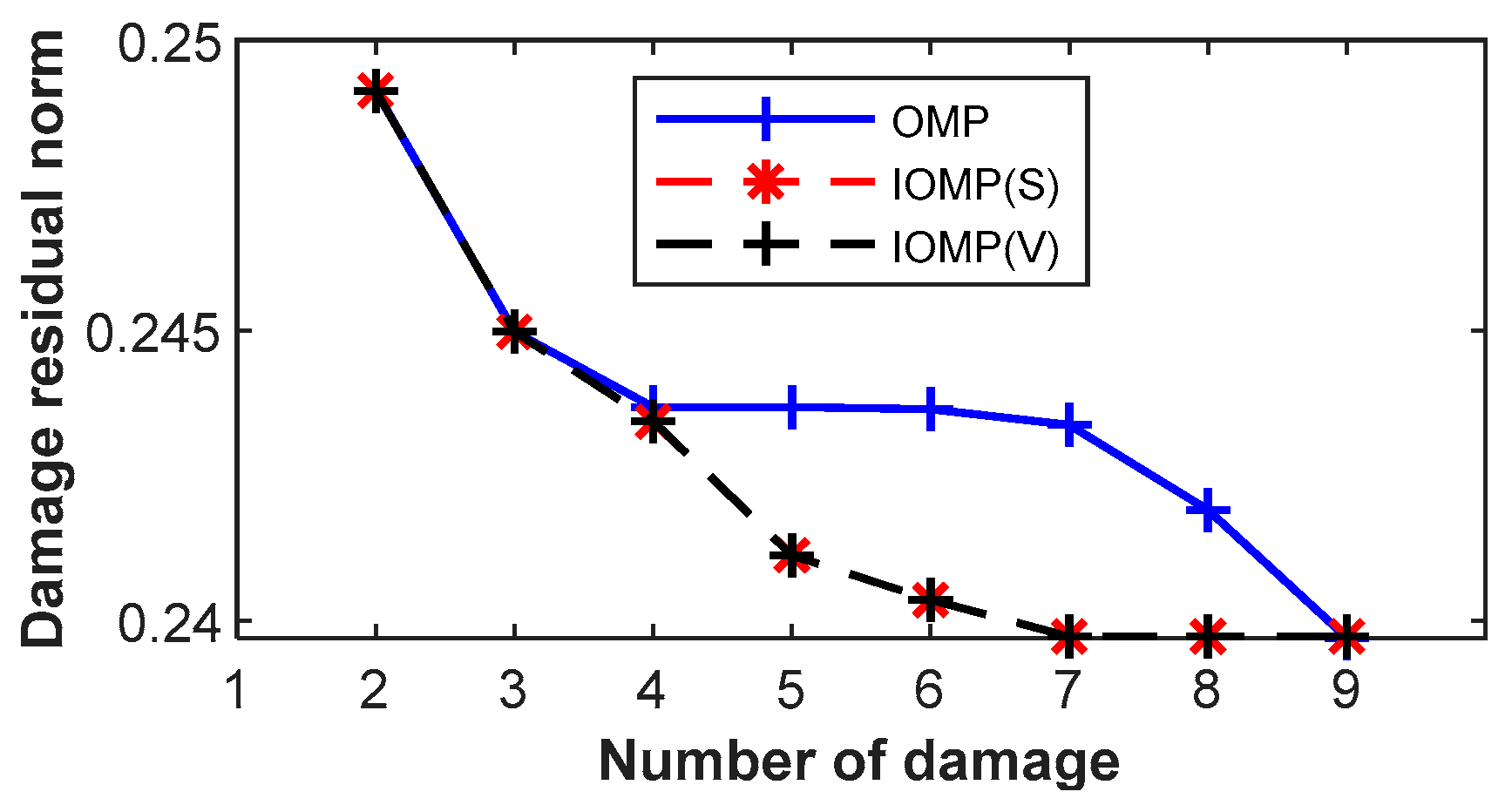
| Substructure | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| OMP | 0.5087 | 1 | 0.4675 | 1 | 1 | 1 | 1 | 1 | 0.9531 | 0.7076 |
| IOMP(S) | 0.5049 | 1 | 0.5658 | 0.6860 | 1 | 1 | 1 | 1 | 1 | 0.6076 |
| Actual value | 1 | 1 | 0.7 | 1 | 0.8 | 1 | 1 | 0.6 | 1 | 1 |
| Noise Level (rms) | 5% | 10% | 20% | 30% |
|---|---|---|---|---|
| OMP | [8, 6, 3, 5] | [8, 6, 1, 4] | [8, 5, 4, 10] | [8, 5, 4] |
| [62.36%, 100%, 67.34%, 80.58%] | [54.08%, 89.06%, 54.11%, 79.55%] | [47.20%, 82.30%, 99.51%, 67.78%] | [49.08%, 73.03%, 100%] | |
| IOMP(S) | [8, 5, 3] | [8, 5, 3] | [8, 5, 3] | [8, 5, 3] |
| [62.30%, 80.57%, 67.41%] | [58.12%, 80.44%, 72.88%] | [51.99%, 81.24%, 72.22%] | [64.28%, 75.66%, 68.84%] |
| Type | OMP | IOMP |
|---|---|---|
| Damaged substructures | [3, 29, 15, 30, 48, 1, 6] | [3, 29, 15, 30, 48] |
| Residual stiffness | [49.87%, 60.44%, 69.40%, 79.06%, 80.59%, 93.01%, 92.81%] | [49.92%, 60.50%, 69.50%, 79.09%, 80.62%] |
| Substructure | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 |
|---|---|---|---|---|---|---|---|---|---|
| Mean | 108.27 | 107.13 | 108.27 | 107.13 | 108.27 | 107.13 | 108.27 | 107.13 | 107.13 |
| Substructure | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Actual | 1.000 | 0.670 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.500 |
| OMP | 1.000 | 0.685 | 1.000 | 0.936 | 1.000 | 1.000 | 1.000 | 1.000 | 0.475 |
| IOMP (S) | 1.000 | 0.666 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.470 |
| IOMP (V) | 1.000 | 0.660 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.470 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Xu, D.; Hou, J.; Jankowski, Ł.; Wang, H. Damage Identification Method Using Additional Virtual Mass Based on Damage Sparsity. Appl. Sci. 2021, 11, 10152. https://doi.org/10.3390/app112110152
Zhang Q, Xu D, Hou J, Jankowski Ł, Wang H. Damage Identification Method Using Additional Virtual Mass Based on Damage Sparsity. Applied Sciences. 2021; 11(21):10152. https://doi.org/10.3390/app112110152
Chicago/Turabian StyleZhang, Qingxia, Dengzheng Xu, Jilin Hou, Łukasz Jankowski, and Haiyan Wang. 2021. "Damage Identification Method Using Additional Virtual Mass Based on Damage Sparsity" Applied Sciences 11, no. 21: 10152. https://doi.org/10.3390/app112110152
APA StyleZhang, Q., Xu, D., Hou, J., Jankowski, Ł., & Wang, H. (2021). Damage Identification Method Using Additional Virtual Mass Based on Damage Sparsity. Applied Sciences, 11(21), 10152. https://doi.org/10.3390/app112110152






