Applying Heuristics to Generate Test Cases for Automated Driving Safety Evaluation
Abstract
:1. Introduction
1.1. Motivation and Aim
1.2. Related Work
1.3. Main Contribution
1.4. Paper Structure
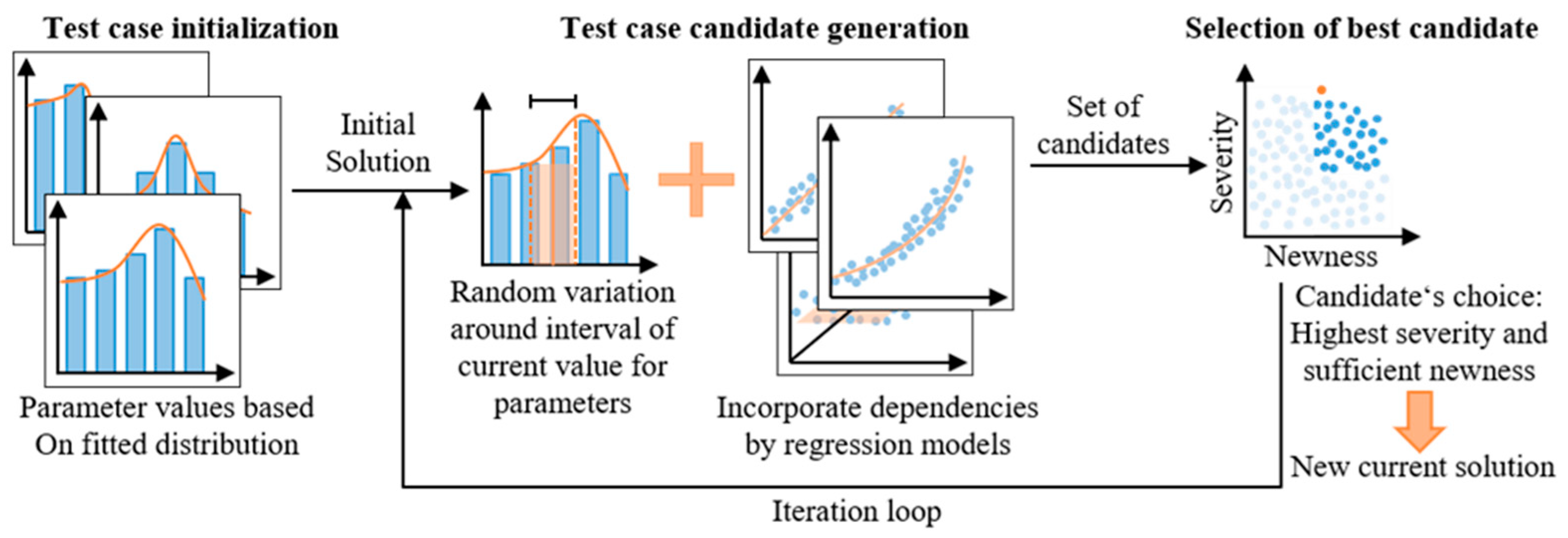
2. Heuristics Methodology
2.1. Evaluation of Severity and Exposure
2.2. Data Split, Distribution Fitting, and Regression Analysis
2.3. Heuristic Generation of Test Cases
- Set parameters only influenced by independent parameters;
- Set parameters influenced by either parameters set, according to rule 2 or by independent parameters;
- Set all remaining dependent parameters, according to their regression models from lower to higher R2 order.
3. Prototypical Application to Cut-In Dataset
3.1. Data Set
3.2. Cut-In Scenario Definition, Detection, and Grouping
3.3. Data Distribution and Regression Analysis
3.4. Application of Heuristic and Resulting Test Cases
4. Assessment of Generated Cut-In Test Cases
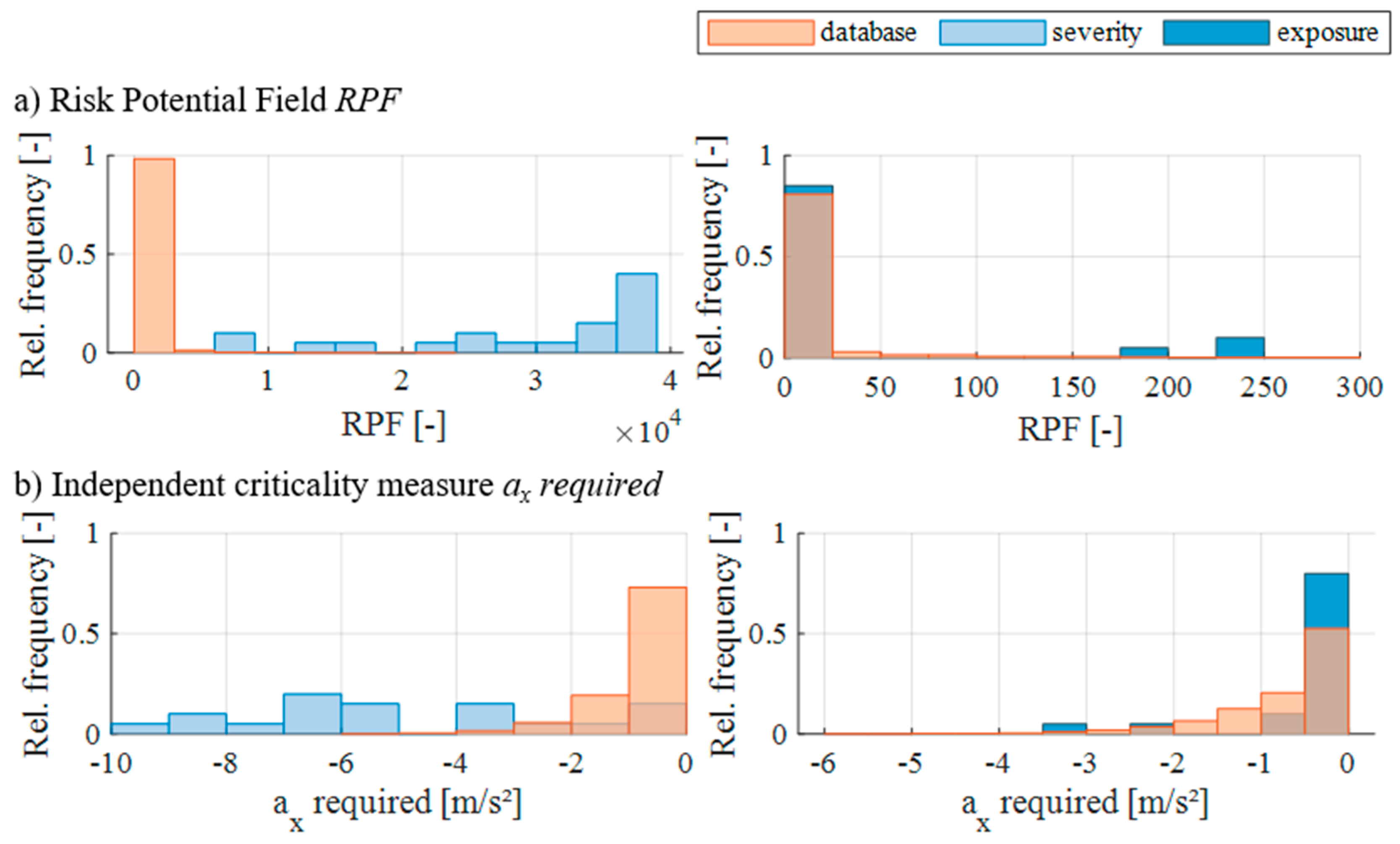
4.1. Evaluation of Criticality of Severity and Exposure Test Suites
4.2. Evaluation of Coverage of Severity and Exposure Test Suites
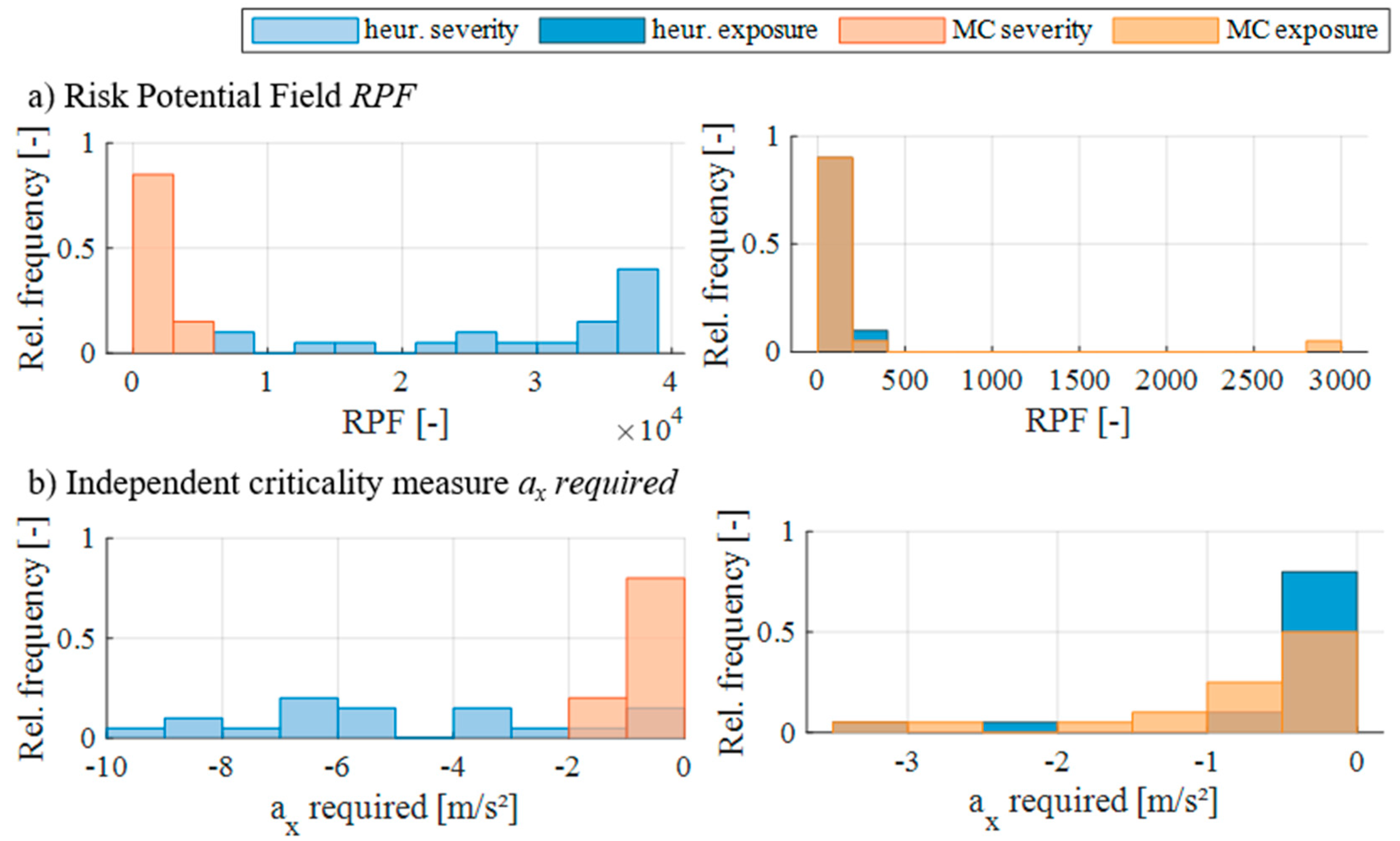
4.3. Comparison to Monte Carlo-Based Test Case Generation
5. Discussion
5.1. Efficiency of the Test Case Generation Process
5.2. Results from the Criticality Assessment
5.3. Results from the Coverage Assessment
5.4. Results from the Comparison with Monte Carlo Sampling
5.5. General Implications of the Methodology
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Test Case No. | vx,VuT [km/h] | ax,VuT [m/s2] | vx,chall [km/h] | vy,chall [m/s] | ax,chall [m/s2] | dx [m] |
|---|---|---|---|---|---|---|
| Severity Test Cases | ||||||
| 1 | 86.9 | −0.6 | 80.0 | 1.1 | −0.3 | 21.8 |
| 2 | 81.1 | 0.0 | 76.1 | 1.2 | 0.1 | 25.6 |
| 3 | 100.2 | −0.5 | 91.6 | 0.9 | 0.6 | 11.3 |
| 4 | 98.0 | 0.5 | 92.2 | 1.1 | −0.2 | 13.4 |
| 5 | 100.5 | 0.1 | 90.3 | 1.1 | 0.0 | 24.3 |
| 6 | 96.8 | 0.6 | 88.7 | 0.5 | 0.7 | 10.4 |
| 7 | 122.5 | 0.7 | 110.4 | 0.6 | 0.4 | 14.6 |
| 8 | 88.8 | −0.1 | 82.7 | 1.0 | 0.8 | 10.2 |
| 9 | 95.6 | −0.3 | 85.5 | 0.7 | −0.1 | 17.5 |
| 10 | 110.4 | 0.1 | 101.7 | 1.4 | 0.6 | 18.2 |
| 11 | 101.6 | 0.8 | 92.6 | 1.1 | 0.4 | 16.0 |
| 12 | 113.7 | −1.2 | 109.9 | 1.0 | −0.3 | 18.3 |
| 13 | 132.1 | −0.3 | 125.0 | 1.2 | 0.6 | 15.8 |
| 14 | 114.4 | 0.0 | 102.0 | 0.5 | 0.4 | 16.0 |
| 15 | 87.3 | 0.0 | 76.9 | 1.3 | 0.2 | 15.1 |
| 16 | 110.8 | −1.9 | 117.4 | 1.1 | −0.6 | 15.0 |
| 17 | 90.2 | −0.6 | 80.1 | 0.8 | 0.0 | 21.1 |
| 18 | 85.5 | −0.6 | 81.9 | 1.2 | 0.8 | 16.3 |
| 19 | 106.8 | −0.7 | 109.2 | 0.7 | 0.4 | 15.0 |
| 20 | 126.3 | −0.4 | 125.8 | 0.6 | 0.4 | 12.7 |
| Exposure Test Cases (Normal driving) | ||||||
| 1 | 111.2 | −1.2 | 111.5 | 0.7 | 0.0 | 54.5 |
| 2 | 104.6 | −0.1 | 107.1 | 0.6 | 0.4 | 30.3 |
| 3 | 118.6 | 0.1 | 101.5 | 1.2 | 0.4 | 32.7 |
| 4 | 135.9 | 0.0 | 120.6 | 0.9 | 0.2 | 51.5 |
| 5 | 95.3 | −0.8 | 73.0 | 1.2 | −0.4 | 52.0 |
| 6 | 113.9 | −0.1 | 106.2 | 1.2 | 0.0 | 24.0 |
| 7 | 143.0 | −1.0 | 140.6 | 1.0 | 0.6 | 33.5 |
| 8 | 127.8 | −0.6 | 123.7 | 0.9 | −0.3 | 61.0 |
| 9 | 128.9 | 0.2 | 125.1 | 1.2 | 0.1 | 62.8 |
| 10 | 116.9 | 0.2 | 118.7 | 1.0 | 0.2 | 57.0 |
| 11 | 134.6 | 0.0 | 125.1 | 0.9 | 0.1 | 36.5 |
| 12 | 105.9 | 1.2 | 90.6 | 0.8 | 0.2 | 65.5 |
| 13 | 114.1 | −1.0 | 95.4 | 0.4 | −0.2 | 32.3 |
| 14 | 128.8 | 0.5 | 107.3 | 0.8 | 0.2 | 30.7 |
| 15 | 140.5 | 0.7 | 137.2 | 0.5 | 0.5 | 59.3 |
| 16 | 135.7 | 0.1 | 121.8 | 0.6 | 0.3 | 35.0 |
| 17 | 134.9 | 0.5 | 102.5 | 1.2 | 0.3 | 48.7 |
| 18 | 137.2 | −0.8 | 127.7 | 0.5 | 0.0 | 64.3 |
| 19 | 114.7 | 0.7 | 117.0 | 1.0 | 0.3 | 70.1 |
| 20 | 102.0 | 0.9 | 95.5 | 1.0 | 0.6 | 12.4 |
References
- Andreas, P.; Adrian, Z.; Jörg, K.; Julian, B.; Lutz, E. Database Approach for the Sign-Off Process of Highly Automated Vehicles. In 25th International Technical Conference on the Enhanced Safety of Vehicles (ESV), Detroit, MI, USA, 5–8 June 2017; National Highway Traffic Safety Administration: Washington, DC, USA, 2017. [Google Scholar]
- Steimle, M.; Bagschik, G.; Menzel, T.; Wendler, J.T.; Maurer, M. Ein Beitrag zur Terminologie für den szenarienbasierten Testansatz automatisierter Fahrfunktionen. In Proceedings of the AAET-Automatisiertes und vernetztes Fahren: Beiträge zum gleichnamigen 19, Stadthalle, Braunschweig, Germany, 14–15 March 2018; ITS Mobility e.V.: Braunschweig, Germany, 2018; pp. 10–32, ISBN 978-3-937655-44-4.
- PEGASUS. Pegasus Method: An Overview, Ehra-Lessien. 2019. Available online: https://www.pegasusprojekt.de/files/tmpl/Pegasus-Abschlussveranstaltung/PEGASUS-Gesamtmethode.pdf (accessed on 21 May 2019).
- Uchimura, T. Connected and Automated Driving Project in Japan “SIP-adus”. In PEGASUS Symposium, Aachen, Germany, 9th November 2017; Deutsches Zentrum für Luft- und Raumfahrt e. V.: Cologne, Germany, 2017. [Google Scholar]
- Antona-Makoshi, J.; Uchida, N.; Imanaga, H.; Kitajima, S.; Taniguchi, S.; Ozawa, K.; Kitahara, E. Towards global AD safety assurance. In 2019 Automated Vehicles Symposium, Orlando, FL, USA, 19 July 2017; Association for Unmanned Systems International (AUVSI): Arlington, VA, USA; Transportation Research Board (TRB): Washington, DC, USA, 2017. [Google Scholar]
- Taniguchi, S. Safety Validation Investigation in Japan: AVS Breakout Session, 18 July 2018; Japan Automobile Manufacturers Association (JAMA): Tokyo, Japan, 2018. [Google Scholar]
- Znamiec, H. Methodik zur Gesamtsystemerprobung für das hochautomatisierte Fahren. In Ko-HAF Zwischenpräsentation, Aschaffenburg, 18 May 2017; Projektträger Mobilität und Verkehrstechnologien: Cologne, Germany, 2017. [Google Scholar]
- Znamiec, H.; Rauber, B.; Henze, R. Prozesse zur Qualifikationsprüfung automatisierter Fahrfunktionen. In Proceedings of the AAET Automatisiertes und Vernetzes Fahren: Beiträge zum gleichnamigen 20, Stadthalle, Braunschweig, Germany, 6–7 February 2019; pp. 330–346. [Google Scholar]
- Transport Systems Catapult. Taxonomy of Scenarios for Automated Driving, Milton Keynes, UK, 2017. Available online: https://s3-eu-west-1.amazonaws.com/media.ts.catapult/wp-content/uploads/2017/04/25114137/ATS34-Taxonomy-of-Scenarios-for-Automated-Driving.pdf (accessed on 20 November 2019).
- Elrofai, H.; Paardekooper, J.-P.; de Gelder, E.; Kalisvaart, S.; Op den Camp, O. StreetWise: Scenario-Based Safety Validation of Connected and Automated Driving; TNO: Helmond, The Netherlands, 2018. [Google Scholar]
- Schuldt, F.; Reschka, A.; Maurer, M. A Method for an Efficient, Systematic Test Case Generation for Advanced Driver Assistance Systems in Virtual Environments. In Automotive Systems Engineering II; Winner, H., Prokop, G., Maurer, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 147–175. ISBN 978-3-319-61607-0. [Google Scholar]
- Winner, H.; Chan, C.-Y. Safety Assurance for Automated Vehicles. In Road Vehicle Automation 4; Meyer, G., Beiker, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 165–175. ISBN 978-3-319-60934-8. [Google Scholar]
- Cohen, D.M.; Dalal, S.R.; Fredman, M.L.; Patton, G.C. The AETG system: An approach to testing based on combinatorial design. IIEEE Trans. Softw. Eng. 1997, 23, 437–444. [Google Scholar] [CrossRef] [Green Version]
- Anand, S.; Burke, E.K.; Chen, T.Y.; Clark, J.; Cohen, M.B.; Grieskamp, W.; Harman, M.; Harrold, M.J.; McMinn, P.; Bertolino, A.; et al. An orchestrated survey of methodologies for automated software test case generation. J. Syst. Softw. 2013, 86, 1978–2001. [Google Scholar] [CrossRef]
- Cohen, M.B.; Colbourn, C.J.; Gibbons, P.B.; Mudgrdge, W.B. Constructing Test Suites for Interaction Testing. In Proceedings of the 25th International Conference on Software Engineering, Portland, OR, USA, 3–10 May 2003; IEEE Computer Society: Washington, DC, USA, 2003. ISBN 076951877X. [Google Scholar]
- Kuhn, R. Introduction to Combinatorial Testing; Carnegie-Mellon University: Pittsburgh, PA, USA, 2011. [Google Scholar]
- Katzourakis, D.; de Winter, J.C.; de Groot, S.; Happee, R. Driving simulator parameterization using double-lane change steering metrics as recorded on five modern cars. Simul. Model. Pract. Theory 2012, 26, 96–112. [Google Scholar] [CrossRef]
- Ali, S.; Briand, L.C.; Hemmati, H.; Panesar-Walawege, R.K. A Systematic Review of the Application and Empirical Investigation of Search-Based Test Case Generation. IEEE Trans. Softw. Eng. 2010, 36, 742–762. [Google Scholar] [CrossRef] [Green Version]
- Tung, Y.-W.; Aldiwan, W.S. Automating test case generation for the new generation mission software system. In Proceedings of the 2000 IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 18–25 March 2000; IEEE: Piscataway, NJ, USA, 2000; pp. 431–437, ISBN 0-7803-5846-5. [Google Scholar]
- Hauer, F.; Gerostathopoulos, I.; Schmidt, T.; Pretschner, A. Clustering Traffic Scenarios Using Mental Models as Little as Possible. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1007–1012, ISBN 978-1-7281-6673-5. [Google Scholar]
- Zhao, J.; Fang, J.; Ye, Z.; Zhang, L. Large Scale Autonomous Driving Scenarios Clustering with Self-Supervised Feature Extraction. 2021. Available online: http://arxiv.org/pdf/2103.16101v1 (accessed on 6 June 2021).
- Wang, W.; Zhang, W.; Zhu, J.; Zhao, D. Understanding V2V Driving Scenarios Through Traffic Primitives. IEEE Trans. Intell. Transport. Syst. 2020, 1–10. [Google Scholar] [CrossRef]
- Ding, W.; Xu, M.; Zhao, D. CMTS: A Conditional Multiple Trajectory Synthesizer for Generating Safety-Critical Driving Scenarios. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA; pp. 4314–4321, ISBN 978-1-7281-7395-5. [Google Scholar]
- Zhou, J.; del Re, L. Identification of critical cases of ADAS safety by FOT based parameterization of a catalogue. In Proceedings of the 2017 Asian Control Conference Gold Coast, Australia, Gold Coast, QLD, Australia, 17–20 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 453–458, ISBN 978-1-5090-1573-3. [Google Scholar]
- Winner, H.; Wachenfeld, W.; Junietz, P. Validation and Introduction of Automated Driving. In Automotive Systems Engineering II; Winner, H., Prokop, G., Maurer, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 177–196. ISBN 978-3-319-61607-0. [Google Scholar]
- Thal, S.; Znamiec, H.; Henze, R.; Nakamura, H.; Imanaga, H.; Antona-Makoshi, J.; Uchida, N.; Taniguchi, S. Incorporating safety relevance and realistic parameter combinations in test-case generation for automated driving safety assessment. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Zhao, D.; Lam, H.; Peng, H.; Bao, S.; LeBlanc, D.J.; Nobukawa, K.; Pan, C.S. Accelerated Evaluation of Automated Vehicles Safety in Lane-Change Scenarios Based on Importance Sampling Techniques. IEEE Trans. Intell. Transport. Syst. 2017, 18, 595–607. [Google Scholar] [CrossRef] [Green Version]
- Akagi, Y.; Kato, R.; Kitajima, S.; Antona-Makoshi, J.; Uchida, N. A Risk-index based Sampling Method to Generate Scenarios for the Evaluation of Automated Driving Vehicle Safety. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 667–672, ISBN 978-1-5386-7024-8. [Google Scholar]
- Calo, A.; Arcaini, P.; Ali, S.; Hauer, F.; Ishikawa, F. Generating Avoidable Collision Scenarios for Testing Autonomous Driving Systems. In Proceedings of the 2020 IEEE 13th International Conference on Software Testing, Validation and Verification (ICST), Porto, Portugal, 24–28 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 375–386, ISBN 978-1-7281-5778-8. [Google Scholar]
- Calò, A.; Arcaini, P.; Ali, S.; Hauer, F.; Ishikawa, F. Simultaneously searching and solving multiple avoidable collisions for testing autonomous driving systems. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2020; Coello, C.C.A., Ed.; ACM: New York, NY, USA, 2020; pp. 1055–1063, ISBN 9781450371285. [Google Scholar]
- Beglerovic, H.; Stolz, M.; Horn, M. Testing of autonomous vehicles using surrogate models and stochastic optimization. In Proceedings of the IEEE ITSC 2017, 20th International Conference on Intelligent Transportation Systems: Mielparque Yokohama in Yokohama, Kanagawa, Japan, 16–19 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6, ISBN 978-1-5386-1526-3. [Google Scholar]
- Ben Abdessalem, R.; Nejati, S.; Briand, L.C.; Stifter, T. Testing advanced driver assistance systems using multi-objective search and neural networks. In Proceedings of the 31st IEEE/ACM International Conference on Automated Software Engineering, Singapore, 3–7 September 2016; Lo, D., Apel, S., Khurshid, S., Eds.; ACM: New York, NY, USA, 2016; pp. 63–74, ISBN 9781450338455. [Google Scholar]
- Feng, S.; Feng, Y.; Yu, C.; Zhang, Y.; Liu, H.X. Testing Scenario Library Generation for Connected and Automated Vehicles, Part I: Methodology. IEEE Trans. Intell. Transport. Syst. 2020, 22, 1573–1582. [Google Scholar] [CrossRef] [Green Version]
- Akagi, Y.; Raksincharoensak, P. Longitudinal and lateral motion planning method for avoidance of multi-obstacles in urban environments based on inverse collision probability. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 827–832, ISBN 978-1-5090-1821-5. [Google Scholar]
- Sato, D.; Nunobiki, E.; Inoue, S.; Raksincharoensak, P. Motion Planning and Control in Highway Merging Maneuver Based on Dynamic Risk Potential Optimization. In Proceedings of the 5th International Symposium on Future Active Safety Technology toward Zero Accidents (FAST-zero ‘19), Blacksburg, VA, USA, 9–11 September 2019. [Google Scholar]
- Weber, H.; Bock, J.; Klimke, J.; Roesener, C.; Hiller, J.; Krajewski, R.; Zlocki, A.; Eckstein, L. A framework for definition of logical scenarios for safety assurance of automated driving. Traffic Inj. Prev. 2019, 20, S65–S70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Osterwald-Lenum, M. A Note with Quantiles of the Asymptotic Distribution of the Maximum Likelihood Cointegration Rank Test Statistics1. Oxf. Bull. Econ. Stat. 1992, 54, 461–472. [Google Scholar] [CrossRef]
- Eick, C.F.; Parmar, R.; Ding, W.; Stepinski, T.F.; Nicot, J.-P. Finding regional co-location patterns for sets of continuous variables in spatial datasets. In Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems 2008 (ACM GIS 2008), Irvine, CA, USA, 5–7 November 2008; Aref, W.G., Mokbel, M.F., Schneider, M., Eds.; Curran: Red Hook, NY, USA, 2009; p. 1, ISBN 9781605583235. [Google Scholar]
- Sonka, A.; Krauns, F.; Henze, R.; Kucukay, F.; Katz, R.; Lages, U. Dual approach for maneuver classification in vehicle environment data. In Proceedings of the 28th IEEE Intelligent Vehicles Symposium, Redondo Beach, CA, USA, 11–14 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 97–102, ISBN 978-1-5090-4804-5. [Google Scholar]
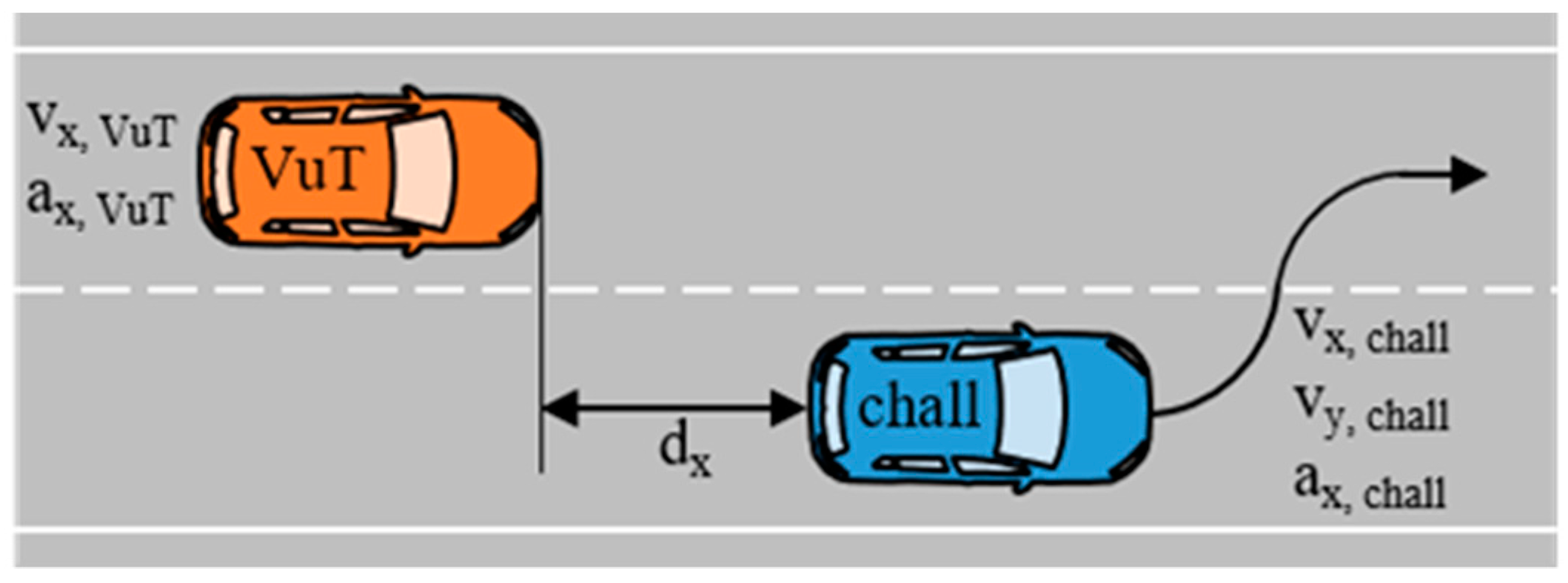
| Vehicle under Test (VuT) | Challenging Vehicle (Chall) | Interaction Parameters |
|---|---|---|
| vx (initial value) | vx (initial value) | Longitudinal distance dx |
| ax (initial value) | vy (max. value) | (initial value) |
| ax (mean value) |
| Parameter Name | Unit | μ | σ | k |
|---|---|---|---|---|
| vx,VuT | km/h | 98.2 | 14.1 | 0.0 |
| ax,VuT | m/s2 | −0.4 | 0.6 | −0.3 |
| vx,chall | km/h | 95.9 | 16.3 | −0.2 |
| vy,chall | m/s | 0.9 | 0.3 | −0.1 |
| ax,chall | m/s2 | 0 | 0.4 | −0.2 |
| dx | m | 14.4 | 4.8 | −0.3 |
| Parameter Name | Unit | μ | σ | k |
|---|---|---|---|---|
| vx,VuT | km/h | 116.7 | 17.6 | −0.5 |
| ax,VuT | m/s2 | −0.3 | 0.5 | −0.2 |
| vx,chall | km/h | 103.8 | 17.3 | −0.3 |
| vy,chall | m/s | 0.7 | 0.2 | 0.0 |
| ax,chall | m/s2 | 0.1 | 0.4 | −0.2 |
| dx | m | 47.1 | 18.2 | −0.3 |
| Dependent Parameter | R2 | Constant Term | Influencing Parameter 1 | Influencing Parameter 2 |
|---|---|---|---|---|
| Severe data set (based on 229 cut-in scenarios) | ||||
| vx,VuT | 0.952 | 0.20 | vx,chall (0.92) | |
| vx,chall | 0.915 | 0.20 | vx,VuT (0.91) | |
| Normal driving data set (based on 2068 cut-in scenarios) | ||||
| vx,VuT | 0.790 | 0.33 | ax,VuT (−0.25) | vx,chall (0.77) |
| vx,chall | 0.857 | 0.33 | vx,VuT (0.84) | ax,VuT (0.23) |
| Test Case No. | vx,VuT [km/h] | ax,VuT [m/s2] | vx,chall [km/h] | vy,chall [m/s] | ax,chall [m/s2] | dx [m] |
|---|---|---|---|---|---|---|
| Severity Test Cases | ||||||
| 1 | 144.8 | 0.0 | 143.9 | 2.2 | 0.0 | 2.1 |
| 2 | 136.9 | −0.5 | 136.4 | 2.2 | 0.7 | 2.1 |
| 3 | 140.0 | −1.6 | 139.4 | 2.2 | 0.1 | 2.1 |
| 4 | 139.0 | −0.3 | 138.4 | 2.2 | −1.0 | 2.1 |
| 5 | 130.8 | 0.0 | 130.5 | 2.1 | 0.3 | 5.5 |
| 6 | 118.1 | 0.0 | 118.5 | 2.2 | 0.8 | 7.7 |
| 7 | 124.1 | −0.8 | 124.2 | 2.2 | 0.1 | 3.4 |
| 8 | 139.6 | 1.5 | 139.0 | 2.2 | 0.0 | 2.8 |
| 9 | 121.0 | 0.2 | 121.2 | 1.6 | 0.2 | 5.1 |
| 10 | 120.2 | 0.0 | 120.5 | 2.2 | −0.6 | 2.1 |
| 11 | 120.6 | −0.8 | 120.8 | 1.4 | −0.2 | 3.5 |
| 12 | 144.3 | 1.5 | 143.5 | 2.2 | 1.2 | 2.1 |
| 13 | 136.5 | 0.6 | 136.0 | 2.2 | −0.6 | 5.0 |
| 14 | 113.7 | −0.3 | 114.3 | 2.1 | −0.1 | 6.2 |
| 15 | 124.7 | 0.9 | 127.7 | 2.2 | 0.3 | 8.4 |
| 16 | 144.2 | 0.0 | 143.3 | 2.2 | 1.6 | 2.1 |
| 17 | 144.6 | −1.7 | 143.7 | 2.2 | 1.3 | 2.1 |
| 18 | 116.4 | −0.2 | 116.8 | 1.3 | 0.1 | 9.9 |
| 19 | 131.0 | 0.7 | 130.8 | 2.2 | 1.0 | 2.3 |
| 20 | 112.3 | −0.1 | 112.9 | 1.9 | 0.3 | 13.0 |
| Exposure Test Cases (Normal driving) | ||||||
| 1 | 146.7 | 0.0 | 139.4 | 0.2 | 0.0 | 19.5 |
| 2 | 137.3 | 1.5 | 144.3 | 2.2 | 1.5 | 101.5 |
| 3 | 144.5 | −1.7 | 116.3 | 1.4 | 0.2 | 101.5 |
| 4 | 130.8 | 0.4 | 122.4 | 1.1 | 1.4 | 47.8 |
| 5 | 149.7 | −1.0 | 133.3 | 2.2 | 0.8 | 29.7 |
| 6 | 136.6 | 0.8 | 135.9 | 0.6 | 0.3 | 101.5 |
| 7 | 137.8 | 0.2 | 129.5 | 2.0 | 0.4 | 78.7 |
| 8 | 149.7 | −1.7 | 127.7 | 0.3 | 1.5 | 36.7 |
| 9 | 135.9 | 1.5 | 142.5 | 1.4 | −0.8 | 39.1 |
| 10 | 117.9 | 1.4 | 117.0 | 1.5 | 0.9 | 64.6 |
| 11 | 140.1 | 1.5 | 148.1 | 0.5 | 1.0 | 30.8 |
| 12 | 123.8 | 1.0 | 120.7 | 2.1 | 0.3 | 39.0 |
| 13 | 149.7 | −0.9 | 134.7 | 0.9 | 0.3 | 64.4 |
| 14 | 142.3 | 0.6 | 140.5 | 1.5 | 0.5 | 25.9 |
| 15 | 129.9 | 1.5 | 134.4 | 0.3 | −0.2 | 54.3 |
| 16 | 122.5 | 0.6 | 114.2 | 2.0 | 1.3 | 93.7 |
| 17 | 148.3 | −0.3 | 137.8 | 0.5 | 0.1 | 48.8 |
| 18 | 147.9 | −0.4 | 136.0 | 1.4 | 1.5 | 95.8 |
| 19 | 144.6 | 0.3 | 140.1 | 0.2 | 1.3 | 78.0 |
| 20 | 139.7 | 1.1 | 143.6 | 1.3 | 1.0 | 79.6 |
| vx,VuT | ax,VuT | vx,chall | vy,chall | ax,chall | dx |
|---|---|---|---|---|---|
| Severity test cases | |||||
| [46.8%] | 93.5% | [30.5%] | 43.1% | 98.2% | 41.5% |
| Exposure test cases (Normal driving) | |||||
| [46.0%] | 100% | [37.5%] | 100% | 100% | 83.5% |
| vx,VuT | ax,VuT | vx,chall | vy,chall | ax,chall | dx |
|---|---|---|---|---|---|
| Severity test cases | |||||
| [72.3%] | 75.2% | [48.9%] | 47.1% | 51.7% | 58.5% |
| Exposure test cases (Normal driving) | |||||
| [68.9%] | 77.9% | [74.6%] | 40.5% | 42.1% | 58.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stepien, L.; Thal, S.; Henze, R.; Nakamura, H.; Antona-Makoshi, J.; Uchida, N.; Raksincharoensak, P. Applying Heuristics to Generate Test Cases for Automated Driving Safety Evaluation. Appl. Sci. 2021, 11, 10166. https://doi.org/10.3390/app112110166
Stepien L, Thal S, Henze R, Nakamura H, Antona-Makoshi J, Uchida N, Raksincharoensak P. Applying Heuristics to Generate Test Cases for Automated Driving Safety Evaluation. Applied Sciences. 2021; 11(21):10166. https://doi.org/10.3390/app112110166
Chicago/Turabian StyleStepien, Leonard, Silvia Thal, Roman Henze, Hiroki Nakamura, Jacobo Antona-Makoshi, Nobuyuki Uchida, and Pongsathorn Raksincharoensak. 2021. "Applying Heuristics to Generate Test Cases for Automated Driving Safety Evaluation" Applied Sciences 11, no. 21: 10166. https://doi.org/10.3390/app112110166
APA StyleStepien, L., Thal, S., Henze, R., Nakamura, H., Antona-Makoshi, J., Uchida, N., & Raksincharoensak, P. (2021). Applying Heuristics to Generate Test Cases for Automated Driving Safety Evaluation. Applied Sciences, 11(21), 10166. https://doi.org/10.3390/app112110166






