Analysis of Water Consumption in Fruit and Vegetable Processing Plants with the Use of Artificial Intelligence
Abstract
:1. Introduction
2. The Literature Review
- How can the variability of water consumption by plants in this industry be explained?
- How can the optimum water consumption in a given plant be determined?
- Lack of fully closed circuits of process water (e.g., from washing) and (mainly) cooling water [23];
- Ineffective recovery of the condensate;
- Lack of water consumption optimization in the washing processes (both automatic and manual); the leakage of pipelines, valves, and machinery; and the lack of full supervision over water consumption in specific technological processes.
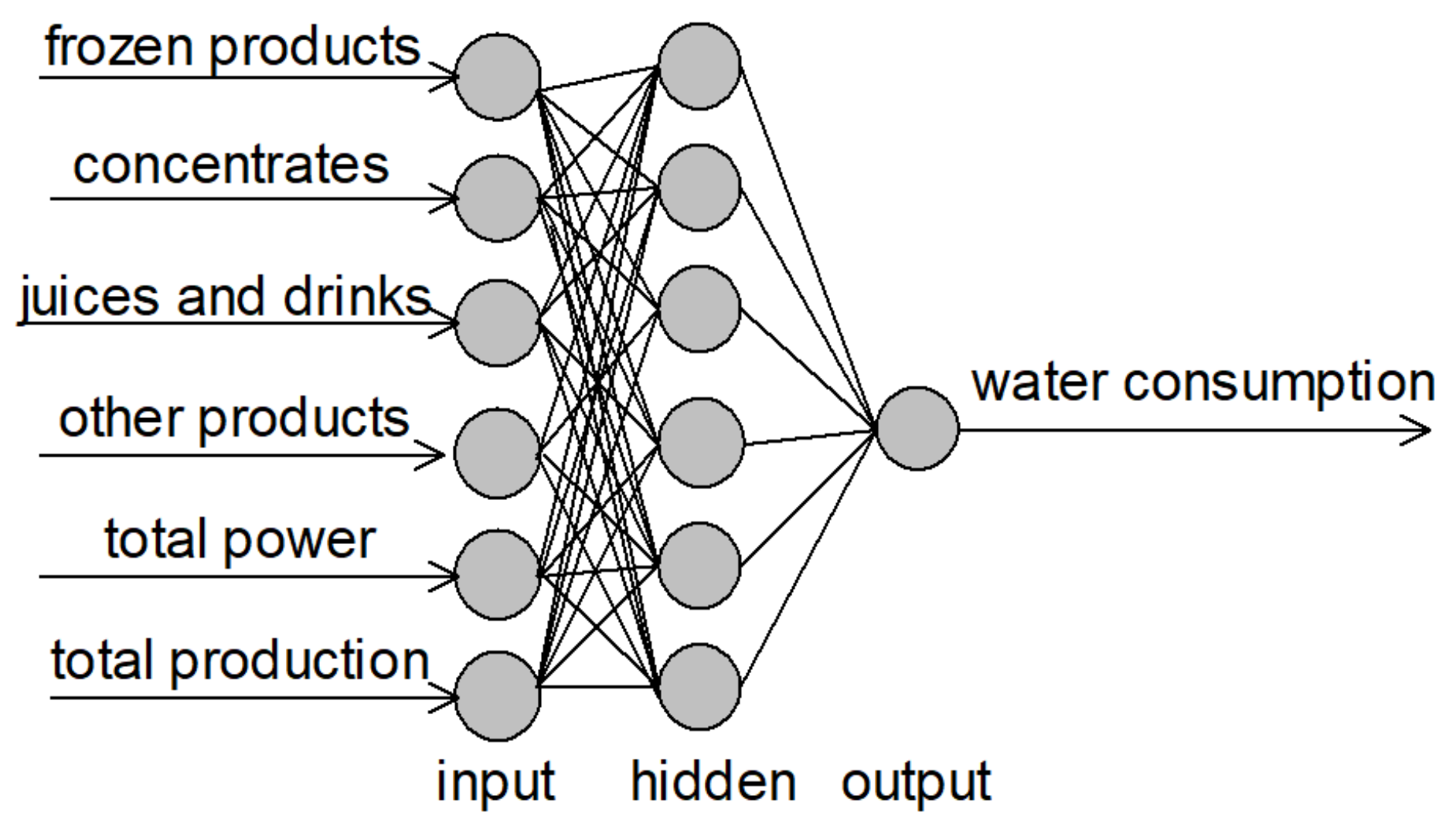
3. Neural Model of Water Consumption
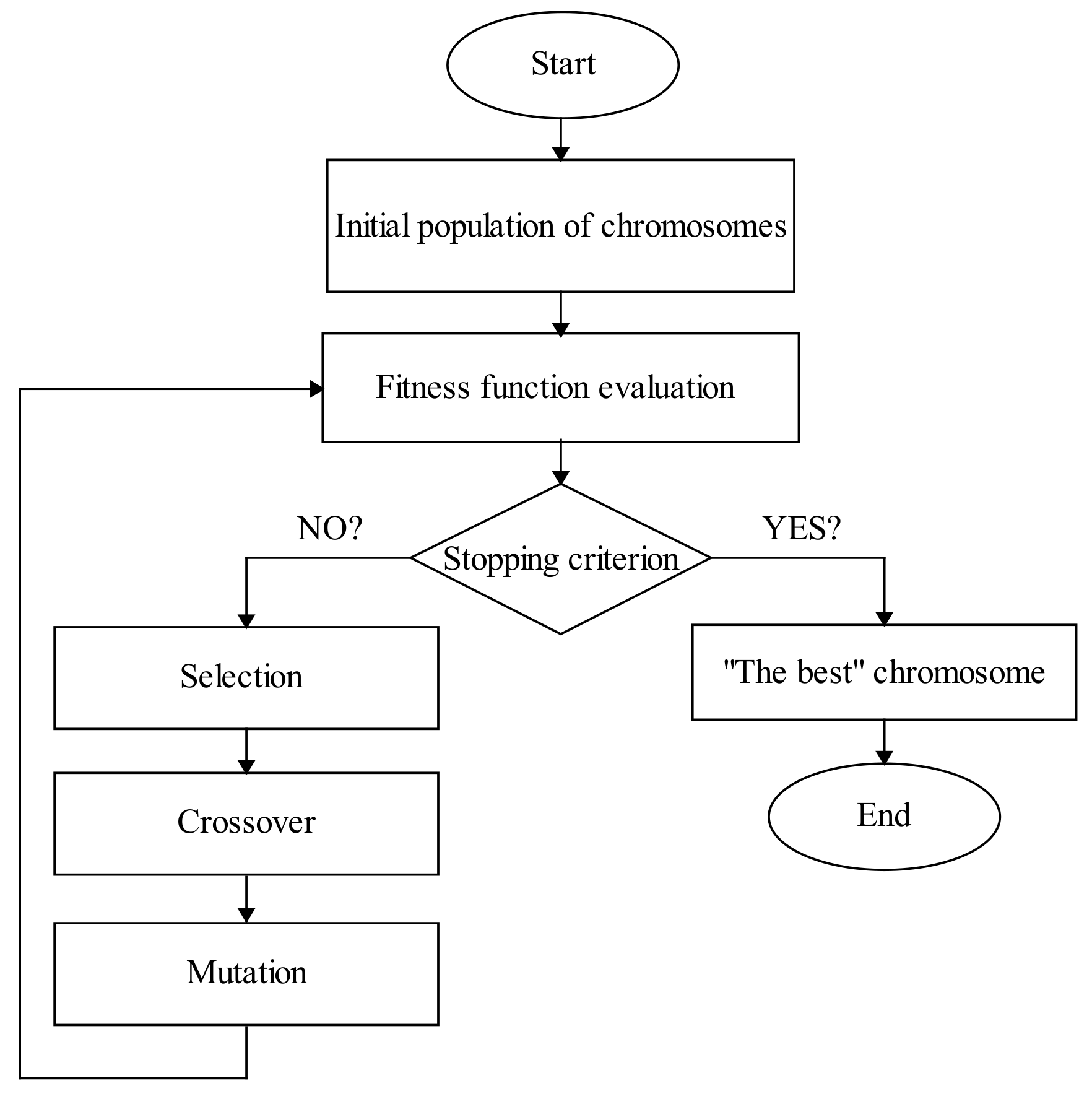
4. Optimizing Water Consumption
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Selma, M.V.; Allende, A.; Lopez-Galvez, F.; Conesa, M.A.; Gil, M.I. Disinfection potential of ozone, ultraviolet-C and their combination in wash water for the fresh-cut vegetable industry. Food Microbiol. 2008, 25, 809–814. [Google Scholar] [CrossRef]
- Gil, M.I.; Selma, M.V.; López-Gálvez, F.; Allende, A. Fresh-cut product sanitation and wash water disinfection: Problems and solutions. Int. J. Food Microbiol. 2009, 134, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Khaki, S.; Pham, H.; Wang, L. Simultaneous Corn and Soybean Yield Prediction from Remote Sensing Data Using Deep Transfer Learning. Sci. Rep. 2021, 11, 11132. [Google Scholar] [CrossRef]
- Moon, T.; Park, J.; Son, J.E. Prediction of the Fruit Development Stage of Sweet Pepper (Capsicum Annum Var. Annuum) by an Ensemble Model of Convolutional and Multilayer Perceptron. Biosyst. Eng. 2021, 210, 171–180. [Google Scholar] [CrossRef]
- Ziółkowski, J.; Oszczypała, M.; Małachowski, J.; Szkutnik-Rogoż, J. Use of Artificial Neural Networks to Predict Fuel Con-sumption on the Basis of Technical Parameters of Vehicles. Energies 2021, 14, 2639. [Google Scholar] [CrossRef]
- Yadav, A.; Prasad, B.B.V.S.V.; Mojjada, R.K.; Kothamasu, K.K.; Joshi, D. Application of Artificial Neural Network and Ge-netic Algorithm Based Artificial Neural Network Models for River Flow Prediction. Revue d’Intelligence Artif. 2020, 34, 745–751. [Google Scholar] [CrossRef]
- Lewicki, P.P.; Skierkowski, K.; Wrzeszcz, S. Przemysł Fermentacyjny i Owocowo-Warzywny; Wydawnictwo Czasopism i Ksiazek Technicznych SIGMA-NOT Sp. z o.o: Warszawa, Poland, 1981; pp. 40–42. [Google Scholar]
- Lipińska-Łuczyn, E. Best Available Techniques (BAT)-Guidelines for the Food Industry: Fruit and Vegetable; Ministry of the Environment: Warszawa, Poland, 2005; pp. 24–27.
- Henkel, M.; Richter, M. Situation und Aufgaben der Betriebswirtschaft in der obst- und gemüseverarbeitenden Industrie. Wasserwirtsch. -Wassertech. 1981, 10, 358–359. [Google Scholar]
- Rüffer, H.; Rosenwinkel, K.H. Treatment of Industrial Wastewater; Oficyna Wydawnicza Projprzem-EKO: Bydgoszcz, Poland, 1998; pp. 81–98. [Google Scholar]
- Neryng, A.; Wojdalski, J.; Budny, J.; Krasowski, E. Energy and Water in the Agri-Food Industry; WNT: Warszawa, Poland, 1990; pp. 280–281. [Google Scholar]
- Masanet, E.; Woorrell, E.; Graus, W.; Galitsky, C. Energy Efficiency Improvement and Cost Saving Opportunities for the Fruit and Vegetable Processing Industry; University of California: Berkeley, CA, USA, 2007; pp. 115–126. [Google Scholar]
- Kwas, A. Determinants of the Consumption of Energy Carriers in a Fruit Processing Plant. Master’s Thesis, Wydział Inżynierii Produkcji, SGGW, Warszawa, Poland, 2018. [Google Scholar]
- Grzybek, A. The impact of selected technologies on the environment and energy consumption in fruit and vegetable processing. Rozprawy habilitacyjne nr 12. Inżynieria Rolnicza 2003, 2. [Google Scholar]
- WS Atkins International. Environmental Protection in the Agri-Food Industry. Environmental Standards; FAPA: Warszawa, Poland, 1998; Volume 57, p. 88. [Google Scholar]
- Strzelczyk, M.; Steinhoff-Wrześniewska, A.; Rajmund, A. Indicators of water consumption and the quantity of wastewater formed in selected branches of food industry. Polish J. Chem. Technol. 2010, 12, 6–10. [Google Scholar] [CrossRef] [Green Version]
- Steinhoff-Wrześniewska, A.; Rajmund, A.; Godzwon, J. Water consumption in selected branches of food industry. Inżynieria Ekologiczna 2013, 32, 164–171. [Google Scholar] [CrossRef] [Green Version]
- Lehto, M.; Sipilä, I.; Alakukku, L.; Kymäläinen, H.R. Water consumption and wastewaters in fresh-cut vegetable production. Agric. Food Sci. 2014, 23, 245–256. [Google Scholar] [CrossRef]
- Kubicki, M. Environmental Protection in the Fruit and Vegetable Industry; FAPA: Warszawa, Poland, 1998; pp. 34–35, 38–43. [Google Scholar]
- Evrard, D.; Villot, J.; Armiyaou, C.; Gaucher, R.; Bouhrizi, S.; Laforest, V. Best Available Techniques: An integrated method for multicriteria assessment of reference installations. J. Clean. Prod. 2018, 176, 1034–1044. [Google Scholar] [CrossRef]
- Wojdalski, J.; Dróżdż, B. Basics of analysis of energy consumption in production of agricultural and food industry plants. MOTROL Motoryzacja i Energetyka Rolnictwa 2006, 8A, 294–304. [Google Scholar]
- Wojdalski, J.; Dróżdż, B.; Lubach, M. Factors influencing water consumption in fruit and vegetable processing plants. Postępy Techniki Przetwórstwa Spożywczego 2005, 1, 39–43. [Google Scholar]
- Montgomery, J.M. Water Recycling in the Fruit and Vegetable Processing Industry; Office of Water Recycling, California State Water Resources Control Board: Sacramento, CA, USA, 1981. [Google Scholar]
- Derden, A.; Vercaemst, P.; Dijkmans, R. Best available techniques (BAT) for the fruit and vegetable processing industry. Resour. Conserv. Recycl. 2002, 34, 261–271. [Google Scholar] [CrossRef]
- Lipowski, J. Possibilities of reducing water consumption during the thermal preservation of canned goods. In Proceedings of the Seminar in the Series “Relationships between Science and Practice”. POLEKO’96, Poznań, Poland; 1996; pp. 117–124. [Google Scholar]
- Miłek, B.; Stelmach, Z.; Stankiewicz, K. Technical possibilities of using waste heat and reducing water consumption in selected technological processes of the fruit and vegetable industry. Przemysł Ferment. Owocowo-Warzywny 1991, 3, 13–14. [Google Scholar]
- MathWorks-Matlab. Available online: www.mathworks.com (accessed on 21 October 2021).
- Winiczenko, R.; Kaleta, A.; Górnicki, K. Application of a MOGA Algorithm and ANN in the Optimization of Apple Drying and Rehydration. Processes 2021, 9, 1415. [Google Scholar] [CrossRef]
- Hickey, M.; Hoogers, R.; Singh, R.; Christen, E.; Henderson, C.; Ashcroft, B.; Hoffmann, H. Maximising Returns from Water in the Australian Vegetable Industry: National Report; NSW Department of Primary Industries: Orange, NSW, Australia, 2006. [Google Scholar]
- Kumar, R.S.; Manimegalai, G. Fruit and Vegetable Processing Industries and Environment. Industrial Pollution & Management; Kumar, A., Ed.; APH Publishing Corporation: New Delhi, India, 2004; pp. 97–117. [Google Scholar]
- Asgharnejad, H.; Khorshidi Nazloo, E.; Madani Larijani, M.; Hajinajaf, N.; Rashidi, H. Comprehensive review of water management and wastewater treatment in food processing industries in the framework of water-food-environment nexus. Compr. Rev. Food Sci. Food Saf. 2021, 20, 4779–4815. [Google Scholar] [CrossRef]
- Almató, M.; Sanmartí, E.; Espun, A.; Puigjaner, L. Rationalizing the water use in the batch process industry. Comput. Chem. Eng. 1997, 21, S971–S976. [Google Scholar] [CrossRef]
- Carrasquer, B.; Uche, J.; Martínez-Gracia, A. A new indicator to estimate the efficiency of water and energy use in agro-industries. J. Clean. Prod. 2017, 143, 462–473. [Google Scholar] [CrossRef]
- Mundi, G.S.; Zytner, R.G.; Warriner, K.; Gharabaghi, B. Predicting fruit and vegetable processing wash-water quality. Water Sci. Technol. 2018, 2017, 256–269. [Google Scholar] [CrossRef] [PubMed]
- Valta, K.; Kosanovič, T.; Malamis, D.; Moustakas, K.; Loizidou, M. Overview of water usage and wastewater management in the food and beverage industry. Desalination Water Treat. 2015, 53, 3335–3347. [Google Scholar] [CrossRef]
- Volschenk, P.J. Investigating Water and Wastewater Management in the South African Fruit and Vegetable Processing Industry. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2020. Available online: https://scholar.sun.ac.za (accessed on 21 October 2021).


| Production, Water Intake Directions | Unit water Consumption Indices (m3/mg of Product) | Source | ||
|---|---|---|---|---|
| Index Range * | Numerical Value | |||
Tomato juice thickening in rotary evaporators
| A | 94.5 101.1 85.3 | [7] | |
| Fruit washing Vegetable washing Vegetable peeling Blanching Refrigerating | T | 1.0–4.0 1.8–2.5 3.0–5.0 0.5–1.0 0.5–1.5 | [8] | |
| Marmalades, preserves Fruit juices Retort fruit preserves Retort vegetable preserves Salad preserves | T | 6.5 4.5 2.5–4.0 3.5–6.0 3.0 | [9,10] | |
| Nectars Liquid fruit Tomato juice Concentrated fruit juices | T | 16.0 9.0–11.0 13.0 140.0 | [11] | |
| Canned fruit Canned vegetables Frozen vegetables Fruit juices Jams Preserves for children | T | 2.5–4 3.5–6 5.0–8.5 6.5 6.0 6.0–9.0 | [12] | |
| Frozen fruit | Z | 1.3–4.0 | [13] | |
| Fruit processing Vegetable processing | Z | 2.2–8.2 5.8–20.3 | [14] | |
| Fruit and vegetable processing plants | Poland | Z | 12.0–32.0 ** | [15] |
| 5.0–61.3 | [16,17] | |||
| Finland | Z | 1.5–5.0 | [18] | |
| South Africa | Z | 0.7–1.9 ** | [19] | |
| Group of Factors | Meaning, Physical Sense | Applied Markings |
| I | Value generally characterizing the plant | V1, |
| II | Elements of the structure of installed power of the plants | P1, |
| III | Structure of daily production | Z1, Z2, Z3 |
| IV | Level of technical and technological equipment and production organization | K2 |
| Group of Independent Variables | Multiple Regression Equations | R2 | Independent Variables | |
|---|---|---|---|---|
| Determination, Dimension | Numerical Range | |||
| I | Aw = −1777.0 + 150. 88 · | 0.395 | V1 (m3) | 10,008–572,645 |
| II | Aw = 408.4 + 2.30 ·P1 | 0.543 | P1 (kW) | 41–1715 |
| III | Aw = 2180.0 − 1420.0/Z1 + 661.6 · logZ2 +140.50 · | 0.476 | Z1 (mg) Z2 (mg) Z3 (mg) | 3.8–105.0 64.0–773.0 11.1–191.1 |
| IV | Ww = 1.4 +0.005K2 | 0.843 | K2 (m3/mg) | 563–307,692 |
| Simulation No. | Division of Each Sample into Train-Valid-Test Sets | Activation Function in the Hidden Layer | Number of Neurons in the Hidden Layer | Activation Function in the Output Layer | Statistical Performance | ||
|---|---|---|---|---|---|---|---|
| MSE | R-Value | R—Adjusted | |||||
| 1 | 60-20-20 | log-sig | 10 | log-sig | 0.00909 | 0.92052 | 0.94955 |
| 2 | 60-20-20 | log-sig | 14 | log-sig | 0.01295 | 0.85946 | 0.80006 |
| 3 | 60-20-20 | log-sig | 6 | pureline | 0.00882 | 0.90510 | 0.92124 |
| 4 | 60-20-20 | log-sig | 10 | pureline | 0.01115 | 0.89047 | 0.93475 |
| 5 | 60-20-20 | log-sig | 14 | pureline | 0.00569 | 0.93186 | 0.92554 |
| 6 | 60-20-20 | tansig | 6 | pureline | 0.01105 | 0.87170 | 0.93544 |
| 7 | 60-20-20 | tansig | 10 | pureline | 0.01012 | 0.88376 | 0.98881 |
| 8 | 60-20-20 | tansig | 14 | pureline | 0.00724 | 0.94758 | 0.96594 |
| 9 | 60-20-20 | tansig | 6 | log-sig | 0.01227 | 0.85771 | 0.84561 |
| 10 | 60-20-20 | tansig | 10 | log-sig | 0.01046 | 0.90830 | 0.83945 |
| 11 | 60-20-20 | tansig | 14 | log-sig | 0.01151 | 0.91263 | 0.94033 |
| 12 | 70-15-15 | log-sig | 6 | log-sig | 0.00656 | 0.94070 | 0.88573 |
| 13 | 70-15-15 | log-sig | 10 | log-sig | 0.00839 | 0.90687 | 0.99758 |
| 14 | 70-15-15 | log-sig | 14 | log-sig | 0.01024 | 0.91473 | 0.96854 |
| 15 | 70-15-15 | log-sig | 6 | pureline | 0.00779 | 0.88962 | 0.88017 |
| 16 | 70-15-15 | log-sig | 10 | pureline | 0.01127 | 0.90074 | 0.99739 |
| 17 | 70-15-15 | log-sig | 14 | pureline | 0.01032 | 0.90545 | 0.89289 |
| 18 | 70-15-15 | tansig | 6 | pureline | 0.00977 | 0.89027 | 0.97076 |
| 19 | 70-15-15 | tansig | 10 | pureline | 0.00856 | 0.91127 | 0.71730 |
| 20 | 70-15-15 | tansig | 14 | pureline | 0.01171 | 0.85632 | 0.83473 |
| 21 | 70-15-15 | tansig | 6 | log-sig | 0.01130 | 0.89255 | 0.97375 |
| 22 | 70-15-15 | tansig | 10 | log-sig | 0.00654 | 0.92229 | 0.83440 |
| 23 | 70-15-15 | tansig | 14 | log-sig | 0.01516 | 0.80701 | 0.99803 |
| 24 | 80-10-10 | log-sig | 6 | log-sig | 0.00411 | 0.95967 | 0.94904 |
| 25 | 80-10-10 | log-sig | 10 | log-sig | 0.00788 | 0.92798 | 0.90828 |
| 26 | 80-10-10 | log-sig | 14 | log-sig | 0.01172 | 0.87754 | 0.92124 |
| 27 | 80-10-10 | log-sig | 6 | pureline | 0.02016 | 0.82914 | 0.92241 |
| 28 | 80-10-10 | log-sig | 10 | pureline | 0.00986 | 0.91291 | 0.91322 |
| 29 | 80-10-10 | log-sig | 14 | pureline | 0.01231 | 0.88508 | 0.99082 |
| 30 | 80-10-10 | tansig | 6 | pureline | 0.00637 | 0.9521 | 0.94621 |
| 31 | 80-10-10 | tansig | 10 | pureline | 0.01315 | 0.88489 | 0.9999 |
| 32 | 80-10-10 | tansig | 14 | pureline | 0.01241 | 0.85400 | 0.85677 |
| 33 | 80-10-10 | tansig | 6 | log-sig | 0.00761 | 0.90785 | 0.96694 |
| 34 | 80-10-10 | tansig | 10 | log-sig | 0.00901 | 0.94803 | 0.95231 |
| 35 | 80-10-10 | tansig | 14 | log-sig | 0.00782 | 0.92660 | 0.96451 |
| Neural Network | Sensitivity Analysis | |||||
|---|---|---|---|---|---|---|
| X6 | X5 | X3 | X2 | X1 | X4 | |
| MLP 6-6-1 | 3.19527 | 2.136989 | 1.804672 | 1.763347 | 1.628497 | 1.494883 |
| Population Size | Crossover Probability | Mutation Probability | Number of Generations |
|---|---|---|---|
| 80 | 0.8 | 0.01 | 3000 |
| Frozen Products (mg/day) | Concentrates (mg/day) | Juices and Drinks (mg/day) | Other Products (mg/day) | Total Power (kW) | Total Production (mg/day) |
|---|---|---|---|---|---|
| 35.06 | 505.05 | 237.68 | 0.44 | 946 | 778.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trajer, J.; Winiczenko, R.; Dróżdż, B. Analysis of Water Consumption in Fruit and Vegetable Processing Plants with the Use of Artificial Intelligence. Appl. Sci. 2021, 11, 10167. https://doi.org/10.3390/app112110167
Trajer J, Winiczenko R, Dróżdż B. Analysis of Water Consumption in Fruit and Vegetable Processing Plants with the Use of Artificial Intelligence. Applied Sciences. 2021; 11(21):10167. https://doi.org/10.3390/app112110167
Chicago/Turabian StyleTrajer, Jędrzej, Radosław Winiczenko, and Bogdan Dróżdż. 2021. "Analysis of Water Consumption in Fruit and Vegetable Processing Plants with the Use of Artificial Intelligence" Applied Sciences 11, no. 21: 10167. https://doi.org/10.3390/app112110167






