Polymerization of Isobutylene in a Rotating Packed Bed Reactor: Experimental and Modeling Studies
Abstract
:1. Introduction
2. Materials and Methods
2.1. Reagents
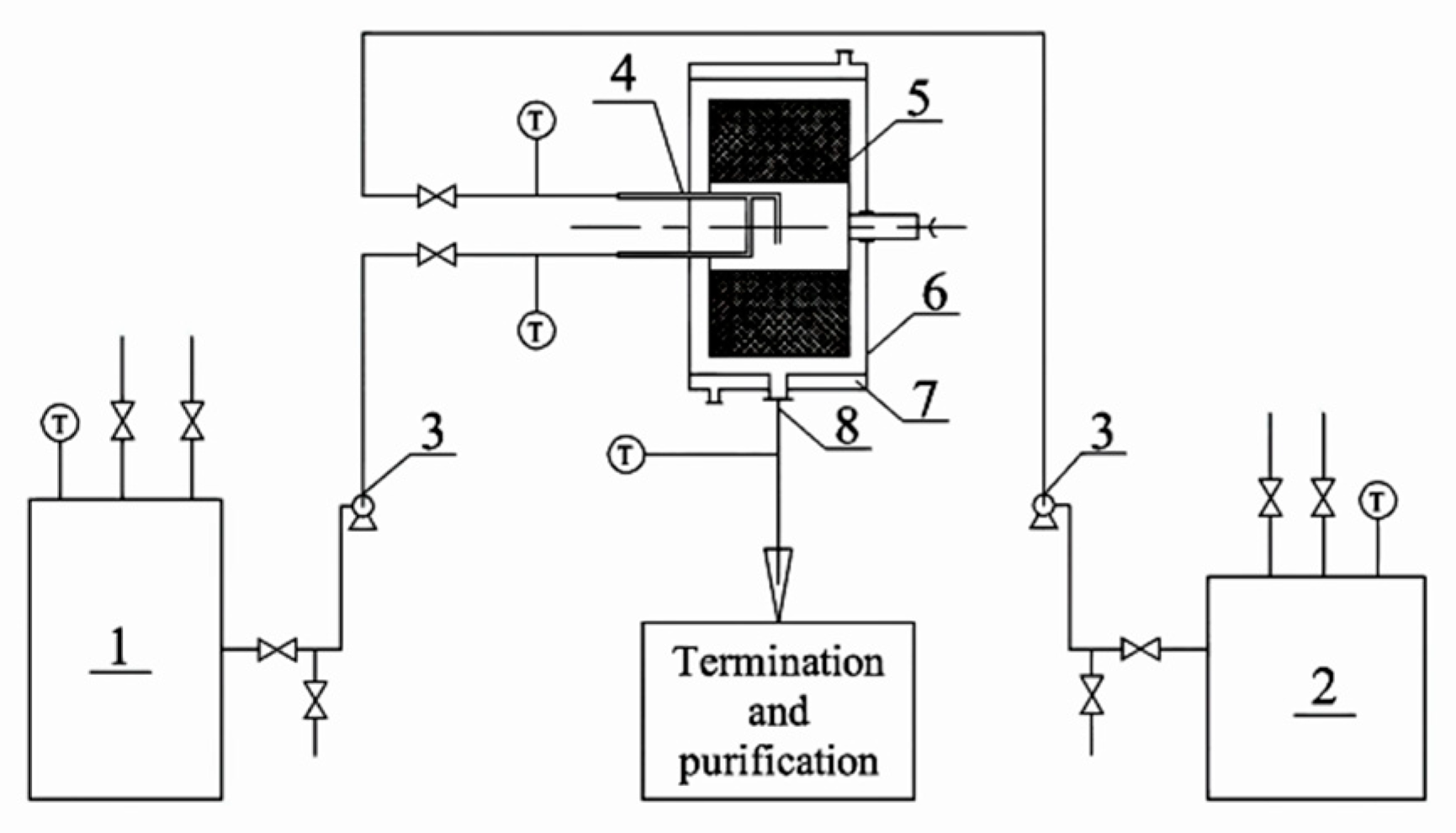
2.2. Experimental Procedures
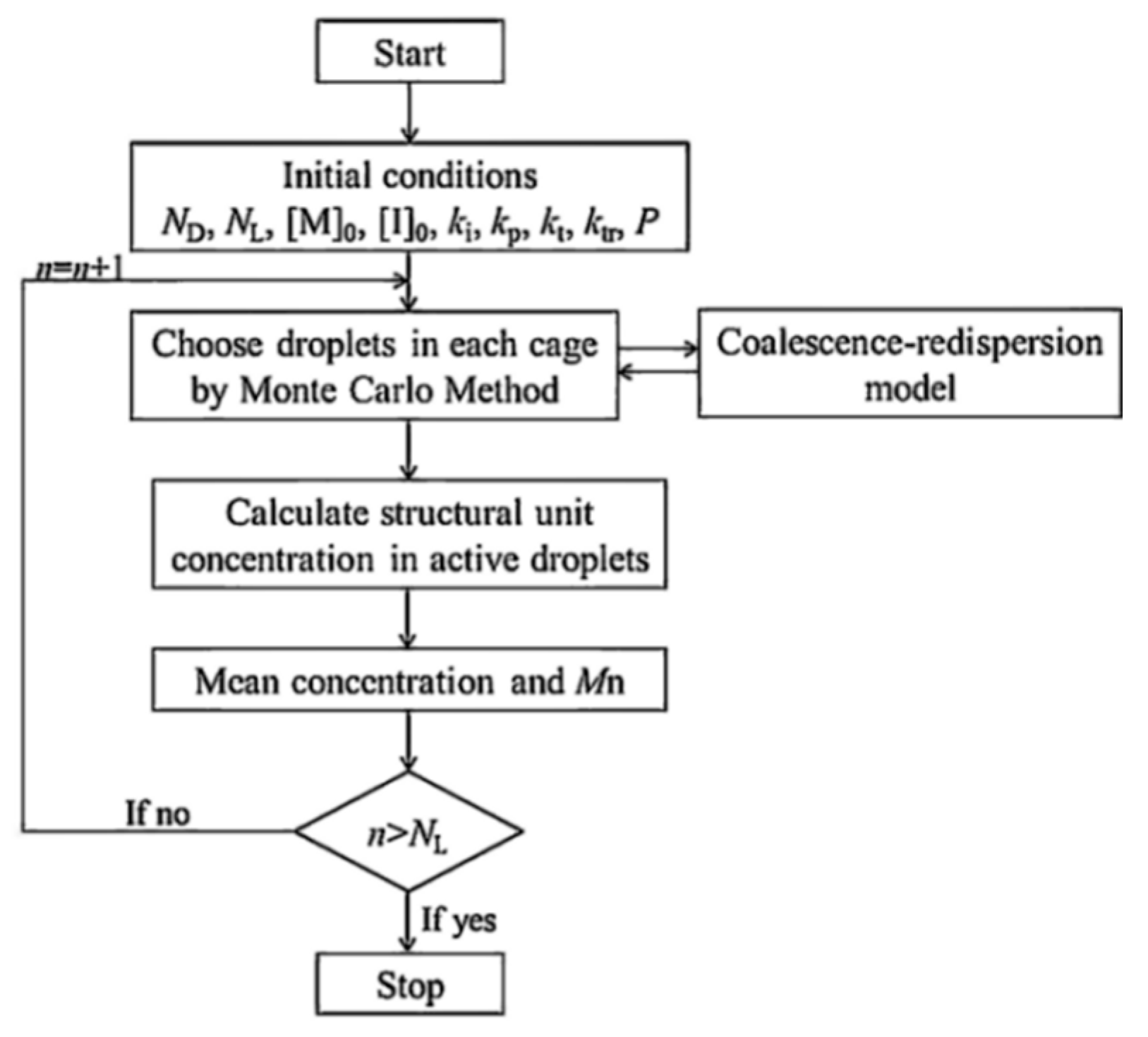
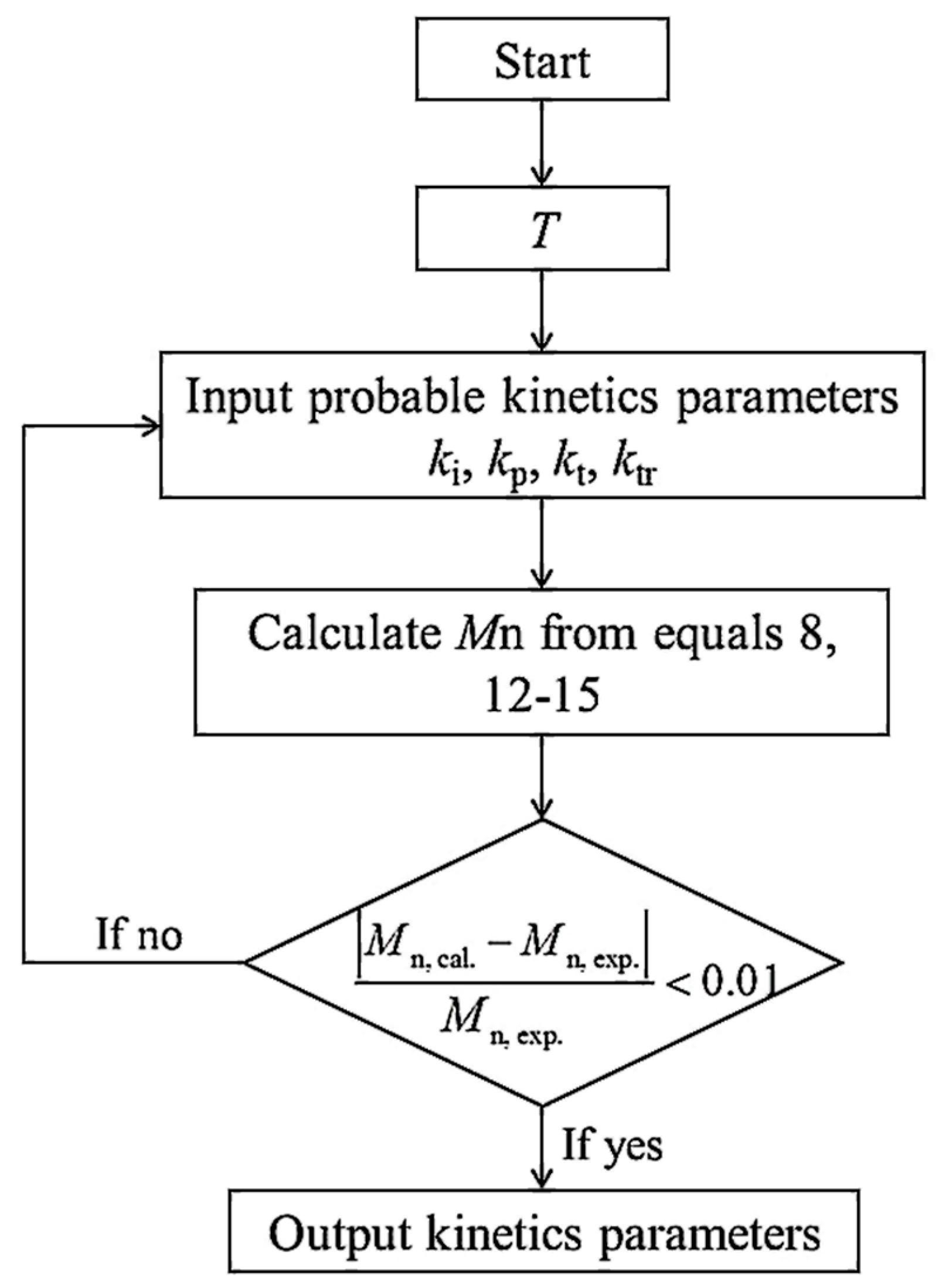
2.3. Model Development
2.3.1. Modeling for the Polymerization of IB in RPB
2.3.2. Presumptive-Steady-State Analysis for the Polymerization
2.3.3. Calculation of Mn
3. Results
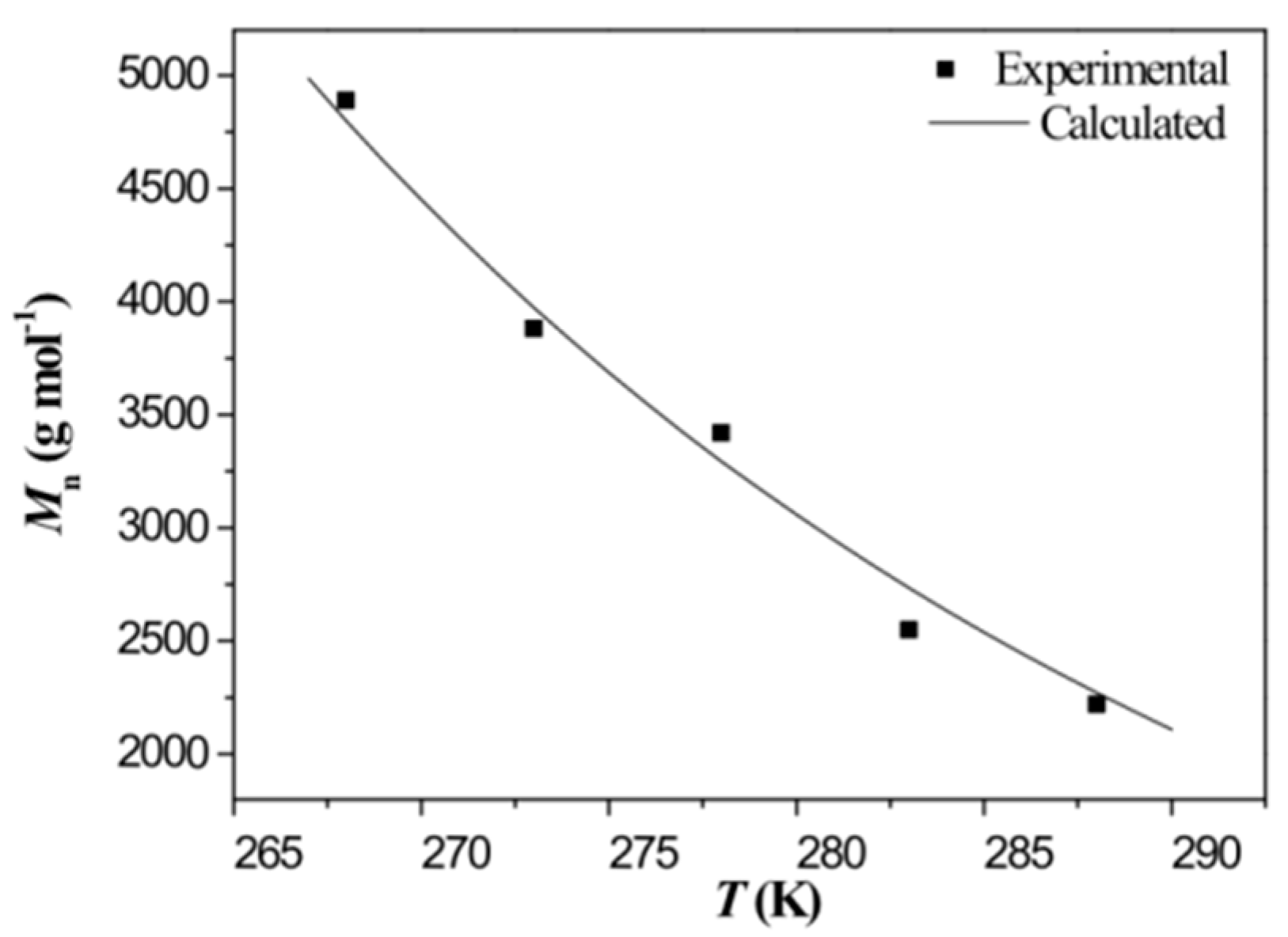
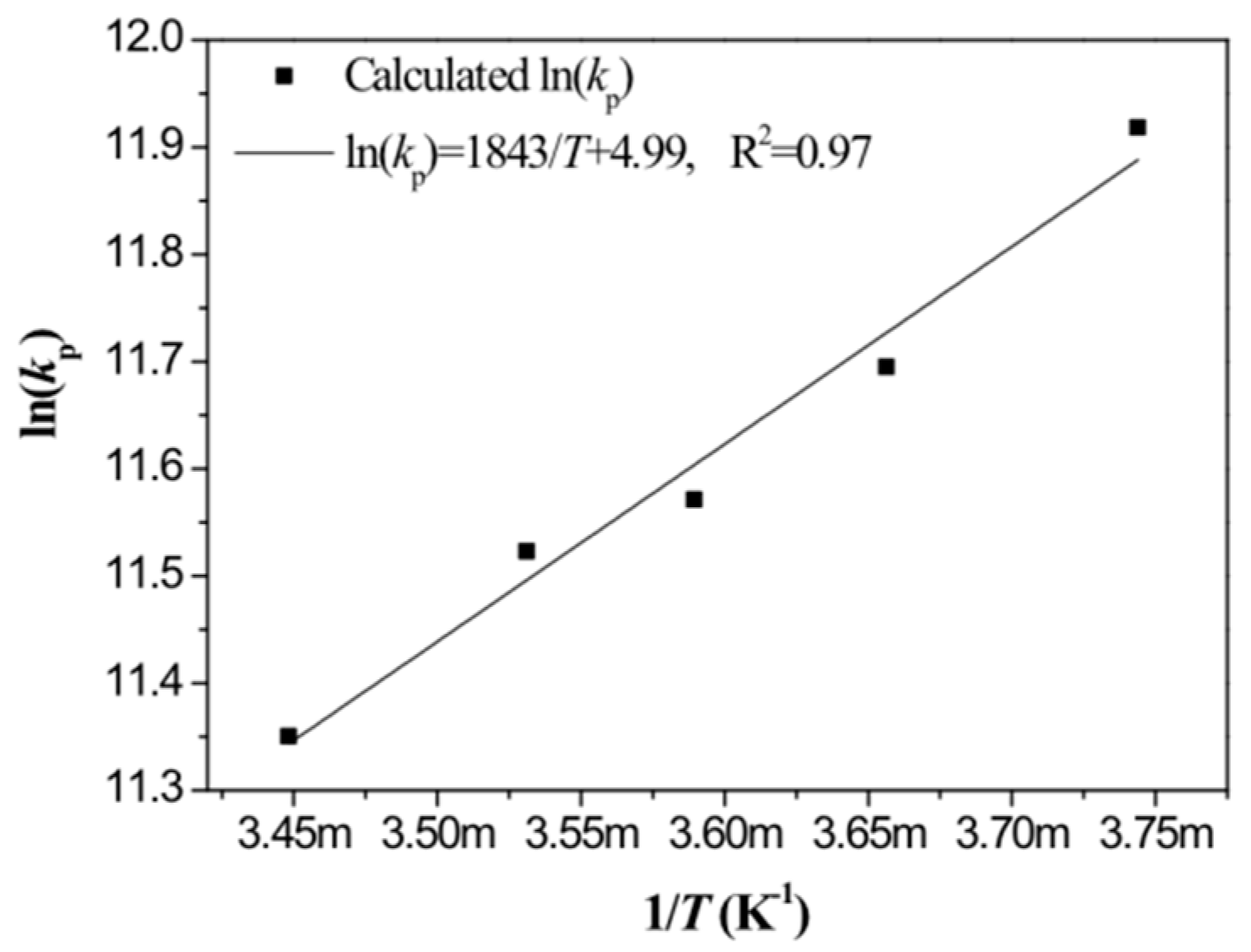
3.1. Effect of T and Estimation of Reaction Rate Constant
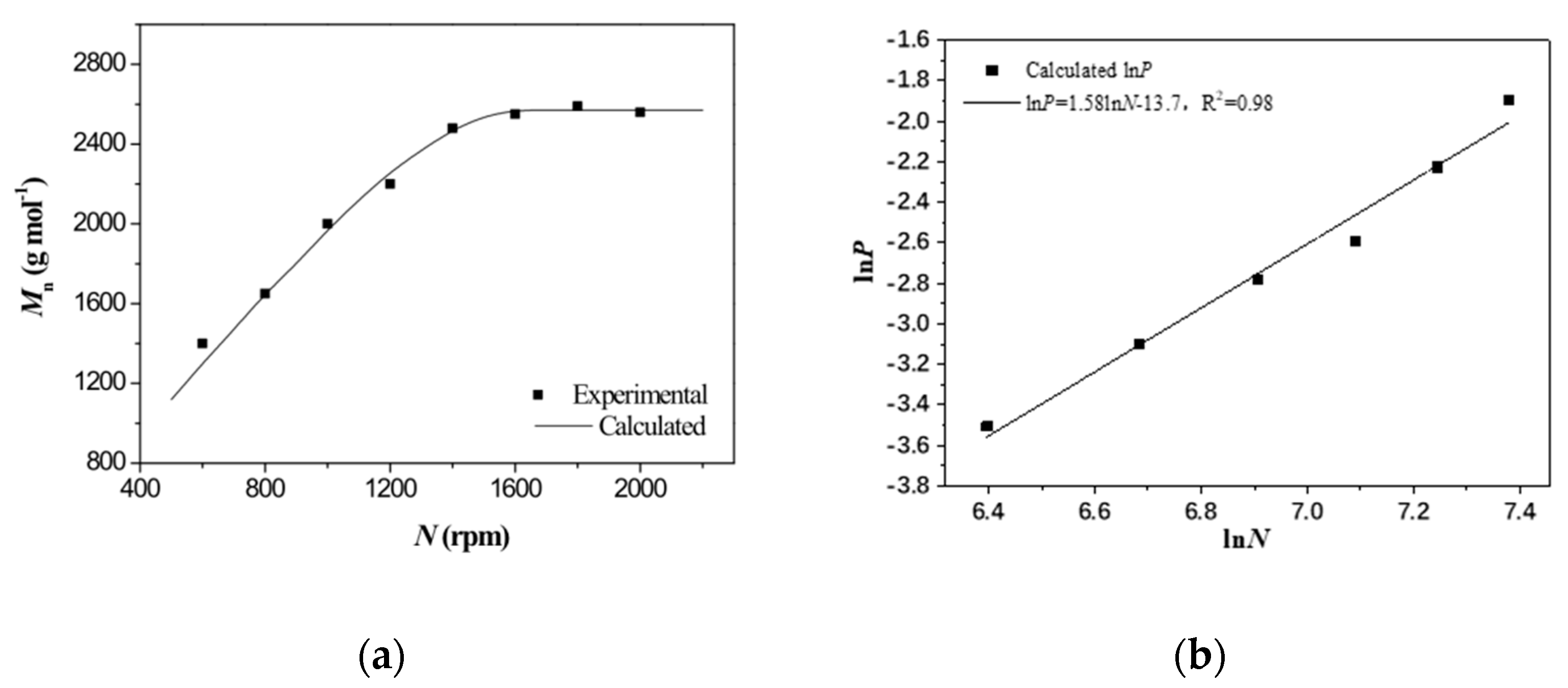
3.2. Effect of N and Estimation of P
3.3. Effect of [M]0/[I]0
3.4. Model Error Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notation
| T | polymerization temperature, K |
| N | rotating speed of rotator in RPB, rpm (r·min−1) |
| Mn | number-average molecular weight, g·mol−1 |
| [M]t | concentration of IB in tank, mol·L−1 |
| [M]0 | initial concentration of IB in RPB, mol·L−1 |
| [M] | concentration of IB in RPB, mol·L−1 |
| [I]t | concentration of initiating system in tank, mol·L−1 |
| [I]0 | initial concentration of initiating system in RPB, mol·L−1 |
| [I] | concentration of initiating system in RPB, mol·L−1 |
| QM | volumetric flow rate of IB solution, L·h−1 |
| QI | volumetric flow rate of initiating system solution, L·h−1 |
| D | packing thickness in RPB, mm |
| NL | total cage number of packing |
| ND | droplets number in every cage |
| Ri | inner radius of rotator in RPB, mm |
| Ro | outer radius of rotator in RPB, mm |
| ri | initiation rate, mol·L−1·s−1 |
| rp | propagation rate, mol·L−1·s−1 |
| rtr | chain transfer rate, mol·L−1·s−1 |
| rt | termination rate, mol·L−1·s−1 |
| concentration of active left, mol·L−1 | |
| concentration of polymer with j units, mol·L−1 | |
| concentration of polymer with j units out of packing, mol·L−1 | |
| ki | rate constant for initiation, L·mol−1·s−1 |
| kp | rate constant for propagation, L·mol−1·s−1 |
| ktr | rate constant for chain transfer to monomer, L·mol−1·s−1 |
| kt | rate constant for termination, s−1 |
| Mj | 56j molecular weight of polymer with j units, g·mol−1 |
| tm | micromixing characteristic time, ms |
| t1/2 | reactive characteristic time, ms |
| k0 | pre-exponential factor |
| R | molar gas constant, J·mol−1·K−1 |
| Ea | apparent activation energy, kJ·mol−1 |
| P | coalescence probability |
| Greek letters | |
| δ | distance between adjacent cages, mm |
References
- Liu, Q.; Wu, Y.X.; Yan, P.F.; Zhang, Y.; Xu, R.W. Polyisobutylene with High Exo-olefin Content via β-H Elimination in the Cationic Polymerization of Isobutylene with H2O/FeCl3/dialkyl ether Initiating System. Macromolecules 2011, 44, 1866–1875. [Google Scholar] [CrossRef]
- Vasilenko, I.V.; Kostjuk, S.V. Homogeneous and heterogeneous catalysts for the synthesis of highly reactive polyisobutylene: Discovery, development and perspectives. J. Macromol. Sci. Part A 2021, 1–11. [Google Scholar] [CrossRef]
- Rajasekhar, T.; Singh, G.; Kapur, G.S.; Ramakumar, S.S.V. Recent Advances in Catalytic Chain Transfer Polymerization of Isobutylene: A Review. RSC Adv. 2020, 10, 18180–18191. [Google Scholar] [CrossRef]
- Kostjuk, S.V. Recent Progress in the Lewis Acid Co-Initiated Cationic Polymerization of Isobutylene and 1,3-Dienes. RSC Adv. 2015, 5, 13125–13144. [Google Scholar] [CrossRef]
- Li, Y.; Cokoja, M.; Kühn, F.E. Inorganic/Organometallic Catalysts and Initiators Involving Weakly Coordinating Anions for Isobutene Polymerisation. Coord. Chem. Rev. 2011, 255, 1541–1557. [Google Scholar]
- Kostjuk, S.V.; Yeong, H.Y.; Voit, B. Cationic Polymerization of Isobutylene at Room Temperature. J. Polym. Sci. A Polym. Chem. 2013, 51, 471–486. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, Y.X.; Zhang, Y.; Yan, P.F.; Xu, R.W. A cost-effective process for highly reactive polyisobutylenes via cationic polymerization coinitiated by AlCl3. Polymer 2010, 51, 5960–5969. [Google Scholar] [CrossRef]
- Sigwalt, P.; Moreau, M. Carbocationic Polymerization: Mechanisms and Kinetics of Propagation Reactions. Prog. Polym. Sci. 2006, 31, 44–120. [Google Scholar] [CrossRef]
- Matyjaszewski, K.; Pugh, C. Mechanistic aspects of cationic polymerization of alkenes. In Cationic Polymerization: Mechanisms, Synthesis, and Applications; Dekker M Press: New York, NY, USA, 1996; pp. 192–204. [Google Scholar]
- Qiu, Y.X.; Wu, Y.X.; Xu, X.; Ran, F.; Wu, G.Y. Propagation Rate Constants for the Cationic Polymerization of Vinyl Monomer. Chin. Polym. Bull. 2006, 4, 1–10. [Google Scholar]
- Plesch, P.H. The Propagation Rate Constants of the Cationic Polymerization of Alkenes. Prog. React. Kinet. 1993, 18, 1–62. [Google Scholar]
- Puskas, J.E.; Shaikh, S.; Yao, K.Z.; McAuley, K.B.; Kaszas, G. Kinetic Simulation of Living Carbocationic Polymerizations. II. Simulation of Living Isobutylene Polymerization using a mechanistic model. Eur. Polym. J. 2005, 41, 1–14. [Google Scholar] [CrossRef]
- Wu, G.Y.; Wu, Y.X. Controlling Cationic Polymerization and Its Application; Chem. Ind. Press: Beijing, China, 2005. [Google Scholar]
- Liu, D.H. Handbook of Synthetic Rubber Industry; Chem. Ind. Press: Beijing, China, 1991. [Google Scholar]
- Kennedy, J.P.; Macrechal, E. Carbocationic Polymerization; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Chen, G.T. Foundation of Polymer Reactive Engineering; China Petrochemical Press: Beijing, China, 1991. [Google Scholar]
- Chen, J.F.; Gao, H.; Zou, H.K.; Chu, G.W.; Zhang, L.; Shao, L.; Xiang, Y.; Wu, Y.X. Cationic Polymerization in Rotating Packed Bed Reactor: Experimental and Modeling. AIChE J. 2010, 56, 1053–1062. [Google Scholar] [CrossRef]
- Chen, J.F.; Wang, Y.H.; Guo, F.; Wang, X.M.; Zheng, C. Synthesis of Nanoparticles with Novel Technology: High-gravity Reactive Precipitation. Ind. Eng. Chem. Res. 2000, 39, 948–954. [Google Scholar] [CrossRef]
- Munjal, S.; Dudukovc, M.P.; Ramachandran, P. Mass Transfer in Rotating Packed Beds-I. Development of Gas-liquid and Liquid-solid Mass-transfer Correlations. Chem. Eng. Sci. 1989, 44, 2245–2256. [Google Scholar] [CrossRef]
- Ramshaw, C.; Mallinson, R. Mass Transfer Process. U.S. Patent 4,263,255, 11 August 1981. [Google Scholar]
- Chen, J.F. High Gravity Technology and Application-a New Generation of Reaction and Separation Technology; Chem. Ind. Press: Beijing, China, 2003. (In Chinese) [Google Scholar]
- Chen, J.F.; Shao, L.; Guo, F.; Wang, X.M. Synthesis of Nano-fibers of Aluminum Hydroxide in Novel Rotating Packed Bed Reactor. Chem. Eng. Sci. 2003, 58, 569–575. [Google Scholar] [CrossRef]
- Wang, M.; Zou, H.K.; Shao, L.; Chen, J.F. Controlling Factors and Mechanism of Preparing Needlelike CaCO3 under High-gravity Environment. Powder Technol. 2004, 142, 166–174. [Google Scholar] [CrossRef]
- Chen, J.F.; Shao, L. Mass Production of Nanoparticles by High Gravity Reactive Precipitation Technology with Low Cost. China Particuology 2003, 1, 64–69. [Google Scholar] [CrossRef]
- Guo, K.; Guo, F.; Feng, Y.D.; Chen, J.F.; Zheng, C.; Gardner, N.C. Synchronous Visual and RTD Study on Liquid Flow in Rotating Packed Bed Contactor. Chem. Eng. Sci. 2000, 55, 1699–1706. [Google Scholar] [CrossRef]
- Chen, J.F.; Zhou, M.Y.; Shao, L.; Wang, Y.Y.; Yun, J.; Chew, N.Y.K.; Chan, H.K. Feasibility of Preparing Nanodrugs by High-gravity Reactive Precipitation. Int. J. Pharm. 2004, 269, 267–274. [Google Scholar] [CrossRef]
- Chen, Y.H.; Chang, C.Y.; Su, W.L.; Chen, C.C.; Chiu, C.Y.; Yu, Y.H.; Chiang, P.C.; Chiang, S.I.M. Modeling Ozone Contacting Process in a Rotating Packed Bed. Ind. Eng. Chem. Res. 2004, 43, 228–236. [Google Scholar] [CrossRef]
- Yang, H.J.; Chu, G.W.; Zhang, J.W.; Shen, Z.G.; Chen, J.F. Micromixing Efficiency in a Rotating Packed Bed: Experiments and Simulation. Ind. Eng. Chem. Res. 2005, 44, 7730–7737. [Google Scholar] [CrossRef]
- Chen, J.F.; Gao, H.; Wu, Y.X.; Zou, H.K.; Chu, G.W.; Zhang, L. Method for Synthesis of Butyl Rubber. U.S. Patent 12,307,121, 17 August 2010. [Google Scholar]
- Curl, R.L. Disperse Phase Mixing I: Theory and Effects in Simple Reactors. AIChE J. 1963, 9, 175–181. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.T. Kinetic Models of Homogeneous Ionic Polymerization. J. Polym. Sci. Pol. Chem. Edit. 1982, 20, 2915–2934. [Google Scholar] [CrossRef]
- Wu, G.; Wu, Y. Control Cationic Polymerization and Its Application; Chemical Industry Press: Beijing, China, 2004; pp. 166–173. [Google Scholar]
- Wang, J.D. Real-time Dynamic Simulation of Low Density Polyethylene Reactor under High Pressure. Master’s Thesis, Beijing University of Chemical Technology, Beijing, China, 1997. [Google Scholar]
- Wang, W.S.; Li, S.F. Conditional Contractivity of Runge-Kutta Methods for Nonlinear Differential Equations with Many Variable Delays. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 399–408. [Google Scholar] [CrossRef]
- Thomas, Q.A.; Storey, R.F. Effect of Reaction Conditions on Apparent TiCl4 Reaction Order in Quasiliving Isobutylene Polymerization at High [initiator]/[TiCl4] Ratios. Macromolecules 2003, 36, 10120–10125. [Google Scholar] [CrossRef]
- Pan, Z.R. Polymer Chemistry; Chem. Ind. Press: Beijing, China, 2002. [Google Scholar]
- Fordor, Z.; Bae, Y.C.; Faust, R. Temperature Effects on the Living Cationic Polymerization of Isobutylene: Determination of Spontaneous Chain-transfer Constants in the Presence of Terminative Chain Transfer. Macromolecules 1998, 31, 4439–4446. [Google Scholar] [CrossRef]
- Yang, H.J.; Chu, G.W.; Xiang, Y.; Chen, J.F. Characterization of Micro-mixing Efficiency in Rotating Packed Beds by Chemical Methods. Chem. Eng. J. 2006, 121, 147–152. [Google Scholar] [CrossRef]


| ND | NL | δ/mm | Ri/mm | Ro/mm |
|---|---|---|---|---|
| 600 | 40 | 0.9 | 40 | 76 |
| T/K | Mn/(g·mol−1) | kp/(104 L·mol−1·s−1) |
|---|---|---|
| 267 | 4890 | 15.0 |
| 274 | 3880 | 12.0 |
| 279 | 3420 | 10.6 |
| 283 | 2550 | 10.1 |
| 290 | 2220 | 8.5 |
| N/rpm | Mn/(g·mol−1) | P |
|---|---|---|
| 600 | 1400 | 0.030 |
| 800 | 1650 | 0.045 |
| 1000 | 2000 | 0.062 |
| 1200 | 2200 | 0.075 |
| 1400 | 2480 | 0.108 |
| 1600 | 2550 | 0.150 |
| 1800 | 2590 | 0.151 |
| 2000 | 2560 | 0.150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, W.; Wang, W.; Xiang, Y.; Li, Y.; Chu, G.; Zou, H.; Sun, B. Polymerization of Isobutylene in a Rotating Packed Bed Reactor: Experimental and Modeling Studies. Appl. Sci. 2021, 11, 10194. https://doi.org/10.3390/app112110194
Hou W, Wang W, Xiang Y, Li Y, Chu G, Zou H, Sun B. Polymerization of Isobutylene in a Rotating Packed Bed Reactor: Experimental and Modeling Studies. Applied Sciences. 2021; 11(21):10194. https://doi.org/10.3390/app112110194
Chicago/Turabian StyleHou, Wenhui, Wei Wang, Yang Xiang, Yingjiao Li, Guangwen Chu, Haikui Zou, and Baochang Sun. 2021. "Polymerization of Isobutylene in a Rotating Packed Bed Reactor: Experimental and Modeling Studies" Applied Sciences 11, no. 21: 10194. https://doi.org/10.3390/app112110194
APA StyleHou, W., Wang, W., Xiang, Y., Li, Y., Chu, G., Zou, H., & Sun, B. (2021). Polymerization of Isobutylene in a Rotating Packed Bed Reactor: Experimental and Modeling Studies. Applied Sciences, 11(21), 10194. https://doi.org/10.3390/app112110194







