Determination of Local Stresses and Strains within the Notch Strain Approach: Efficient Implementation of Notch Root Approximations
Abstract
:1. Introduction
- On the one hand, the local elastic-plastic stresses and strains can be estimated using the notch root approximation according to Neuber [27] with the extension according to Seeger and Heuler [28]. For each closed hysteresis detected from the local stress-strain paths estimated in this way, a load parameter PRAM, Equation (1), is calculated.
- On the other hand, the local stresses and strains can be estimated using the notch root approximation according to Seeger and Beste [30,31,32]. The evaluation of the damage of the individual hystereses is carried out with the PRAJ load parameter, which is a refined version of the PJ parameter according to Vormwald [21,24].
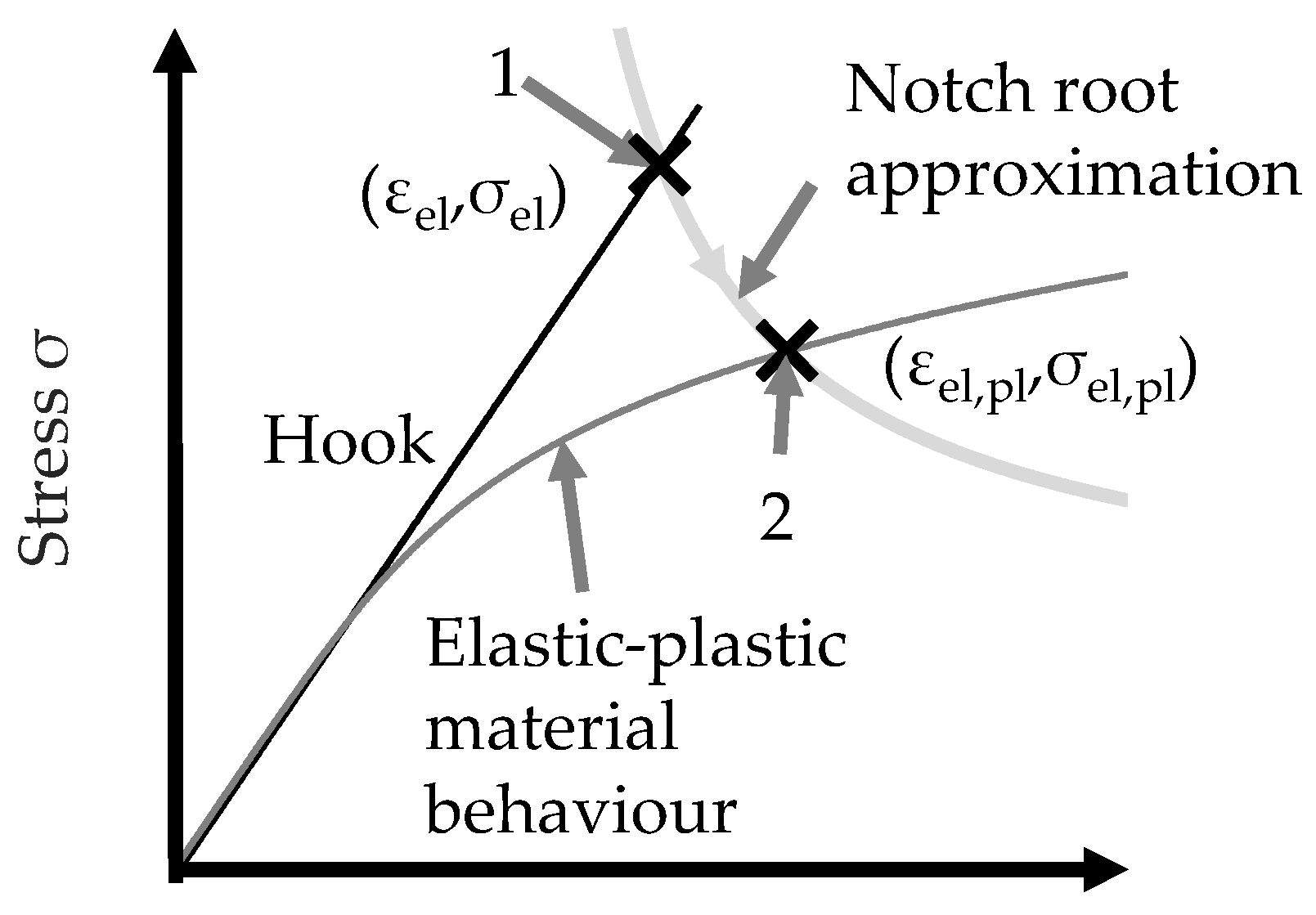
2. Notch Root Approximations in the FKM Guideline Nonlinear
2.1. Extended Version of Neuber’s Rule
2.2. Notch Root Approximation according to Seeger and Beste
3. Issues concerning the Implementation of Notch Root Approximations
- Is the formulation of the root finding problem a good option to ensure consistent accuracy over the entire load range?
- How can the derivative f’ of the functions for the notch root approximation used in Newton’s method be obtained? Is it better to perform the derivation analytically or numerically?
- Is the termination criterion specified in [25] for Newton’s method with a fixed number of 10 iterations suitable for reliably performing the notch root approximations? As alternative termination criteria, criteria based on an accuracy value could also be considered, which would lead to a variable number of iterations.
- Are there other aspects to be considered with regard to a (numerically) stable and reliable implementation?
3.1. Formulation of the Root Finding Problem for Use in Newton’s Method
3.2. Derivatives of the Functions for Use in Newton’s Method
3.3. Termination Criteria for Newton’s Method
- Termination after a predefined number of iterations.
- Termination when the value of the root finding problem falls below , i.e., when Equation (27) is fulfilled. This is the case if the function value of the root finding problem is sufficiently close to zero; compare Figure 4.
- Termination after 10 fixed steps, as suggested in [25].
- Termination after falling below a function value .
- using f according to Equations (10) and (14) (i.e., finding the root of the difference of ) and .
- using f according to Equations (20) and (21) (i.e., finding the root of the quotient of ) and .
- A small remaining strain deviation in criterion 2a has a high influence, especially at low stresses.
- ○
- For example, for steel (Young’s modulus ), a value of leads to a deviation in the stress direction of 0.02 MPa at 1 MPa, which corresponds to a relative deviation of 2%.
- ○
- With increasing loads, the deviation of 0.02 MPa remains almost constant, so the relative error decreases.
- ○
- The maximum error is .
- If the absolute deviation of 0.02 MPa from the previous point is now applied to a load height of 20 MPa, then the following value results for for termination criterion 2b:
- ○
- or since in Equations (20) and (21), 1 is subtracted. The result is .
3.4. Consideration of the Numerical Stability
4. Evaluation of Performance and Accuracy of Different Implementations
- The accuracy with which the notch root approximations are carried out affects the results of the fatigue strength assessment.
- The calculation resources required for the application or the required computing time matter for an efficient implementation. When performing single calculations on a single or a few individual locations of a component to be verified, this aspect is not important. However, in regard to performing many assessments, e.g., when applied to a whole FE surface mesh of a component, the calculation time becomes a decisive factor.
4.1. Database
- Maximum linear-elastic stress range relevant for the strength verification .
- Tensile strength Rm for estimation of Ramberg-Osgood parameters according to [25].
- Limit load factor Kp.
4.2. Implementation into Software Code
- The software environment MATLAB (version 2020b) was used to represent script languages and
- Fortran (Intel Ifort 2019 Update 5 using “-O3” optimization) was used to represent compiled languages in machine code.
- Enhanced Neuber using the analytical derivative and termination after 10 fixed steps
- Enhanced Neuber using the analytical derivative, termination if Equation (10) falls below
- Enhanced Neuber using the analytical derivative, termination if Equation (20) falls below
- Seeger/Beste using the analytical derivative, termination after 10 fixed steps
- Seeger/Beste using the analytical derivative, termination if Equation (14) falls below
- Seeger/Beste using the analytical derivative, termination if Equation (21) falls below
- Seeger/Beste using the numerical approximation of the derivative, termination after 10 fixed steps
- Seeger/Beste using the numerical approximation of the derivative, termination if Equation (14) falls below
- Seeger/Beste using the numerical approximation of the derivative, termination if Equation (21) falls below
4.3. Results and Discussion
5. Conclusions
- 10 Newton steps, as suggested in [25], almost always lead to a desired accuracy but are not required in most cases.
- In the case of a script language, here represented by MATLAB, the formulation of the root finding problem in the form of a quotient between the strain calculated via the material law and the strain calculated via the notch root approximation leads to the best computational performance.
- In the case of a language compiled in machine code, here represented by Fortran, the formulation of the root finding problem in the form of a difference in the strain calculated via the material law and strain calculated via the notch root approximation leads to the best computational performance.
- If Seeger and Beste’s notch root approximations are used and an incorrect termination criterion is selected, then there is a risk that the automated calculation will produce complex numbers that cannot be interpreted meaningfully in terms of a service life calculation. Here, the use of the termination criteria with a desired accuracy leads to the most stable solution, in the sense that no complex number arose in the examined parameter field.
- The analytical derivative of the notch root approximation according to Seeger and Beste cannot be trivially used. The numerical approximation via the difference quotient is much easier to handle and leads to minor losses in performance when used in MATLAB and to comparable performance when used in Fortran.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| E | Young’s modulus |
| function placeholder of the root finding problem | |
| f’ | function placeholder of the derivative of the root finding problem |
| FE | finite element |
| FKM | Abbreviation for the german research association “Forschungskuratorium Maschinenbau” |
| H | step size |
| k | mean stress correction factor |
| cyclic hardening coefficient | |
| limit load factor | |
| reference load for local yielding | |
| reference load for plastic collapse | |
| cyclic hardening exponent | |
| NRA | notch root approximation |
| PRAJ | load parameter |
| PRAM | load parameter |
| cyclic yield strength | |
| RO | Ramberg Osgood |
| range of stress/strain of a hysteresis | |
| effective elastic-plastic strain range | |
| effective elastic-plastic stress range | |
| strain amplitude of the detected stress-strain hysteresis | |
| linear-elastic local strain | |
| substitution strain for net section plasticity | |
| elastic-plastic local strain | |
| placeholder for the convergence threshold | |
| convergence threshold when finding the root of the difference | |
| convergence threshold when finding the root of the quotient | |
| start value of elastic-plastic stress for the newton iteration | |
| stress amplitude of the detected stress-strain hysteresis | |
| linear-elastic local stress | |
| elastic-plastic local stress | |
| mean stress of the detected stress-strain hysteresis | |
| value of elastic-plastic stress in the n-th newton iteration |
Appendix A. Derivation of the Root Finding Equations
Appendix A.1. Root Finding Equations Formulated by Taking the Difference
Appendix A.2. Root Finding Equations Formulated by Taking the Quotient
Appendix B. Derivatives of the Root Finding Equations
References
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Dowling, N.E. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture and Fatigue; Pearson: London, UK, 2013. [Google Scholar]
- Nihei, M.; Heuler, P.; Boller, C.; Seeger, T. Evaluation of means tress effect on fatigue life by use of damage parameters. Int. J. Fatigue 1986, 8, 119–126. [Google Scholar] [CrossRef]
- Heuler, P. Procedures for fatigue evaluation of automotive structures. In Proceedings of the 8th Portuguese Conference on Fracture, Vila Real, Portugal, 20–22 February 2002; pp. 225–243. [Google Scholar]
- Lampman, S.R. ASM Handbook Volume 19. Fatigue and Fracture, 7th ed.; ASM International: Novelty, OH, USA, 2012. [Google Scholar] [CrossRef] [Green Version]
- Molski, K.; Glinka, G. A method of elastic-plastic stress and strain calculation at a notch root. Mater. Sci. Eng. 1981, 50, 93–100. [Google Scholar] [CrossRef]
- James, M.N.; Dimitriou, C.; Chandler, H.D. Low cycle fatigue lives of notched components. Fatigue Fract. Eng. Mater. Struct. 1989, 3, 213–225. [Google Scholar] [CrossRef]
- Ellyin, F.; Kujawski, D. Generalization of notch analysis and its extension to cyclic loading. Eng. Fract. Mech. 1989, 32, 819–826. [Google Scholar] [CrossRef]
- Newport, A.; Glinka, G. Effect of Notch-strain Calculation Method on Fatigue-crack-initiation Life Predictions. Exp. Mech. 1990, 30, 208–216. [Google Scholar] [CrossRef]
- Ye, D.; Matsuaoka, S.; Suzuki, N.; Maeda, Y. Further investigation of Neuber’s rule and the equivalent strain energy density (ESED) method. Int. J. Fatigue 2004, 26, 447–455. [Google Scholar] [CrossRef]
- Ye, D.; Hertel, O.; Vormwald, M. A unified expression of elastic-plastic notch stress-strain calculation in bodies subjected to multiaxial cyclic loading. Int. J. Solids Struct. 2008, 45, 6177–6189. [Google Scholar] [CrossRef] [Green Version]
- Kujawski, D.; Sree, P.C.R. On deviatoric interpretation of Neuber’s rule and the SWT parameter. Theor. Appl. Frac. Mech. 2014, 71, 44–50. [Google Scholar] [CrossRef]
- Ince, A.; Glinka, G. Innovative computational modelling of multiaxial fatigue analysis for notched components. Int. J. Fatigue 2016, 82, 134–145. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.-P.; Li, C.-W. Elastic-plastic stress-strain calculation at notch root under monotonic, uniaxial and multiaxial loadings. Theor. Appl. Frac. Mech. 2017, 92, 33–46. [Google Scholar] [CrossRef]
- Ball, D.L. Estimation of elastic-plastic strain response at twodimensional notches. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1895–1916. [Google Scholar] [CrossRef]
- Burghardt, R.; Wächter, M.; Esderts, A. Über den Einfluss der Abschätzung des elastisch-plastischen Beanspruchungszustandes auf die rechnerische Lebensdauervorhersage. In Proceedings of the 4. Symposium Materialtechnik, Clausthal-Zellerfeld, Germany, 25–26 February 2021; pp. 426–435. [Google Scholar] [CrossRef]
- Smith, R.N.; Watson, P.; Topper, T.H. A stress-strain parameter for the fatigue of metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Haibach, E. The influence of cyclic material properties on fatigue life prediction by amplitude transformation. Int. J. Fatigue 1979, 1, 7–16. [Google Scholar] [CrossRef]
- Bergmann, J.W.; Seeger, T. On the influence of cyclic stress-strain curves, damage parameters and various evaluation concepts on the prediction by the local approach. In Proceedings of the 2nd European Coll. on Fracture, VDI-Report of Progress, Darmstadt, Germany, 9–11 October 1979; Volume 18. No. 6. [Google Scholar]
- Heitmann, H.; Vehoff, H.; Neumann, P. Random load fatigue of steels: Service life prediction based on the behaviour of microcracks. In Proceedings of the International Conference on Application of Fracture Mechanics to Materials and Structures, Freiburg, Germany, 20–24 June 1983. [Google Scholar]
- Vormwald, M.; Seeger, T. The Consequences of short crack closure on fatigue crack growth under variable amplitude loading. Fatigue Fract. Eng. Mater. Struct. 1991, 14, 205–225. [Google Scholar] [CrossRef]
- Dowling, N.E. Mean-stress effects in strain-life fatigue. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 1004–1019. [Google Scholar] [CrossRef]
- Ince, A.; Glinka, G. A modification of Morrow and Smith-Watson-Topper mean stress correction models. Fatigue Fract. Eng. Mater. Struct. 2011, 34, 854–867. [Google Scholar] [CrossRef]
- Vormwald, M. Classification of Load Sequence Effects in Metallic Structures. Procedia Eng. 2015, 101, 534. [Google Scholar] [CrossRef] [Green Version]
- Fiedler, M.; Wächter, M.; Varfolomeev, I.; Esderts, A.; Vormwald, M. Rechnerischer Festigkeitsnachweis für Maschinenbauteile unter Expliziter Erfassung Nichtlinearen Werkstoffverformungsverhaltens, 1st ed.; VDMA-Verlag: Frankfurt, Germany, 2019. [Google Scholar]
- Fiedler, M.; Vormwald, M. Introduction to the new FKM guideline which considers nonlinear material behaviour. MATEC Web Conf. 2018, 165, 10014. [Google Scholar] [CrossRef]
- Neuber, H. Theory of Stress Concentration for Shear-Strained Prismatical Bodies with Arbitary Nonlinear Stress-Strain Law. Trans. ASME J. Appl. Mech. 1961, 28, 544–550. [Google Scholar] [CrossRef]
- Seeger, T.; Heuler, P. Generalized application of Neuber’s rule. J. Test. Eval. 1980, 8, 199–204. [Google Scholar] [CrossRef]
- Bergmann, J. Zur Betriebsfestigkeitsbemessung Gekerbter Bauteile auf der Grundlage der Örtlichen Beanspruchungen. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 1983. [Google Scholar]
- Seeger, T.; Beste, A. Zur Weiterentwicklung von Näherungsformeln für die Berechnung von Kerbbeanspruchungen im elastisch-plastischen Bereich. Kerben Bruch. VDI-Fortschr. 1977, 18, 1–56. [Google Scholar]
- Amstutz, H.; Seeger, T. Elastic-plastic finite element calculations of notched plates. In Proceedings of the 1st International Conference on Numerical Methods in Fracture Mechanics, University College Swansea, Swansea, UK, 9–13 January 1978; pp. 581–594. [Google Scholar]
- Seeger, T.; Beste, A.; Amstutz, H. Elastic-plastic stress-strain behaviour of monotonic and cyclic loaded notched plates. In Proceedings of the Fracture 1977 Fourth International Conference on Fracture, Waterloo, ON, Canada, 19–24 June 1977; Volume 2, pp. 943–951. [Google Scholar]
- Clormann, U.H.; Seeger, T. RAINFLOW-HCM Ein Zählverfahren für Betriebsfestigkeitsnachweise auf werkstoffmechanischer Grundlage. Stahlbau 1986, 55, 65–71. [Google Scholar]
- Masing, G. Eigenspannungen und Verfestigung beim Messing. In Proceedings of the 2nd International Congress of Applied Mechanics, Zürich, Switzerland, 12–17 September 1926; pp. 332–335. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; Technical Note No. 902; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943.
- Wächter, M.; Esderts, A. Contribution to the Evaluation of Stress-Strain and Strain-Life Curves. In Proceedings of the Symposium on Fatigue and Fracture Test. Planning, Test. Data Acquisitions and Analysis ASTM STP1598, San Antonio, TX, USA, 4–5 May 2017; ASTM International: West Conshohocken, PA, USA, 2017; pp. 151–185. [Google Scholar] [CrossRef]
- SEP 1240. Testing and Documentation Guideline for the Experimental Determination of Mechanical Properties of Steel Sheets for CAE-Calculations; VDEh: Düsseldorf, Germany, 2006. [Google Scholar]
- Wächter, M. Zur Ermittlung von zyklischen Werkstoffkennwerten und Schädigungsparameterwöhlerlinien. Ph.D. Thesis, Technische Universität Clausthal, Clausthal-Zellerfeld, Germany, 2016. [Google Scholar] [CrossRef]
- Wächter, M.; Esderts, A. On the estimation of cyclic material properties—Part 2: Introduction of a new estimation method. Mater. Test. 2018, 60, 953–959. [Google Scholar] [CrossRef]
- Burghardt, R.; Wächter, M.; Masendorf, L.; Esderts, A. Estimation of elastic-plastic notch strains and stresses using artificial neural networks. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 2718–2735. [Google Scholar] [CrossRef]
- Rennert, R.; Kullig, E.; Vormwald, M.; Esderts, A.; Luke, M. Rechnerischer Festigkeitsnachweis für Maschinenbauteile, 7th ed.; VDMA-Verlag: Frankfurt, Germany, 2020. [Google Scholar]
- Kujawski, D.; Ellyin, F. An energy-based methods for stress and strain calculation at notches. In Proceedings of the Transactions of the 8th International Conference on Structural Mechanics in Reactor Technology, Amsterdam, The Netherlands, 19–23 August 1985; pp. 173–178. [Google Scholar]
- Burghardt, R.; Wächter, M.; Esderts, A. Determination of Local Stresses and Strains within the Notch Strain Approach: Efficient Implementation of Notch Root Approximations—Software Code (v1.0). Zenodo. 2021. Available online: https://zenodo.org/record/5552576#.YYOZYRwRV9B (accessed on 6 October 2021).






| Parameter | Value |
|---|---|
| K’ in MPa | 902.2915 |
| n’ | 0.187 |
| Kp | 1.7 |
| leading to numerical stable behavior in MPa | 110.022454508070 |
| leading to numerical unstable behavior in MPa | 110.022454507071 |
| Parameter | Symbol | Range | Number of Equidistant Steps in the Range |
|---|---|---|---|
| Limit load factor | Kp | 1–8 | 10 |
| Tensile strength | Rm | 300–1200 MPa | 100 |
| (resulting) Cyclic hardening coefficient | K’ | 640–3500 MPa | (same as Rm) |
| (resulting) Cyclic hardening exponent | n’ | 0.187 | 1 |
| (resulting) Cyclic yield strength | 200–1100 MPa | (same as Rm) | |
| Maximum linear-elastic stress range | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burghardt, R.; Masendorf, L.; Wächter, M.; Esderts, A. Determination of Local Stresses and Strains within the Notch Strain Approach: Efficient Implementation of Notch Root Approximations. Appl. Sci. 2021, 11, 10339. https://doi.org/10.3390/app112110339
Burghardt R, Masendorf L, Wächter M, Esderts A. Determination of Local Stresses and Strains within the Notch Strain Approach: Efficient Implementation of Notch Root Approximations. Applied Sciences. 2021; 11(21):10339. https://doi.org/10.3390/app112110339
Chicago/Turabian StyleBurghardt, Ralf, Lukas Masendorf, Michael Wächter, and Alfons Esderts. 2021. "Determination of Local Stresses and Strains within the Notch Strain Approach: Efficient Implementation of Notch Root Approximations" Applied Sciences 11, no. 21: 10339. https://doi.org/10.3390/app112110339
APA StyleBurghardt, R., Masendorf, L., Wächter, M., & Esderts, A. (2021). Determination of Local Stresses and Strains within the Notch Strain Approach: Efficient Implementation of Notch Root Approximations. Applied Sciences, 11(21), 10339. https://doi.org/10.3390/app112110339






