Experimental and Numerical Analysis of 3D Printed Polymer Tetra-Petal Auxetic Structures under Compression
Abstract
:1. Introduction
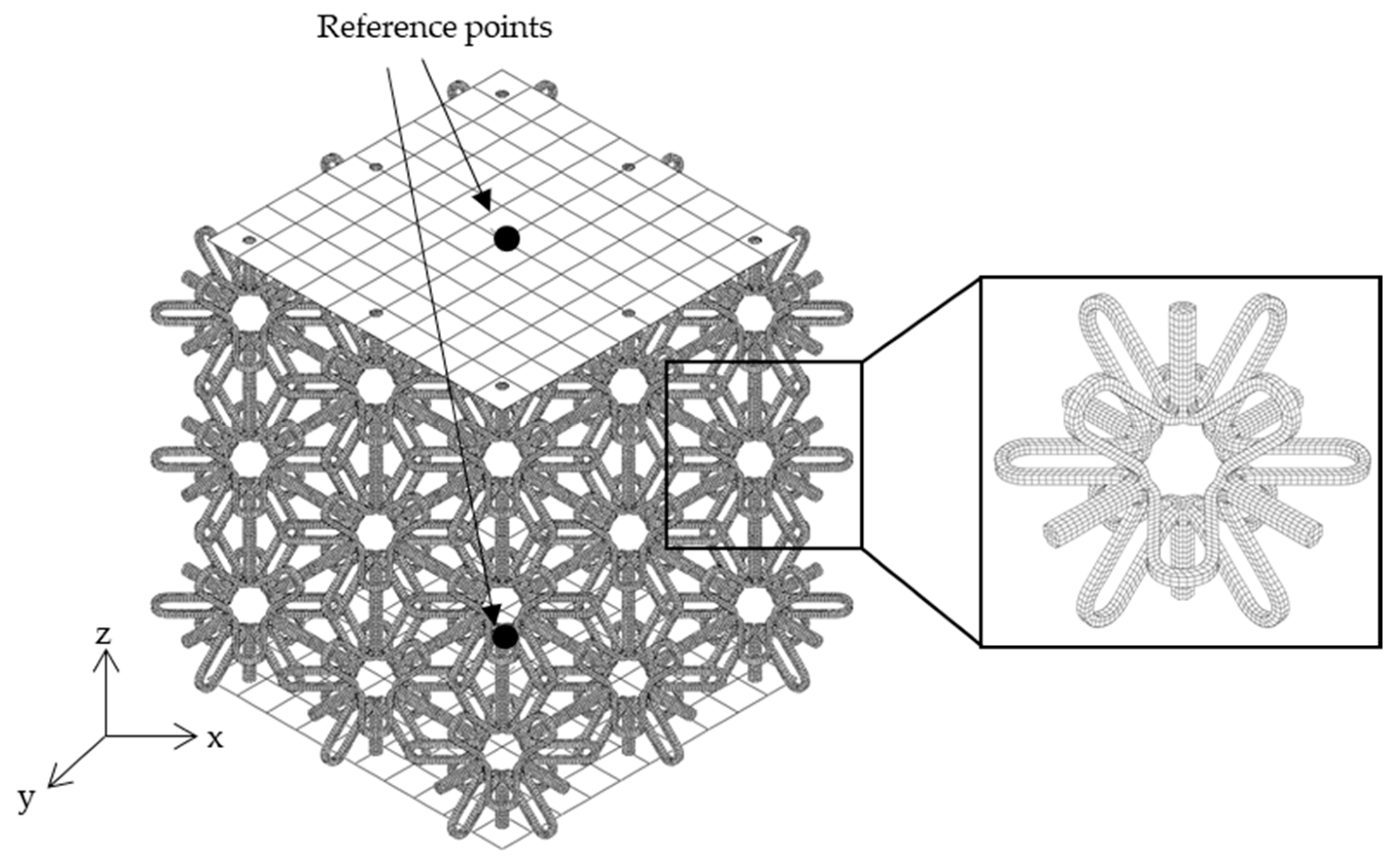
2. Simulation-Driven Parametric Design of Auxetic Structures
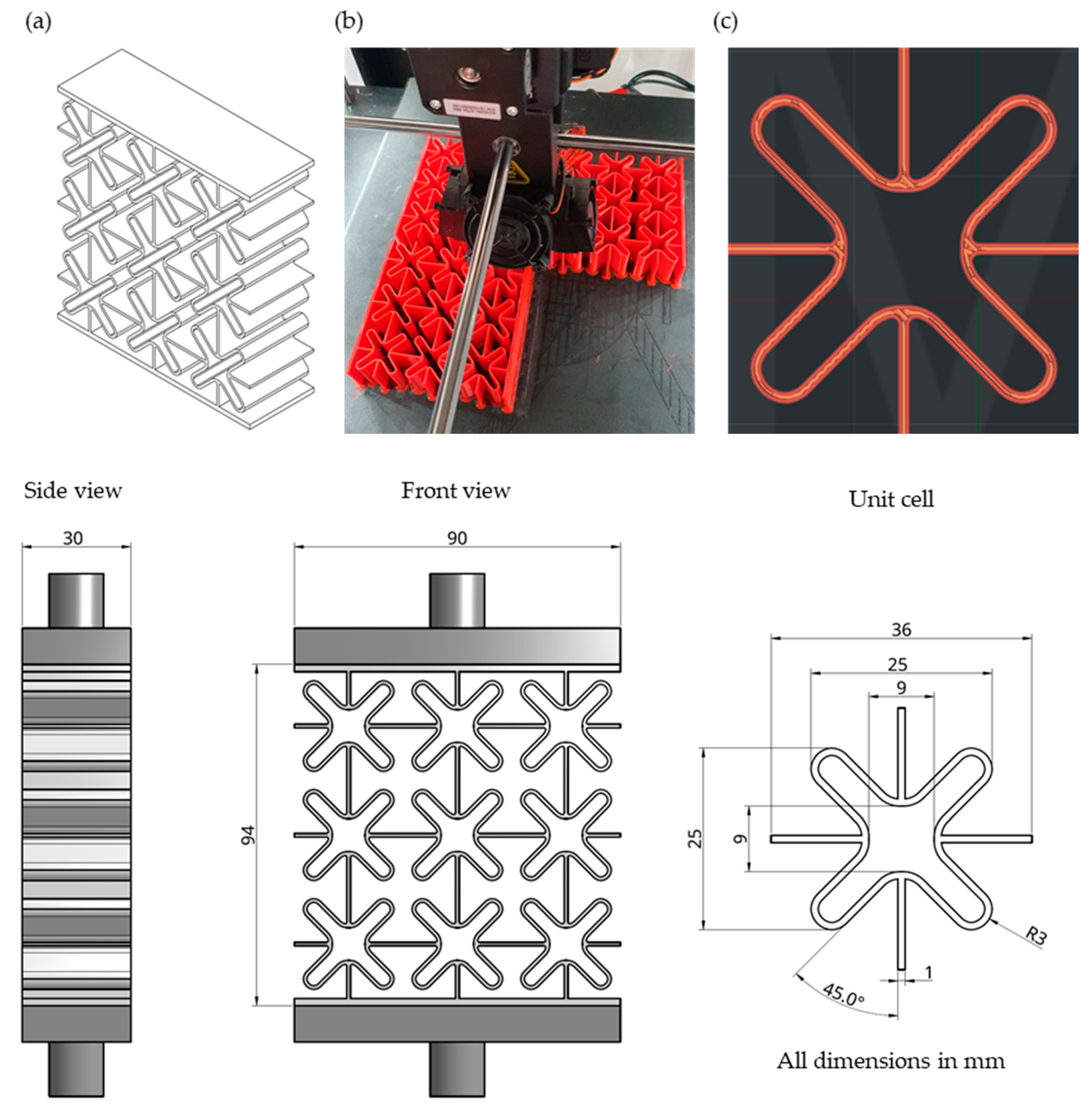
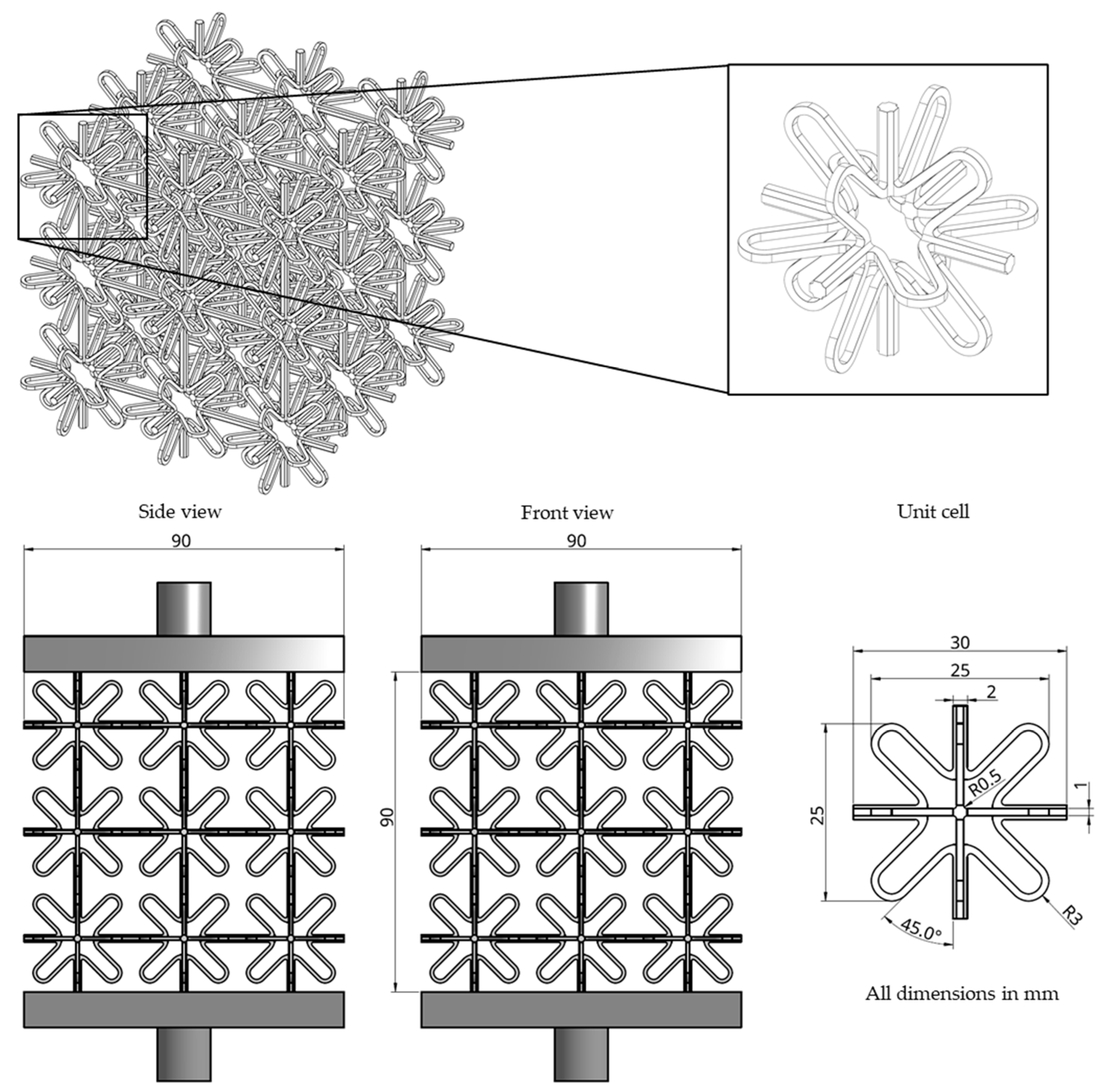
3. Fabrication of Prototypes Sample by Means of 3D Printing
4. Experimental Mechanical Testing of 3D Printed Auxetic Structures
4.1. Experimental Setup
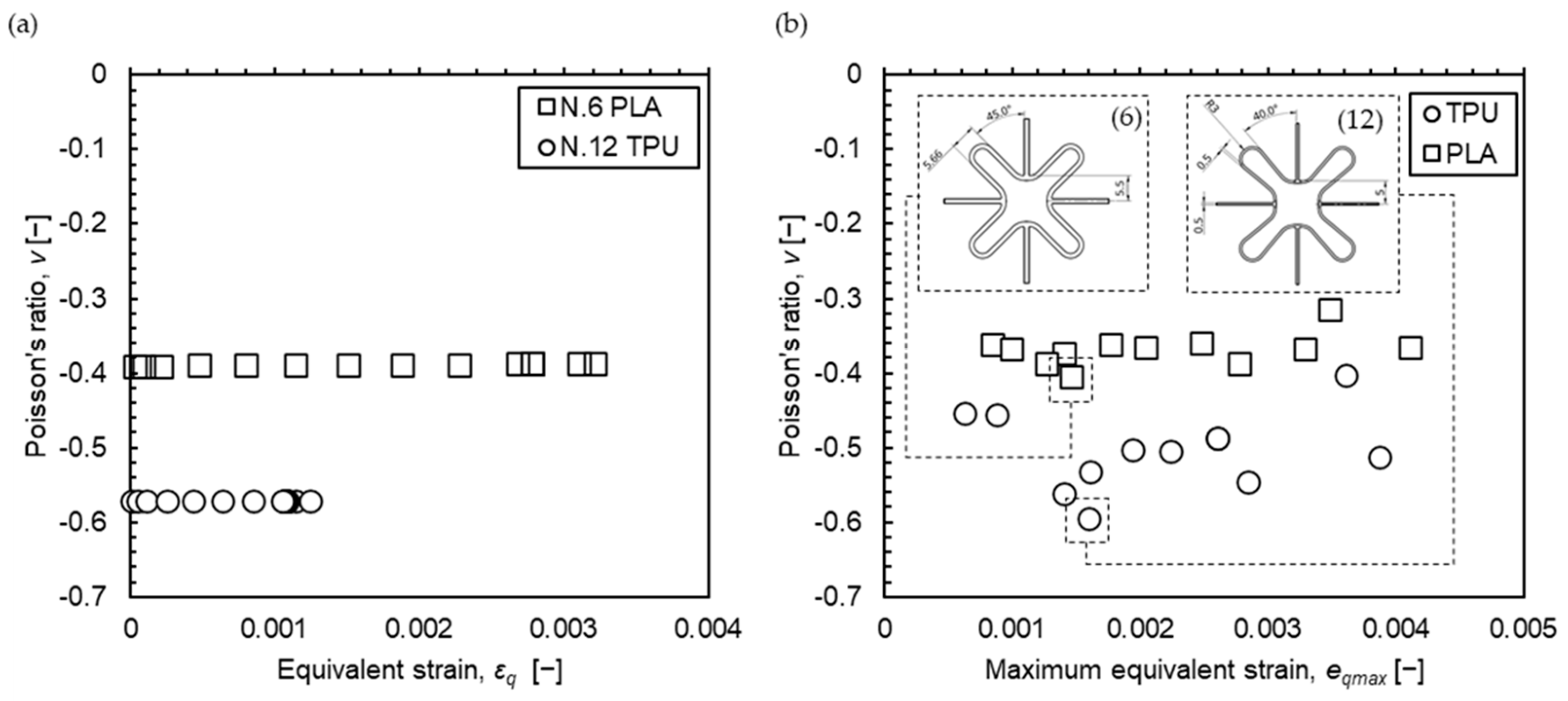
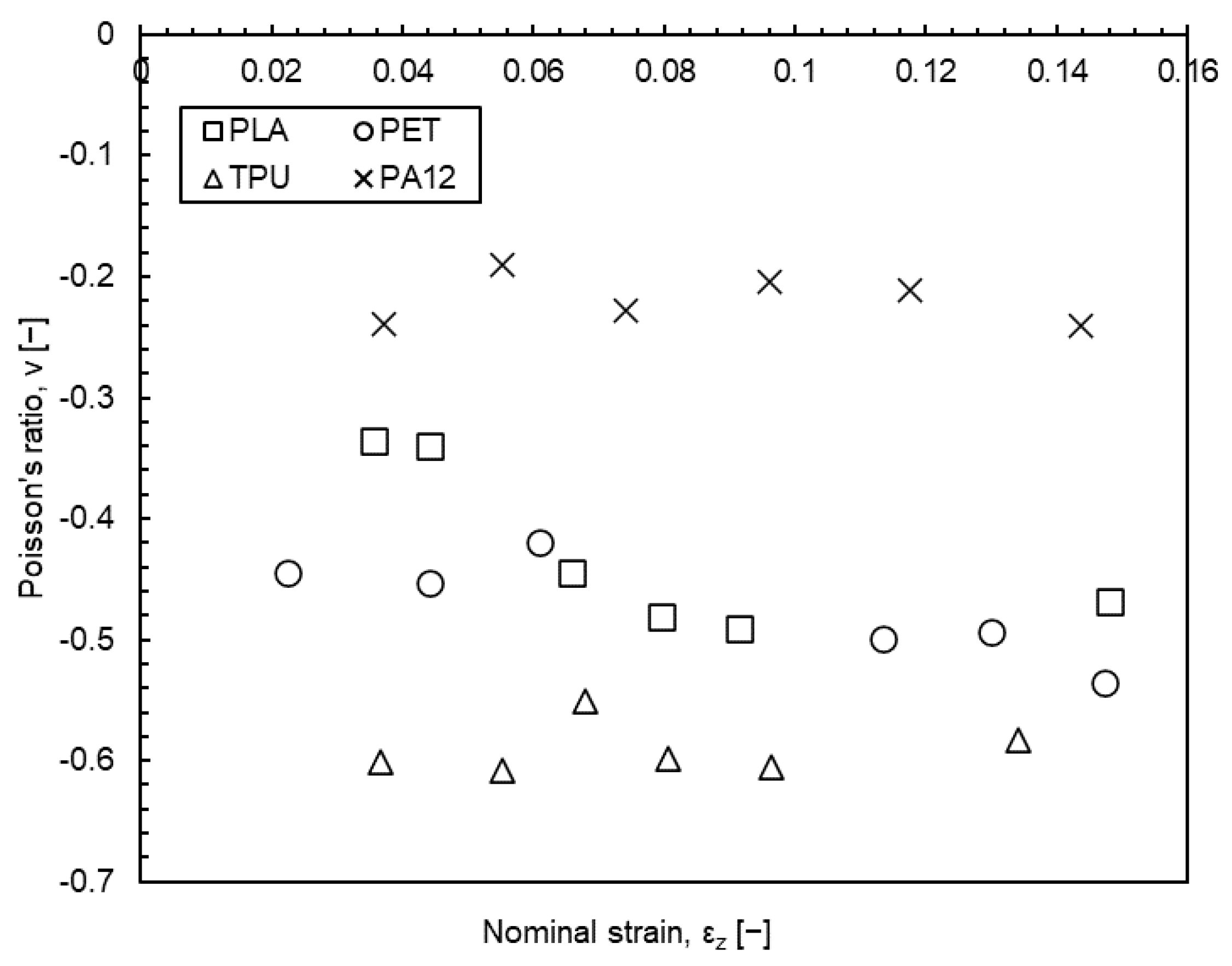
4.2. Experimental Results
5. Numerical FE Modelling of Auxetic Systems’ Mechanical Behavior
6. Discussion and Conclusions
7. Outlook and Future Research
- Use the rendered knowledge for the 3D printing of auxetic structures with metallic alloys by means of powder bed fusion for lightweight energy absorption applications and for human bone implants with adapted stiffness properties;
- Implement material properties in the finite element model derived from the experimental mechanical characterization of samples created by the particular 3D printing process, i.e., FDM or SLS, with specific process parameters, in order to replicate irregularities and possible anisotropy in the real built-up material;
- Enhance the finite element model definition to include contact conditions between and within the auxetic unit cells, plasticity behavior, and fracture criteria;
- Perform experimental testing at higher impact speeds to characterize the auxetic behavior at high strain rates.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Imbalzano, G.; Linforth, S.; Ngo, T.D.; Lee, P.V.S.; Tran, P. Blast resistance of auxetic and honeycomb sandwich panels: Comparisons and parametric designs. Compos. Struct. 2018, 183, 242–261. [Google Scholar] [CrossRef]
- Castanie, B.; Bouvet, C.; Ginot, M. Review of composite sandwich structure in aeronautic applications. Compos. Part C Open Access 2020, 1, 100004. [Google Scholar] [CrossRef]
- Tarlochan, F. Sandwich Structures for Energy Absorption Applications: A Review. Materials 2021, 14, 4731. [Google Scholar] [CrossRef]
- Hunady, R. A Sensitivity Analysis of the Dynamic Behavior of Aluminium Honeycomb Sandwich Panels. Am. J. Mech. Eng. 2016, 4, 236–240. [Google Scholar]
- Strek, T.; Jopek, H.; Nienartowicz, M. Dynamic response of sandwich panels with auxetic cores. Phys. Status Solidi 2015, 252, 1540–1550. [Google Scholar] [CrossRef]
- Xiao, D.; Chen, X.; Li, Y.; Wu, W.; Fang, D. The structure response of sandwich beams with metallic auxetic honeycomb cores under localized impulsive loading-experiments and finite element analysis. Mater. Des. 2019, 176, 107840. [Google Scholar] [CrossRef]
- Photiou, D.; Prastiti, N.; Sarris, E.; Constantinides, G. On the conical indentation response of elastic auxetic materials: Effects of Poisson’s ratio, contact friction and cone angle. Int. J. Solids Struct. 2016, 81, 33–42. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Zadpoor, A.A. Auxetic mechanical metamaterials. RSC Adv. 2017, 7, 5111–5129. [Google Scholar] [CrossRef] [Green Version]
- Foster, L.; Peketi, P.; Allen, T.; Senior, T.; Duncan, O.; Alderson, A. Application of Auxetic Foam in Sports Helmets. Appl. Sci. 2018, 8, 354. [Google Scholar] [CrossRef] [Green Version]
- Duncan, O.; Shepherd, T.; Moroney, C.; Foster, L.; Venkatraman, P.; Winwood, K.; Allen, T.; Alderson, A. Review of Auxetic Materials for Sports Applications: Expanding Options in Comfort and Protection. Appl. Sci. 2018, 8, 941. [Google Scholar] [CrossRef] [Green Version]
- Imbalzano, G.; Tran, P.; Ngo, T.D.; Lee, P.V. Three-dimensional modelling of auxetic sandwich panels for localised impact resistance. J. Sandw. Struct. Mater. 2017, 19, 291–316. [Google Scholar] [CrossRef]
- Guo, C.; Zhao, D.; Liu, Z.; Ding, Q.; Gao, H.; Yan, Q.; Sun, Y.; Ren, F. The 3D-Printed Honeycomb Metamaterials Tubes with Tunable Negative Poisson’s Ratio for High-Performance Static and Dynamic Mechanical Properties. Materials 2021, 14, 1353. [Google Scholar] [CrossRef]
- Dudek, K.K.; Attard, D.; Gatt, R.; Grima-Cornish, J.N.; Grima, J.N. The Multidirectional Auxeticity and Negative Linear Compressibility of a 3D Mechanical Metamaterial. Materials 2020, 13, 2193. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Yu, T.; Wang, X. Study on a Chiral Structure with Tunable Poisson’s Ratio. Materials 2021, 14, 3338. [Google Scholar] [CrossRef]
- Photiou, D. Computational Modeling of Nanoindentation on Emerging Materials: Auxetics, Hard Thin Films and Cohesive-Frictional Solids. Ph.D. Thesis, Cyprus University of Technology, Limassol, Cyprus, 2019. [Google Scholar]
- Bilski, M.; Pigłowski, P.M.; Wojciechowski, K.W. Extreme Poisson’s Ratios of Honeycomb, Re-Entrant, and Zig-Zag Crystals of Binary Hard Discs. Symmetry 2021, 13, 1127. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids; Cambridge University Press: Cambridge, UK, 1997; ISBN 9781139878326. [Google Scholar]
- Lakes, R. Deformation mechanisms in negative Poisson’s ratio materials: Structural aspects. J. Mater. Sci. 1991, 26, 2287–2292. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Non-chiral, molecular model of negative Poisson ratio in two dimensions. J. Phys. A Math. Gen. 2003, 36, 11765–11778. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Alderson, A.; Evans, K.E. Rotation and dilation deformation mechanisms for auxetic behaviour in the $α$-cristobalite tetrahedral framework structure. Phys. Chem. Miner. 2001, 28, 711–718. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating triangles. J. Mater. Sci. 2006, 41, 3193–3196. [Google Scholar] [CrossRef]
- Grima, J.N.; Chetcuti, E.; Manicaro, E.; Attard, D.; Camilleri, M.; Gatt, R.; Evans, K.E. On the auxetic properties of generic rotating rigid triangles. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 810–830. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Ellul, B.; Chetcuti, E. Auxetic behaviour in non-crystalline materials having star or triangular shaped perforations. J. Non-Cryst. Solids 2010, 356, 1980–1987. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Negative Poisson’s ratios from rotating rectangles. Comput. Methods Sci. Technol. 2004, 10, 137–145. [Google Scholar] [CrossRef] [Green Version]
- Grima, J.N.; Gatt, R.; Farrugia, P.-S. On the properties of auxetic meta-tetrachiral structures. Phys. Status Solidi 2008, 245, 511–520. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Alderson, A.; Evans, K.E. On the origin of auxetic behaviour in the silicate α-cristobalite. J. Mater. Chem. 2005, 15, 4003. [Google Scholar] [CrossRef]
- Grima, J.N.; Manicaro, E.; Attard, D. Auxetic behaviour from connected different-sized squares and rectangles. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 439–458. [Google Scholar] [CrossRef] [Green Version]
- Narojczyk, J.W.; Wojciechowski, K.W. Elastic properties of degenerate f.c.c. crystal of polydisperse soft dimers at zero temperature. J. Non-Cryst. Solids 2010, 356, 2026–2032. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G.; Hoover, C.G. Searching for auxetics with DYNA3D and ParaDyn. Phys. Status Solidi 2005, 242, 585–594. [Google Scholar] [CrossRef] [Green Version]
- Alderson, A.; Alderson, K.L.; Attard, D.; Evans, K.E.; Gatt, R.; Grima, J.N.; Miller, W.; Ravirala, N.; Smith, C.W.; Zied, K. Elastic constants of 3-, 4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading. Compos. Sci. Technol. 2010, 70, 1042–1048. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wang, Q.; Yang, Z.; Lu, Z. Novel auxetic structures with enhanced mechanical properties. Extrem. Mech. Lett. 2019, 27, 59–65. [Google Scholar] [CrossRef]
- Harris, J.A.; McShane, G.J. Metallic stacked origami cellular materials: Additive manufacturing, properties, and modelling. Int. J. Solids Struct. 2020, 185–186, 448–466. [Google Scholar] [CrossRef]
- Grima, J.N.; Mizzi, L.; Azzopardi, K.M.; Gatt, R. Auxetic Perforated Mechanical Metamaterials with Randomly Oriented Cuts. Adv. Mater. 2016, 28, 385–389. [Google Scholar] [CrossRef] [PubMed]
- Rafsanjani, A.; Pasini, D. Bistable auxetic mechanical metamaterials inspired by ancient geometric motifs. Extrem. Mech. Lett. 2016, 9, 291–296. [Google Scholar] [CrossRef] [Green Version]
- Babaee, S.; Shim, J.; Weaver, J.C.; Chen, E.R.; Patel, N.; Bertoldi, K. 3D Soft Metamaterials with Negative Poisson’s Ratio. Adv. Mater. 2013, 25, 5044–5049. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Garcia, A.F.; Du Plessis, A.; Rans, C.; Mirzaali, M.J.; Zadpoor, A.A. Fatigue performance of auxetic meta-biomaterials. Acta Biomater. 2021, 126, 511–523. [Google Scholar] [CrossRef]
- Khan, S.Z.; Masood, S.H.; Cottam, R. Mechanical properties in tensile loading of H13 re-entrant honeycomb auxetic structure manufactured by direct metal deposition. MATEC Web Conf. 2015, 34, 01004. [Google Scholar] [CrossRef]
- Meena, K.; Singamneni, S. A new auxetic structure with significantly reduced stress concentration effects. Mater. Des. 2019, 173, 107779. [Google Scholar] [CrossRef]
- Wang, Z.; Luan, C.; Liao, G.; Liu, J.; Yao, X.; Fu, J. Progress in Auxetic Mechanical Metamaterials: Structures, Characteristics, Manufacturing Methods, and Applications. Adv. Eng. Mater. 2020, 22, 2000312. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, G.; You, Z. Large deformation and energy absorption of additively manufactured auxetic materials and structures: A review. Compos. Part B Eng. 2020, 201, 108340. [Google Scholar] [CrossRef]
- Wang, Z.-P.; Poh, L.H.; Dirrenberger, J.; Zhu, Y.; Forest, S. Isogeometric shape optimization of smoothed petal auxetic structures via computational periodic homogenization. Comput. Methods Appl. Mech. Eng. 2017, 323, 250–271. [Google Scholar] [CrossRef] [Green Version]
- Koutsianitis, P.I.; Tairidis, G.K.; Stavroulakis, G.E. Shunted piezoelectric patches on auxetic microstructures for the enhancement of band gaps. Arch. Appl. Mech. 2021, 91, 739–751. [Google Scholar] [CrossRef]
- Koutsianitis, P.I.; Tairidis, G.K.; Drosopoulos, G.A.; Stavroulakis, G.E. Conventional and star-shaped auxetic materials for the creation of band gaps. Arch. Appl. Mech. 2019, 89, 2545–2562. [Google Scholar] [CrossRef]
- Dassault Systèmes. ABAQUS: Theory Manual; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2011; Available online: http://130.149.89.49:2080/v6.11/pdf_books/THEORY.pdf (accessed on 30 October 2021).
- Zhao, Y.; Chen, Y.; Zhou, Y. Novel mechanical models of tensile strength and elastic property of FDM AM PLA materials: Experimental and theoretical analyses. Mater. Des. 2019, 181, 108089. [Google Scholar] [CrossRef]
- Lindberg, A.; Alfthan, J.; Pettersson, H.; Flodberg, G.; Yang, L. Mechanical performance of polymer powder bed fused objects—FEM simulation and verification. Addit. Manuf. 2018, 24, 577–586. [Google Scholar] [CrossRef]






| Technology | Auxetic Type | Material |
|---|---|---|
| Polyjet | 2D/3D chiral, 2D re-entrant, missing ribs | Veroblue, VeroWhite, TangoPlus, VeroGray |
| FDM | 2D/3D chiral, 2D re-entrant | PLA |
| SLA | 2D/3D chiral, 2D re-entrant | Tough resin, Photosensitive resin |
| SLS | 2D/3D chiral | Polyamide 12 |
| SLM | 3D chiral, 3D re-entrant | AlSi10Mg, SS 316L, Ti56Ni44 |
| EBM | 3D re-entrant | Ti-6Al-4V |
| Von Mises Plastic Material | Hyperelastic Mooney–Rivlin Material | ||
|---|---|---|---|
| Property | Value | Property | Value |
| Density, | 1240 kg/m3 | Density, | 1200 kg/m3 |
| Elastic modulus, | 973 MPa | Poisson’s ratio, | 0.45 |
| Poisson’s ratio, | 0.36 | Tensile strength, | 30 MPa |
| Yield strength, | 15.7 MPa | Mooney–Rivlin coef. | −1.1 MPa |
| Mooney–Rivlin coef. | 5.2 MPa | ||
| Mooney–Rivlin coef. | −846.5 MPa | ||
| Mooney–Rivlin coef. | 451.7 MPa | ||
| Mooney–Rivlin coef. | 398.7 MPa | ||
| Auxetic Sample | 3D Printing Method | Geometry |
|---|---|---|
| PLA | FDM | 2D |
| PET | FDM | 2D |
| TPU | FDM | 2D |
| PA12 | SLS | 3D |
| Duraform Flex | SLS | 3D |
| Process Parameter | Materials | Units | ||
|---|---|---|---|---|
| PLA | PETG | TPU | ||
| Filament diameter | 1.75 | 1.75 | 1.75 | mm |
| Nozzle diameter | 0.4 | 0.4 | 0.4 | mm |
| Extrusion width * | 0.44 | 0.44 | 0.44 | mm |
| Nozzle temperature | 205 | 240 | 225 | °C |
| Bed temperature | 60 | 80 | 60 | °C |
| Printing speed | 50 | 45 | 25 | mm/s |
| Layer height | 0.2 | 0.2 | 0.2 | mm |
| Infill density | 100 | 100 | 100 | % |
| Process Parameter | Value | Units |
|---|---|---|
| Machine type | EOS P 396 | - |
| Material (powder) | EOS PA2200 (PA12) | - |
| Laser type | CO2 | - |
| Laser power | 40 | W |
| Laser spot diameter | F-theta lens, Standard focus | μm |
| Laser speed | 4000 | mm/s |
| Layer thickness | 100 | μm |
| Hatch distance | 0.3 | mm |
| Process Parameter | Value | Units |
|---|---|---|
| Machine type | DTM Sinterstation 2500 Plus | - |
| Material (powder) | Duraform FLEX, infiltrated | - |
| Laser type | CO2 | - |
| Laser power | 30 | W |
| Laser spot diameter | 300 | μm |
| Laser speed | 5000 | mm/s |
| Layer thickness | 150 | μm |
| Hatch distance | 0.3 | mm |
| Auxetic Sample | Stiffness (N/mm) | Max. Force (N) | Aver. Poisson’s Ratio (-) | Young’s Modulus (N/mm2) | Tensile Strength (N/mm2) |
|---|---|---|---|---|---|
| 2D Auxetic Samples made by FDM | |||||
| PLA | 28.5 | 480 | −0.43 | 2636 | 46.6 |
| PET | 16.3 | 320 | −0.47 | 1472 | 31.9 |
| TPU | 0.5 | 65 | −0.59 | 9.4 | 29.0 |
| 3D Auxetic Sample made by SLS | |||||
| PA12 | 1.6 | 34 | −0.22 | 1700 | 48.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Photiou, D.; Avraam, S.; Sillani, F.; Verga, F.; Jay, O.; Papadakis, L. Experimental and Numerical Analysis of 3D Printed Polymer Tetra-Petal Auxetic Structures under Compression. Appl. Sci. 2021, 11, 10362. https://doi.org/10.3390/app112110362
Photiou D, Avraam S, Sillani F, Verga F, Jay O, Papadakis L. Experimental and Numerical Analysis of 3D Printed Polymer Tetra-Petal Auxetic Structures under Compression. Applied Sciences. 2021; 11(21):10362. https://doi.org/10.3390/app112110362
Chicago/Turabian StylePhotiou, Demetris, Stelios Avraam, Francesco Sillani, Fabrizio Verga, Olivier Jay, and Loucas Papadakis. 2021. "Experimental and Numerical Analysis of 3D Printed Polymer Tetra-Petal Auxetic Structures under Compression" Applied Sciences 11, no. 21: 10362. https://doi.org/10.3390/app112110362
APA StylePhotiou, D., Avraam, S., Sillani, F., Verga, F., Jay, O., & Papadakis, L. (2021). Experimental and Numerical Analysis of 3D Printed Polymer Tetra-Petal Auxetic Structures under Compression. Applied Sciences, 11(21), 10362. https://doi.org/10.3390/app112110362







