Estimation of Burst Pressure of PVC Pipe Using Average Shear Stress Yield Criterion: Experimental and Numerical Studies
Abstract
:1. Introduction
2. Theoretical Analysis
2.1. The Average Shear Stress Yield Criterion
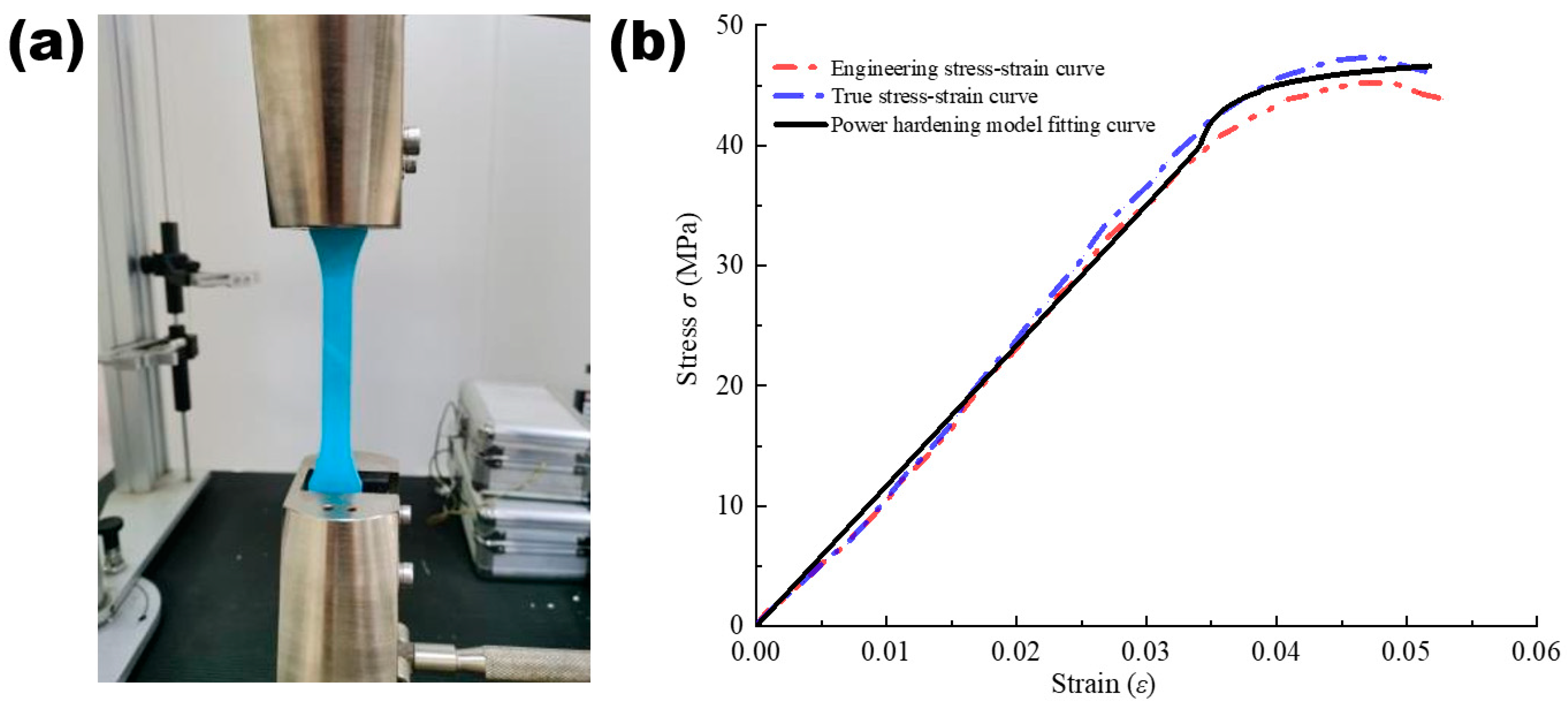
2.2. Stress–Strain Relationship of PVC
2.3. Burst Pressure Solution Based ASSY
3. Experimental Study
3.1. Tensile Testing
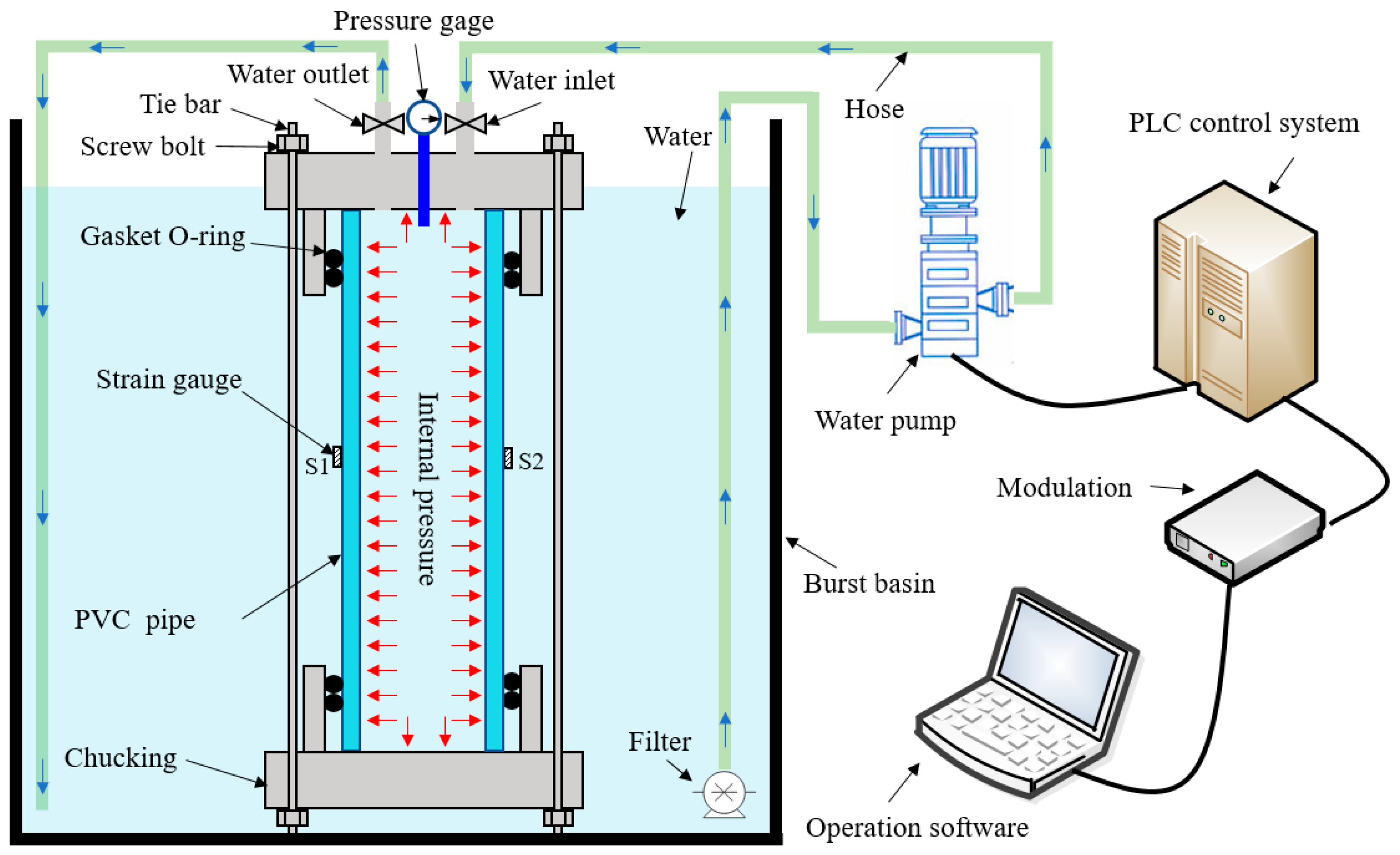
3.2. Burst Tests
4. Finite Element Modeling
4.1. Tool Geometry and Mesh
4.2. Definition of Burst Pressure
5. Result Analysis
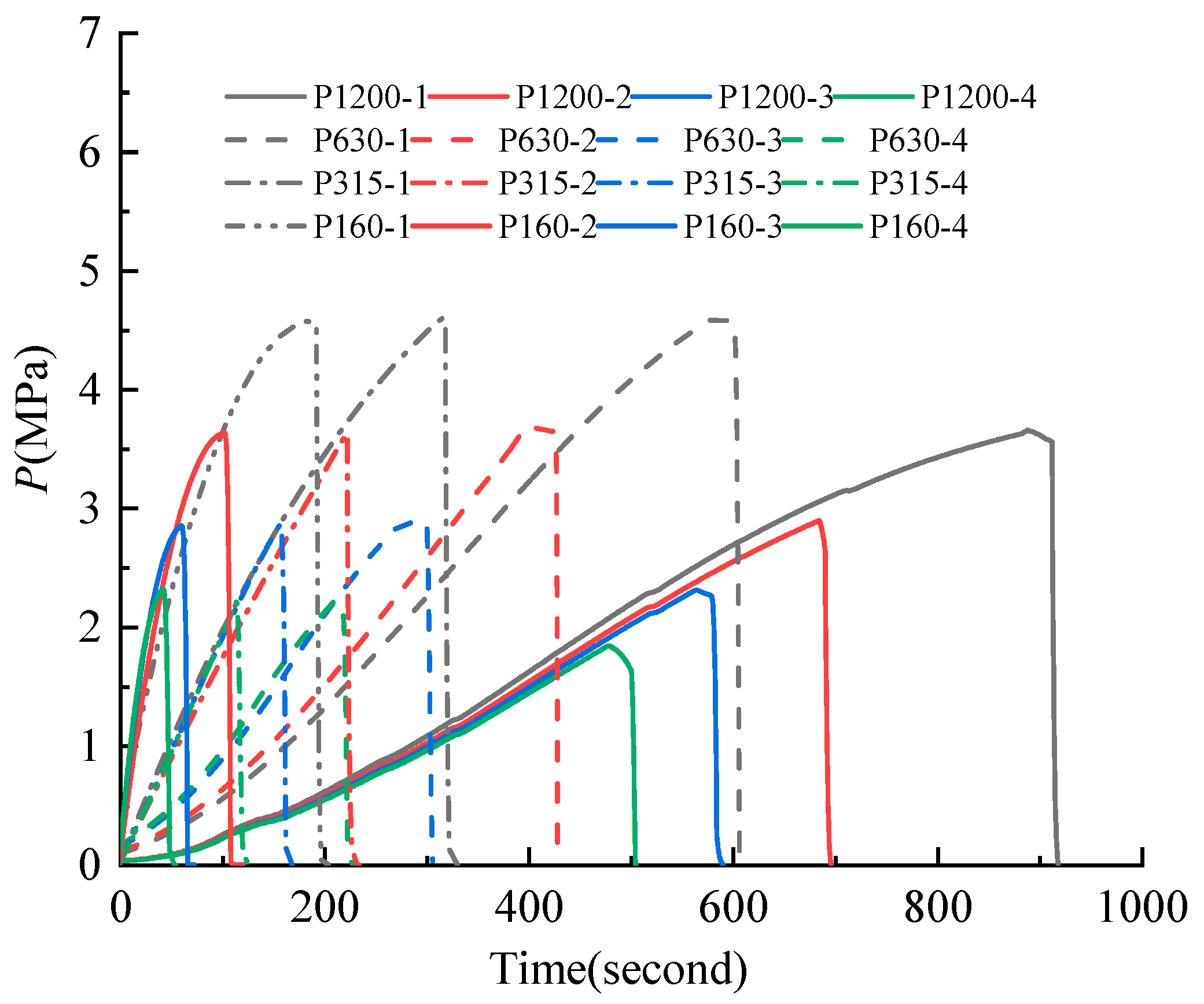
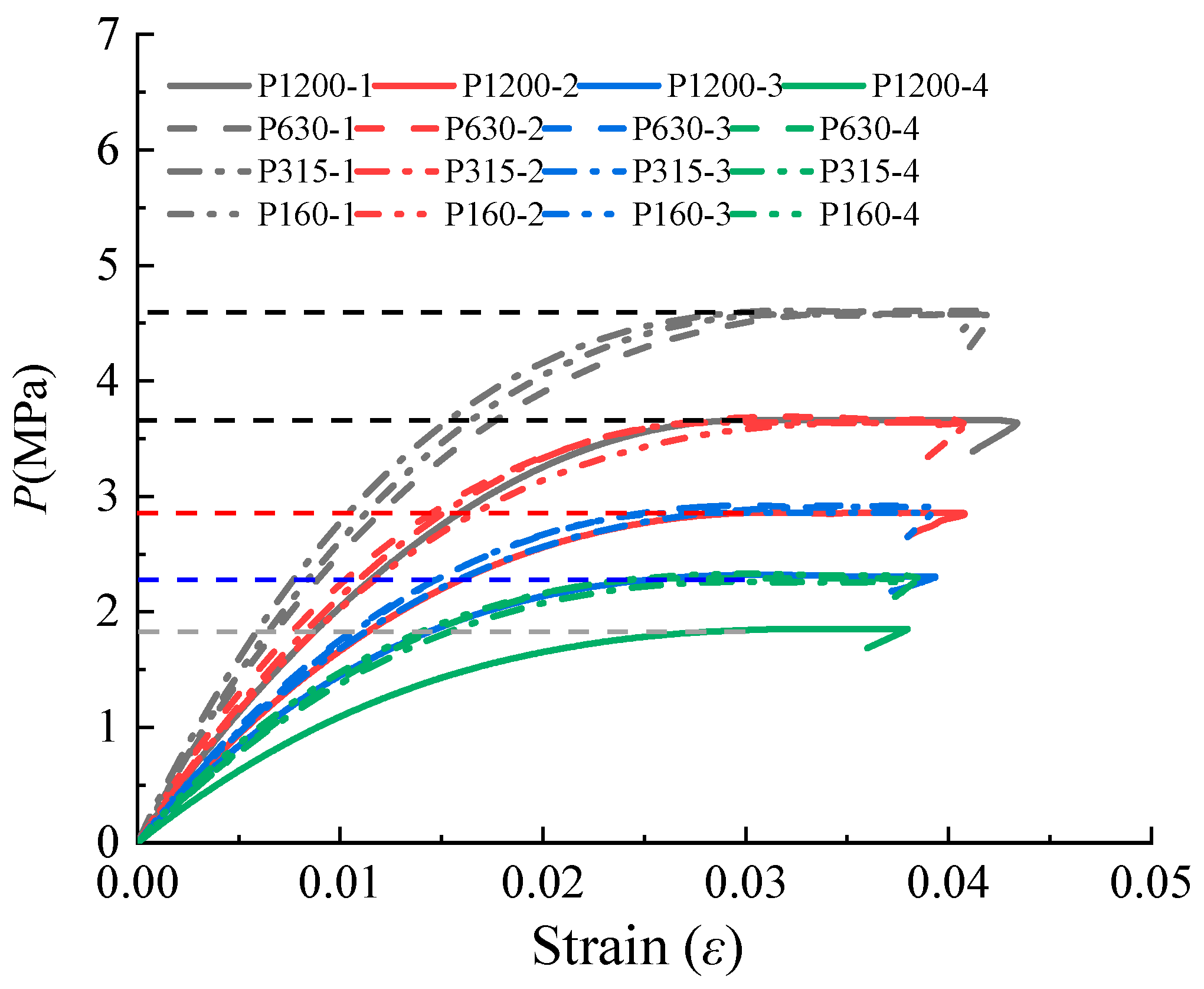
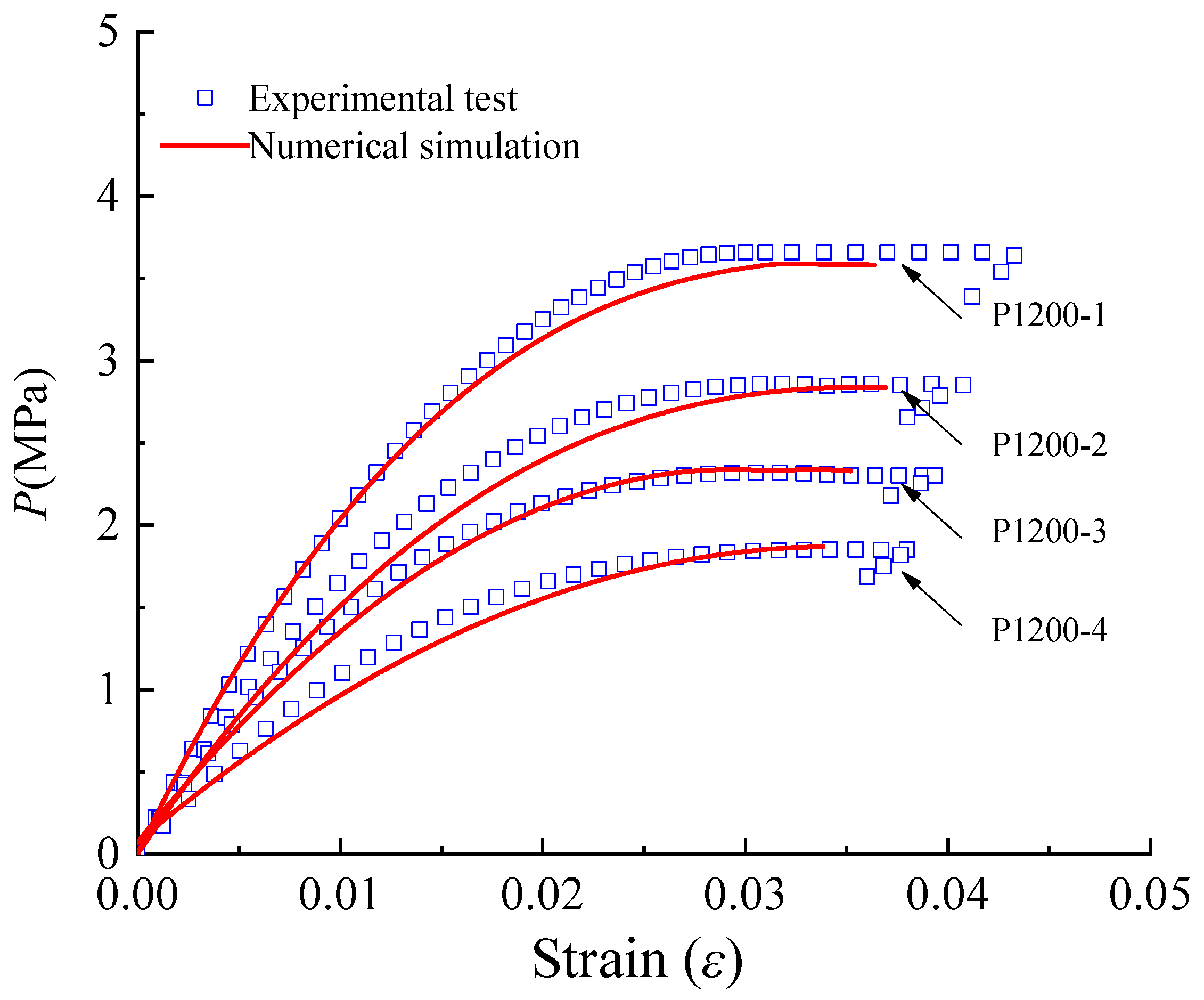
5.1. Burst Test Results
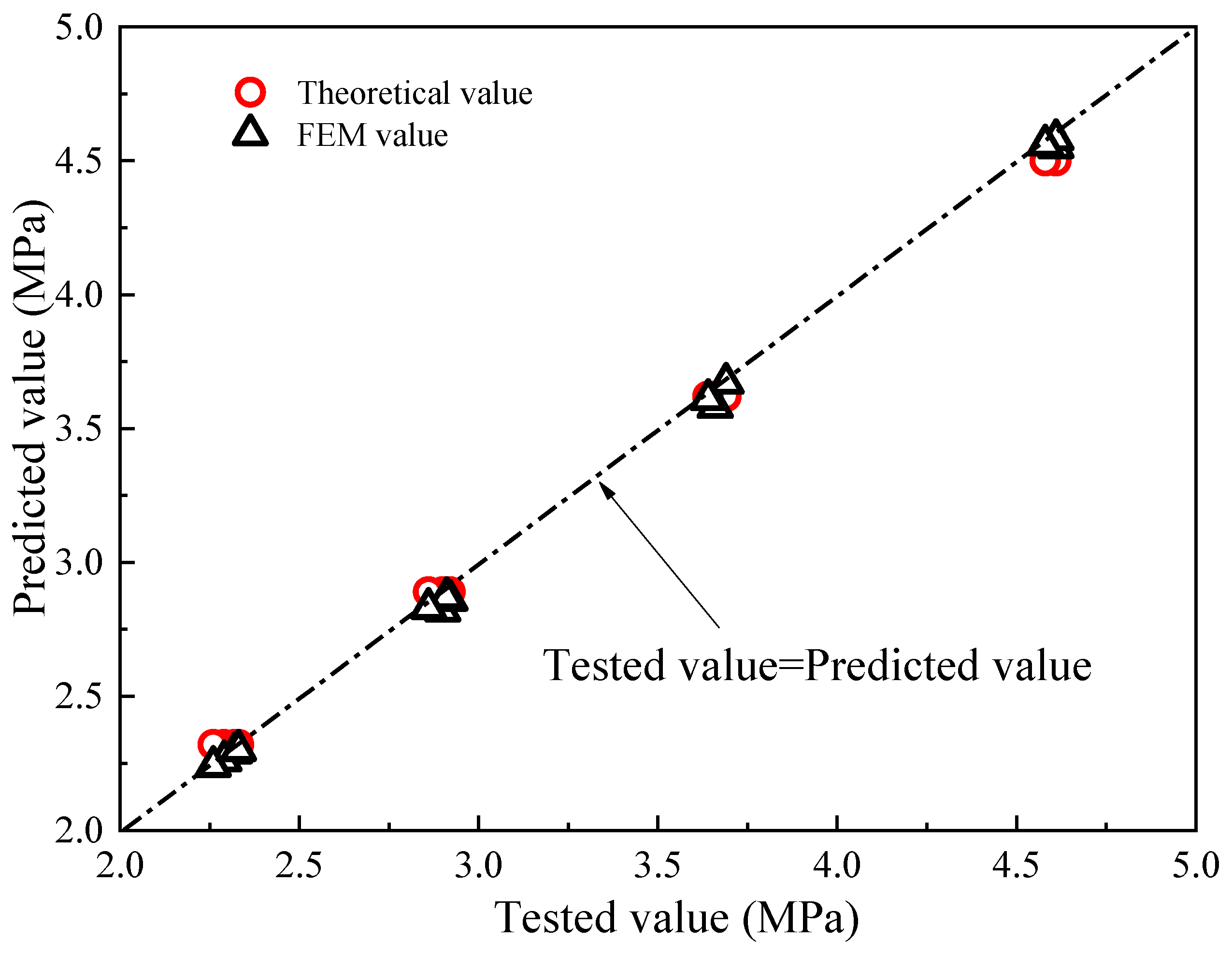
5.2. Analysis of Simulation and Test Results
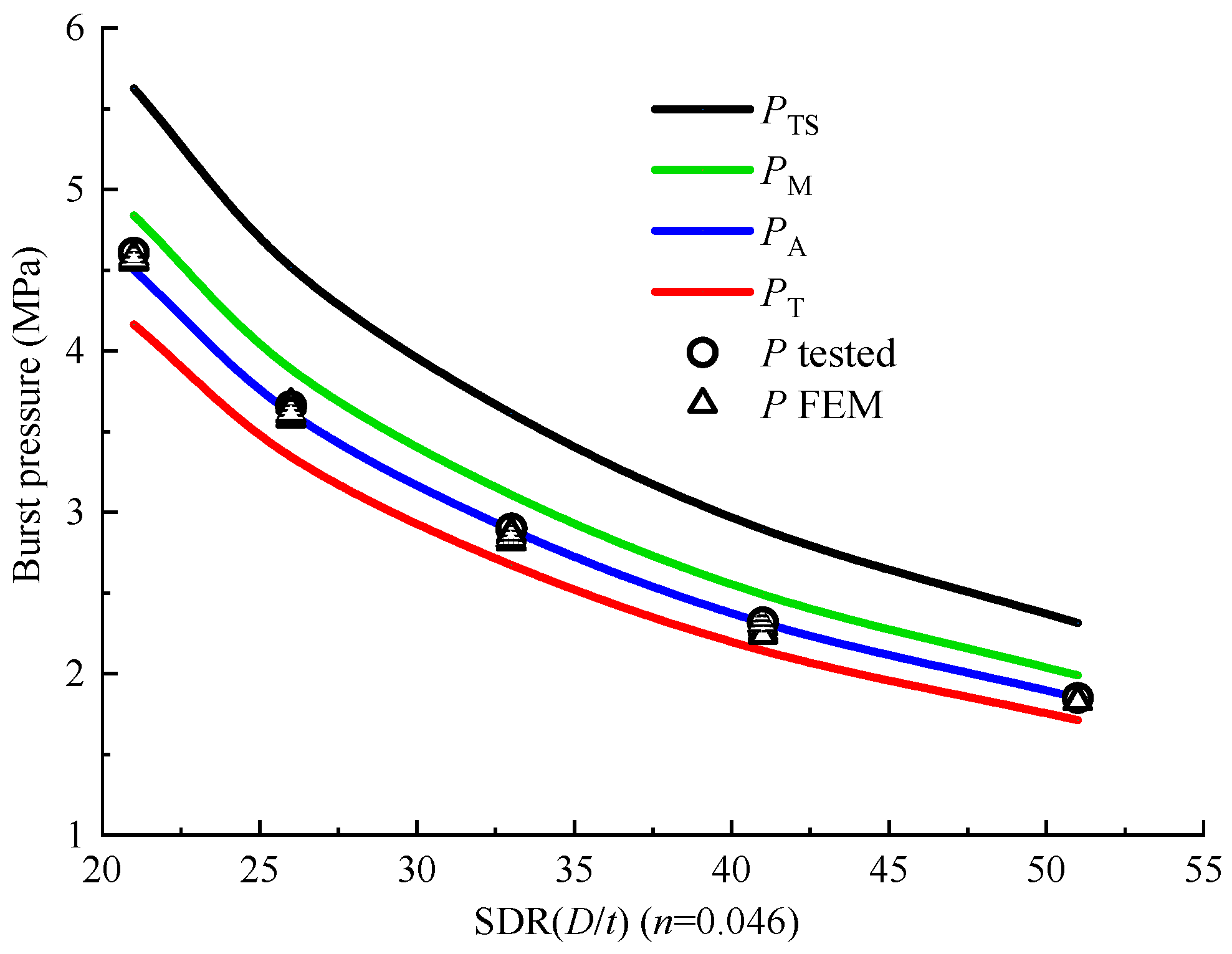
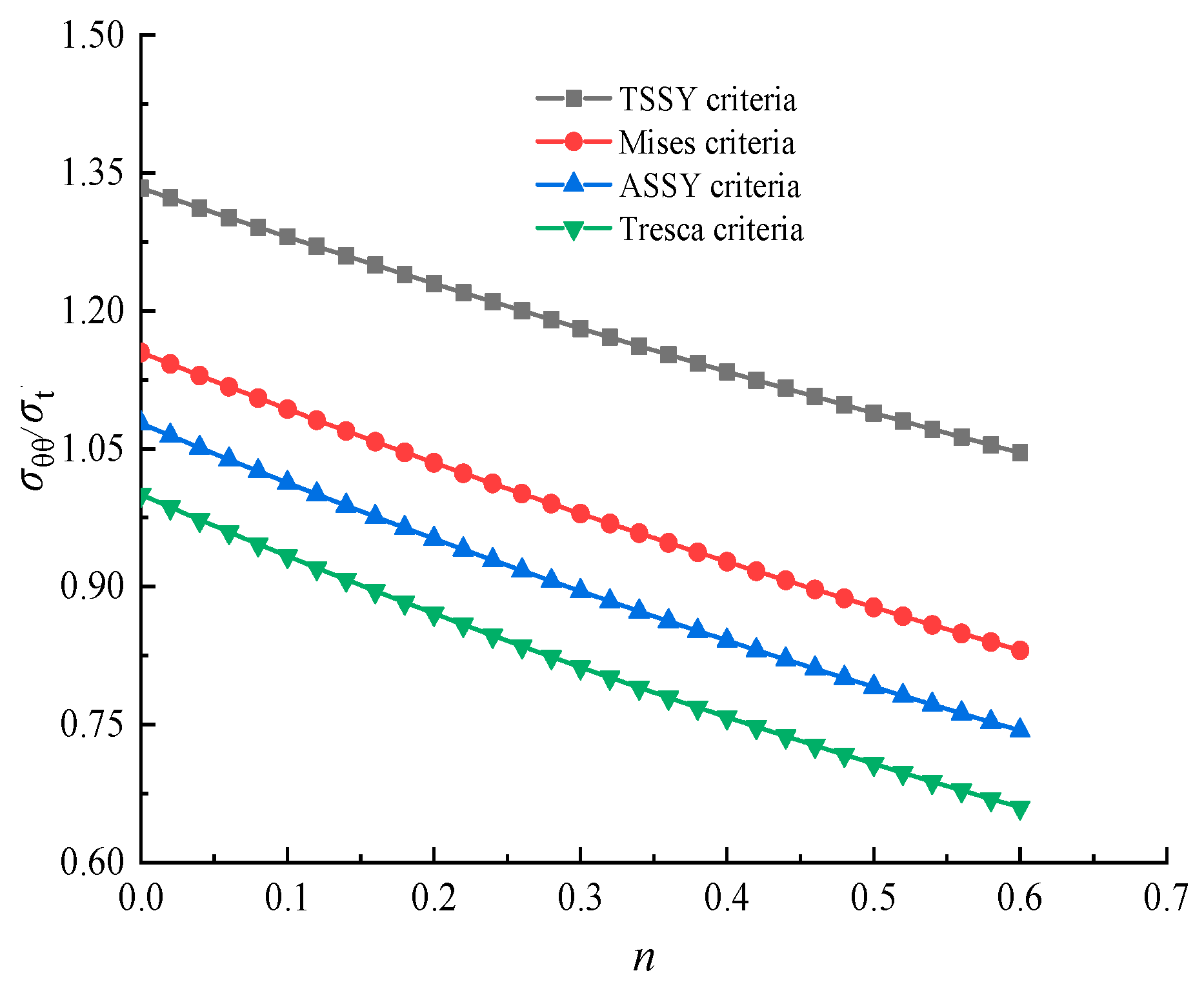
5.3. Discussion of Burst Pressure
6. Conclusions
- (1)
- The comparison between the theoretical value of the ASSY approach with the experimental and numerical results confirmed that the burst pressure solution-based ASSY can fit test data for PVC pipes well and is more applicable and accurate than other criteria.
- (2)
- The test data revealed that the ASSY approach exhibited excellent performance in evaluating PVC pipe burst pressure. The TSSY approach and Tresca criterion provided an upper and lower bound, respectively, while they overestimated or underestimated burst pressure to a certain extent.
- (3)
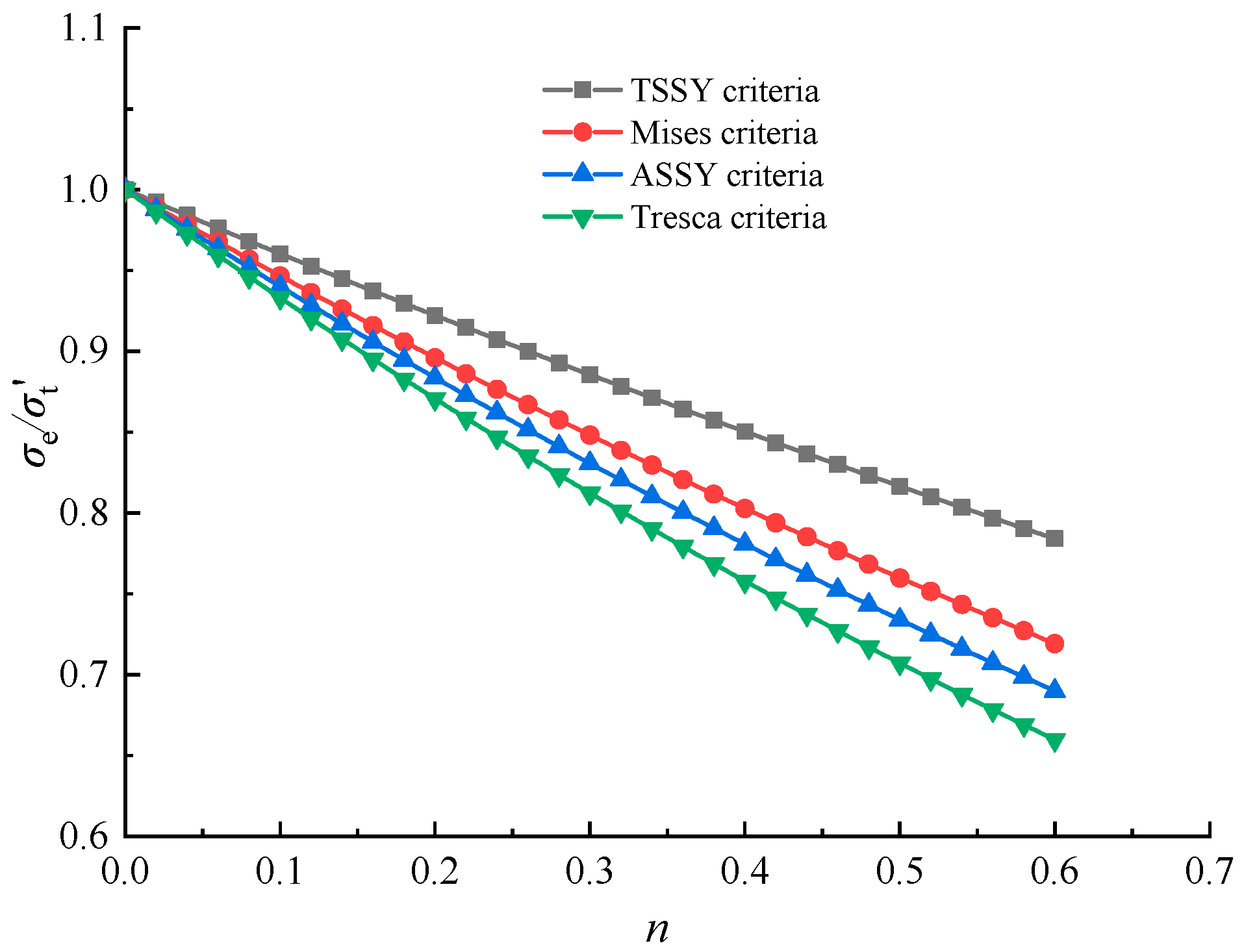
- The theoretical value of water burst pressure was reduced with increasing strain hardening exponent n-value, while it increased with increasing SDR. The equivalent stress and the hoop stress derived from the four theoretical solutions showed a similar tendency. However, a significant discrepancy among them can be recognized.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| b | Material parameter | ỹi | Predictive value |
| C | Material parameter | α | The tensile and compression strength ratio |
| D | Pipe mean diameter | β | Material parameter |
| D0 | Initial diameter | σ′ | Uniaxial true stress |
| E | Young’s modulus | σA | Equivalent stress based on ASSY |
| k | Coefficient determined by yield criterion | σc | Compressive strength |
| K | Strengthening coefficient | σe | Equivalent stress |
| L | Pipe length | σM | Equivalent stress based on Mises |
| n | Strain hardening index | σt | Uniaxial engineering tensile strength |
| Pi | Internal pressure | σt′ | Uniaxial true tensile strength |
| PA | Burst pressure based on ASSY | σT | Equivalent stress based on Tresca |
| Pb,TES | Burst pressure determined by TES criterion | σTS | Equivalent stress based on TSSY |
| Pb,TI | Burst pressure determined by TI criterion | σr | The radial stress |
| Pb,ZS | Burst pressure determined by ZS criterion | σθ | The hoop stress |
| PM | Burst pressure based on the von Mises yield criterion | σz | The axial stress |
| PN | The nominal pressure of pipe | σy | The yield strength |
| Ps | Tested burst pressure | ε′ | Uniaxial true strain |
| PT | Burst pressure based on the Tresca yield criterion | εt′ | Uniaxial true tensile strain |
| PTS | Burst pressure based on TSSY | εt | Uniaxial engineering strain |
| t | Wall thickness | εr | The radial stress |
| t0 | Initial wall thickness | εθ | The hoop stress |
| yi | Tested value | εz | The axial stress |
References
- Jemii, H.; Bahri, A.; Boubakri, A.; Hammiche, D.; Elleuch, K.; Guermazi, N. On the mechanical behaviour of industrial PVC pipes under pressure loading: Experimental and numerical studies. J. Polym. Res. 2020, 27, 1–13. [Google Scholar] [CrossRef]
- Folkman, S. Water Main Break Rates in the USA and Canada a Comprehensive Study; Utah State University Buried Structures Laboratory: Logan, UT, USA, 2018; pp. 1–48. [Google Scholar]
- Wéber, R.; Huzsvár, T.; Hős, C. Vulnerability analysis of water distribution networks to accidental pipe burst. Water Res. 2020, 184, 116178. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Li, S.; Zhou, Y. Analysis of Chinese Pipe Burst Events Reported by Web Media in 2013. In Proceedings of the American Society of Civil Engineers International Conference on Pipelines and Trenchless Technology, Xiamen, China, 21 November 2014; pp. 320–333. [Google Scholar]
- Ayed, L.; Hafsi, Z. Experimental and Numerical Investigations of Multi-leaks Detection in a Nonhomogenous Pipeline System. Arab. J. Sci. Eng. 2021, 3, 1–11. [Google Scholar] [CrossRef]
- Adewole, J.K.; Jensen, L.; Al-Mubaiyedh, U.A.; von Solms, N.; Hussein, I.A. Transport properties of natural gas through polyethylene nanocomposites at high temperature and pressure. J. Polym. Res. 2012, 19, 9814. [Google Scholar] [CrossRef]
- Citarella, R.; Giannella, V.; Lepore, M.A.; Fellinger, J. FEM-DBEM approach to analyse crack scenarios in a baffle cooling pipe undergoing heat flux from the plasma. AIMS Mater. Sci. 2017, 4, 391–412. [Google Scholar] [CrossRef]
- Fellinger, J.; Citarella, R.; Giannella, V.; Lepore, M.A.; Sepe, R.; Czerwinski, M.; Herold, F.; Stadler, R. Overview of fatigue life assessment of baffles in Wendelstein 7-X. Fusion Eng. Des. 2018, 136, 292–297. [Google Scholar] [CrossRef] [Green Version]
- Peres, F.M.; Schön, C.G. An alternative approach to the evaluation of the slow crack growth resistance of polyethylene resins used for water pipe extrusion. J. Polym. Res. 2007, 14, 181–189. [Google Scholar] [CrossRef]
- Duong, B.P.; Kim, J.; Jeong, I.; Kim, C.H.; Kim, J.-M. Acoustic Emission Burst Extraction for Multi-Level Leakage Detection in a Pipeline. Appl. Sci. 2020, 10, 1933. [Google Scholar] [CrossRef] [Green Version]
- Ge, P.; Xia, H.; Liu, Q.; Shi, C.; Xiao, W.; Jia, X.; Xu, Y. Prediction of ultimate burst pressure and comparison of failure criteria for thermoplastic composite pipes. IOP Conf. Ser. Earth Environ. Sci. 2021, 725, 012004. [Google Scholar] [CrossRef]
- Germain, Y. Burst pressure prediction of polyamide pipes. Polym. Eng. Sci. 1998, 38, 657–661. [Google Scholar] [CrossRef]
- Zheng, J.; Shi, J.; Shi, J.; Zhong, S.; Rao, J.; Li, G.; Li, X. Short-term burst pressure of polyethylene pipe reinforced by winding steel wires under various temperatures. Compos. Struct. 2015, 121, 163–171. [Google Scholar] [CrossRef]
- Zhou, W.G.; Huang, X. Model error assessments of burst capacity models for corroded pipeline. Int. J. Press. Vessel. Pip. 2012, 99–100, 1–8. [Google Scholar] [CrossRef]
- Law, M.; Bowie, G. Prediction of failure strain and burst pressure in high yield-to-tensile strength ratio linepipe. Int. J. Press. Vessel. Pip. 2007, 84, 487–492. [Google Scholar] [CrossRef]
- Mattos, H.D.C.; Paim, L.; Reis, J. Analysis of burst tests and long-term hydrostatic tests in produced water pipelines. Eng. Fail. Anal. 2012, 22, 128–140. [Google Scholar] [CrossRef]
- Zhu, X.-K.; Leis, B.N. Evaluation of burst pressure prediction models for line pipes. Int. J. Press. Vessel. Pip. 2012, 89, 85–97. [Google Scholar] [CrossRef]
- Cooper, W.E. The Significance of The Tensile Test to Pressure Vessel Design. Weld. J. Weld. Res. Suppl. 1957, 36, 49–56. [Google Scholar]
- Law, M.; Bowie, G. Failure strain in high yield-to-tensile ratio linepipes. J. Pipeline Syst. Eng. 2006, 5, 25–36. [Google Scholar]
- Giannella, V.; Citarella, R.; Fellinger, J.; Esposito, R. LCF assessment on heat shield components of nuclear fusion experiment “Wendelstein 7-X” by critical plane criteria. Procedia Struct. Integr. 2018, 8, 318–331. [Google Scholar] [CrossRef]
- Giannella, V.; Fellinger, J.; Perrella, M.; Citarella, R. Fatigue life assessment in lateral support element of a magnet for nuclear fusion experiment “Wendelstein 7-X”. Eng. Fract. Mech. 2017, 178, 243–257. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Zhu, W.; Di, Q.; Wang, W. Prediction of Burst Pressure of Pipes with Geometric Eccentricity. J. Press. Vessel. Technol. 2015, 137, 061201. [Google Scholar] [CrossRef] [Green Version]
- Sudduth, R.D. Comparison of the failure conditions for creep, stress relaxation, and constant strain rate measurements to predict pipe burst for two ABS materials using the universal viscoelastic model. J. Appl. Polym. Sci. 2004, 93, 247–260. [Google Scholar] [CrossRef]
- Zhang, Y.; Ben Jar, P.-Y. Comparison of Mechanical Properties between PE80 and PE100 Pipe Materials. J. Mater. Eng. Perform. 2016, 25, 4326–4332. [Google Scholar] [CrossRef]
- Gerdeen, M. Effect of strain gradient and curvature on forming limit diagrams for anisotropic sheets. J. Mater. Shap. Technol. 1991, 9, 253. [Google Scholar]
- Majid, F.; Safe, M.; Elghorba, M. Burst behavior of CPVC compared to HDPE thermoplastic polymer under a controlled internal pressure. Procedia Struct. Integr. 2017, 3, 380–386. [Google Scholar] [CrossRef]
- Guidara, M.A.; Bouaziz, M.; Schmitt, C.; Capelle, J.; Taïeb, E.H.; Azari, Z.; Hariri, S. Structural integrity assessment of defected high density poly-ethylene pipe: Burst test and finite element analysis based on J-integral criterion. Eng. Fail. Anal. 2015, 57, 282–295. [Google Scholar] [CrossRef]
- Chen, Y.; Hong, Z.; Zhang, J.; Xin, L.; Jing, Z. Failure analysis of high strength pipeline with single and multiple corrosions. Mater. Des. 2015, 67, 552–557. [Google Scholar] [CrossRef]
- Mondal Chandra, B.; Dhar Sutra, A. Finite-element evaluation of burst pressure models for corroded pipelines. J. Press. Vessel. Technol. 2017, 139, 021702. [Google Scholar] [CrossRef]
- Hasan, M.; Khan, F.; Kenny, S. Identification of the Cause of Variability of Probability of Failure for Burst Models Recommended by Codes/Standards. J. Press. Vessel. Technol. 2011, 133, 041101. [Google Scholar] [CrossRef]
- Jafari, S.; Alashti, R.A.; Hosseinipour, S.J. Comparison of Ductile Fracture Models on Load Bearing Capacity of a Dented Aluminum Pipe Subjected to Internal Pressure. Arab. J. Sci. Eng. 2014, 39, 8031–8049. [Google Scholar] [CrossRef]
- Wang, N.; Zarghamee, M.S. Evaluating Fitness-for-Service of Corroded Metal Pipelines: Structural Reliability Bases. J. Pipeline Syst. Eng. Pract. 2014, 5, 04013012. [Google Scholar] [CrossRef]
- Ma, B.; Shuai, J.; Liu, D.; Xu, K. Assessment on failure pressure of high strength pipeline with corrosion defects. Eng. Fail. Anal. 2015, 32, 209–219. [Google Scholar] [CrossRef]
- Rezaei, H.; Ryan, B.; Stoianov, I. Pipe Failure Analysis and Impact of Dynamic Hydraulic Conditions in Water Supply Networks. Procedia Eng. 2015, 119, 253–262. [Google Scholar] [CrossRef] [Green Version]
- Yu, M.-H. Twin shear stress yield criterion. Int. J. Mech. Sci. 1983, 25, 71–74. [Google Scholar] [CrossRef]
- Zhu, X.-K.; Leis, B.N. Average shear stress yield criterion and its application to plastic collapse analysis of pipelines. Int. J. Press. Vessel. Pip. 2006, 83, 663–671. [Google Scholar] [CrossRef]
- Zike, S.; Sørensen, B.F.; Mikkelsen, L.P. Experimental determination of the micro-scale strength and stress-strain relation of an epoxy resin. Mater. Des. 2016, 98, 47–60. [Google Scholar] [CrossRef] [Green Version]
- Payghan, V.; Jadhav, D.N.; Savant, G.Y.; Bharadwaj, S. Design & Analysis of Steam Drum Based on ASME Boiler and Pressure Vessel Code, Section VIII Div.2 & Div.3. Appl. Mech. Mater. 2016, 852, 511–517. [Google Scholar] [CrossRef]
- Guidara, M.A.; Bouaziz, M.A.; Schmitt, C.; Capelle, J.; Hariri, S. Burst Test and J-Integral Crack Growth Criterion in High Density Polyethylene Pipe Subjected to Internal Pressure; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 391–399. [Google Scholar]
- Benyahia, H.; Tarfaoui, M.; EL Moumen, A.; Ouinas, D.; Hassoon, O. Mechanical properties of offshoring polymer composite pipes at various temperatures. Compos. Part B Eng. 2018, 152, 231–240. [Google Scholar] [CrossRef]
- González-Arévalo, N.; Velázquez, J.; Díaz-Cruz, M.; Cervantes-Tobón, A.; Terán, G.; Hernández-Sanchez, E.; Capula-Colindres, S. Influence of aging steel on pipeline burst pressure prediction and its impact on failure probability estimation. Eng. Fail. Anal. 2021, 120, 104950. [Google Scholar] [CrossRef]










| Parameters | σy (MPa) | σt (MPa) | εt | E (MPa) | σt′ (MPa) | εt′ | n | K |
|---|---|---|---|---|---|---|---|---|
| value | 43.67 | 45.15 | 0.047 | 1259.43 | 47.28 | 0.046 | 0.046 | 57.05 |
| Pipe Number | Length (L/mm) | Wall Thickness (t/mm) | Mean Diameter (D/mm) | SDR(D/t) | Burst Pressure (Ps/MPa) |
|---|---|---|---|---|---|
| P1200-1 | 1800 | 45.9 | 1200 | 26 | 3.66 |
| P1200-2 | 1800 | 36.7 | 1200 | 33 | 2.90 |
| P1200-3 | 1800 | 29.4 | 1200 | 41 | 2.32 |
| P1200-4 | 1800 | 23.5 | 1200 | 51 | 1.85 |
| P630-1 | 1200 | 30.0 | 630 | 21 | 4.61 |
| P630-2 | 1200 | 24.1 | 630 | 26 | 3.69 |
| P630-3 | 1200 | 19.3 | 630 | 33 | 2.92 |
| P630-4 | 1200 | 15.4 | 630 | 41 | 2.29 |
| P315-1 | 800 | 15.0 | 315 | 21 | 4.61 |
| P315-2 | 800 | 12.1 | 315 | 26 | 3.64 |
| P315-3 | 800 | 9.7 | 315 | 33 | 2.91 |
| P315-4 | 800 | 7.7 | 315 | 41 | 2.26 |
| P160-1 | 800 | 7.7 | 160 | 21 | 4.58 |
| P160-2 | 800 | 6.2 | 160 | 26 | 3.64 |
| P160-3 | 800 | 4.9 | 160 | 33 | 2.86 |
| P160-4 | 800 | 4.0 | 160 | 41 | 2.33 |
| Pipe Number | Test Value (MPa) | Theoretical Value (MPa) | Error (%) | FEM Value (MPa) | Error (%) |
|---|---|---|---|---|---|
| P1200-1 | 3.66 | 3.62 | −1.09 | 3.58 | −2.19 |
| P1200-2 | 2.90 | 2.89 | −0.34 | 2.82 | −2.76 |
| P1200-3 | 2.32 | 2.32 | 0.00 | 2.29 | −1.29 |
| P1200-4 | 1.85 | 1.85 | 0.00 | 1.83 | −1.08 |
| P630-1 | 4.61 | 4.50 | −2.39 | 4.55 | −1.30 |
| P630-2 | 3.69 | 3.62 | −1.90 | 3.67 | −0.54 |
| P630-3 | 2.92 | 2.89 | −1.03 | 2.86 | −2.05 |
| P630-4 | 2.29 | 2.32 | 1.31 | 2.26 | −1.31 |
| P315-1 | 4.61 | 4.50 | −2.39 | 4.58 | −0.65 |
| P315-2 | 3.64 | 3.62 | −0.55 | 3.61 | −0.82 |
| P315-3 | 2.91 | 2.89 | −0.69 | 2.87 | −1.37 |
| P315-4 | 2.26 | 2.32 | 2.65 | 2.24 | −0.88 |
| P160-1 | 4.58 | 4.50 | −1.75 | 4.56 | −0.44 |
| P160-2 | 3.64 | 3.62 | −0.55 | 3.61 | −0.82 |
| P160-3 | 2.86 | 2.89 | 1.05 | 2.83 | −1.05 |
| P160-4 | 2.33 | 2.32 | −0.43 | 2.3 | −1.29 |
| Evaluation Indicators | RMSE (MPa) | MAE (MPa) | ME (MPa) | R2 |
|---|---|---|---|---|
| ASSY solution | 0.05 | 0.04 | 0.11 | 0.99960 |
| FEM approach | 0.04 | 0.04 | 0.08 | 0.99975 |
| TSSY solution | 0.78 | 0.77 | 1.05 | 0.99962 |
| Tresca solution | 0.28 | 0.27 | 0.45 | 0.99960 |
| von Mises solution | 0.22 | 0.21 | 0.26 | 0.99961 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Hu, S. Estimation of Burst Pressure of PVC Pipe Using Average Shear Stress Yield Criterion: Experimental and Numerical Studies. Appl. Sci. 2021, 11, 10477. https://doi.org/10.3390/app112110477
Yang J, Hu S. Estimation of Burst Pressure of PVC Pipe Using Average Shear Stress Yield Criterion: Experimental and Numerical Studies. Applied Sciences. 2021; 11(21):10477. https://doi.org/10.3390/app112110477
Chicago/Turabian StyleYang, Jinhui, and Shaowei Hu. 2021. "Estimation of Burst Pressure of PVC Pipe Using Average Shear Stress Yield Criterion: Experimental and Numerical Studies" Applied Sciences 11, no. 21: 10477. https://doi.org/10.3390/app112110477
APA StyleYang, J., & Hu, S. (2021). Estimation of Burst Pressure of PVC Pipe Using Average Shear Stress Yield Criterion: Experimental and Numerical Studies. Applied Sciences, 11(21), 10477. https://doi.org/10.3390/app112110477





