Global Dynamics of a Stochastic Viral Infection Model with Latently Infected Cells

Abstract

In this paper, we study the global dynamics of a stochastic viral infection model with humoral immunity and Holling type II response functions. The existence and uniqueness of non-negative global solutions are derived. Stationary ergodic distribution of positive solutions is investigated. The solution fluctuates around the equilibrium of the deterministic case, resulting in the disease persisting stochastically. The extinction conditions are also determined. To verify the accuracy of the results, numerical simulations were carried out using the Euler–Maruyama scheme. White noise’s intensity plays a key role in treating viral infectious diseases. The small intensity of white noises can maintain the existence of a stationary distribution, while the large intensity of white noises is beneficial to the extinction of the virus.

1. Introduction

Mathematical models have been introduced to define the within-host dynamical behaviors of various viral infections, mainly focusing on virus-to-cell spread in the bloodstream, such as human immunodeficiency virus (HIV) [1], COVID-19 [2,3], hepatitis C virus (HCV) [4,5], hepatitis B virus (HBV) [6], human T cell lymphotropic virus I (HTLV-1) [7], etc. Those classical viral infection models are composed of interactions among susceptible cells, infected target cells, and free viruses. Further, some authors include latent infection to describe the mechanism of latency. Wang et al. [8] investigated the HIV model with latent infection incorporating both modes of time delays, transmissions between viral entry and viral production or integration and also discussed the basic reproductive number and existence results of asymptotic stability of the endemic equilibrium points. Wen et al. [9] studied the virus-to-cell and cell-to-cell HIV virus transmission dynamics with latently infected cells. Pan et al. [10] discussed the HCV infection model, which includes the routes of infection and spread, like, virus-to-cell and cell-to-cell transmission dynamics, and explained numerically the four different HCV models.

The virus can weaken and suppress the immune response, which leads to persistent infections. Immune system response refers to the process that when the virus entry to the human body, the immune system receives the signal of virus attack and spreads it to the immune organs, which secrete lymphocytes to purge the virus. Moreover, the adaptive immune response plays a crucial role in the control of the infection process. When a virus spreads to the human body, the human body produces double modes of immune responses: one is the B-cell, which causes a humoral immune response and the second is the Cytotoxic T Lymphocyte (CTL), which causes a cellular immune response. Previous studies have showed that the humoral immune response is more active than the cellular immune responses. Elaiw et al. [11] discussed the dynamical behaviors of viral infection models with latently infected cells, humoral immune response, and general nonlinear incidence rate function. The authors in [12] investigated the global asymptotic stability of a reaction–diffusion virus infection model with homogeneous environments, nonlinear incidence in heterogeneous, and humoral immunity. Wang et al. [13] discussed the global stability results of HIV viral infection model with latently infected cells, B-cell immune response, Beddington–DeAngelis functional response, and various time delays. The authors in [14] reported the stability and bifurcation results of generalized viral infection system with humoral immunity and distributed delays in virus production and cell infection, and used time lags to describe the time needed to activate the immune response.

Stochastic modeling of viral infectious disease plays an important role and gives an extra degree of realism when compared to their corresponding deterministic models [15]. Generally, viral infection models, infective virus particles, and different cells reacting in the same environment can often provide different results. In reality, due to continuous fluctuations in the environment, the parameters involved in the system always fluctuate around some average values ([16,17,18]). Wang et al. [19] formulated the HIV viral infection model with latently infectious and random noise and also studied the existing results of stationary distribution/stochastic persistence. The authors in [20] discussed the stationary distribution and extinction results of stochastic HBV viral infection model with a time lag in the transmission coefficient make the periodic outbreaks. Sun et al. [21] investigated the existence of solution for the stochastic viral infectious system with CTL responses and distributed delay, moreover, the diseases will be eradicated while the stochastic reproductive number is less than one and if the stochastic reproductive ratio is greater than one, the viral infection will be stochastic persistence/ergodic stationary distribution. Rihan et al. [22] derived the existence of solution and stationary distribution of stochastic HBV model with intracellular delay, moreover, the solution fluctuates around endemic equilibrium of the corresponding deterministic model and leads to the stochastic persistence of the disease.

Motivated by the above-mentioned studies, in this paper, we formulate and analyze the dynamical behaviors of a virus–immune system with white noise. The presence and uniqueness of the global non-negative solution of the stochastic viral infection model with a Holling type II functional response is investigated. Using a stochastic Lyapunov function combined with Ito’s formula, we provide a sufficient condition for determining the existing results of stationary distribution and extinction of such considered model. The rest of this paper is organized as follows: In Section 2, we formulate the viral infection model and study the existence of global positive solution. Stationary distribution and extinction results of such a model are derived in Section 3 and Section 4. Some numerical simulations are given in Section 5 to verify the obtained theoretical results. Section 6 contains the conclusion.

2. Model Formulation

In the process of viral infection, the immune system plays a critical role. Viral dynamics can be modeled properly to provide insights into understanding the disease and the clinical treatments used to treat it. In adaptive immune responses, lymphocytes are responsible for specificity and memory. The two main types of lymphocytes are B cells and T cells. The function of T cells is to recognize and kill infected cells, while the function of B cells is to produce antibodies to neutralize the viruses. Researchers have studied the effects of immune responses such as CTL responses and antibody responses [23,24,25,26,27]. Some other researchers have also taken into account the effect of CTL responses and intracellular delays [5,28,29]. The mathematical model that describes the effect of humoral immune response on virus dynamics is presented in [27]

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)& =\lambda -d_{1}x\left(t\right)-{\beta }_{11}x\left(t\right)v\left(t\right)-{\beta }_{22}x\left(t\right)y\left(t\right),\hfill \\ \hfill \dot{y}\left(t\right)& ={\beta }_{1}x\left(t\right)v\left(t\right)+{\beta }_{2}x\left(t\right)y\left(t\right)-ay\left(t\right),\hfill \\ \hfill \dot{v}\left(t\right)& =ky\left(t\right)-\mu v\left(t\right)-\xi v\left(t\right)w\left(t\right),\hfill \\ \hfill \dot{w}\left(t\right)& =gv\left(t\right)w\left(t\right)-hw\left(t\right).\hfill \end{array}$$

(1)

This model consists of uninfected target cells $x\left(t\right)$, actively infected cells $y\left(t\right)$, free viruses $v\left(t\right)$, and antibodies/B cells $w\left(t\right)$. The uninfected cells $x\left(t\right)$ are produced at a rate constant $\lambda$ and death rate $d_1$. ${\beta }_{11}$ is the infection rate by free virus and uninfected cells being converted to productively infected ones at a rate ${\beta }_{22}$ per both cells. $a,\mu ,h$ are the death rate of infected cells, free virus particles, and antibodies/B cells, respectively. Free virus particle are produced from productively infected cells at the rate k and $\xi$ is the rate of neutralization by antibodies. g is the rate of antibodies activated against the virus.

Herein, we upgrade model (1) to include the latent infection component. We assume that the uninfected cell $x\left(t\right)$ gets infected by a free virus $v\left(t\right)$ or by direct contact with an infected cell $y\left(t\right)$ at the rate ${\displaystyle \frac{{\beta }_{1}x\left(t\right)v\left(t\right)}{1+v\left(t\right)}+\frac{{\beta }_{2}x\left(t\right)y\left(t\right)}{1+y\left(t\right)}}$ with a Holling type II functional response. ${\beta }_1>0$ and ${\beta }_2>0$ represent the virus to cell infection rate and cell to cell transmission rate, respectively [30]. We also assume that $(1-\phi )$ and $\phi \in (0,1)$ are the proportions of infection that lead to latency and productivity, respectively. Additionally, in order to reflect a more realistic situation of disease development, we incorporated the effect of randomization within the host by introducing nonlinear perturbations on the natural death rate with white noise into each equation. Therefore, the extended model takes the following form:

$$\begin{array}{cc}\hfill dx\left(t\right)& =(\lambda -d_{1}x\left(t\right)-\frac{{\beta }_{1}x\left(t\right)v\left(t\right)}{1+v\left(t\right)}-\frac{{\beta }_{2}x\left(t\right)y\left(t\right)}{1+y\left(t\right)})dt+{\sigma }_{1}x\left(t\right)d{W}_1\left(t\right),\hfill \\ \hfill dl\left(t\right)& =((1-\phi )\left(\frac{{\beta }_{1}x\left(t\right)v\left(t\right)}{1+v\left(t\right)}+\frac{{\beta }_{2}x\left(t\right)y\left(t\right)}{1+y\left(t\right)}\right)-(m+\gamma )l\left(t\right))dt+{\sigma }_{2}l\left(t\right)d{W}_2\left(t\right),\hfill \\ \hfill dy\left(t\right)& =(\phi \left(\frac{{\beta }_{1}x\left(t\right)v\left(t\right)}{1+v\left(t\right)}+\frac{{\beta }_{2}x\left(t\right)y\left(t\right)}{1+y\left(t\right)}\right)+\gamma l\left(t\right)-ay\left(t\right))dt+{\sigma }_{3}y\left(t\right)d{W}_3\left(t\right),\hfill \\ \hfill dv\left(t\right)& =(ky\left(t\right)-\mu v\left(t\right)-\xi v\left(t\right)w\left(t\right))dt+{\sigma }_{4}v\left(t\right)d{W}_4\left(t\right),\hfill \\ \hfill dw\left(t\right)& =(gv\left(t\right)w\left(t\right)-hw\left(t\right))dt+{\sigma }_{5}w\left(t\right)d{W}_5\left(t\right),\hfill \end{array}$$

(2)

with initial values $x\left(0\right)>0,l\left(0\right)>0,y\left(0\right)>0,v\left(0\right)>0,w\left(0\right)>0$. $l\left(t\right)$ denotes the concentrations of infected cells in latent stage at t. m be the death rate of $l\left(t\right)$ and latent infection become productively infected cells at the rate $\gamma$. ${\sigma }_1^2,{\sigma }_2^2,{\sigma }_3^2,{\sigma }_4^2,{\sigma }_5^2$ are intensities of the environmental white noises. $W_1\left(t\right),W_2\left(t\right),W_3\left(t\right),W_4\left(t\right),W_5\left(t\right)$ are mutually independent standard Brownian motions with $W_i\left(0\right)=0$ ($i=1,2,3,4,5$). We define the basic concepts of probability theory and SDEs. Let $(\mathsf{\Omega },\mathfrak{F},{\left\{{\mathfrak{F}}_t\right\}}_{t\ge 0},P)$ be complete probability space with filtration ${\left\{{\mathfrak{F}}_t\right\}}_{t\ge 0}$ satisfies the usual conditions and see more details about Ito’s formula (see [31,32,33]).

Definition 1.

Let $\mathcal{U}$ denote the family of all continuous non-decreasing functions $u_1:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ such that $u_1\left(0\right)=0$ and $u_1\left(r\right)>0$ if $r>0$. For $h>0$, let ${\mathbb{S}}_h=\{y_1\in {\mathbb{R}}^n:|y_1|<h\}$. A continuous function $V(y_1,t)$ defined on ${\mathbb{S}}_h\times [t_0,\infty )$ is said be Lyapunov function if

(i).

$V(0,t)=0$ and for some $u_1\in \mathcal{U}$, $u_1\left(\right|y_1\left|\right)\le V(y_1,t),$ for every $(y_1,t)\in {\mathbb{S}}_h\times [t_0,\infty ).$

(ii).

$V(y_1,t)\in C^{2,1}({\mathbb{S}}_h\times [t_0,\infty ),{\mathbb{R}}_{+})$ such that $LV(y_1,t)\le 0.$

Let $y_1\left(t\right)$ be a regular time-homogeneous Markov process in ${\mathbb{R}}^n$ defined by SDE

$$\begin{array}{c}\hfill d{y}_1\left(t\right)=f\left(y_1\left(t\right)\right)dt+g\left(y_1\left(t\right)\right)dW\left(t\right).\end{array}$$

(3)

The diffusion matrix of the process $y_1\left(t\right)$ is described as $\mathcal{A}\left(y_1\right)=\left(b_{ij}\left(y_1\right)\right)$, $b_{ij}\left(y_1\right)=g^i\left(y_1\right)g^j\left(y_1\right).$

Lemma 1.

([34]) The Markov process $y_1\left(t\right)$ has a unique ergodic stationary distribution $\pi (·)$ if there exists a bounded open domain $\mathcal{D}\subset {\mathbb{R}}^n$ with regular boundary $\mathsf{\Gamma }$, having the following properties:

• the diffusion matrix $\mathcal{A}\left(y_1\right)$ is strictly positive definite for all $y_1\in \mathcal{D}$.
• there exists a non-negative $C^2-$ function $\mathcal{V}$ such that $L\mathcal{V}$ is negative for any ${\mathbb{R}}^n\backslash \mathcal{D}$.

Theorem 1.

Assume that $g<\xi <h,{\beta }_{1}k<\mu +g,({\beta }_2+1)<\frac{a}{k}$, the model (2) has a unique positive solution $\left(x\right(t),l(t),y(t),v(t),w(t\left)\right)$ on $t\ge 0$ with $(x\left(0\right),l\left(0\right),y\left(0\right),v\left(0\right),w\left(0\right))\in R_{+}^5$, and the solution will remain in ${\mathbb{R}}_{+}^5$ with probability 1.

Proof. 

Basically, the coefficients of the system (2) satisfy the local Lipschitz condition, then (2) has a unique local solution $\left(x\right(t),l(t),y(t),v(t),w(t\left)\right)$ on $[0,{\tau }_e]$, where ${\tau }_e$ is an exposure time. Then, we prove that ${\tau }_e=+\infty .$ Let us follow the similar proof of Theorem 3.1 in [32]. The major step is to describe a non-negative $C^2$ function $V:{\mathbb{R}}_{+}^5\to {\mathbb{R}}_{+}$ such that ${lim}_{h_1\to \infty ,(x,l,y,v,w)\in {\mathbb{R}}_{+}^5\backslash D_{h_1}}infV(x,l,y,v,w)=+\infty ,andLV(x,l,y,v,w)\le \mathcal{K},$ where $D_{h_1}=(\frac{1}{h_1},h_1)\times (\frac{1}{h_1},h_1)\times (\frac{1}{h_1},h_1)\times (\frac{1}{h_1},h_1)\times (\frac{1}{h_1},h_1),$ and $\mathcal{K}$ is non-negative constant. Define a function $V:{\mathbb{R}}_{+}^5\to {\mathbb{R}}_{+}$ as follows

$$V(x,l,y,v,w)=(x-1-lnx)+(l-1-lnl)+(y-1-lny)+(v-1-lnv)+(w-1-lnw).$$

The non-negativity of this function can be seen from $\vartheta -1-ln\vartheta \ge 0$, $\forall \vartheta >0.$ By applying the Ito’s formula, we can obtain

$$\begin{array}{cc}\hfill dV(x,l,y,v,w)=& LV(x,l,y,v,w)dt+{\sigma }_1(x-1)d{W}_1\left(t\right)+{\sigma }_2(l-1)d{W}_2\left(t\right)+\hfill \\ & {\sigma }_3(y-1)d{W}_3\left(t\right)+{\sigma }_4(v-1)d{W}_4\left(t\right)+{\sigma }_5(w-1)d{W}_5\left(t\right),\hfill \\ \hfill LV(x,l,y,v,w)=& (1-\frac{1}{x})(\lambda -d_{1}x\left(t\right)-\frac{{\beta }_{1}x\left(t\right)v\left(t\right)}{1+v\left(t\right)}-\frac{{\beta }_{2}x\left(t\right)y\left(t\right)}{1+y\left(t\right)})+\hfill \\ & (1-\frac{1}{l})((1-\phi )\left(\frac{{\beta }_{1}x\left(t\right)v\left(t\right)}{1+v\left(t\right)}+\frac{{\beta }_{2}x\left(t\right)y\left(t\right)}{1+y\left(t\right)}\right)-\hfill \\ & (m+\gamma )l\left(t\right))+(1-\frac{1}{y})(\phi \left(\frac{{\beta }_{1}x\left(t\right)v\left(t\right)}{1+v\left(t\right)}+\frac{{\beta }_{2}x\left(t\right)y\left(t\right)}{1+y\left(t\right)}\right)+\gamma l\left(t\right)-ay\left(t\right))+\hfill \\ & (1-\frac{1}{v})(ky\left(t\right)-\mu v\left(t\right)-\xi v\left(t\right)w\left(t\right))+(1-\frac{1}{w})(gv\left(t\right)w\left(t\right)\hfill \\ & -hw\left(t\right))+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2+{\sigma }_4^2+{\sigma }_5^2}{2},\hfill \\ \hfill \le & \lambda +d_1+m+\gamma +a+\mu +h+(\xi -h)w+(g-\xi )vw+({\beta }_{1}k-(\mu +g))v\hfill \\ & +(({\beta }_2+1)k-a)y+\frac{{\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2+{\sigma }_4^2+{\sigma }_5^2}{2}.\hfill \end{array}$$

Using the assumptions $g<\xi <h,{\beta }_{1}k<\mu +g,({\beta }_2+1)<\frac{a}{k}$, there exists a positive constant $\mathcal{K}$ such that $LV\le \mathcal{K}.$ The rest of proof follows that of [31,32] and hence, is omitted.  □

3. Existence of Ergodic Stationary Distribution

Here, we discuss the stationary distribution results for the model (2), which helps to identify whether the diseases are persistent or can be eradicated.

Theorem 2.

Assume that ${\mathcal{R}}_0^s:=\frac{\lambda \gamma k{\beta }_1(1-\phi )}{d_1\widehat{a}\widehat{\gamma }\widehat{\mu }}>1,$ then for any $((x\left(0\right),l\left(0\right),y\left(0\right),v\left(0\right),w\left(0\right))\in {\mathbb{R}}_{+}^5$, the model $\left(2\right)$ has a unique ergodic stationary distribution $\pi (·),$ where $\widehat{\gamma }=m+\gamma +\frac{{\sigma }_2^2}{2},\widehat{a}=a+\frac{{\sigma }_3^2}{2},\widehat{\mu }=\mu +\frac{{\sigma }_4^2}{2}.$

Proof. 

The diffusion matrix of (2) is calculated as below

$$\mathcal{A}=\left(\begin{array}{ccccc}{\sigma }_1^2{x}^2& 0& 0& 0& 0\\ 0& {\sigma }_2^2{l}^2& 0& 0& 0\\ 0& 0& {\sigma }_3^2{y}^2& 0& 0\\ 0& 0& 0& {\sigma }_4^2{v}^2& 0\\ 0& 0& 0& 0& {\sigma }_5^2{w}^2\end{array}\right),$$

which is positive definite for any compact subset of ${\mathbb{R}}_{+}^5$, the condition (i) in Lemma 1 is verified.

Define the $C^2-$ function $V:{\mathbb{R}}_{+}^5\to \mathbb{R}$ as

$$\begin{array}{cc}\hfill V(x,l,y,v,w)& =M\left(-lnx-c_{1}lnl-c_{2}lny-c_{3}lnv-lnw\right)-lnx-lnl-lny-lnv\hfill \\ & +\frac{1}{\rho +1}{(x+l+y+v+w)}^{\rho +1},\hfill \\ \hfill & =M{V}_1+V_2+V_3+V_4+V_5+V_6,\hfill \end{array}$$

where $c_1=\frac{\lambda {\beta }_1\gamma k(1-\phi )}{{\widehat{\gamma }}^2\widehat{a}\widehat{\mu }},c_2=\frac{\lambda {\beta }_1\gamma k(1-\phi )}{\widehat{\gamma }{\widehat{a}}^2\widehat{\mu }},c_3=\frac{\lambda {\beta }_1\gamma k(1-\phi )}{\widehat{\gamma }\widehat{a}{\widehat{\mu }}^2},0<\rho <1$ satisfying $\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)>0$ and $M>0$ is constant, satisfying the condition $-M\nu +N_1\le -2,N_1=d_1+(M+1)\frac{{\sigma }_1^2}{2}+Mh+M\frac{{\sigma }_5^2}{2}+(M+1){\beta }_{2}y+{\beta }_{1}v+N_2+m+\gamma +\frac{{\sigma }_2^2}{2}+a+\frac{{\sigma }_3^2}{2}+\mu +\frac{{\sigma }_4^2}{2}$ and $\nu =d_1\left({\mathcal{R}}_0^s-1\right)>0.$ Further, $V(x,l,y,v,w)$ is not only continuous, but also goes to $+\infty$ as $(x,l,y,v,w)$ tends to the boundary of ${\mathbb{R}}_{+}^5$ and $\parallel (x,l,y,v,w)\parallel \to \infty .$V must have a minimum point $\left(x\right(0),l(0),y(0),v(0),w(0\left)\right)$ in the interior of ${\mathbb{R}}_{+}^5.$ Define a $C^2-$ function $\tilde{V}:{\mathbb{R}}_{+}^5\to {\mathbb{R}}_{+}$ as

$$\tilde{V}(x,l,y,v,w)=V(x,l,y,v,w)-V(x\left(0\right),l\left(0\right),y\left(0\right),v\left(0\right),w\left(0\right)).$$

Applying Ito’s formula L on the functions $V_1,\dots ,V_6$ and assume ${\beta }_1<g<\xi ,k<a$ and $\eta =max\{d_1,m,a,\mu ,h\}$

$$\begin{array}{cc}\hfill L{V}_1& \le -\frac{\lambda }{x}-\frac{c_1}{l}(1-\phi ){\beta }_{1}xv-\frac{\gamma l{c}_2}{y}-\frac{ky{c}_3}{v}+d_1+{\beta }_{2}y+c_1(m+\gamma )+a{c}_2+\mu c_3+\xi w{c}_3\hfill \\ & -(g-{\beta }_1)v+h+\frac{{\sigma }_1^2+c_1{\sigma }_2^2+c_2{\sigma }_3^2+c_3{\sigma }_4^2+{\sigma }_5^2}{2},\hfill \\ \hfill & \le -4\sqrt[4]{c_1{c}_2{c}_3\lambda (1-\phi ){\beta }_1\gamma k}+d_1+\frac{{\sigma }_1^2}{2}+c_1(m+\gamma +\frac{{\sigma }_2^2}{2})+c_2(a+\frac{{\sigma }_3^2}{2})+c_3(\mu +\frac{{\sigma }_4^2}{2})\hfill \\ & +h+\frac{{\sigma }_5^2}{2}+{\beta }_{2}y+\xi w{c}_3,\hfill \\ \hfill & \le -\frac{\lambda (1-\phi ){\beta }_1\gamma k}{\widehat{\gamma }\widehat{a}\widehat{\mu }}+d_1+\frac{{\sigma }_1^2}{2}+h+\frac{{\sigma }_5^2}{2}+{\beta }_{2}y+\xi w{c}_3,\hfill \\ \hfill & \le -\nu +\frac{{\sigma }_1^2}{2}+h+\frac{{\sigma }_5^2}{2}+{\beta }_{2}y+\xi w{c}_3,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill L{V}_2& \le -\frac{\lambda }{x}+d_1+{\beta }_{1}v+{\beta }_{2}y+\frac{{\sigma }_1^2}{2},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill L{V}_3& =-\frac{1}{l}(1-\phi )\left(\frac{{\beta }_{1}xv}{1+v}+\frac{{\beta }_{2}xy}{1+y}\right)+m+\gamma +\frac{{\sigma }_2^2}{2},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill L{V}_4& =-\frac{\phi {\beta }_{1}xv}{y(1+v)}-\frac{\phi {\beta }_{2}x}{1+y}-\frac{\gamma l}{y}+a+\frac{{\sigma }_3^2}{2},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill L{V}_5& =-\frac{ky}{v}+\mu +\xi w+\frac{{\sigma }_4^2}{2},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill L{V}_6& \le {(x+l+y+v+w)}^{\rho }[\lambda -\eta (x+l+y+v+w)]+\frac{\rho }{2}{(x+l+y+v+w)}^{\rho -1}\hfill \\ & \times [{\sigma }_1^2{x}^2+{\sigma }_2^2{l}^2+{\sigma }_3^2{y}^2+{\sigma }_4^2{v}^2+{\sigma }_5^2{w}^2],\hfill \\ \hfill & \le {(x+l+y+v+w)}^{\rho }[\lambda -\eta (x+l+y+v+w)]+\frac{\rho }{2}{(x+l+y+v+w)}^{\rho +1}\hfill \\ & \times ({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2),\hfill \\ \hfill & \le \lambda {(x+l+y+v+w)}^{\rho }-{(x+l+y+v+w)}^{\rho +1}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)],\hfill \\ \hfill & \le N_2-\frac{1}{2}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)](x^{\rho +1}+l^{\rho +1}+y^{\rho +1}+v^{\rho +1}+w^{\rho +1}),\hfill \end{array}$$

(9)

where

$$\begin{array}{cc}\hfill N_2& =\underset{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5}{sup}\{\lambda {(x+l+y+v+w)}^{\rho }-\frac{1}{2}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]\hfill \\ & {(x+l+y+v+w)}^{\rho +1}\}<\infty .\hfill \end{array}$$

From Equations (4)–(9), we have

$$\begin{array}{cc}\hfill L\tilde{V}& \le -\frac{\lambda }{x}-M\nu +(M{c}_3+1)\xi w-\frac{1}{l}(1-\phi ){\beta }_{1}xv-\frac{\phi {\beta }_{2}x}{1+y}-\frac{ky}{v}-\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\hfill \\ & \vee {\sigma }_4^2\vee {\sigma }_5^2\left)\right](x^{\rho +1}+l^{\rho +1}+y^{\rho +1}+v^{\rho +1}+w^{\rho +1})-\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]\hfill \\ & \times (x^{\rho +1}+l^{\rho +1}+y^{\rho +1}+v^{\rho +1}+w^{\rho +1})+d_1+(M+1)\frac{{\sigma }_1^2}{2}+Mh+M\frac{{\sigma }_5^2}{2}\hfill \\ & +(M+1){\beta }_{2}y+{\beta }_{1}v+N_2+m+\gamma +\frac{{\sigma }_2^2}{2}+a+\frac{{\sigma }_3^2}{2}+\mu +\frac{{\sigma }_4^2}{2}.\hfill \end{array}$$

(10)

For $ϵ>0,$ define a bounded closed set

$$\mathcal{D}=\left\{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5:ϵ\le x\le \frac{1}{ϵ},{ϵ}^5\le l\le \frac{1}{{ϵ}^5},{ϵ}^2\le y\le \frac{1}{{ϵ}^2},{ϵ}^3\le v\le \frac{1}{{ϵ}^3},ϵ\le w\le \frac{1}{ϵ}\right\}.$$

In the set ${\mathbb{R}}_{+}^5\backslash \mathcal{D},$ let us choose $ϵ$ satisfies the following conditions

$$\begin{array}{cc}\hfill & -\frac{\lambda }{ϵ}+M_1\le -1,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & -\frac{(1-\phi ){\beta }_1}{ϵ}+M_1\le -1,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & -\frac{\phi {\beta }_2ϵ}{1+{ϵ}^2}+M_1\le -1,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & -\frac{k}{ϵ}+M_1\le -1,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & 0<ϵ<\frac{1}{(M{c}_3+1)\xi },\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & -\frac{1}{4}\left[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)\right]\frac{1}{{ϵ}^{\rho +1}}+M_1\le -1,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & -\frac{1}{4}\left[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)\right]\frac{1}{{ϵ}^{2(\rho +1)}}+M_1\le -1,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & -\frac{1}{4}\left[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)\right]\frac{1}{{ϵ}^{3(\rho +1)}}+M_1\le -1,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & -\frac{1}{4}\left[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)\right]\frac{1}{{ϵ}^{5(\rho +1)}}+M_1\le -1,\hfill \end{array}$$

(19)

where $M_1={sup}_{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5}\left\{(M{c}_3+1)\xi w-\frac{1}{4}\left[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)\right](x^{\rho +1}+l^{\rho +1}+y^{\rho +1}+v^{\rho +1}+w^{\rho +1})+d_1+(M+1)\frac{{\sigma }_1^2}{2}+Mh+M\frac{{\sigma }_5^2}{2}+(M+1){\beta }_{2}y+{\beta }_{1}v+N_2+m+\gamma +\frac{{\sigma }_2^2}{2}+a+\frac{{\sigma }_3^2}{2}+\mu +\frac{{\sigma }_4^2}{2}\right\}.$ We need to verity the Lemma 1, to show that $L\tilde{V}\le -1$ for $(x,l,y,v,w)\in {\mathbb{R}}_{+}^5\backslash \mathcal{D}$ and ${\mathbb{R}}_{+}^5\backslash \mathcal{D}={\bigcup }_{i=1}^{10}{\mathcal{D}}_i,$ where

$$\begin{array}{cc}\hfill {\mathcal{D}}_1& =\{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5;0<x<ϵ\},\hfill \\ \hfill {\mathcal{D}}_2& =\{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5;0<l<{ϵ}^5,x\ge ϵ,v\ge {ϵ}^3\},\hfill \\ \hfill {\mathcal{D}}_3& =\{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5;0<y<{ϵ}^2,x\ge ϵ\},\hfill \\ \hfill {\mathcal{D}}_4& =\{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5;0<v<{ϵ}^3,y\ge {ϵ}^2\},\hfill \\ \hfill {\mathcal{D}}_5& =\{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5;0<w<ϵ\},\hfill \\ \hfill {\mathcal{D}}_6& =\{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5;x>\frac{1}{ϵ}\},\hfill \\ \hfill {\mathcal{D}}_7& =\{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5;l>\frac{1}{{ϵ}^5}\},\hfill \\ \hfill {\mathcal{D}}_8& =\{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5;y>\frac{1}{{ϵ}^2}\}\hfill \\ \hfill {\mathcal{D}}_9& =\{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5;v>\frac{1}{{ϵ}^3}\},\hfill \\ \hfill {\mathcal{D}}_{10}& =\{(x,l,y,v,w)\in {\mathbb{R}}_{+}^5;w>\frac{1}{ϵ}\}.\hfill \end{array}$$

Case (i) For $(x,l,y,v,w)\in {\mathcal{D}}_1$, by (10) we get

$$\begin{array}{cc}\hfill L\tilde{V}& \le -\frac{\lambda }{x}+(M{c}_3+1)\xi w-\frac{1}{4}\left[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)\right](x^{\rho +1}+l^{\rho +1}+y^{\rho +1}+v^{\rho +1}\hfill \\ & +w^{\rho +1})+d_1+(M+1)\frac{{\sigma }_1^2}{2}+Mh+M\frac{{\sigma }_5^2}{2}+(M+1){\beta }_{2}y+{\beta }_{1}v+N_2+\hfill \\ & m+\gamma +\frac{{\sigma }_2^2}{2}+a+\frac{{\sigma }_3^2}{2}+\mu +\frac{{\sigma }_4^2}{2},\hfill \\ \hfill & \le -\frac{\lambda }{ϵ}+M_1\le -1,\hfill \end{array}$$

which obtained from (11).

Case (ii) For $(x,l,y,v,w)\in {\mathcal{D}}_2,$ we have

$$\begin{array}{cc}\hfill L\tilde{V}& \le -\frac{1}{l}(1-\phi ){\beta }_{1}xv+M_1,\hfill \\ \hfill & \le -\frac{1}{ϵ}(1-\phi ){\beta }_1+M_1\le -1,\hfill \end{array}$$

which is obtained from (12).

Case (iii) For $(x,l,y,v,w)\in {\mathcal{D}}_3,$ we have

$$\begin{array}{cc}\hfill L\tilde{V}& \le -\frac{\phi {\beta }_{2}x}{1+y}+M_1,\hfill \\ \hfill & \le -\frac{\phi {\beta }_2ϵ}{1+{ϵ}^2}+M_1\le -1,\hfill \end{array}$$

which is obtained from (13).

Case (iv) For $(x,l,y,v,w)\in {\mathcal{D}}_4,$ we have

$$\begin{array}{cc}\hfill L\tilde{V}& \le -\frac{ky}{v}+M_1,\hfill \\ \hfill & \le -\frac{k}{ϵ}+M_1\le -1,\hfill \end{array}$$

which is obtained from (14).

Case (v) For $(x,l,y,v,w)\in {\mathcal{D}}_5,$ we have

$$\begin{array}{cc}\hfill L\tilde{V}& \le -M\nu +(M{c}_3+1)\xi w+N_1,\hfill \\ \hfill & \le -M\nu +(M{c}_3+1)\xi ϵ+N_1<-1,\hfill \end{array}$$

which is obtained from (15) and $-M\nu +N_1\le -2.$

Case (vi) For $(x,l,y,v,w)\in {\mathcal{D}}_6,$ we get

$$\begin{array}{cc}\hfill L\tilde{V}& \le -\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]x^{\rho +1}+M_1,\hfill \\ \hfill & \le -\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]\frac{1}{{ϵ}^{\rho +1}}+M_1\le -1,\hfill \end{array}$$

which is obtained from (16).

Case (vii) For $(x,l,y,v,w)\in {\mathcal{D}}_7,$ it yields

$$\begin{array}{cc}\hfill L\tilde{V}& \le -\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]l^{\rho +1}+M_1,\hfill \\ \hfill & \le -\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]\frac{1}{{ϵ}^{5(\rho +1)}}+M_1\le -1,\hfill \end{array}$$

which is obtained from (19).

Case (viii) For $(x,l,y,v,w)\in {\mathcal{D}}_8,$ we get

$$\begin{array}{cc}\hfill L\tilde{V}& \le -\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]y^{\rho +1}+M_1,\hfill \\ \hfill & \le -\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]\frac{1}{{ϵ}^{2(\rho +1)}}+M_1\le -1,\hfill \end{array}$$

which is obtained from (17).

Case (ix) For $(x,l,y,v,w)\in {\mathcal{D}}_9,$ it yields

$$\begin{array}{cc}\hfill L\tilde{V}& \le -\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]v^{\rho +1}+M_1,\hfill \\ \hfill & \le -\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]\frac{1}{{ϵ}^{3(\rho +1)}}+M_1\le -1,\hfill \end{array}$$

which is obtained from (18).

Case (x) For $(x,l,y,v,w)\in {\mathcal{D}}_{10},$ we get

$$\begin{array}{cc}\hfill L\tilde{V}& \le -\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]w^{\rho +1}+M_1,\hfill \\ \hfill & \le -\frac{1}{4}[\eta -\frac{\rho }{2}({\sigma }_1^2\vee {\sigma }_2^2\vee {\sigma }_3^2\vee {\sigma }_4^2\vee {\sigma }_5^2)]\frac{1}{{ϵ}^{\rho +1}}+M_1\le -1,\hfill \end{array}$$

which is obtained from (16).

Therefore, follows the above discussion, there exists a $ϵ>0,$ such that $L\tilde{V}(x,l,y,v,w)\le -1,$ for all $(x,l,y,v,w)\in {\mathbb{R}}_{+}^5\backslash \mathcal{D}.$ Based on Lemma 1, the model (2) has a unique ergodic stationary distribution.  □

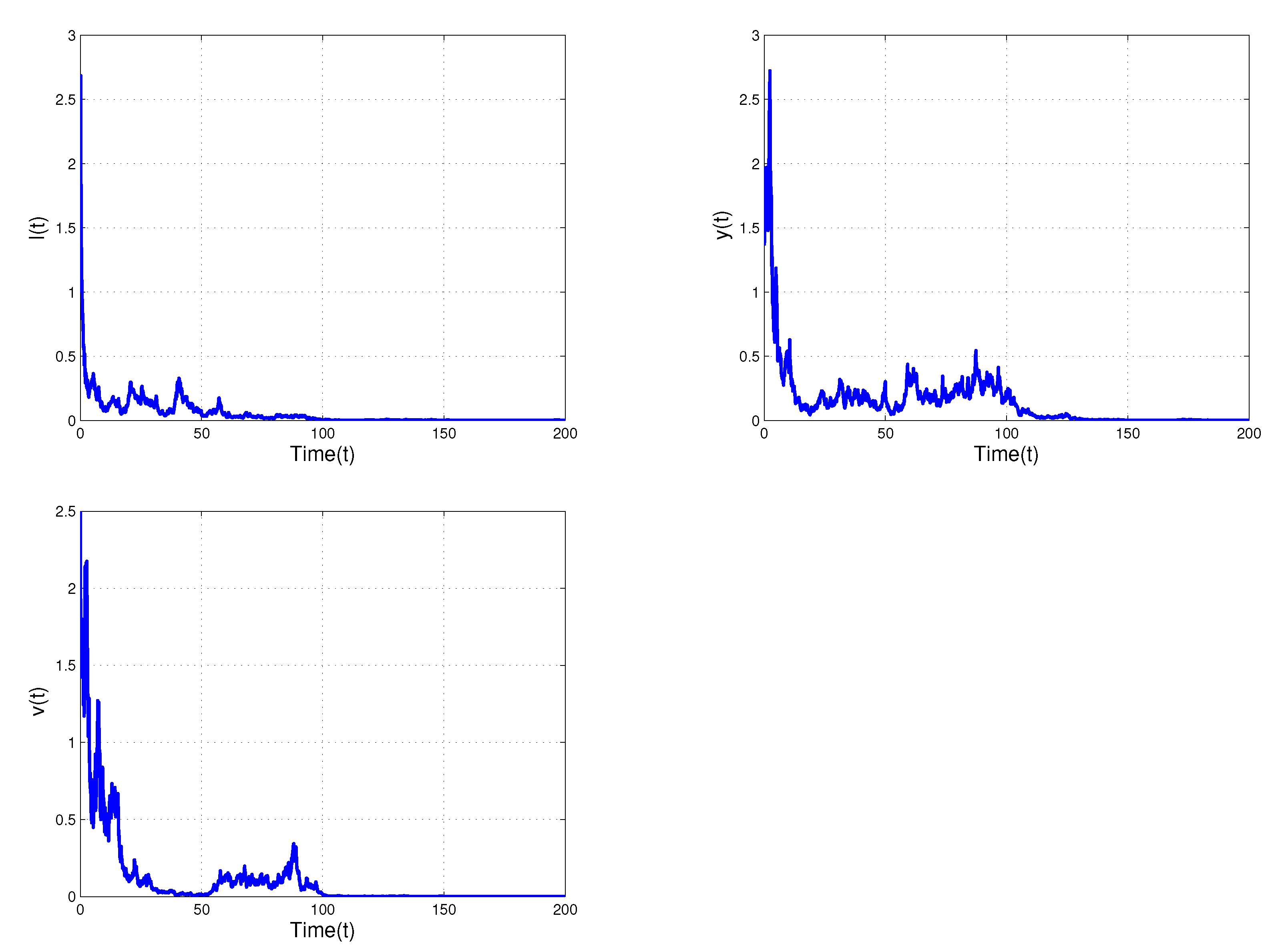
4. Extinction

Now, we establish the conditions under which extinction of the disease.

Theorem 3.

Let $\left(x\right(t),l(t),y(t),v(t),w(t\left)\right)$ be the solution of (2), $\left(x\right(0),l(0),y(0),v(0),w(0\left)\right)$$\in {\mathbb{R}}_{+}^5$, if ${\tilde{R}}_0^s:=\frac{3({\beta }_1+{\beta }_2)\lambda }{d_1((m+\frac{{\sigma }_2^2}{2})\wedge ((a-k)+\frac{{\sigma }_3^2}{2})\wedge (\mu +\frac{{\sigma }_4^2}{2}))}<1,$ which implies that

$$\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}x\left(s\right)ds\le \frac{\lambda }{d_1},\underset{t\to \infty }{lim}l\left(t\right)=0,\underset{t\to \infty }{lim}y\left(t\right)=0,\underset{t\to \infty }{lim}v\left(t\right)=0.a.s.$$

Proof. 

By Theorem 1, the solution of (2) is positive,

$$\begin{array}{c}\hfill dx\left(t\right)\le (\lambda -d_{1}x)dt+{\sigma }_{1}xd{W}_1\left(t\right).\end{array}$$

Consider the auxiliary stochastic equation of the above equation

$$\begin{array}{cc}\hfill d{x}_1\left(t\right)& =(\lambda -d_1{x}_1)dt+{\sigma }_1{x}_{1}d{W}_1\left(t\right),x_1\left(0\right)=x\left(0\right)>0,\hfill \end{array}$$

we get $\begin{array}{cc}\hfill \underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^t{x}_1\left(s\right)ds& =\frac{\lambda }{d_1}a.s.\hfill \end{array}$

Using the comparison theorem of stochastic equation [32], we get $x\left(t\right)\le x_1\left(t\right)a.s.$ Then

$$\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}x\left(s\right)ds\le \underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^t{x}_1\left(s\right)ds=\frac{\lambda }{d_1}.a.s.$$

Define $ln\left(l\right(t)+y(t)+v(t\left)\right)$ and apply the Ito’s formula, assume $k<a$, we get

$$\begin{array}{cc}\hfill & d\left(ln\right(l\left(t\right)+y\left(t\right)+v\left(t\right)\left)\right)\hfill \\ & =\frac{1}{l\left(t\right)+y\left(t\right)+v\left(t\right)}\left\{\frac{{\beta }_{1}xv}{1+v}+\frac{{\beta }_{2}xy}{1+y}-ml-(a-k)y-\mu v-\xi vw\right\}dt\hfill \\ \hfill & -\frac{({\sigma }_2^2{l}^2+{\sigma }_3^2{y}^2+{\sigma }_4^2{v}^2)}{2{(l+y+v)}^2}dt+\frac{{\sigma }_{2}l}{l+y+v}d{W}_2\left(t\right)+\frac{{\sigma }_{3}y}{l+y+v}d{W}_3\left(t\right)+\frac{{\sigma }_{4}v}{l+y+v}d{W}_4\left(t\right),\hfill \\ \hfill & \le ({\beta }_1+{\beta }_2)xdt-\frac{(m+\frac{{\sigma }_2^2}{2})l^2+((a-k)+\frac{{\sigma }_3^2}{2})y^2+(\mu +\frac{{\sigma }_4^2}{2})v^2}{{(l+y+v)}^2}dt+\frac{{\sigma }_{2}l}{l+y+v}d{W}_2\left(t\right)+\hfill \\ & +\frac{{\sigma }_{3}y}{l+y+v}d{W}_3\left(t\right)+\frac{{\sigma }_{4}v}{l+y+v}d{W}_4\left(t\right),\hfill \\ \hfill & \le ({\beta }_1+{\beta }_2)xdt-\frac{1}{3}((m+\frac{{\sigma }_2^2}{2})\wedge ((a-k)+\frac{{\sigma }_3^2}{2})\wedge (\mu +\frac{{\sigma }_4^2}{2}))dt+\frac{{\sigma }_{2}l}{l+y+v}d{W}_2\left(t\right)\hfill \\ & +\frac{{\sigma }_{3}y}{l+y+v}d{W}_3\left(t\right)+\frac{{\sigma }_{4}v}{l+y+v}d{W}_4\left(t\right).\hfill \end{array}$$

Taking integration from 0 to t on both sides and divide by t,

$$\begin{array}{cc}\hfill & \frac{ln\left(l\right(t)+y(t)+v(t\left)\right)}{t}-\frac{ln\left(l\right(0)+y(0)+v(0\left)\right)}{t}\hfill \\ & \le \frac{{\beta }_1+{\beta }_2}{t}{\int }_0^{t}x\left(s\right)ds-\frac{1}{3}((m+\frac{{\sigma }_2^2}{2})\wedge ((a-k)+\frac{{\sigma }_3^2}{2})\hfill \\ & \wedge (\mu +\frac{{\sigma }_4^2}{2}))+\frac{{\sigma }_2}{t}{\int }_0^t\frac{l}{l+y+v}d{W}_2\left(s\right)+\frac{{\sigma }_3}{t}\hfill \\ & \times {\int }_0^t\frac{y}{l+y+v}d{W}_3\left(s\right)+\frac{{\sigma }_4}{t}{\int }_0^t\frac{v}{l+y+v}d{W}_4\left(s\right),\hfill \\ \hfill & \underset{t\to \infty }{lim}sup\frac{ln\left(l\right(t)+y(t)+v(t\left)\right)}{t}\hfill \\ & \le ({\beta }_1+{\beta }_2)\frac{\lambda }{d_1}-\frac{1}{3}((m+\frac{{\sigma }_2^2}{2})\wedge ((a-k)+\frac{{\sigma }_3^2}{2})\wedge (\mu +\frac{{\sigma }_4^2}{2})),\hfill \\ \hfill & \le \frac{1}{3}({\tilde{R}}_0^s-1)((m+\frac{{\sigma }_2^2}{2})\wedge ((a-k)+\frac{{\sigma }_3^2}{2})\wedge (\mu +\frac{{\sigma }_4^2}{2}))<0a.s.\hfill \end{array}$$

It implies that ${lim}_{t\to \infty }l\left(t\right)=0,{lim}_{t\to \infty }y\left(t\right)=0,{lim}_{t\to \infty }v\left(t\right)=0.a.s.$  □

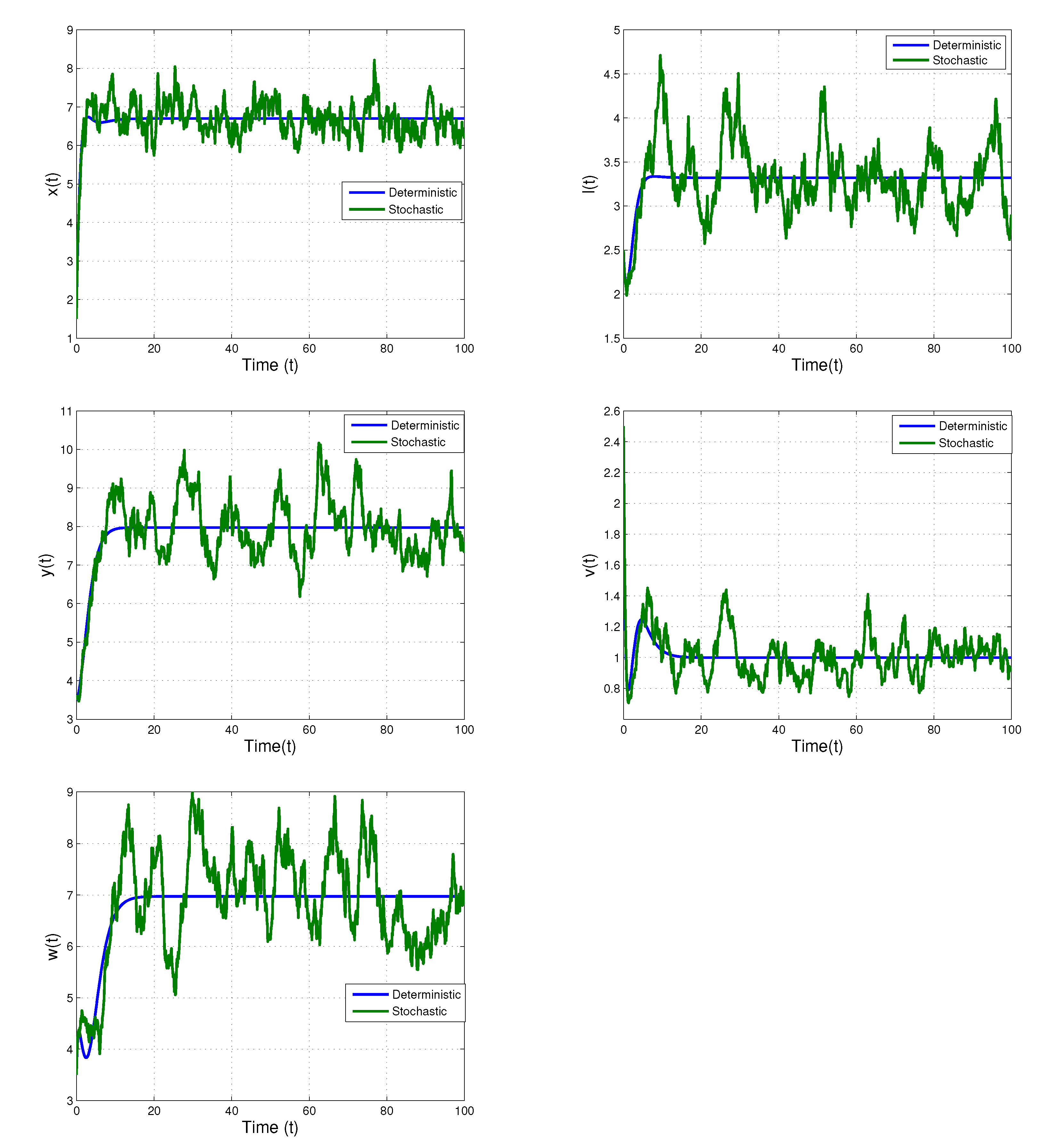
5. Numerical Simulations

In this section, we use Euler–Maruyama method for solving SDEs, as was discussed in detail in [32,35], to have the discretization transformation of (2), as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill x_{j+1}& =x_j+[\lambda -d_1{x}_j-\frac{{\beta }_1{x}_j{v}_j}{1+v_j}-\frac{{\beta }_2{x}_j{y}_j}{1+y_j}]\Delta t+{\sigma }_1{x}_j\sqrt{\Delta t}{\zeta }_{1,j},\hfill \\ \hfill l_{j+1}& =l_j+[(1-\phi )\left(\frac{{\beta }_1{x}_j{v}_j}{1+v_j}+\frac{{\beta }_2{x}_j{y}_j}{1+y_j}\right)-(m+\gamma )l_j]\Delta t+{\sigma }_2{l}_j\sqrt{\Delta t}{\zeta }_{2,j},\hfill \\ \hfill y_{j+1}& =y_j+[\phi \left(\frac{{\beta }_1{x}_j{v}_j}{1+v_j}+\frac{{\beta }_2{x}_j{y}_j}{1+y_j}\right)+\gamma l_j-a{y}_j]\Delta t+{\sigma }_3{y}_j\sqrt{\Delta t}{\zeta }_{3,j},\hfill \\ \hfill v_{j+1}& =v_j+[k{y}_j-\mu v_j-\xi v_j{w}_j]\Delta t+{\sigma }_4{v}_j\sqrt{\Delta t}{\zeta }_{4,j},\hfill \\ \hfill w_{j+1}& =w_j+[g{v}_j{w}_j-h{w}_j\left(t\right)]\Delta t+{\sigma }_5{w}_j\sqrt{\Delta t}{\zeta }_{5,j},\hfill \end{array}\end{array}$$

(20)

where $\Delta t>0$ is time increment, ${\zeta }_{i,j},(i=1,2,3,4,5)$ are independent Gaussian random variables which follow the distribution $N(0,1)$.

We assign the following parameter values: $\lambda =10,d=0.1,{\beta }_1=2,{\beta }_2=2,\phi =0.5,$$m=0.5,\gamma =5,a=10,k=2,\mu =10,\xi =3,g=2,h=4.$

We insert the different values of the white noises to discuss dynamical behaviors for the model (2). Initially, we consider the white noise values ${\sigma }_1=0.9,{\sigma }_2=0.9,{\sigma }_3=0.7,{\sigma }_4=0.9,$${\sigma }_5=0.8,$ the threshold conditions of unique stationary distribution $R_0^s=1.5886>1$ is satisfied. Figure 1 displays the time trajectories of the corresponding deterministic model of (2), which shows a stable behavior and also shows that the uninfected cells $x\left(t\right)$, latently infected cells $l\left(t\right)$, actively infected cells $y\left(t\right)$, free virus $v\left(t\right)$, and antibodies $w\left(t\right)$ of (2) fluctuate randomly with respective stochastic mean respectively.

Next, we increase the white noise values ${\sigma }_1=3.9,{\sigma }_2=3.9,{\sigma }_3=3.7,{\sigma }_4=3.9,{\sigma }_5=3.8,$ we obtain the condition of extinction results in Theorem 3 such that ${\tilde{R}}_0^s=0.5665<1$ is satisfied. Figure 2 shows that infected cells $l\left(t\right)$, actively infected cells $y\left(t\right)$, and free virus $v\left(t\right)$ can all die out as the white noise value increases. As a result, this indicates that white noise intensity can significantly reduce the number of virally infected cells and inhibit the growth of infected cells, as well as eliminate all latently, actively, and free virally infected cells.

Remark 1.

Under certain conditions, the disease can be eradicated. Through numerical simulations, it has been shown that a small intensity of white noises can maintain a stationary distribution, whereas a large intensity of white noises can result in the extinction of the disease.

6. Concluding Remarks

In this work, we discussed the fluctuations in cell dynamics of a new stochastic viral infection model with latently infected cells and a Holling type II functional response. We derived the existence of a global positive solution for such a considered model. By using the concept of Ito’s formula and Lyapunov function, we derived the sufficient conditions for unique stationary distribution/stochastic persistence of viral infection model and extinction of latently infected, actively infected cell and free virus particle. The derived theoretical condition for stochastic persistence $R_0^s=1.5886>1$ and extinction ${\tilde{R}}_0^s=0.5665<1$, then numerical simulations are verified. Moreover, theoretical and numerical analyses show that the intensity of noise effect is a prominent factor for controlling, survival, suppression, and extinction of viral infected cell growth in presence of immune cells.

Stochastic epidemic models with Markovian switching and time delays are the focus of our future research.