Applications of Bioelectrical Impedance Vector Analysis (BIVA) in the Study of Body Composition in Athletes

Featured Application

This work proposes an innovative and specific strategy for body composition assessment in athletes by applying BIVA, currently used in clinical practice, to sports.

Abstract

The study of body composition (BC) allows evaluating nutritional status, optimizing competitive performance, and monitoring the success of training regimens in athletes. Since BC reference techniques are expensive and/or invasive, in practice simpler, less expensive, and safer methods such as anthropometry are often used. The problem is that anthropometry requires a qualified anthropometrist, a rigorous measurement protocol using validated equipment, and a lengthy procedure because of its limited accuracy. Bioimpedance analysis (BIA) is an indirect method for estimating BC in a simple, fast, inexpensive, noninvasive, accurate, and reproducible manner. Despite the limitations of conventional BIA, it is still the most commonly used method for assessing BC in athletes. However, bioelectrical impedance vector analysis (BIVA) allows qualitative assessment of body cell mass (BCM) and hydration status without the need for biological assumptions and without being subject to conventional BIA errors. The purpose of this article was to demonstrate the uses and applications of BIA in the study of the BC and physical characteristics of athletes. For example, several practical cases of athletes from different sports were compared. The results obtained from somatotype studies, conventional BIA, and BIVA were included. BIVA interpretation and somatotype were consistent for all cases analyzed, but BIVA also provided information about hydration and BCM. The application of BIVA in the assessment of athletes can improve BC studies in sports because it is fast, simple, and reliable and neither imposes two-compartment-model limitations on BC estimation nor requires any biological assumptions.

1. Introduction

The study of body composition (BC) is an essential tool for evaluating nutritional status, optimizing competitive performance, and monitoring the success of training regimens in athletes [1,2,3]. BC assessment enables the identification of possible problems and proposes solutions that allow athletes to reach their maximum athletic potential. Therefore, it should be a habitual practice to control and monitor athletes.

The Ad Hoc Research Working Group on Body Composition Health and Performance, under the auspices of the International Olympic Committee (I.O.C.) Medical Commission, conducted a survey of BC assessment practices among international sporting organizations [4]. Despite the possibilities offered by BC, the majority of participants (69%) responded that it raised issues such as a lack of standardization, a high level of technical training needed for accurate assessment, and a need for more research. In this context, there is an obvious need for simple, fast, safe, and cost-effective techniques; standardized protocols; and specific reference values for sport BC assessment.

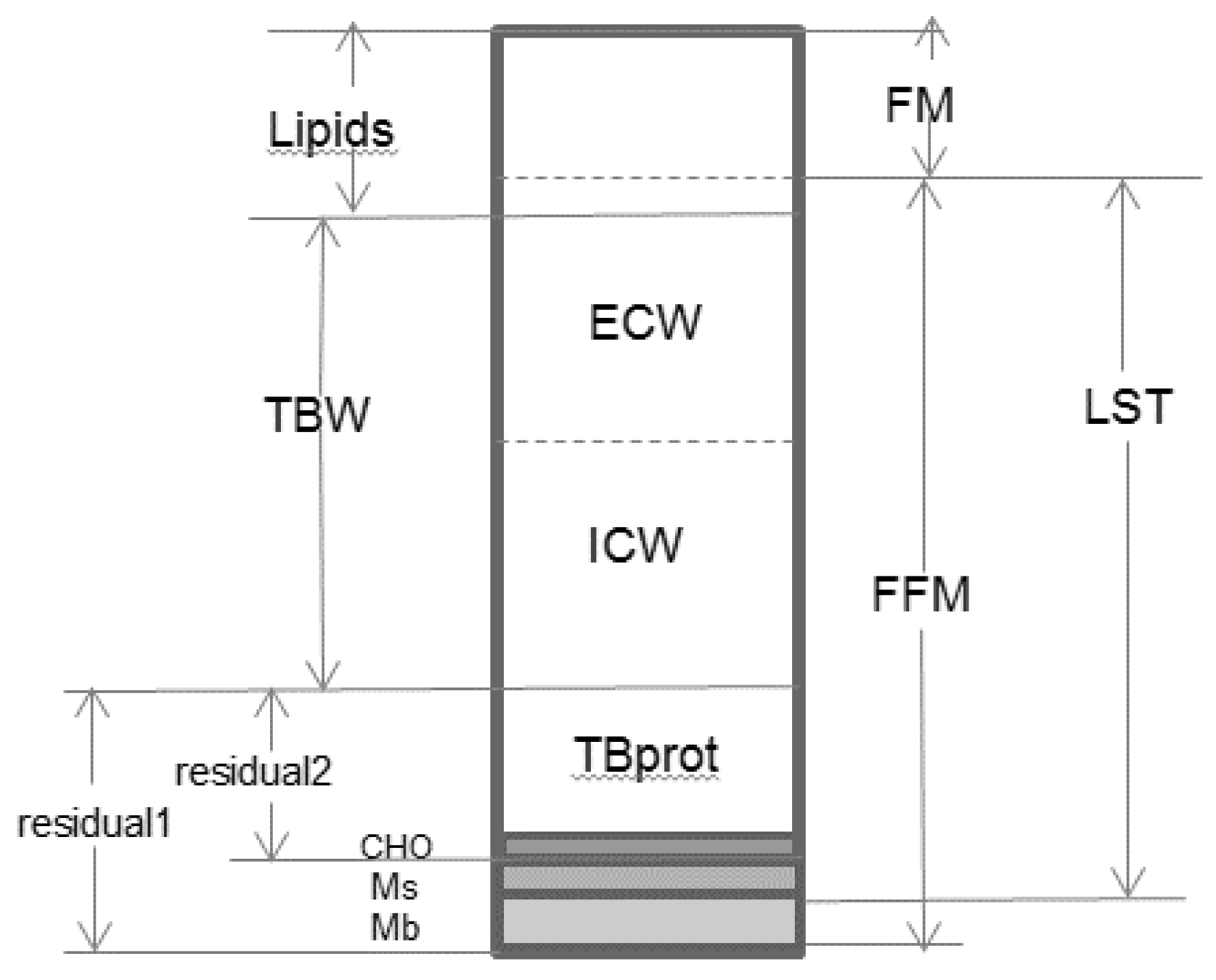
Wang et al. defined BC research as “a branch of human biology that has three interconnecting areas: body-composition levels and their organizational rules, measurement techniques, and biological factors that influence body composition”. They proposed a five-level model, with each level having different components (compartments), for organizing BC research [5]. However, depending on the BC model used, the main compartments of each level can be combined in different ways. Let us take as an example how the different components are grouped at the molecular level (Figure 1):

-

Two-compartment model: body mass is the sum of fat mass (FM) and fat-free mass (FFM).

-

Three-compartment model: body mass combines FM, total body water (TBW), and residual1 (i.e., the sum of glycogen (HCO), minerals (M), and protein); it may also include FM, bone mineral (BM), and lean soft tissue (LST).

-

Four-compartment model: body mass is measured by adding up FM, TBW, M, and residual2 (i.e., the sum of glycogen and protein).

The two-compartment model is most commonly used in practice to estimate BC, despite the fact that it assumes some biological considerations that are not always valid, such as stable FFM, hydration, and density. As a result, the estimation of compartments fails under certain specific physiological and pathological conditions (e.g., childhood, growth, elderly, or disproportionate fluid accumulation) [7,8]. The proper use of the multicompartment model is more useful for accurate estimation of changes in body compartments, especially in non-steady-state conditions [9].

An essential aspect of multicompartment models for BC studies is that they do not make biological assumptions; however, they require the use of different and specific instruments [10]. All these models were developed from equations that may include unknown components, known components, and/or measurable properties. Reference techniques such as hydrostatic weighing, dilution techniques, and dual energy X-ray absorptiometry were used to create these regression models. Considering the high cost, inexperience of practitioners, and potential side effects of the reference techniques, this model is not very commonly used in daily practice.

Today, the most widely used method for BC assessment in sports nutrition is anthropometry through the application of the International Society for the Advancement of Kinanthropometry (ISAK) protocol [11]. Anthropometric characteristics, especially when they are employed to identify the somatotype, allow the identification of morphological characteristics (endomorphic, mesomorphic, and ectomorphic components) of athletes. Although somatotype study is a relatively inexpensive technique with great advantages in evaluating and monitoring athletes, it also has disadvantages, which include the need for a well-trained anthropometrist who knows how to apply a specific protocol, validated equipment, and certain measurement time. The most widely used approach to somatotype is that proposed by Heath and Carter, which can be calculated by measuring two circumferences, skinfold thickness at four points, and two breadths, as well as weight and height, for a total of ten body dimensions [12]. Therefore, the correct assessment of somatotype according to the Heath–Carter method depends on the qualifications of the anthropometrist and the quality of the measuring instruments, including possible technical errors that may limit the accuracy of the anthropometric measurements and, therefore, the somatotype analysis [13].

Bioelectrical impedance analysis (BIA) is an easy-to-use and noninvasive technique with highly reproductivity and accurate measurements that can be repeated frequently using robust and portable equipment, making it truly suitable for use in “on-site work”. In addition, BIA does not require the active cooperation of patients and is fast and economically acceptable [14,15]. For these reasons, the use of BIA is also being popularized in sports. Although conventional BIA is based on a two-compartment model of body composition, BIA offers other practical possibilities that obviate the aforementioned limitations of two-compartment models.

The purpose of this article was to review the use and applications of BIA in sports and to explore the new possibilities that BIVA can offer to the study of BC in athletes, providing some examples as practical cases for comparing different approaches.

2. Bioelectrical Impedance Analysis (BIA)

BIA is an indirect technique for estimating body composition that determines the electrical impedance of a tissue to an alternating current with very low intensity and specific frequency. Electrical impedance (Z) consists of two components: resistance (R) and reactance (Xc). R is defined as the opposition to the flow of an alternating current through the intra- and extracellular ionic solutions. In the model, membranes behave like a capacitor that charges and discharges when current flows. Then, Xc (the inverse of the capacitance) is defined as the delay in the conduction of the current flow produced by cell membranes and tissue interfaces. In way, a lag is generated during the current flow that is expressed as a phase shift called the phase angle (AF) [16,17].

When a low-frequency current (0–5 kHz) flows, it is distributed exclusively through the extracellular space and Z is the same as R. Medium-frequency currents (50 kHz, most commonly used in single-frequency BIA) pass through some membranes and tissue interfaces. In this way, the current flows through the extracellular space and partly through the intracellular space, such that Z is determined by its two components: R and Xc. Finally, when a high-frequency current (>100 kHz) flows, the capacitances of membranes and interfaces are exceeded, and the current is distributed through all water compartments (total body water) and Z is also the same as R [16].

The estimation of the volume and body compartments of the BIA is based on Ohm’s law, which states that the opposition to the flow of an electrical current (Z) through a uniform cylindrically shaped conductor (in this case, the human body or its segments) is directly proportional to the length of the conductor (L) and indirectly proportional to the cross-sectional area of the conductor (A): Z = ρ L/A (where ρ is the resistivity coefficient of the conductor). Multiplying the numerator and denominator by L, Z is directly proportional to the square of the length and inversely proportional to the volume of the conductor (multiplying the cross-sectional area and the length). From this ratio, the volume of the conductor can be calculated (V = ρ L²/Z). Obviously, for the human body, L is equivalent to height (H).

The application of BIA to body composition analysis involves measuring the Z-value of a conductor (the human body) or its components (R and Xc). Transforming these electrical properties into body composition variables requires a two-compartment model. Total body water (TBW) is the largest component of the FFM and the best electrical current conductor of the human body. The TBW compartment is composed of water placed inside the cells (intracellular water (ICW)) and outside the cells (extracellular water (ECW)). Both are excellent current conductors, and they are separated by cell membranes that act as capacitors as described above.

Estimation of body compartments by BIA requires the use of predictive equations. Because of the strong linear relationship that exists between the “impedance index” (T²/Z) and TBW, all predictive models include it as a variable. In fact, the “resistance index” (T²/R) is often used instead of the “impedance index” because when the current is flowing at 50 kHz, the main component of Z is R (Xc represents a very small percentage of the total Z), so R and Z can be equated. Predictive models typically include other variables such as weight, height, age, sex, Xc, etc. [16,17,18].

In habitual practice, the most commonly used BIA is the single-frequency BIA (SF-BIA), an analysis characterized by a fixed low-current AC at 50 kHz flowing through the body. Based on the body part and electrode arrangement, whole body-BIA, through the use of a tetrapolar hand-to-foot electrode placement, is the most commonly selected analysis for SF-BIA, MF-BIA, BIVA, and BIS by technicians. In this method, two injector electrodes should be located dorsally on the right hand proximal to the metacarpophalangeal joint and on the right foot proximal to the metatarsophalangeal joint, and two voltage detector electrodes should be placed: one on the midline between the prominent ends of the right radius and ulna of the wrist, and one on the midline between the prominent ends of the medial and lateral malleoli of the right ankle. The current injection and detection of electrodes should be 5 cm apart [18]. Some BIA equipment uses a hand-to-hand or foot-to-foot configuration.

After the BIA application, the obtained data can be interpreted using two different patterns:

Conventional BIA: TBW and FFM are estimated by predictive models and.When FFM is subtracted from the total weight of the body, FM is obtained. This modality assumes some considerations that are not always true:

(a)

The human body (or body segments: trunk, arms, and legs) is considered as a cylindrical conductor with variable length, uniform cross-section, and homogeneous composition. However, it is composed of five cylinders with different lengths and cross-sections (the trunk and four extremities), with each one contributing in a different proportion to total body Z. This assumption is not respected in most cases of anomalies in body geometry (amputated limbs, etc.) [16].

(b)

FFM is estimated by assuming that, in a healthy body, hydration is a constant, so TBW is 73.2% of FFM (FFM = TBW/0.732 and FM = Weight-FFM). However, this is not true for certain diseases that present hydration alterations; in addition, FFM hydration changes with age [16,19].

These limitations necessitate the application of predictive models developed for predicting BC in similar populations (in terms of sex, age, race, physiological situation, pathology, etc.) [17,20].

This is one of the main reasons why the use and interpretation of the phase angle has been extended during the last years. Phase angle is defined as an angle consisting of the R and Xc vectors, quantified as the arctangent of Xc/R, and expressed in degrees. The phase angle is an indicator of the nutritional and functional status of the elderly, and it provides information about prognosis and mortality [15,20,21]. Its interpretation is based on its gross value and does not depend on predictive models.

Conventional BIA presents less intraobserver variability compared to anthropometry (intraobserver variability <2 Ohm for R and Xc and <1° for AF; test-retest variability = 1%) [22,23], provided that the assumptions previously commented on are respected and the most appropriate estimation models are used in each case. Furthermore, this technique can be used in bedridden patients and does not require specialized personnel or the active cooperation of the subjects. These aspects have contributed to the greater incorporation of conventional BIA into clinical practice and population studies in the last decades.

Bioelectrical impedance vector analysis (BIVA or vector-BIA) is a semiquantitative analysis method, because it does not employ mathematical models to estimate (absolutely or relatively) one or more body compartments. Hydration status and body cell mass (BCM) are evaluated by expressing the impedance vector, measured at 50 kHz, normalized to standing height (R/H and Xc/H), in a graph of R/H–Xc/H of the reference population (in terms of age, race, and sex) (Figure 2). This reference graph is made up of three concentric ellipses corresponding to the 50th, 75th, and 95th percentiles of the normal distribution of the values of the reference population (tolerance ellipses). Vectors that fall outside the 75th tolerance ellipse indicate an abnormal impedance [24]. The impedance vector displacements in the reference diagram provide information about the hydration and BCM of the subject. Since R is inversely proportional to ICW and ECW, and Xc is directly related to BCM, the vector length shows the tissue hydration status (vector displacements parallel to the major axis of tolerance ellipses indicate changes in hydration status: dehydration with long vectors, hyperhydration with short vectors), while the vector direction (phase angle) shows the BCM (vector displacements parallel to the short axis indicate changes in BCM: malnutrition, cachexia, or anorexia with smaller phase angles; obesity and high muscle mass subjects with larger phase angles) [15,24]. (Figure 2).

The BIVA model does not presume anything about body compartments, weight, geometry, or hydration status. Moreover, since it does not quantify body compartments, it is not subject to the sources of error associated with conventional BIA (errors due to regression models associated with gold standard techniques, cylindrical and homogeneous body assumptions, etc.).

Bioelectrical Impedance Analysis (BIA) in Sport

The accuracy of estimating body compartments (FM, FFM, and TBW) by applying conventional BIA in athletes depends on the predictive models used (specific to the sports population or a particular discipline) and on the previously mentioned assumptions, such as constant tissue hydration, a condition that is not always met in these subjects [15,25]. Therefore, the most appropriate predictive equations for FFM estimation in sports are those obtained from a multicompartment model containing the TBW determination [25,26].

To date, most predictive models for estimating FFM from BIA have been developed in the general population and are therefore not suitable for athletes, as they tend to overestimate and underestimate FM and FFM, respectively, depending on the athlete [26]. However, if athlete-specific equations are used, and the BIA analysis is performed under ideal conditions following a standardized measurement protocol, this technique could provide BC estimates similar to other methods based on a bicompartmental model, such as hydrostatic weighing or air displacement plethysmography.

Recently, a predictive model to estimate FFM in the adult athlete population (men and women from different sports disciplines: basketball, handball, judo and wrestling, karate and taekwondo, pentathlon, rugby, sailing, soccer, swimming, tennis, track and field athletics, triathlon, and volleyball) was developed and validated against a four-compartment model (R² = 0.94; concordance correlation coefficient = 0.94) [25]. This formula allows estimating accurately the FFM for all types of athletes, regardless of their somatotype or sport categorization. The same research group previously developed specific equations for estimating TBW and ECW in male and female athletes and in 15 different sports, validating the models against isotope dilution [27].

Over the last few years, the application of BIVA to the study of BCM (body cell mass), hydration, and changes in these variables during training or exercise has been intensively studied because of the limitations of conventional BIA in quantifying TBW or BC and the lack of specific predictive models for athletes [28,29,30]. It is important to re-emphasize that BIVA directly analyzes electrical variables and is not based on predictive models; therefore, it is not subject to errors or noncompliance with conventional BIA assumptions. Since impedance vector migration shows changes in TBW and the relation ICW/ECW (determined by the phase angle), some studies have shown that BIVA allowed the detection of the dehydration produced by intense exercise, as well as a more efficient posterior rehydration method (changes in body mass or respiratory and urinary/fecal water losses) than the usual method [30,31,32].

Furthermore, some articles have reflected a similar impedance vector distribution in elite athletes, with significantly different patterns from the general population (impedance vectors migrating to the left, outside the 50% ellipse of the reference population) [28,32,33]. Therefore, it is necessary to construct reference tolerance ellipses for the athlete population (by age, sex, and race) or for each sport-specific situation [29]. The Campa research group published tolerance ellipses for male and female athletes based on the analysis of 1556 athletes from 23 different sports disciplines [28]. This work also observed different bioelectrical properties in athletes depending on the type of sport: endurance, velocity/power, or team sports.

3. Discussion

It is evident that practicing sports, especially at the elite level, invariably requires an adequate BC and physique. An accurate description of these aspects allows identifying and optimizing the somatic and morphological characteristics of athletes according to their sporting practices. As a result, a training methodology that facilitates athlete-specific BC and physique development as well as good physical fitness can assist athletes in standing out in their sporting events [34]. Therefore, BC assessment is an essential component for monitoring athletes and for adapting to training and nutritional interventions aimed at optimizing their morphological conditions while controlling their health [35].

BC analysis requires different measuring instruments and specific expertise. Unfortunately, the use of reference methods for BC assessment (e.g., hydrostatic weighing or dilution techniques) is not always feasible because of the unavailability of extremely specific equipment, long scan times, potential deleterious effects, and high costs and experience required. Although Ackland et al. concluded that all of the techniques in common use have some inherent problems, these techniques are required for ordinary practice [1]. Anthropometry and conventional BIA are widely used as methods for field tests because of their ease of application and affordability [35,36]. However, the classical BC assessment using anthropometry or conventional BIA involves estimating BC at a molecular level using the two-compartment model; consequently, both make a number of biological assumptions that are not always applicable to athletes. On the other hand, the predictive equations applied in molecular anthropometry and conventional BIA have been developed and validated from general population samples, which could make them less valid for athletes [37].

In sports, the models more widely used for anthropometric assessment of BC are based on body fractionation. These methods identify up to five body components (skin, fat, muscle, bone, and visceral component) and involve estimating BC at the tissue level [5]. Although the five-level model has been used for BC estimation in diverse populations and is used in the standardized and validated protocols of the International Society for the Advancement of Kinanthropometry (ISAK), there is no evidence of its validation compared to the reference methods for different sports [11,35].

From another point of view, anthropometric measurements could also be implemented to analyze the morphological characteristics of athletes by calculating the three essential components of the somatotype (endomorphic, mesomorphic, and ectomorphic). According to the approach proposed by Heath and Carter, different combinations among the three morphological components allow the classification of the athlete’s body shape into one of thirteen categories [12]. This method can be used to characterize athletes because anthropometric features and somatotype vary according to different sports disciplines. In practice, the growing interest in the analysis of morphological characteristics and BC at the molecular level (FM and FFM) is becoming even more evident in sports, where the principal aim is to obtain the optimal BC that predisposes the athlete to achieve the highest performance [2].

As already mentioned in previous sections, the fundamental problem is that somatotype assessment involves a great deal of measurement time and requires a qualified anthropometrist and different validated tools [38]. Consequently, the accuracy of the Heath–Carter model in properly evaluating somatotype depends on the training of the anthropometrist and the quality of the measurement tools as well as possible technical errors that may reduce the precision and accuracy of the analysis [13].

Regarding conventional BIA, besides the inherent limitations of the two-compartment model and the lack of athlete-specific equations for different disciplines and levels of sports practice, there is often a lack of knowledge about the predictive equations used by BIA manufacturers to estimate FFM and/or FM. For all these reasons, the error of estimation may constitute a real handicap to the use of BIA, because, as expected, a smaller difference is observed between FM/FFM estimated by BIA and by reference methods (DXA) when BIA data are used in athlete-specific equations.

Inconsistent results have been found in studies that compared anthropometry and conventional BIA to the gold standard techniques (i.e., DXA) for BC assessment in sports. López-Taylor et al. demonstrated that in a group of professional male soccer players, only 12 of 31 anthropometric equations for body FM% estimation presented nonsignificant differences with DXA. Only 4 of them showed narrower limits of agreement [39]. Lozano Berges et al. also observed significant differences in the estimation of FM% by using DXA, anthropometry (Slaughter equation), conventional BIA, and air displacement plethysmography in young soccer players, concluding that such methods do not present good agreement in this population [40]. According to all the authors, the results of body composition analysis are extremely dependent on the methods used.

Although the most common use of conventional BIA is to estimate body compartments (i.e., FM, FFM, and/or TBW), BIA analysis offers more possibilities, such as other types of quantitative BC assessments and the qualitative analysis of BIVA. BIVA has the significant advantage of not making biological assumptions that rarely hold true in sports [32]. It is equally possible to obtain a great deal of information about BC using raw data, for example, the phase angle, the parameter that best represents the ICW/ECW ratio and reflects the integrity of the cell membranes [30].

BIA analysis is a simple, inexpensive, and extremely fast technique that can be used for both large-scale evaluations and individualized monitoring of athletes at “on-site work”. As a result, despite its limitations, conventional BIA, especially BIVA, is often employed to evaluate BC in sports [13,41,42]. Campa et al. have focused their research on the application of BIVA in sports. They showed that it was possible to discriminate between different categories of somatotypes by the bioelectrical properties of athletes. This was due to the predictive role of their raw measurements on muscle mass and body fluid distribution, which change according to FM and FFM [13]. They concluded that BIA and especially BIVA could be utilized to monitor the nutritional status and seasonal changes in body composition of athletes as well as to provide accurate intra- and interathlete comparisons [43].

4. Practical Applications of BIVA in Sports

Some examples of BIA, BIVA, and somatotype characteristics applied to sports are presented below along with corresponding interpretation. This section presents a series of cases, by way of example, in which SF-BIA was applied and interpreted according to the two previously reviewed patterns as well as other techniques widely used in athlete BC research. The sports included are:

-

Endurance sports: rhythmic gymnastics.

-

Velocity/power sports: athletics (team sprints and relay races) and canoeing.

-

Team sports: rugby.

Anthropometric measurements were performed according to standard procedures [44]. An electronic scale and a SECA stadiometer (Hamburg, Germany) were used to measure body weight (W, kg; precision: 100 g) and height (H, m; precision: 0.1 cm). Body circumferences were determined using a flexible and nonextendable steel tape (to the nearest 1 cm). Somatotypes were calculated by employing the Heath–Carter method [12].

Bioimpedance analysis (BIA) was conducted by single-frequency mode (at 50 kHz, 400 μARMS) using a tetrapolar electrode configuration with a BIA 101, AKERN-Srl bioimpedance measuring device (Florence, Italy). The measurement method was standardized in accordance with the protocol used by Lukaski [18]. Measurement errors of the system were determined using a precision resistor and capacitor, with <1% for R and <2% for capacitance. Fat-free mass (FFM) was estimated using the equation of Matías et al. [25], and fat mass (FM) was calculated as the difference between body weight and FFM. For bioelectrical impedance vector analysis, the components of the impedance vector (R and Xc) were normalized by the subject’s height (R/H (ohm/m) and Xc/H (ohm/m), respectively) and were expressed on the R–Xc graph (abscissa axis: R/H; ordinate axis: Xc/H). Individual impedance vectors were compared with the vector distribution of Campa et al.’s reference sports population [28] (50%, 75%, and 95% tolerance ellipses) (software provided by A. Piccoli—BIVA Programs, released in 2002).

The study was conducted according to the guidelines of the Declaration of Helsinki and was approved by the Clinical Research Ethics Committee (CEIC) of Valladolid–East Health Area (Protocol code: PI 16–512 of 17 January 2017).

Systematized exposure of the casework was carried out. Athlete data are presented in tabular form:

-

BMI, classified according to WHO criteria [45,46].

-

BC, determined by conventional BIA (FFM and FM). Reference values were obtained by the author who validated the equation [25].

-

Somatotype. Values and interpretations thereof are included in the table. Reference values for each discipline are also included [47].

-

Phase angle value.

-

BIVA graph.

4.1. Endurance Sports: Rhythmic Gymnastics

Subject: Female, 19 Years Old

Interpretation: With a BMI of 17.1 kg/m², the subject analyzed in

Table 1. Descriptive characteristics of the female athlete performing rhythmic gymnastics.

Somatotype		BIVA Nomogram
	Measurements		Reference Values 1
BMI (kg/m2)	17.1		18.5–24.9
SOMATOTYPE (Endo/Meso/Ecto)	2.8/1.9/4.9		1.9/2.4/5
FFM (kg/%)	34.4/75.1		47.0 (6.1)/—
FM (kg/%)	11.4/24.9		15.7 (4.9)/24.6 (4.8)
Phase angle	5.6		6.8 ± 0.8

BMI: body mass index; Endo: endomorph; Meso: mesomorph; Ecto: ectomorph; FFM: fat-free mass; FM: fat mass. ¹ Reference values: BMI [48]; somatotype [25]; phase angle [49].

was underweight. Her somatotype was classified as an endomorphic ectomorph (EnEc); while the reference for rhythmic gymnastics was a balanced ectomorph (BEc), both categories have a dominant ectomorphic component. Despite the low body mass of the subject, she presented significant adiposity. BC analysis by conventional BIA showed a similar distribution of body compartments to the reference population. However, the BIVA nomogram showed the mean impedance vector for a gymnast located outside the 95th ellipse in the upper right quadrant, indicating that the subject was very slim with a reduced active cell mass with respect to her reference population. Similar characteristics were also reflected separately in the reduced phase angle. These interpreted findings were consistent with the somatotype classification.

Conclusion: The athlete was very thin, with a reduced active cell mass and a relative adiposity. These specific characteristics were shown by both somatotype classification and BIVA analysis.

4.2. Velocity/Power Sports: Athletics (Team Sprints and Relay Races)

4.2.1. Subject: Female, 21 Years Old

Interpretation: BMI was at the midpoint of the nutritionally normal range; the subject detailed in

Table 2. Descriptive characteristics of the female athlete performing team sprints and relay races.

Somatotype		BIVA Nomogram
	Measurements		Reference Values 1
BMI (kg/m2)	21.6		18.5–24.9
SOMATOTYPE (Endo/Meso/Ecto)	2.4/3.3/2.8		2.4/3.3/3.3
FFM (kg/%)	46.5/74.3		47.0 (6.1)/—
FM (kg/%)	16.1/25.7		15.7 (4.9)/24.6 (4.8)
Phase angle	7.7		6.8 ± 0.8

BMI: body mass index; Endo: endomorph; Meso: mesomorph; Ecto: ectomorph; FFM: fat-free mass; FM: fat mass. ¹ Reference values: BMI [48]; somatotype [25]; phase angle [49].

was classified as normal weight. Her somatotype was quite similar to that of her reference population, although it presented a discrete smaller ectomorphic component, indicating a relative linearity of large volume per unit of height. The BC analysis agreed with the reference population. The mean impedance vector was located at the 50th percentile in the center of the reference ellipse, which reflected a normal BCM, as did the phase angle value (7.7).

Conclusion: Different methods classified this athlete as nutritionally normal, with BC characteristics similar to those of her reference population.

4.2.2. Subject: Male, 25 Years Old

Interpretation: The subject studied in

Table 3. Descriptive characteristics of the male athlete performing team sprints and relay races.

Somatotype		BIVA Nomogram
	Measurements		Reference Values 1
BMI (kg/m2)	25.0		18.5–24.9
SOMATOTYPE (Endo/Meso/Ecto)	2.0/5.3/2.0		1.8/5.2/2.7
FFM (kg/%)	72.1/87.8		65.2 (9.1)/—
FM (kg/%)	10.0/12.2		11.0 (4.7)/14.1 (4.6)
Phase angle	9.0		7.7 ± 0.8

BMI: body mass index; Endo: endomorph; Meso: mesomorph; Ecto: ectomorph; FFM: fat-free mass; FM: fat mass. ¹ Reference values: BMI [48]; somatotype [25]; phase angle [49].

showed a BMI within the limits of overweight. However, BC analysis by conventional BIA indicated a high FFM (low FM), discretely above the reference values. The somatotype suggested a balanced mesomorphic subject, which implied good musculoskeletal development. In the BIVA graph, the impedance vector was located in the 75th ellipse, in the upper left quadrant, indicating that the subject was athletic, coinciding with the somatotype. The phase angle value was extremely high, also reflecting an elevated BCM.

Conclusion: Although the BMI indicated overweight status, the BC, somatotype, and BIVA nomogram demonstrated that the subject was athletic and muscular.

4.3. Velocity/Power Sports: Canoeing

4.3.1. Subject: Female, 21 Years Old

Interpretation: The subject in

Table 4. Descriptive characteristics of the female athlete performing canoeing.

Somatotype		BIVA Nomogram
	Measurements		Reference Values 1
BMI (kg/m2)	24.7		18.5–24.9
SOMATOTYPE (Endo/Meso/Ecto)	3.1/6.2/1.2		3.4/4.8/2.3
FFM (kg/%)	54.3/79.8		47.0 (6.1)/—
FM (kg/%)	13.7/20.2		15.7 (4.9)/24.6 (4.8)
Phase angle	9.1		6.8 ± 0.8

BMI: body mass index; Endo: endomorph; Meso: mesomorph; Ecto: ectomorph; FFM: fat-free mass; FM: fat mass. ¹ Reference values: BMI [48]; somatotype [25]; phase angle [49].

was a female with a BMI in the upper limit of normality, but she had a lower FM percentage than her reference population. The somatotype of the subject was dominated by the mesomorphic component, implying good musculoskeletal development. BIVA confirmed this observation, as the impedance vector was located in the 95th ellipse on the left side above the short axis, reflecting a high muscle mass. The very high value of the phase angle also supported this finding.

Conclusion: As in the previous case, the subject had good musculoskeletal development.

4.3.2. Subject: Male, 33 Years Old

Interpretation and Conclusion: This subject detailed in

Table 5. Descriptive characteristics of the male athlete performing canoeing.

Somatotype		BIVA Nomogram
	Measurements		Reference Values 1
BMI (kg/m2)	28.4		18.5–24.9
SOMATOTYPE (Endo/Meso/Ecto)	2.3/8.0/0.8		2.4/6.5/1.4
FFM (kg/%)	77.4/86.0		65.2 (9.1)/—
FM (kg/%)	12.6/14.0		11.0 (4.7)/14.1 (4.6)
Phase angle	9.0		7.7 ± 0.8

BMI: body mass index; Endo: endomorph; Meso: mesomorph; Ecto: ectomorph; FFM: fat-free mass; FM: fat mass. ¹ Reference values: BMI [48]; somatotype [25]; phase angle [49].

was a male from the same sport discipline as the athlete discussed Section 4.3.1 (canoeing). He had a higher BMI, which was classified as overweight, but his BC characteristics and somatotype classification were similar to those of the athlete discussed in Section 4.3.1, indicating very remarkable musculoskeletal development.

4.4. Team Sports: Rugby

Subject: Female, 26 Years Old

Interpretation: The subject described in

Table 6. Descriptive characteristics of the female athlete performing rugby.

Somatotype		BIVA Nomogram
	Measurements		Reference Values 1
BMI (kg/m2)	37.5		18.5–24.9
SOMATOTYPE (Endo/Meso/Ecto)	3.9/4.1/2.3		3.6/4.9/1.9
FFM (kg/%)	83.8/70.8		47.0 (6.1)/—
FM (kg/%)	34.7/29.3		15.7 (4.9)/24.6 (4.8)
Phase angle	6.7		6.8 ± 0.8

BMI: body mass index; Endo: endomorph; Meso: mesomorph; Ecto: ectomorph; FFM: fat-free mass; FM: fat mass. ¹ Reference values: BMI [48]; somatotype [25]; phase angle [49].

was a female rugby defensive player. With a BMI of 37.5 kg/m², she appeared obese (class II). Although the FM percentage was higher than her reference population, the BC values did not reflect as much adiposity as the BMI suggested. The somatotype was more dominated by the endomorphic component than that in her reference population, indicating moderate relative adiposity and moderate relative musculoskeletal development. The mean impedance vector was located between the 75th and 95th ellipses, in the lower left quadrant, which reflects that the athlete presented a high BCM and high adiposity.

Conclusion: Based on the BC characteristics, somatotype, and BIVA nomogram, the athlete was highly muscular and had high adiposity, but not as much as expected considering the elevated BMI value registered.

5. Conclusions

BIVA is a quantitative analytical method for the study of body composition based on the measurement of tissue electrical impedance. It is currently employed in clinical practice because of its rapidity, ease of use, harmlessness, high reproduction rate, and lack of active patient cooperation. All these aspects are common to both BIVA and BIA; however, in addition, BIVA does not presume anything about body compartments, weight, geometry or hydration status, so it does not present the limitations of the two-compartment model for BC evaluation and thus produces fewer estimation errors to quantify TBW or BC. Because of to the excellent results of BIVA in clinical practice, it is here proposed for use in sports. Recent studies have shown that BIVA can be applied to monitor athletes by using both quantitative and qualitative parameters, as a new regression equation has been developed specifically for athletes [25], and the impedance vector distribution is similar to that of elite athletes, with clear differences from the general population [28,32].

As shown in the examples provided, BIVA is consistent with somatotype and coherent with BC interpretation; however, BIVA also provides information about hydration and BCM. Furthermore, there is evidence that it can also detect dehydration caused by intense exercise and posterior rehydration more efficiently than conventional methods. In conclusion, the application of BIVA in the evaluation and monitoring of athletes could improve BC studies in sports if used and interpreted correctly. However, further validation of BIVA for different sports and disciplines is necessary, which is equally useful to develop reference tolerance ellipses for the athlete population (by sport, age, gender, and race).