Handling Imbalanced Datasets for Robust Deep Neural Network-Based Fault Detection in Manufacturing Systems

Abstract

Over the recent years, Industry 4.0 (I4.0) technologies such as the Industrial Internet of Things (IIoT), Artificial Intelligence (AI), and the presence of Industrial Big Data (IBD) have helped achieve intelligent Fault Detection (FD) in manufacturing. Notably, data-driven approaches in FD apply Deep Learning (DL) techniques to help generate insights required for monitoring complex manufacturing processes. However, due to the ratio of instances where actual faults occur, FD datasets tend to be imbalanced, leading to training challenges that result in inefficient DL-based FD models. In this paper, we propose Dual Logits Weights Perturbation (DLWP) loss, a method featuring weight vectors for improved dataset generalization in FD systems. The weight vectors act as hyperparameters adjusted on a case-by-case basis to regulate focus accorded to individual minority classes during training. In particular, our proposed method is suitable for imbalanced datasets from safety-related FD tasks as it generates DL models that minimize false negatives. Subsequently, we integrate human experts into the workflow as a strategy to help safeguard the system. A subset of the results, model predictions with uncertainties exceeding a preset threshold, are considered a preliminary output subject to cross-checking by human experts. We demonstrate that DLWP achieves improved Recall, AUC, F1 scores.

1. Introduction

With advancements in modern-day manufacturing, rapid automation through industry 4.0 (I4.0) [1,2,3,4,5,6] has led to increased and improved access to real-time data from complex industrial operations. Subsequently, reliable fault detection (FD) systems have become essential for safety, efficiency, and sustained product quality under these dynamic industrial environments. For large-scale systems in manufacturing, FD data comes from numerous process variables which feature complex interactions, resulting from nonlinear and highly correlated process variables captured using a multitude of sensors installed over entire distributed control systems (DCS) [7].

However, FD data are captured under extreme manufacturing conditions, leading to noisy measurements coupled with multiple sensor failures that result in incomplete data due to missing data points. Further, for a relatively stable industrial operation, the data generation process is such that actual incidences of fault, even though probable, are far fewer than incidences considered normal, resulting in imbalanced datasets available for FD methods [8]. Although data-driven FD methods [9,10,11,12] have proven to be more reliable, it is imperative to develop robust models that tackle the problem of imbalanced datasets, especially in the wake of safety-related scenarios. In particular, for safety-related FD systems, undetected failures resulting from false-negative predictions can be catastrophic, leading to the total shut down of the entire operation and even in other cases resulting in loss of life [13].

Current works on data-driven FD models have led to the advancement of FD systems built using multivariate statistical methods or machine learning techniques, including Deep Neural Networks (DNNs) [14]. Nevertheless, further research issues persist due to the following: (1) most existing models do not explicitly deal with the problem of real-world imbalanced datasets, (2) models tackling imbalanced datasets depend on sophisticated data augmentation techniques, robust feature extraction (i.e., these models are application-specific), while others employ either one-class or one-vs-all classification strategies, which do not scale well as the number of target classes increases, (3) for safety-related and high-cost applications, it is necessary to limit the occurrence of false-negatives or type II errors while also providing informative measures of uncertainty regarding model predictions.

Recently, DL applications have achieved state-of-the-art (SOTA) performance in a wide variety of tasks [15,16,17,18,19,20]. The underlying assumption has been that datasets used in training these application models have a target class distribution that is reasonably well balanced across all the classes. However, real-world datasets are usually imbalanced with a long-tailed data distribution that feature under-represented classes [21,22,23]. Such skewed target class distributions exist in a variety of manufacturing application areas [8,24,25,26,27], including in many other real-world applications such as autonomous driving, fraud detection, network intrusion, and rare disease detection where the datasets are characteristically imbalanced [15,28,29,30]. Therefore, a classifier encounters an imbalanced classification problem when trained on an imbalanced dataset where samples from the minority class are scarce compared to the majority class. Classifiers trained on imbalanced datasets generate models that can achieve a perceived high overall model accuracy, even while misclassifying all of the samples from the minority class since they only make up a relatively small portion of the entire dataset [15,31].

In this paper, we seek to develop a DL-based FD system by generating effective models backed by coordinated reinforcements from human experts. Further, we acknowledge a significant trade-off between safety and operational efficiency for DL-based FD systems and seek to address this in our proposed solution. In particular, our approach involves designing a DL method that generates robust models from imbalanced datasets together with a data-informed call to action that enlists human experts for feedback on a subset of the model predictions with high uncertainty exceeding a preset threshold. Therefore, we propose a classifier-level method known as Dual Logit Weight Perturbation (DLWP) loss for DL-based FD systems. Based on our approach, our main contributions can be summarized as follows:

• We propose a classifier-level method called DLWP loss, which can be applied directly to DNNs, preserving the original dataset distribution during training while improving overall classifier performance on the imbalanced dataset.
• We introduce logit weight vectors, a set of tunable network hyperparameters adjustable on a case-by-case basis, meant for regulating the levels of focus accorded to each of the distinct target classes during training.
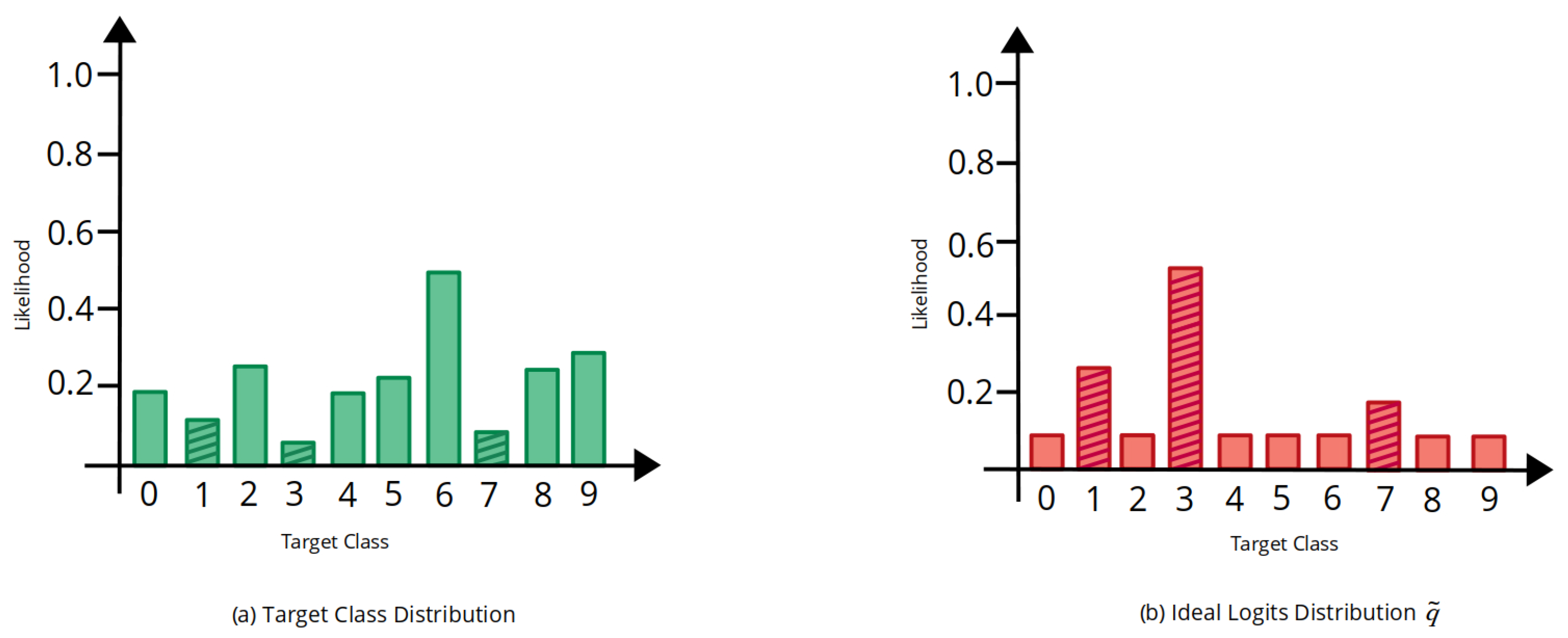
• We show that information from the imbalanced target class distribution can be strategically used to generate a suitable logit weight vector that predisposes a DNN to focus on minority samples during critical periods of training.
• We introduce a training regime that facilitates switching between predefined logit weight vectors, one for each training phase of a DNN, achieving improved classifier performance on the minority samples while still effectively generalizing the entire dataset.
• We propose a data-informed strategy for safety-related FD systems first by generating models that prioritize recall, followed by a call to action enlisting human experts for feedback on a subset of the results; model predictions with high uncertainty requiring further action.

The remainder of this paper is structured as follows. In Section 2, we present a review of the literature and related work on methods used to address imbalanced dataset classification problems. In Section 3, we describe associated concepts from which we build upon our proposed method and weight vector selection strategies. We also present the implementation details, uncertainty estimation methods, datasets, and the evaluation techniques used for the experiments. In Section 4, we discuss the results of our experiments. Finally, in Section 5, we conclude the paper with an overview of our contributions and future work.

2. Review

The three main categories of FD include model-based, knowledge-based and, data-driven approaches [9,10,11]. In this work, we focus on data-driven methods that are more suitable in the context of I4.0 as they rely upon industrial big data (IBD), containing valuable historical information on the operation processes. The data-driven approach used in this paper is a supervised method [32] that depends on labeled data, providing prior information about the fault subspace or region in data space. General approaches designed for tackling imbalanced datasets can be split into two types: re-sampling and reweighting. Data re-sampling techniques such as undersampling and oversampling have been used as a solution to tackle the imbalanced dataset problem [31,33,34]. Undersampling-based methods work by reducing the number of samples from the majority class to achieve a more balanced target class distribution. These methods are synonymous with data purging, a practice that always leads to the loss of information from the original dataset [35]. In cases where the original dataset is not large enough, undersampling further reduces the size of the dataset, hence limiting the capacity to train a robust classifier [33]. Oversampling-based methods, on the other hand, solve the imbalance problem by generating random replica samples from the minority class to balance the distribution of the target classes. These additional copies end up increasing the likelihood of over-fitting by the classifier. Another downside in cases where the original dataset is already large is that oversampling creates even more data that has to be evaluated by the classifier, leading to an increase in the workload [31,34].

Oh and Lee [36] propose a Gaussian Process Regression (GPR) and Generative Adversarial Network (GAN) framework through which complete data are generated, first by replacing missing values using GPR and finally applying GAN to generate refinements including new data similar to the real data. Saqlain et al. [25] use data augmentation techniques to oversample the minority and combine this with a convolutional neural network (CNN) to automatically extract effective features of various defect classes. Lee et al. [37] develop a fault detection and classification (FDC) model out of stacked denoising autoencoders to perform robust feature extraction from data that contains noise induced by mechanical and electrical disturbances. In [38], the authors proposed an FDC-CNN model that makes use of special receptive fields as feature extractors, achieving high performance on FDC tasks while improving training speed. We also note that FD models depending on robust feature extraction can be application-specific, requiring explicit knowledge of relations between process variables. Nonetheless, models dependent on feature extraction can easily be extended using our classifier-level method to factor in imbalanced datasets. Lee et al. [27] employ the use of one-class classification, while Adam et al. [24] propose a hybrid ANN-Naive Bayes classifier for a two-class imbalanced dataset. Both these strategies face challenges scaling up as the number of target classes increase. Further, Cho et al. [39] propose a transfer learning-based approach, a method to counter imbalanced datasets by pre-training a Neural Network (NN) using a larger dataset as the source domain and eventually transferring the knowledge to train an NN using the imbalanced dataset in the target domain.

Our method falls in the data reweighting category, thereby preserving dataset integrity. Cost-sensitive reweighting is a widely used strategy where adaptive weights are applied to different classes based on a chosen criteria. Refs. [40,41] propose unique formulations for computing a class-balancing weight hyperparameter. They use the class weighting approach on the loss function to balance the losses from the minority and majority samples.

Mikolov et al. [42] use inverse class frequencies with thresholding to help subsample more frequent words out of a corpus hence countering the imbalance with the rare words. Refs. [43,44,45] use a reweighting scheme generating class weights from the inverse of their frequency. However, from [45], we observe that reweighting methods negatively impact the optimization of deep models, especially for large datasets with extreme data imbalance.

Additionally, Cui et al. [23] demonstrate that reweighting by inverse class frequency has limited gains and instead yields poor performance on frequent classes. Further, the approach in [23] introduces the concept of the weights made up of quantities inversely proportional to the effective number of samples per class. Our work builds upon this concept and also compares methods from [23] as one of the baselines. Recently, Lin et al. [46] introduced a different form of weighted loss called focal loss (FL). The composition of FL is such that a penalty factor ${(1-p\left(\mathit{correct}\right))}^{\gamma }$ is applied to cross-entropy loss. $\gamma$ is a manually tuned focusing hyperparameter that is adjusted to reduce the relative loss of well-classified (easy) samples and increase the loss for misclassified (hard) samples during training. We note that FL loss by design is more effective to intra-class as opposed to inter-class imbalance. Our method works well with inter-class imbalance, which is more suitable for DL-based FD systems where datasets are made up of labeled in-sample (IS) and out-of-sample (OOS) process data.

Inspired by the idea of regularization, the approach in [47] prioritizes regularization of minority classes, achieving improved generalization error for the minority classes without sacrificing the model’s ability to fit the majority classes. The idea, label-distribution-aware margin (LDAM) loss, requires a label-dependent regularizer that depends on both the weight matrices and the labels alike to differentiate between the majority and minority samples. Anantrasirichai et al. [48] propose DefectNet featuring a hybrid loss for multiclass FD with an imbalanced dataset. The DefectNet network architecture is composed of two parallel CNN paths to detect different target sizes.

In

Table 1. Summary of approaches used in tackling imbalanced datasets.

Research	Specification	Remarks
Oversampling [31,33,34]	Data re-sampling technique for imbalanced datasets	Generates random replica samples from the minority class to balance the distribution of the target classes. Increases likelihood of over-fitting.
Undersampling [31,33,34,35]	Data re-sampling technique for imbalanced datasets	Reduces the number of samples from the majority class to achieve a more balanced target class distribution. Loss of information through data purging of the original dataset.
GPR-based GAN [36]	Data re-sampling and imputation for imbalanced datasets	Combines the use of Gaussian Process Regression and Generative Adversarial Network to impute missing data points and generate new samples.
Convolutional Neural Network for Automatic Wafer Defect Identification (CNN-WDI) [25]	Data re-sampling and feature extraction for imbalanced datasets	Combines CNN feature extraction and oversampling through data augmentation for imbalanced dataset. Data augmentation techniques can be application specific.
One-class Fault detection [27]	One-class learning for imbalanced datasets	Multi-network architecture with a fault-detection module based on one-class learning. Challenges scaling up as the number of target classes increase.
Cost-sensitive reweighting [23,40,41,42,43,44,45]	Class-balancing weights for imbalanced datasets	Class-balancing weight hyperparameter for loss functions. Reweighting by inverse class frequency has been shown to have limited gains.
Focal Loss (FL) [46]	Class-balancing penalty factor for imbalanced datasets	Balances loss for well-classified (easy) vs. misclassified (hard) samples during training. FL loss is more effective to intra-class data imbalance.
Label-Distribution Aware Margin (LDAM) loss [47]	Label-dependent regularizer for imbalanced datasets	Label-dependent regularizer that depends on both the weight matrices and the labels for class-rebalancing.
DefectNet for Fault Detection [48]	Class-rebalancing and feature extraction for imbalanced datasets	Combines CNN feature extraction and hybrid loss function for imbalanced dataset. Feature extraction module can be application specific.
Transfer Learning-Based Fault Diagnosis [39]	Transfer Learning for imbalanced datasets	Transfer of knowledge from neural networks trained in domains with enough data to others in domains that encounter an imbalanced dataset. Performs well in scenarios where target and source domain a more similar.

, we provide a summary of the approaches used in tackling imbalanced dataset problem for real-world datasets. For the comparable cost-sensitive learning methods, there remains a challenge as there is no clear way of determining the optimal class weight vector to be used as a class-balancing weight hyperparameter for the loss function. Based on our approach, we propose a method, DLWP loss, focused on imbalance across the classes through a class-specific weight vector that introduces relevant perturbations to the logit layer to help the classifier generalize better on imbalanced datasets. We also provide proposed guides on how to select the ideal logit weight, a class-specific weight vector we use as the class-balancing weight hyperparameter for the loss function.

3. Materials and Methods

In this section, we describe the concept of dual logit weight perturbation for DNNs. First of all, we briefly describe temperature-scaled softmax for DNNs. Second, we describe a closely related concept known as logit perturbation and draw its relationship with noise-based logit regularization. Third, we formalize the implementation of logit perturbation in DNNs and the basis for which we perform the switching logit weight vectors during training. Fourth we provide some weight selection strategies, followed by an application and implementation section. We then describe some of the uncertainty estimation methods we apply to predicted samples. Finally, we outline the datasets used and the evaluation techniques we use in our experiments.

3.1. Preliminaries

Consider a set of N i.i.d. labeled samples from an imbalanced dataset $\mathcal{D}={\left\{\left({\mathit{x}}_n,{\mathit{y}}_n\right)\right\}}_{n=1}^N$ where ${\mathit{y}}_n$ represents the corresponding ground-truth label for the input sample ${\mathit{x}}_n$. In this paper, our goal is to generate a predictor $f(\mathit{x},\mathit{\theta })$ with good enough network parameters $\mathit{\theta }$ that can enable us to minimize the average loss on the imbalanced dataset $\mathcal{D}$ while still improving prediction accuracy over the minority samples. For a classification problem with $C=\{1,\dots ,C\}$ classes, we train a DNN that produces, as set of extracted features, the logit vector $\mathit{z}={\mathit{\theta }}^{\top }\mathit{x}\in {\mathbb{R}}^C$ in the penultimate layer. These features are then passed onto the softmax activation function [49] (p. 79) to produce the probability vector representing a relative measure of confidence in each of the individual C classes. The softmax activation function $\sigma {\left(\mathit{z}\right)}_i$ generates a conditional probability $\mathit{p}(y=i|\mathit{x})\in {\mathbb{R}}^C\mathrm{for}i\in \{1,\dots ,C\}$.

3.2. Temperature-Scaled Softmax for DNNs

For knowledge transfer between DNNs, Hinton et al. [50] used temperature scaling in softmax to modulate the probability distributions produced by the different models. Temperature scaling in DNNs is achieved by softmax activation in the following functional form:

$$\mathit{p}(y=i|\mathit{x})=\frac{exp\left({\mathit{z}}_i/\mathcal{T}\right)}{{\sum }_{j=1}^{C}exp\left({\mathit{z}}_j/\mathcal{T}\right)}$$

(1)

$\mathcal{T}$ is a temperature hyperparameter that is normally set to 1. Ref. [50] show that using higher values for $\mathcal{T}$ produces softer probability scores over classes resulting in distributions that tend more towards a uniform distribution. On the other hand, lower $\mathcal{T}$ values place most of the probability mass onto the most probable state resulting in a more spiked non-uniform distribution. In their work, ref. [50] demonstrate that temperatures in the range $\mathbf{2}.\mathbf{5}$ to $\mathbf{4}$ worked significantly better than higher or lower temperatures. They eventually settle on $\mathcal{T}=\mathbf{2}$ as the ultimate temperature value for their model. Guo et al. [51] use temperature scaling to achieve confidence calibration for neural networks. Through the use of higher $\mathcal{T}$ values, improved confidence calibration is obtained from network outputs that feature softer probability scores over classes. The softer probability scores lead to higher entropy and penalized network overconfidence. Furthermore, model accuracy is not affected since the temperature scaling parameter $\mathcal{T}$ softens the class probabilities uniformly. Setting the temperature scaling value $\mathcal{T}$ to 1 reverts the solution to the already familiar softmax activation function in [49] (p. 79).

Extending to multiclass classifiers, Kull et al. [52] propose a multiclass calibration method derived from Dirichlet distributions, inspired by a generalized beta calibration method for binary classification. The multiclass calibration idea replaces the single temperature-parameter $\mathcal{T}>0$ over all classes with a calibration map from Dirichlet distributions.

3.3. Logit Perturbation

Logit perturbation involves the introduction of noise to logits in the penultimate layer of a DNN to bring about relevant deviations in the output. A closely related concept, logit squeezing [53] works by adding a regularization term to the training objective to improve adversarial robustness. The regularization term in logit squeezing penalizes the norm of logits retaining only norms that have smaller magnitudes.

For some logit vector $\mathit{z}\in {\mathbb{R}}^C$, logit perturbation is achieved by adding $\mathit{\epsilon }\in {\mathbb{R}}^C$, the noise vector as follows:

$${\mathit{z}}_{\epsilon }=(\overrightarrow{\mathbf{1}}+\mathit{\epsilon })\odot \mathit{z}$$

(2)

where $\overrightarrow{\mathbf{1}}\in {\mathbb{R}}^C$ a is a vector of C ones and ⊙ represents Hadamard (element-wise) product. Refs. [54,55] show that the logit regularization fine-tunes the logits leading to improved classifier robustness. Temperature scaling can be considered as a form of logit perturbation where $\mathcal{T}$, the temperature parameter used in temperature scaling is set up as noise penalty added to the original logit. Let $\mathit{\epsilon }\in {\mathbb{R}}^C$, be a noise vector with all C elements ${\epsilon }_i=({\mathcal{T}}_{-1}-1)$. For the logit vector $\mathit{z}\in {\mathbb{R}}^C$, the perturbation is achieved as follows:

$${\mathit{z}}_{\epsilon }=(\overrightarrow{\mathbf{1}}+\mathit{\epsilon })\odot \mathit{z},\{\left({\epsilon }_1,\dots ,{\epsilon }_C\right)\in {\mathbb{R}}^C:{\epsilon }_i=({\mathcal{T}}_{-1}-1)\forall i\}$$

(3)

Formally, the temperature parameter in Equation (1) can be interpreted as having the same effect as the perturbation caused by noise vector $\mathit{\epsilon }$ in Equation (3).

3.4. Class Rebalanced Noise Logit Perturbation for DNNs

In the context of imbalanced datasets, we seek to introduce noise that has the effect of rebalancing the logits to counter the effects that dominating majority classes have over the minority classes. Therefore, we propose the introduction of noise to the logits in the form of weight vectors that amplify logits from minority classes while suppressing the logits from majority classes. To achieve this effect, we replace the noise vector in Equation (3) with a class rebalancing weight vector $\mathit{q}$. The individual ${\mathit{q}}_i$ elements in vector $\mathit{q}$ correspond to inverse class frequencies meant to rebalance class logits by assigning higher weights to logits from the minority classes and lower weights to logits from the majority classes. Unlike temperature scaling, perturbation noise from weight vector $\mathit{q}$ does not uniformly soften the class probabilities, potentially altering the maximum of the softmax function. The modified logit perturbation equation is as follows:

$${\mathit{z}}_{\epsilon }=(\overrightarrow{\mathbf{1}}+\mathit{\epsilon })\odot \mathit{z},\{\left({\epsilon }_1,\dots ,{\epsilon }_C\right)\in {\mathbb{R}}^C:{\epsilon }_i=({\mathit{q}}_i-1)\forall i\}$$

(4)

For our implementation, we begin by generating a set of logit weights, hyperparameter $\tilde{\mathit{q}}$, that represents an ideal case scenario for the classifier given the imbalanced dataset. This is the noise vector, which we term the ideal logit weights. To this end, we argue that by generating an ideal logit weights vector $\tilde{\mathit{q}}$ that is reflective of the level of imbalance in the dataset, we can implement a class rebalanced logit output layer to help bias the DNNs inference in favor of the target classes belonging to the minority. Therefore, we propose two methods as guidelines for generating the ideal logit weights vector $\tilde{\mathit{q}}$; (1) relative likelihood approach and (2) effective number of samples approach.

① Relative Likelihood Approach: To generate the ideal logit weights vector, we go back to the preliminary stage of dataset exploration. During this stage, we examine the target class distribution to infer the actual extent of dataset imbalance. We note that our problem setting is such that the samples of interest almost always fall in the minority classes. With this information, we can formulate a weight vector representing the classifier ideal case scenario where minority class samples are given more priority over the majority class samples.

Determination of the ideal logit weights vector involves carrying out subjective judgment on each of the individual classes from the target classes to reflect our personal belief of what the precise ideal logit weight for a given target class should be. The process of carrying out subjective judgment to obtain relative class weights is the human expert input that produces logit weight vectors, applied to the DNN as hyperparameters. Ideally, expert elicitation in industrial settings comes from experienced human experts (manufacturers) who understand what target classes are more important than others and their desired priority levels.

To enable us to maintain the correlation of magnitudes between weights across all classes, we choose to represent the ideal logit weights vector as a proper probability distribution. Therefore, to generate the weight vector as a probability distribution, we use the relative likelihood approach [56] (p. 64), a technique from the method; subjective determination of prior density. This technique rates the class probabilities relative to each other in terms of “most likely” and “least likely”. For multiclass problem settings, one of the classes could be chosen as the point of reference and the others compared to it in terms of the relative likelihoods such as half as likely, twice as likely, n times as likely, where $n\in {\mathbb{R}}^{+}$, etc.

Take, for instance, the target class distribution illustrated on the left-hand side of Figure 1. It represents an imbalanced dataset comprising of $C=10$ target classes where $\{1,3,7\}$ are the minority classes with different levels of likelihood. We apply the relative likelihood approach first by selecting class 0 as the reference class. We then weight all the majority classes to be equally likely to occur compared to class 0. Further, for the minority, we weight classes 1, 3, and 7 to be, respectively, three, six, and two times as likely compared to class 0. The result is a logit weight vector $\tilde{\mathit{q}}\in {\mathbb{R}}^C$ represented in terms of a probability distribution over all the C classes, as illustrated on the right-hand side of Figure 1.

② Effective Number of Samples Approach: Following the proposed theoretical framework in [23], the effective number of samples per class is used in place of the usual class frequencies. The effective number of samples for some class i can be calculated by the formula $E_{n_i}=\frac{(1-{\beta }_i^{n_i})}{(1-{\beta }_i)}$ where $\beta \in [0,1)$ is a hyperparameter and $n_i$ is the number of samples in total for class i. To help achieve a class-balanced loss, $\mathit{\alpha }\in {\mathbb{R}}^C$, a vector of weighting factors composed of C individual elements, each inversely proportional to the effective number of samples per class $i:{\mathit{\alpha }}_i\propto 1/E_{n_i}$ is used to perform rebalancing on the loss. We note that, in order to perform useful penalization of the loss function, the composition of $\mathit{\alpha }$ is such that minority classes are weighted higher compared to majority classes. This is the same type of blueprint we use to formulate an ideal logit weights vector using the relative likelihood approach. We perform further normalization on the weight vector $\mathit{\alpha }$ to reduce the magnitude of individual elements, which otherwise have the potential to introduce incoherent perturbations to the logit layer. From this method, vector $\mathit{\alpha }$ is our ideal logit weights vector $\tilde{\mathit{q}}$.

Applying either of the two approaches proposed above, we can generate the ideal logit weights vector $\tilde{\mathit{q}}$ that is biased towards the minority classes and will be used as part of the inference drawing process in the DNN. Introducing weight vector $\tilde{\mathit{q}}$ as perturbation to the logit layer $\mathit{z}$ and using formula (4) results in a softmax of the following functional form:

$$\mathit{p}(y=i|\mathit{x})=\frac{exp\left({\mathit{z}}_i\odot \tilde{\mathit{q}}\right)}{{\sum }_{j=1}^{C}exp\left({\mathit{z}}_j\odot \tilde{\mathit{q}}\right)}$$

(5)

The training set-up thus far enables us to achieve a model that predicts most of the positive samples correctly; in our case, these are the minority class samples. However, this is not the desired result as the model ends up performing unfavorably when it comes to majority class samples hence failing to generalize effectively on the entire dataset.

3.5. Switching Logit Weights for Improved Classifier Generalization

The idea of switching logit weights stems from the fact that, in principle, training of a DNN can be categorized into two critical phases. Achille et al. [57] in their study observe that the early stages of DNN training is a crucial time in the development of skills necessary for satisfactory classifier performance.

They show that relative to the quality of input data, neural networks in the first few epochs develop strong connections that appear not to change even with additional training. Further, they outline two distinct phases in the training life-cycle of a DNN; first, the memorization phase during which rapid growth of information about the data is experienced together with a significant increase in the strength of the connections, followed by the compression or forgetting phase phase during which redundant connections are eliminated and non-relevant variability in the data is discarded. Refs. [58,59] both study the evolution of the loss landscape during optimization by analyzing the Hessian spectrum of DNNs. Their study reveals that the curvature of the loss landscape changes rapidly during the early phase of training and is later on reshaped such that a few large eigenvalues emerge with a majority of the remaining tending to zero while the negatives become very small. In addition, Gur-Ari et al. [59] observe that after a short period of training, the gradient converges to a very small subspace spanned by the top k eigenvectors of the Hessian where k is the number of classes in the dataset. Two phases of training emerge from [59]; the early phase when the loss landscape around the network state appears to change rapidly with the Hessian splitting slowly into two varying subspaces, and the second phase when learning appears to concentrate in a small subspace with all Frankle et al. [60] uncover three sub-phases, the early phase where gradient magnitudes are anomalously large and motion is rapid followed by the second phase where gradients overshoot to smaller magnitudes before leveling off while performance increases rapidly, and lastly, the third phase where learning slowly begins to decelerate. Following the categorization put forward in [57], two critical phases from the training life-cycle of a DNN emerge. We propose the use of two distinct types of weight vectors during training, one for each phase to help achieve improved classifier generalization over the entire training dataset.

The first phase of training is the memorization phase, which is characterized by the rapid growth of information about the data and an increase in the formation of strong network connections. From the observations we made in Section 3.4, the ideal logit weight vector $\tilde{\mathit{q}}$ allows us to condition the DNN to focus on the minority samples. This type of conditioning, if applied at this crucial learning stage of the DNN, ensures that most of the information captured and connections formed are relevant to our samples of interest from the minority.

The second phase of training, the compression phase, is characterized by the elimination of the redundant connections and discarding of non-relevant variability in data. We observe that the benefits attained in this phase are useful to all the classes in the dataset. On the other hand, the ideal logit weight vector $\tilde{\mathit{q}}$ as composed gives an advantage only to samples from the minority classes during training. To transform this training strategy into one that provides equal opportunity across all classes, we switch to $\overline{\mathit{q}}$, a uniform logit weight vector modeled after a uniform distribution, hence allocating equal weighting to all the classes involved. For the remainder of the training cycle, we use the uniform logit weight vector $\overline{\mathit{q}}$.

We note that by replacing the ideal logit weight vector $\tilde{\mathit{q}}$ in Equation (5) with the uniform logit weight vector $\overline{\mathit{q}}$ as the noise perturbation vector, we improve classifier generalization by allowing the classifier to focus equally on all the classes, including the majority of classes previously suppressed. During the initial epochs, the model focuses on the minority classes, followed by the switch at epoch 80 from when the model focuses uniformly on the entire target class distribution, improving overall model generalization (see Figure 2).

Therefore the model architecture of DLWP Loss involves a two stage training process where in the initial stage, the logits are perturbed using the ideal logit weight vector $\tilde{\mathit{q}}$ (see Figure 3a) and followed by a switch to the second stage in which the logits are perturbed using the uniform logit weight vector $\overline{\mathit{q}}$ (see Figure 3b).

3.6. Weight Selection Strategies

DLWP loss is a cost-sensitive learning-based method that utilizes logit weight vectors to rebalance the relative loss across classes and help mitigate the effects from the imbalanced target class distribution. Together with some of the techniques used in baselines LDAM [47] and Class Balanced loss [23], we outline the strategies applied in this paper. First, the following strategies are used to generate the class balancing weights applied to the loss function:

• Empirical Risk Minimization (ERM): minimizes the empirical expectation of losses obtained by applying a prescribed loss function over some labeled training set. All training samples from all the classes are weighted equally.
• Inverse Class Reweighting [23]: class balanced-loss for each training sample is obtained by reweighting the prescribed loss function by the inverse class frequency for its class.
• Effective Number Reweighting [23]: class balanced-loss for each training sample is obtained by reweighting the prescribed loss function by the inverse of the effective number of samples for its class.
• Delayed Effective Number Reweighting [47]: the class balanced-loss is obtained by applying the standard ERM until the last learning rate decay when the inverse effective number of sample-based reweighting is applied.

Secondly, for the logit weight vectors, we use the strategies highlighted in Section 3.4, i.e., the relative likelihood approach or the effective number of samples approach. In conjunction with some of the weighting strategies listed above, we propose the following variants:

• Effective Number Probability (ENPr): inverse of the effective number of samples per class is converted to logit weight class probabilities and applied to the DLWP loss method as the ideal logit weights probability distribution.
• Delayed Effective Number Probability (DENPr): standard ERM until the last learning rate decay when the inverse of the effective number of samples per class is converted to class probabilities and applied to the DLWP loss method as the ideal logit weights probability distribution.
• Relative Likelihood Probability (RLPr): relative likelihood method is used to generate the class probabilities applied to the DLWP loss method as the ideal logit weights probability distribution.

3.7. Application and Implementation Details

In this paper, we analyze the effectiveness of our proposed method on two real-world industrial datasets; APS Failure at Scania Trucks dataset and the Steel Plates Faults dataset.

3.7.1. APS Failure at Scania Trucks Dataset

The APS Failure at Scania Trucks dataset [61] is an imbalanced dataset meant for failure prediction in the Air Pressure System (APS) of Scania Trucks. APS is an essential part of the vehicle pneumatic system in which pressurized, compressed air is used for power distribution [62]. The APS control unit intelligently manages pressurized air, engaging and disengaging the compressor to regulate energy during functions such as braking and gear changes. APS is particularly useful in compressed air brake systems found in large commercial and passenger vehicles such as trucks, busses, trailers, and railroad trains. As a result, FD systems involving APS are safety-related, owing to the catastrophic consequences of road accidents resulting from brake system failures. Notably, safety-related FD systems exhibiting high rates of false negatives are counterproductive, resulting in faults not only going undetected but incorrectly declared normal.

The APS Failure at Scania Trucks dataset [61] has a misclassification cost metric whose objective seeks to minimize the number of false negatives. In particular, false positives (Type I errors) associated with unnecessary checks performed by a mechanic at the workshop bear a penalty cost of 10 each while on the other hand, false negatives (Type II errors), associated with missing a faulty truck and eventually leading to a breakdown, bear a penalty cost of 500 each. The dataset consists of sensor data collected from APS equipment in heavy Scania trucks mapping out their everyday usage. The result is a labeled dataset in which the positive class represents failures from a specific component in the APS [61]. However, the dataset is extensively imbalanced, with the negative class vastly outnumbering the positive class (see Figure 4b). In addition, the dataset features missing values for some attributes due to sensor failures, making it unsuitable for most of the Multivariate Statistical Process Control (MSPC) methods [63,64,65].

Therefore, we implement a neural network-based FD system, which uses the available mapping between process variables and faults to identify the system faults [66,67,68,69]. The neural network can model complex nonlinear dynamic processes through a learning algorithm that extracts features from historical training data and subsequently apply pattern classification to detect the faults. This feature makes the neural networks robust to datasets with missing and incorrect data. In particular, deep learning technologies can harness the vast amounts of industrial process data made available through I4.0 technologies such as the Industrial Internet of Things (IIoT) and IBD, effectively extracting features required to create robust FD systems [70].

For experiments on the APS Failure at Scania Trucks dataset [61], we utilize a deep feed forward neural network. The architecture is made up of three fully-connected layers (492, 328, and 82 output features), each layer followed by ReLU nonlinearity [71], Batch Normalization layer [72] and a Dropout layer [73]. The loss layer for the neural network is the DLWP loss or one of the other SOTA methods depending on the evaluation being carried out. We train for 200 epochs using the Adam optimizer [74] and a base learning rate of 0.1, which is through a learning rate scheduler adaptively changed to 0.01 at epoch 150 and 0.001 at epoch 180 during training. As pointed out in [75], tuning the Adam optimizer $ϵ$ hyperparameter can improve performance. Upon further tuning, we ultimately settle on Adam with $ϵ$ values of ${10}^{-5}$ for the APS Failure at Scania Trucks dataset. We use a larger batch size of 256 for all experiments as we are dealing with imbalanced datasets, and this increases the chances of having samples from the minority classes included in each batch during training.

Consistent with the misclassification cost objective from the APS Failure at Scania Trucks dataset [61], we seek to build a reliable safety-related FD model that limits the number of false negatives, hence minimizing the misclassification cost. We achieve this by prioritizing recall, introducing reweighting strategies for the logit and the loss layer to help the classifier focus on the minority classes during training. The formulation in [23] applied to the Scania Trucks dataset target class distribution produces a vector $\mathit{\alpha }\propto 1/E_{\mathbf{n}}$ = (0.1139, 0.8861) to be used as class weights in the ENPr and DENPr schemes during training. Providing an initial class weight vector $\mathit{\alpha }$ is subjectively adjusted to (0.03, 0.97), obtaining the RLPr class weight vector that we use in our experiments.

We compare the results from our DL-based FD system with the ones reported in the GPR-based GAN framework [36] as the baseline FD system. The results are displayed in

Table 2. Results for fault detection systems. We consider metrics Precision, Recall F1, and False Positives (FP) and False Negatives (FN). The total misclassification cost is featured in the last column.

	PRECISION			RECALL			F1			CM		Total
Method	Macro↑	N↑	P↑	Macro↑	N↑	P↑	Macro↑	N↑	P↑	FP↓	FN↓	Cost↓
GPR-based GAN	0.80	99.0	0.60	0.91	0.98	0.84	0.84	0.99	0.70	207	59	31,570
DLWP-RLPr-RLPr	0.70	1.0	0.39	0.97	0.96	0.98	0.77	0.98	0.56	569	9	10,190
DLWP-RLPr-ENPr	0.70	1.0	0.40	0.97	0.96	0.98	0.77	0.98	0.56	558	9	10,080
DLWP-RLPr-None	0.67	1.0	0.35	0.97	0.96	0.98	0.75	0.98	0.51	690	6	9900
DLWP-None-ENPr	0.84	1.0	0.69	0.93	0.99	0.88	0.88	0.99	0.77	147	46	24,470
DLWP-None-DENPr	0.84	1.0	0.67	0.94	0.99	0.89	0.88	0.99	0.77	160	43	23,100

and further discussed in Section 4.

3.7.2. Steel Plates Faults Dataset

The Steel Plates Faults dataset [76,77,78] consists of a total of 1941 instances meant for the classification of surface defects in stainless steel plates. The dataset instances are grouped into 7 distinct typologies of faults: Pastry, Z Scratch, K Scatch, Stains, Dirtiness, Bumps and Other Faults. Each recorded instance consists of 27 attributes representing the geometric shape of the fault and its contour. The target class distribution reveals an imbalanced dataset (see Figure 4a).

For experiments on the Steel Plates Faults dataset [76,77,78], we utilize a deep feed forward neural network with an architecture similar to the one used for the previous dataset but a comparably smaller size of the fully connected layers (81, 54 and 13 output features) for each layer. We train for 200 epochs using the Adam optimizer [74] and a base learning rate of 0.1, which is through a learning rate scheduler adaptively changed to 0.01 at epoch 150 and 0.001 at epoch 180 during training. For the optimizer tuning, we ultimately settle on Adam with $ϵ$ values of ${10}^{-4}$.

We maintain a similar objective of a safety-related FD system for this experiment, minimizing the number of false negatives, achieved through prioritizing recall and weighting strategies for the logit and the loss layer. From the target class distribution of the Steel Plates Faults dataset, we observe that two classes, ‘Stains’ and ‘Dirtiness’, represent the minority. Applying the effective number of samples formulation [23] to this target class distribution yields $\mathit{\alpha }\propto 1/E_{\mathbf{n}}=$ (0.1262, 0.1051, 0.0516, 0.2758, 0.3607, 0.0502, 0.0304). $\mathit{\alpha }$ is the vector composed of per class inverse effective number and is used as the class weight quantities for in the ENPr and DENPr schemes during training. Analyzing the composition of $\mathit{\alpha }$, we observe that it provides us with an initial vector that acts as a guideline on which we employ the RLPr strategy to obtain a class weight vector. In particular, based on the techniques highlighted in Section 3.4, we perform an alteration on the original $\mathit{\alpha }$ vector to obtain (0.1262, 0.1051, 0.0516, 0.2, 0.4365, 0.0502, 0.0304) as our RLPr class weight vector.

Finally, for both the two datasets, we compare our class rebalancing loss implementation against other SOTA methods, LDAM [47], Focal loss [46] and Class Balanced loss [23], as baselines, including a combination of different weighting strategies recommended in Section 3.6. The results are discussed in Section 4. We implement all the algorithms and experiments in PyTorch (ver. 1.4.0) [79].

3.8. Uncertainty Estimation

DLWP loss uses softmax of the functional form represented in Equation (5), providing point estimates for the sample class probabilities without the associated uncertainties. Uncertainty estimation generates uncertainty measures for the associated sample class probabilities, enabling us to develop threshold-based isolation criteria. In particular, a subset of the results, the model predictions with high uncertainties exceeding some preset threshold, are set aside as preliminary outputs and passed on to human experts for cross-checking (see

Table 3. A final report showcasing inference results from the Steel Plates Faults dataset. A threshold set at 50% implies the human expert has to cross-check only the first three records.

Fault	Entropy	Uncertainty (%)
Dirtiness	5.903 × ${10}^{-1}$	59.025
Dirtiness	5.280 × ${10}^{-1}$	52.802
Stains	5.096 × ${10}^{-1}$	50.961
Dirtiness	4.610 × ${10}^{-1}$	46.096
Dirtiness	4.497 × ${10}^{-1}$	44.968
Stains	4.461 × ${10}^{-1}$	44.606
Stains	3.894 × ${10}^{-1}$	38.942
Stains	2.716 × ${10}^{-1}$	27.163
Dirtiness	2.335 × ${10}^{-1}$	23.354
Dirtiness	1.893 × ${10}^{-1}$	18.926

). The threshold setting for the minimum acceptable level of uncertainty is decided on a case-by-case basis depending on the level of precaution expected from the generated models.

For our implementation, we make use of the following uncertainty estimation methods applied to the generated class probabilities [80,81,82,83,84,85]:

• Entropy: $\mathbb{H}\left(x\right)=\underset{x}{argmax}\left\{-{\sum }_{i=1}^{C}P\left(y_i\mid x_i\right)logP\left(y_i\mid x_i\right)\right\}$ for a given set of C point estimates from a model prediction, we use the Entropy [81] method, which computes the entropy of the prediction as a score. The higher the entropy score, the more uncertain the model’s prediction.
• Jain’s Fairness Index: $\mathcal{J}\left(x\right)=\underset{x}{argmax}\left\{{\left({\sum }_{i=1}^{C}P\left(y_i\mid x_i\right)\right)}^2/C·{\sum }_{i=1}^{C}P{\left(y_i\mid x_i\right)}^2\right\}$ for a given set of C point estimates from a model prediction, we use the Jain’s fairness index [85] or score defined where $P\left(y_i\right|x_i)\in {\mathbb{R}}^C$. The result ranges from 1/C representing the lowest to 1 as the highest fairness score. The higher the fairness score, the more uncertain the model’s prediction.

Uncertainty estimation enables the implementation of a data-informed call to action, only invoking human experts for feedback on a subset of the output results requiring further assessment. This way, we improve operational efficiency by maintaining the number of queries to the human experts at a manageable size while still improving overall system safety.

3.9. Evaluation Techniques

Accuracy, commonly used as the metric of evaluation for a multiclass classification model, is the ratio of correct predictions to the total number of predictions made. However, accuracy has limitations in the context of classification on imbalanced datasets [86].

With safety-related systems, the cost of false negatives far outweighs that of false positives. For this reason, we prioritize recall. The recall metric, also known as sensitivity, represents the true positive rate [86]. As proposed in [87,88], we use the measures Receiver Operating Curve (ROC) and ROC Area Under Curve (ROC-AUC) in place of accuracy as metrics of classifier performance when training on imbalanced datasets. ROC [86,89] is a two-dimensional representation of the classifier performance, plotting the true positive rate against the false positive rate for all possible prediction thresholds. Interpretation of ROC is such that the closer the curve is to the top left corner, the better the classifier, effectively maximizing the true positive rate while minimizing the false positive rate. ROC-AUC [86] on the other hand, provides a single scalar quantity that summarizes the classifier’s expected performance. It represents a measure of the degree of separability between classes by the classifier. Actual values of ROC-AUC range from 0 to 1 and interpretation is such that the higher the quantity, the better the classifier performance.

For additional analysis of the classifier performance, we generate a Confusion Matrix (CM) [90]. Interpretation of the CM is such that the numbers along the leading diagonal represent the correct decisions made, while off-diagonal elements represent the errors or confusion between classes. The authors of [91] describe the entries on the CM as one that is made up of the predicted class values as its columns and the actual class values as its rows.

We use Scikit-learn (ver. 0.23.2), a machine learning library written in Python [92], to generate the metrics ROC, ROC-AUC, and CM from the classifier results.

3.10. Datasets

In our empirical studies, we make use of two datasets; Steel Plates Faults dataset [76,77,78] and APS Failure at Scania Trucks dataset [61].

• Steel Plates Faults dataset consists of a total of 1941 instances meant for the classification of surface defects in stainless steel plates. The dataset instances are grouped into 7 distinct typologies of faults. Each recorded instance consists of 27 attributes representing the geometric shape of the fault and its contour. The target class distribution reveals an imbalanced dataset.
• APS Failure at Scania Trucks dataset is an imbalanced dataset consisting of a total of 76,000 instances meant for the prediction of failures in the Air Pressure System (APS) of Scania Trucks. The dataset instances are instances divided into 60,000 training set instances (59,000 negative, 1000 positive) and 16,000 test set instances (15,625 negative, 375 positive). The dataset consists of 171 attributes per recorded instance, where all attribute names have been anonymized for proprietary reasons.

4. Results and Discussion

In Table 2, we present experimental results from an FD task on the imbalanced APS Failure at Scania Trucks dataset [61]. We compare our method, DWLP and its different weight combination variants against the GPR-based GAN [36]. Following the main objective of a safety-related FD system, requiring low misclassification cost and minimal false negatives, the DLWP-RLPr-None method applying RLPr generated weights to the logits and no reweighting to the loss function achieves the lowest misclassification cost of 9900 as it yields 6, the lowest number of false negatives. DLWP-RLPr-RLPr and DLWP-RLPr-ENPr methods also achieve low misclassification costs of 10,190 and 10,080 with equally good Recall macro scores of 0.97.

GPR-based GAN does not perform well in this regard, achieving a high misclassification cost of 31,570 and a total of 59 false negatives, but it achieves good Precision and F1 macro scores of 0.80 and 0.84. However, the variants DLWP-None-ENPr and DLWP-None-DENPr, which implement uniform logit noise together with weights ENPr and DENPr, achieve the best precision and F1 macro scores of 0.84 and 0.88 each. These methods are more suitable for systems that are not safety-related but require the minimization of false-positives or false alarms.

4.1. Further Experiments and Results

Our proposed method falls under the category of cost-sensitive learning. The evaluation compares DLWP against other SOTA methods; LDAM [47], Focal loss [46] and Class Balanced loss [23] as baselines. To compile a comprehensive list of experiments, we combine different reweighting strategies with the loss functions and obtain

Table A1. Extended results from experiments on the APS Failure at Scania Trucks dataset. We consider the metrics Precision, PRC-AUC, Recall-Macro, ROC-AUC, F1, and CM (Confusion Matrix)—false positives (FP) and false negatives (FN). Class N (0: Negative) is the majority class, Class P (1: Positive) is the minority class. Total misclassification cost was calculated from the last two columns where FP = 10 units and FN = 500 units; lower cost implies better classifier.

	PRECISION			PRC-AUC		RECALL			ROC-AUC		F1			CM		Total
Method	Macro↑	0↑	1↑	0↑	1↑	Macro↑	0↑	1↑	0↑	1↑	Macro↑	0↑	1↑	FP↓	FN↓	Cost↓
CE-None	0.79	1.0	0.58	1.0	0.54	0.95	0.98	0.92	0.95	0.95	0.85	0.99	0.71	246	31	17,960
CE-RW	0.75	1.0	0.50	1.0	0.47	0.96	0.98	0.95	0.96	0.96	0.82	0.99	0.65	361	18	12,610
CE-DRW	0.79	1.0	0.58	1.0	0.54	0.95	0.98	0.92	0.95	0.95	0.85	0.99	0.71	246	31	17,960
CE-RLPr	0.72	1.0	0.44	1.0	0.42	0.96	0.97	0.95	0.96	0.96	0.80	0.98	0.61	450	17	13,000
Focal-None	0.74	1.0	0.49	1.0	0.45	0.95	0.98	0.93	0.95	0.95	0.81	0.99	0.64	365	28	17,650
Focal-RW	0.73	1.0	0.45	1.0	0.44	0.97	0.97	0.96	0.97	0.97	0.80	0.99	0.62	432	15	11,820
Focal-DRW	0.74	1.0	0.49	1.0	0.45	0.95	0.98	0.93	0.95	0.95	0.81	0.99	0.64	365	28	17,650
Focal-RLPr	0.67	1.0	0.35	1.0	0.34	0.96	0.96	0.97	0.96	0.96	0.74	0.98	0.51	684	11	12,340
LDAM-None	0.70	1.0	0.40	1.0	0.38	0.96	0.97	0.95	0.96	0.96	0.77	0.98	0.57	527	19	14,770
LDAM-RW	0.68	1.0	0.36	1.0	0.35	0.97	0.96	0.97	0.97	0.97	0.75	0.98	0.52	655	10	11,550
LDAM-DRW	0.70	1.0	0.40	1.0	0.38	0.96	0.97	0.95	0.96	0.96	0.77	0.98	0.57	527	19	14,470
LDAM-RLPr	0.75	1.0	0.49	1.0	0.47	0.97	0.98	0.96	0.97	0.97	0.82	0.99	0.65	368	16	11,680
DLWP-None-None	0.83	1.0	0.67	1.0	0.57	0.92	0.99	0.86	0.92	0.92	0.87	0.99	0.75	161	54	28,610
DLWP-None-ENPr	0.84	1.0	0.69	1.0	0.61	0.93	0.99	0.88	0.93	0.93	0.88	0.99	0.77	147	46	24,470
DLWP-None-DENPr	0.84	1.0	0.67	1.0	0.60	0.94	0.99	0.89	0.94	0.94	0.88	0.99	0.77	160	43	23,100
DLWP-None-RLPr	0.75	1.0	0.40	1.0	0.47	0.96	0.98	0.95	0.96	0.96	0.82	0.99	0.65	365	18	12,650
DLWP-RW-None	0.70	1.0	0.39	1.0	0.38	0.96	0.96	0.97	0.96	0.96	0.77	0.98	0.56	561	13	12,110
DLWP-RW-ENPr	0.73	1.0	0.47	1.0	0.44	0.96	0.97	0.94	0.96	0.96	0.80	0.99	0.62	407	21	14,570
DLWP-RW-DENPr	0.70	1.0	0.40	1.0	0.30	0.96	0.97	0.96	0.96	0.96	0.77	0.98	0.56	545	15	12,950
DLWP-RW-RLPr	0.76	1.0	0.52	1.0	0.49	0.96	0.98	0.94	0.96	0.96	0.83	0.99	0.67	329	21	13,790
DLWP-DRW-None	0.83	1.0	0.67	1.0	0.57	0.92	0.99	0.86	0.92	0.92	0.87	0.99	0.75	161	54	28,610
DLWP-DRW-ENPr	0.84	1.0	0.69	1.0	0.61	0.93	0.99	0.88	0.93	0.93	0.88	0.99	0.77	147	46	24,470
DLWP-DRW-DENPr	0.70	1.0	0.40	1.0	0.38	0.96	0.97	0.96	0.96	0.96	0.77	0.98	0.56	545	15	12,950
DLWP-DRW-RLPr	0.75	1.0	0.49	1.0	0.47	0.96	0.98	0.95	0.96	0.96	0.82	0.99	0.65	365	18	12,650
DLWP-RLPr-None	0.67	1.0	0.35	1.0	0.34	0.97	0.96	0.98	0.97	0.97	0.75	0.98	0.51	690	6	9900
DLWP-RLPr-ENPr	0.70	1.0	0.40	1.0	0.39	0.97	0.96	0.98	0.97	0.97	0.77	0.98	0.56	558	9	10,080
DLWP-RLPr-DENPr	0.73	1.0	0.47	1.0	0.45	0.97	0.97	0.96	0.97	0.97	0.81	0.99	0.63	404	16	12,040
DLWP-RLPr-RLPr	0.70	1.0	0.39	1.0	0.38	0.97	0.96	0.98	0.97	0.97	0.77	0.98	0.56	569	9	10,190

and

Table A2. Extended results from experiments on the Steel Plates Faults dataset. We consider the metrics Precision, PRC-AUC, Recall-Macro, ROC-AUC, F1, and CM (Confusion Matrix) leading diagonal non-normalized scores for Classes 3 and 4. Class 3 (Stains) and Class 4 (Dirtiness) represent the minority classes out of the 7 classes from the dataset.

	PRECISION			PRC-AUC		RECALL			ROC-AUC		F1			CM
Method	Macro↑	3↑	4↑	3↑	4↑	Macro↑	3↑	4↑	3↑	4↑	Macro↑	3↑	4↑	3↑	4↑
CE-None	0.71	0.78	0.74	0.74	0.58	0.79	0.95	0.77	0.97	0.88	0.74	0.86	0.76	21	17
CE-RW	0.68	0.68	0.66	0.65	0.57	0.80	0.95	0.86	0.97	0.92	0.71	0.79	0.75	21	19
CE-DRW	0.72	0.84	0.60	0.80	0.50	0.81	0.95	0.82	0.97	0.90	0.75	0.89	0.69	21	18
CE-RLPr	0.70	0.72	0.66	0.69	0.57	0.81	0.95	0.86	0.97	0.92	0.73	0.82	0.75	21	19
Focal-None	0.72	0.75	0.74	0.72	0.58	0.79	0.95	0.77	0.97	0.88	0.74	0.84	0.76	21	17
Focal-RW	0.69	0.72	0.73	0.69	0.64	0.81	0.95	0.86	0.97	0.93	0.72	0.82	0.79	21	19
Focal-DRW	0.69	0.78	0.59	0.74	0.52	0.81	0.95	0.86	0.97	0.92	0.73	0.86	0.70	21	19
Focal-RLPr	0.68	0.75	0.53	0.72	0.48	0.78	0.95	0.91	0.97	0.94	0.72	0.84	0.67	21	20
LDAM-None	0.63	0.86	0.0	0.75	0.40	0.68	0.86	0.0	0.93	0.50	0.65	0.86	0.0	19	0
LDAM-RW	0.68	0.70	0.66	0.67	0.57	0.80	0.95	0.86	0.97	0.92	0.71	0.81	0.75	21	19
LDAM-DRW	0.69	0.77	0.54	0.70	0.47	0.79	0.91	0.86	0.95	0.92	0.73	0.83	0.67	20	19
LDAM-RLPr	0.63	0.64	0.48	0.61	0.44	0.79	0.95	0.91	0.97	0.93	0.67	0.76	0.62	21	20
DLWP-None-None	0.75	0.84	0.86	0.80	0.71	0.80	0.95	0.82	0.97	0.91	0.77	0.89	0.84	21	18
DLWP-None-ENPr	0.77	0.83	0.95	0.76	0.83	0.80	0.91	0.86	0.95	0.93	0.78	0.87	0.90	20	19
DLWP-None-DENPr	0.79	0.91	0.82	0.83	0.68	0.79	0.91	0.82	0.95	0.91	0.79	0.91	0.82	20	18
DLWP-None-RLPr	0.79	0.91	0.85	0.83	0.67	0.79	0.91	0.77	0.95	0.88	0.79	0.91	0.81	20	17
DLWP-RW-None	0.70	0.72	0.73	0.69	0.64	0.81	0.95	0.86	0.97	0.93	0.73	0.82	0.79	21	19
DLWP-RW-ENPr	0.70	0.72	0.59	0.69	0.52	0.81	0.95	0.86	0.97	0.92	0.73	0.82	0.70	21	19
DLWP-RW-DENPr	0.71	0.72	0.74	0.69	0.68	0.81	0.95	0.91	0.97	0.95	0.75	0.82	0.82	21	20
DLWP-RW-RLPr	0.69	0.81	0.53	0.77	0.46	0.81	0.95	0.86	0.97	0.92	0.73	0.88	0.66	21	19
DLWP-DRW-None	0.70	0.75	0.68	0.72	0.59	0.81	0.95	0.86	0.97	0.92	0.74	0.84	0.76	21	19
DLWP-DRW-ENPr	0.77	0.83	0.95	0.76	0.83	0.80	0.91	0.86	0.95	0.93	0.78	0.87	0.90	20	19
DLWP-DRW-DENPr	0.70	0.81	0.61	0.77	0.55	0.81	0.95	0.91	0.97	0.94	0.73	0.88	0.73	21	20
DLWP-DRW-RLPr	0.71	0.78	0.59	0.74	0.52	0.82	0.95	0.86	0.97	0.92	0.74	0.86	0.70	21	19
DLWP-RLPr-None	0.70	0.72	0.66	0.69	0.57	0.80	0.95	0.86	0.97	0.92	0.73	0.75	0.82	21	19
DLWP-RLPr-ENPr	0.70	0.75	0.62	0.72	0.51	0.81	0.95	0.82	0.97	0.90	0.73	0.84	0.71	21	18
DLWP-RLPr-DENPr	0.67	0.72	0.63	0.69	0.55	0.80	0.95	0.86	0.97	0.92	0.71	0.82	0.73	21	19
DLWP-RLPr-RLPr	0.68	0.70	0.43	0.67	0.41	0.82	0.95	0.95	0.97	0.95	0.72	0.81	0.59	21	21

. The combination is structured as follows: LOSS type—LOSS WEIGHT strategy—LOGIT WEIGHT strategy.

4.1.1. APS Failure at Scania Trucks Results

In Table A1, we present extended experimental results from an FD task on the imbalanced APS Failure at APS Failure at Scania Trucks dataset [61]. First, we compare our method DLWP loss against all the other baselines when no class-balancing weight parameter has been applied to the loss function. DLWP loss with no reweighting and no selected logit weight vector (DLWP-None-None) shows improved Precision (0.83) and F1 (0.87) macro scores over the counterparts CE-None, Focal-None, and LDAM-None. The variations in this category of no reweighting, DLWP-None-ENPr, DLWP-None-DENPr, both achieve improved and highest Precision (0.84) and F1 (0.88) macro scores for the same dataset. Comparing the methods from the different categories, Figure 5 shows the method variations that yield the best Type I error count and Type II error count on the APS Failure at Scania Trucks dataset.

We observe that higher recall scores are associated with lower misclassification costs across all the compared methods. Applying RPLr generated weights as logit perturbation weights is effective in minimizing recall and misclassification costs compared to other weight schemes. Notably, even baselines reweighted using our proposed RLPr weight generation scheme (CE-RLPr, Focal-RLPr, and LDAM-RLPr) achieve higher recall scores compared to the baselines reweighted with strategies proposed in [23,46,47]. Figure 6, compares the misclassification costs across the different categories revealing DLWP-RPLr as best performing.

The reweighting strategy DRW involves a delay that, in effect, applies reweighting during the later stages of training (beyond 80% epoch). We note that for all methods, this delay causes no effect as the result is similar to the one in methods where the reweighting is not at all applied. Method pairs (CE-None and CE-DRW), (Focal-None and Focal-DRW), (LDAM-None and LDAM-DRW), and (DLWP-None-None and DLWP-DRW-None) all have similar results, showing that there is no effect of delaying the reweighting in these cases.

4.1.2. Steel Plates Faults Results

In Table A2, we present extended experimental results from an FD task on the imbalanced Steel Plates Faults dataset [76,77,78]. For the method DLWP-RLPr-RLPr, we report improved recall macro (0.82) spread over all the seven classes and improved recall metrics, especially for the minority classes ‘Dirtiness’ (0.95) and ‘Stains’ (0.95). We also report the improved ROC-AUC for the two minority classes. DLWP-RLPr-RLPr also delivers improved non-normalized confusion matrix scores in the leading diagonal for the minority classes, achieving 21 for the ‘Stains’ class and 21 for the ‘Dirtiness’ class both out of a possible total of 22 samples. We also note that methods CE-RW and Focal-RW perform comparably well on some metrics but not better than DLWP-RPLr-RPLr.

DLWP loss with no reweighting and no selected logit weight vector (DLWP-None-None) shows improved Precision (0.75), Recall (0.80) and F1 (0.77) macro scores over the counterparts CE-None, Focal-None, and LDAM-None. Still in this category, the no reweighting strategy can be combined with a different logit weight vector for the DLWP loss method to achieve three other variations. The DLWP-None-DENPr, DLWP-None-RLPr methods that combine no reweighting and logit weight vector derived from the RLPr and DENPr methods attain the highest Precision (0.79) and F1 (0.79) macro scores compared to all the other methods used in the experiments. These are higher precision models suitable for use cases that require low false positives or false alarms.

5. Conclusions

In this paper, we propose DLWP loss, a new approach that enhances the training of DL-based FD systems on imbalanced datasets. Through DLWP loss, we apply logit weight vectors to the penultimate layer of a DNN, introducing relevant perturbations meant to influence the network output strategically. In particular, we implement a training regime that facilitates the switching between logit vectors to help the classifier focus on samples from the minority classes while still effectively generalizing the entire dataset. The logit weight vectors as constituted act as network hyperparameters adjusted on a case-by-case basis to regulate the focus accorded to the various minority classes during training.

For safety-related FD systems, we reduce the likelihood of predicting false negatives by generating models that prioritize recall, ensuring the bulk of positive samples are classified correctly despite the possible drawback of encountering a few incorrect predictions. Consequently, we apply a data-informed call to action, invoking human experts for feedback on a subset of the results, the model predictions with high uncertainties exceeding some preset threshold. Our results show that DLWP loss outperforms SOTA methods on the metrics Recall, ROC AUC, and per-class accuracy. We then extend our analysis to results from further experiments in which we reveal the effects of applying different reweighting and derivation strategies for the logit weight vector. In particular, our newly proposed reweighting strategy, the RLPr, shows improved results even for the SOTA methods.

Finally, training on imbalanced datasets with DLWP loss eliminates the unintended additional workload or loss of data that comes with data re-sampling techniques. In the future, we aim to extend our study to include a formula that connects the generated logit weight vector to the precise level of imbalance in datasets. Additionally, we aim to improve our method by applying methods providing broader reasoning around uncertainty, such as ensemble-based methods and Bayesian models.