Nonlinear Suppression of a Dual-Tube Coriolis Mass Flowmeter Based on Synchronization Effect
Abstract
:Featured Application
Abstract
1. Introduction
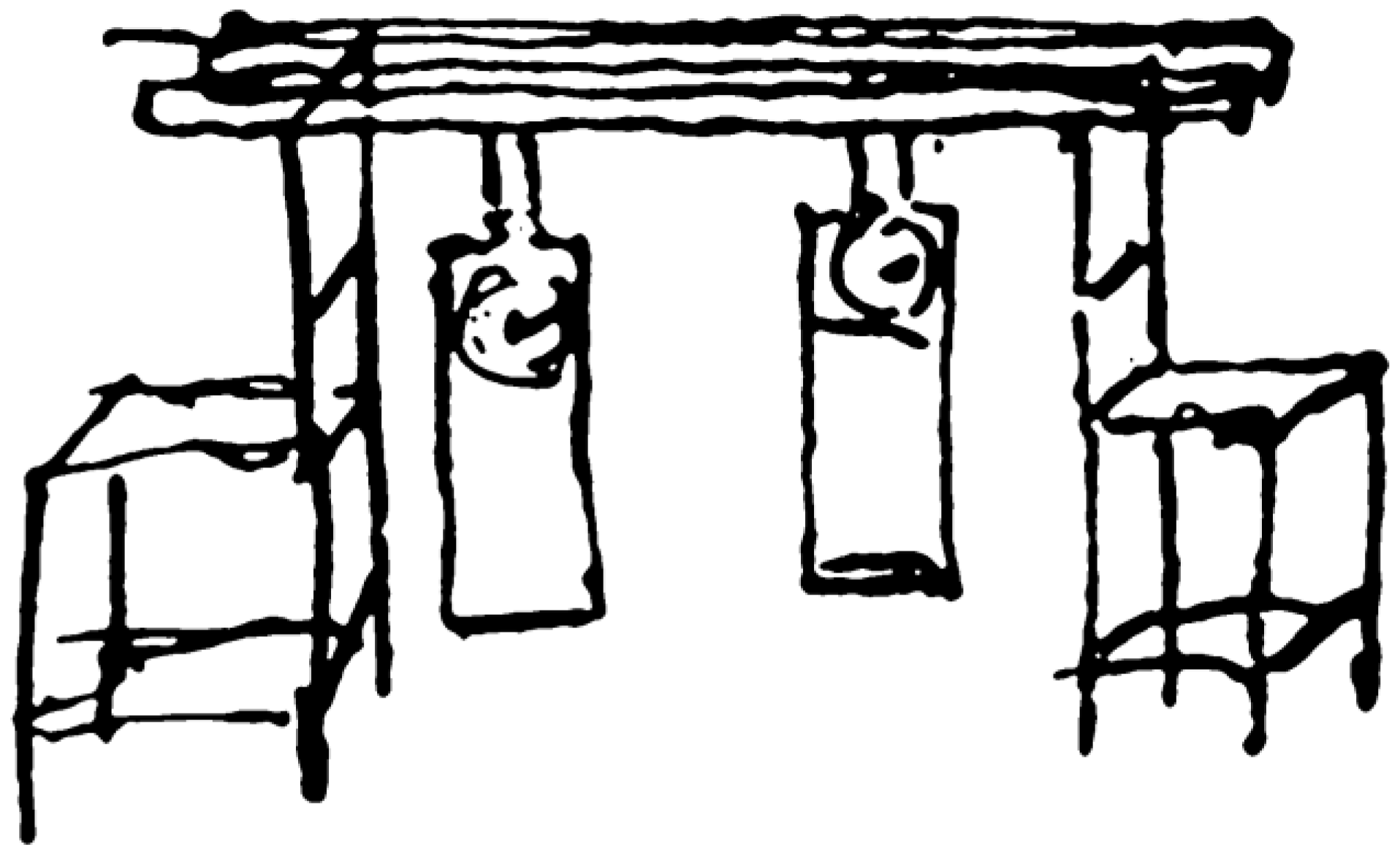
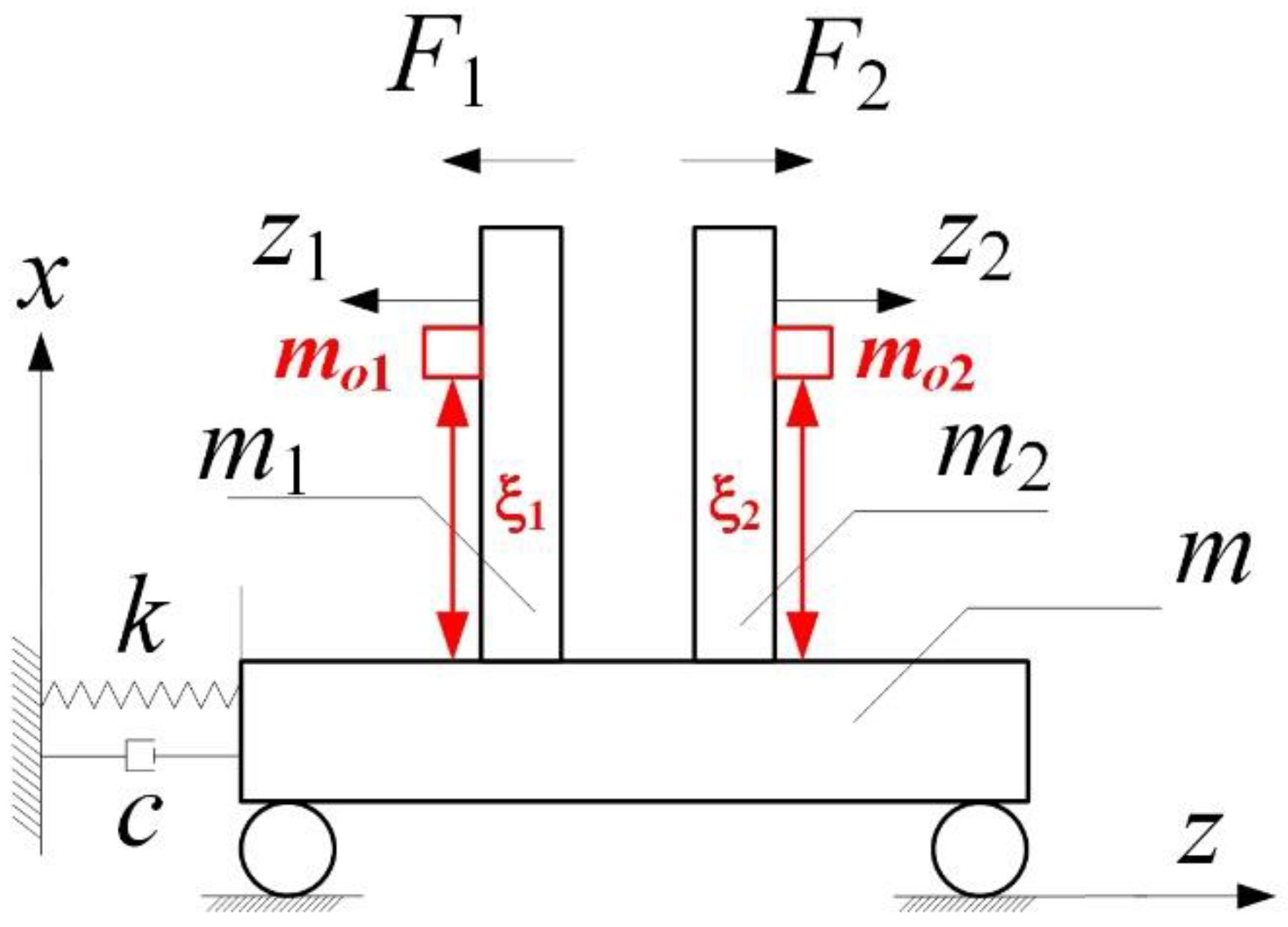
2. Nonlinear Analysis on Coupled Vibration of Dual-Tube Model with Additional Mass
- (1)
- Generalized coordinate
- (2)
- Generalized coordinate
3. Numerical Solution and Analysis
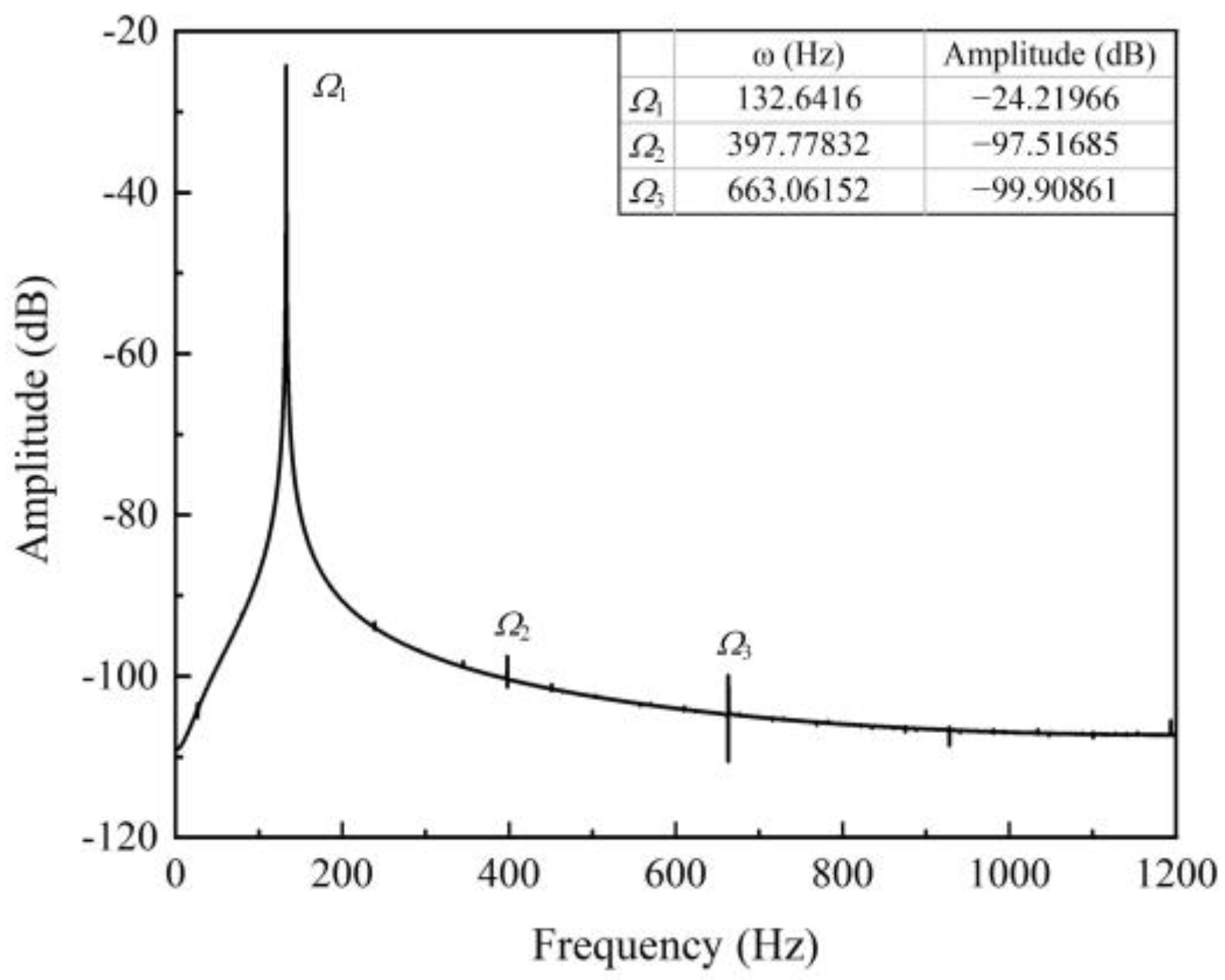
3.1. No Additional Mass
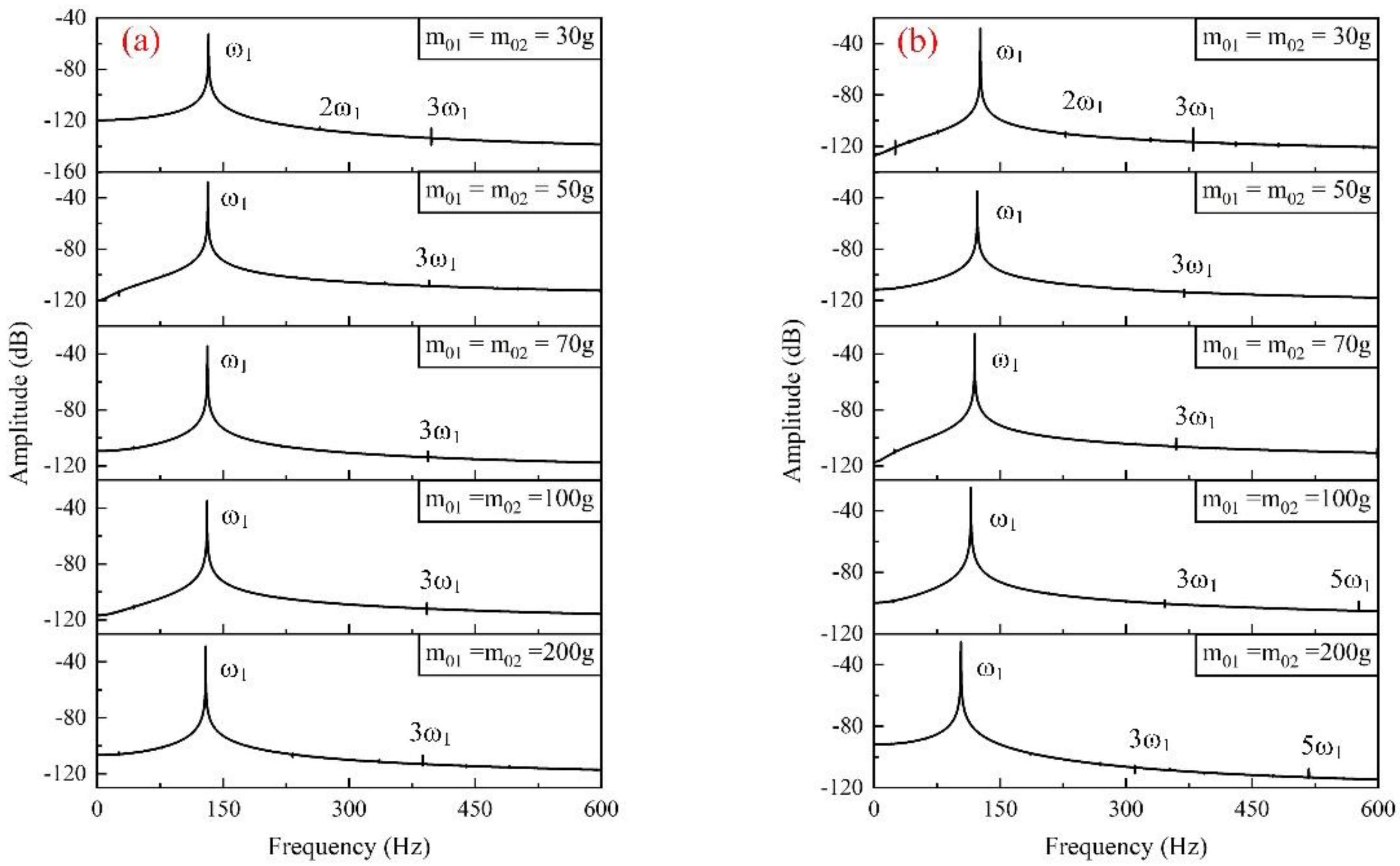
3.2. Symmetric Additional Mass
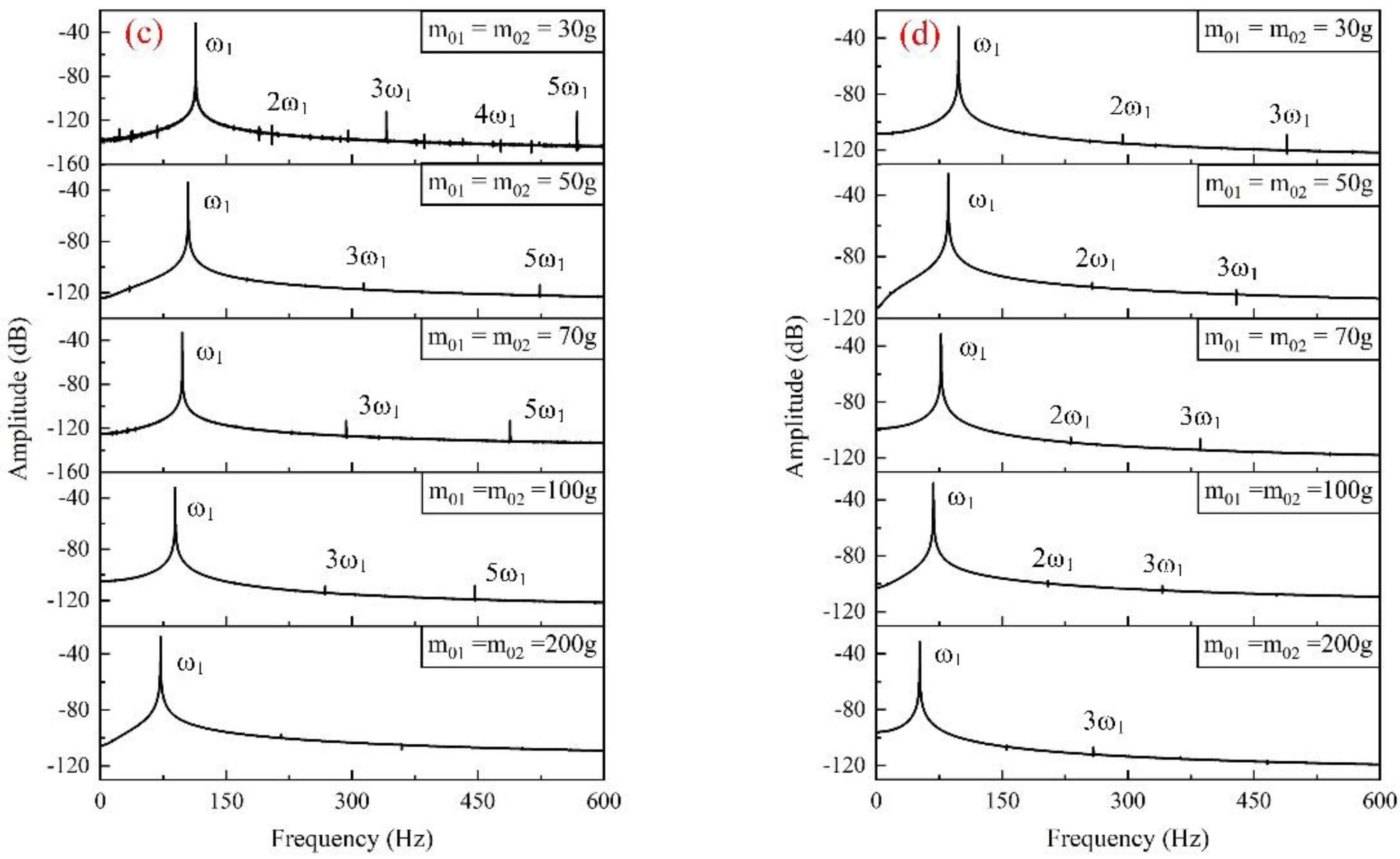
3.3. Asymmetric Additional Mass
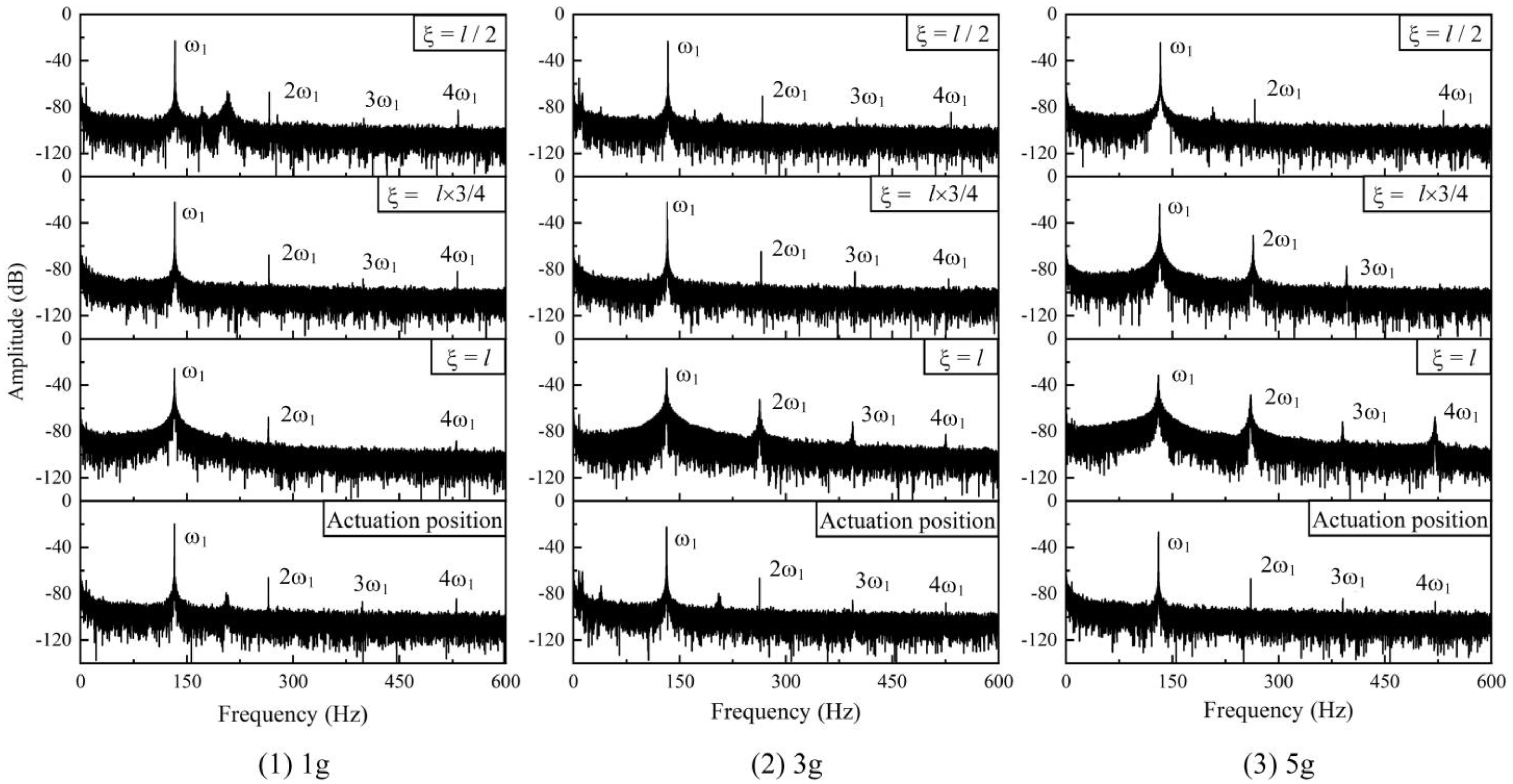
4. Experiment and Analysis
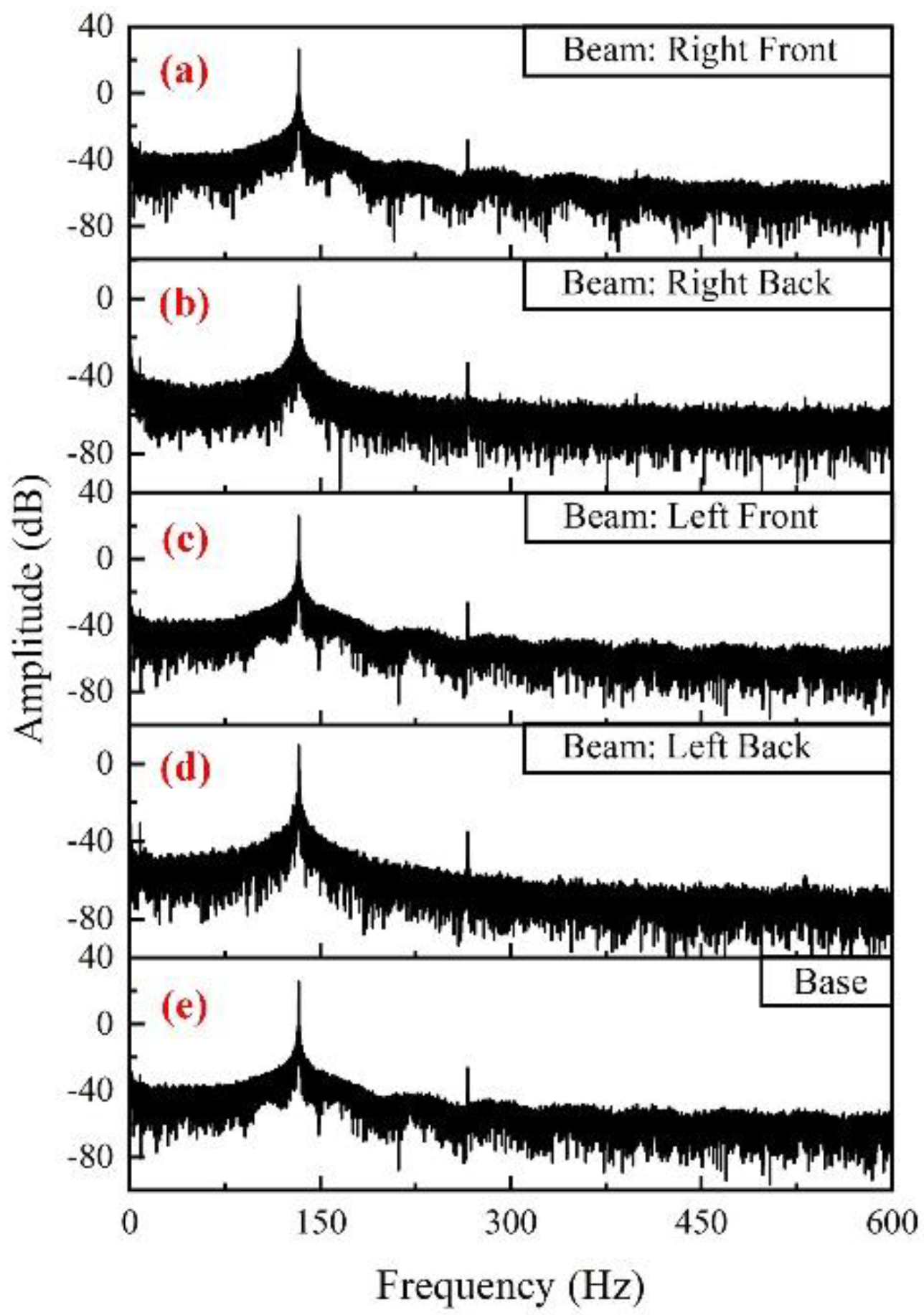
4.1. CMF without Additional Mass
4.2. CMF with Symmetric Additional Mass
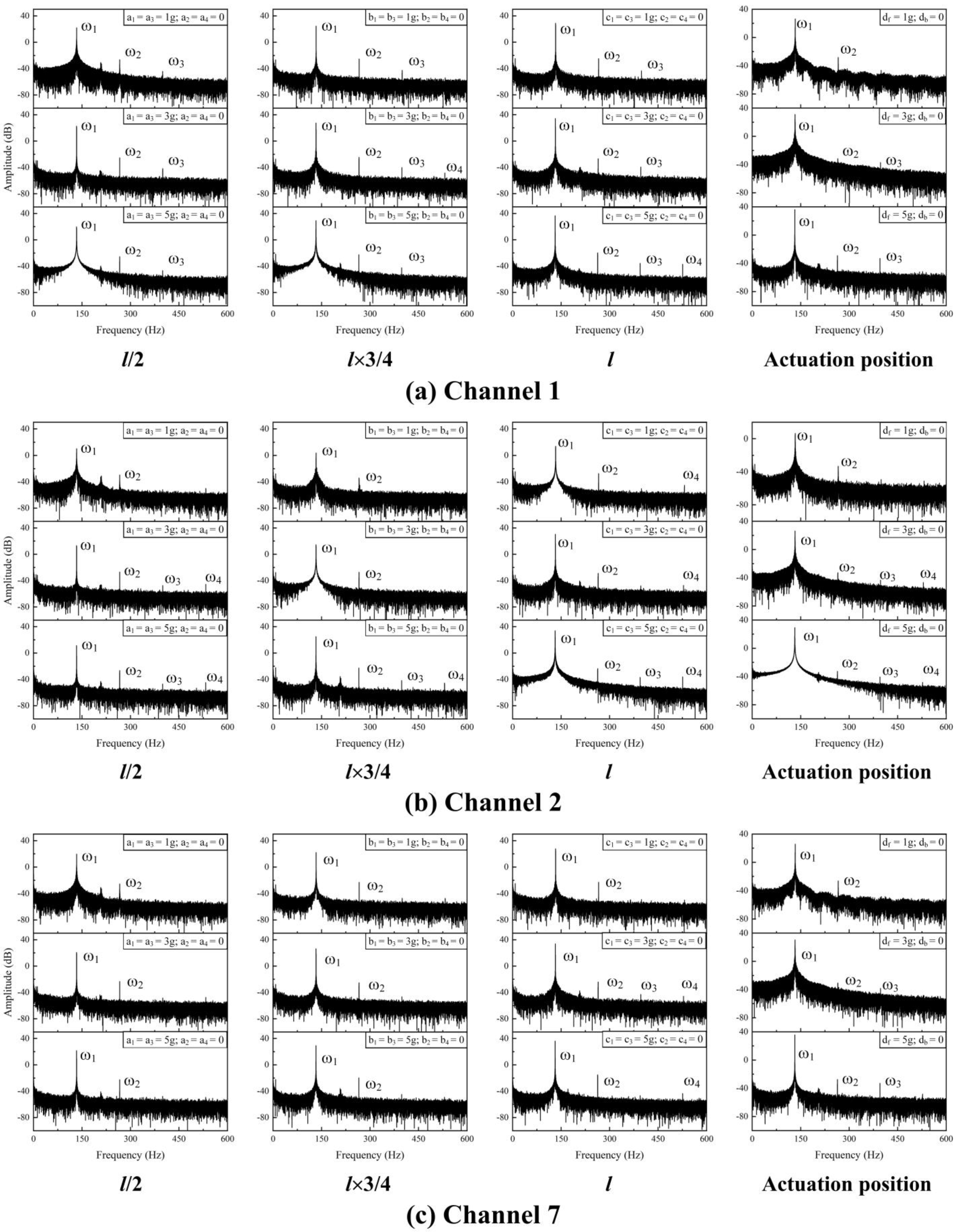
4.3. CMF with Asymmetric Additional Mass
5. Conclusions and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, D.; Wang, S.; Fan, S. Nonlinear Vibration Characteristics of Coriolis Mass Flowmeter. Chin. J. Aeronaut. 2009, 22, 198–205. [Google Scholar] [CrossRef] [Green Version]
- Zheng, D.; Wang, S.; Liu, B.; Fan, S. Theoretical analysis and experimental study of Coriolis mass flow sensor sensitivity. J. Fluids Struct. 2016, 65, 295–312. [Google Scholar] [CrossRef]
- Belhadj, A.; Cheesewright, R.; Clark, C. The simulation of coriolis meter response to pulsating flow using a general purpose F.E. code. J. Fluids Struct. 2000, 14, 613–634. [Google Scholar] [CrossRef]
- Chen, S.-S. Dynamic Stability of Tube Conveying Fluid. J. Eng. Mech. Div. 1971, 97, 1469–1485. [Google Scholar] [CrossRef]
- Enz, S.; Thomsen, J.J. Predicting phase shift effects for vibrating fluid-conveying pipes due to Coriolis forces and fluid pulsation. J. Sound Vib. 2011, 330, 5096–5113. [Google Scholar] [CrossRef]
- Wang, T.; Baker, R. Manufacturing variation of the measuring tube in a Coriolis flowmeter. Comput. Control. Eng. J. 2003, 14, 38–39. [Google Scholar] [CrossRef]
- Bobovnik, G.; Mole, N.; Kutin, J.; Štok, B.; Bajsić, I. Coupled finite-volume/finite-element modelling of the straight-tube Coriolis flowmeter. J. Fluids Struct. 2005, 20, 785–800. [Google Scholar] [CrossRef]
- Bobovnik, G.; Kutin, J.; Mole, N.; Štok, B.; Bajsić, I. Numerical analysis of installation effects in Coriolis flowmeters: Single and twin tube configurations. Flow Meas. Instrum. 2015, 44, 71–78. [Google Scholar] [CrossRef]
- Keita, N. Contribution to the understanding of the zero shift effects in Coriolis mass flowmeters. Flow Meas. Instrum. 1989, 1, 39–43. [Google Scholar] [CrossRef]
- Thomsen, J.J.; Dahl, J. Phase shift effects for fluid conveying pipes on non-ideal supports. J. Sound Vib. 2010, 329, 3065–3081. [Google Scholar] [CrossRef]
- Thomsen, J.J.; Dahl, J.; Fuglede, N.; Enz, S. Predicting phase shift of elastic waves in pipes due to fluid flow and imperfections. In Proceedings of the 16th International Congress on Sound and Vibration, ICSV16, Krakow, Poland, 5–9 July 2009; p. 8. [Google Scholar]
- Hemp, J.; Kutin, J. Theory of errors in Coriolis flowmeter readings due to compressibility of the fluid being metered. Flow Meas. Instrum. 2006, 17, 359–369. [Google Scholar] [CrossRef]
- Fuglede, N. Coriolis Flowmeter Accuracy and Precision; Technical University of Denmark: Lyngby, Denmark, 2009. [Google Scholar]
- Gagliano, S.; Cairone, F.; Amenta, A.; Bucolo, M. A Real Time Feed Forward Control of Slug Flow in Microchannels. Energies 2019, 12, 2556. [Google Scholar] [CrossRef] [Green Version]
- Gagliano, S.; Stella, G.; Bucolo, M. Real-Time Detection of Slug Velocity in Microchannels. Micromachines 2020, 11, 241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Senator, M. Synchronization of two coupled escapement-driven pendulum clocks. J. Sound Vib. 2006, 291, 566–603. [Google Scholar] [CrossRef]
- Neda, Z.; Ravasz, E.; Brechet, Y.; Vicsek, T.; Barabasi, A. The sound of many hands clapping. Nat. Cell Biol. 2000, 403, 849–850. [Google Scholar] [CrossRef]
- Néda, Z.; Ravasz, E.; Vicsek, T.; Brechet, Y.; Barabasi, A. Physics of the rhythmic applause. Phys. Rev. E 2000, 61, 6987–6992. [Google Scholar] [CrossRef] [Green Version]
- Kapitaniak, M.; Czolczynski, K.; Perlikowski, P.; Stefanski, A.; Kapitaniak, T. Synchronization of clocks. Phys. Rep. 2012, 517, 1–69. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Wang, N.; Li, L.; Xiao, J. Anti-phase synchronization of two coupled mechanical metronomes. CHAOS Interdiscip. J. Nonlinear Sci. 2012, 22, 23146. [Google Scholar] [CrossRef]
- Xin, X.; Liu, Y. Analysis of synchronization phenomena of two metronomes on a cart using describing function approach. In Proceedings of the 2015 American Control Conference, Chicago, IL, USA, 1–3 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1345–1350. [Google Scholar]
- Li, Z.X.; Hu, C.; Zheng, D.Z.; Fan, S.C. Synchronization Theory-Based Analysis of Coupled Vibrations of Dual-Tube Coriolis Mass Flowmeters. Sensors 2020, 20, 6340. [Google Scholar] [CrossRef] [PubMed]
- Esu, O.E.; Wang, Y.; Chryssanthopoulos, M.K. Local vibration mode pairs for damage identification in axisymmetric tubular structures. J. Sound Vib. 2021, 494, 115845. [Google Scholar] [CrossRef]
- G Krishnanunni, C.; N Rao, B. Indirect health monitoring of bridges using Tikhonov regularization scheme and signal averaging technique. Struct. Control Health Monit. 2021, 28, e2686. [Google Scholar]





| Parameter | Value |
|---|---|
| Length of single beam | 0.232 m |
| Diameter of single beam | 0.01 m |
| Density | 7890 kg/ |
| Base mass | 3 kg |
| Elastic modulus | 206 GPa |
| Additional- Mass Position | Frequencies (Hz) | Amplitudes (dB) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 g | 50 g | 70 g | 100 g | 200 g | 30 g | 50 g | 70 g | 100 g | 200 g | |||
| l/4 | ω1 | 132.57 | 131.76 | 131.40 | 130.88 | 129.20 | A1 | −52.62 | −27.75 | −34.36 | −34.77 | −28.82 |
| 2ω1 | 265.21 | - | - | - | - | A2 | −124.95 | - | - | - | - | |
| 3ω1 | 397.78 | 395.14 | 394.12 | 392.58 | 387.74 | A3 | −125.80 | −104.52 | −109.48 | −107.90 | −106.79 | |
| l/2 | ω1 | 126.64 | 123.12 | 119.82 | 115.43 | 103.49 | A1 | −27.96 | −34.73 | −25.68 | −24.84 | −25.21 |
| 2ω1 | 253.27 | 369.07 | 359.47 | 346.14 | 310.55 | A2 | −111.97 | −111.41 | −100.41 | −98.39 | −105.53 | |
| 3ω1 | 379.91 | - | - | 577.00 | 517.60 | A3 | −106.00 | - | - | −98.99 | −107.75 | |
| l×3/4 | ω1 | 113.67 | 104.74 | 97.71 | 89.28 | 71.85 | A1 | −31.80 | −34.12 | −32.73 | −31.81 | −27.63 |
| 2ω1 | 227.34 | - | - | - | - | A2 | −133.98 | - | - | - | - | |
| 3ω1 | 341.02 | 314.28 | 293.04 | 267.99 | - | A3 | −111.89 | −112.65 | −113.15 | −108.63 | - | |
| 4ω1 | 454.69 | - | - | - | - | A4 | −139.24 | - | - | - | - | |
| 5ω1 | 568.36 | 523.75 | 488.38 | 446.56 | - | A5 | −112.00 | −113.98 | −113.08 | −108.53 | - | |
| l | ω1 | 97.85 | 85.77 | 77.20 | 68.19 | 51.78 | A1 | −31.78 | −26.24 | −31.22 | −28.02 | −31.22 |
| 2ω1 | 195.04 | 257.30 | 231.74 | 204.57 | - | A2 | −109.85 | −97.07 | −105.29 | −97.89 | - | |
| 3ω1 | 293.55 | 428.91 | 386.13 | 341.02 | 258.91 | A3 | −109.07 | −101.73 | −106.45 | −101.23 | −106.76 | |
| B | R1 | R2 | H1 | H2 | H3 | H4 | D (Tube Wall Thickness) |
|---|---|---|---|---|---|---|---|
| 260 | 60 | 54 | 240 | 180 | 23 | 48 | 1 |
| No. | Sensitivity |
|---|---|
| 1 | 9.962 |
| 2 | 10.333 |
| 3 | 9.892 |
| 4 | 10.198 |
| 7 | 9.982 |
| ω1 | 2ω1 | 3ω1 | A(ω1) − A(2ω1) (dB) | A(2ω1) − A(3ω1) (dB) | |
|---|---|---|---|---|---|
| Beam | 133.22 | 266.45 | 399.67 | 45.72 | 17.57 |
| Detection position | 133.22 | 266.45 | 399.67 | 45.72 | 17.57 |
| Base | 133.22 | 266.45 | - | 42.89 | - |
| Frequencies (Hz) | |||||||||||||
| Channel 1 | Additional- mass position | 1 g | 3 g | 5 g | |||||||||
| ω1 | 2ω1 | 3ω1 | 4ω1 | ω1 | 2ω1 | 3ω1 | 4ω1 | ω1 | 2ω1 | 3ω1 | 4ω1 | ||
| l/2 | 133.29 | 266.57 | 399.55 | - | 133.19 | 266.42 | 399.61 | - | 133.13 | 266.32 | 399.55 | - | |
| l×3/4 | 133.10 | 266.16 | 399.26 | - | 132.81 | 265.66 | 398.47 | 531.32 | 132.56 | 265.15 | 397.72 | - | |
| l | 132.85 | 265.69 | 398.54 | - | 132.15 | 264.33 | 396.48 | - | 131.46 | 262.94 | 394.43 | 525.89 | |
| Ap | 132.91 | 265.85 | - | - | 132.34 | 264.49 | 396.80 | - | 131.65 | 263.32 | 395.00 | - | |
| Channel 2 | 1 g | 3 g | 5 g | ||||||||||
| ω1 | 2ω1 | 3ω1 | 4ω1 | ω1 | 2ω1 | 3ω1 | 4ω1 | ω1 | 2ω1 | 3ω1 | 4ω1 | ||
| l/2 | 133.26 | 266.57 | - | - | 133.19 | 266.39 | 399.61 | 532.80 | 133.16 | 266.32 | 399.48 | 532.64 | |
| l×3/4 | 132.94 | 265.79 | - | - | 132.81 | 265.66 | - | - | 132.59 | 265.19 | 397.75 | 530.34 | |
| l | 132.88 | 265.69 | - | 531.38 | 132.15 | 264.30 | - | 528.60 | 131.49 | 262.98 | 394.40 | 525.89 | |
| Ap | 132.91 | 265.82 | - | - | 132.31 | 264.68 | 396.80 | 529.14 | 131.71 | 263.32 | 395.03 | 526.68 | |
| Channel 7 | 1 g | 3 g | 5 g | ||||||||||
| ω1 | 2ω1 | 3ω1 | 4ω1 | ω1 | 2ω1 | 3ω1 | 4ω1 | ω1 | 2ω1 | 3ω1 | 4ω1 | ||
| l/2 | 133.29 | 266.57 | - | - | 133.19 | 266.42 | - | - | 133.16 | 266.35 | - | - | |
| l×3/4 | 133.10 | 266.16 | - | - | 132.85 | 265.66 | - | - | 132.59 | 265.15 | - | - | |
| l | 132.85 | 265.69 | - | - | 132.15 | 264.30 | 396.45 | 528.63 | 131.46 | 262.94 | - | 525.92 | |
| Ap | 132.91 | 265.82 | - | - | 132.31 | 264.65 | 396.80 | - | 131.65 | 263.32 | 395.00 | 526.68 | |
| Amplitudes (dB) | |||||||||||||
| Channel 1 | 1 g | 3 g | 5 g | ||||||||||
| A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | ||
| l/2 | 21.90 | −26.40 | −44.22 | - | 22.67 | −25.31 | −41.60 | - | 18.94 | −25.67 | −46.66 | - | |
| l×3/4 | 24.53 | −25.41 | −42.52 | - | 27.39 | −24.61 | −40.22 | −48.34 | 29.20 | −22.57 | −42.42 | - | |
| l | 28.74 | −24.95 | −43.45 | - | 34.29 | −27.18 | −39.43 | - | 35.03 | −19.88 | −35.81 | −37.03 | |
| Ap | 26.37 | −28.26 | - | - | 30.94 | −31.47 | −37.08 | - | 33.73 | −29.10 | −33.03 | - | |
| Channel 2 | 1 g | 3 g | 5 g | ||||||||||
| A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | ||
| l/2 | 10.23 | −30.28 | - | - | 13.21 | −29.87 | −47.43 | −45.67 | 11.30 | −26.50 | −46.98 | −44.79 | |
| l×3/4 | 3.68 | −34.22 | - | - | 14.51 | −27.19 | - | - | 24.94 | −22.69 | −41.70 | −45.55 | |
| l | 13.84 | −27.43 | - | −45.44 | 30.40 | −28.86 | - | −47.29 | 33.84 | −23.63 | −36.96 | −36.19 | |
| Ap | 6.40 | −33.11 | - | - | 24.38 | −32.80 | −43.37 | −46.86 | 29.24 | −32.68 | −40.62 | −48.38 | |
| Channel 7 | 1 g | 3 g | 5 g | ||||||||||
| A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | ||
| l/2 | 19.63 | −25.35 | - | - | 20.74 | −23.24 | - | - | 21.43 | −22.46 | - | - | |
| l×3/4 | 22.21 | −22.90 | - | - | 26.24 | −25.31 | - | - | 29.27 | −19.68 | - | - | |
| l | 27.65 | −22.70 | - | - | 33.81 | −24.03 | −43.12 | −45.71 | 34.36 | −15.20 | - | −43.60 | |
| Ap | 25.73 | −26.36 | - | - | 27.57 | −30.70 | −38.31 | - | 33.10 | −27.46 | −32.78 | −48.11 | |
| Frequencies (Hz) | |||||||||||||
| Channel 1 | Additional- mass position | 1 g | 3 g | 5 g | |||||||||
| ω1 | ω2 | ω3 | ω4 | ω1 | ω2 | ω3 | ω4 | ω1 | ω2 | ω3 | ω4 | ||
| l/2 | 133.29 | 266.57 | 399.55 | - | 133.19 | 266.42 | 399.61 | - | 133.13 | 266.32 | 399.55 | - | |
| l×3/4 | 133.10 | 266.16 | 399.26 | - | 132.81 | 265.66 | 398.47 | 531.32 | 132.56 | 265.15 | 397.72 | - | |
| l | 132.85 | 265.69 | 398.54 | - | 132.15 | 264.33 | 396.48 | - | 131.46 | 262.94 | 394.43 | 525.89 | |
| Ap | 132.91 | 265.85 | - | - | 132.34 | 264.49 | 396.80 | - | 131.65 | 263.32 | 395.00 | - | |
| Channel 2 | 1 g | 3 g | 5 g | ||||||||||
| ω1 | ω2 | ω3 | ω4 | ω1 | ω2 | ω3 | ω4 | ω1 | ω2 | ω3 | ω4 | ||
| l/2 | 133.26 | 266.57 | - | - | 133.19 | 266.39 | 399.61 | 532.80 | 133.16 | 266.32 | 399.48 | 532.64 | |
| l×3/4 | 132.94 | 265.79 | - | - | 132.81 | 265.66 | - | - | 132.59 | 265.19 | 397.75 | 530.34 | |
| l | 132.88 | 265.69 | - | 531.38 | 132.15 | 264.30 | - | 528.60 | 131.49 | 262.98 | 394.40 | 525.89 | |
| Ap | 132.91 | 265.82 | - | - | 132.31 | 264.68 | 396.80 | 529.14 | 131.71 | 263.32 | 395.03 | 526.68 | |
| Channel 7 | 1 g | 3 g | 5 g | ||||||||||
| ω1 | ω2 | ω3 | ω4 | ω1 | ω2 | ω3 | ω4 | ω1 | ω2 | ω3 | ω4 | ||
| l/2 | 133.29 | 266.57 | - | - | 133.19 | 266.42 | - | - | 133.16 | 266.35 | - | - | |
| l×3/4 | 133.10 | 266.16 | - | - | 132.85 | 265.66 | - | - | 132.59 | 265.15 | - | - | |
| l | 132.85 | 265.69 | - | - | 132.15 | 264.30 | 396.45 | 528.63 | 131.46 | 262.94 | - | 525.92 | |
| Ap | 132.91 | 265.82 | - | - | 132.31 | 264.65 | 396.80 | - | 131.65 | 263.32 | 395.00 | 526.68 | |
| Amplitudes(dB) | |||||||||||||
| Channel 1 | 1 g | 3 g | 5 g | ||||||||||
| A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | ||
| l/2 | 21.90 | −26.40 | −44.22 | - | 22.67 | −25.31 | −41.60 | - | 18.94 | −25.67 | −46.66 | - | |
| l×3/4 | 24.53 | −25.41 | −42.52 | - | 27.39 | −24.61 | −40.22 | −48.34 | 29.20 | −22.57 | −42.42 | - | |
| l | 28.74 | −24.95 | −43.45 | - | 34.29 | −27.18 | −39.43 | - | 35.03 | −19.88 | −35.81 | −37.03 | |
| Ap | 26.37 | −28.26 | - | - | 30.94 | −31.47 | −37.08 | - | 33.73 | −29.10 | −33.03 | - | |
| Channel 2 | 1 g | 3 g | 5 g | ||||||||||
| A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | ||
| l/2 | 10.23 | −30.28 | - | - | 13.21 | −29.87 | −47.43 | −45.67 | 11.30 | −26.50 | −46.98 | −44.79 | |
| l×3/4 | 3.68 | −34.22 | - | - | 14.51 | −27.19 | - | - | 24.94 | −22.69 | −41.70 | −45.55 | |
| l | 13.84 | −27.43 | - | −45.44 | 30.40 | −28.86 | - | −47.29 | 33.84 | −23.63 | −36.96 | −36.19 | |
| Ap | 6.40 | −33.11 | - | - | 24.38 | −32.80 | −43.37 | −46.86 | 29.24 | −32.68 | −40.62 | −48.38 | |
| Channel 7 | 1 g | 3 g | 5 g | ||||||||||
| A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | ||
| l/2 | 19.63 | −25.35 | - | - | 20.74 | −23.24 | - | - | 21.43 | −22.46 | - | - | |
| l×3/4 | 22.21 | −22.90 | - | - | 26.24 | −25.31 | - | - | 29.27 | −19.68 | - | - | |
| l | 27.65 | −22.70 | - | - | 33.81 | −24.03 | −43.12 | −45.71 | 34.36 | −15.20 | - | −43.60 | |
| Ap | 25.73 | −26.36 | - | - | 27.57 | −30.70 | −38.31 | - | 33.10 | −27.46 | −32.78 | −48.11 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.-X.; Hu, C.; Han, M.-Z.; Fan, S.-C.; Zheng, D.-Z. Nonlinear Suppression of a Dual-Tube Coriolis Mass Flowmeter Based on Synchronization Effect. Appl. Sci. 2021, 11, 9916. https://doi.org/10.3390/app11219916
Li Z-X, Hu C, Han M-Z, Fan S-C, Zheng D-Z. Nonlinear Suppression of a Dual-Tube Coriolis Mass Flowmeter Based on Synchronization Effect. Applied Sciences. 2021; 11(21):9916. https://doi.org/10.3390/app11219916
Chicago/Turabian StyleLi, Zhong-Xiang, Chun Hu, Ming-Zhe Han, Shang-Chun Fan, and De-Zhi Zheng. 2021. "Nonlinear Suppression of a Dual-Tube Coriolis Mass Flowmeter Based on Synchronization Effect" Applied Sciences 11, no. 21: 9916. https://doi.org/10.3390/app11219916







