Prediction of Shear Strength of Reinforced High-Strength Concrete Beams Using Compatibility-Aided Truss Model
Abstract
:1. Introduction
2. Shear Analytical Model for RC Elements with High-Strength Concrete
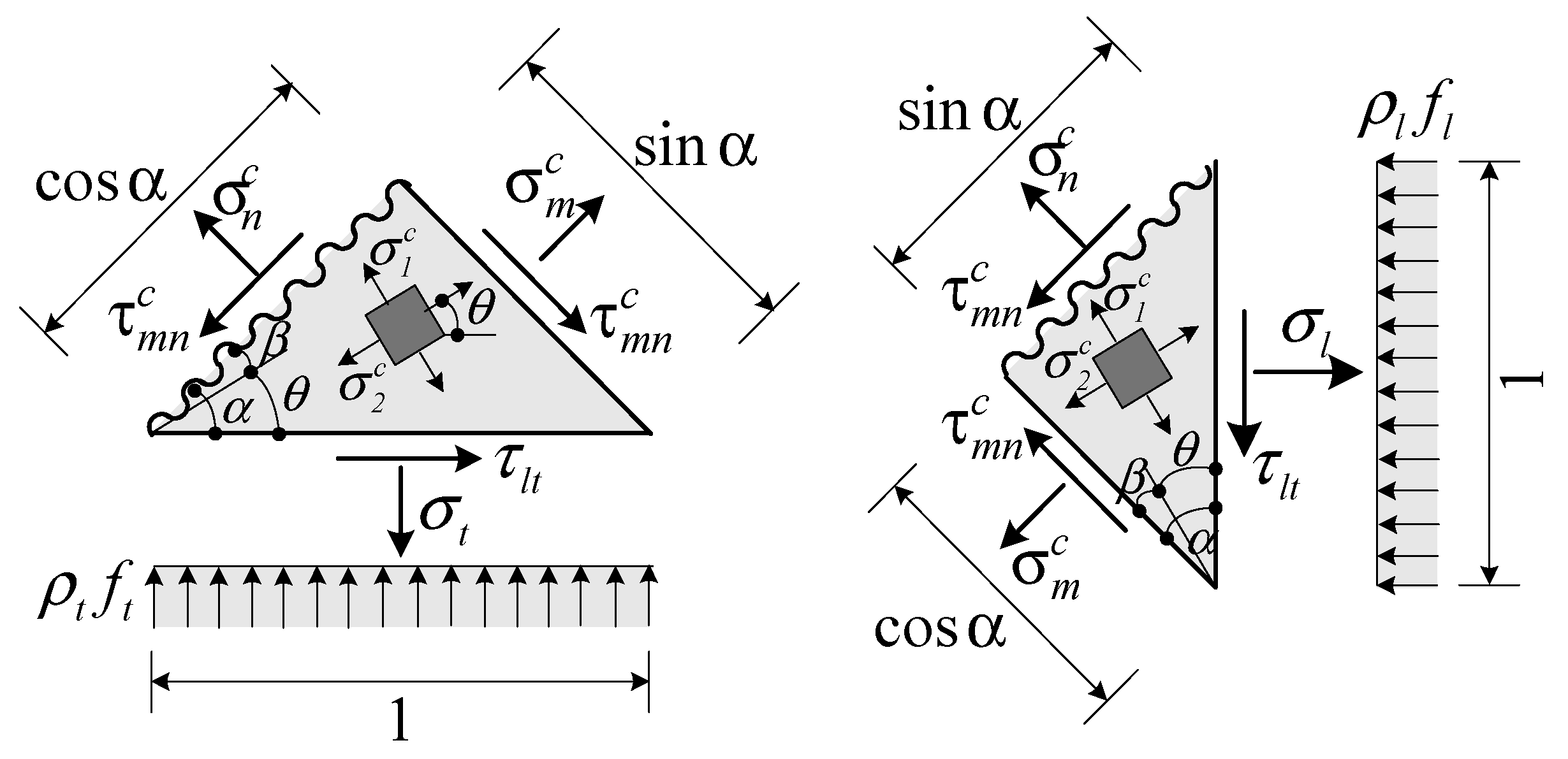
2.1. Equilibrium Conditions
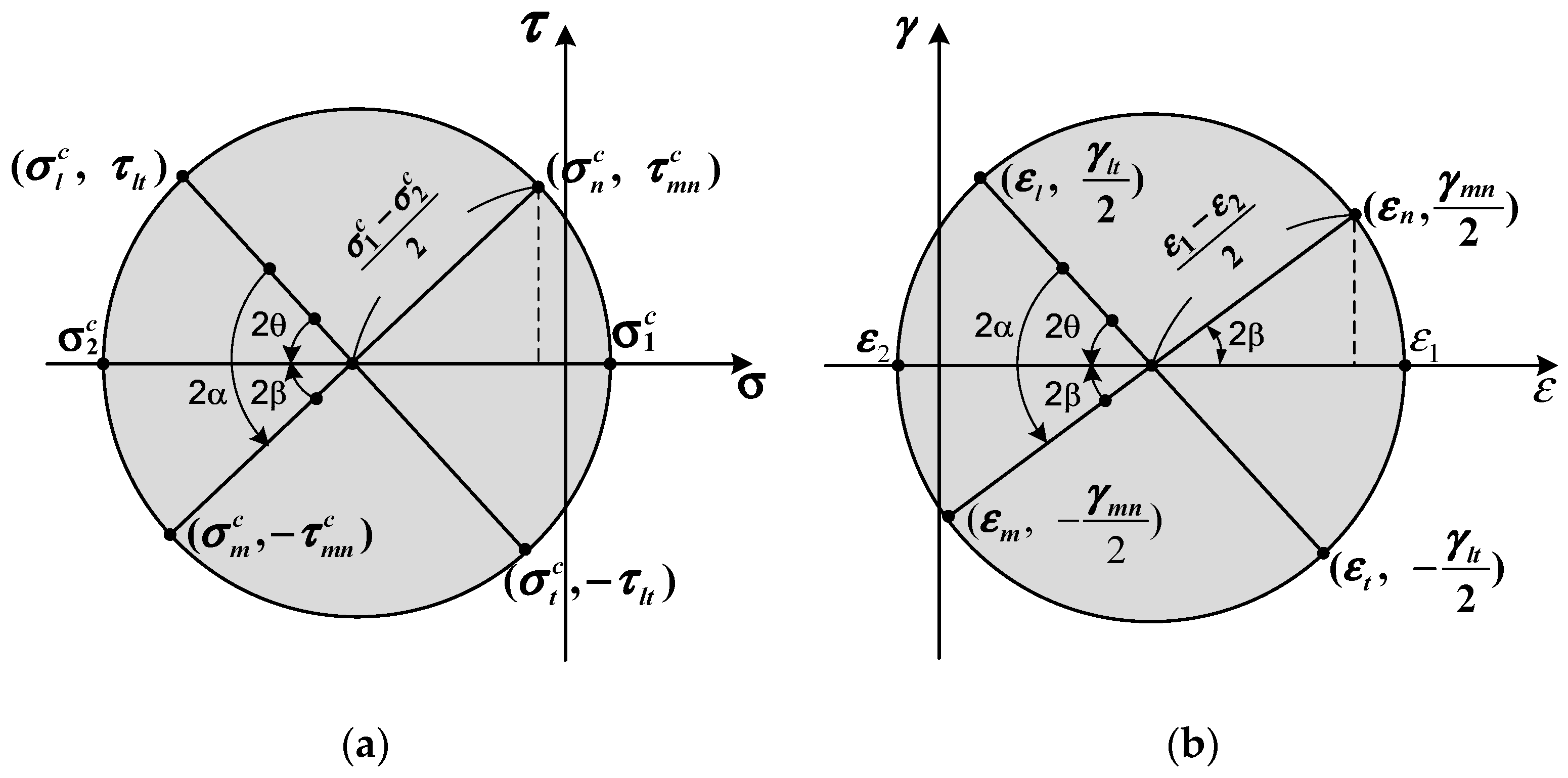
2.2. Compatibility Conditions
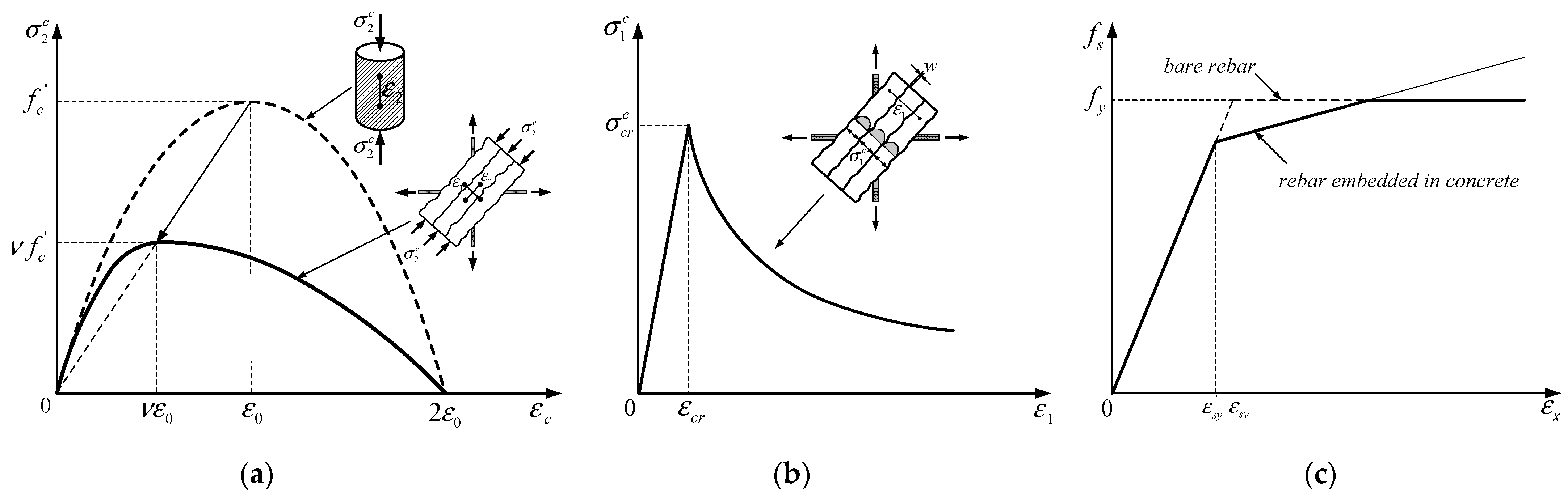
2.3. Constitutive Laws
3. Application of Proposed Model to Reinforced High-Strength Concrete Beams
3.1. Consideration of Bending Moment
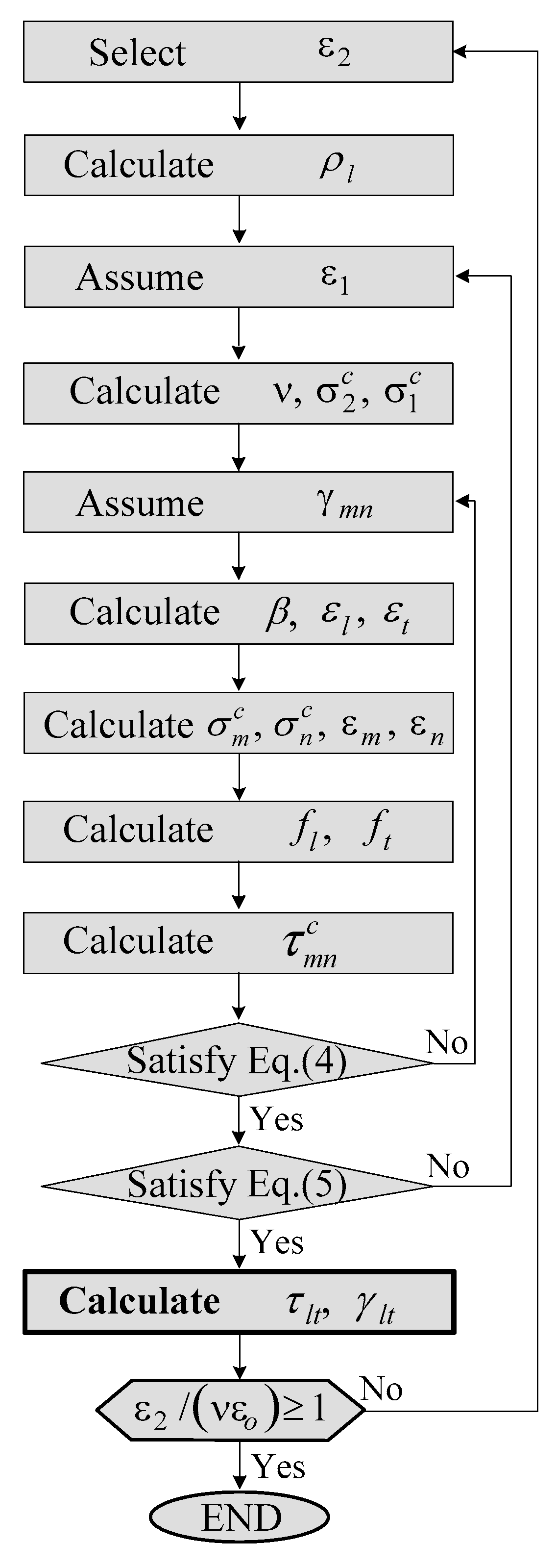
3.2. Calculation Procedure
4. Prediction of Shear Strength of Reinforced High-Strength Concrete Beams
5. Conclusions
- (1)
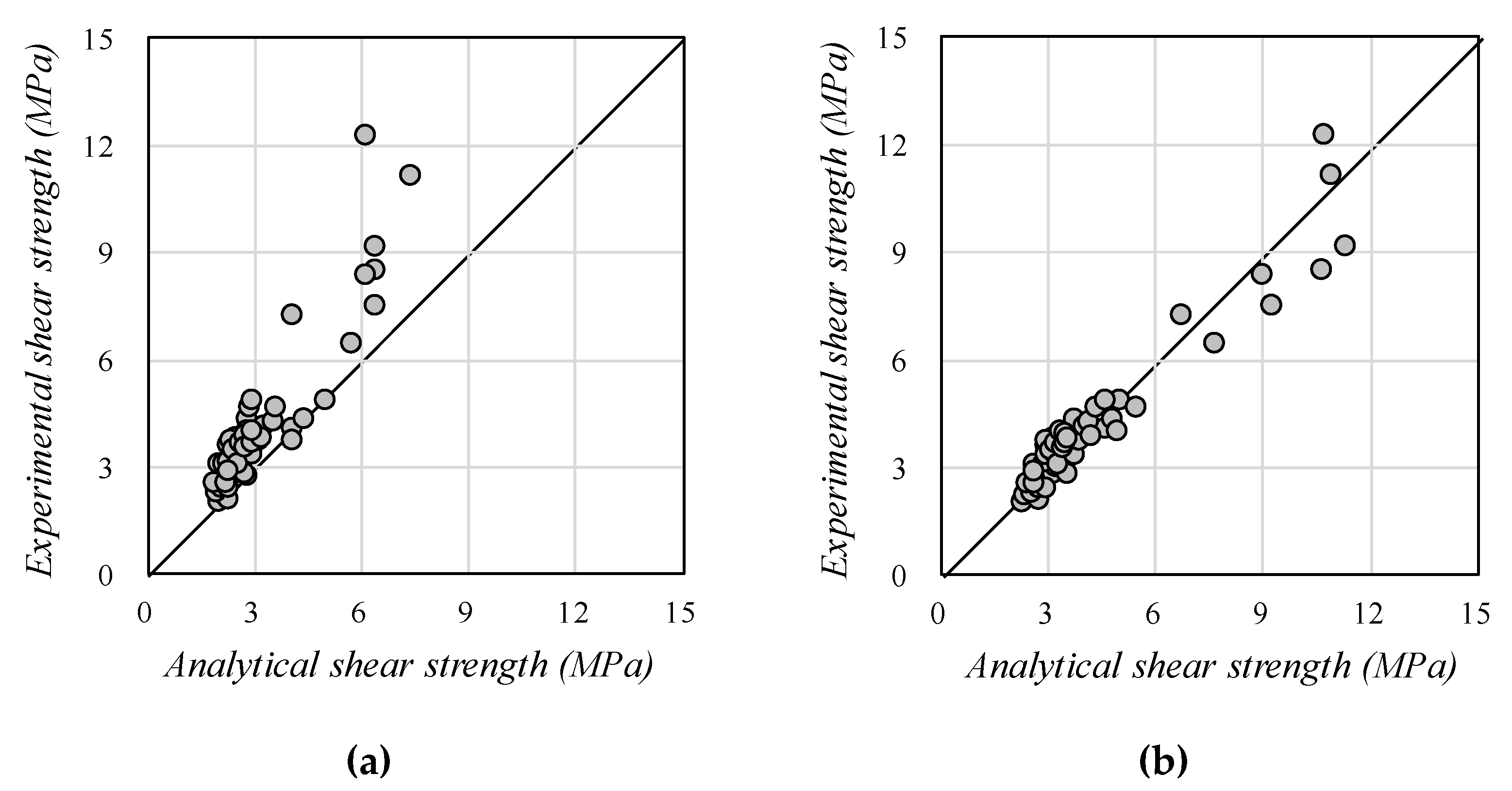
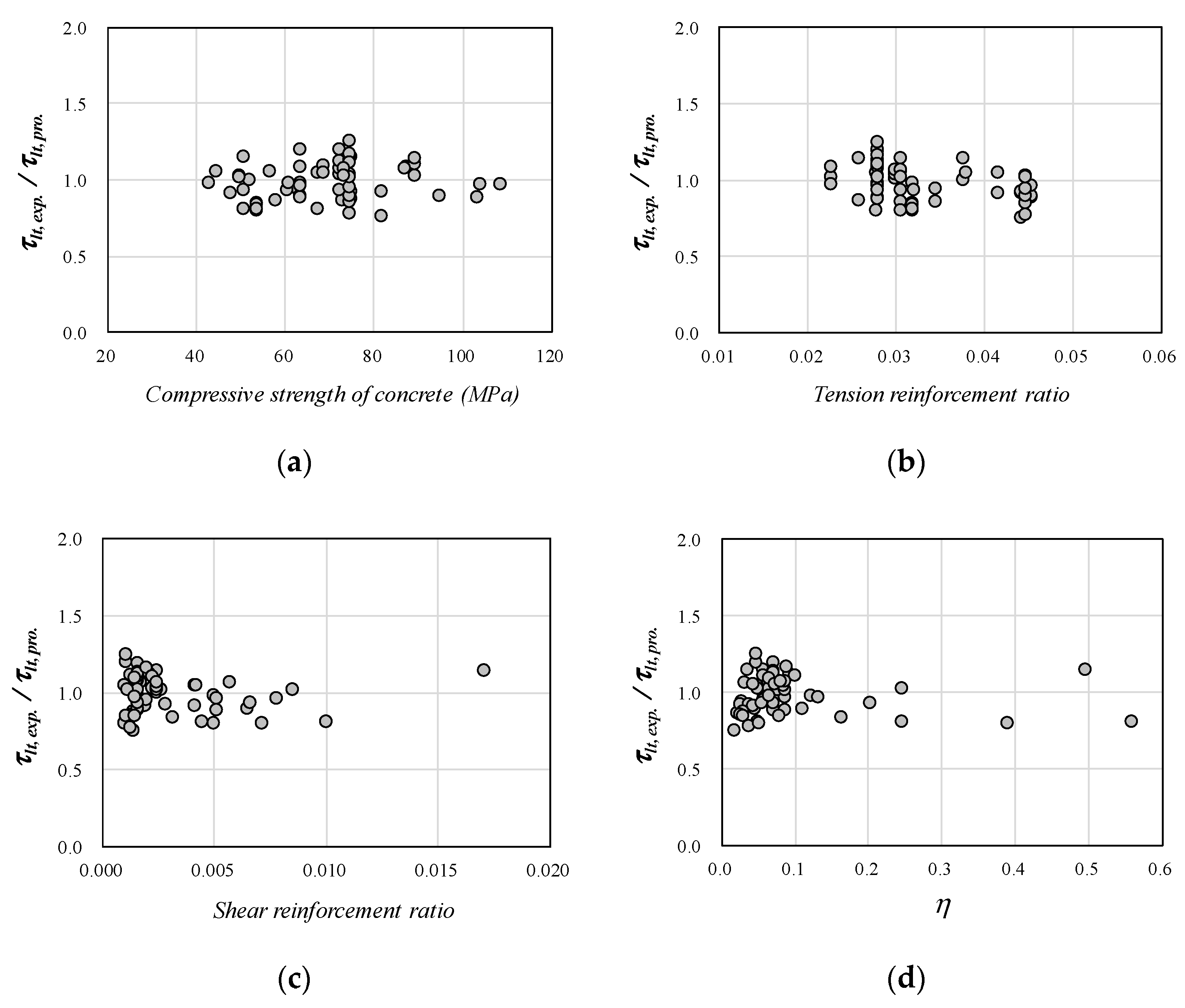
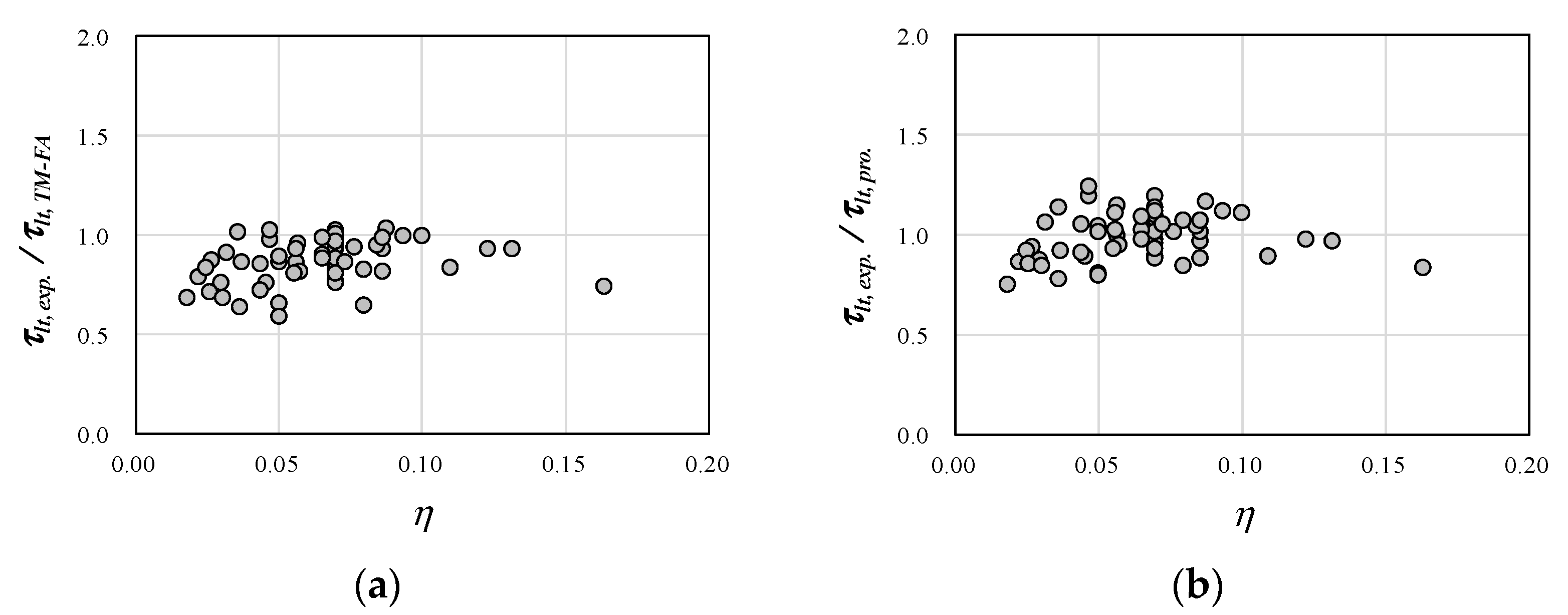
- The proposed shear analytical model was extended for application to high-strength concrete. The material models, including the shear transfer model by aggregate interlock, were replaced with those suitable for high-strength concrete. A total of 61 experimental results were well predicted, with a mean of 0.98 and a COV of 12.1%, without being affected by the concrete compressive strength.
- (2)
- A comparison with the experimental results confirmed that the analytical results were barely affected by various shear-span-to depth ratios. Thus, the proposed method for considering the bending moment effect can be used for reinforced high-strength concrete beams.
- (3)
- RC beams generally exhibit a large difference between the longitudinal and transverse reinforcement ratios. To consider this property of the RC beams, the proposed model based on the fixed angle theory allows the principal stresses and strains to rotate as the load increases. When 64 experimental results were predicted using the same model as the proposed analytical model but the principal stresses did not rotate, the accuracy was significantly reduced. This result confirmed that the proposed transformation angle system is applicable to reinforced high-strength concrete beams.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Elzanaty, A.H.; Nilson, A.H.; Slate, F.O. Shear capacity of reinforced concrete beams using high-strength concrete. ACI J. Proc. 1986, 83, 290–296. [Google Scholar]
- Ahmad, S.H.; Khaloo, A.A.; Poveda, A. Shear capacity of reinforced high-strength concrete beams. ACI J. Proc. 1986, 83, 297–305. [Google Scholar]
- Johnson, M.K.; Ramirez, J.A. Minimum shear reinforcement in beams with higher strength concrete. ACI Struct. J. 1989, 86, 376–382. [Google Scholar]
- Sarsam, K.F.; Al-Musawi, J.M.S. Shear design of high- and normal strength concrete beams with web reinforcement. ACI Struct. J. 1992, 89, 658–664. [Google Scholar]
- El-Sayed, A.K.; El-Salakawy, E.F.; Benmokrane, B. Shear capacity of high-strength concrete beams reinforced with FRP bars. ACI Struct. J. 2006, 103, 383–389. [Google Scholar]
- Jumaa, G.B.; Yousif, A.R. Size effect in shear failure of high strength concrete beams without stirrup reinforced with basalt FRP Bars. KSCE J. Civ. Eng. 2019, 23, 1–12. [Google Scholar] [CrossRef]
- Tahenni, T.; Chemrouk, M.; Lecompte, T. Effect of steel fibers on the shear behavior of high strength concrete beams. Constr. Build. Mater. 2016, 105, 14–28. [Google Scholar] [CrossRef]
- Biolzi, L.; Cattaneo, S. Response of steel fiber reinforced high strength concrete beams: Experiments and code predictions. Cem. Concr. Compos. 2017, 77, 1–13. [Google Scholar] [CrossRef]
- Mansour, W.; Tayeh, B.A. Shear Behaviour of RC Beams Strengthened by Various Ultrahigh Performance Fibre-Reinforced Concrete Systems. Adv. Civ. Eng. 2020, 2020, 1–18. [Google Scholar] [CrossRef]
- Mansour, W.; Sakr, M.; Seleemah, A.; Tayeh, B.A.; Khalifa, T. Development of shear capacity equations for RC beams strengthened with UHPFRC. Comput. Concr. 2021, 27, 473–487. [Google Scholar]
- Mitchell, D.; Collins, M.P. Diagonal compression field theory—A rational model for structural concrete in pure torsion. ACI J. Proc. 1974, 71, 396–408. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. The modified compression-field theory for reinforced concrete elements subjected to shear. ACI Struct. J. 1986, 83, 219–231. [Google Scholar]
- Hsu, T.T.C. Softened truss model theory for shear and torsion. ACI Struct. J. 1988, 85, 624–635. [Google Scholar]
- Hsu, T.T.C. Nonlinear analysis of concrete membrane elements. ACI Struct. J. 1991, 88, 552–561. [Google Scholar]
- Pang, X.B.; Hsu, T.T.C. Fixed angle softened truss model for reinforced concrete. ACI Struct. J. 1996, 93, 197–207. [Google Scholar]
- Hsu, T.T.C.; Zhang, L.X. Nonlinear analysis of membrane elements by fixed-angle softened-truss model. ACI Struct. J. 1997, 97, 483–492. [Google Scholar]
- Lee, J.-Y.; Kim, S.-W.; Mansour, M.Y. Nonlinear analysis of shear-critical reinforced concrete beams using fixed angle theory. J. Struct. Eng. 2011, 137, 1017–1029. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Kim, K.-H.; Kim, S.-W. Non-linear shear analysis of reinforced concrete columns by fixed-angle theory. Struct. Build. 2013, 166, 165–181. [Google Scholar] [CrossRef]
- Collins, M.P.; Porasz, A. Shear Design for High-Strength Concrete; Bulletin d’Information No. 193; Comité Euro-International du Béton: Lausanne, Switzerland, 1989; pp. 77–83. [Google Scholar]
- Belarbi, A.; Hsu, T.T.C. Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete. ACI Struct. J. 1994, 91, 465–474. [Google Scholar]
- Wilby, C.B. The strength of reinforced concrete beams in shear. Mag. Concr. Res. 1951, 3, 23–30. [Google Scholar] [CrossRef]
- Al-Alusi, A.F. Diagonal tension strength of reinforced concrete T-beams with varying shear span. ACI J. Proc. 1957, 53, 1067–1077. [Google Scholar]
- Taub, J.; Neville, A.M. Resistance to shear of reinforced concrete beams. ACI J. Proc. 1960, 57, 193–220. [Google Scholar]
- Shin, S.-W.; Lee, K.-S.; Moon, J.-I.; Ghosh, S.K. Shear strength of reinforced high-strength concrete beams with shear span-to-depth ratios between 1.5 and 2.5. ACI Struct. J. 1999, 96, 549–556. [Google Scholar]
- Xie, Y.; Ahmad, S.H.; Yu, T.; Hino, S.; Chung, W. Shear ductility of reinforced concrete beams of normal and high-strength concrete. ACI Struct. J. 1994, 91, 140–149. [Google Scholar]
- Ozcebe, G.; Ersoy, U.; Tankut, T. Evaluation of minimum shear reinforcement requirements for higher strength concrete. ACI Struct. J. 1999, 96, 361–368. [Google Scholar]
- Kong, P.Y.L.; Rangan, B.V. Shear strength of high-performance concrete beams. ACI Struct. J. 1998, 95, 677–688. [Google Scholar]
- Placas, A.; Regan, P.E. Shear failure of reinforced concrete beams. ACI J. Proc. 1971, 68, 763–773. [Google Scholar]
- Haddadin, M.J.; Hong, S.-T.; Mattock, A.H. Stirrup effectiveness in reinforced concrete beams with axial force. J. Struct. Div. ASCE 1971, 97, 2277–2297. [Google Scholar] [CrossRef]
- Kokusho, S.; Kobayashi, K.; Mitsugi, S.; Kumagai, H. Ultimate shear strength of RC beams with high tension shear reinforcement and high strength concrete. J. Struct. Constr. Eng. AIJ 1987, 373, 83–91. (In Japanese) [Google Scholar]
- Iwai, Y.; Enomoto, H.; Watanabe, F.; Muguruma, H. Study on the shear strength of beams using high-strength concrete. J. Archit. Build. Sci. AIJ 1991, 106, 269–270. (In Japanese) [Google Scholar]
- Yoo, D.-Y.; Yang, J.-M. Effects of stirrup, steel fiber, and beam size on shear behavior of high-strength concrete beams. Cem. Concr. Compos. 2018, 87, 137–148. [Google Scholar] [CrossRef]
- Cladera, A.; Mari, A.R. Experimental study on high-strength concrete beams failing in shear. Eng. Struct. 2005, 27, 1519–1527. [Google Scholar] [CrossRef]
- ACI Committee. Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary (ACI 318R-19); American Concrete Institute: Farmington Hills, MI, USA, 2019; 623p. [Google Scholar]


| Ref. | Specimens | (MPa) | a/d | (MPa) | (MPa) | (MPa) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [24] | HB2.5-25 | 73.0 | 2.5 | 0.0377 | 414.0 | 0.00240 | 372.5 | 0.057 | 4.30 | 1.54 | 1.14 |
| [24] | MHB2.5-25 | 52.0 | 2.5 | 0.0377 | 414.0 | 0.00240 | 372.5 | 0.057 | 3.67 | 1.47 | 0.99 |
| [25] | NNW-3 | 42.9 | 3.0 | 0.0320 | 406.2 | 0.00494 | 324.0 | 0.123 | 3.37 | 1.13 | 0.97 |
| [25] | NHW-3 | 103.4 | 3.0 | 0.0454 | 421.0 | 0.00510 | 324.0 | 0.086 | 4.07 | 1.01 | 0.88 |
| [25] | NHW-3a | 94.8 | 3.0 | 0.0454 | 421.0 | 0.00650 | 324.0 | 0.110 | 4.30 | 0.98 | 0.89 |
| [25] | NHW-3b | 108.7 | 3.0 | 0.0454 | 421.0 | 0.00780 | 324.0 | 0.132 | 4.87 | 0.98 | 0.96 |
| [25] | NHW-4 | 104.1 | 4.0 | 0.0454 | 421.0 | 0.00510 | 324.0 | 0.086 | 3.73 | 0.92 | 0.96 |
| [26] | ACI56 | 58.0 | 5.0 | 0.0346 | 450.0 | 0.00139 | 255.0 | 0.023 | 2.01 | 1.01 | 0.86 |
| [26] | TH56 | 63.0 | 5.0 | 0.0346 | 450.0 | 0.00167 | 255.0 | 0.027 | 2.23 | 1.05 | 0.94 |
| [26] | ACI59 | 82.0 | 5.0 | 0.0443 | 425.0 | 0.00139 | 255.0 | 0.019 | 2.08 | 0.91 | 0.75 |
| [26] | TH59 | 75.0 | 5.0 | 0.0443 | 425.0 | 0.00187 | 255.0 | 0.025 | 2.57 | 1.06 | 0.91 |
| [26] | TS59 | 82.0 | 5.0 | 0.0443 | 425.0 | 0.00279 | 255.0 | 0.038 | 2.70 | 0.96 | 0.92 |
| [26] | ACI36 | 75.0 | 3.0 | 0.0259 | 450.0 | 0.00139 | 255.0 | 0.030 | 2.26 | 1.14 | 0.87 |
| [26] | TH36 | 75.0 | 3.0 | 0.0259 | 450.0 | 0.00167 | 255.0 | 0.037 | 3.03 | 1.48 | 1.14 |
| [26] | ACI39 | 73.0 | 3.0 | 0.0307 | 439.0 | 0.00139 | 255.0 | 0.026 | 2.40 | 1.16 | 0.85 |
| [26] | TH39 | 73.0 | 3.0 | 0.0307 | 439.0 | 0.00170 | 255.0 | 0.032 | 3.07 | 1.43 | 1.06 |
| [27] | S1-1 | 63.6 | 2.5 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 3.13 | 1.26 | 0.98 |
| [27] | S1-2 | 63.6 | 2.5 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 2.85 | 1.14 | 0.89 |
| [27] | S1-3 | 63.6 | 2.5 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 2.82 | 1.13 | 0.88 |
| [27] | S1-4 | 63.6 | 2.5 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 3.81 | 1.53 | 1.19 |
| [27] | S1-5 | 63.6 | 2.5 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 3.47 | 1.39 | 1.08 |
| [27] | S1-6 | 63.6 | 2.5 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 3.07 | 1.23 | 0.96 |
| [27] | S2-1 | 72.5 | 2.5 | 0.0280 | 452.0 | 0.00105 | 569.0 | 0.047 | 3.57 | 1.55 | 1.19 |
| [27] | S2-2 | 72.5 | 2.5 | 0.0280 | 452.0 | 0.00126 | 569.0 | 0.057 | 3.18 | 1.31 | 1.03 |
| [27] | S2-3 | 72.5 | 2.5 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 3.47 | 1.33 | 1.07 |
| [27] | S2-4 | 72.5 | 2.5 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 3.01 | 1.16 | 0.93 |
| [27] | S2-5 | 72.5 | 2.5 | 0.0280 | 452.0 | 0.00209 | 569.0 | 0.094 | 3.86 | 1.33 | 1.12 |
| [27] | S3-3 | 67.4 | 2.5 | 0.0279 | 452.0 | 0.00101 | 632.0 | 0.051 | 3.12 | 1.37 | 1.04 |
| [27] | S3-4 | 67.4 | 2.5 | 0.0279 | 452.0 | 0.00101 | 632.0 | 0.051 | 2.39 | 1.05 | 0.80 |
| [27] | S4-4 | 87.3 | 2.5 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 3.54 | 1.28 | 1.08 |
| [27] | S5-1 | 89.4 | 3.0 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 3.31 | 1.19 | 1.10 |
| [27] | S5-2 | 89.4 | 2.7 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 3.56 | 1.28 | 1.13 |
| [27] | S5-3 | 89.4 | 2.5 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 3.34 | 1.20 | 1.02 |
| [27] | S7-1 | 74.8 | 3.3 | 0.0447 | 433.0 | 0.00105 | 569.0 | 0.031 | 2.96 | 1.13 | 0.85 |
| [27] | S7-2 | 74.8 | 3.3 | 0.0447 | 433.0 | 0.00126 | 569.0 | 0.037 | 2.79 | 1.02 | 0.77 |
| [27] | S7-3 | 74.8 | 3.3 | 0.0447 | 433.0 | 0.00157 | 569.0 | 0.046 | 3.35 | 1.15 | 0.89 |
| [27] | S7-4 | 74.8 | 3.3 | 0.0447 | 433.0 | 0.00196 | 569.0 | 0.058 | 3.72 | 1.18 | 0.94 |
| [27] | S7-5 | 74.8 | 3.3 | 0.0447 | 433.0 | 0.00224 | 569.0 | 0.066 | 4.14 | 1.25 | 1.02 |
| [27] | S7-6 | 74.8 | 3.3 | 0.0447 | 433.0 | 0.00262 | 569.0 | 0.077 | 4.23 | 1.20 | 1.01 |
| [27] | S8-1 | 74.6 | 2.5 | 0.0280 | 452.0 | 0.00105 | 569.0 | 0.047 | 3.73 | 1.60 | 1.24 |
| [27] | S8-2 | 74.6 | 2.5 | 0.0280 | 452.0 | 0.00126 | 569.0 | 0.057 | 3.44 | 1.41 | 1.11 |
| [27] | S8-4 | 74.6 | 2.5 | 0.0280 | 452.0 | 0.00157 | 569.0 | 0.071 | 3.64 | 1.39 | 1.12 |
| [27] | S8-5 | 74.6 | 2.5 | 0.0280 | 452.0 | 0.00196 | 569.0 | 0.088 | 3.96 | 1.39 | 1.16 |
| [27] | S8-6 | 74.6 | 2.5 | 0.0280 | 452.0 | 0.00224 | 569.0 | 0.101 | 3.89 | 1.29 | 1.11 |
| [28] | R21 | 47.9 | 3.6 | 0.0416 | 617.6 | 0.00410 | 278.6 | 0.044 | 3.86 | 1.42 | 0.91 |
| [28] | T26 | 56.7 | 3.6 | 0.0416 | 617.6 | 0.00410 | 278.6 | 0.044 | 4.63 | 1.62 | 1.05 |
| [29] | F3 | 44.7 | 2.5 | 0.0381 | 514.7 | 0.00419 | 343.1 | 0.073 | 4.85 | 1.66 | 1.05 |
| [30] | B-570-4.1 | 53.8 | 1.7 | 0.0320 | 798.0 | 0.00147 | 1392.2 | 0.080 | 4.63 | 1.29 | 0.84 |
| [30] | B-570-6.0 | 53.8 | 1.7 | 0.0320 | 798.0 | 0.00314 | 1333.3 | 0.164 | 6.43 | 1.12 | 0.83 |
| [30] | B-570-7.4 | 53.8 | 1.7 | 0.0320 | 798.0 | 0.00444 | 1421.7 | 0.247 | 7.49 | 1.17 | 0.81 |
| [30] | B-570-9.2 | 53.8 | 1.7 | 0.0320 | 798.0 | 0.00711 | 1402.0 | 0.390 | 8.48 | 1.33 | 0.79 |
| [30] | B-570-11.0 | 53.8 | 1.7 | 0.0320 | 798.0 | 0.01000 | 1431.4 | 0.561 | 9.16 | 1.44 | 0.80 |
| [31] | B-1 | 50.7 | 1.7 | 0.0306 | 952.9 | 0.00498 | 297.1 | 0.051 | 3.97 | 1.35 | 0.80 |
| [31] | B-4 | 50.7 | 1.7 | 0.0306 | 952.9 | 0.00660 | 902.0 | 0.204 | 8.35 | 1.35 | 0.93 |
| [31] | B-5 | 50.7 | 1.7 | 0.0306 | 953.2 | 0.01710 | 846.3 | 0.496 | 12.27 | 1.99 | 1.14 |
| [31] | B-6 | 73.5 | 1.7 | 0.0306 | 952.9 | 0.00569 | 411.3 | 0.080 | 7.19 | 1.75 | 1.07 |
| [31] | B-7 | 73.5 | 1.7 | 0.0306 | 953.2 | 0.00850 | 846.3 | 0.247 | 11.15 | 1.50 | 1.02 |
| [32] | S-F0 | 60.5 | 3.2 | 0.0322 | 498.0 | 0.00159 | 566.0 | 0.056 | 3.08 | 1.22 | 0.93 |
| [33] | H50/2 | 49.9 | 3.1 | 0.0228 | 500.0 | 0.00109 | 530.0 | 0.051 | 2.52 | 1.33 | 1.02 |
| [33] | H50/4 | 49.9 | 3.1 | 0.0299 | 500.0 | 0.00239 | 540.0 | 0.086 | 3.51 | 1.28 | 1.01 |
| [33] | H60/2 | 60.8 | 3.1 | 0.0228 | 500.0 | 0.00141 | 530.0 | 0.066 | 2.55 | 1.16 | 0.97 |
| [33] | H75/2 | 68.9 | 3.1 | 0.0228 | 500.0 | 0.00141 | 530.0 | 0.066 | 2.89 | 1.26 | 1.09 |
| [33] | H75/4 | 68.9 | 3.1 | 0.0299 | 500.0 | 0.00239 | 530.0 | 0.085 | 3.64 | 1.23 | 1.04 |
| [33] | H100/4 | 87.0 | 3.1 | 0.0299 | 500.0 | 0.00239 | 540.0 | 0.086 | 3.80 | 1.19 | 1.06 |
| Mean | 1.28 | 0.98 | |||||||||
| COV | 16.4% | 12.1% | |||||||||
| Types | Num. of Beams | |||||||
|---|---|---|---|---|---|---|---|---|
| TM-NM | TM-FA | Proposed | ||||||
| Mean | COV | Mean | COV | Mean | COV | |||
| 42.9~68.9 MPa | 29 | 0.76 | 12.7% | 0.83 | 13.9% | 0.95 | 11.5% | |
| 72.5~108.7 MPa | 35 | 0.76 | 15.3% | 0.89 | 12.1% | 1.01 | 12.0% | |
| Supports | Simple beam | 54 | 0.74 | 13.6% | 0.87 | 11.7% | 1.00 | 11.2% |
| Restrained beam | 10 | 0.84 | 11.9% | 0.81 | 19.3% | 0.90 | 14.2% | |
| Total | 64 | 0.76 | 14.0% | 0.86 | 13.1% | 0.98 | 12.1% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-W. Prediction of Shear Strength of Reinforced High-Strength Concrete Beams Using Compatibility-Aided Truss Model. Appl. Sci. 2021, 11, 10585. https://doi.org/10.3390/app112210585
Kim S-W. Prediction of Shear Strength of Reinforced High-Strength Concrete Beams Using Compatibility-Aided Truss Model. Applied Sciences. 2021; 11(22):10585. https://doi.org/10.3390/app112210585
Chicago/Turabian StyleKim, Sang-Woo. 2021. "Prediction of Shear Strength of Reinforced High-Strength Concrete Beams Using Compatibility-Aided Truss Model" Applied Sciences 11, no. 22: 10585. https://doi.org/10.3390/app112210585
APA StyleKim, S.-W. (2021). Prediction of Shear Strength of Reinforced High-Strength Concrete Beams Using Compatibility-Aided Truss Model. Applied Sciences, 11(22), 10585. https://doi.org/10.3390/app112210585






