A Convenient Way to Determine the Optimum Angle of Incidence of Fizeau Interferometer
Abstract
:1. Introduction
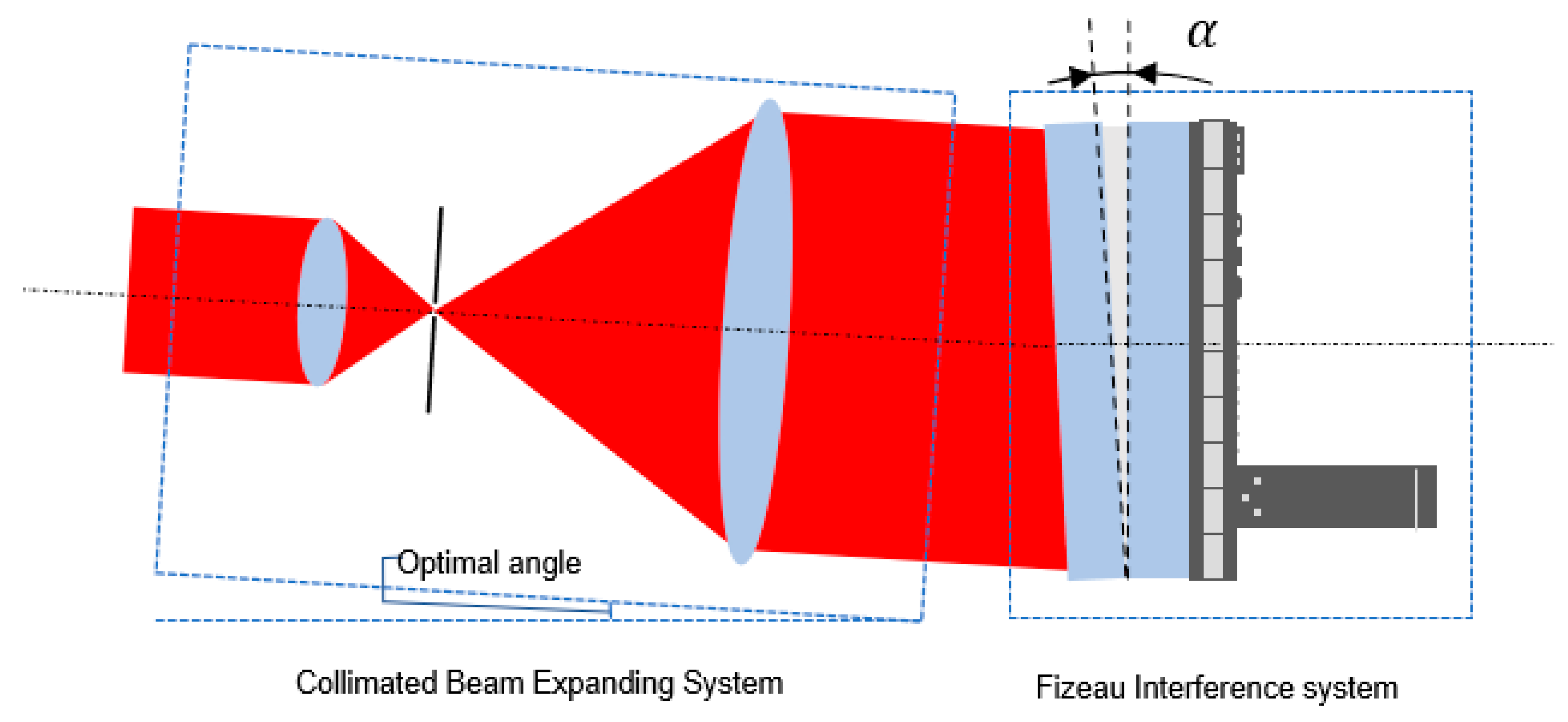
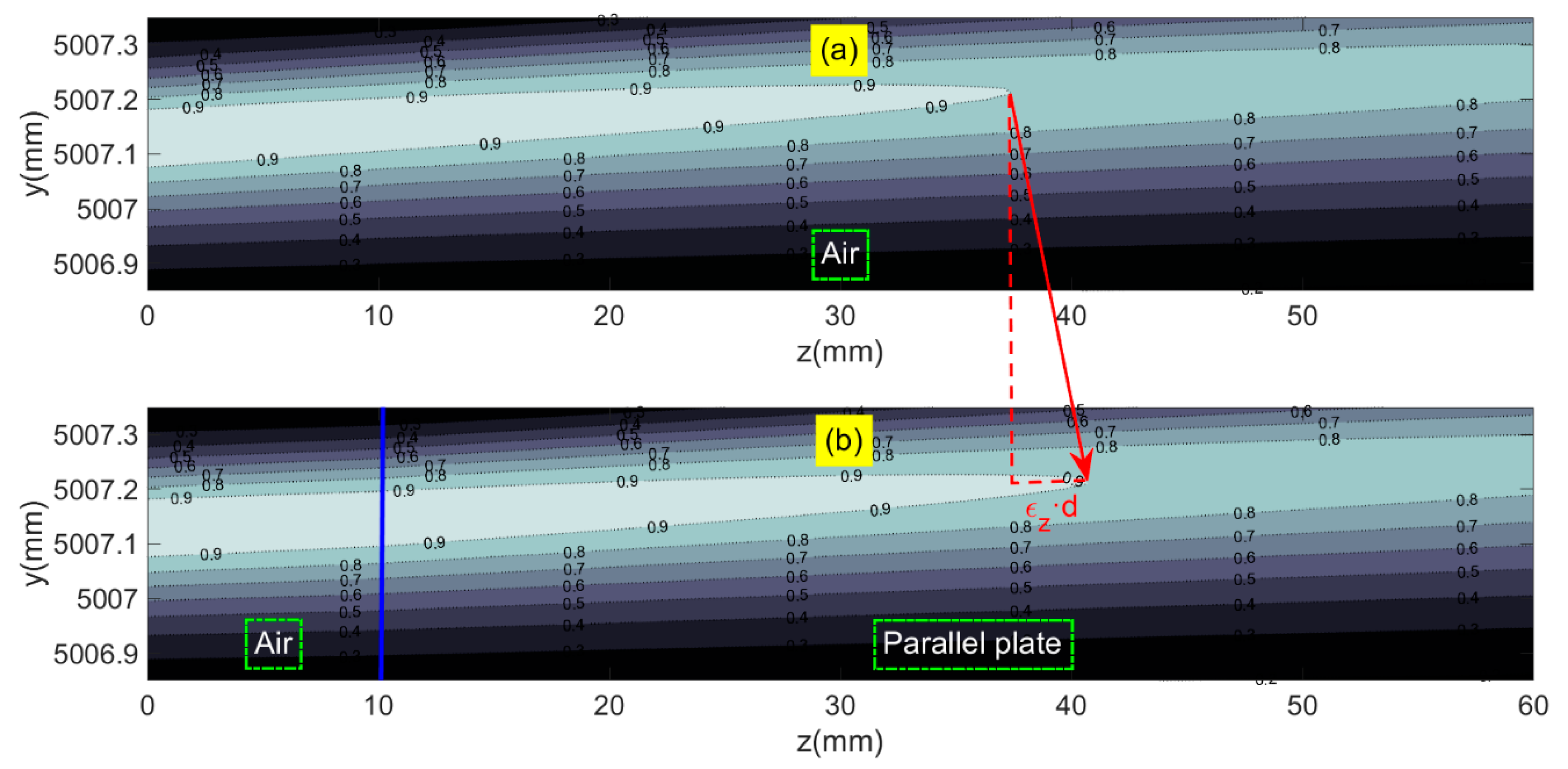
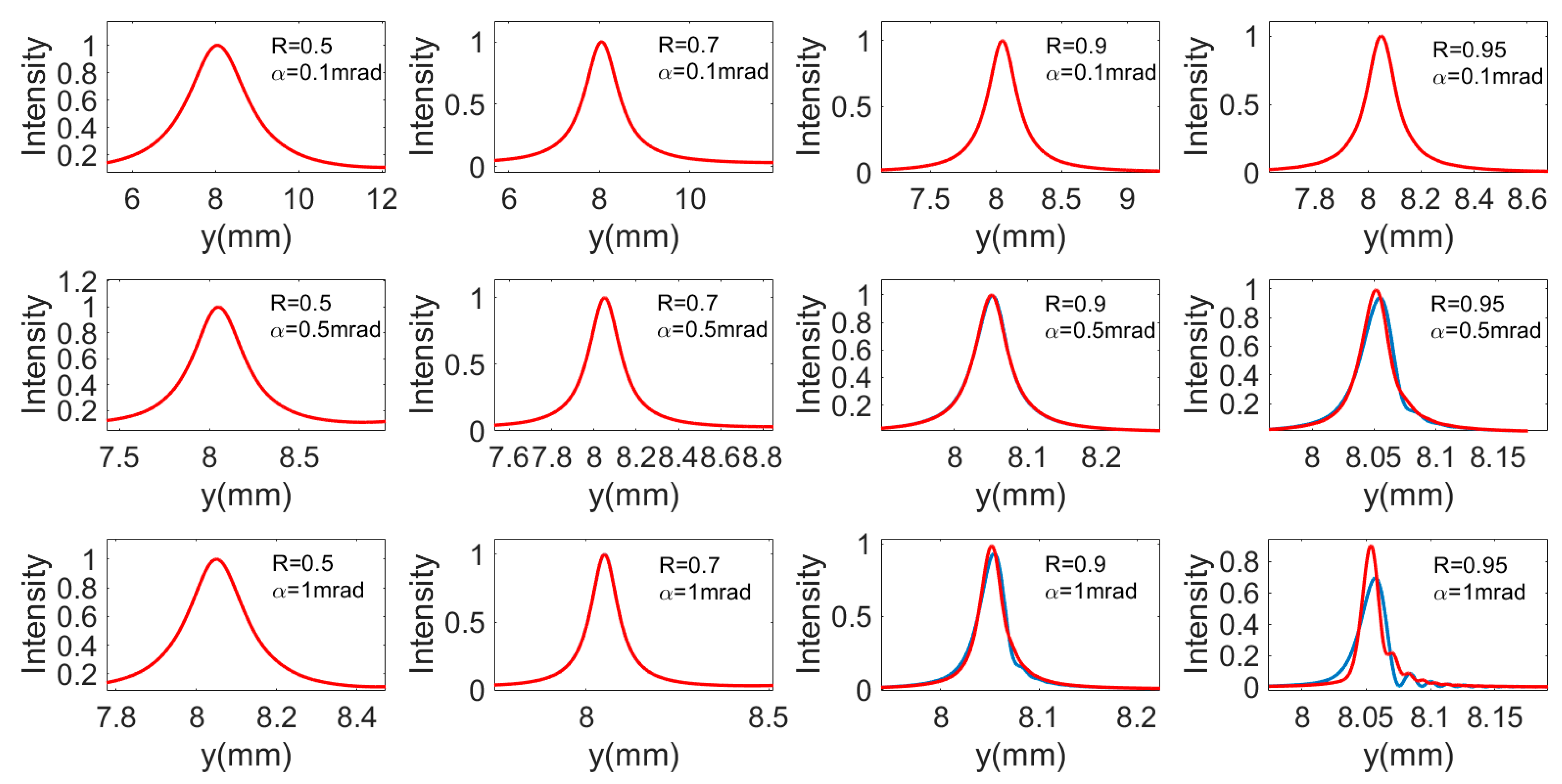
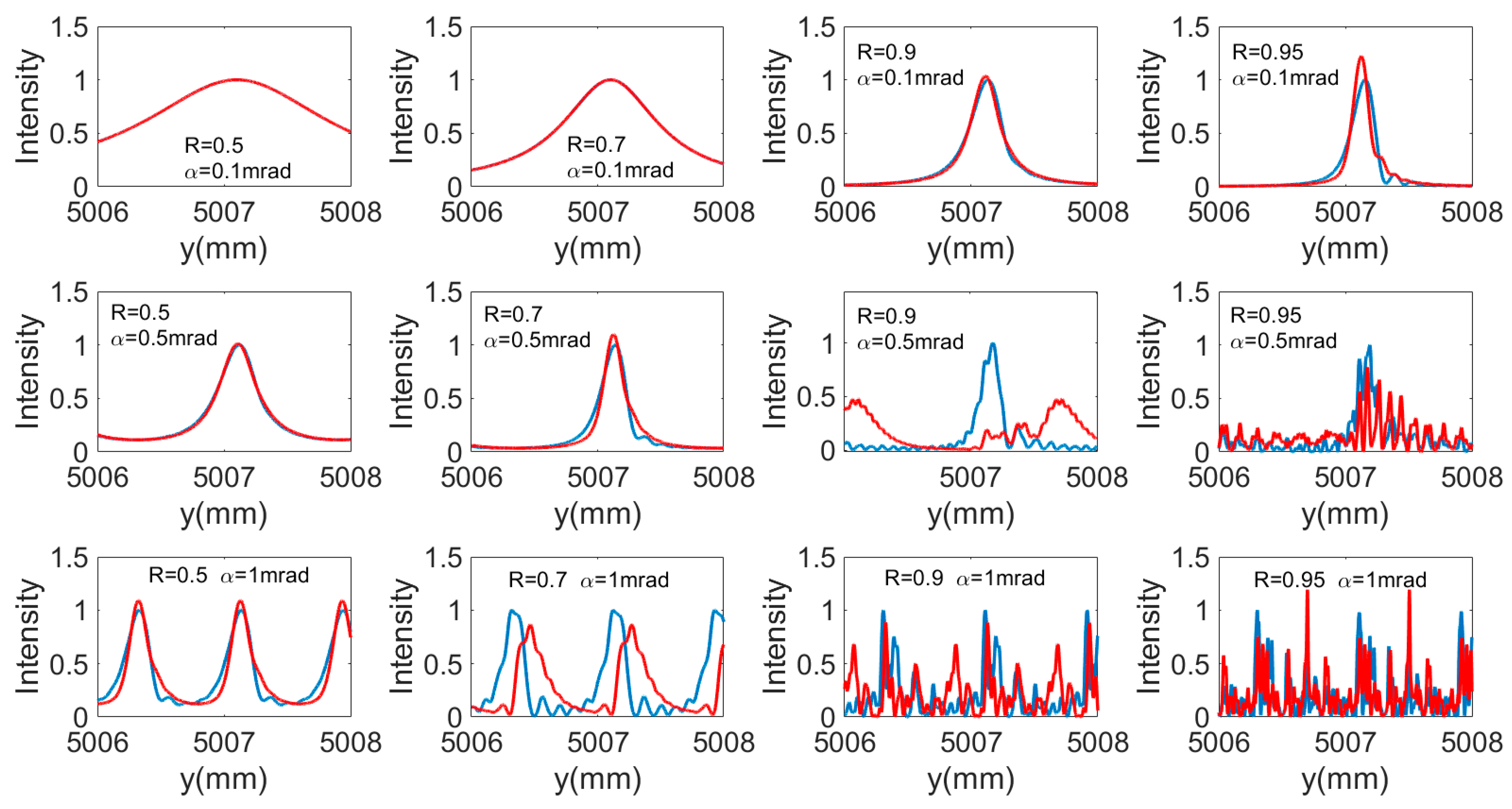
2. Analysis of Spatial Light Intensity Distribution
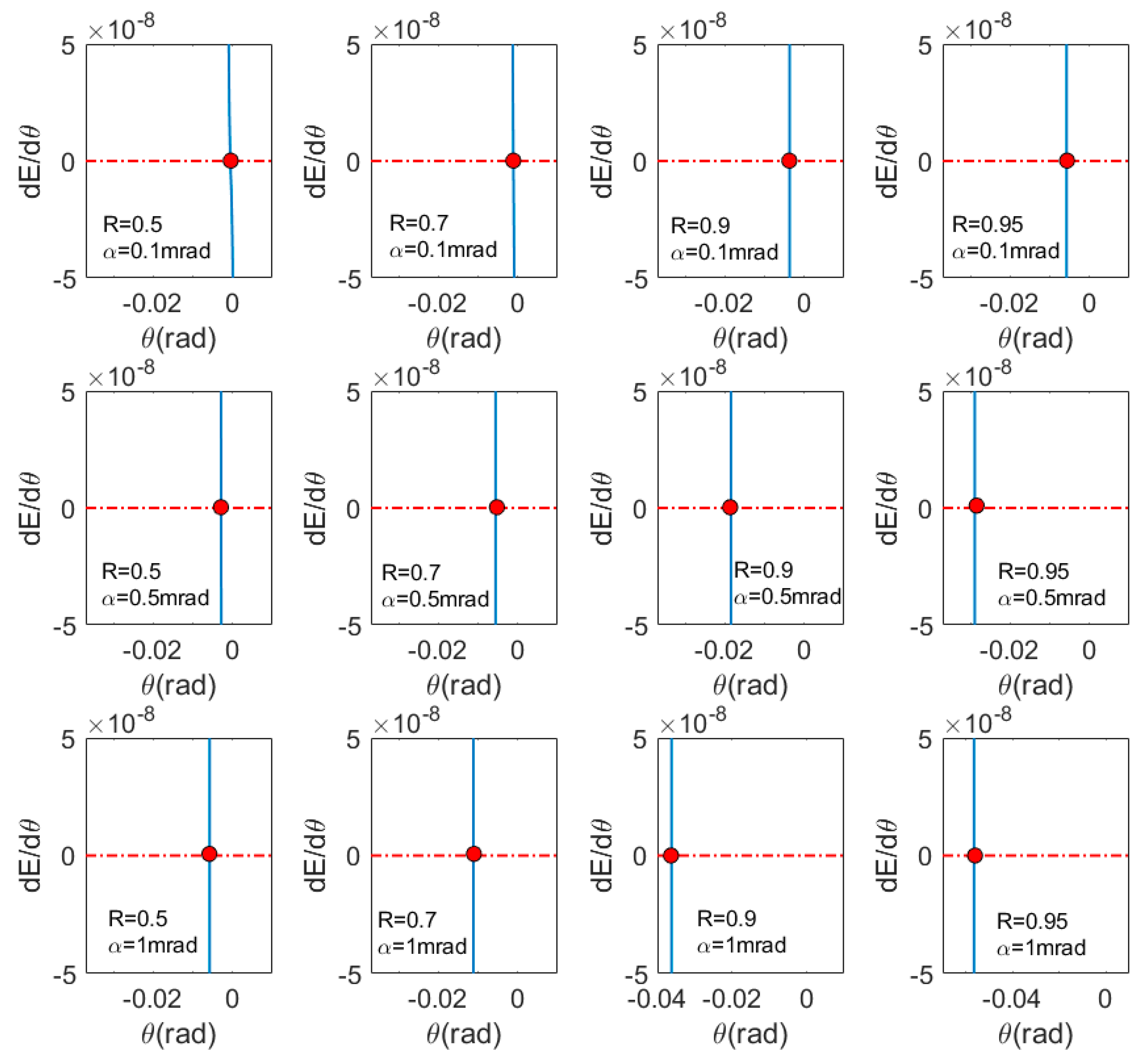
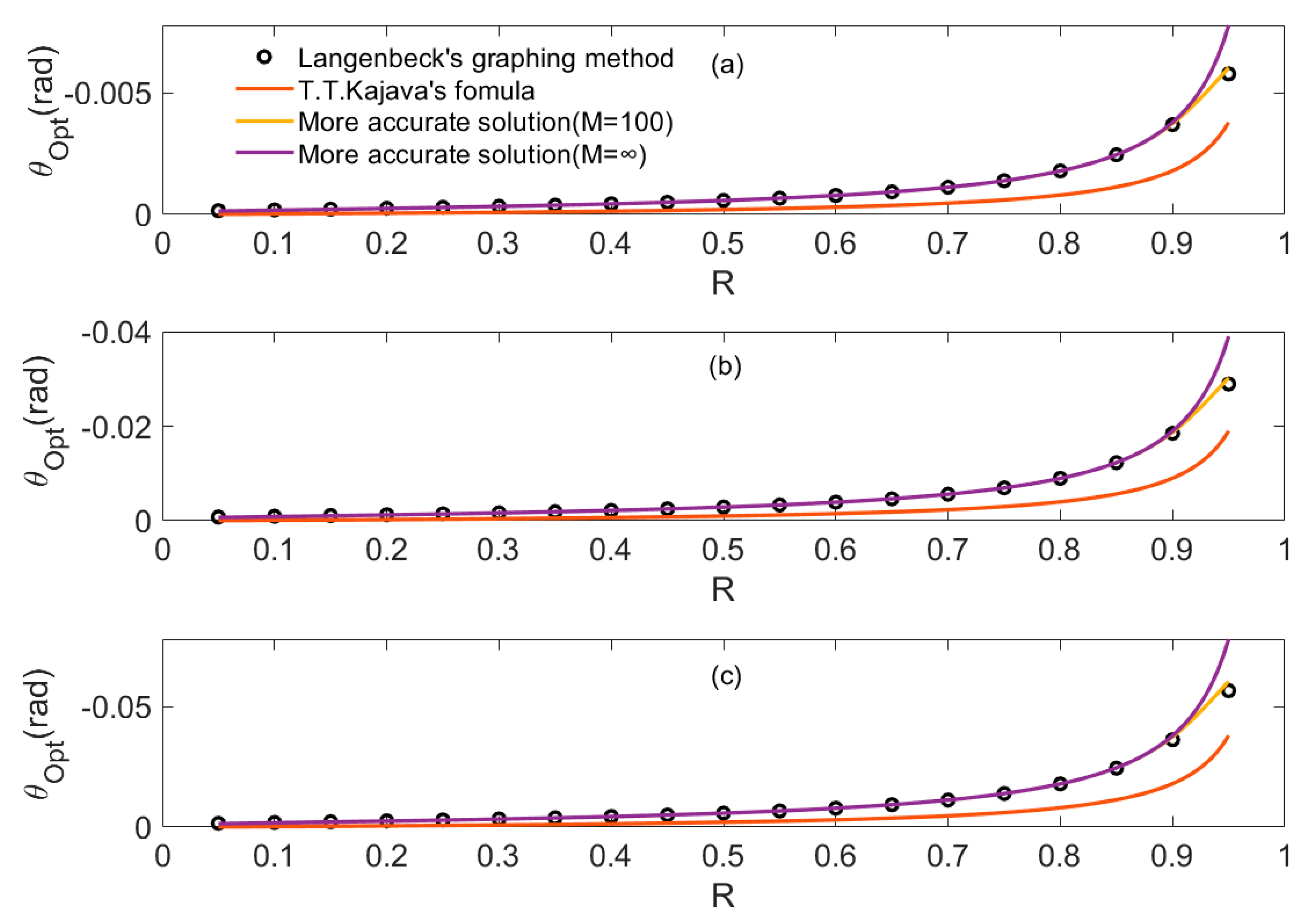
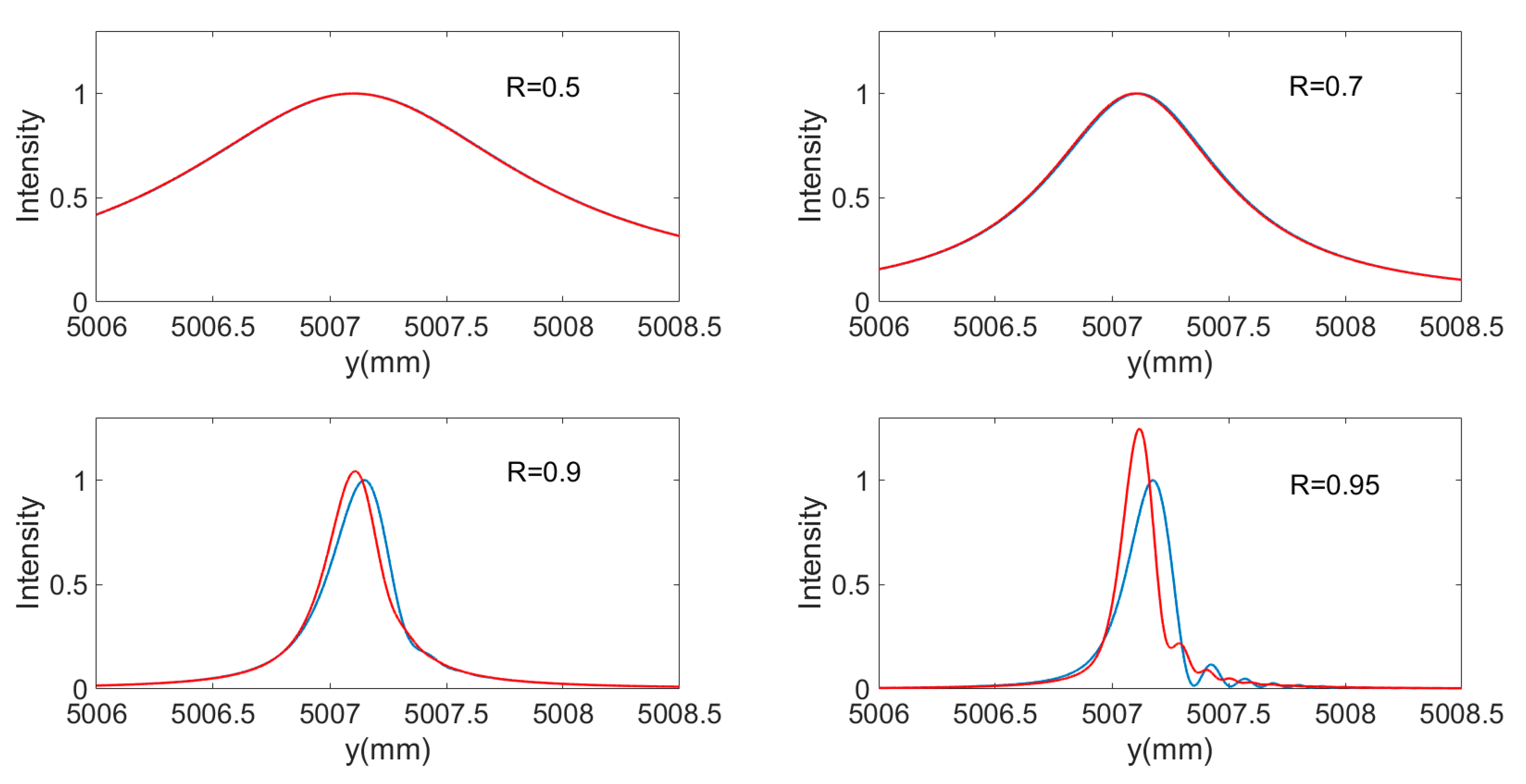
3. Determination of the Optimum Incident Angle
4. Intensity Optimization
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gillard, F.; Ferrec, Y.; Guérineau, N.; Rommeluère, S.; Taboury, J.; Chavel, P. Angular acceptance analysis of an infrared focal plane array with a built-in stationary Fourier transform spectrometer. JOSA A 2012, 29, 936–944. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guerineau, N.; Rommeluere, S.; Deschamps, J.; De Borniol, E.; Million, A.; Chamonal, J.P.; Destefanis, G. Infrared focal plane array with a built-in stationary fourier-transform spectrometer: First experimental results. In Proceedings of the Fourier Transform Spectroscopy, Alexandria, VA, USA, 31 January–3 February 2005. [Google Scholar]
- Guerineau, N.; Suffis, S.; Cymbalista, P.; Primot, J. Conception of a stationary Fourier transform infrared spectroradiometer for field measurements of radiance and emissivity. In Proceedings of the Optical Design and Engineering, St. Etienne, France, 18 February 2004; Volume 5249, pp. 441–448. [Google Scholar]
- Gillard, F.; Rommeluère, S.; de la Barrière, F.; Druart, G.; Guérineau, N.; Ferrec, Y.; Lefebvre, S.; Fendler, M.; Taboury, J. Towards a handheld cryogenic FTIR spectrometer. In Proceedings of the Fourier Transform Spectroscopy, Toronto, ON, Canada, 10–14 July 2011. [Google Scholar]
- Ferrec, Y.; Rommeluère, S.; Lefebvre, S.; Benoît, C.; Gillard, F.; Guérineau, N. Infrared focal plane array with a built-in stationary Fourier-transform spectrometer (MICROSPOC): Physical limitations and numerical solutions. In Proceedings of the Fourier Transform Spectroscopy, Toronto, ON, Canada, 10–14 July 2011. [Google Scholar]
- Ferrec, Y.; de la Barrière, F.; le Coarer, E.; Diard, T.; Guérineau, N.; Martin, G.; Rommeluère, S.; Schmitt, B.; Thomas, F. Current status and perspectives for Microspoc, the miniature Fourier transform spectrometer. In Proceedings of the Fourier Transform Spectroscopy, Lake Arrowhead, CA, USA, 1–4 March 2015. [Google Scholar]
- Rommeluère, S.; Haïdar, R.; Guérineau, N.; Deschamps, J.; De Borniol, E.; Million, A.; Chamonal, J.P.; Destefanis, G. Single-scan extraction of two-dimensional parameters of infrared focal plane arrays utilizing a Fourier-transform spectrometer. Appl. Opt. 2007, 46, 1379–1384. [Google Scholar] [CrossRef] [PubMed]
- Novák, O.; Falconer, I.S.; Sanginés, R.; Lattemann, M.; Tarrant, R.N.; McKenzie, D.R.; Bilek, M.M.M. Fizeau interferometer system for fast high-resolution studies of spectral line shapes. Rev. Sci. Instrum. 2011, 82, 023105. [Google Scholar] [CrossRef] [PubMed]
- Bae, W.; Kim, Y. Phase extraction formula for glass thickness measurement using Fizeau interferometer. J. Mech. Sci. Technol. 2021, 35, 1623–1632. [Google Scholar] [CrossRef]
- Kim, Y.; Hibino, K.; Sugita, N.; Mitsuishi, M. Error-compensating phase-shifting algorithm for surface shape measurement of transparent plate using wavelength-tuning Fizeau interferometer. Opt. Lasers Eng. 2016, 86, 309–316. [Google Scholar] [CrossRef]
- Emadi, A.; Wu, H.; de Graaf, G.; Wolffenbuttel, R. Design and implementation of a sub-nm resolution microspectrometer based on a Linear-Variable Optical Filter. Opt. Express 2012, 20, 489–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DeCorby, R.G.; Ponnampalam, N.; Epp, E.; Allen, T.; McMullin, J.N. Chip-scale spectrometry based on tapered hollow Bragg waveguides. Opt. Express 2009, 17, 16632–16645. [Google Scholar] [CrossRef] [PubMed]
- Langenbeck, P. Fizeau interferometer–fringe sharpening. Appl. Opt. 1970, 9, 2053–2058. [Google Scholar] [CrossRef] [PubMed]
- Kajava, T.T.; Lauranto, H.M.; Friberg, A.T. Interference pattern of the Fizeau interferometer. JOSA A 1994, 11, 2045–2054. [Google Scholar] [CrossRef]
- Vasil’ev, K.K.; Dement’ev, V.E.; Andriyanov, N.A. Doubly stochastic models of images. Pattern Recognit. Image Anal. 2015, 25, 105–110. [Google Scholar] [CrossRef]
- Shirokanev, A.S.; Kibitkina, A.S.; Ilyasova NY, E.; Degtyaryov, A.A. Methods of mathematical modeling of fundus laser exposure for therapeutic effect evaluation. Comput. Opt. 2020, 44, 809–820. [Google Scholar] [CrossRef]
- Shirokanev, A.S.; Andriyanov, N.A.; Ilyasova, N.Y. Development of vector algorithm using CUDA technology for three-dimensional retinal laser coagulation process modeling. Comput. Opt. 2021, 45, 427–437. [Google Scholar] [CrossRef]
- Brossel, J. Multiple-beam localized fringes: Part I.-Intensity distribution and localization. Proc. Phys. Soc. 1947, 59, 224. [Google Scholar] [CrossRef]
- Brossel, J. Multiple-beam localized fringes: Part II.-Conditions of observation and formation of ghosts. Proc. Phys. Soc. 1947, 59, 234. [Google Scholar] [CrossRef]
- Meyer, Y.H. Fringe shape with an interferential wedge. JOSA 1981, 71, 1255–1263. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, B.; Zheng, Y.; Lin, C.; Zhang, H. A Convenient Way to Determine the Optimum Angle of Incidence of Fizeau Interferometer. Appl. Sci. 2021, 11, 10678. https://doi.org/10.3390/app112210678
Du B, Zheng Y, Lin C, Zhang H. A Convenient Way to Determine the Optimum Angle of Incidence of Fizeau Interferometer. Applied Sciences. 2021; 11(22):10678. https://doi.org/10.3390/app112210678
Chicago/Turabian StyleDu, Bowen, Yuquan Zheng, Chao Lin, and Hang Zhang. 2021. "A Convenient Way to Determine the Optimum Angle of Incidence of Fizeau Interferometer" Applied Sciences 11, no. 22: 10678. https://doi.org/10.3390/app112210678





