1. Introduction
The commissioning of mechatronic systems has been accompanied by the appearance of failures and breakdowns that develop over time. These failures are not yet well mastered. Therefore, to identify these failures is necessary in order to ensure the systems reliability [
1,
2]. The transistor is one of the important components in these systems. This element played a great role in the revolution of the design and development of such systems. For the most developed systems like airborne systems, we find that the origin of most of their failures is their high-power amplifiers (HPA), a large percentage of these failures are caused by high electron mobility transistors (HEMT) [
3,
4].
The high electron mobility transistor (HEMT), based on aluminum gallium nitride/gallium nitride (AlGaN/GaN), is an important electronic component thanks to its structure and materials. Gallium nitride GaN is characterized by high mobility, very high electrical breakdown field and high thermal conductivity [
5,
6]. Thanks to these characteristics, these components have been used in different high-temperature and high-frequency applications [
7,
8], such as airborne systems, telecommunication and electronic warfare [
9,
10]. HEMT has also been used in several systems such as high-power amplifiers, satellites and radars [
11].
The failures in HEMT technology are strongly related to its operating temperature exceeding the critical values because of the component self-heating. The operating temperature is an important factor, it can influence the HEMT reliability because most of its characteristics, such as electron mobility, saturation rate [
12], thermal conductivity and others, are temperature-dependent [
13,
14]. All these characteristics degrade and decrease with the rise of temperature due to the self-heating phenomenon [
3,
15]. The phenomenon of self-heating can give rise to different degradations such as gate burial, damage to the connection chip-package [
8], electron mobility degradation and current reduction [
16].
More authors have realized electrothermal or thermal modeling in order to determine the thermal behavior of the HEMT as a function of its electrical parameters, and they apply a voltage between the transistor terminals and observe the temperature variation [
17,
18]. However, this method is very complex because we need to integrate several electrical and thermal equations and parameters, which makes the modeling difficult and the finite element model becomes very expensive in terms of necessary parameters and calculation time. In this paper, we propose another simple method of modeling that is based on the injection of the power dissipated at the active area instead of applying the voltage or current at the terminals of the component [
19]. In the rest of this work, we will detail this method and the results obtained. In addition, we have developed an approach to estimating the reliability of the HEMT technology using the approximation methods SORM and FORM. These methods allow us to evaluate the reliability index and the failure probability of our system. We have developed a coupling between two models: a finite element model using Comsol multiphysics and the reliability model coded with Matlab software. This coupling allows us to evaluate the reliability index and the probability of failures in our component.
In a first step, we will present a description of the HEMT technology and its structure, in order to have a clear idea about its topology as well as the thermal properties of its material. Then, we will develop a finite element model with Comsol multiphysics software in its thermal part, which will allow us to manipulate the different parameters: geometry, thermal properties and loads, and so forth. Afterwards, we will study the influence of some parameters, such as the power dissipation and the reference temperature, on the operating temperature of the HEMT. In the other section, the FORM and SORM methods used to estimate the reliability index and the failure probability will be presented. In the final section, we will present the result of the reliability analysis—failure probability and the reliability index—obtained thanks to the coupling between thermal model and the reliability model using Matlab software.
2. Device Description
The HEMT, based on aluminum gallium nitride/gallium nitride (AlGaN/GaN), is a highly developed electronic component due to its structure and materials. One of this materials is Gallium nitride (GaN); it is characterized by high mobility, high electrical breakdown field, and high thermal conductivity. The HEMT appears as an evolution of the MESFET; the difference is that the HEMT uses a heterojunction, that is to say, a junction between materials having different energy bands, to make the electrons constituting the drain-source current pass through a non-doped semiconductor, to decrease the transit time and thus increase the frequency performance. The electrons’ speed is all the greater when the doping of the semiconductor is weak, because the dispersion of ionized impurities is reduced [
20].
The field effect transistor based on the GaN heterostructure uses a 2-dimensional electron gas (2DEG) as a conductive channel, where electrons circulate in a lightly doped material and result from the occupation of the energy levels of the potential well that is characteristic of the heterojunction. Three electrodes, commonly called source, gate and drain allow controlling the current and the voltage of the transistor operation. The source and drain contacts are Ohmic type, the gate contact is Schottky type. For power amplified applications, the common source arrangement is used and the source electrode is connected to the ground. The gate allows the control of the current density circulating in the transistor by acting electro-statically on the electron gas; it is the low power control electrode. The drain allows the control of the operating voltage; it is the high power control electrode [
3,
21].
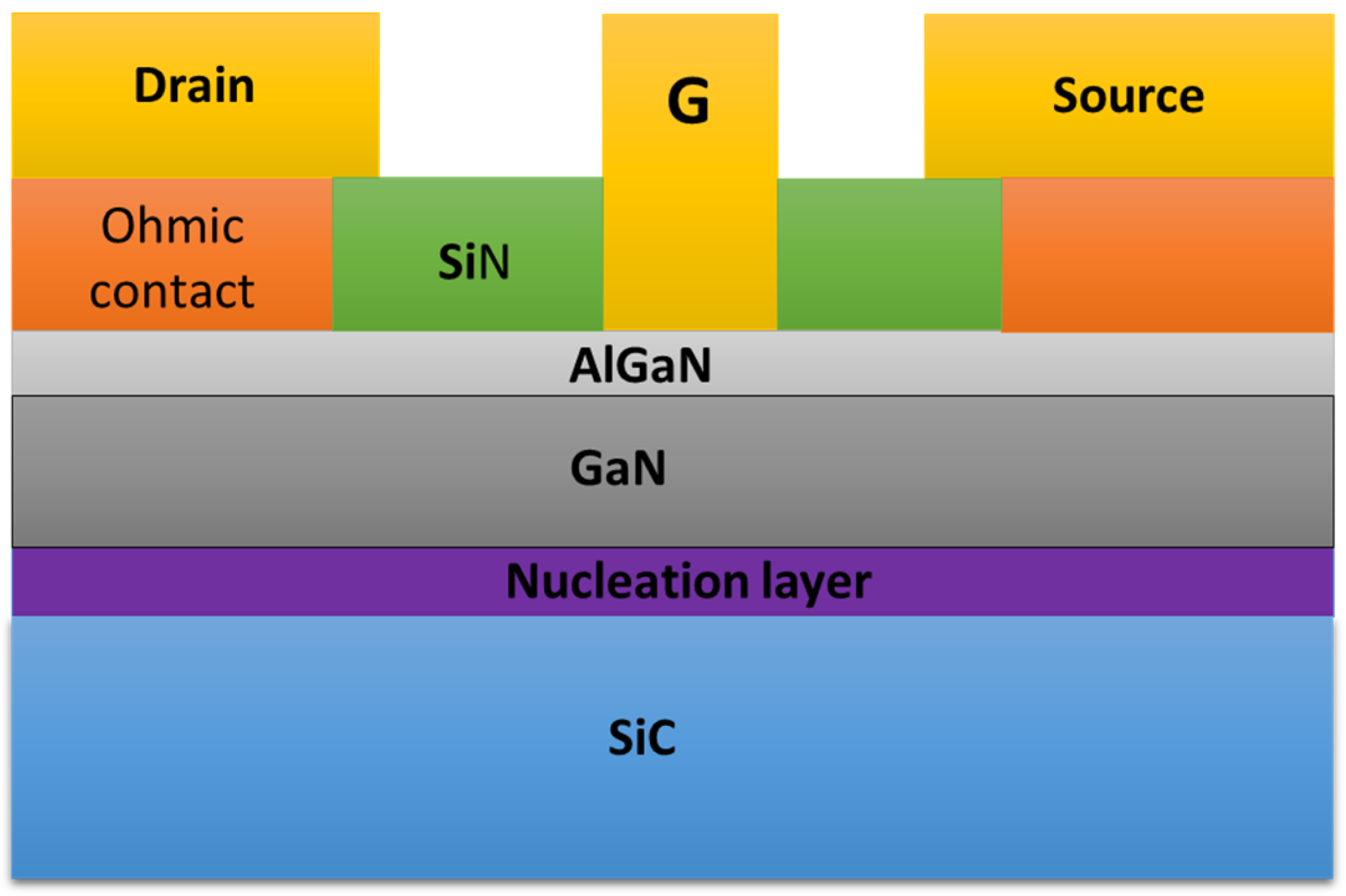
The HEMT has a particular structure that consists of many layers with different materials (
Figure 1). A silicon carbide (SiC) is used as a substrate on which the component is grown. The nucleation layer or the thermal boundary resistance (TBR) serves to realize a mesh tuning for the SiC and GaN layer; its other function is to reduce mechanical stress and defects in the GaN layer. The GaN layer contains the 2DEG at the upper part, and the AlGaN layer is used to create a heterojunction with the GaN layer; there are many layers that provide several functions. After a bibliographic study, we found that the HEMT has several structures. It was also noticed that there is a difference between these structures regarding the topology and materials used; all this leads us to conclude that the HEMT is a technology that is still developing and improving in order to find the best structure that increases its performance and reliability [
4,
14].
3. Electrothermal Modeling of the HEMT
We will detail the electrothermal modeling approach in this part, which allows us to study the thermal behavior of the high electron mobility transistor as a function of operating conditions. During its operation, the transistor dissipated power at the active area at the output of the gate [
22]. The dissipated power is related to the current flowing in this transistor and the voltage applied to its terminals such as [
19,
21]:
where
and
are, respectively, the voltage and the current flowing between its terminals: drain and source. For studying the electro-thermal behavior of the HEMT, the approach that we will use is based on injecting the dissipated power at its active zone. Then we will study the heat distribution at its structure. This transfer is principally done by conduction mode; the other modes of transfer (convection and radiation) are negligible because they represent just less than 1.5% of the global transfer [
21,
23]. Based on the principal transfer mode, the heat equation will be [
24]:
where:
- -
Q: dissipated power (J);
- -
: thermal conductivity
- -
: density
- -
: thermal mass capacity
- -
T: the temperature
Equation (
2) describes the HEMT’s thermal behavior; for better modeling, we will use the finite element method that allows us to solve this problem using Comsol multiphysics software [
25]. The electrothermal modeling of the transistor is done in the form of a 3D finite element model with Comsol multiphysics software, to observe the influence of the dissipated power in the active area of the transistor during its operation, and that of the reference temperature at the substrate. The system is composed of several materials whose properties are shown in
Table 1 [
26]. Using these properties, numerical simulations of the HEMT were performed, then the variation of the operating temperature as a function of the dissipated power
and the reference temperature
was studied.
3.1. Influence of the Dissipated Power
The dissipated power in the active area is one of the operating conditions of the HEMT. To observe its effect on the thermal behavior of the transistor, we vary the linear density of this power in the finite element model developed previously, and we keep the other parameters constant. The reference temperature was 25 °C.
Figure 2 shows the temperature distribution in the whole structure of the HEMT. We can see that the temperature is high in the AlGaN layer at the exit of the gate and around the passivation layer and along the gate.
To study the evolution of the operating temperature as a function of the dissipated power, we performed several numerical simulations. The obtained results are presented in
Figure 3 with the experimental results that were obtained by the optical Raman-Micro-Spectrometry method. According to the figure, we notice that the HEMT temperature increases according to the dissipated power by a non-linear variation; it reaches rather important values at a very high dissipated power. The curve of the results of simulations and experiments are in good correlation. The small deviation between the curves, and especially in the case of high power, is due to the fact that we neglected the other modes of heat transfer, as we have previously mentioned. We will consider that this criterion is sufficient to validate the finite element model developed.
3.2. Influence of the Reference Temperature
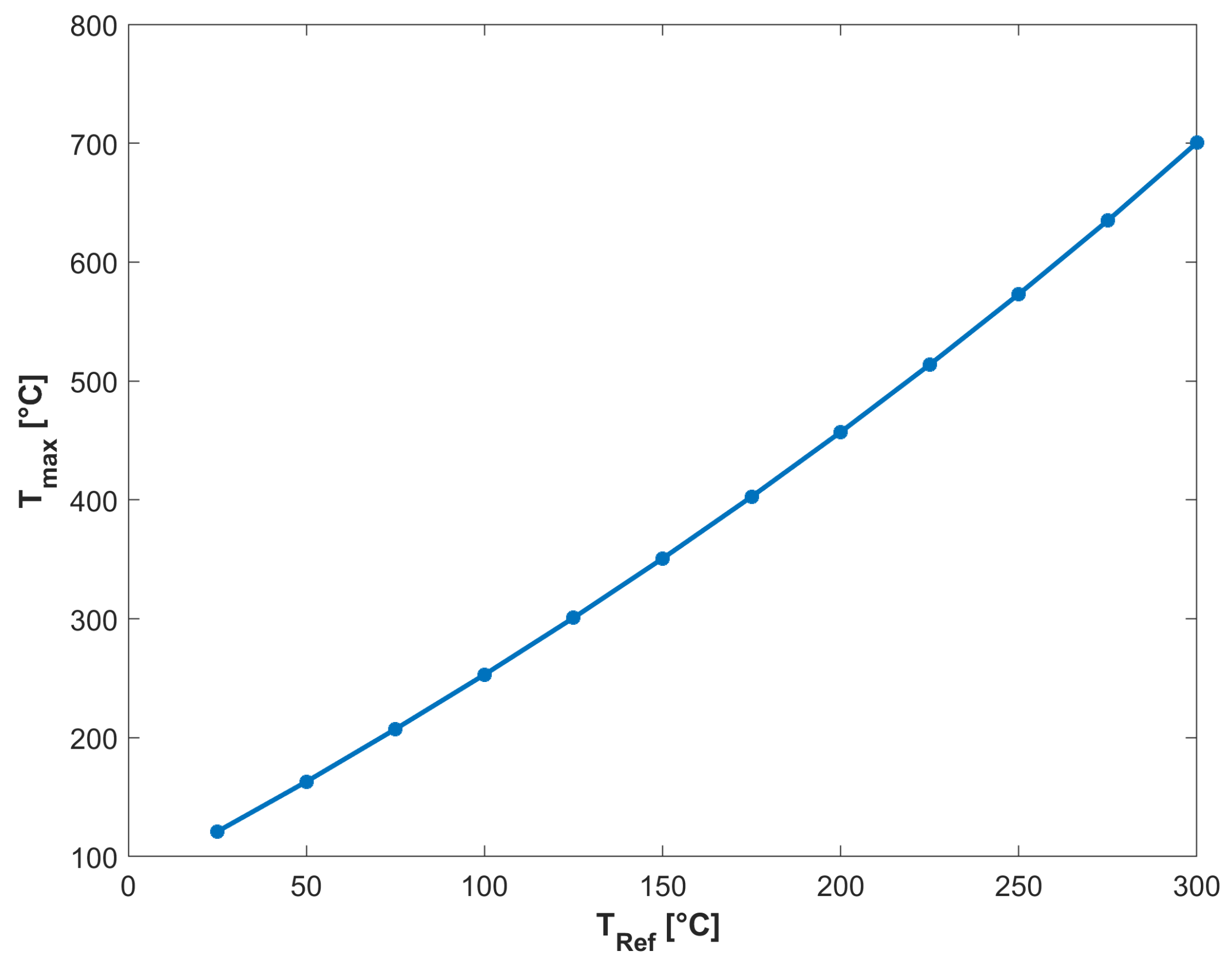
The reference temperature represents the temperature received from the external environment. It applies below the substrate. To identify the relationship between the reference temperature and the operating temperature of the HEMT, numerical simulations have to be carried out based on the finite element model (FEM) developed, by varying the reference temperature between 25 and 300 °C.
Figure 4 shows the numerical results. It represents the evolution of the maximum temperature of the transistor as a function of the reference temperature; with a fixed power dissipation of 5 W/mm, it is clear that the temperature of the component increases with the variation of Tref.
4. Analysis of Systems Reliability
Reliability is defined by AFNOR (French Association of Normalisation) as the ability of systems to assure a required function in given conditions within a specified period [
27]. In the case of complex systems and mechatronic systems, reliability is a challenge for developers and industrialists today, because reliability analysis represents an important step in the development process of many systems and different structures. Evaluating the reliability
R is related to the evaluation of the failure probability
using the following expression:
The precedent expression serves to evaluate reliability from the value of the probability of failure. In addition, the probability of failure is related to several parameters:
where
G(
X) is the limit state function (performance function), it is a function of random variable
X such that:
- -
: the security domain of the system.
- -
: the boundary of state surface.
- -
: the failure domain of the system.
To evaluate the failure probability
or the reliability
R, it is necessary to calculate the integral in the Expression (
4). However, the calculation is analytically difficult and mostly impossible, especially if the random variable X has a large dimension. For this reason, we should use approximation methods [
21,
27].
There are two methods that are very efficient for evaluating the reliability of systems: the First Order Reliability Method (FORM) and the Second Order Reliability Method (SORM) are based principally on the search for the Most Probable Failure Point (MPFP). With FORM and SORM, we can calculate the failure probability and reliability from the reliability index. The FORM method allows us to calculate
using this expression:
where
represents the reduced centered normal distribution function. The FORM method consists of replacing the boundary state surface by the tangent hyperplane at the design point (
Figure 5). However, when the the performance function is strongly nonlinear, this approximation can result in an incorrect probability of failure.
The SORM method makes it possible to calculate
, but differently from the FORM method, using the following formula:
where
are the main curves of the performance function
G at the MPFP (Most Probable Failure Point). The SORM method consists of replacing the limit state surface at the most probable point of failure by the quadratic surface (
Figure 6).
The reliability index can be evaluated with different methods. Hasofer and Lind have proposed to estimate
in the space of the reduced centered normal and statistically independent random variables [
27]. For this reason, the random vector
X will be transformed into the random vector
U, such as:
The random variables follow the reduced centered normal distribution and, regardless of
,
and
, are independent of each other. The probabilistic transformation T necessitates knowing the statistical distributions of every one of the random variables. The performance function after transformation becomes:
The reliability index of Hasofer and Lind
can be defined as the Euclidean distance between the origin of the standard normal space and the boundary state surface
. We consider
u a realization of the random vector
U, with
. Therefore,
will be a realization of the random variable
. To evaluate the reliability index, it is necessary to solve this minimization problem with constraint:
The solution of this minimization problem will be the requested reliability index [
21,
27]. Another reliability index is the Rjanitzyn–Cornell, which is based on considering that the limit state function G(X) follows a normal distribution. The Cornell index is obtained from the mean
and standard deviation
[
27], as such:
The major inconvenience of this index is that it gives different values for different expressions of the limit state function.
5. Evaluation of the HEMT Reliability
To estimate the reliability of the component, many authors have studied the effect of the electrical characteristics on its structural performance [
28,
29]. However, the thermal behavior also has a great impact on the HEMT’s reliability, by different degradation forms such as gate burial, degradation of the feed metals interconnection and degradation of the Schottky contact [
4].
Thermal modeling has identified the parameters that have a great impact on the operating temperature, such as the power dissipation
and the reference temperature
. We consider that these two variables follow a normal law. If
is the maximum temperature that the system must not exceed, and
T is the maximum temperature calculated by the finite element model, the performance function is written as:
The temperature
is evaluated by the FEM developed in the preceding section. It is calculated as a function of random variables vector
X. These variables represent the parameters of dissipated power and reference temperature. In this work, we have considered these parameters as random variables following a normal distribution. All parameters and their values are classified in
Table 2.
Our reliability analysis process is based on thermo-reliability coupling. The probability model of SORM and FORM methods coded on Matlab allows us to estimate the limit state function and calculate the reliability index and the failure probability. The FEM using Comsol multiphysics allows the calculation of the temperature as a function of the random variables. The process will stop if we obtain the best value of
. The results obtained—the reliability index
, failure probability, and reliability
R of the transistor, calculated by both SORM and FORM approximation methods using the precedent process—are classified in
Table 2. The reliability index obtained by the SORM method is 0.123 and by the FORM method is 0.124. Both methods allowed estimation of the reliability level but the SORM method is more accurate. From these results, we can see clearly that the HEMT’s reliability level needs to be optimized to improve its performance.
6. Conclusions
In this paper, the reliability analysis of the high electron mobility transistor was described. Thanks to the approximate methods, the First and Second Order Reliability Methods (FORM and SORM, respectively), we have estimated the reliability index and the failure probability. Our approach is based on the coupling between two models. The finite elements model using Comsol multiphysics software allowed us to observe the influence of and on the operating temperature. The reliability model coded using Matlab software ensures the probabilistic calculation of the reliability analysis. The results obtained using this approach show that the operating conditions influence the reliability of the high electron mobility transistor and can increase its failure probability. Therefore, the performance of this technology needs to be improved using an optimization approach, for example. However, the approximate methods, SORM and FORM, are generally satisfactory, as well as the calculation time, for the reliability analysis.