4.1. Dataset
We used the available dataset from [
9], which contains real cases for few-shot charges prediction, and the dataset has three subsets of different sizes, denoted as Criminal-S (small), Criminal-M (medium), and Criminal-L (large). Each case has a good structure, including fact description, charge, related article, and prison term. This paper chooses the fact description part of the case as input and extracts the charge label by regular expression. Since this paper explores the few-shot prediction task, and the dataset contains cases with multiple defendants and multiple charges, which increase the complexity of the charge prediction task, we filtered these multi-label cases. We kept 149 distinct charges with at least 10 cases. The detailed statistics are shown in
Table 3. All datasets were divided into training set, validation set, and test set in the ratio of 8:1:1. In addition, this paper counted the statistical results of the number of distribution of charges in Criminal-S. It can be seen from the
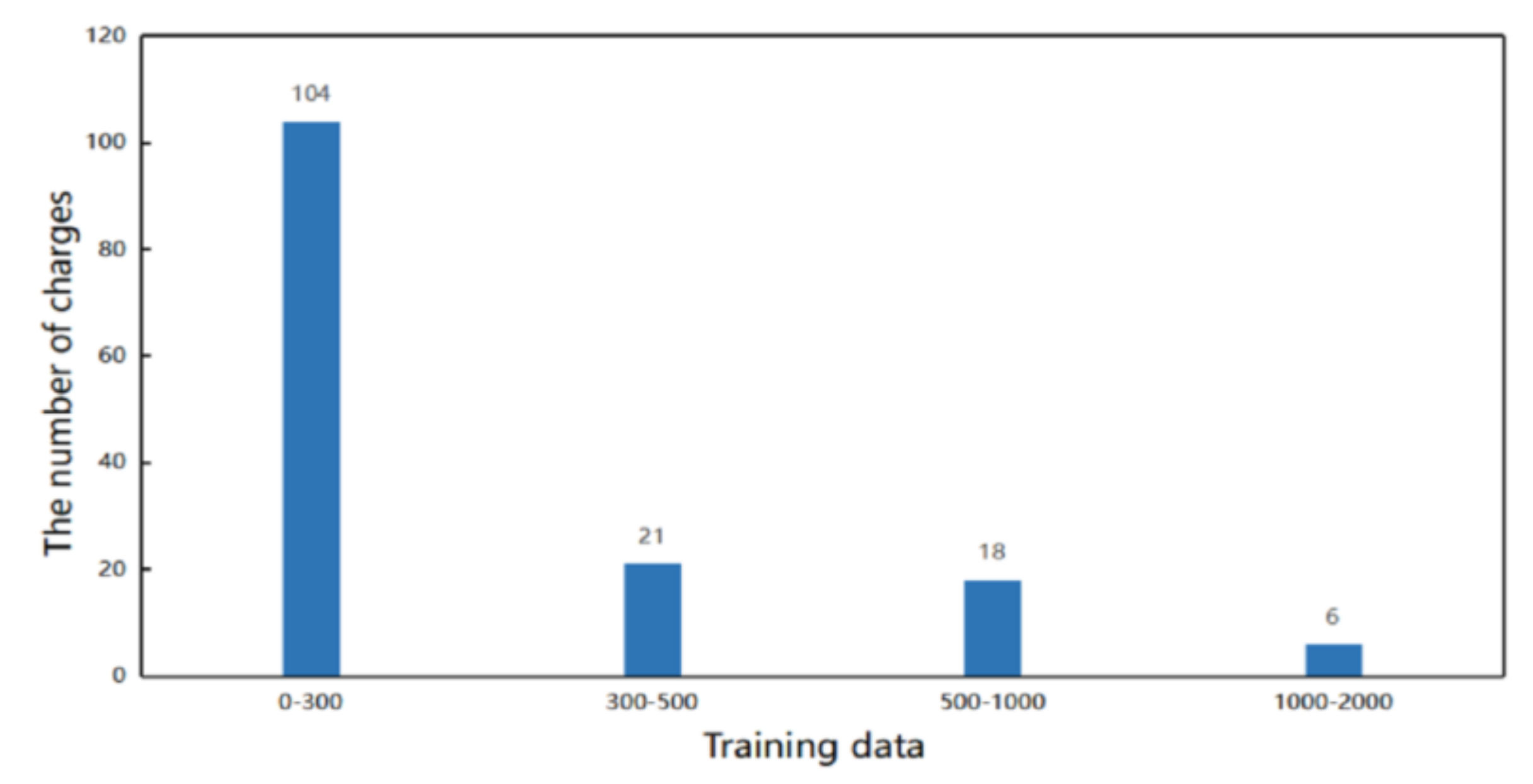
Figure 6 that the distribution of charges was extremely unbalanced. More than 50% of the charges had less than 200 training data, while there were only 10 charges with more than 2000 training data.
The overall model was divided into two parts: data augmentation module and feature augmentation module. Tensorflow was uniformly used to build the neural network model. In the data augmentation module, in order to improve the data quality, we firstly cleaned the data and removed some invalid samples, then we discretized a large amount of information, normalizing the license plate number, mobile phone number, bank card number, and other information. The regular expression was used to extract the fact description from cases, THULAC was used for word separation, and the skip-gram algorithm of word2vec for word vector modeling: setting the vector dimension to 200, setting the maximum text length to 500, truncating if it was too long, and filling it with 0 if it was less than 500. The maximum document length was 32 sentences, words with a word frequency of less than five were regarded as unknown words, and the dimension of GRU hidden layer was set to 256. The dropout was set to 0.5, the mixing factor was obtained from the beta distribution () sampling, the parameter was , the batch size was 64, and the learning rate was 0.01.
In the feature augmentation module, the charge definition was also segmented, the word vector was modeled by using the skip-gram algorithm of word2vec; the vector dimension was set to 200, the window size was set as 20, and the dropout to 0.5. All neural network models were trained by random gradient descent (SGD), and Adam [
41] was used as the optimizer. Iterative training was repeated during the experiment until the difference between two consecutive iterations was small enough, and the maximum epochs were 20. We employed accuracy (Acc.), macro-precision (MP), macro-recall (MR), and macro-F1 (F1) as our evaluation metrics.
4.2. Baselines
We selected a basic neural network model and several state-of-the-art models of LJP as a baseline. The effectiveness of our model is proved by comparative analysis. The descriptions of the baseline models are as follows:
CNN [
42]: A text classification model based on CNN. Text features are extracted using CNNs with different width filters, combined with fully connected neural networks to predict the charges.
HAN [
31]: A hierarchical attention network model for document classification. The model uses word-level GRU to extract features, an attention mechanism to aggregate words into sentences and further extract features from sentence-level GRU, and an attention mechanism to classify documents.
Few-attribute [
9]: A model for few-shot charges prediction. The model introduces legal attributes as external knowledge, and multi-task joint modeling is used to predict both charges and attributes.
MPBFN [
20]: A multi-perspective bi-feedback network for legal judgment prediction. The network effectively utilizes the dependencies among subtasks of LJP, and a word collection attention mechanism is proposed to increase the accuracy of penalty prediction.
LADAN [
8]: A model for confusing charges prediction. The model uses a graph neural network to extract the differences between legal articles and re-encode the case descriptions to predict the charges.
In the experimental process, this paper treated the charge prediction as a classification problem, selected a set of optimal experimental parameters by reviewing the range of experimental parameters given in the original paper, conducted three iterations of the experiment, and took the best single result as the final result.
4.3. Results and Analysis
The experimental results on the criminal dataset are shown in
Table 4. † indicates significant improvements (
p < 0.05) compared with the best baseline. It can be observed that our model achieves better performance on three different-sized datasets, which showcases the robustness and wide applicability over various application scenarios of our proposed method for charge prediction. Our model is basically similar to other models on a certain metric of a dataset, such as the Acc (93.3) of LADAN and ours (93.5) are close to each other in Criminal-S. Through our annotation, it can be found that at least two indicators of our model are significantly improved in different datasets, especially in MR and F1. Thus, we can infer that the model in this paper significantly outperforms other baseline models on different datasets by looking at all the metrics for a particular dataset. In addition, the experimental results of different-sized datasets are compared horizontally, and it is found that the prediction results become more and more accurate with the increase of data volume, which proves that the amount of data can affect the training effect of the model, and the training data of large datasets are more adequate.
Further comparing the experimental results, it can be observed that our model outperforms all the baseline models, and the existing models generally perform poorly on the F1 metric. This is mainly because of the imbalance of training samples among different charges and indicates the shortage of prediction for few-shot charges. In contrast, our model achieves an absolute improvement of 5.5%, 2.9%, and 3.1% in F1 over the current optimal model on the three datasets, respectively. It proves the effectiveness and robustness of the method in this paper under different scenarios (sufficient or insufficient data).
Among these evaluation metrics, MR and F1 are the preferred evaluation metrics for classification problems, especially in the scenario of unbalanced data. The above analysis shows that our model is superior in F1. Therefore, we compared the performance with MR metric, and further compared the generalization performance of our model and the baseline model in a statistical sense. Firstly, we compared six different models on three datasets, and then sorted them on each dataset according to MR values and assigned ordinal values (1, 2, …). As shown in
Table 5, the last row is average ordinal values. Then, the “Friedman test” was used to judge whether the performance of these models was the same. Let
be the average ordinal values of the
models. We assumed a variable
, where
is the number of models and
is the number of datasets. We obtained the
when
and
are large and
obeys distribution
. Then, we used the variable
, which follows the
distribution with degrees of freedom
and
. Then, we obtained the
by referring to the table of common critical values for the F test, when significance level
,
. Therefore, the assumption that all models have the same performance was rejected. Then we used the “Nemenyi follow-up test” by referring the common critical values for the “Nemenyi test”. We obtained the critical value
when
and
. The “Nemenyi test” calculates the critical range
of the difference between the average ordinal values. Finally, we compared the average ordinal values gap and
:
. This shows that, compared with the ordinary neural network model (CNN and HAN), the performance of our model is particularly superior. In addition, compared with other legal judgment prediction models, our model predicts a higher MR value, which is slightly better than other models in statistical sense.
By comparing the ordinary neural network model and the charge prediction model, it is found that the charge prediction model is significantly better than the ordinary neural network in various indexes, which indicates that in-depth analysis of various factors affecting LJP can effectively improve the prediction effect by introducing external knowledge or multi-task joint learning.
Comparing on three different size datasets, the advantage of our model is particularly obvious on the Criminal-S dataset, mainly due to the adoption of the Mixup method in this paper. The two most basic metrics in the classification domain are Acc. and MR, and, comparing our model with LADAN and HAN, the accuracy is basically close, but the recall differs greatly. The main reason is that low-frequency and confusing charges account for a lower proportion, while the LADAN model can effectively distinguish confusing charges through DGCN, so the MR is improved. Through data enhancement and feature enhancement, our model can not only distinguish easily confused charges, but also has a good prediction effect on few-shot charges.
To further demonstrate the advantage of our model in the case of few-shot charges, MPBFN and LADAN models, which are more effective in the baseline model, were compared with our model under different frequency charges. Here, according to the frequency of the charge, we divided them into three parts: the number of cases included in the low-frequency charges is less than 10 and the number of cases included in the high-frequency charges is more than 100. As shown in
Table 6, the effects of the three models in high-frequency charges are close, but compared with the baseline model, our model improves 3.95% and 4.74% in low-frequency charges, respectively, which fully proves the advantages of our model in predicting few-shot charges.
In addition, it can be seen from
Figure 6 that the charge distribution of data in the legal field is imbalanced. In order to prove the effectiveness of this model in an unbalanced data scenario, we select a new evaluation metrics for comparative experiments. As shown in
Table 4, in the ordinary neural network model the prediction effect of HAN is better than the CNN. In the LJP models, the Few-attribute model is specially used to solve the few-shot charge problem. Therefore, we selected HAN and Few-attribute from the baseline model. At the same time, the loss function of our model was replaced by the ordinary cross entropy; the variant is named cross-loss. We compared the above three models with our model on the Criminal-L set with sufficient data. Then the AUC evaluation index was used to explore the effectiveness of the model in the unbalanced data scenario. The experimental results are shown in the
Table 7. It can be seen from the table that the AUC value of HAN is the lowest, which indicates the limitation of the ordinary neural network model for the category imbalance problem, and the accuracy can be effectively improved by integrating external knowledge. Therefore, the prediction result of Few-attribute is significantly improved, and the AUC value of our model is the highest. When the ordinary cross-entropy loss function is used, the AUC value decreases significantly, but it is still higher than other models. It can be seen that the data augmentation and feature augmentation strategies in this paper can initially solve the problem of category imbalance. More importantly, the fusion of category priors has a significant effect on solving the problem of unbalanced data.
Further, we selected “theft” and “fire crime” as the representative of high-frequency charges and low-frequency charges respectively and used a PR curve (precision-recall) to intuitively explore the performance of our model and Few-attribute on different frequency charges. As shown in
Figure 7, it can be observed that the prediction effect of the model on “theft” is higher than that on “fire crime”, and, in the prediction of “theft”, the prediction effects of the two models are basically close. This shows that the two models have the same prediction effect on high-frequency charges and also reflects that low-frequency charges in the dataset can affect the effect of the model. However, for low-frequency charges, the PR curve of our model completely covers another one, so our model is obviously better than the Few-attribute model. It can be seen that the method proposed in this paper is particularly excellent for few-shot charges.