Applications of Multi-Agent Deep Reinforcement Learning: Models and Algorithms
Abstract
:1. Introduction
2. Background of Multi-Agent Deep Reinforcement Learning: Reinforcement Learning and Multi-Agent Reinforcement Learning
2.1. Reinforcement Learning
| Algorithm 1: Q-learning algorithm. |
1: Procedure 2: Observe current state 3: Select action 4: Receive immediate reward 5: Update Q-value using Equation (1) 6: End Procedure |
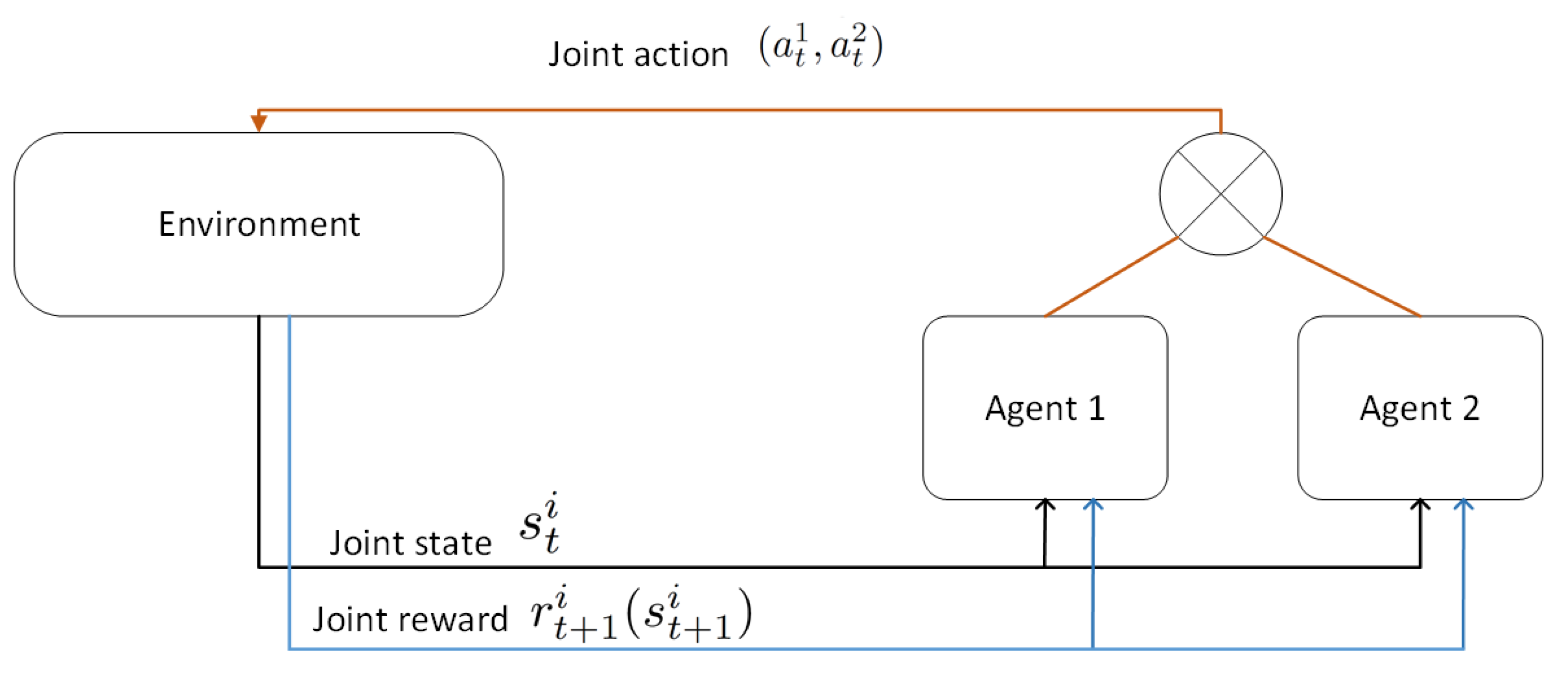
2.2. Multi-Agent Reinforcement Learning
| Algorithm 2: MARL algorithm. |
1: Procedure 2: Observe current state 3: Send Q-value to neighboring agents 4: Receive from agent 5: Select action 6: Receive immediate reward 7: Update Q-value using Equation (2) 8: End Procedure |
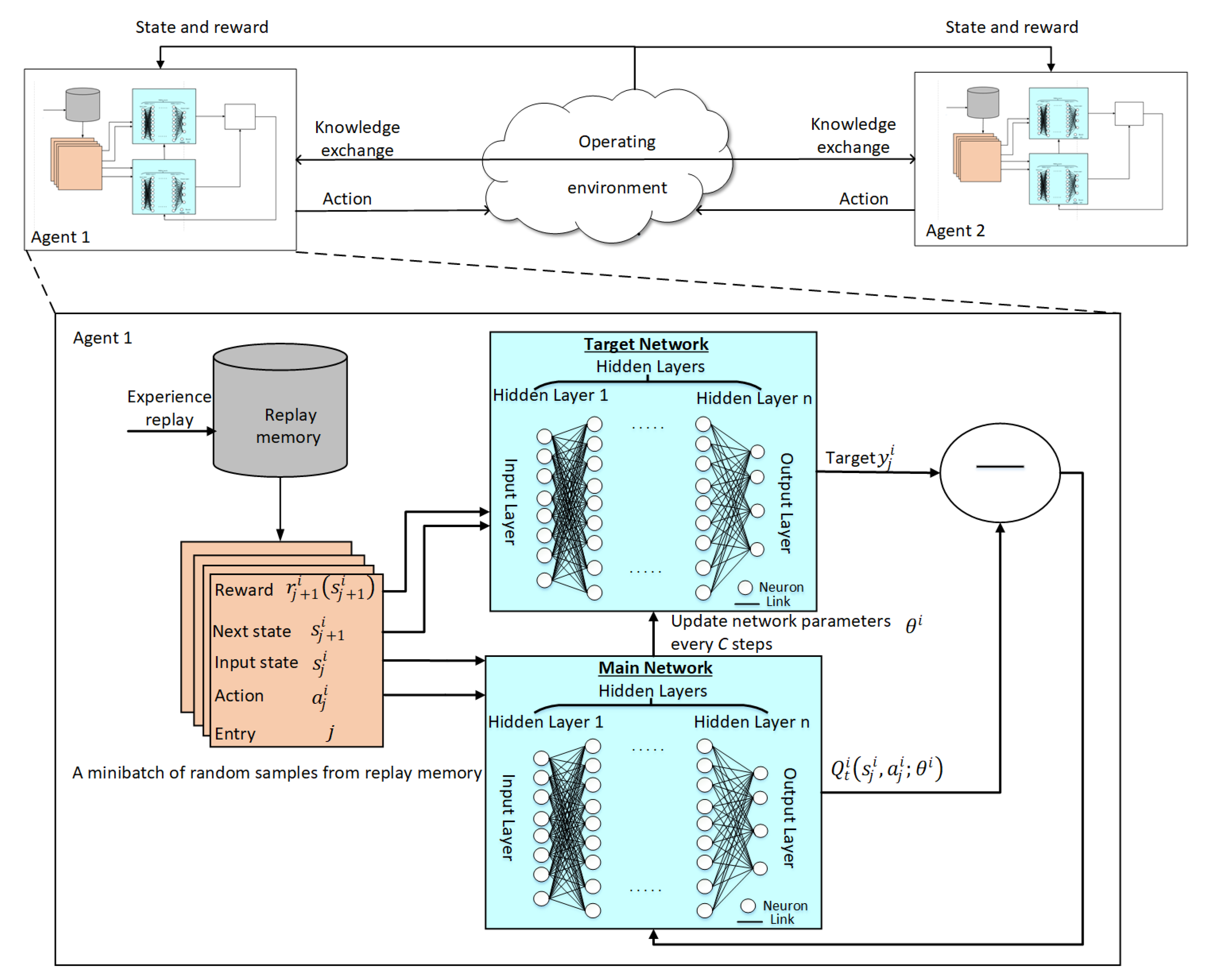
3. Multi-Agent Deep Reinforcement Learning
3.1. Deep Reinforcement Learning
| Algorithm 3: DQN algorithm. |
1: Procedure 2: for episode = 1 : M do 3: Observe current state 4: for time t = 1 : T do 5: Select action 6: Receive immediate reward and next state 7: Store experience in replay memory 8: Sample a minibatch of N experiences from replay memory 9: for step j = 1 : N do 10: Set target 11: Perform gradient descent on with respect to main network parameters using Equation (5) 12: end for 13: Perform every C steps 14: end for 15: end for 16: End Procedure |
3.2. Multi-Agent Deep Q-Network
| Algorithm 4: MADQN algorithm. |
1: Procedure 2: for episode = 1 : M do 3: Observe current state 4: Send Q-value to neighboring agents 5: Receive from agent 6: for : T do 7: Preform steps 5 to 12 in Algorithm 3 8: end for 9: Update every C steps 10: Update Q-value using Equation (6) 11: end for 12: End Procedure |
4. Research Methodology
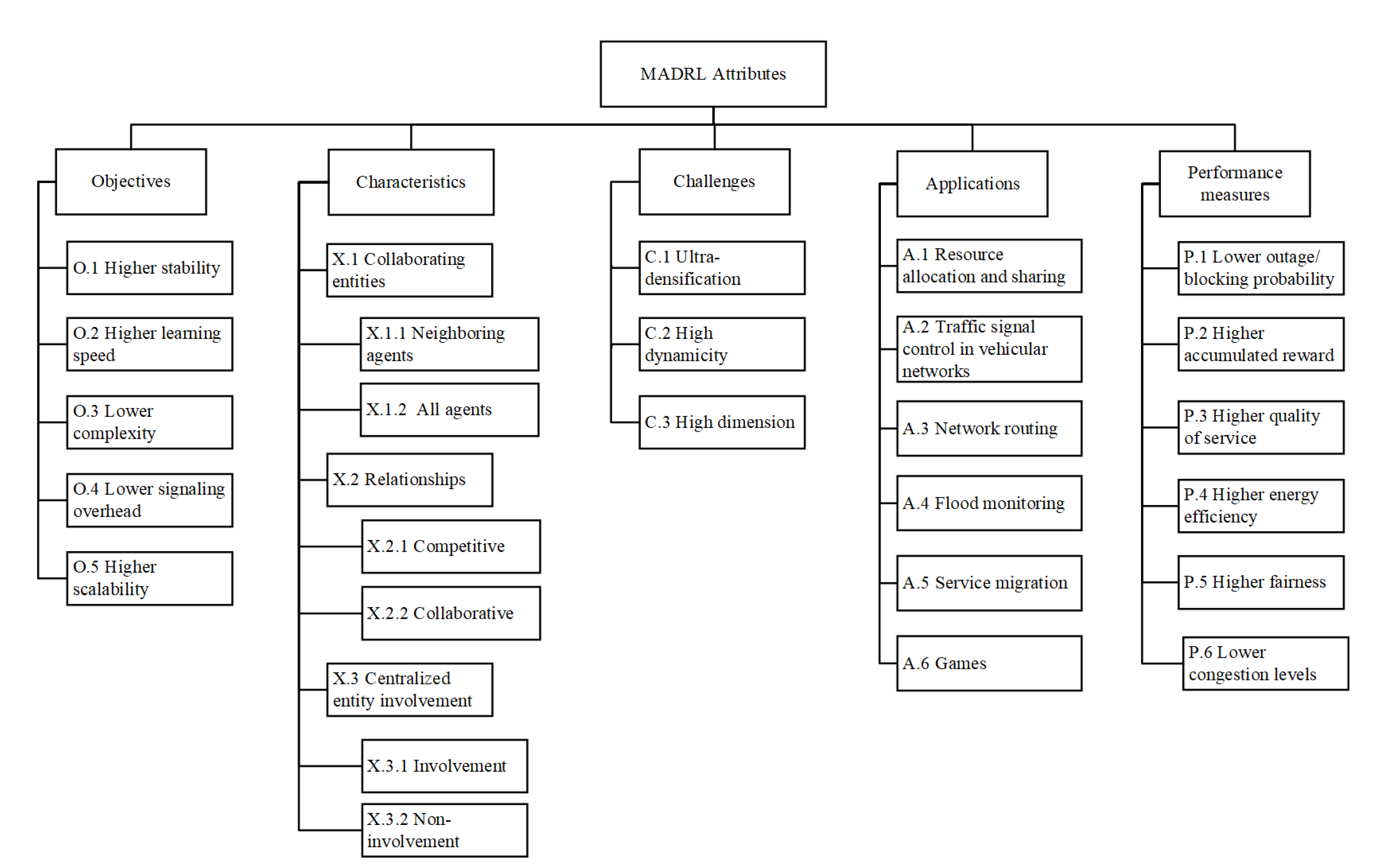
5. Attributes of Multi-Agent Deep Reinforcement Learning
5.1. Objectives
- O.1
- Higher stability ensures the convergence to the optimal joint action. It mitigates instability caused by several factors: (a) the dynamic and unpredictable operating environment; and (b) the dynamic and unpredictable actions are taken in a simultaneous (or nonsequential) manner by multiple agents. As an example, in order to improve the stability of the multi-agent environment: (a) distributed agents apply knowledge from the centralized entity to select their respective actions [35]; and (b) a common reward is given to distributed agents to encourage cooperation among themselves [51].
- O.2
- Higher learning (or convergence) speed reduces the number of iterations required to converge to the optimal joint action in the presence of large state and action spaces. As an example, in order to improve the learning speed in a multi-agent environment: (a) distributed agents select samples based on their priorities from the replay memory, whereby learned samples are prioritized, and redundant samples are removed [52,53]; and (b) distributed agents prioritize knowledge received from adjacent agents and scale down knowledge received from non-adjacent agents in order to increase the effects of local knowledge which is more correlated with their local states.
- O.3
- Lower complexity reduces the computational and hardware implementation complexities of DNN in multi-agent environments. It addresses the complexity of learning among distributed agents and the large number of iterations required for training (e.g., computing the value function). As an example, in order to reduce complexity in a multi-agent environment: (a) distributed agents segregate and distribute a complex task among themselves according to their respective capabilities [35]; and (b) the loss function of each training step is sampled and differentiated with respect to network parameters in order to update the Q-network with reduced complexity [52].
- O.4
- Lower signaling overhead reduces the frequency of message exchange between centralized and distributed entities. It addresses the increase of message exchange when the system size grows. A lower signaling overhead has been shown to reduce co-channel interference and improve fairness among distributed agents in wireless networks [52]. As an example, in order to reduce signaling overhead in a multi-agent environment: (a) distributed agents transfer the complex training process to the centralized entity [52]; and (b) the centralized entity gathers data from selected distributed agents rather than all of them [35].
- O.5
- Higher scalability enhances a system with a large number of agents. It addresses the challenges of segregating a centralized scheme and the need of exchanging a large amount of knowledge or information [35]. For example, distributed agents select a subset of states from a large complex set of states [35]. Higher scalability helps to improve various aspects of a system with a large number of distributed agents, including achieving a higher learning speed, a lower complexity, and a lower signaling overhead.
5.2. Characteristics
- X.1
- Collaborating entities represent the agents that share knowledge in a multi-agent environment as follows:
- X.1.1
- Neighboring agents indicates that an agent shares knowledge with neighboring agents only.
- X.1.2
- All agents indicates that an agent shares knowledge with all agents in the environment.
- X.2
- Relationship indicates the relationship between agents in a multi-agent environment as follows:
- X.2.1
- Competitive indicates that agents compete with each other for network services or resources (e.g., transmission opportunities).
- X.2.2
- Collaborative indicates that agents collaborate with each other to achieve a common goal.
- X.3
- Centralized entity represents the centralized controller with a higher amount of resources (e.g., higher computing power) to perform centralized and complex tasks in a multi-agent environment. Thus, distributed agents perform distributed and simple tasks.
- X.3.1
- Involvement from the centralized entity indicates that the centralized controller performs complex tasks in a centralized manner.
- X.3.2
- Non-involvement from the centralized entity indicates that distributed agents perform complex tasks in a distributed manner.
5.3. Challenges
- C.1
- Ultra-densification is attributed to the presence of a large number of agents (e.g., user devices) in the operating environment. Consequently, it affects the capability of multiple agents to exchange knowledge among themselves in a shared operating environment. For instance, in [35], the centralized entity performs learning by gathering data from a predefined number of neighboring distributed agents, and distributes knowledge to them so that they can select actions independently.
- C.2
- High dynamicity is attributed to the rapid changes of the operating environment (e.g., due to high mobility of agents), including states and rewards. Consequently, it affects learning and decision making. For instance, in [6], historical information (i.e., actions) related to distributed agents are part of the input information (i.e., state) of the DNN in order to adapt to the highly dynamic operating environment.
- C.3
- High dimension is attributed to the presence of a large state and action spaces. For instance, in [54], distributed agents receive knowledge about each other (e.g., delayed rewards and Q-values), use a function approximator to store and keep track of a smaller number of features instead of a large number of state–action pairs, and then use them to select their respective actions.
5.4. Applications
- A.1
- Resource allocation and sharing enable agents to allocate and manage resources, such as distributed renewable energy sources (e.g., power grids) [55], and meet system demands in a distributed manner. In [35], in a wireless network, a node pair, which is a distributed agent, selects its operating channel for device-to-device (D2D) communication in a distributed manner. D2D enables neighboring nodes to communicate with each other directly without passing through a base station. MADRL can mitigate the instability of a multi-agent environment, whereby a centralized entity learns and shares learned knowledge with the node pairs, who subsequently make decisions independently. This helps to increase throughput. In [56], in a home network, a controller switches on or off home appliances based on their activities in the past 24 h and the user’s presence to meet the user’s resource (i.e., energy) demands and reduce resource consumption. MADRL addresses ultra-densification in which resources are limited in the presence of a large number of distributed agents. The centralized agent learns and performs action selection rather than the distributed agents, which also helps to increase energy efficiency.
- A.2
- Traffic signal control in vehicular networks enables traffic signal controllers at intersections to manage and control traffic, such as selecting traffic phases (e.g., the north–south and west–east bounds) following traffic rules (e.g., vehicles cannot make a right turn) for reducing congestion at intersections [57,58]. In [33], traffic signal controllers select their respective traffic phases in a distributed manner. MADRL addresses the ultra-densification and high dynamicity challenges using actors and critics that share knowledge (i.e., historical actions) with neighboring distributed agents cooperatively in order to select their respective actions. This helps to reduce the congestion level.
- A.3
- Network routing enables source nodes to establish routes and send packets to destination nodes in networks with dynamically changing traffic patterns. In [6], MADRL addresses the ultra-densification, high dynamicity, and high dimension challenges by learning based on historical knowledge while making optimal decisions in route selection. This helps to reduce latency.
- A.4
- Flood monitoring enables distributed agents to sense and monitor water levels based on real-time data to predict the complex flood levels [59,60]. In [61], multiple aircraft update their respective positions in a distributed manner, enabling them to predict and report water levels at different locations. MADRL addresses the challenge of high dimension by enabling the distributed agents to share a common reward in a cooperative manner. This helps to increase the accumulated reward.
- A.5
- Service migration enables intelligent devices, such as connected vehicles, to offload computing-intensive tasks (e.g., video and data processing, route planning, and traffic management in networks) from resource-limited distributed entities (e.g., vehicles and local servers) to centralized entities (e.g., edge servers at the edge of the network, and data centers) with extensive computing resources in order to achieve the expected service level. In [62], a service entity chooses whether or not to offload tasks to edge servers based on the utility (e.g., latency and energy) of a vehicle. MADRL addresses the ultra-densification and high dynamicity challenges by enabling distributed agents to share knowledge (i.e., historical actions) with neighboring distributed agents cooperatively in order to select their respective actions. This helps to reduce latency.
- A.6
- Games enable agents to achieve the goals of games, such as winning the games or increasing human players’ engagement. In [63], two players select their movements (i.e., up or down) in a pong game. MADRL addresses the challenge of high dynamicity using a common reward received after winning a game to encourage cooperative behavior among the players. This helps to increase the accumulated rewards.
5.5. Performance Measures
- P.1
- Lower outage (or blocking) probability reflects the reliability of a system to sustain its normal operation (e.g., achieving a required data rate in networking) based on: (a) internal factors (e.g., a higher amount of internal resources reduces the outage probability [31]); and (b) external factors (e.g., a communication channel with a lower interference level reduces the outage probability [35]).
- P.2
- Higher accumulated reward increases the total immediate rewards received by agents over time [35].
- P.3
- P.4
- P.5
- P.6
6. Application of Multi-Agent Deep Reinforcement Learning: State of the Art
6.1. SADRL Applied to Distributed Agents in a Multi-Agent Environment
6.1.1. Chen’s SADRL Approach in a Multi-Agent Environment
6.1.2. Vila’s SADRL Approach in a Multi-Agent Environment
6.1.3. Shilu’s SADRL Approach in a Multi-Agent Environment
6.1.4. Ruoyun’s SADRL Approach in a Multi-Agent Environment
6.1.5. Shing’s SADRL Approach in a Multi-Agent Environment
6.1.6. You’s SADRL Approach in a Multi-Agent Environment
6.1.7. Zhao’s SADRL Approach in a Multi-Agent Environment
6.1.8. Luis’s SADRL Approach in a Multi-Agent Environment
6.1.9. Chen’s SADRL Approach in a Multi-Agent Environment
6.2. Donghan’s SADRL Approach for a Hierarchical Multi-Agent Environment
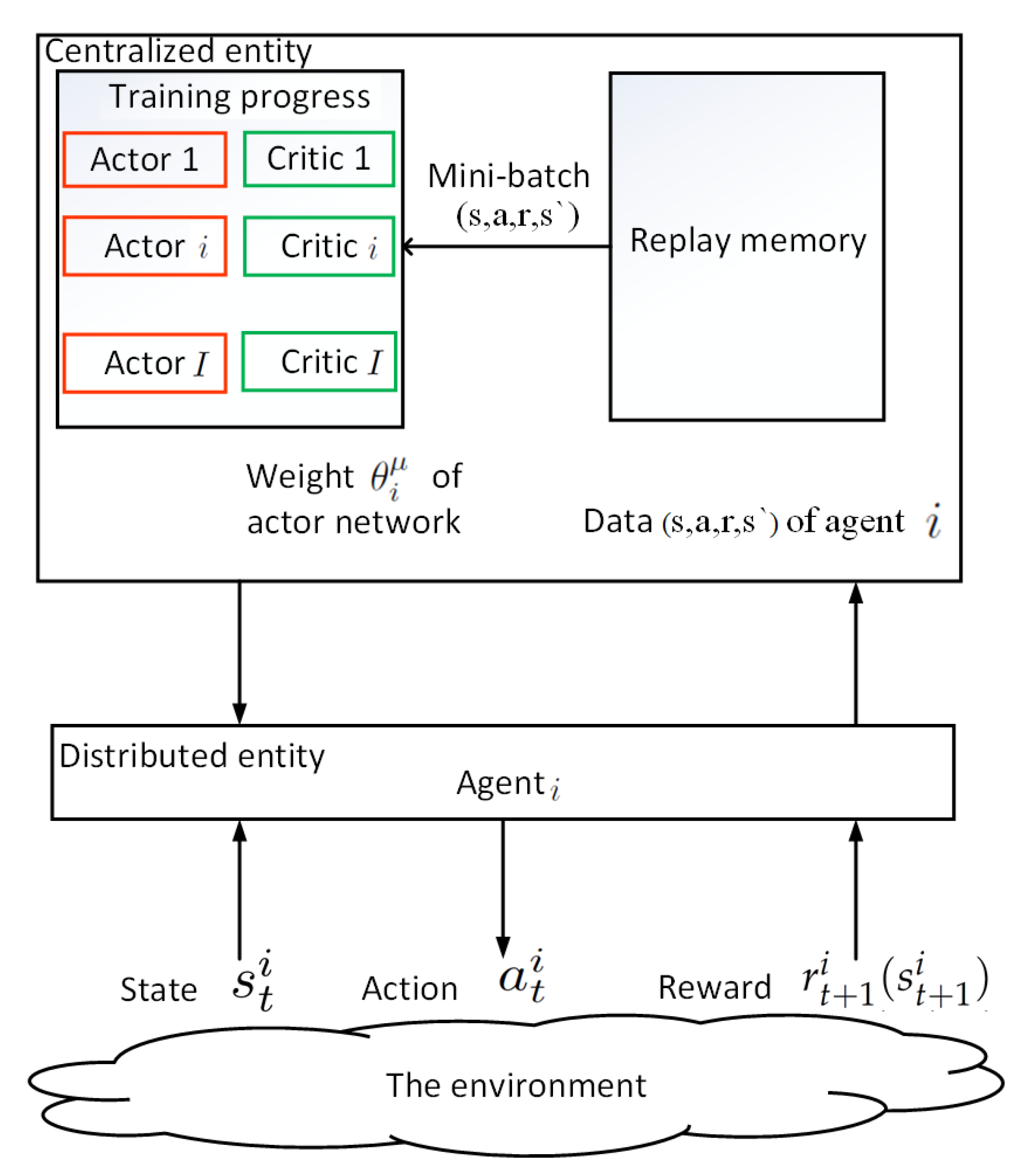
6.3. SADRL with Actors and Critics Applied to Centralized Entities in a Hierarchical Multi-Agent Environment
- Actor network is parameterized by weight . It updates the weight of agent i using sampled policy gradient according to where and represents environment.
- Target actor network is a copy of the actor network that updates the weight slowly (e.g., with a small value) to ensure convergence.
- Critic network is parameterized by weight . It updates the weight of agent i by minimizing its loss where .
- Target critic network is a copy of the critic network that updates the weight slowly.
| Algorithm 5: Actor-Critic RL algorithm. |
1: Procedure 2: /*Critic*/ 3: Observe current state 4: Select action 5: Receive immediate reward 6: Calculate temporal difference 7: /*Actor*/ 8: Update Q-value 9: End Procedure |
Li’s Hybrid SADRL Approach with Actors and Critics
6.4. SADRL with Actors and Critics Applied to Distributed Entities in a Hierarchical Multi-Agent Environment
6.4.1. Chen’s SADRL Approach with Actors and Critics
6.4.2. Zou’s SADRL Approach with Actors and Critics
6.5. MADRL with Actors and Critics Applied to Distributed Entities in a Multi-Agent Environment
6.5.1. Chu’s MADRL Approach with Actors and Critics
6.5.2. Hurmat’s MADRL Approach with Actors and Critics
6.5.3. Li’s MADRL Approach with Actors and Critics
6.6. Wu’s MADRL Approach Using Target Updated with Neighboring Agents’ States and Actions Information
6.7. Ge’s MADRL Approach Using Target Updated with Neighboring Agents’ Q-Values
6.8. Tian’s MADRL Approach with Bootstrapping in a Multi-Agent Environment
6.9. Baldazo’s MADRL Approach with Shared Reward
6.10. Lei’s MADRL with Action Discovery Strategy
6.11. Yu’s Fully Distributed MADRL with Hierarchical Characteristics
6.12. Elhadji’s MADRL with Concurrent Learning
7. Open Issues and Future Directions
7.1. Enhancing Communication between Agents in Large Scale MADRL
7.2. Ensuring a Balanced Trade-off between Complexity and Network-Wide Performance in MADRL
7.3. Ensuring Convergence in Cooperative MADRL
7.4. Enhancing Training Performance in MADRL Using Delayed Rewards
7.5. Enhancing Learning in Large Scale MADRL
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. A brief survey of deep reinforcement learning. arXiv 2017, arXiv:1708.05866. [Google Scholar] [CrossRef] [Green Version]
- Arel, I.; Liu, C.; Urbanik, T.; Kohls, A.G. Reinforcement learning-based multi-agent system for network traffic signal control. IET Intell. Transp. Syst. 2010, 4, 128–135. [Google Scholar] [CrossRef] [Green Version]
- Su, S.; Tham, C.K. SensorGrid for real-time traffic management. In Proceedings of the 2007 3rd International Conference on Intelligent Sensors, Sensor Networks and Information, Melbourne, VIC, Australia, 3–6 December 2007; pp. 443–448. [Google Scholar]
- Lasheng, Y.; Marin, A.; Fei, H.; Jian, L. Studies on hierarchical reinforcement learning in multi-agent environment. In Proceedings of the 2008 IEEE International Conference on Networking, Sensing and Control, Sanya, China, 6–8 April 2008; pp. 1714–1720. [Google Scholar]
- Jang, B.; Kim, M.; Harerimana, G.; Kim, J.W. Q-learning algorithms: A comprehensive classification and applications. IEEE Access 2019, 7, 133653–133667. [Google Scholar] [CrossRef]
- You, X.; Li, X.; Xu, Y.; Feng, H.; Zhao, J.; Yan, H. Toward packet routing with fully-distributed multi-agent deep reinforcement learning. arXiv 2019, arXiv:1905.03494. [Google Scholar]
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep reinforcement learning for multiagent systems: A review of challenges, solutions, and applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hernandez-Leal, P.; Kartal, B.; Taylor, M.E. Is multiagent deep reinforcement learning the answer or the question? A brief survey. Learning 2018, 21, 22. [Google Scholar]
- OroojlooyJadid, A.; Hajinezhad, D. A review of cooperative multi-agent deep reinforcement learning. arXiv 2019, arXiv:1908.03963. [Google Scholar]
- Da Silva, F.L.; Warnell, G.; Costa, A.H.R.; Stone, P. Agents teaching agents: A survey on inter-agent transfer learning. Auton. Agents Multi-Agent Syst. 2020, 34, 1–17. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.; Başar, T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. Handb. Reinf. Learn. Control 2021, 325, 321–384. [Google Scholar]
- Gronauer, S.; Diepold, K. Multi-agent deep reinforcement learning: A survey. Artif. Intell. Rev. 2021, 1–49. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Introduction to Reinforcement Learning; MIT Press: Cambridge, MA, USA, 1998; Volume 135. [Google Scholar]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Bennett, C.C.; Hauser, K. Artificial intelligence framework for simulating clinical decision-making: A Markov decision process approach. Artif. Intell. Med. 2013, 57, 9–19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watkins, C.J.C.H. Learning from Delayed Rewards; King’s College: Cambridge, UK, 1989; pp. 1–229. Available online: http://www.cs.rhul.ac.uk/~chrisw/thesis.html (accessed on 30 September 2021).
- Bowling, M.; Burch, N.; Johanson, M.; Tammelin, O. Heads-up limit hold’em poker is solved. Science 2015, 347, 145–149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsitsiklis, J.N. Asynchronous stochastic approximation and Q-learning. Mach. Learn. 1994, 16, 185–202. [Google Scholar] [CrossRef] [Green Version]
- Even-Dar, E.; Mansour, Y.; Bartlett, P. Learning Rates for Q-learning. J. Mach. Learn. Res. 2003, 5, 1–25. [Google Scholar]
- Tsitsiklis, J.N.; Van Roy, B. An analysis of temporal-difference learning with function approximation. IEEE Trans. Autom. Control 1997, 42, 674–690. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Wellman, M.P. Multiagent reinforcement learning: Theoretical framework and an algorithm. ICML 1998, 98, 242–250. [Google Scholar]
- Littman, M.L. Markov games as a framework for multi-agent reinforcement learning. In Proceedings of the Machine Learning Proceedings, New Brunswick, NJ, USA, 10–13 July 1994; pp. 157–163. [Google Scholar]
- Bernstein, D.S.; Givan, R.; Immerman, N.; Zilberstein, S. The complexity of decentralized control of Markov decision processes. Math. Oper. Res. 2002, 27, 819–840. [Google Scholar] [CrossRef]
- Hansen, E.A.; Bernstein, D.S.; Zilberstein, S. Dynamic programming for partially observable stochastic games. AAAI 2004, 4, 709–715. [Google Scholar]
- Laurent, G.J.; Matignon, L.; Fort-Piat, L. The world of independent learners is not Markovian. Int. J. Knowl.-Based Intell. Eng. Syst. 2011, 15, 55–64. [Google Scholar] [CrossRef] [Green Version]
- Guestrin, C.; Lagoudakis, M.; Parr, R. Coordinated reinforcement learning. ICML 2002, 2, 227–234. [Google Scholar]
- Busoniu, L.; De Schutter, B.; Babuska, R. Multiagent Reinforcement Learning with Adaptive State Focus. In BNAIC Proceedings of the Seventeenth Belgium-Netherlands Conference on Artificial Intelligence, Brussels, Belgium, 17–18 October 2005; pp. 35–42.
- Busoniu, L.; Babuska, R.; De Schutter, B. A comprehensive survey of multiagent reinforcement learning. IEEE Trans. Syst. Man, Cybern. Part C 2008, 38, 156–172. [Google Scholar] [CrossRef] [Green Version]
- Stettner, Ł. Zero-sum Markov games with stopping and impulsive strategies. Appl. Math. Optim. 1982, 9, 1–24. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjel, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Chen, X.; Li, B.; Proietti, R.; Zhu, Z.; Yoo, S.B. Multi-agent deep reinforcement learning in cognitive inter-domain networking with multi-broker orchestration. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 3–7 March 2019; Optical Society of America: Washington, DC, USA, 2019. [Google Scholar]
- Rasheed, F.; Yau, K.L.A.; Noor, R.M.; Wu, C.; Low, Y.C. Deep Reinforcement Learning for Traffic Signal Control: A Review. IEEE Access 2020, 8, 208016–208044. [Google Scholar] [CrossRef]
- Ge, H.; Song, Y.; Wu, C.; Ren, J.; Tan, G. Cooperative deep Q-learning with Q-value transfer for multi-intersection signal control. IEEE Access 2019, 7, 40797–40809. [Google Scholar] [CrossRef]
- Tan, M. Multi-agent reinforcement learning: Independent vs. cooperative agents. In Proceedings of the Tenth International Conference on Machine Learning, Amherst, MA, USA, 27–29 July 1993; pp. 330–337. [Google Scholar]
- Li, Z.; Guo, C. Multi-Agent Deep Reinforcement Learning based Spectrum Allocation for D2D Underlay Communications. IEEE Trans. Veh. Technol. 2019, 69, 1828–1840. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Zhou, P.; Liu, K.; Yuan, Y.; Wang, X.; Huang, H.; Wu, D.O. Multi-Agent Deep Reinforcement Learning for Urban Traffic Light Control in Vehicular Networks. IEEE Trans. Veh. Technol. 2020, 69, 8243–8256. [Google Scholar] [CrossRef]
- Fan, J.; Wang, Z.; Xie, Y.; Yang, Z. A theoretical analysis of deep Q-learning. In Proceedings of the Learning for Dynamics and Control, Berkeley, CA, USA, 10–11 June 2020; pp. 486–489. [Google Scholar]
- Sorokin, I.; Seleznev, A.; Pavlov, M.; Fedorov, A.; Ignateva, A. Deep attention recurrent Q-network. arXiv 2015, arXiv:1512.01693. [Google Scholar]
- Bowling, M. Convergence problems of general-sum multiagent reinforcement learning. ICML 2000, 89–94. [Google Scholar]
- Littman, M.L. Friend-or-foe Q-learning in general-sum games. ICML 2001, 1, 322–328. [Google Scholar]
- Tesauro, G. Extending Q-learning to general adaptive multi-agent systems. Adv. Neural Inf. Process. Syst. 2003, 16, 871–878. [Google Scholar]
- Kapetanakis, S.; Kudenko, D. Reinforcement learning of coordination in heterogeneous cooperative multi-agent systems. In Adaptive Agents and Multi-Agent Systems II; Springer: Berlin/Heidelberg, Germany, 2004; pp. 119–131. [Google Scholar]
- Lauer, M.; Riedmiller, M. An algorithm for distributed reinforcement learning in cooperative multi-agent systems. In Proceedings of the Seventeenth International Conference on Machine Learning, San Francisco, CA, USA, 29 June-2 July 2000. [Google Scholar]
- Melo, F.S.; Meyn, S.P.; Ribeiro, M.I. An analysis of reinforcement learning with function approximation. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 664–671. [Google Scholar]
- Ernst, D.; Geurts, P.; Wehenkel, L. Tree-based batch mode reinforcement learning. J. Mach. Learn. Res. 2005, 6, 503–556. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 1889–1897. [Google Scholar]
- Jaderberg, M.; Mnih, V.; Czarnecki, W.M.; Schaul, T.; Leibo, J.Z.; Silver, D.; Kavukcuoglu, K. Reinforcement learning with unsupervised auxiliary tasks. arXiv 2016, arXiv:1611.05397. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 March 2016; Volume 30. [Google Scholar]
- Wang, Z.; Schaul, T.; Hessel, M.; Hasselt, H.; Lanctot, M.; Freitas, N. Dueling network architectures for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 1995–2003. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 1928–1937. [Google Scholar]
- Liang, L.; Ye, H.; Li, G.Y. Spectrum sharing in vehicular networks based on multi-agent reinforcement learning. IEEE J. Sel. Areas Commun. 2019, 37, 2282–2292. [Google Scholar] [CrossRef] [Green Version]
- Budhiraja, I.; Kumar, N.; Tyagi, S. Deep Reinforcement Learning Based Proportional Fair Scheduling Control Scheme for Underlay D2D Communication. IEEE Internet Things J. 2020, 8, 3143–3156. [Google Scholar] [CrossRef]
- Yang, H.; Alphones, A.; Zhong, W.D.; Chen, C.; Xie, X. Learning-based energy-efficient resource management by heterogeneous RF/VLC for ultra-reliable low-latency industrial IoT networks. IEEE Trans. Ind. Inform. 2019, 16, 5565–5576. [Google Scholar] [CrossRef]
- Zhao, N.; Liang, Y.C.; Niyato, D.; Pei, Y.; Wu, M.; Jiang, Y. Deep reinforcement learning for user association and resource allocation in heterogeneous cellular networks. IEEE Trans. Wirel. Commun. 2019, 18, 5141–5152. [Google Scholar] [CrossRef]
- Xi, L.; Yu, L.; Xu, Y.; Wang, S.; Chen, X. A novel multi-agent DDQN-AD method-based distributed strategy for automatic generation control of integrated energy systems. IEEE Trans. Sustain. Energy 2019, 11, 2417–2426. [Google Scholar] [CrossRef]
- Tai, C.S.; Hong, J.H.; Fu, L.C. A Real-time Demand-side Management System Considering User Behavior Using Deep Q-Learning in Home Area Network. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 4050–4055. [Google Scholar]
- Zhao, L.; Liu, Y.; Al-Dubai, A.; Zomaya, A.Y.; Min, G.; Hawbani, A. A novel generation adversarial network-based vehicle trajectory prediction method for intelligent vehicular networks. IEEE Internet Things J. 2020, 8, 2066–2077. [Google Scholar] [CrossRef]
- Aljeri, N.; Boukerche, A. Mobility Management in 5G-enabled Vehicular Networks: Models, Protocols, and Classification. ACM Comput. Surv. (CSUR) 2020, 53, 1–35. [Google Scholar] [CrossRef]
- Bui, D.T.; Ngo, P.T.T.; Pham, T.D.; Jaafari, A.; Minh, N.Q.; Hoa, P.V.; Samui, P. A novel hybrid approach based on a swarm intelligence optimized extreme learning machine for flash flood susceptibility mapping. Catena 2019, 179, 184–196. [Google Scholar] [CrossRef]
- Yang, S.N.; Chang, L.C. Regional Inundation Forecasting Using Machine Learning Techniques with the Internet of Things. Water 2020, 12, 1578. [Google Scholar] [CrossRef]
- Baldazo, D.; Parras, J.; Zazo, S. Decentralized Multi-Agent deep reinforcement learning in swarms of drones for flood monitoring. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), A Coruna, Spain, 2–6 September 2019; pp. 1–5. [Google Scholar]
- Yuan, Q.; Li, J.; Zhou, H.; Lin, T.; Luo, G.; Shen, X. A Joint Service Migration and Mobility Optimization Approach for Vehicular Edge Computing. IEEE Trans. Veh. Technol. 2020, 69, 9041–9052. [Google Scholar] [CrossRef]
- Li, S.; Li, B.; Zhao, W. Joint Optimization of Caching and Computation in Multi-Server NOMA-MEC System via Reinforcement Learning. IEEE Access 2020, 8, 112762–112771. [Google Scholar] [CrossRef]
- Kerk, S.G.; Hassan, N.U.; Yuen, C. Smart Distribution Boards (Smart DB), Non-Intrusive Load Monitoring (NILM) for Load Device Appliance Signature Identification and Smart Sockets for Grid Demand Management. Sensors 2020, 20, 2900. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.F.; Yau, K.L.A.; Noor, R.M.; Imran, M.A. Survey and taxonomy of clustering algorithms in 5G. J. Netw. Comput. Appl. 2020, 154, 102539. [Google Scholar] [CrossRef]
- Rasheed, F.; Yau, K.L.A.; Low, Y.C. Deep reinforcement learning for traffic signal control under disturbances: A case study on Sunway city, Malaysia. Future Gener. Comput. Syst. 2020, 109, 431–445. [Google Scholar] [CrossRef]
- Yau, K.L.A.; Qadir, J.; Khoo, H.L.; Ling, M.H.; Komisarczuk, P. A survey on reinforcement learning models and algorithms for traffic signal control. ACM Comput. Surv. (CSUR) 2017, 50, 1–38. [Google Scholar] [CrossRef]
- Luo, Z.; Chen, Q.; Yu, G. Multi-Agent Reinforcement Learning Based Unlicensed Resource Sharing for LTE-U Networks. In Proceedings of the 2018 IEEE International Conference on Communication Systems (ICCS), Chengdu, China, 19–21 December 2018; pp. 427–432. [Google Scholar]
- Jiang, N.; Deng, Y.; Nallanathan, A.; Chambers, J.A. Reinforcement learning for real-time optimization in NB-IoT networks. IEEE J. Sel. Areas Commun. 2019, 37, 1424–1440. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Yu, J.; Buehrer, R.M. The application of deep reinforcement learning to distributed spectrum access in dynamic heterogeneous environments with partial observations. IEEE Trans. Wirel. Commun. 2020, 19, 4494–4506. [Google Scholar] [CrossRef]
- Jain, A.; Powers, A.; Johnson, H.J. Robust Automatic Multiple Landmark Detection. In Proceedings of the 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI), Iowa City, Iowa, 3–7 April 2020; pp. 1178–1182. [Google Scholar]
- Vilà, I.; Pérez-Romero, J.; Sallent, O.; Umbert, A. A Novel Approach for Dynamic Capacity Sharing in Multi-tenant Scenarios. In Proceedings of the 2020 IEEE 31st Annual International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, 31 August–3 September 2020; pp. 1–6. [Google Scholar]
- Chen, R.; Lu, H.; Lu, Y.; Liu, J. MSDF: A Deep Reinforcement Learning Framework for Service Function Chain Migration. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Korea, 25–28 May 2020; pp. 1–6. [Google Scholar]
- Luis, S.Y.; Reina, D.G.; Marín, S.L.T. A Multiagent Deep Reinforcement Learning Approach for Path Planning in Autonomous Surface Vehicles: The Ypacaraí Lake Patrolling Case. IEEE Access 2021, 9, 17084–17099. [Google Scholar] [CrossRef]
- Chen, S.; Dong, J.; Ha, P.; Li, Y.; Labi, S. Graph neural network and reinforcement learning for multi-agent cooperative control of connected autonomous vehicles. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 838–857. [Google Scholar] [CrossRef]
- Xie, D.; Wang, Z.; Chen, C.; Dong, D. IEDQN: Information Exchange DQN with a Centralized Coordinator for Traffic Signal Control. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Zhong, C.; Lu, Z.; Gursoy, M.C.; Velipasalar, S. A Deep Actor-Critic Reinforcement Learning Framework for Dynamic Multichannel Access. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 1125–1139. [Google Scholar] [CrossRef] [Green Version]
- Zou, Z.; Yin, R.; Chen, X.; Wu, C. Deep Reinforcement Learning for D2D transmission in unlicensed bands. In Proceedings of the 2019 IEEE/CIC International Conference on Communications Workshops in China (ICCC Workshops), Changchun, China, 11–13 August 2019; pp. 42–47. [Google Scholar]
- Chu, T.; Wang, J.; Codecà, L.; Li, Z. Multi-agent deep reinforcement learning for large-scale traffic signal control. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1086–1095. [Google Scholar] [CrossRef] [Green Version]
- Shah, H.A.; Zhao, L. Multi-Agent Deep Reinforcement Learning Based Virtual Resource Allocation Through Network Function Virtualization in Internet of Things. IEEE Internet Things J. 2020, 8, 3410–3421. [Google Scholar] [CrossRef]
- Li, Z.; Yu, H.; Zhang, G.; Dong, S.; Xu, C.Z. Network-wide traffic signal control optimization using a multi-agent deep reinforcement learning. Transp. Res. Part C Emerg. Technol. 2021, 125, 103059. [Google Scholar] [CrossRef]
- Su, Q.; Li, B.; Wang, C.; Qin, C.; Wang, W. A Power Allocation Scheme Based on Deep Reinforcement Learning in HetNets. In Proceedings of the 2020 International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 17–20 February 2020; pp. 245–250. [Google Scholar]
- Tan, T.; Chu, T.; Wang, J. Multi-Agent Bootstrapped Deep Q-Network for Large-Scale Traffic Signal Control. In Proceedings of the 2020 IEEE Conference on Control Technology and Applications (CCTA), Montreal, QC, Canada, 24–26 August 2020; pp. 358–365. [Google Scholar]
- Zhang, Y.; Mou, Z.; Gao, F.; Xing, L.; Jiang, J.; Han, Z. Hierarchical Deep Reinforcement Learning for Backscattering Data Collection with Multiple UAVs. IEEE Internet Things J. 2020, 8, 3786–3800. [Google Scholar] [CrossRef]
- Diallo, E.A.O.; Sugiyama, A.; Sugawara, T. Learning to coordinate with deep reinforcement learning in doubles pong game. In Proceedings of the 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), Cancun, Mexico, 18–21 December 2017; pp. 14–19. [Google Scholar]
- Zhang, Y.; Wang, X.; Wang, J.; Zhang, Y. Deep Reinforcement Learning Based Volt-VAR Optimization in Smart Distribution Systems. arXiv 2020, arXiv:2003.03681. [Google Scholar]
- Zhang, Y.; Cai, P.; Pan, C.; Zhang, S. Multi-agent deep reinforcement learning-based cooperative spectrum sensing with upper confidence bound exploration. IEEE Access 2019, 7, 118898–118906. [Google Scholar] [CrossRef]
- Kassab, R.; Destounis, A.; Tsilimantos, D.; Debbah, M. Multi-Agent Deep Stochastic Policy Gradient for Event Based Dynamic Spectrum Access. arXiv 2020, arXiv:2004.02656. [Google Scholar]
- Tuyls, K.; Weiss, G. Multiagent learning: Basics, challenges, and prospects. Ai Mag. 2012, 33, 41. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Lu, Z. Learning attentional communication for multi-agent cooperation. arXiv 2018, arXiv:1805.07733. [Google Scholar]
- Pesce, E.; Montana, G. Improving coordination in small-scale multi-agent deep reinforcement learning through memory-driven communication. Mach. Learn. 2020, 109, 1727–1747. [Google Scholar] [CrossRef] [Green Version]
- Gupta, J.K.; Egorov, M.; Kochenderfer, M. Cooperative multi-agent control using deep reinforcement learning. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, São Paulo, Brazil, 8–12 May 2017; Springer: Cham, Switzerland, 2017; pp. 66–83. [Google Scholar]
- Terry, J.K.; Grammel, N.; Hari, A.; Santos, L.; Black, B.; Manocha, D. Parameter sharing is surprisingly useful for multi-agent deep reinforcement learning. arXiv 2020, arXiv:2005.13625. [Google Scholar]
- Seo, M.; Vecchietti, L.F.; Lee, S.; Har, D. Rewards prediction-based credit assignment for reinforcement learning with sparse binary rewards. IEEE Access 2019, 7, 118776–118791. [Google Scholar] [CrossRef]
- Gaina, R.D.; Lucas, S.M.; Pérez-Liébana, D. Tackling sparse rewards in real-time games with statistical forward planning methods. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1691–1698. [Google Scholar]
- Shoham, Y.; Powers, R.; Grenager, T. If multi-agent learning is the answer, what is the question? Artif. Intell. 2007, 171, 365–377. [Google Scholar] [CrossRef] [Green Version]
- Roy, J.; Barde, P.; Harvey, F.G.; Nowrouzezahrai, D.; Pal, C. Promoting Coordination through Policy Regularization in Multi-Agent Deep Reinforcement Learning. arXiv 2019, arXiv:1908.02269. [Google Scholar]
- De Hauwere, Y.M.; Vrancx, P.; Nowé, A. Learning multi-agent state space representations. In Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems, Toronto, ON, Canada, 10–14 May 2010; Volume 1, pp. 715–722. [Google Scholar]




| Reference, Year | Foci | Approach | Multi-Agent Environment |
|---|---|---|---|
| Nguyen et al. (2020) [7] | The use of transfer learning in MADRL approaches for non-stationarity and partial observable multi-agent environments | Deep Learning |
|
| Hernandez-Leal et al. (2018) [8] | An overview of the MADRL literature on the use of RL and MARL in multi-agent environments, and the computational complexity of MADRL | Deep Learning |
|
| Oroojlooyjadid and Hajinezhad (2019) [9] | Enhancement of MADRL approaches and algorithms (i.e., independent learners, fully observable critic, value function factorization, consensus, and learning to communicate) | Deep Learning |
|
| Da Silva et al. (2020) [10] | Transfer learning in MADRL | Deep Learning |
|
| Zhang et al. (2021) [11] | Theoretical analysis of MADRL convergence guarantees | Game Theory |
|
| Gronauer and Diepold (2021) [12] | Theoretical analysis of MADRL approaches in terms of training schemes and the emergent patterns of agent behavior | Deep Learning |
|
| This survey | MADRL models and algorithms applied to various multi-agent environments | Deep Learning |
|
| Method | Description | Advantages | Disadvantages | Convergence Criteria |
|---|---|---|---|---|
| RL | A single agent interacts with the operating environment to learn the optimal policy, such as the action-value function (or Q-value) in Q-learning |
|
|
|
| MARL | Multiple agents exchange knowledge with each other and interact with the operating environment to learn the optimal policy |
|
|
|
| DQN | A single agent interacts with the operating environment to learn the optimal policy using DNN with experience replay and target network, which addresses the curse of dimensionality (or high-dimensional state–action spaces) |
|
| |
| MADQN | Multiple agents exchange knowledge with each other and interact with the operating environment to learn the optimal policy using DNN with experience replay and target network, which addresses the curse of dimensionality (or high-dimensional state–action spaces) |
|
|
|
| Topic | Keyword |
|---|---|
| General |
|
| Single-agent approaches applied in multi-agent environments |
|
| Multi-agent approaches |
|
| MADRL Approach | Reference, Year | Objective | Characteristic | Challenge | Applications | Performance Measure | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O.1 Higher stability | O.2 Higher learning speed | O.3 Lower complexity | O.4 Lower signaling overhead | O.5 Higher scalability | X.1.1 Neighboring agents | X.1.2 All agents | X.2.1 Competitive | X.2.2 Collaborative | X.3.1 Involvement from the centralized entity | C.1 ultra-densification | C.2 High dynamicity | C.3 High dimension | A.1 Resource allocation | A.2 Traffic signal control in vehicular networks | A.3 Network routing | A.4 Flood monitoring | A.5 Service migration | A.6 Games | P.1 Lower outage/blocking probability | P.2 Higher accumulated reward | P.3 Higher Quality of Service | P.4 Higher energy efficiency | P.5 Higher fairness | P.6 Lower congestion levels | ||
| SADRL applied to distributed agents | Chen et al. (2019) [31] | × | × | × | × | × | ||||||||||||||||||||
| Vila et al. (2020) [72] | × | × | × | × | ||||||||||||||||||||||
| Shilu et al. (2020) [63] | × | × | × | × | × | × | ||||||||||||||||||||
| Ruoyun et al. (2020) [73] | × | × | × | × | ||||||||||||||||||||||
| Shing’s et al. (2019) [56] | × | × | × | × | × | |||||||||||||||||||||
| You et al. (2019) [6] | × | × | × | × | × | × | × | |||||||||||||||||||
| Zhao et al. (2019) [54] | × | × | × | × | × | × | × | × | ||||||||||||||||||
| Luis et al. (2021) [74] | × | × | × | × | × | × | × | |||||||||||||||||||
| Chen et al. (2021) [75] | × | × | × | × | × | × | × | |||||||||||||||||||
| SADRL for hierarchical MA environment | Donghan et al. (2020) [76] | × | × | × | × | × | × | × | × | |||||||||||||||||
| SADRL with AC applied to centralized entities in hierarchical MA environment | Li et al. (2019) [35] | × | × | × | × | × | × | × | × | |||||||||||||||||
| Ishan et al. (2020) [52] | × | × | × | × | × | × | ||||||||||||||||||||
| SADRL with AC applied to distributed entities in hierarchical MA environment | Chen et al. (2019) [77] | × | × | × | × | × | × | |||||||||||||||||||
| Xu et al. (2020) [70] | × | × | × | × | × | × | ||||||||||||||||||||
| Zou et al. (2019) [78] | × | × | × | × | ||||||||||||||||||||||
| MADRL with AC applied to distributed entities | Chu’s et al. (2019) [79] | × | × | × | × | × | × | × | × | × | ||||||||||||||||
| Hurmat et al. (2020) [80] | × | × | × | × | ||||||||||||||||||||||
| Li et al. (2021) [81] | × | × | × | × | × | |||||||||||||||||||||
| MADRL using target updated with neighboring agents’ states and actions | Wu et al. (2020) [36] | × | × | × | × | × | × | × | × | × | ||||||||||||||||
| Qingyong et al. (2020) [82] | × | × | × | × | × | × | × | |||||||||||||||||||
| MADRL using target updated with neighboring agents’ Q-values | Ge et al. (2019) [33] | × | × | × | × | × | × | × | × | × | ||||||||||||||||
| Bootstrapping MADRL | Tian et al. (2020) [83] | × | × | × | × | × | × | × | ||||||||||||||||||
| MADRL with shared reward | Baldazo et al. (2019) [61] | × | × | × | × | × | × | × | ||||||||||||||||||
| MADRL with action discovery strategy | Lei et al. (2019) [55] | × | × | × | × | × | × | |||||||||||||||||||
| Distributed MADRL with hierarchical characteristics | Yu et al. (2020) [84] | × | × | × | × | × | × | |||||||||||||||||||
| MADRL with concurrent learning | Elhadji et al. (2017) [85] | × | × | × | × | × | ||||||||||||||||||||
| Zhang et al. (2020) [86] | × | × | × | × | × | × | × | |||||||||||||||||||
| MADRL Approaches | Description | Advantages |
|---|---|---|
| Actor–critic |
|
|
| MADRL with knowledge exchange |
|
|
| Bootstrapped MADRL |
|
|
| MADRL with action discovery |
|
|
| MADRL with concurrent learning |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, A.M.; Yau, K.-L.A.; Chong, Y.-W.; Wu, C. Applications of Multi-Agent Deep Reinforcement Learning: Models and Algorithms. Appl. Sci. 2021, 11, 10870. https://doi.org/10.3390/app112210870
Ibrahim AM, Yau K-LA, Chong Y-W, Wu C. Applications of Multi-Agent Deep Reinforcement Learning: Models and Algorithms. Applied Sciences. 2021; 11(22):10870. https://doi.org/10.3390/app112210870
Chicago/Turabian StyleIbrahim, Abdikarim Mohamed, Kok-Lim Alvin Yau, Yung-Wey Chong, and Celimuge Wu. 2021. "Applications of Multi-Agent Deep Reinforcement Learning: Models and Algorithms" Applied Sciences 11, no. 22: 10870. https://doi.org/10.3390/app112210870
APA StyleIbrahim, A. M., Yau, K.-L. A., Chong, Y.-W., & Wu, C. (2021). Applications of Multi-Agent Deep Reinforcement Learning: Models and Algorithms. Applied Sciences, 11(22), 10870. https://doi.org/10.3390/app112210870







