Thermal Simulation Studies for the Characterization of a Cyclotron Liquid Target with Thick Niobium Target Windows
Abstract
:1. Introduction
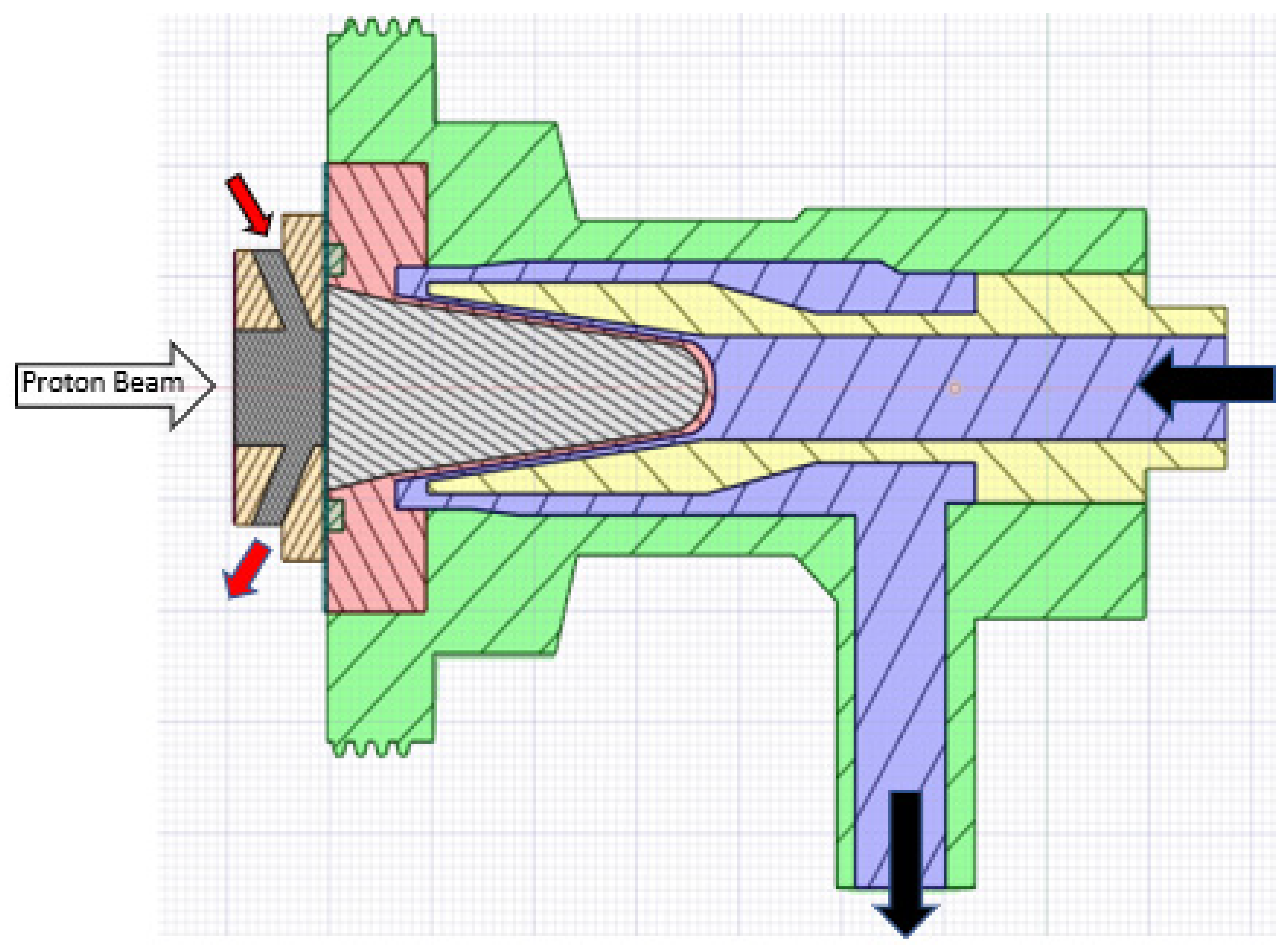
2. Materials and Methods
- the mass flow rates of the helium and the cooling water;
- the initial temperatures of the helium and the cooling water;
- the current of the proton beam (i.e., the energy deposited).
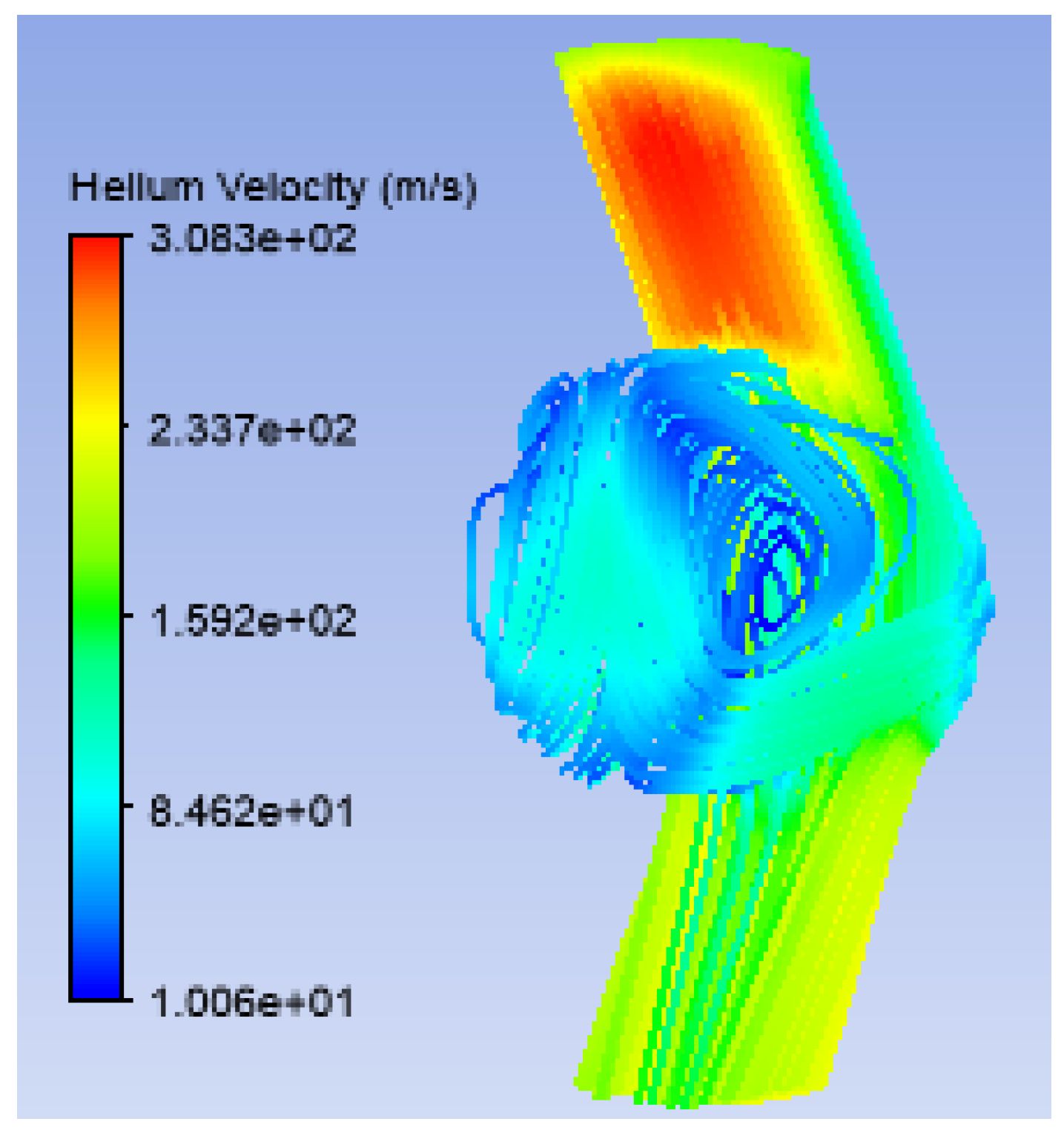
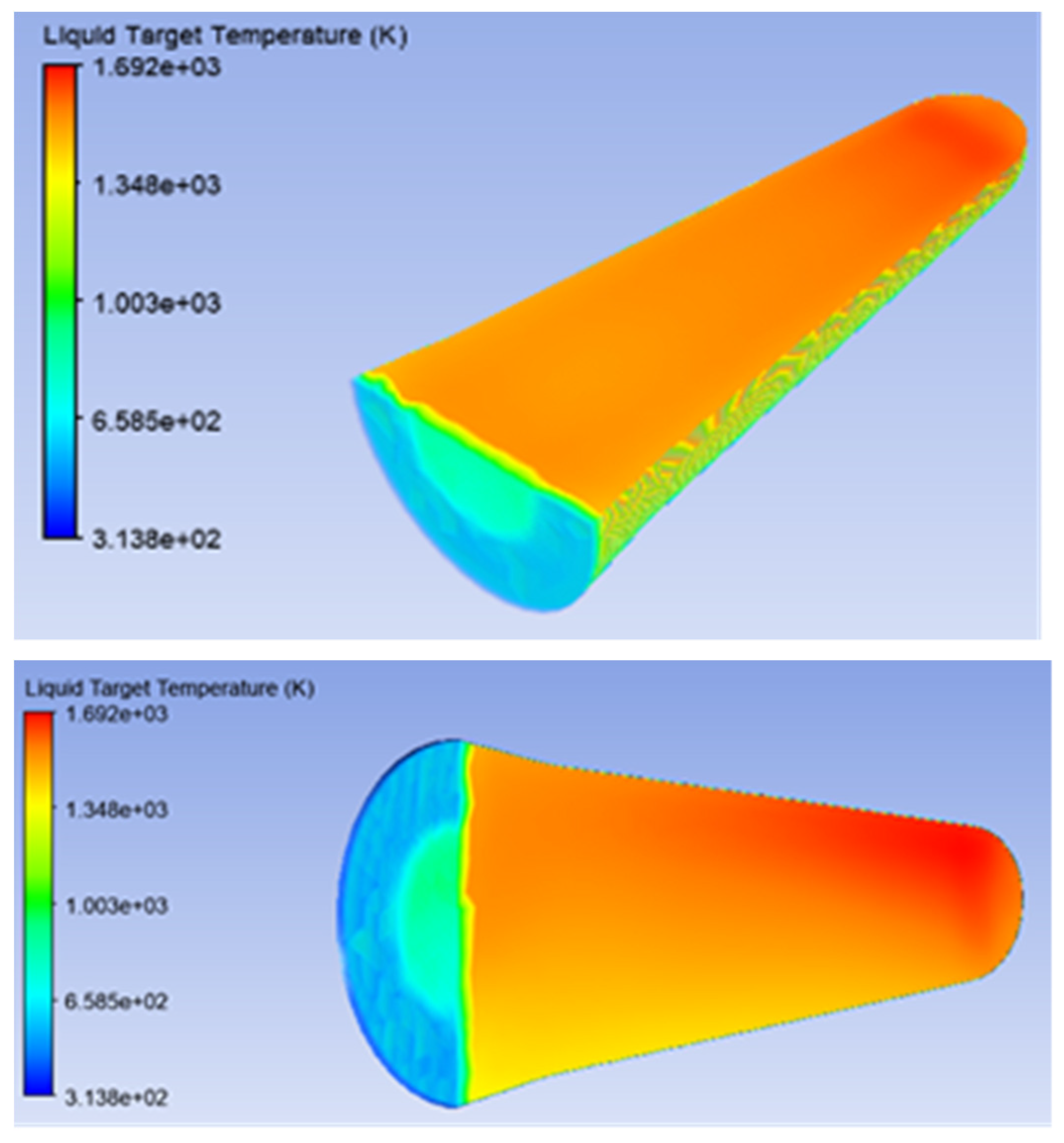
3. Results
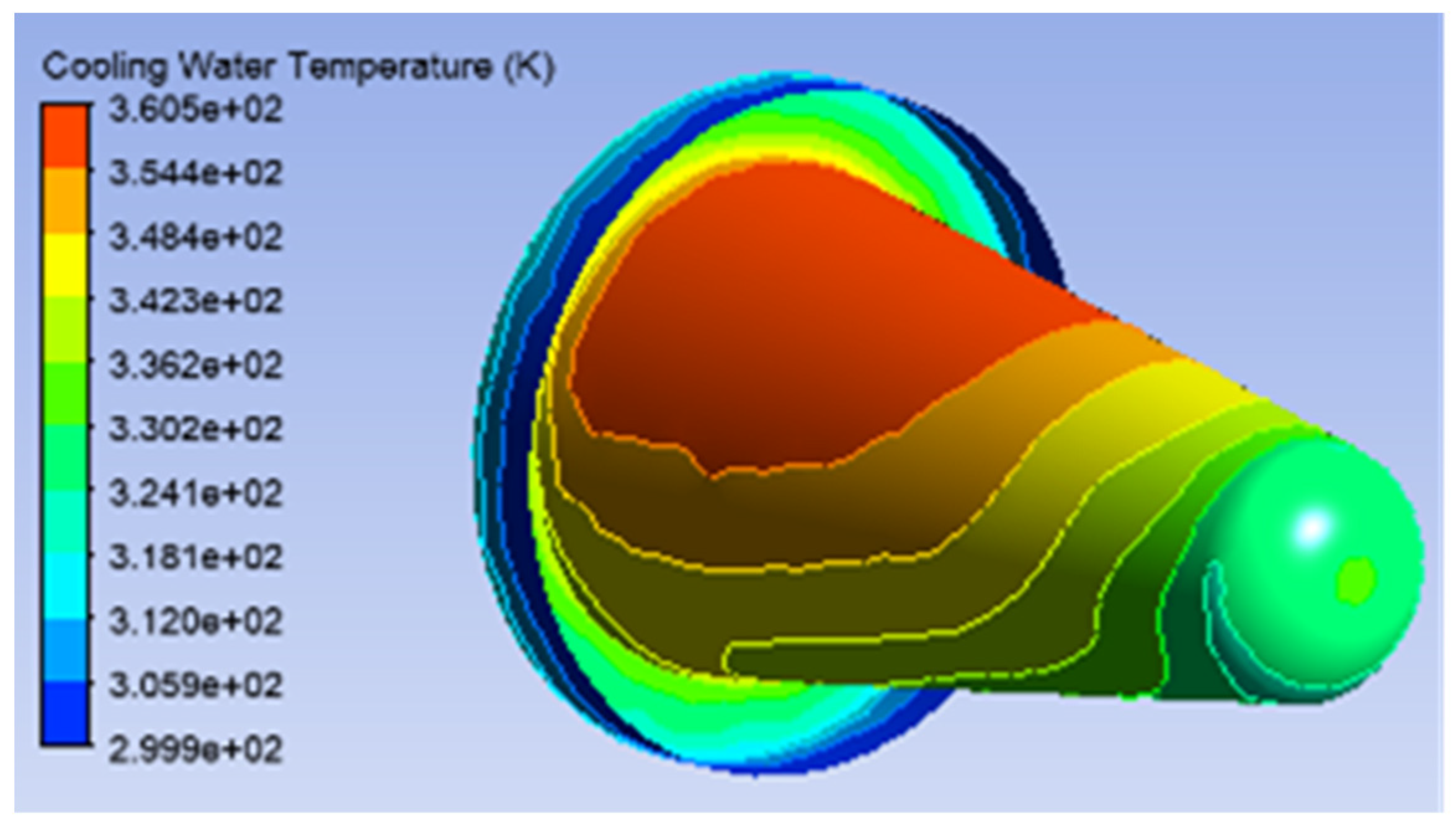
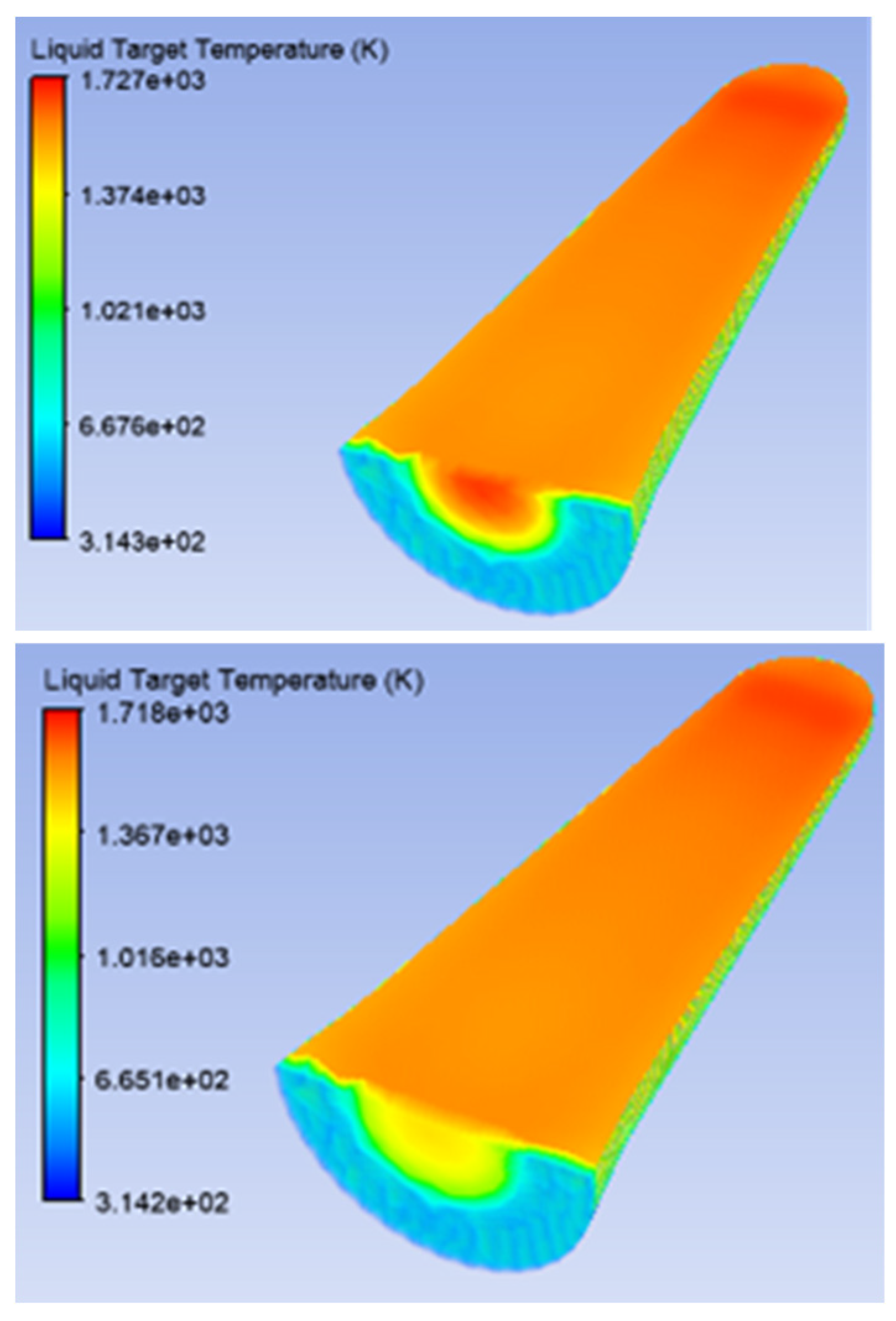
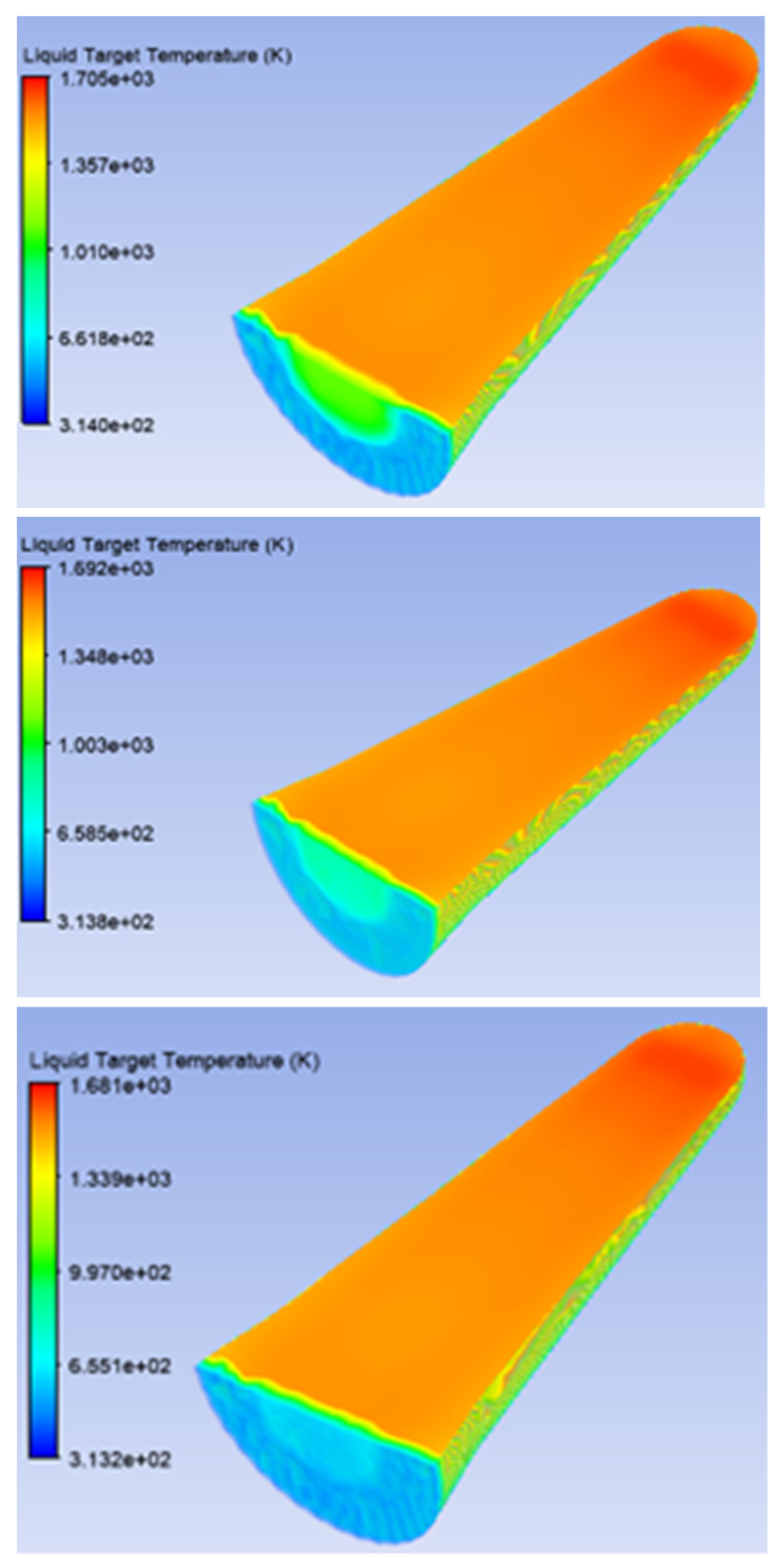
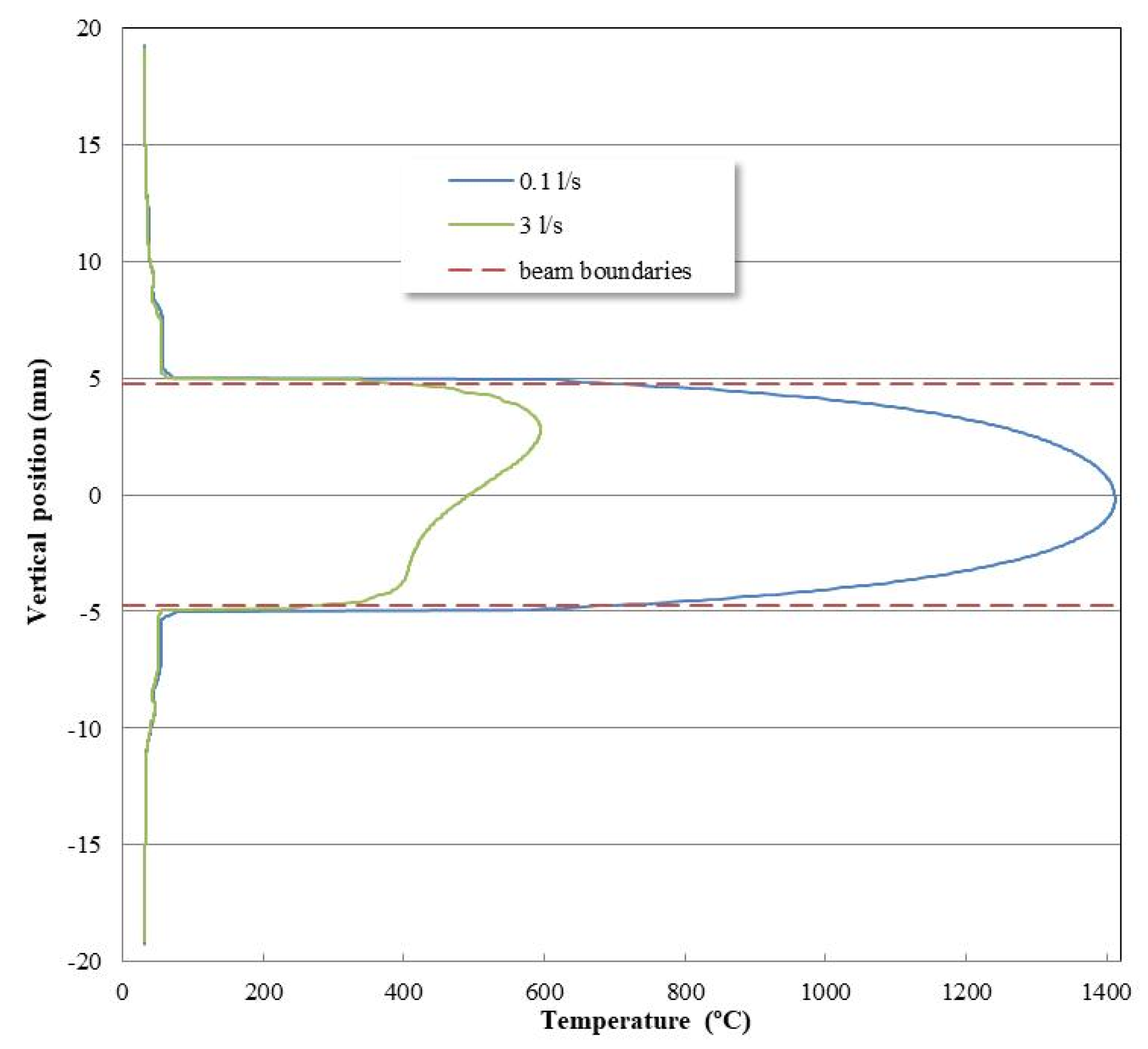
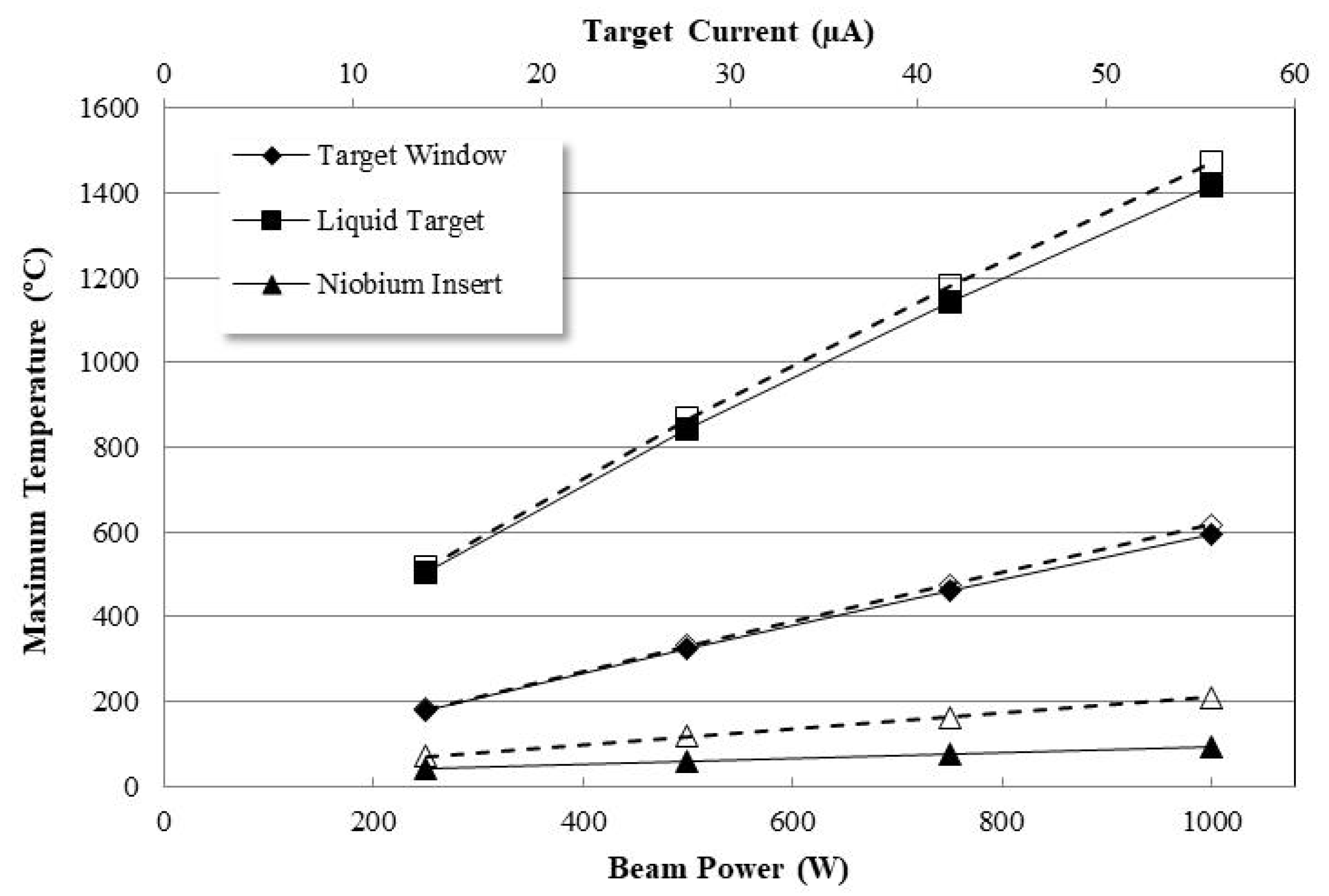
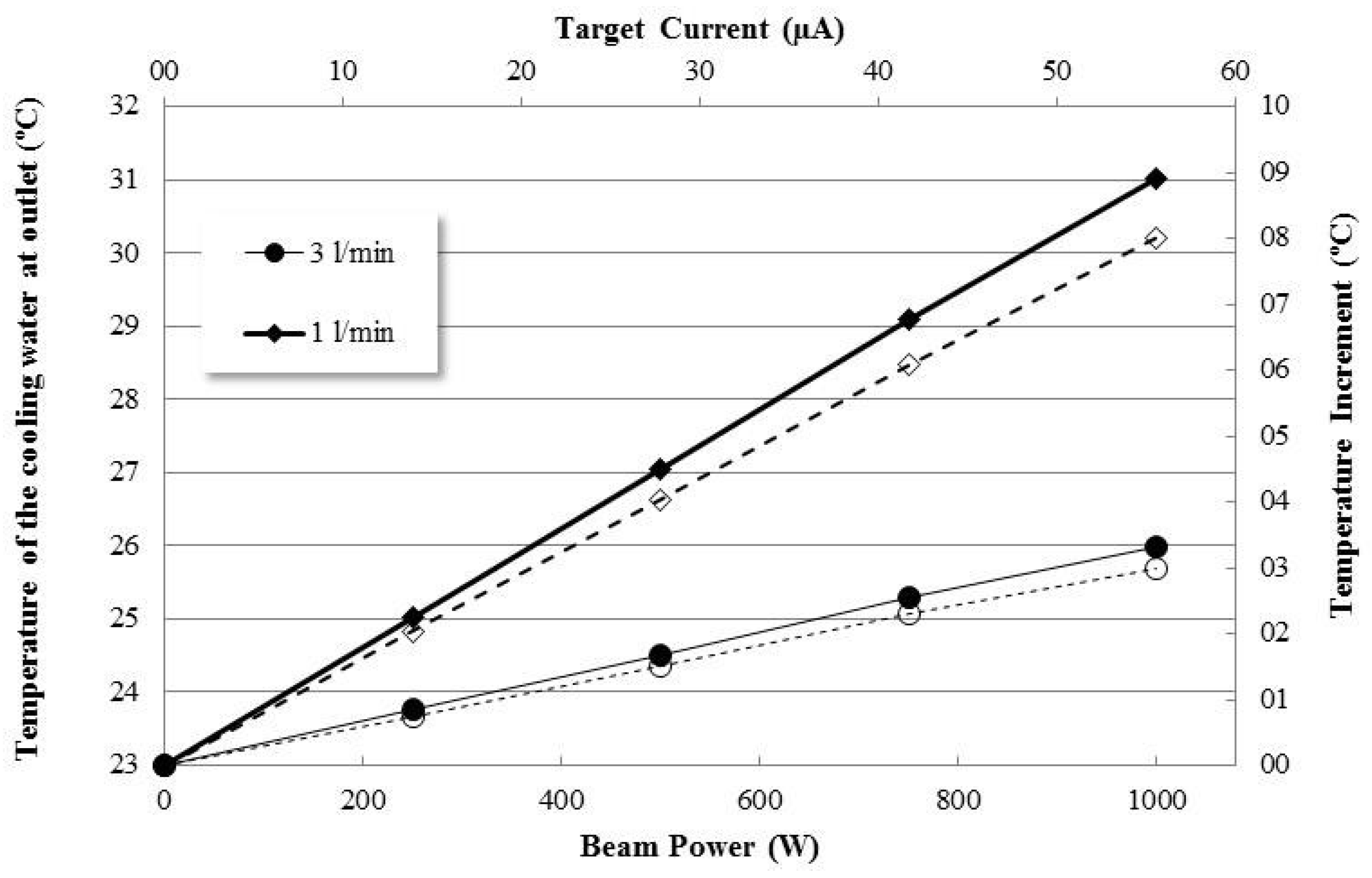
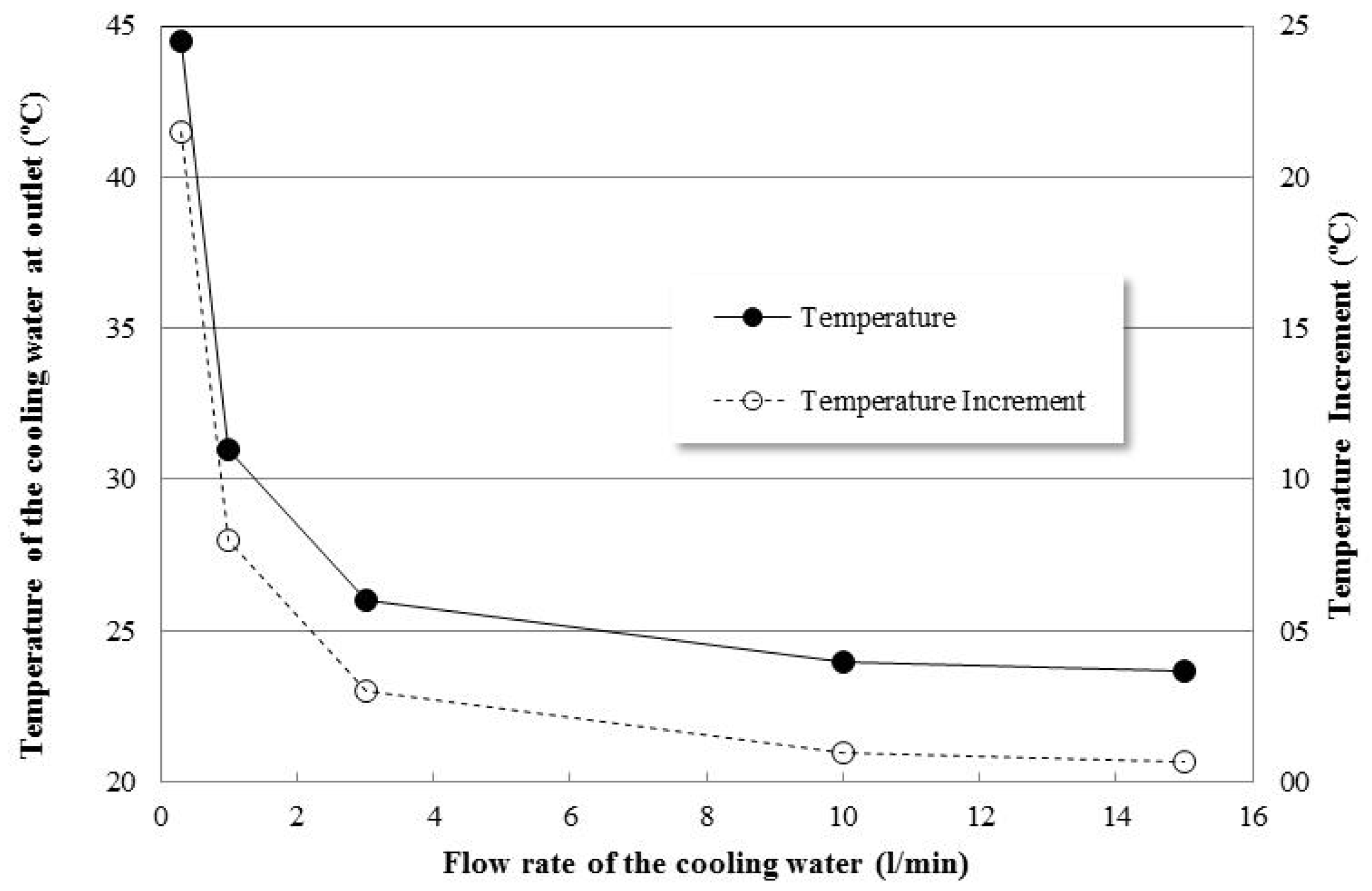
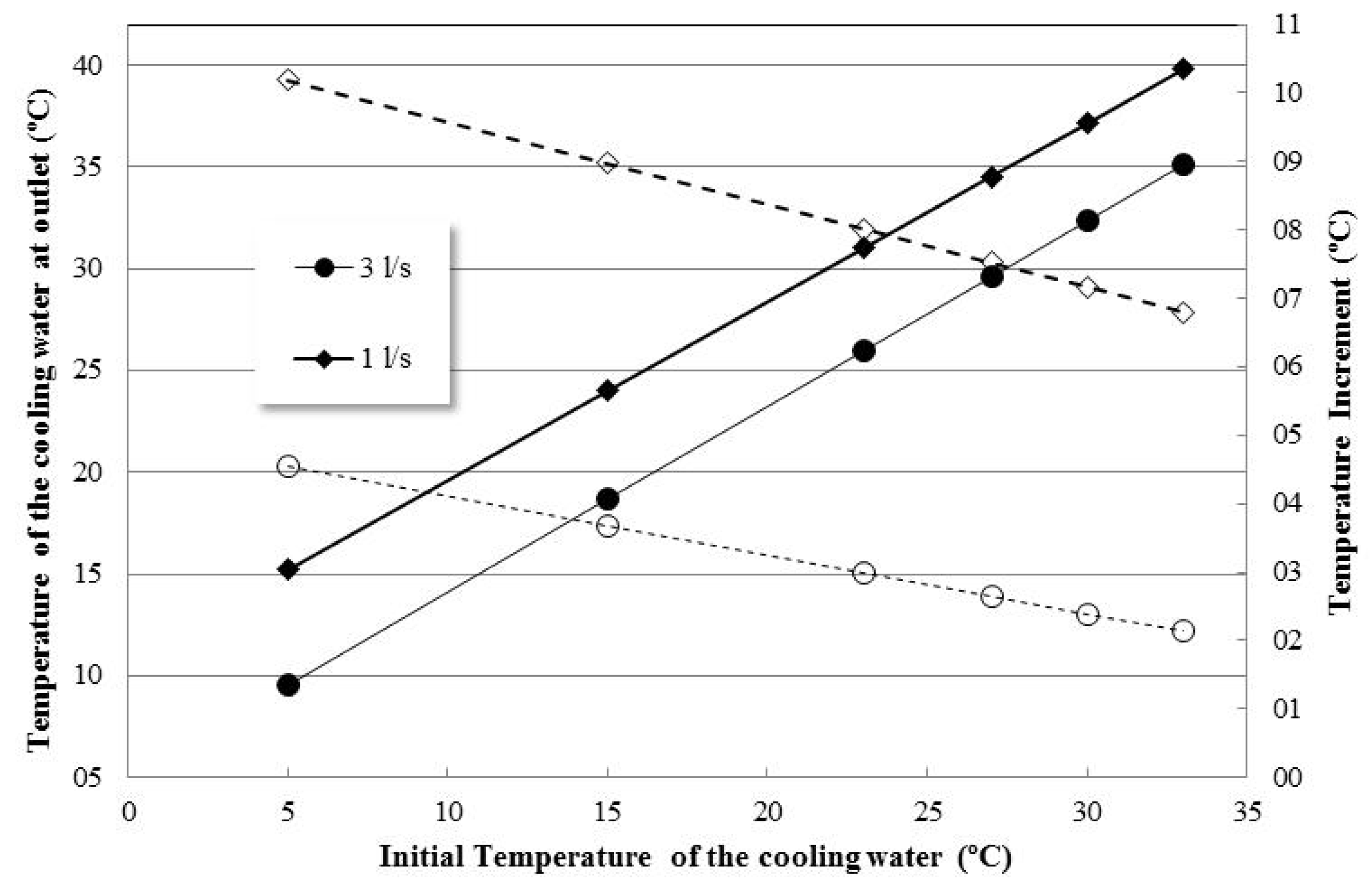
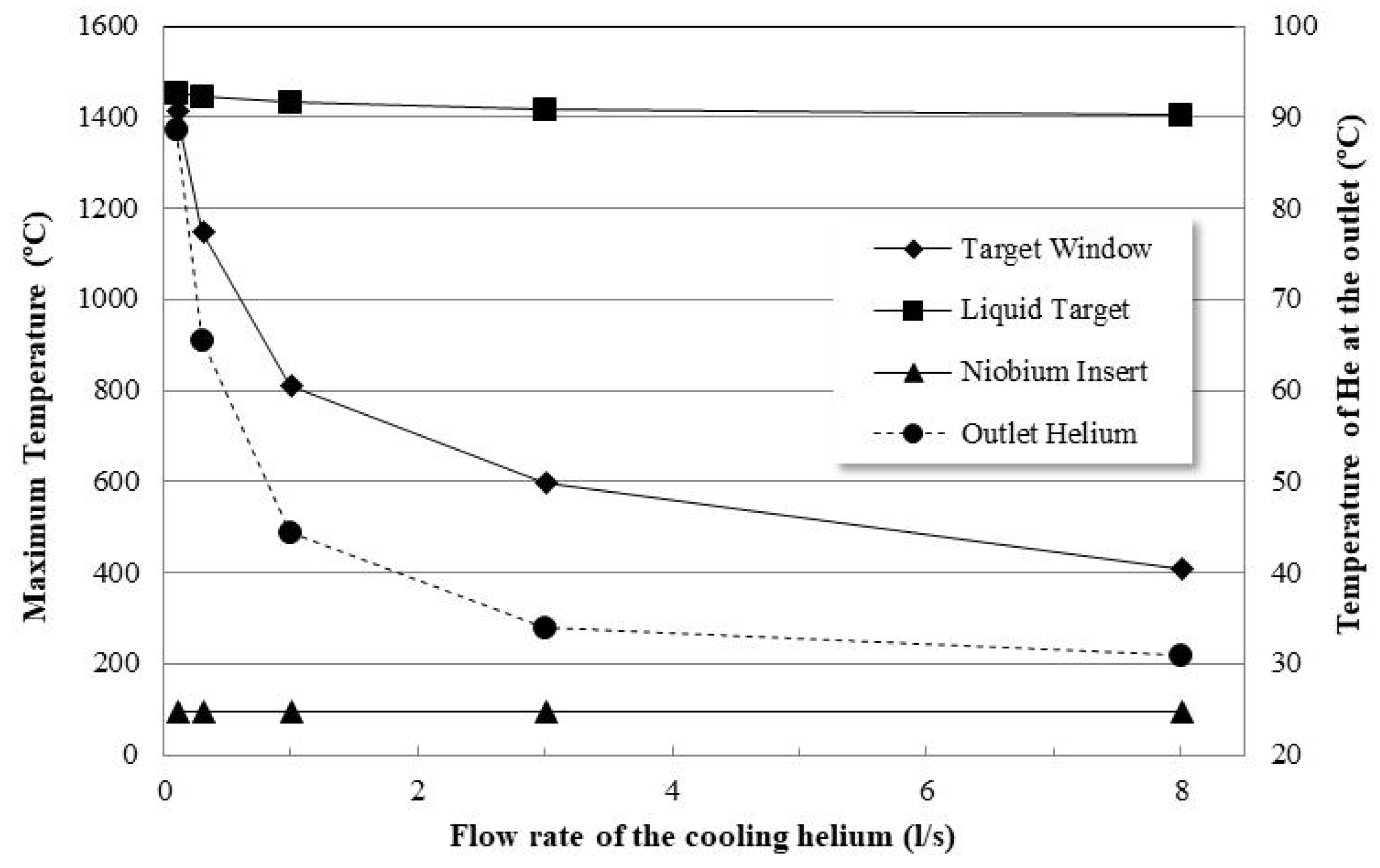
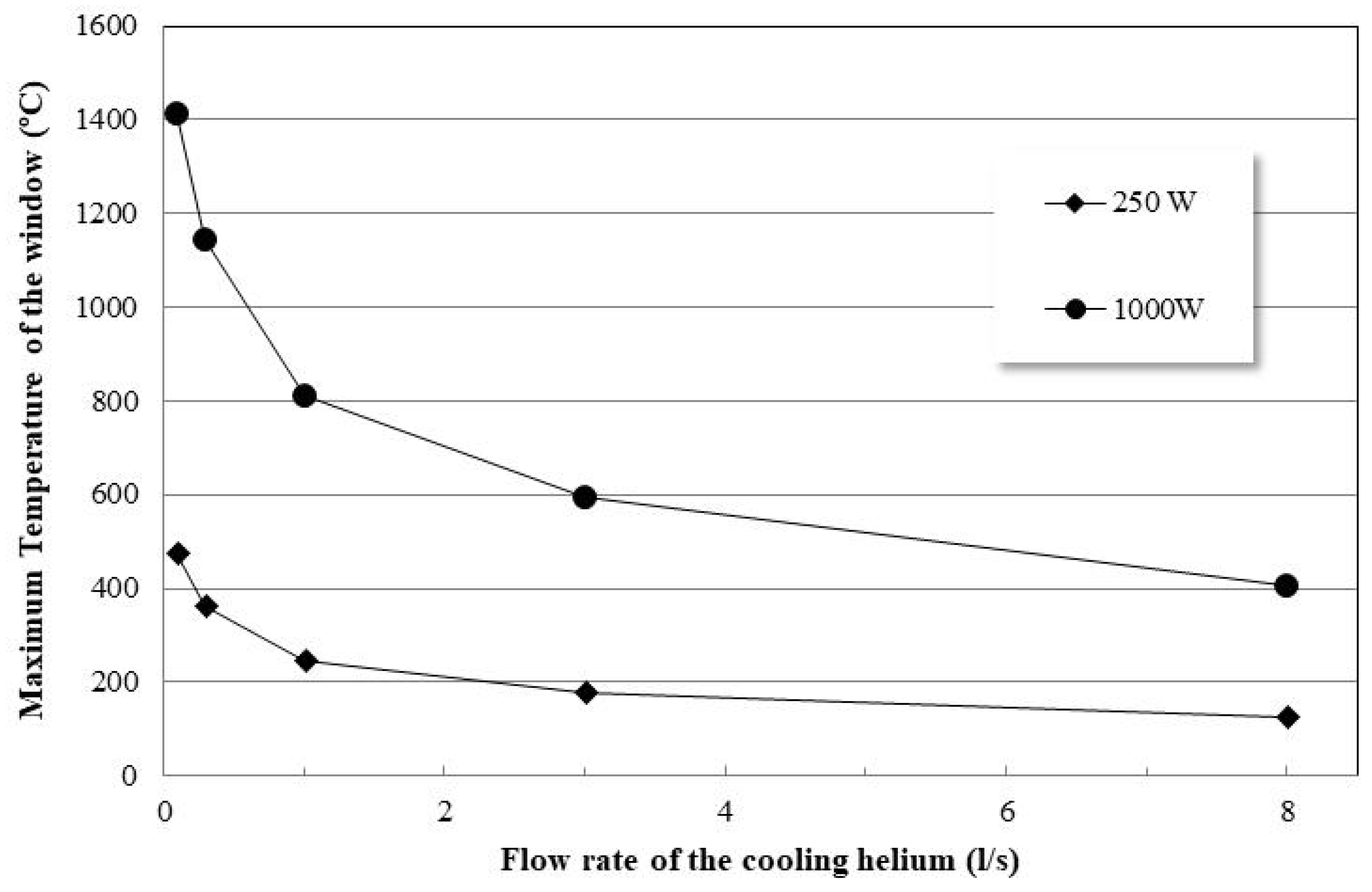
3.1. Standard Target Window
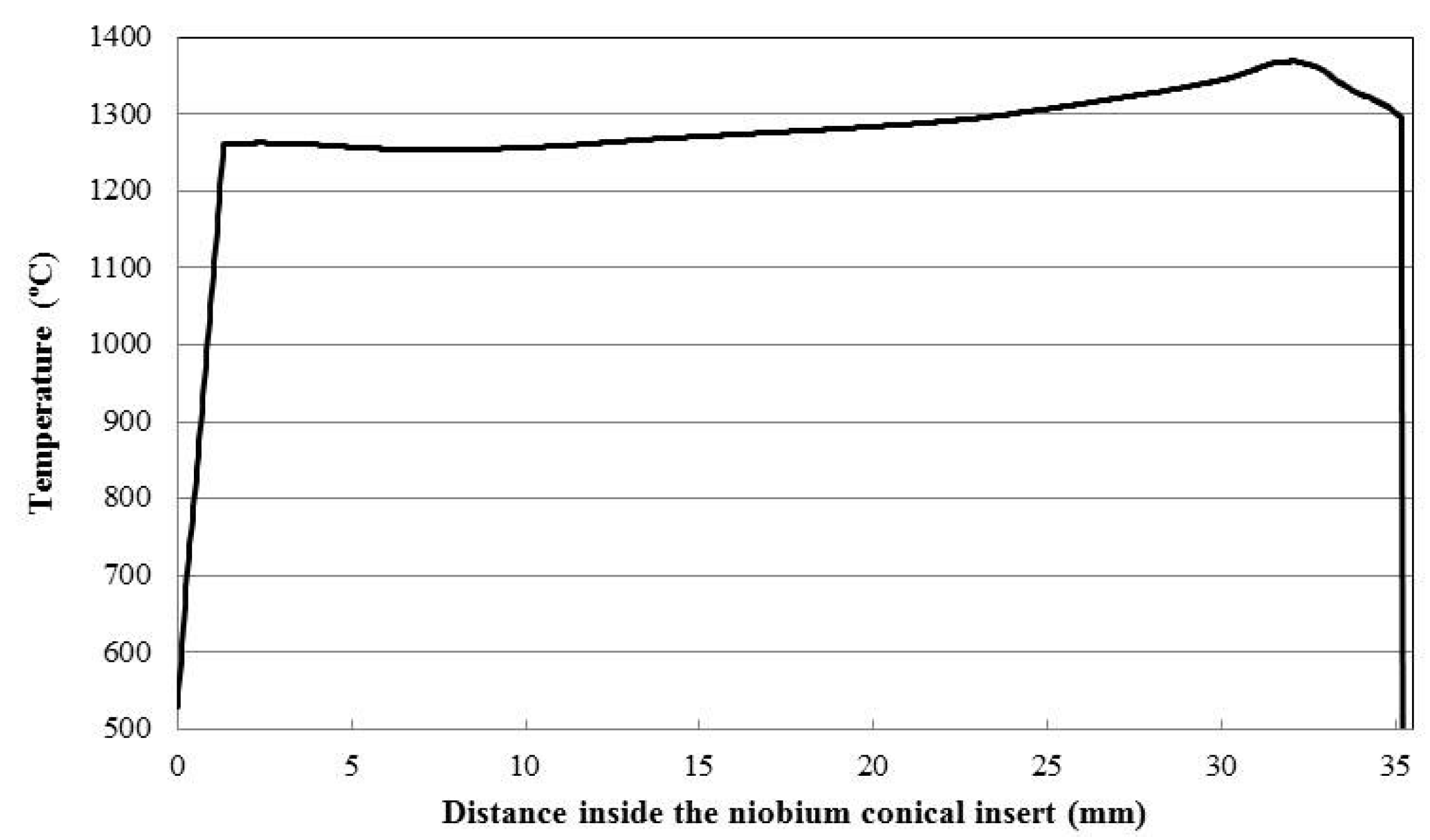
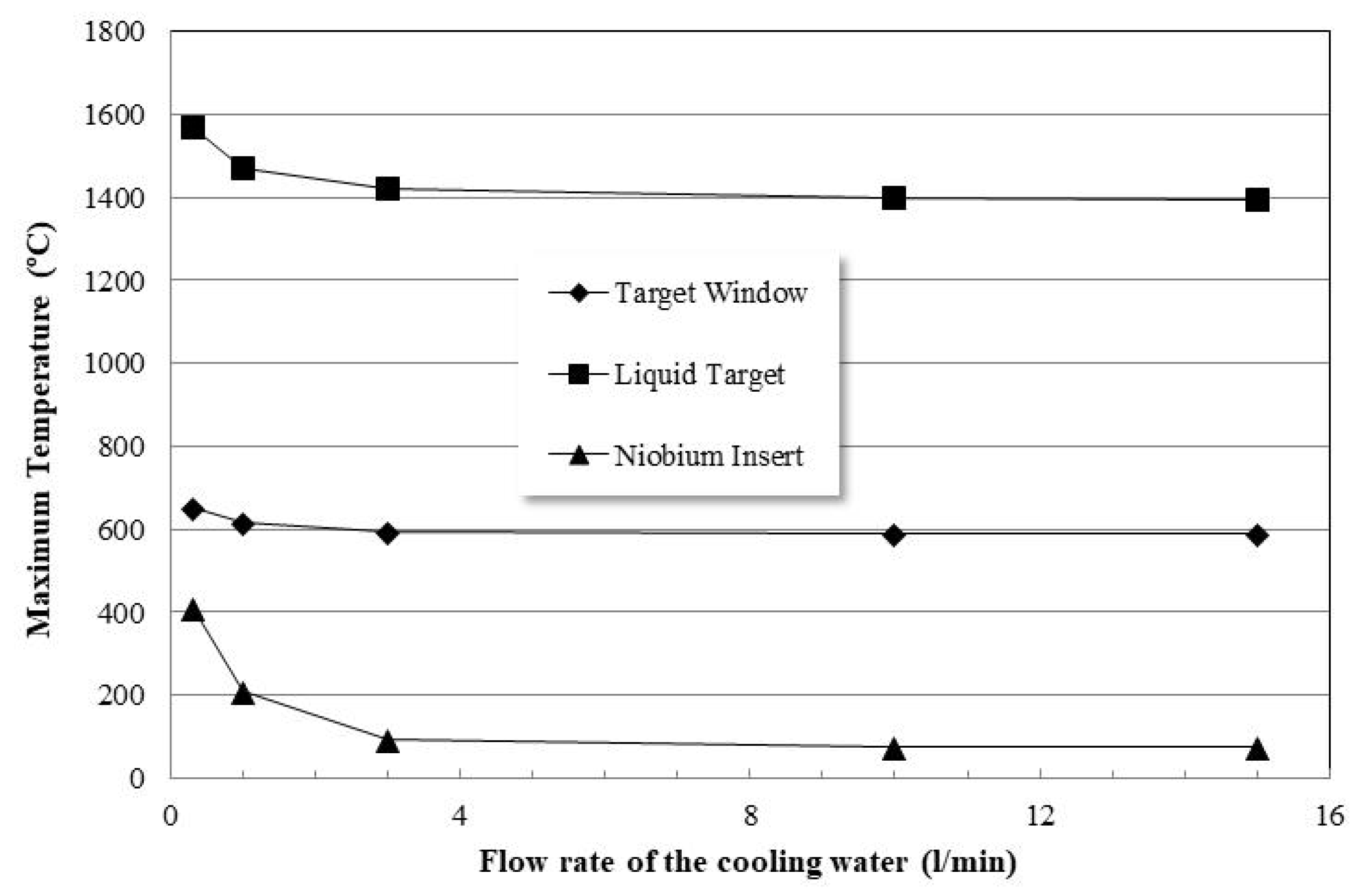
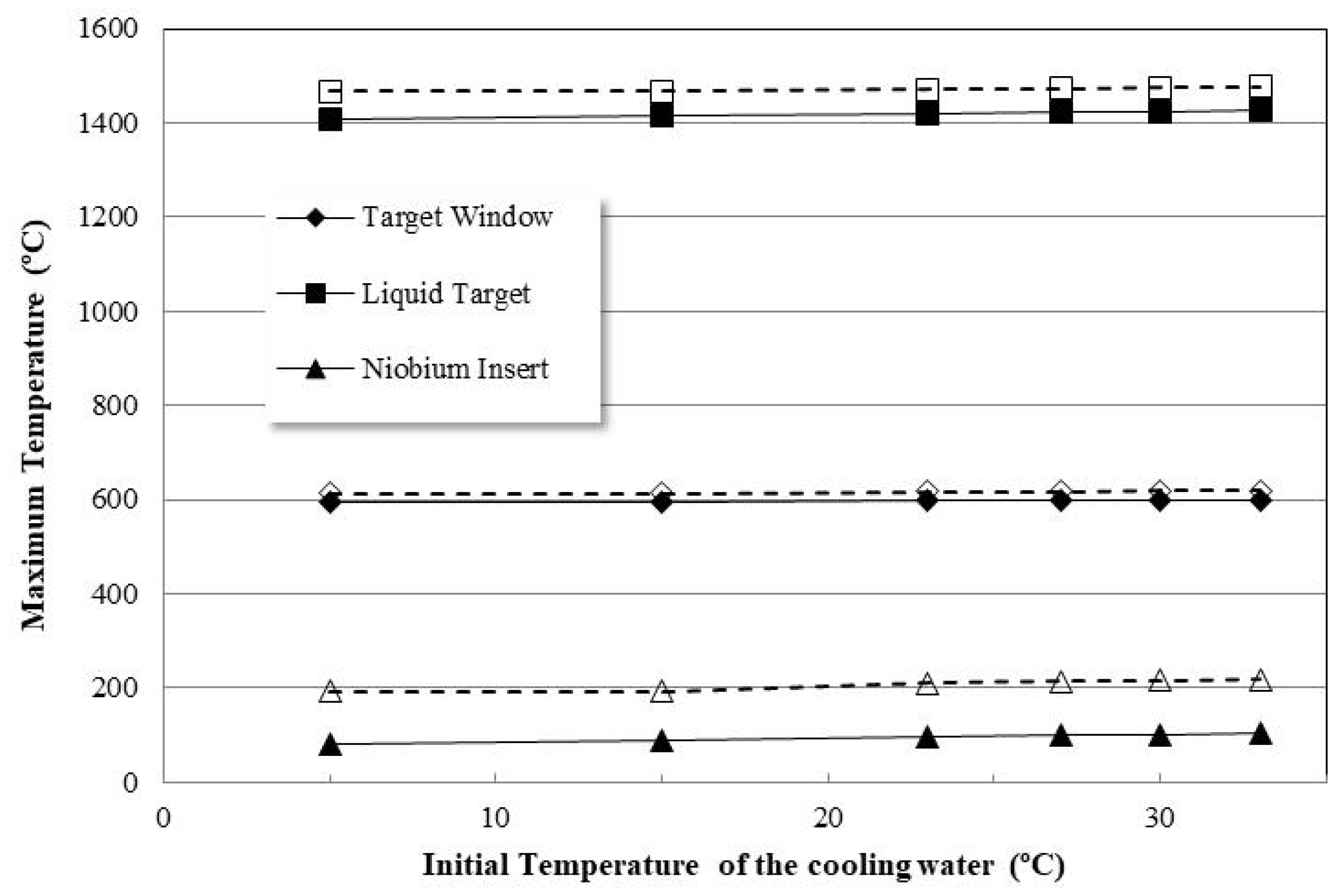
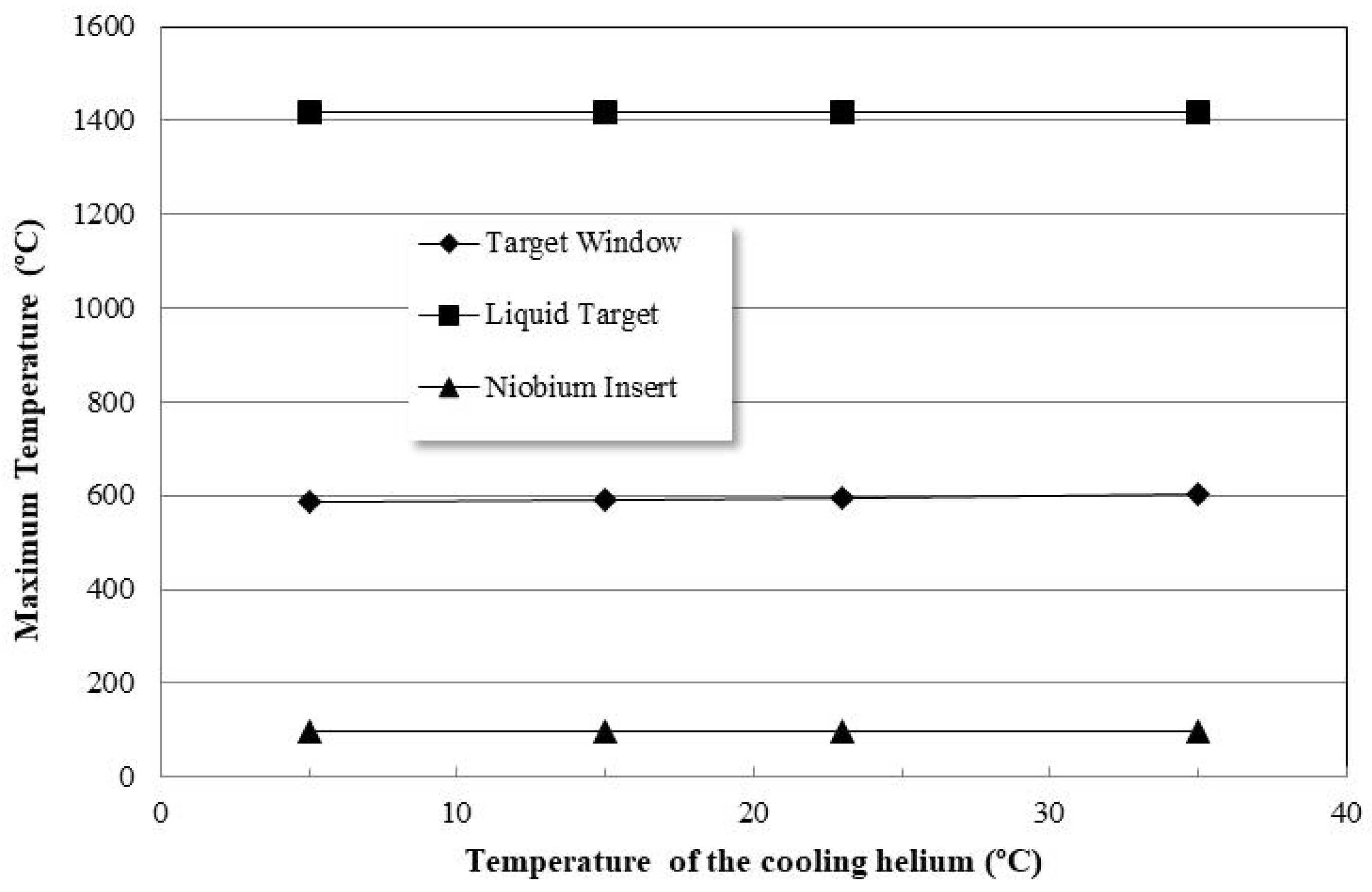
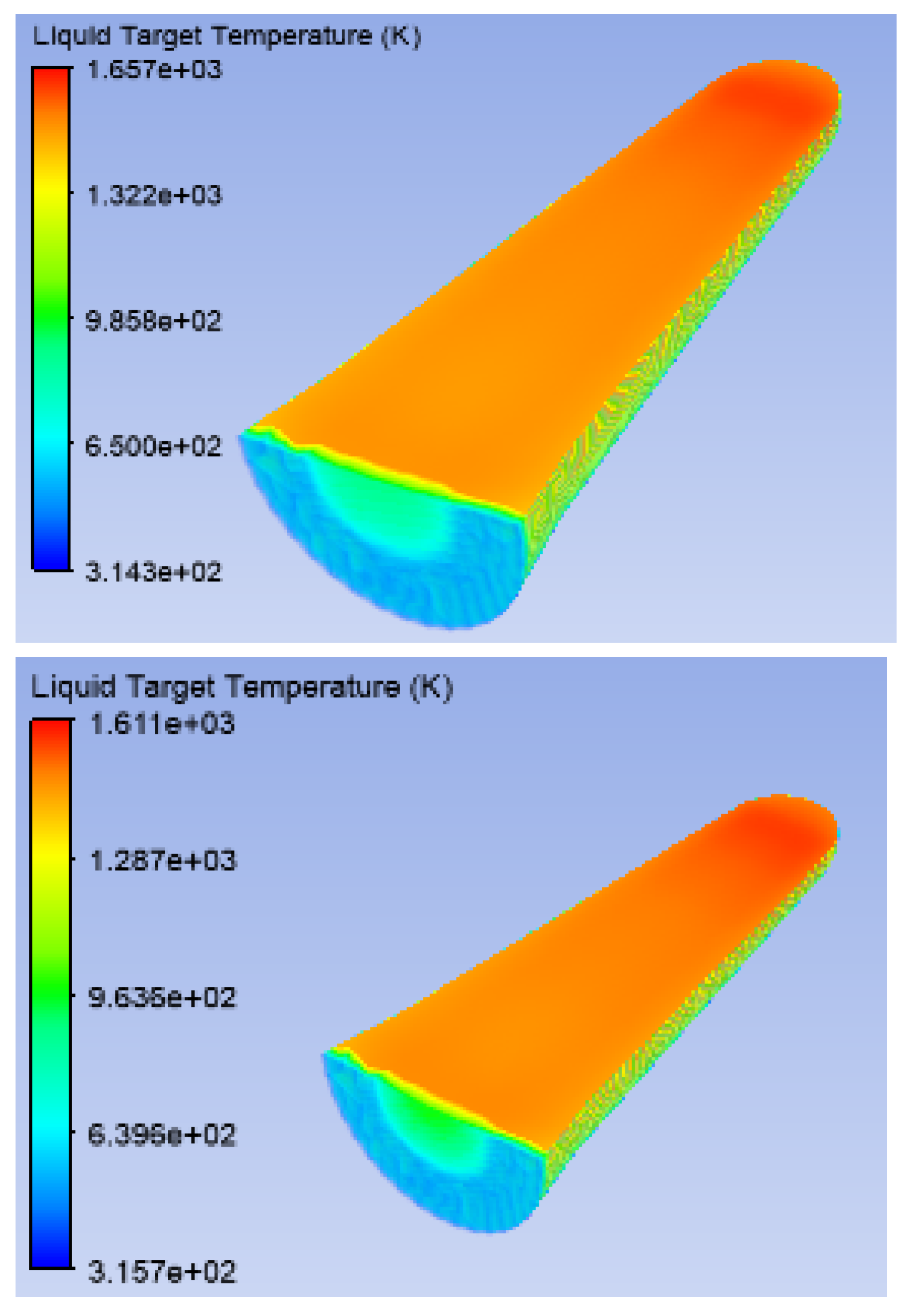
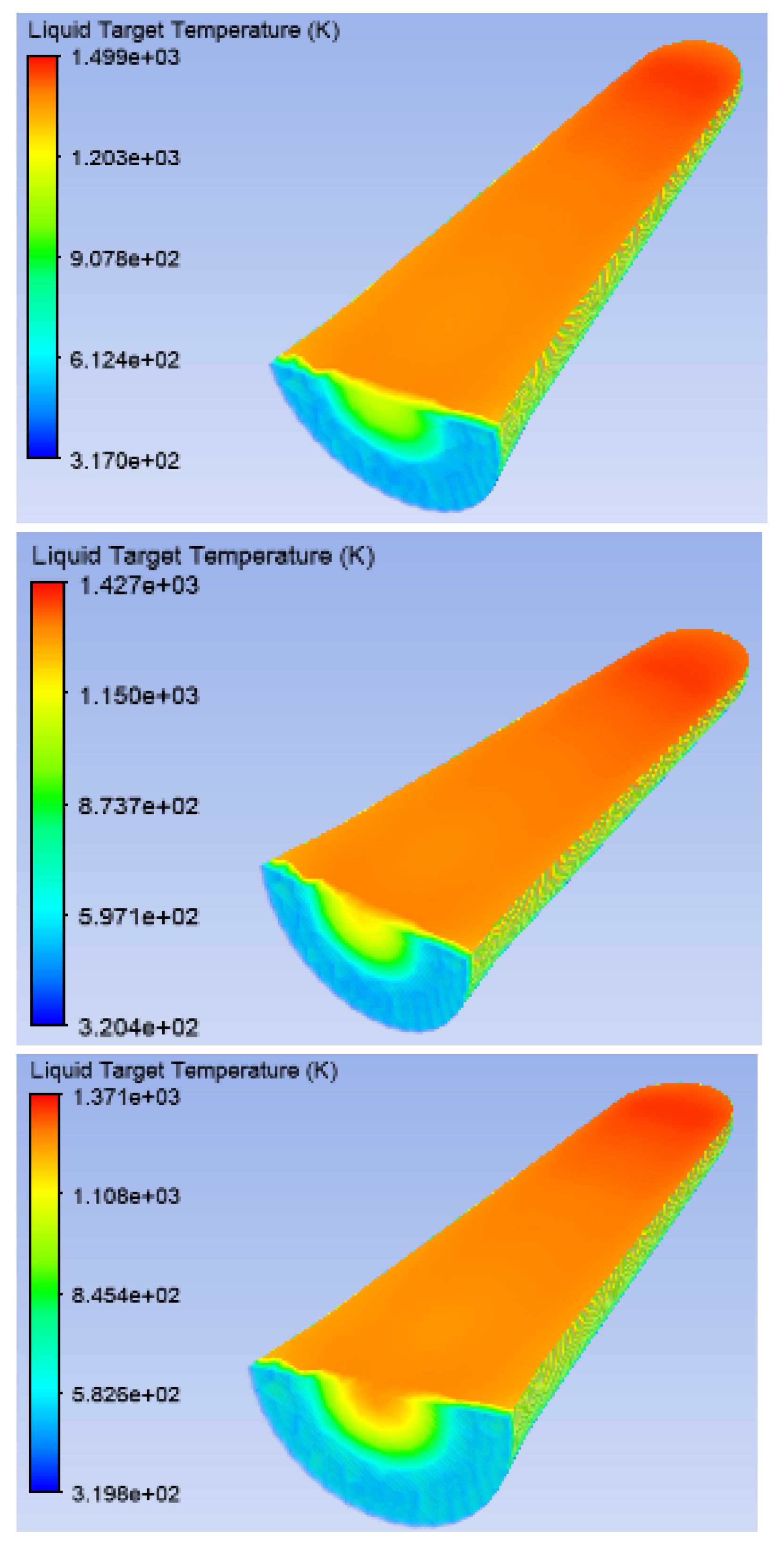
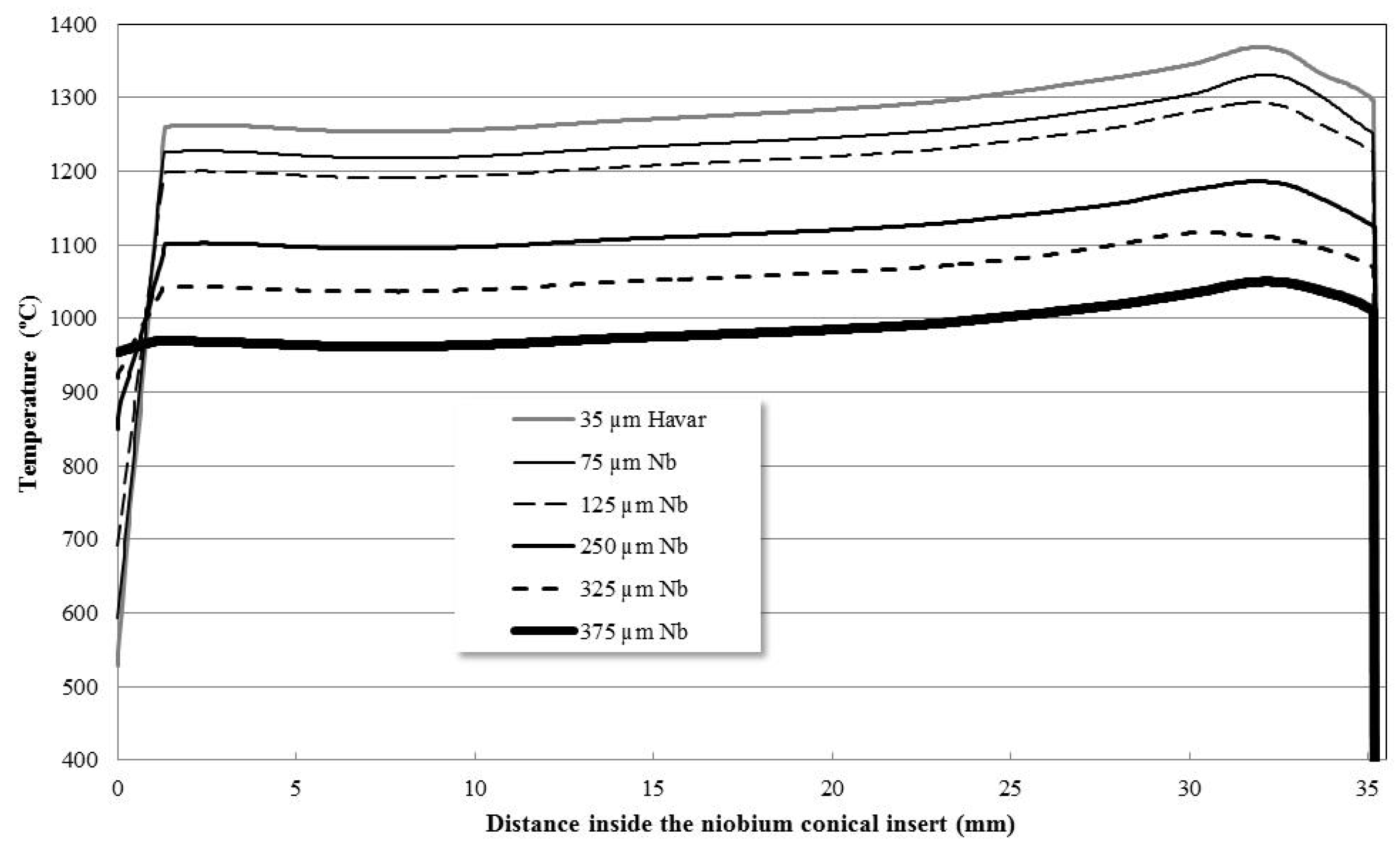
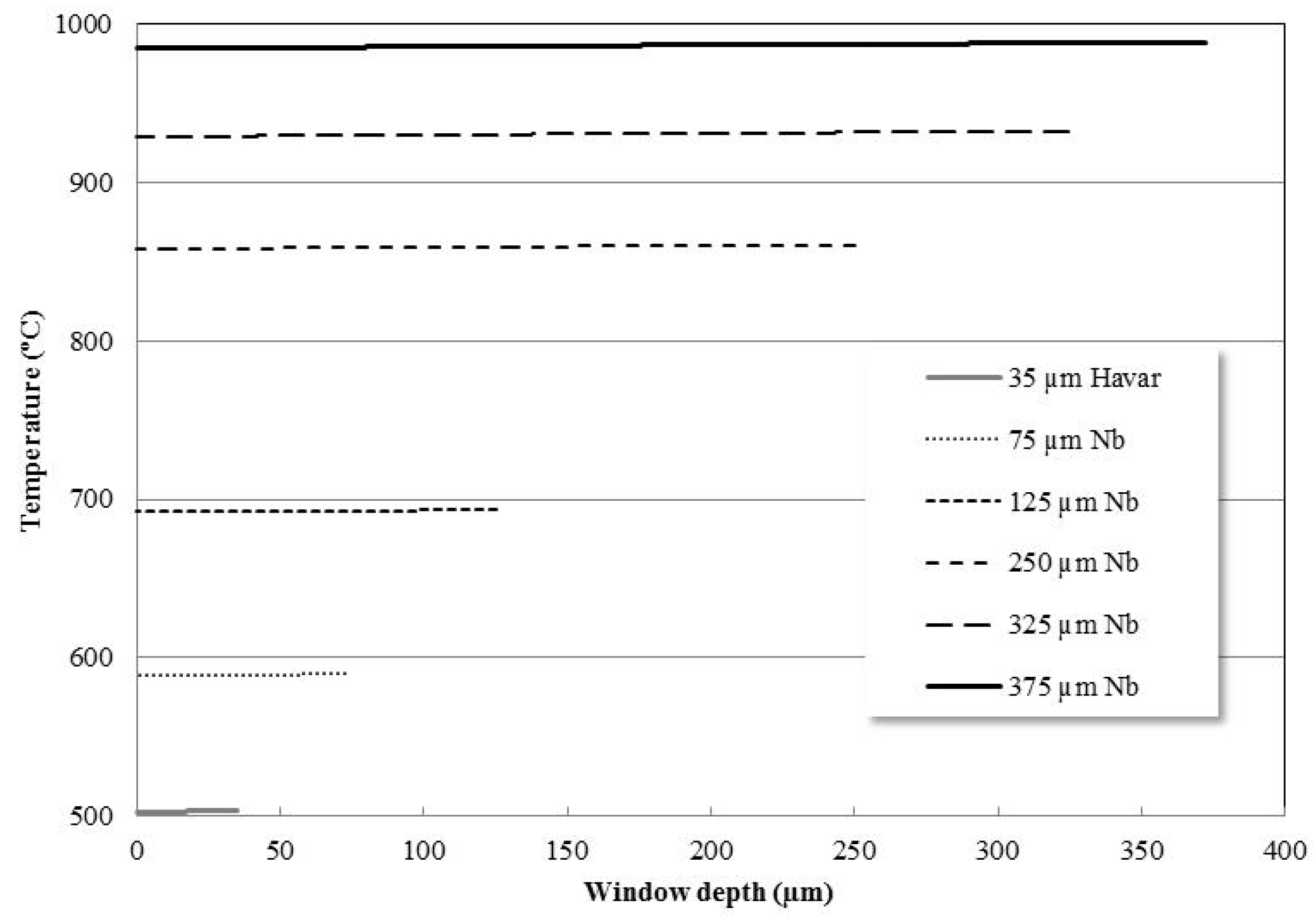
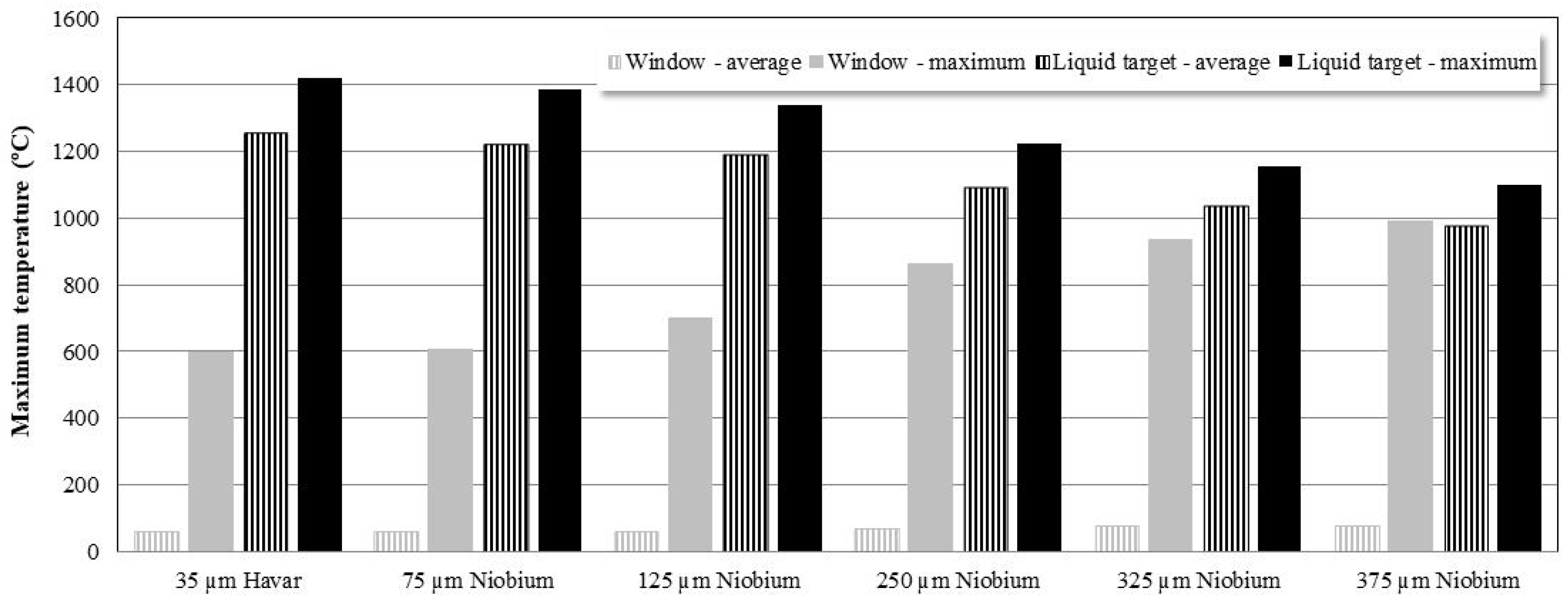
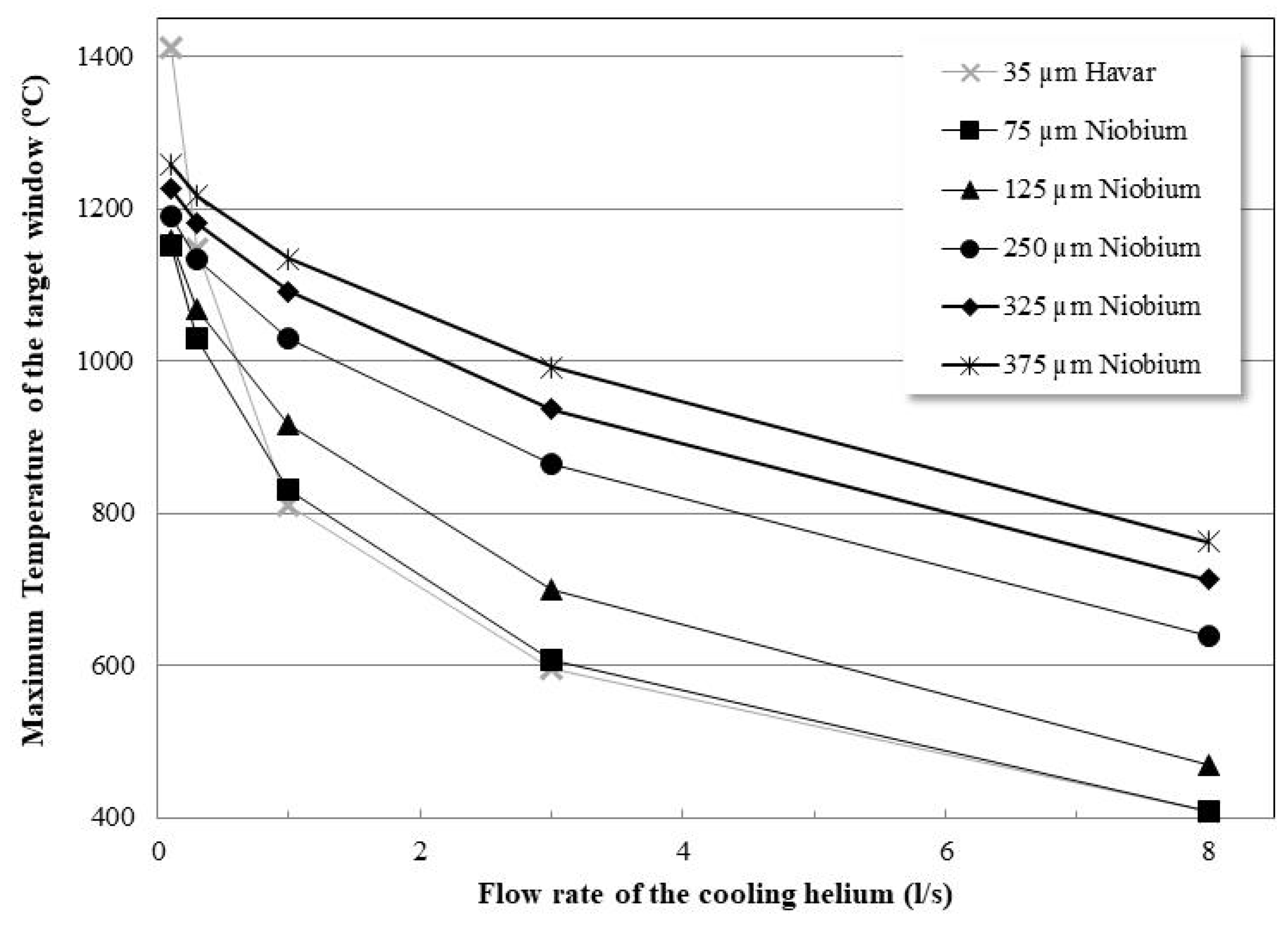
3.2. Thick Niobium Target Windows
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- McQuade, P.; McCarthy, D.W.; Welch, J. Metal Radionuclides for PET Imaging. In Positron Emission Tomography; Bailey, D., Townsend, D.W., Valk, P.E., Maisey, M.N., Eds.; Spinger: London, UK, 2005; pp. 237–250. [Google Scholar]
- Pagani, M.; Stone-Elander, S.; Larsson, S.A. Alternative positron emission tomography with non-conventional positron emitters: Effects of their physical properties on image quality and potential clinical applications. EJNM 1997, 24, 1301–1327. [Google Scholar] [CrossRef] [PubMed]
- do Carmo, S.J.C.; Scott, P.J.H.; Alves, F. Production of radiometals in liquid targets. EJNMMI 2020, 5, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Alves, V.H.P.; Alves, F.; Abrunhosa, A. Process for Producing Gallium-68 through the Irradiation of a Solution Target. EP15170854.2. U.S. Patent 20160358683A1, 8 December 2016. [Google Scholar]
- Alves, F.; Alves, V.H.; Neves, A.C.B.; do Carmo, S.J.C.; Nactergal, B.; Hellas, V.; Kral, E.; Gonçalves-Gameiro, C.; Abrunhosa, A.J.; Gonçalves-gameiro, C. Cyclotron production of Ga-68 for human use from liquid targets: From theory to practice. AIP Conf. Proc. 2017, 1845, 020001(1)–020001(9). [Google Scholar] [CrossRef]
- Oehlke, E.; Hoehr, C.; Hou, X.; Hanemaayer, V.; Zeisler, S.; Adam, M.J.; Ruth, T.J.; Celler, A.; Buckley, K.; Benard, F. Production of Y-86 and other radiometals for research purposes using a solution target system. Nucl. Med. Biol. 2015, 42, 842–849. [Google Scholar] [CrossRef] [PubMed]
- Alves, F.; Alves, V.H.; do Carmo, S.J.C.; Neves, A.C.B.; Silva, M.; Abrunhosa, A.J. Production of copper-64 and gallium-68 with a medical cyclotron using liquid targets. Mod. Phys. Lett. A 2017, 32, 1740013. [Google Scholar] [CrossRef]
- Cyclotron Produced Radionuclides: Operation and Maintenance of Gas and Liquid Targets; IAEA Radioisotopes and Radiopharmaceuticals Series nº4; International Atomic Energy Agency: Vienna, Austria, 2012; Available online: https://www.iaea.org/publications/8783/cyclotron-produced-radionuclides-operation-and-maintenance-of-gas-and-liquid-targets (accessed on 24 May 2021).
- Dury, T.V. Heat transfer to a heavy liquid metal in curved geometry: Code validation and CFD simulation for the Megapie lower target. Nucl. Instr. Meth. A 2006, A562, 859–862. [Google Scholar] [CrossRef]
- Čomor, J.J.; Stevanović, Z.; Rajčević, M.; Košutić, D. Modeling of thermal properties of a TeO2 target for radioiodine production. Nucl. Instr. Meth. A 2004, A521, 161–170. [Google Scholar] [CrossRef]
- Steyn, G.F.; Nortier, F.M.; Mills, S.J. Helium cooling of a double-foil window for external cyclotron beams. Nucl. Instr. Meth. A 1990, A292, 35–44. [Google Scholar] [CrossRef]
- Harutyunyan, G.S. Theoretical justification of the possibility of cryocooling of a solid target at irradiation with proton beam from cyclotron C18. J. Comtemporary Phys. 2016, 51, 102–107. [Google Scholar] [CrossRef]
- Grahn, A.; Kliem, S.; Rohde, U. Coupling of the 3D neutron kinetic core model DYN3D with the CFD software ANSYS-CFX. Ann. Nucl. Energy 2015, 84, 197–203. [Google Scholar] [CrossRef]
- Faugl, M.; Stokely, T.A.; Wieland, M.; Bolotnov, B.W.; Doster, I.A.; Peeples, J.; Poorman, J.L. Modeling a water target with proton range and target density coupling. In Proceedings of the 15th International Workshop on Targetry and Target Chemistry, Prague, Czech Republic, 18–21 August 2015. [Google Scholar]
- O’Brien, E.M.; Doster, J.M.; Nortier, F.M.; Olivas, E.R.; Stokely, M.H. Two-way multi-physics coupling for modeling high power RbCl isotope production targets. Nucl. Instr. Meth. A 2018, 433, 15–22. [Google Scholar] [CrossRef]
- do Carmo, S.J.C.; de Oliveira, P.M.; Alves, F. A Target-Temperature Monitoring System for Cyclotron Targets: Safety Device and Tool to Experimentally Validate Targetry Studies. Instruments 2018, 2, 9. [Google Scholar] [CrossRef] [Green Version]
- Frank, T.; Shi, J.-M.; Burns, A.D. Validation of Eulerian multiphase flow models for nuclear safety application. In Proceedings of the Third International Symposium on Two-Phase Modelling and Experimentation, Pisa, Italy, 22–25 September 2004; pp. 22–25. [Google Scholar]
- Langtry, R.B.; Menter, F.R. Transition modeling for general CFD applications in aeronautics. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. AIAA 2005-522. [Google Scholar]
- Frank, T.; Lifante, C.; Prasser, H.M.; Menter, F. Simulation of turbulent and thermal mixing in T-junctions using URANS and scale-resolving turbulence models in ANSYS CFX. Nucl. Eng. Des. 2010, 240, 2313–2328. [Google Scholar] [CrossRef] [Green Version]
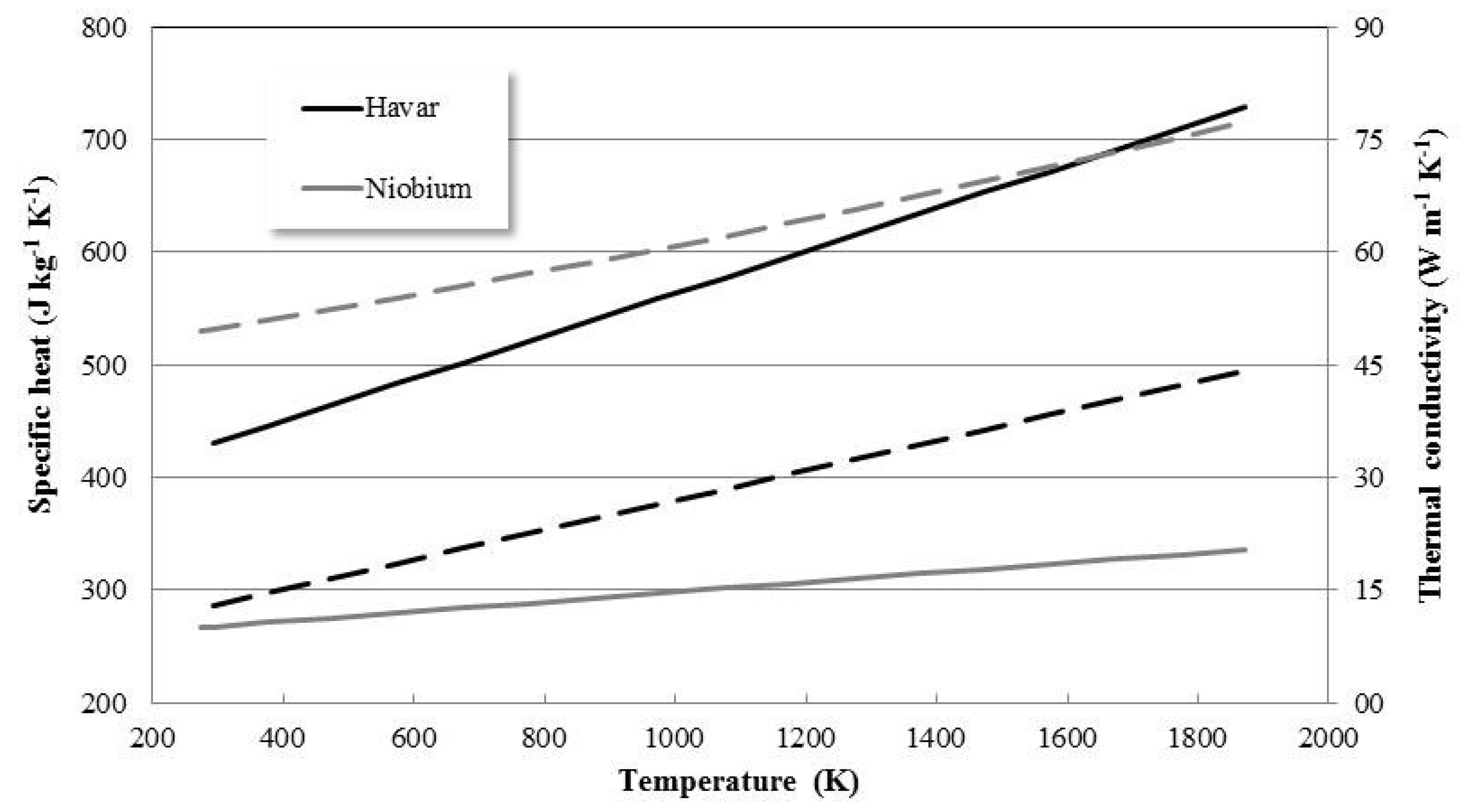
- Goodwin, F.; Guruswamy, S.; Kainer, K.U.; Kammer, C.; Knabl, W.; Koethe, A.; Leichtfried, G.; Schlamp, G.; Stickler, R.; Warlimont, H. Metals. In Springer Handbook of Condensed Matter and Materials Data; Martienssen, W., Warlimont, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 161–430. [Google Scholar]
- Davis, J.R. (Ed.) ASM Specialty Handbook: Nickel, Cobalt, and Their Alloys; ASM International: Materials Park, OH, USA, 2000. [Google Scholar]
- Shabalin, L. Ultra-High Temperature Materials I: Carbon (Graphene/Graphite) and Refractory Metals, 1st ed.; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- de Oliveira, P.M. Thermal Simulation Studies of a Cyclotron Liquid Target with Thick Niobium Window. Master’s Thesis, Physics Department, University of Coimbra, Coimbra, Portugal, 2019. [Google Scholar]





| Number of Elements | 290,293 |
| Number of Nodes | 589,535 |
| Average Skewness | 0.287 ± 0.213 |
| Average Orthogonal Quality | 0.705 ± 0.216 |
| Average Aspect Ratio | 9155 ± 16 |
| Beam Power | Target Window | Cooling Water | Cooling Helium | Initial Temperature of the Solid Elements | |||
|---|---|---|---|---|---|---|---|
| Temperature | Flux | Temperature | Flux | ||||
| (°C) | (L/min) | (°C) | (L/s) | Window Spacer | Insert Diffuser Support | ||
| 1000 W (55.5 µA) | 35 µm thick Havar | 23 | 3 | 23 | 3 | 25 °C with 250 W 27 °C with 500 W 29 °C with 750 W 31 °C with 1000 W (values taken from [16]) | 23 °C |
| Target Window | Energy Loss in the Target Window (MeV) | Energy Loss in the Liquid Target (MeV) |
|---|---|---|
| 35 µm thick havar | 0.51 | 17.49 |
| 75 µm thick niobium | 1.04 | 16.96 |
| 125 µm thick niobium | 1.77 | 16.23 |
| 250 µm thick niobium | 3.70 | 14.30 |
| 325 µm thick niobium | 4.95 | 13.05 |
| 375 µm thick niobium | 5.85 | 12.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
do Carmo, S.J.C.; de Oliveira, P.M.; Alves, F. Thermal Simulation Studies for the Characterization of a Cyclotron Liquid Target with Thick Niobium Target Windows. Appl. Sci. 2021, 11, 10922. https://doi.org/10.3390/app112210922
do Carmo SJC, de Oliveira PM, Alves F. Thermal Simulation Studies for the Characterization of a Cyclotron Liquid Target with Thick Niobium Target Windows. Applied Sciences. 2021; 11(22):10922. https://doi.org/10.3390/app112210922
Chicago/Turabian Styledo Carmo, Sergio J. C., Pedro M. de Oliveira, and Francisco Alves. 2021. "Thermal Simulation Studies for the Characterization of a Cyclotron Liquid Target with Thick Niobium Target Windows" Applied Sciences 11, no. 22: 10922. https://doi.org/10.3390/app112210922
APA Styledo Carmo, S. J. C., de Oliveira, P. M., & Alves, F. (2021). Thermal Simulation Studies for the Characterization of a Cyclotron Liquid Target with Thick Niobium Target Windows. Applied Sciences, 11(22), 10922. https://doi.org/10.3390/app112210922






