Validity and Absolute Reliability of Axial Vertebral Rotation Measurements in Thoracic and Lumbar Vertebrae
Abstract
:1. Introduction
2. Materials and Methods
2.1. Software
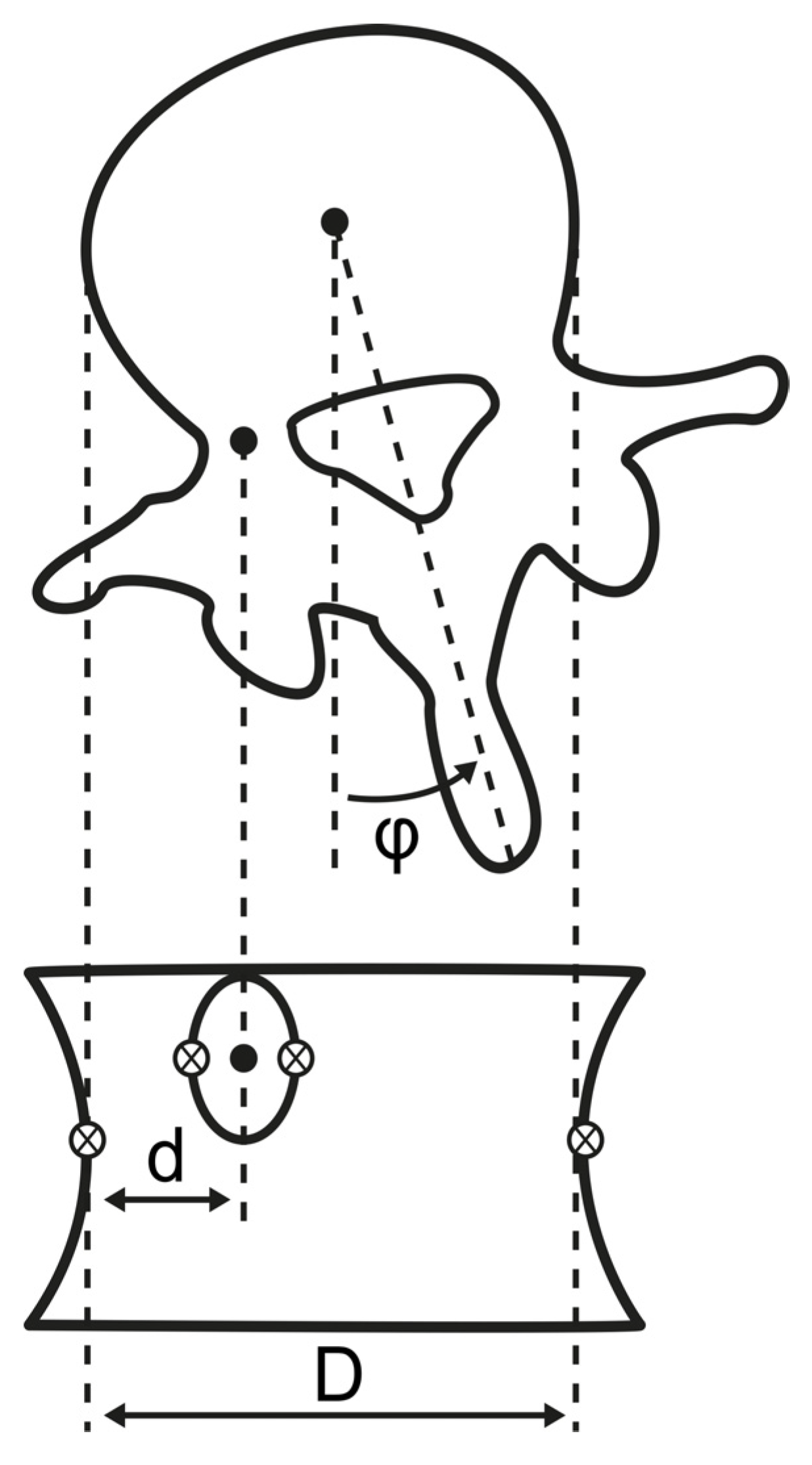
2.2. Study Design and Measurement Protocol
2.3. Statistics
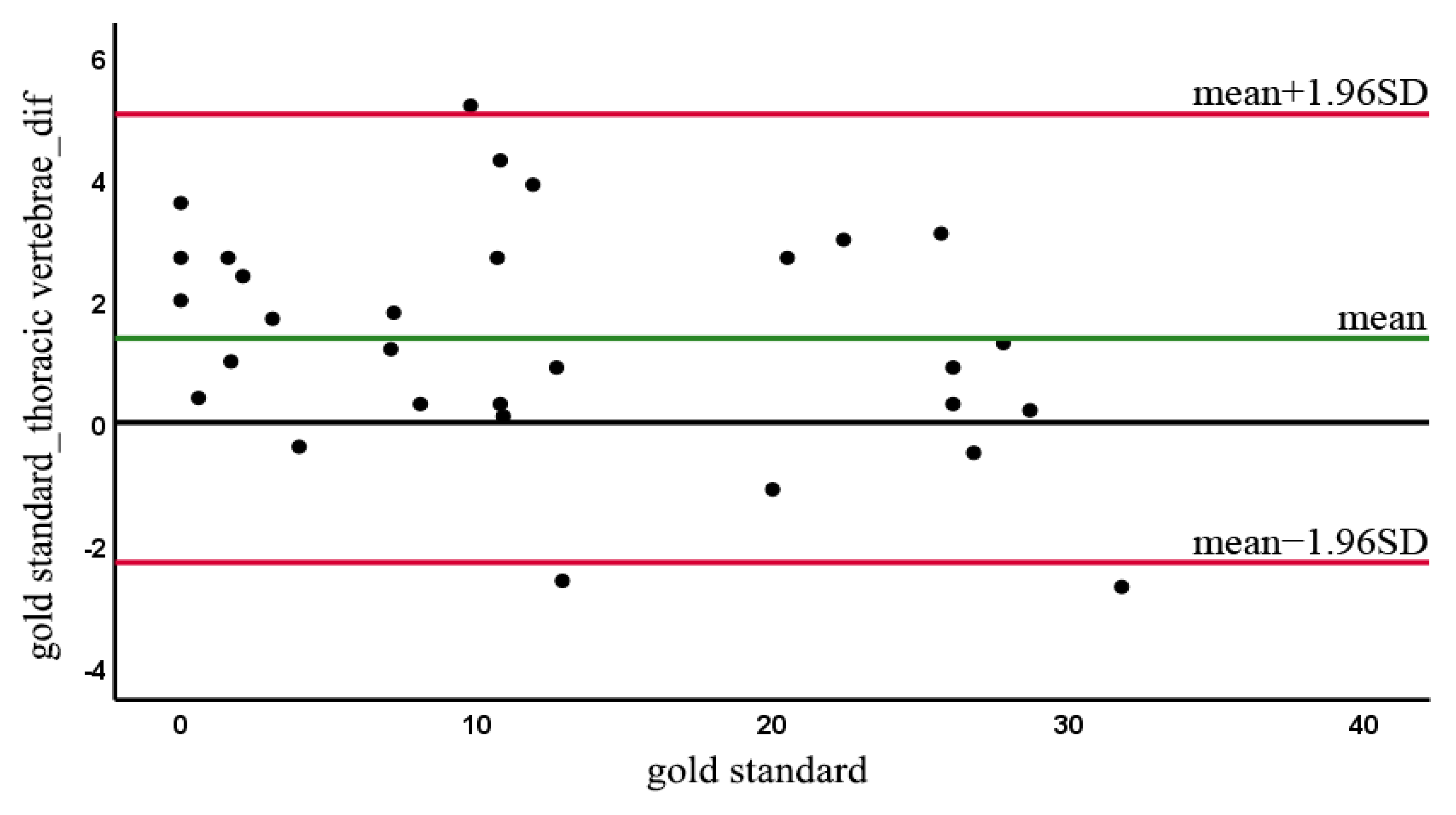
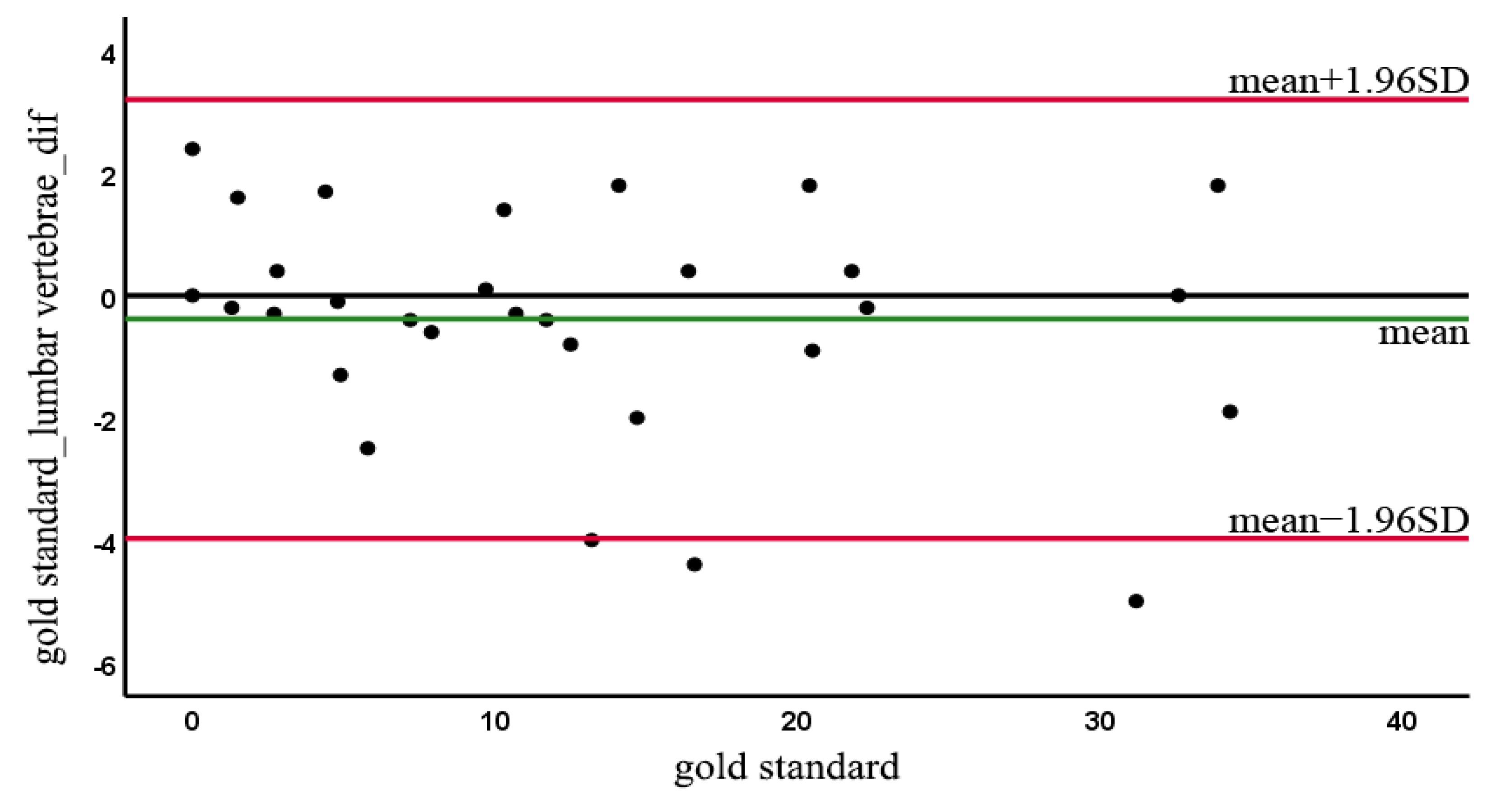
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Ma, Q.; Lin, H.; Wang, L.; Zhao, L.; Chen, M.; Wang, S.; Rao, Z.; Luo, Y. Correlation between spinal coronal balance and static baropodometry in children with adolescent idiopathic scoliosis. Gait Posture 2020, 75, 93–97. [Google Scholar] [CrossRef]
- Hefti, F. Pathogenesis and biomechanics of adolescent idiopathic scoliosis (AIS). J. Child. Orthop. 2013, 7, 17–24. [Google Scholar] [CrossRef] [Green Version]
- Mangone, M.; Raimondi, P.; Paoloni, M.; Pellanera, S.; Di Michele, A.; Di Renzo, S.; Vanadia, M.; Dimaggio, M.; Murgia, M.; Santilli, V. Vertebral rotation in adolescent idiopathic scoliosis calculated by radiograph and back surface analysis-based methods: Correlation between the Raimondi method and rasterstereography. Eur. Spine J. 2013, 22, 367–371. [Google Scholar] [CrossRef]
- Mohanty, S.P.; Pai Kanhangad, M.; Gullia, A. Curve severity and apical vertebral rotation and their association with curve flexibility in adolescent idiopathic scoliosis. Musculoskelet. Surg. 2020, 105, 303–308. [Google Scholar] [CrossRef] [Green Version]
- Stokes, I.A. Three-dimensional terminology of spinal deformity. A report presented to the Scoliosis Research Society by the Scoliosis Research Society Working Group on 3-D terminology of spinal deformity. Spine 1994, 19, 236–248. [Google Scholar] [CrossRef]
- Eijgenraam, S.M.; Boselie, T.F.M.; Sieben, J.M.; Bastiaenen, C.H.G.; Willems, P.C.; Arts, J.J.; Lataster, A. Development and assessment of a digital X-ray software tool to determine vertebral rotation in adolescent idiopathic scoliosis. Spine J. 2017, 17, 260–265. [Google Scholar] [CrossRef]
- Nault, M.-L.; Mac-Thiong, J.-M.; Roy-Beaudry, M.; Turgeon, I.; DeGuise, J.; Labelle, H.; Parent, S. Three-Dimensional Spinal Morphology Can Differentiate between Progressive and Nonprogressive Patients with Adolescent Idiopathic Scoliosis at the Initial Presentation. Spine 2014, 39, E601–E606. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carlson, B.B.; Burton, D.C.; Asher, M.A. Comparison of trunk and spine deformity in adolescent idiopathic scoliosis. Scoliosis 2013, 8, 2. [Google Scholar] [CrossRef] [Green Version]
- Kuklo, T.R.; Potter, B.K.; Schroeder, T.M.; O’Brien, M.F. Comparison of Manual and Digital Measurements in Adolescent Idiopathic Scoliosis. Spine 2006, 31, 1240–1246. [Google Scholar] [CrossRef] [PubMed]
- Tamura, Y.; Sugano, N.; Sasama, T.; Sato, Y.; Tamura, S.; Yonenobu, K.; Yoshikawa, H.; Ochi, T. Surface-based registration accuracy of CT-based image-guided spine surgery. Eur. Spine J. 2005, 14, 291–297. [Google Scholar] [CrossRef] [Green Version]
- Qiao, J.; Zhu, F.; Xu, L.; Zhu, Z.; Qian, B.; Liu, Z.; Qiu, Y. Comparison of the aorta impingement risks between thoracolumbar/lumbar curves with different convexities in adolescent idiopathic scoliosis: A computed tomography study. Eur. Spine J. 2012, 21, 2043–2049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vrtovec, T.; Pernuš, F.; Likar, B. A review of methods for quantitative evaluation of axial vertebral rotation. Eur. Spine J. 2009, 18, 1079–1090. [Google Scholar] [CrossRef] [Green Version]
- Petit, Y.; Aubin, C.-É.; Labelle, H. Spinal shape changes resulting from scoliotic spine surgical instrumentation expressed as intervertebral rotations and centers of rotation. J. Biomech. 2004, 37, 173–180. [Google Scholar] [CrossRef]
- Kadoury, S.; Cheriet, F.; Beauséjour, M.; Stokes, I.A.; Parent, S.; Labelle, H. A three-dimensional retrospective analysis of the evolution of spinal instrumentation for the correction of adolescent idiopathic scoliosis. Eur. Spine J. 2009, 18, 23–37. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weiss, H.-R. Measurement of vertebral rotation: Perdriolle versus Raimondi. Eur. Spine J. 1995, 4, 34–38. [Google Scholar] [CrossRef]
- Defino, H.L.A.; de Araújo, P.H.M. Estudo comparativo da medida da rotação vertebral pelos métodos de Nash & Moe e método de Raimondi. Acta Ortopédica Bras. 2004, 12, 167–173. [Google Scholar] [CrossRef]
- Raimondi, P.; Dupre, J. Evaluation chiffrée de la rotation vertébrale par la méthode de Paolo Raimondi. Kinésithér. Sci. 1996, 358, 2–3. [Google Scholar]
- Raimondi, P. La misurazione della rotazione vertebrale sul piano orizzontale con il Metodo Raimondi. Sci. Mot. 2002, 2, 11–16. [Google Scholar]
- Raimondi, P.; Costanzo, G.; Santaroni, A.P. Evaluation Chiffre de la rotation vertebrale par la mèthode de Paolo Raimondi. Kinésithér. Sci. 1996, 358, 19–22. [Google Scholar]
- Raimondi, P.; Costanzo, G.; Santaroni, A.P.; Bizzarri, F. Ipotesi patogenetica sul ruolo di percezione e postura nello sviluppo delle scoliosi. Résonances Eur. Rachis 1998, 20, 883–889. [Google Scholar]
- Lam, G.C.; Hill, D.L.; Le, L.H.; Raso, J.V.; Lou, E.H. Vertebral rotation measurement: A summary and comparison of common radiographic and CT methods. Scoliosis 2008, 3, 16. [Google Scholar] [CrossRef] [Green Version]
- Hattori, T.; Sakaura, H.; Iwasaki, M.; Nagamoto, Y.; Yoshikawa, H.; Sugamoto, K. In Vivo three-dimensional segmental analysis of adolescent idiopathic scoliosis. Eur. Spine J. 2011, 20, 1745–1750. [Google Scholar] [CrossRef] [Green Version]
- Fletcher, N.D.; Bruce, R.W. Early onset scoliosis: Current concepts and controversies. Curr. Rev. Musculoskelet. Med. 2012, 5, 102–110. [Google Scholar] [CrossRef] [Green Version]
- Yazici, M.; Acaroglu, E.R.; Alanay, A.; Deviren, V.; Cila, A.; Surat, A. Measurement of vertebral rotation in standing versus supine position in adolescent idiopathic scoliosis. J. Pediatr. Orthop. 2001, 21, 252–256. [Google Scholar] [CrossRef]
- Por Imágenes, C.D.; Gentile, L.F.; de Ortopedia, S.A.; Infantil, T. Consenso de escoliosis idiopática del adolescente. Arch. Argent. Pediatr. 2016, 114, 585–594. [Google Scholar] [CrossRef]
- Cerny, P.; Marik, I.; Pallova, I. The radiographic method for evaluation of axial vertebral rotation—Presentation of the new method. Scoliosis 2014, 9, 11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bertolini, M.; Nitrosi, A.; Rivetti, S.; Lanconelli, N.; Pattacini, P.; Ginocchi, V.; Iori, M. A comparison of digital radiography systems in terms of effective detective quantum efficiency. Med. Phys. 2012, 39, 2617–2627. [Google Scholar] [CrossRef]
- Hurtado-Avilés, J.; León-Muñoz, V.J.; Sanz-Mengibar, J.M.; Santonja-Renedo, F.; Andújar-Ortuño, P.; Collazo-Diéguez, M.; Ferrer-López, V.; Roca-González, J.; Kurochka, K.S.; Cabañero-Castillo, M.; et al. Validity and reliability of a computer-assisted system method to measure axial vertebral rotation. Quant. Imaging Med. Surg. 2021, in press. [Google Scholar]
- Safari, A.; Parsaei, H.; Zamani, A.; Pourabbas, B. A Semi-Automatic Algorithm for Estimating Cobb Angle. J. Biomed. Phys. Eng. 2019, 9, 317. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhang, K.; Fan, H.; Huang, Z.; Xiang, Y.; Yang, J.; He, L.; Zhang, L.; Yang, Y.; Li, R.; et al. Development and validation of deep learning algorithms for scoliosis screening using back images. Commun. Biol. 2019, 2, 390. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, Q.; Chen, T.; Wang, H.; Zhu, X.; Fang, Z.; Lu, Y. Evaluation of a computer-aided method for measuring the Cobb angle on chest X-rays. Eur. Spine J. 2019, 28, 3035–3043. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Xu, Q.; Leung, S.; Chung, J.; Chen, B.; Li, S. Accurate automated Cobb angles estimation using multi-view extrapolation net. Med. Image Anal. 2019, 58, 101542. [Google Scholar] [CrossRef] [PubMed]
- Forsberg, D.; Lundström, C.; Andersson, M.; Vavruch, L.; Tropp, H.; Knutsson, H. Fully automatic measurements of axial vertebral rotation for assessment of spinal deformity in idiopathic scoliosis. Phys. Med. Biol. 2013, 58, 1775–1787. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vrtovec, T.; Vengust, R.; Likar, B.; Pernuš, F. Analysis of Four Manual and a Computerized Method for Measuring Axial Vertebral Rotation in Computed Tomography Images. Spine 2010, 35, E535–E541. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, G.; Nevill, A.M. Selected issues in the design and analysis of sport performance research. J. Sports Sci. 2001, 19, 811–827. [Google Scholar] [CrossRef] [Green Version]
- Hopkins, W.G. Measures of Reliability in Sports Medicine and Science. Sports Med. 2000, 30, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Hurtado-Aviles, J.; Roca-González, J.; Kurochka, K.S.; Sanz-Mengibar, J.M.; Santonja-Medina, F. Developing of a Mathematical Model to Perform Measurements of Axial Vertebral Rotation on Computer-Aided and Automated Diagnosis Systems, Using Raimondi’s Method. Radiol. Res. Pract. 2021, 2021, 5523775. [Google Scholar] [CrossRef]
- Shrout, P.E.; Fleiss, J.L. Intraclass correlations: Uses in assessing rater reliability. Psychol. Bull. 1979, 86, 420–428. [Google Scholar] [CrossRef] [PubMed]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Vertebra | Type | AVR | Vertebra | Type | AVR | Vertebra | Type | AVR |
|---|---|---|---|---|---|---|---|---|
| V1 | T4 | 0 | V26 | T6 | 31.8 | V51 | L2 | 16.4 |
| V2 | T11 | 12.4 | V27 | L1 | 14.1 | V52 | T7 | 15.8 |
| V3 | T4 | 8.1 | V28 | L1 | 7.9 | V53 | L1 | 34.3 |
| V4 | L1 | 5.8 | V29 | L1 | 22.3 | V54 | T7 | 0 |
| V5 | T12 | 12.1 | V30 | T8 | 10.8 | V55 | T9 | 25.7 |
| V6 | T8 | 28.7 | V31 | L1 | 13.2 | V56 | L2 | 4.9 |
| V7 | L2 | 12.5 | V32 | L2 | 0 | V57 | T6 | 20.5 |
| V8 | T8 | 0.6 | V33 | L2 | 21.8 | V58 | L2 | 20.5 |
| V9 | L2 | 7.2 | V34 | T7 | 10.9 | V59 | T10 | 26.8 |
| V10 | L1 | 4.4 | V35 | L2 | 10.3 | V60 | T3 | 0 |
| V11 | L2 | 9.7 | V36 | T10 | 22.4 | V61 | T12 | 7.1 |
| V12 | L1 | 1.3 | V37 | L2 | 31.2 | V62 | T7 | 12.9 |
| V13 | T8 | 2.1 | V38 | L1 | 32.6 | V63 | T8 | 1.7 |
| V14 | L2 | 1.5 | V39 | T7 | 3.1 | V64 | L2 | 2.7 |
| V15 | T9 | 27.8 | V40 | T10 | 27.8 | V65 | T10 | 12.7 |
| V16 | T8 | 7.2 | V41 | T4 | 1.6 | V66 | T9 | 1.6 |
| V17 | L2 | 20.4 | V42 | T9 | 29.6 | V67 | L2 | 11.7 |
| V18 | L3 | 4.8 | V43 | T3 | 2.4 | V68 | T8 | 26.1 |
| V19 | T7 | 4 | V44 | T10 | 21.2 | V69 | L1 | 10.7 |
| V20 | T7 | 11.9 | V45 | T4 | 10.8 | V70 | L3 | 2.8 |
| V21 | T3 | 10.8 | V46 | L2 | 14.7 | V71 | T8 | 26.1 |
| V22 | T9 | 12.6 | V47 | T9 | 0 | V72 | L2 | 16.6 |
| V23 | T4 | 0 | V48 | T8 | 20 | V73 | L1 | 33.9 |
| V24 | T9 | 18.5 | V49 | L1 | 0 | V74 | T7 | 10.7 |
| V25 | T4 | 7.8 | V50 | T9 | 9.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hurtado-Avilés, J.; León-Muñoz, V.J.; Andújar-Ortuño, P.; Santonja-Renedo, F.; Collazo-Diéguez, M.; Cabañero-Castillo, M.; Ponce-Garrido, A.B.; González-Ballester, M.; Sánchez-Martínez, F.J.; Fiorita, P.G.; et al. Validity and Absolute Reliability of Axial Vertebral Rotation Measurements in Thoracic and Lumbar Vertebrae. Appl. Sci. 2021, 11, 11084. https://doi.org/10.3390/app112311084
Hurtado-Avilés J, León-Muñoz VJ, Andújar-Ortuño P, Santonja-Renedo F, Collazo-Diéguez M, Cabañero-Castillo M, Ponce-Garrido AB, González-Ballester M, Sánchez-Martínez FJ, Fiorita PG, et al. Validity and Absolute Reliability of Axial Vertebral Rotation Measurements in Thoracic and Lumbar Vertebrae. Applied Sciences. 2021; 11(23):11084. https://doi.org/10.3390/app112311084
Chicago/Turabian StyleHurtado-Avilés, José, Vicente J. León-Muñoz, Pilar Andújar-Ortuño, Fernando Santonja-Renedo, Mónica Collazo-Diéguez, Mercedes Cabañero-Castillo, Ana Belén Ponce-Garrido, Miriam González-Ballester, Francisco Javier Sánchez-Martínez, Pietro G. Fiorita, and et al. 2021. "Validity and Absolute Reliability of Axial Vertebral Rotation Measurements in Thoracic and Lumbar Vertebrae" Applied Sciences 11, no. 23: 11084. https://doi.org/10.3390/app112311084
APA StyleHurtado-Avilés, J., León-Muñoz, V. J., Andújar-Ortuño, P., Santonja-Renedo, F., Collazo-Diéguez, M., Cabañero-Castillo, M., Ponce-Garrido, A. B., González-Ballester, M., Sánchez-Martínez, F. J., Fiorita, P. G., Ruiz-Cambra, N. A., Campuzano-Melgarejo, A., Fuentes-Santos, V. E., & Santonja-Medina, F. (2021). Validity and Absolute Reliability of Axial Vertebral Rotation Measurements in Thoracic and Lumbar Vertebrae. Applied Sciences, 11(23), 11084. https://doi.org/10.3390/app112311084







