Algorithmic Method for the Design of Sequential Circuits with the Use of Logic Elements
Abstract
:1. Introduction
- (a)
- each time the state of the inputs changes, only one input signal changes at a time;
- (b)
- another input signal may change only after the time necessary for the internal state of the system to settle.
- (a)
- decomposition of the system into smaller components that are easier to design,
- (b)
- the use of a computer to assist the designer in solving large numbers of tasks variables.
- (c)
- different from the previously described principles of system construction, and, therefore, also requiring different synthesis methods.
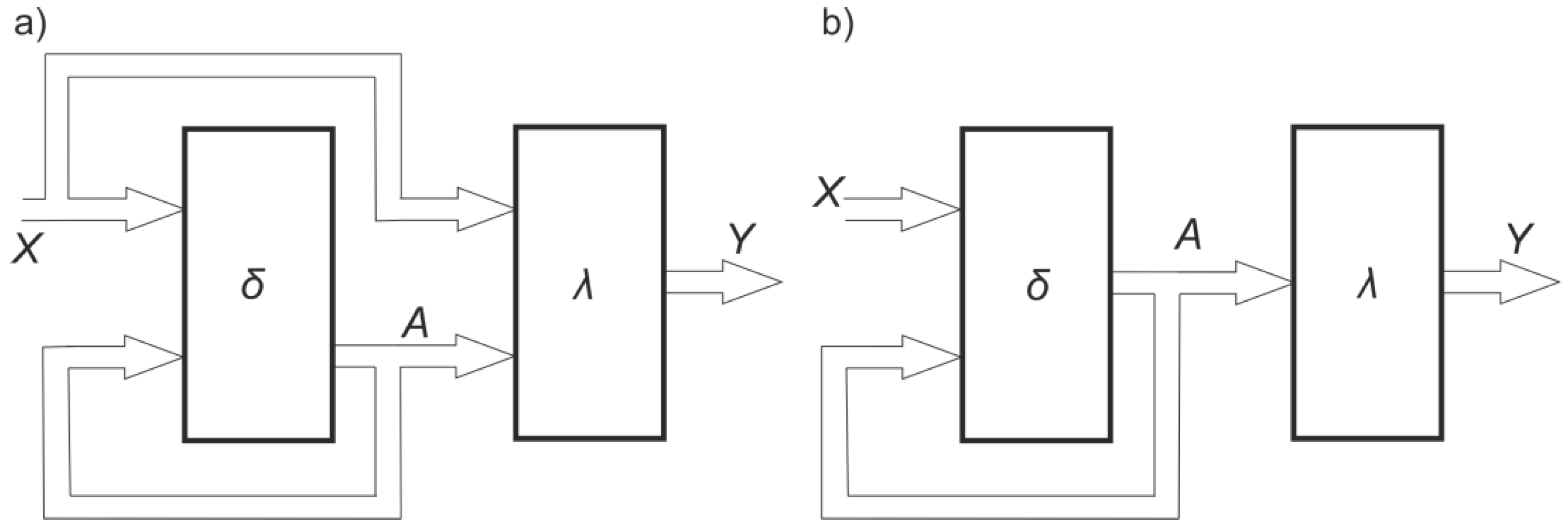
2. Algorithmic Method of Sequential Circuit Design
- the driver element (actuator) used in the project is marked with a capital letter of the alphabet starting from A–Z;
- the sign “+” after the symbol of a given driver element (actuator) means activation (full extension of the piston);
- the sign “−” next to the symbol of a given driver element (actuator) means deactivation of the driver element (extension of the piston);
- the sign “±” next to the symbol of a given element means a short-term actuation of the element;
- each cylinder is equipped with sensors detecting the position of the cylinder piston;
- the position of the driver element (actuator) in the ON state is indicated by the symbol of the given element with the index 0—from logical state 0 (e.g., for element A symbol a0);
- the position of the driver element (actuator) in the OFF state is indicated by the symbol of the given element with the index 1—from logical state 1 (e.g., for element B symbol b1).
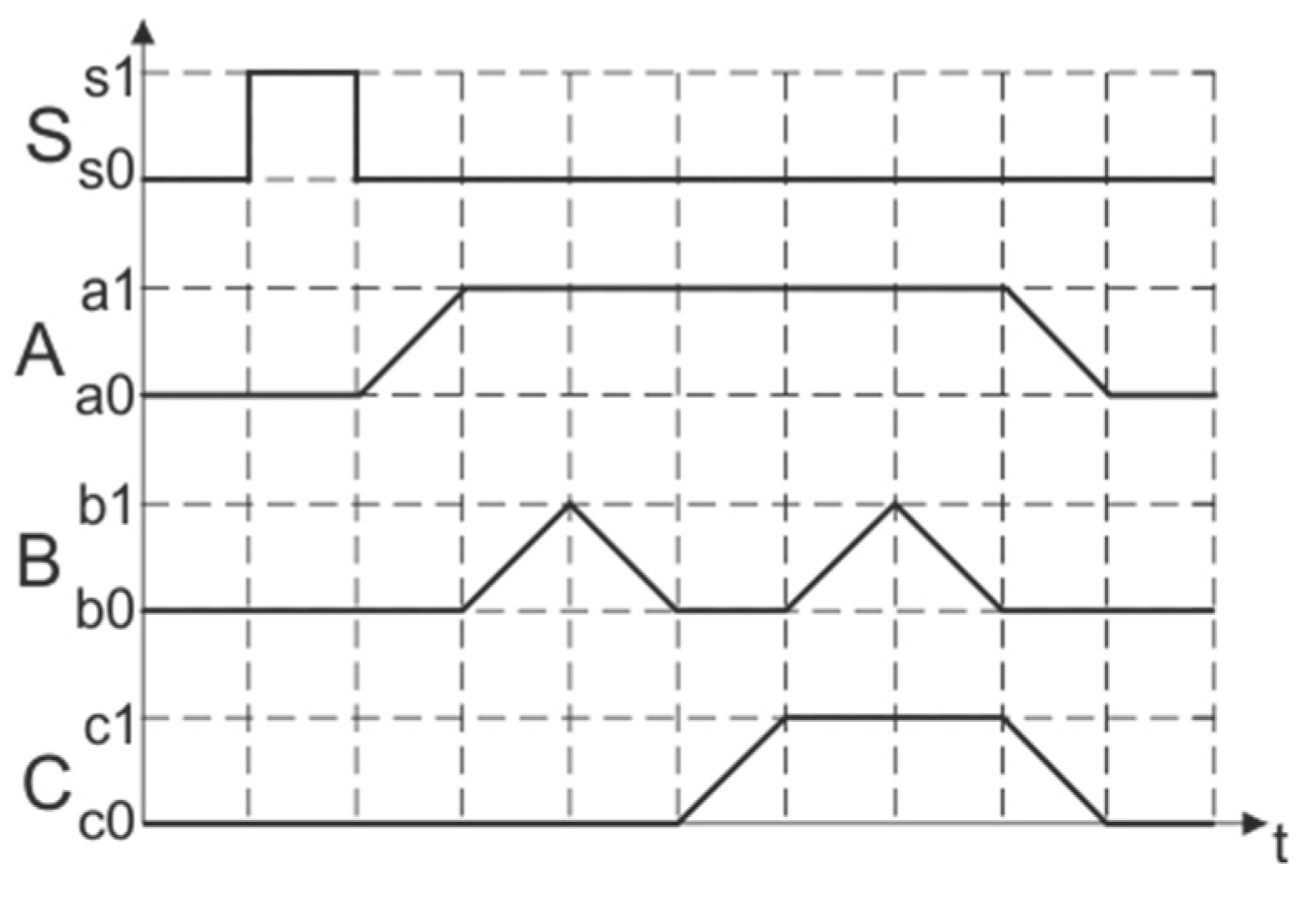
- in the initial state all actuators A, B and C are retracted,
- after pressing the S button, the actuator A begins to extend,
- after the actuator A is extended, the actuator B begins to extend,
- after the actuator B is extended, it is retracted again,
- after the actuator B is retracted, the actuator C begins to extend,
- after the actuator C is extended, the actuator B begins to extend,
- after the actuator B is extended, it is retracted again,
- after the actuator B is retracted, the actuators A and C start to retract simultaneously.
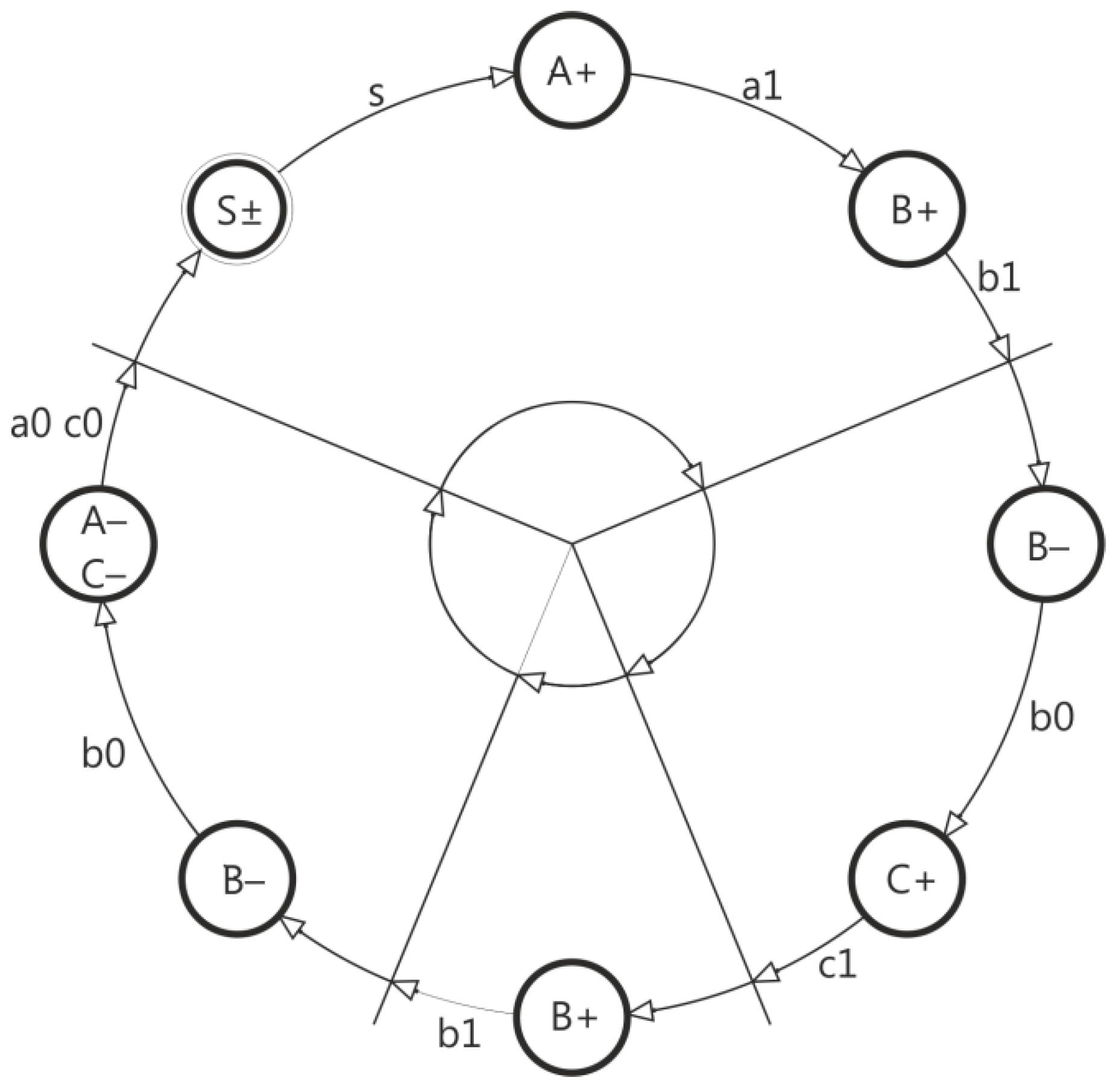
- 1.
- The graph is drawn based on the operating conditions of the system—the connection formula.
- 2.
- The graph is divided into groups in such a way that in each group the state of individual elements occurs only once.
- 3.
- Each separate group is numbered from k1 to kn, starting with the group with the start signal “S”.
- 4.
- The division lines of groups have been marked from x1 to xn, where x1 corresponds to the end of the group k1, while xn to the end of group kn.
- 5.
- Arrows are drawn for each dividing line: from the last circle towards the dividing line.
- 6.
- The arch between the dividing line and the next state is designated as the state in which the arch is located.
- 7.
- The arch between the state and the dividing line directed to the dividing line is designated as signals coming out of that state.
- 8.
- Each dividing line is described by an equation in which we multiply the signals from the arc directed to the dividing line with the value of the state before the dividing line.
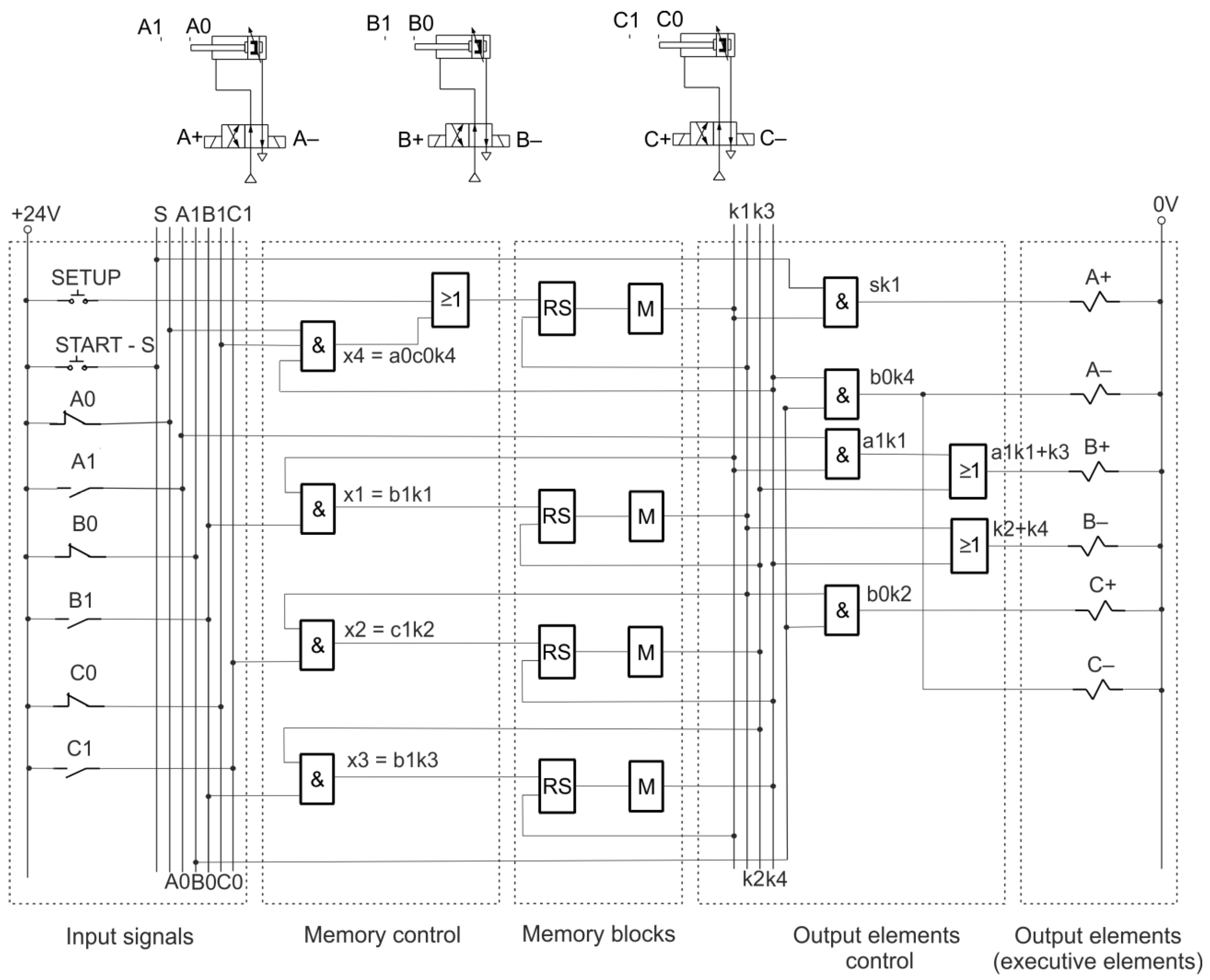
3. Designing of Sequential Circuits Using Logic Elements
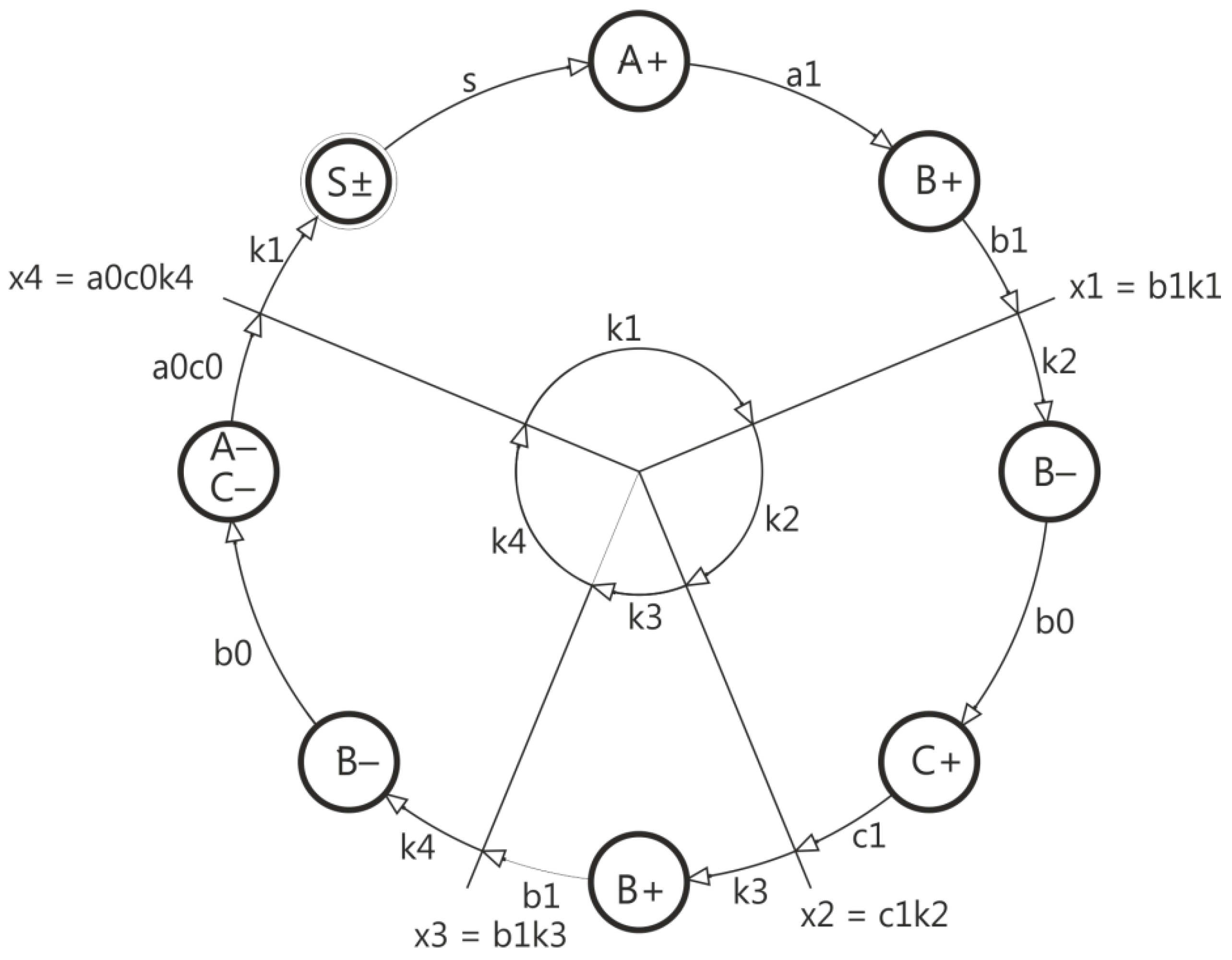
- A+ input requires the product function s k1 to be implemented (s signal from start button, k1 memory status),
- B+ input requires the sum function execution of two components (a1 k1 + k3) because the actuation state of the B actuator occurs twice, where the product a1 k1 is the first state appearing under the influence of the position of the actuator A and the memory state k1, while the second state of activation of the B actuator appears under the influence of the state of memory k3,
- input B− requires the implementation of the function of the sum of two components (k2 + k4) because the B actuator OFF state occurs twice: i.e., under the influence of memory state k2 and memory state k4,
- C+ input requires the product function b0 k2 to be implemented (product of the state of the actuator B position and memory k2),
- inputs C− and A− require the implementation of the product function b0 k4 (product of the state of the actuator B position and the state of memory k4).
- the x1 signal generates the k2 state (through the memory input setting the k2 state), which simultaneously resets the k1 state (through the memory input resetting the k1 state),
- the x2 signal generates the k3 state (through the memory input setting the k3 state), which simultaneously resets the k2 state (through the memory input to reset the k2 state),
- the x3 signal generates the k4 state (through the memory input setting the k4 state), which simultaneously resets the k3 state (through the memory input to reset the k3 state),
- the x4 signal generates the k1 state (through the memory input setting the k1 state), which simultaneously resets the k4 state (through the memory input to reset the k4 state).
- 1.
- Executive elements appearing in the graph are drawn in the general case of A–N, i.e., double-acting actuators cooperating with bistable solenoid valves;
- 2.
- The input signals bus, power signals bus and the memory bus are drawn;
- 3.
- The memory bus reflects the division of the graph from k1–kn;
- 4.
- To the input signals bus A1–N1, A0–N0 measuring sensors of executive elements A–N are connected.
- 5.
- System memory is created consisting of n RS flip-flops and M buffers, generating the memory state k1–kn;
- 6.
- The memory is controlled by signals generated as a result of the radial division of the graph x1–xn, respectively, whereby the signal x1 sets the memory to the state k2, the signal x2 to the state k3, etc., and the signal xn sets the memory to the state k1. The state of k2 clears the state of k1, the state of k3 clears the state of k2, etc., the state of k1 clears the state of kn, through appropriate connections of the setting and resetting inputs of the flip-flops;
- 7.
- The setting signals x1–xn the state of memories k1–kn are produced as the products of the state of the last element present in a given state of memory and the state of that memory; (e.g., x1 = b1k1);
- 8.
- Switching on, switching off the output elements through the solenoid valve coils from A +, A− to N +, N− takes place by creating products of the state signals of the element preceding switching on, switching off the next element and the memory state in which it occurs according to the system graph;
- 9.
- The first element in a given memory state is always controlled by that memory signal;
- 10.
- In the case of multiple occurrences of the actuator state, the executive element switching on/off is performed by summing up the signals that are creating its switching on and off.
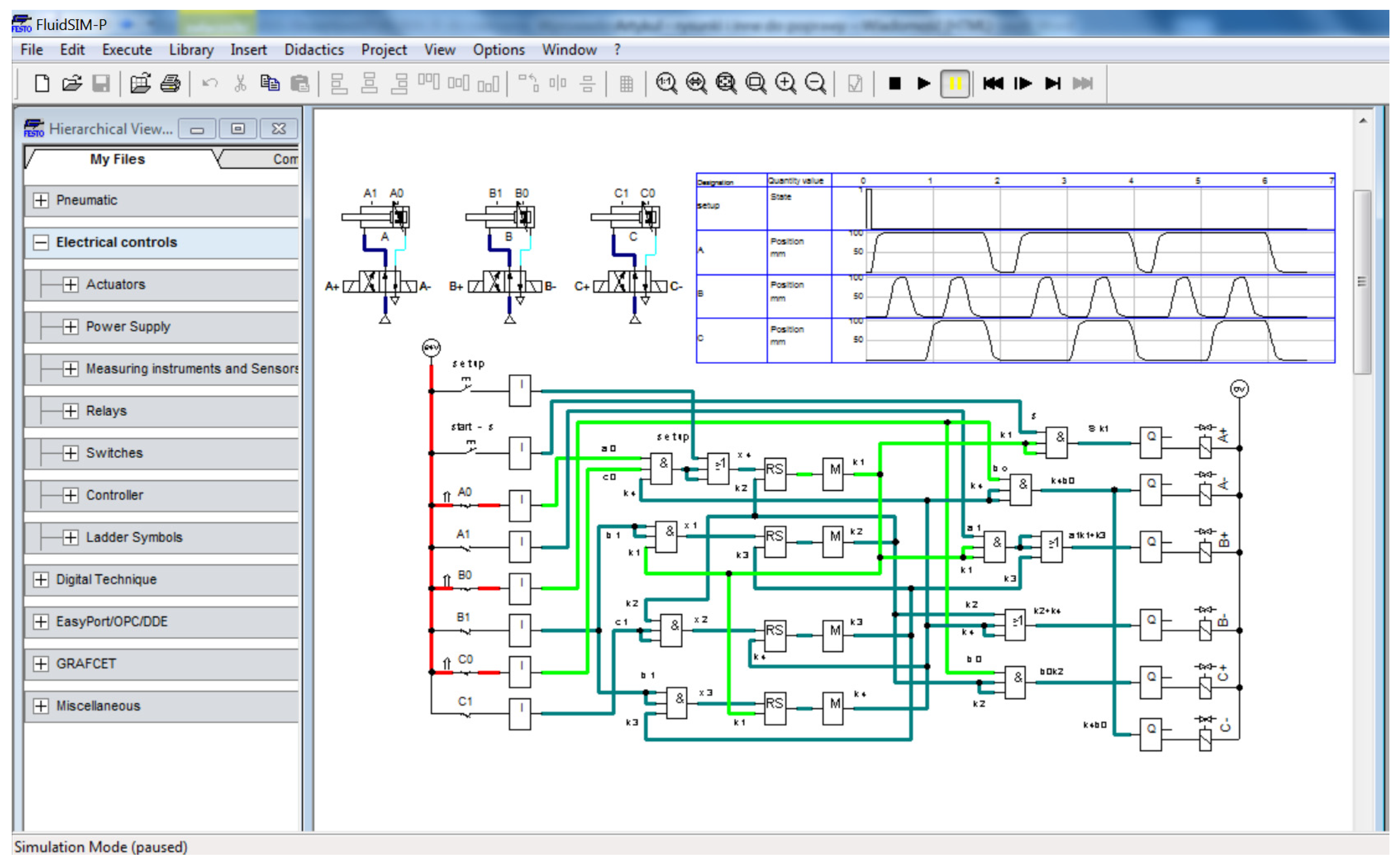
4. Discussion
5. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Borden, T.; Cox, R.A. Technician’s Guide to Programmable Controllers, 6th ed.; Cengage Learning: Boston, MA, USA, 2021; ISBN 978-1111544096. [Google Scholar]
- Wikarek, J.; Sitek, P. A Data-Driven Approach to Constraint Optimization. In Advances in Intelligent Systems and Computing; Springer: Singapore, 2019; Volume 920, pp. 135–144. [Google Scholar]
- Sanver, U.; Yavuz, E.; Eyupoglu, C.; Uzun, T. Design and implementation of a programmable logic controller using PIC18F4580. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow, Russia, 29 January–1 February 2018; pp. 231–235. [Google Scholar]
- Vasu, P.; Chouhan, H.; Naik, N. Design and implementation of optimal soft—Programmable logic controller on multicore processor. In Proceedings of the 2017 International conference on Microelectronic Devices, Circuits and Systems (ICMDCS2017), Vellore, India, 10–12 August 2017; pp. 410–414. [Google Scholar]
- Vinces, L.P.; Fernández, P.; Carpio, C.D.; Rocca, E. An Automatic Control System Using the S7-1200 Programmable Logic Controller for the Ethanol Rectification Process. In Proceedings of the 2018 IEEE XXV International Conference on Electronics, Electrical Engineering and Computing (INTERCON), Lima, Peru, 8–10 August 2018; pp. 96–100. [Google Scholar]
- Gorzałczany, M.B. Układy Cyfrowe—Metody Syntezy. Tom II: Układy Sekwencyjne, Układy Mikroprogramowane; Wydawnictwo Politechniki Świętokrzyskiej: Kielce, Poland, 2003; p. 370. [Google Scholar]
- Tocci, R.; Widmer, N.; Moss, G. Digital Systems, 12th ed.; Pearson: London, UK, 23 March 2016; ISBN 0134220137. [Google Scholar]
- El-Maleh, A. A Note on Moore Model for Sequential Circuits. ResearchGate.com. Published on July 2016. Available online: https://www.researchgate.net/publication/305268049_A_Note_on_Moore_Model_for_Sequential_Circuits (accessed on 10 September 2021).
- Chhillar, K.; Dahiya, S. Design of Sequential Circuits with Timing Analysis and Considerations. Int. J. Eng. Sci. Comput. 2017, 7, 808–11809. [Google Scholar]
- Szcześniak, Z.B. Control of manipulator drive mechanism in smith forging process. Przegląd Elektrotechniczny 2011, 12a, 178–182. [Google Scholar]
- Szcześniak, A.; Szcześniak, Z.B. Designing of Control Systems for Automation of Technological Processes; Kielce University of Technology: Kielce, Poland, 2015. [Google Scholar]
- Li, I.-H.; Lee, L.-W. Design and development of an active suspension system using pneumatic-muscle actuator and intelligent control. Appl. Sci. 2019, 9, 4453. [Google Scholar] [CrossRef] [Green Version]
- Jing, X.; Yong, X.; Jiang, Y.; Li, G.; Yokoi, H. Anthropomorphic prosthetic hand with combination of light weight and diversiform motions. Appl. Sci. 2019, 9, 4203. [Google Scholar] [CrossRef] [Green Version]
- Dávila-Vilchis, J.-M.; LAZ-Avilés; Avilés Vilchis, J.C.; Vilchis-González, A.H. Design methodology for soft wearable devices—The MOSAR case. Appl. Sci. 2019, 9, 4727. [Google Scholar] [CrossRef] [Green Version]
- Szcześniak, A.; Szcześniak, Z.B. Methods and analysis of processing signals of incremental optoelectronic transducer. Rev. Sci. Instrum. 2009, 80, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Szcześniak, A.; Szcześniak, Z.B. Układ sekwencyjnego sterowania elementami wykonawczymi, zwłaszcza elektropneumatycznymi. Patent Application PL432845, 5 February 2020. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szcześniak, A.; Szcześniak, Z. Algorithmic Method for the Design of Sequential Circuits with the Use of Logic Elements. Appl. Sci. 2021, 11, 11100. https://doi.org/10.3390/app112311100
Szcześniak A, Szcześniak Z. Algorithmic Method for the Design of Sequential Circuits with the Use of Logic Elements. Applied Sciences. 2021; 11(23):11100. https://doi.org/10.3390/app112311100
Chicago/Turabian StyleSzcześniak, Adam, and Zbigniew Szcześniak. 2021. "Algorithmic Method for the Design of Sequential Circuits with the Use of Logic Elements" Applied Sciences 11, no. 23: 11100. https://doi.org/10.3390/app112311100
APA StyleSzcześniak, A., & Szcześniak, Z. (2021). Algorithmic Method for the Design of Sequential Circuits with the Use of Logic Elements. Applied Sciences, 11(23), 11100. https://doi.org/10.3390/app112311100





