Physical and Mathematical Modeling of the Interaction of Water Droplets and High-Speed Gas Flow
Abstract
:1. Introduction
2. Recearch Metodology
2.1. Experimental Data
2.2. Numerical Simulation of the Gas Phase
2.3. Description of Data Processing Methods
3. Analysis of Results
4. Conclusions
- 1.
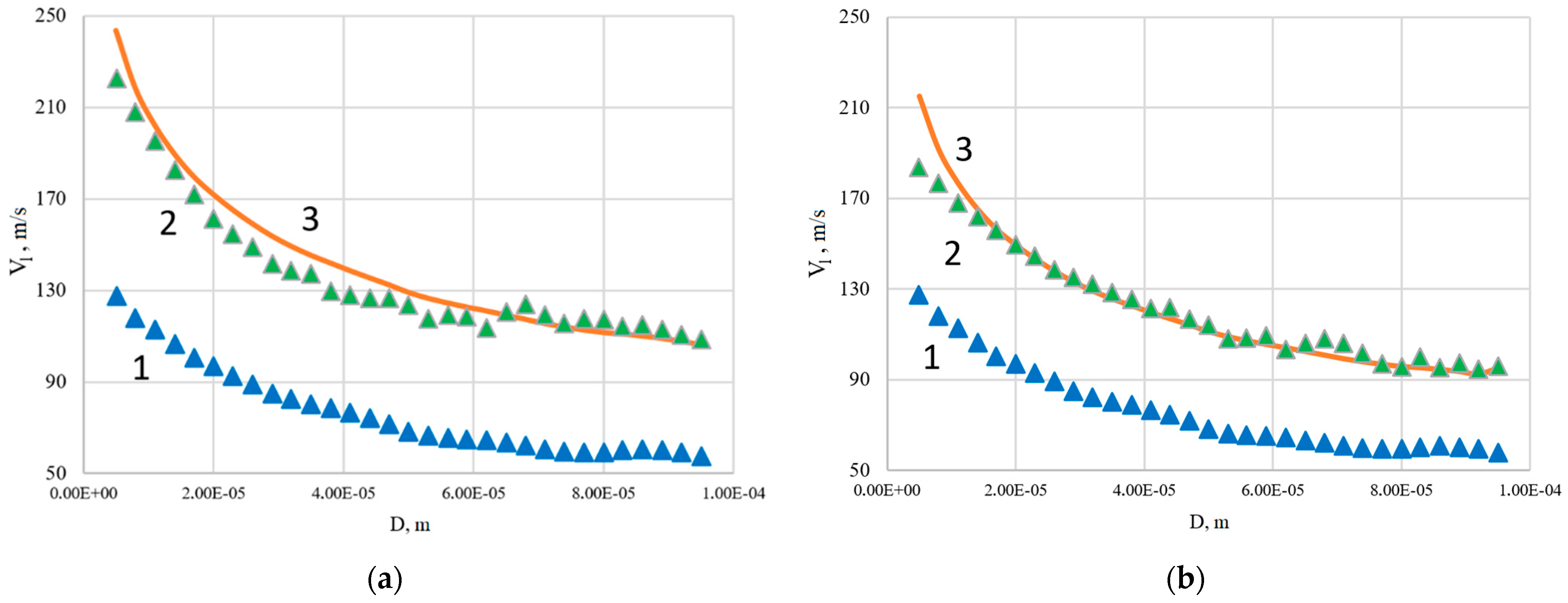
- The piecewise-specified function of the gas velocity and density distribution along the trajectory of liquid droplets with a discontinuity at the intersection of the droplet trajectories with an oblique shock wave can be used for one-dimensional calculations. The velocity and gas density changes at the point where the trajectory of a drop with an oblique shock wave is intercepted can be about 100 m/s and 0.1 kg/m3, respectively. The coordinate of the intersection of the droplet trajectories and shock wave for the considered experimental setup is in the range from 0.01 to 0.04 m depending on the flow Mach number.
- 2.
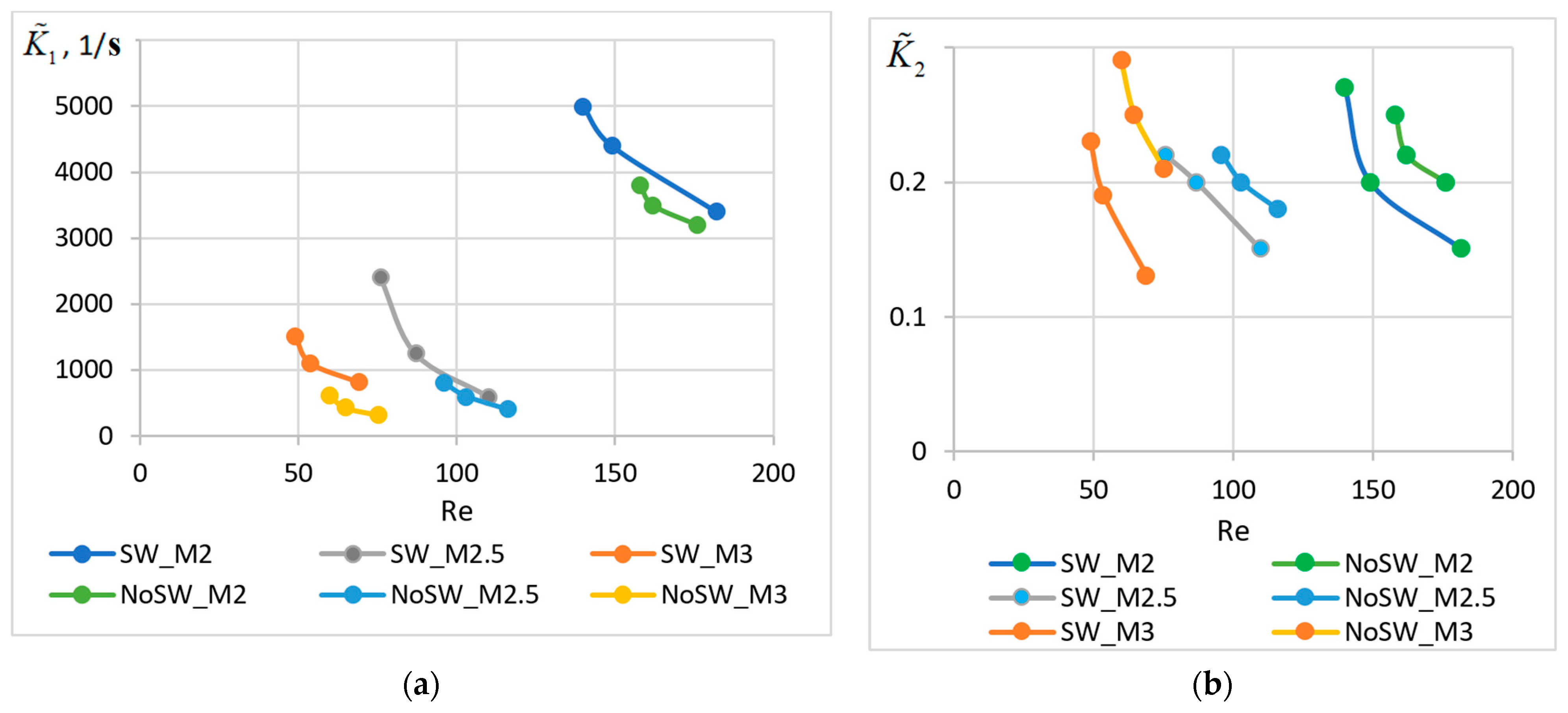
- The presence of an oblique shock wave has an uncertain effect on the rate of liquid droplets gas-dynamic breakup. An oblique shock leads to a decrease of the gas velocity and corresponding decrease of the gas-dynamic breakup rate for almost all pressures of liquid supply in front of the nozzle at Mach numbers less than 2.5. The increase of flow velocity to M = 3 leads to the process of destruction of drops behind the shock wave intensification.
- 3.
- On the basis of a comprehensive analysis of the calculated and experimental data the mathematical model that describes the intensity of gas-dynamic destruction of droplets with a diameter of 5 to 85 microns in a flow with Mach numbers M = 2–3 is proposed. The mathematical model takes into account the influence of the Mach, Weber, Laplace and Reynolds numbers on the rate of gas-dynamic fragmentation of droplets in a high-speed flow. The proposed mathematical model gives a discrepancy with experiment of no more than 3.6%.
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
Abbreviations
| PIV | Particle Image Velocimetry |
| Nd:YAG | Neodymium-doped Yttrium Aluminum Garnet; Nd:Y3Al5O12 |
| RANS | Reynolds-Averaged Navier-Stokes |
| AUSM | Advection Upstream Splitting Method |
| SW | Shock Wave |
Appendix A
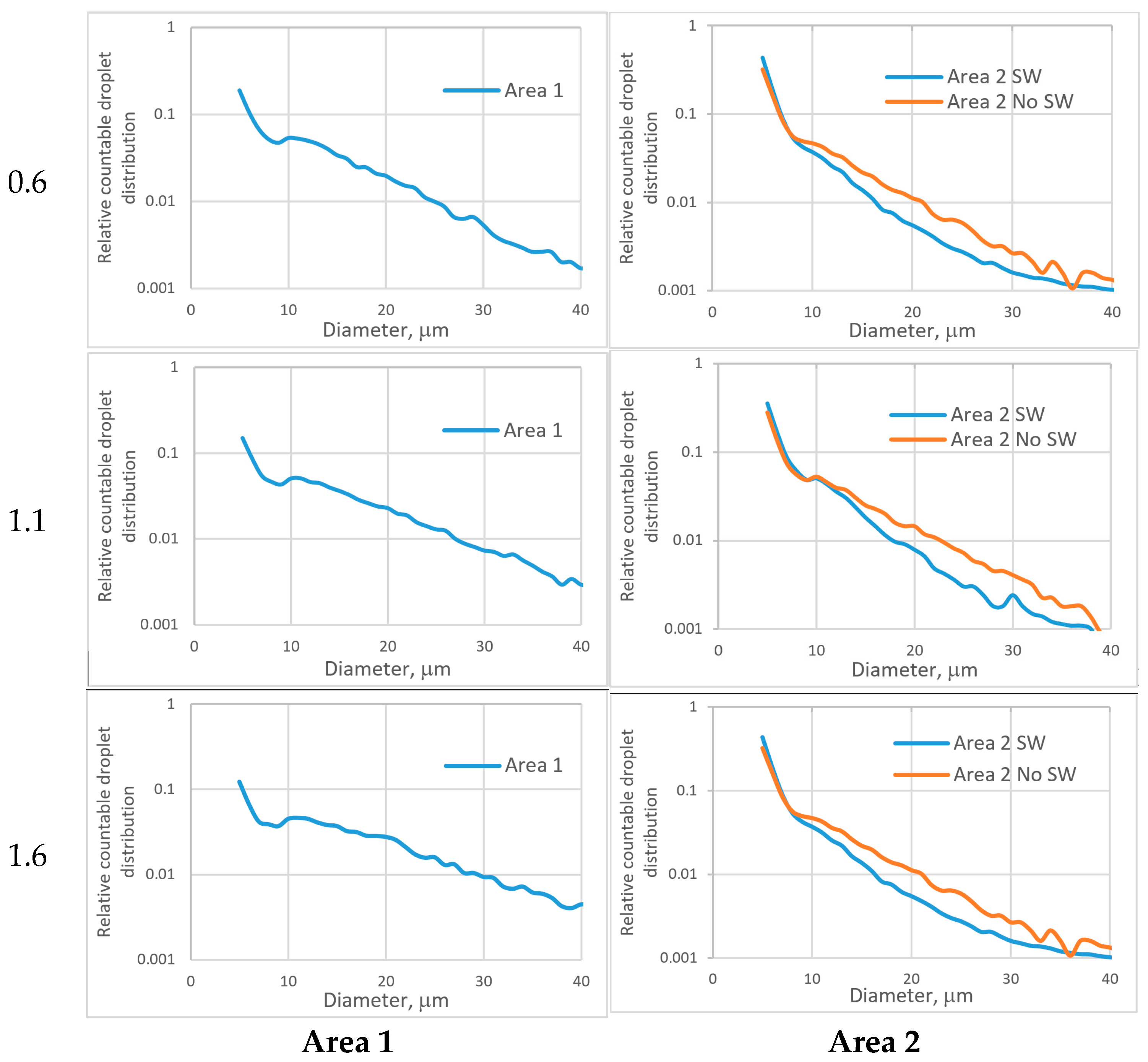
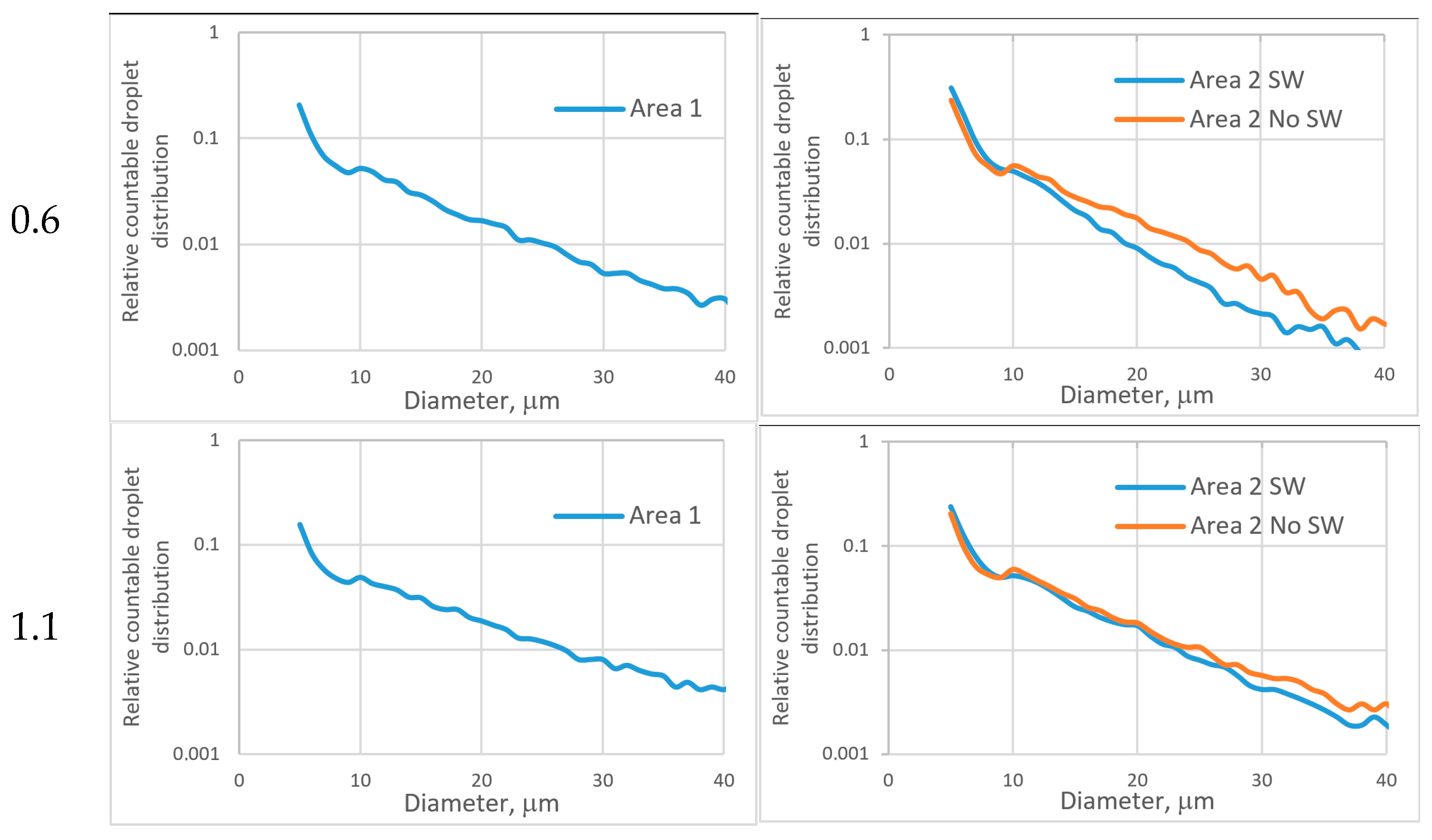
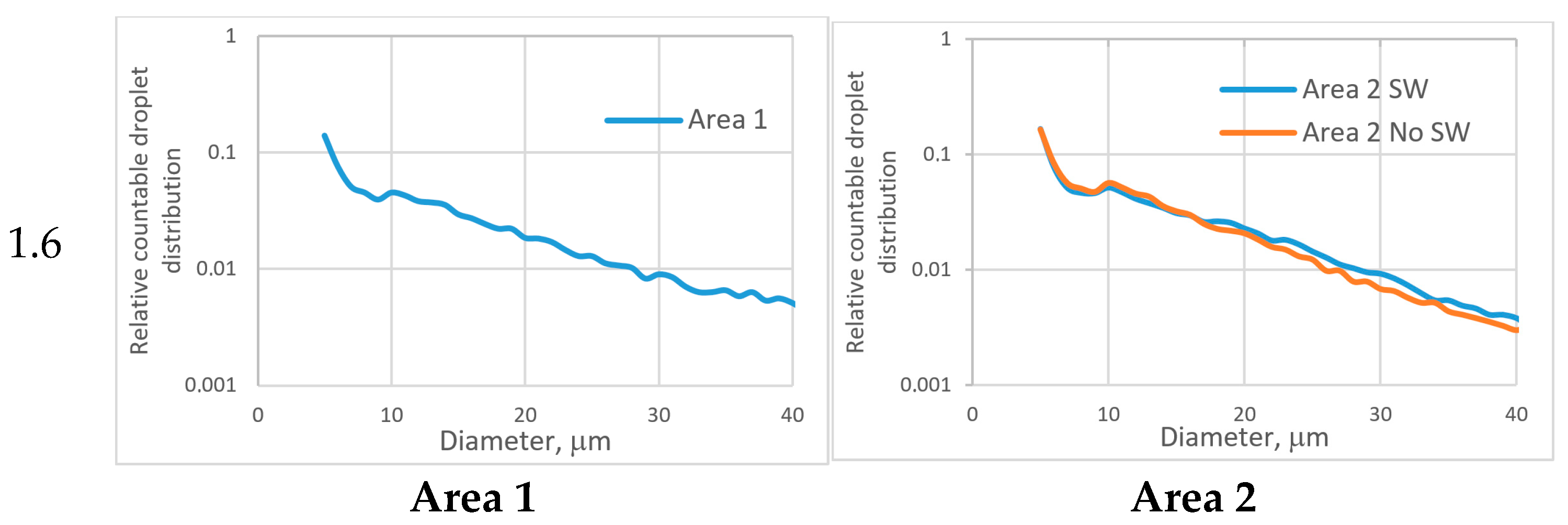


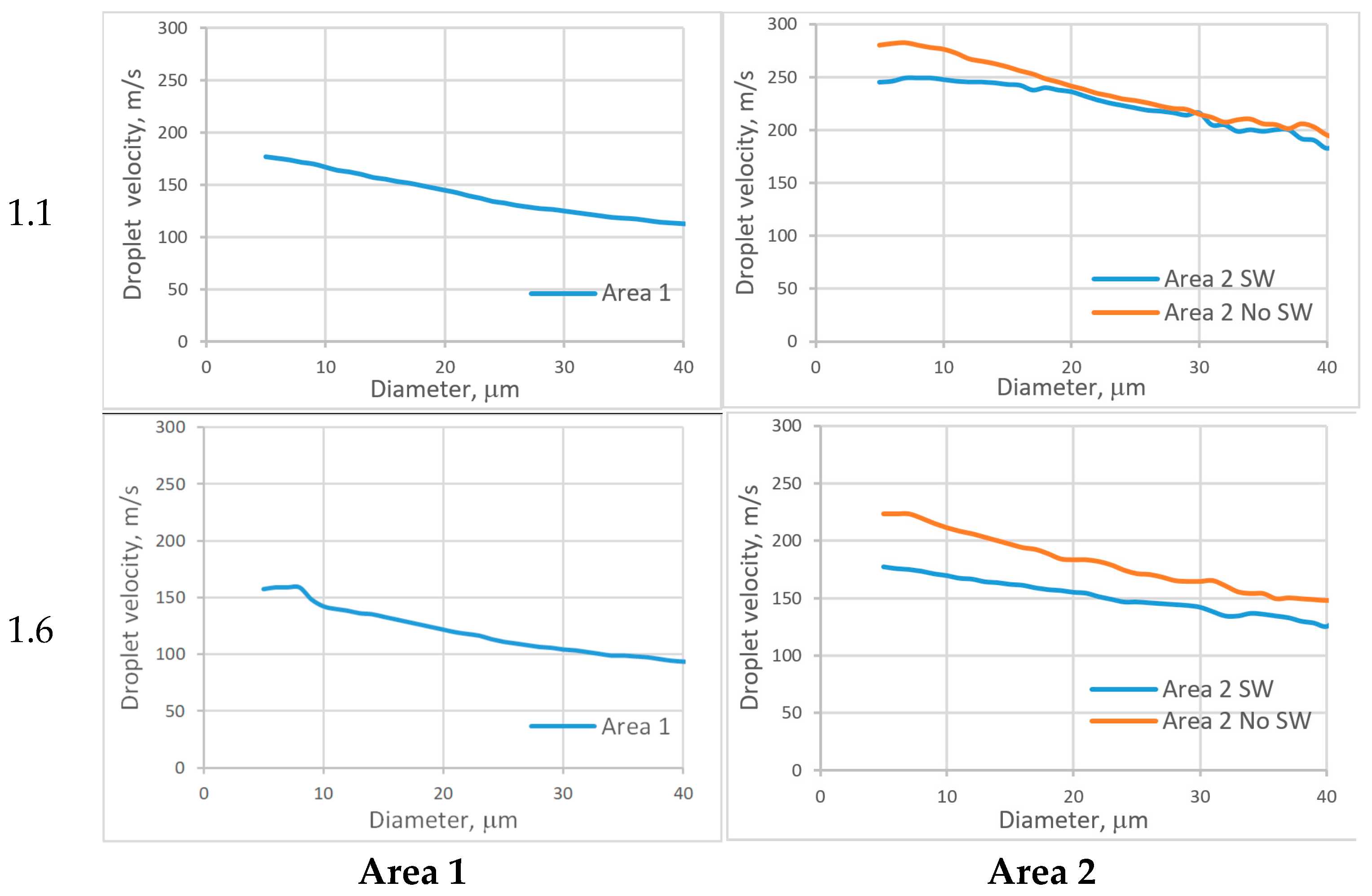
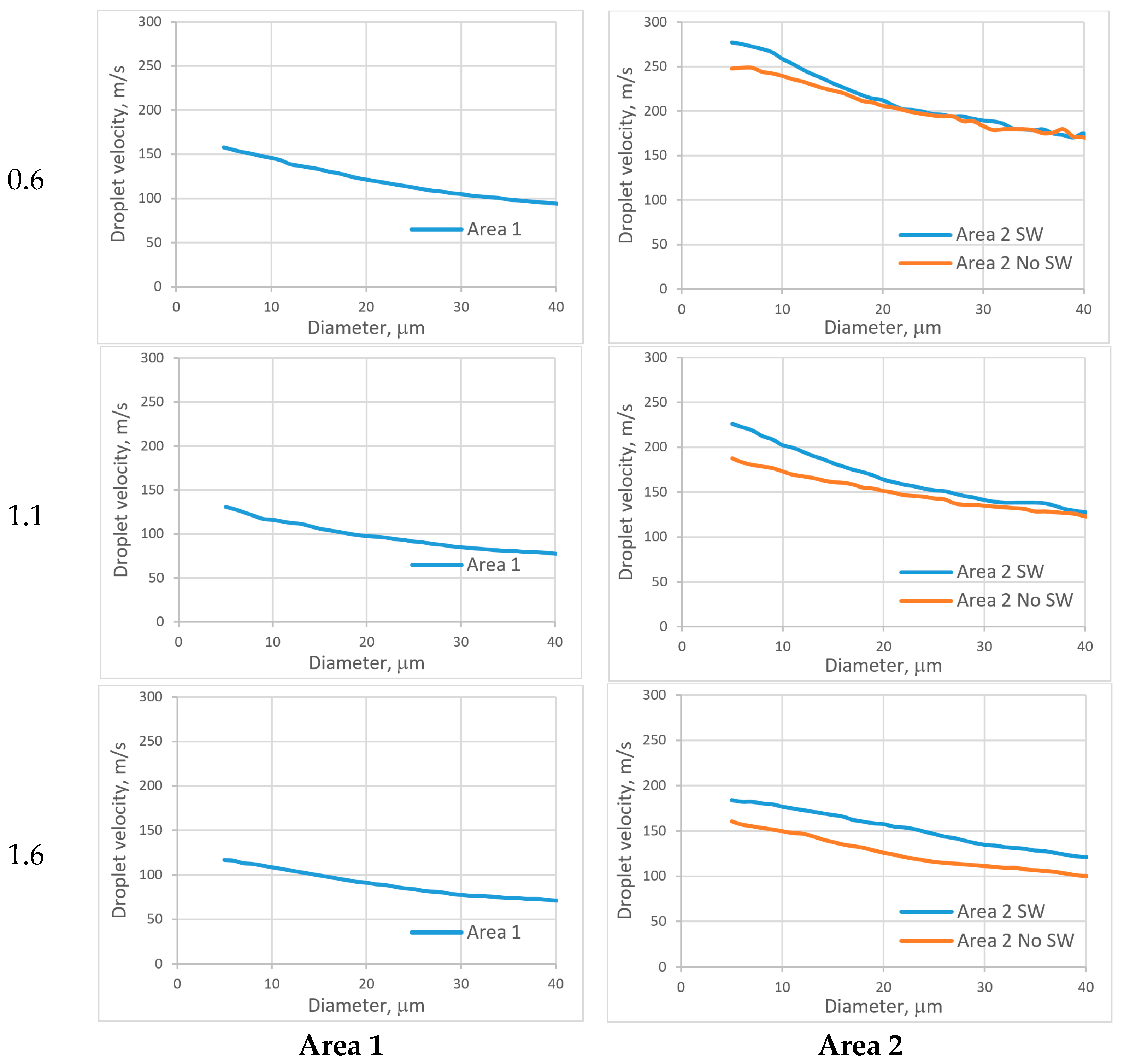
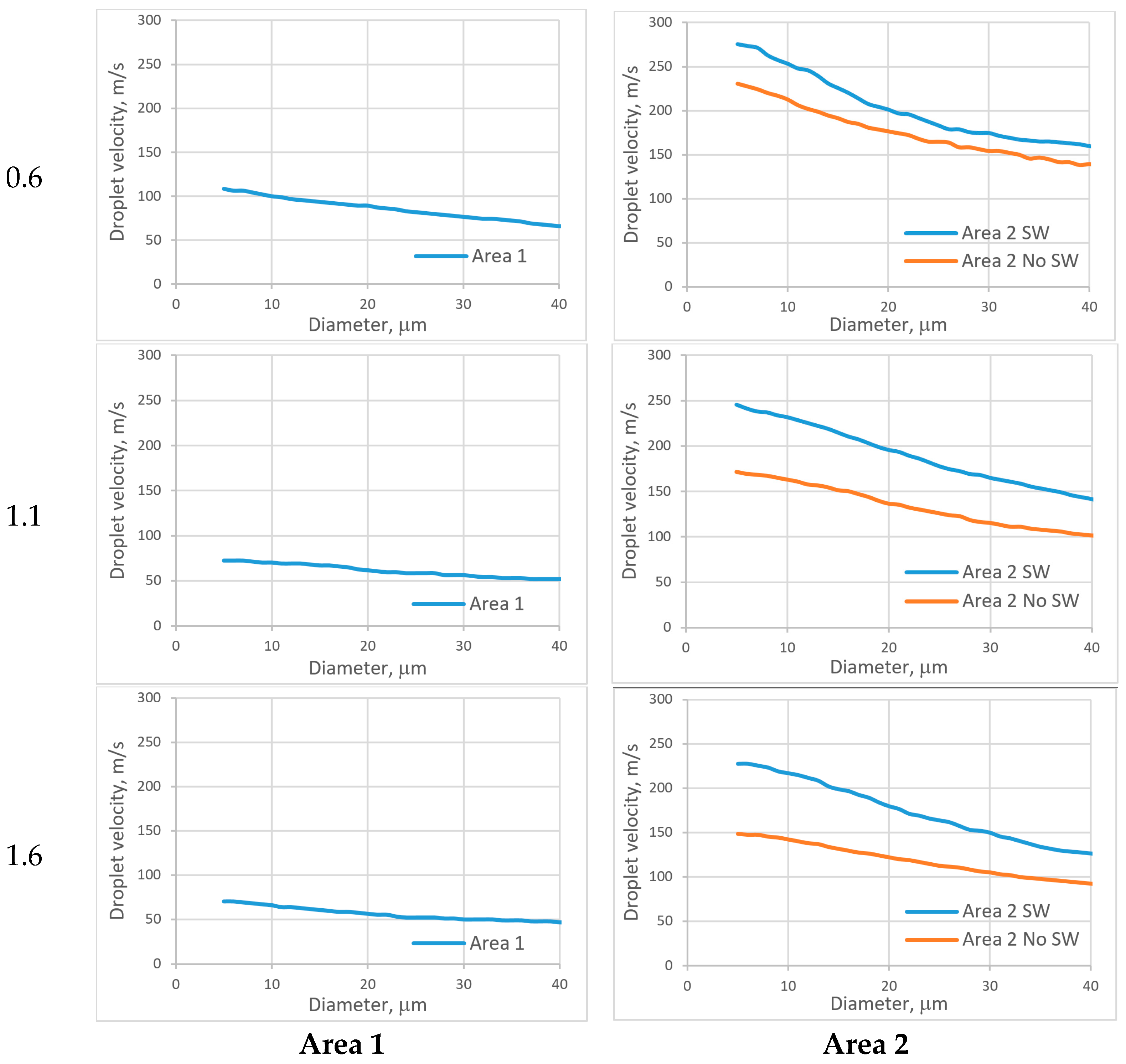
References
- Theofanous, T.G.; Li, G.J. On the Physics of Aerobreakup. Phys. Fluids 2008, 20, 052103. [Google Scholar] [CrossRef]
- Shao, C.; Luo, K.; Yang, Y.; Fan, J. Direct numerical simulation of droplet breakup in homogeneous isotropic turbulence: The effect of the Weber number. Int. J. Multiph. Flow 2018, 107, 263–274. [Google Scholar] [CrossRef]
- Shao, C.; Luo, K.; Fan, J. Detailed numerical simulation of unsteady drag coefficient of deformable droplet. Chem. Eng. J. 2017, 308, 619–631. [Google Scholar] [CrossRef]
- Wang, Z.; Hopfes, T.; Giglmaier, M.; Adams, N.A. Effect of Mach number on droplet aerobreakup in shear stripping regime. Exp. Fluids 2020, 61, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Kékesi, T.; Amberg, G.; Wittberg, L.P. Drop deformation and breakup. Int. J. Multiph. Flow 2014, 66, 1–10. [Google Scholar] [CrossRef]
- Dorschner, B.; Biasiori-Poulanges, L.; Schmidmayer, K.; El-Rabii, H.; Colonius, T. On the formation and recurrent shedding of ligaments in droplet aerobrakeup. J. Fluid Mech. 2020, 904, A20. [Google Scholar] [CrossRef]
- Marcotte, F.; Zaleski, S. Density contrast matters for drop fragmentation thresholds at low Ohnesorge number. Phys. Rev. Fluids 2019, 4, 103604. [Google Scholar] [CrossRef] [Green Version]
- Giffen, E.; Muraszew, A. The Atomization of Liquid Fuels; Chapman & Hall: London, UK, 1953. [Google Scholar]
- Hinze, J.O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1955, 1, 289–295. [Google Scholar] [CrossRef]
- Gelfand, B.E.; Silnikov, M.V.; Takayama, K. Destruction of Liquid Droplets; Polytechnic University Press: Saint Petersburg, Russia, 2008. (In Russian) [Google Scholar]
- Girin, A.G. Hydrodynamic instability and droplet fragmentation models. Eng. Phys. J. 1985, 48, 771–776. (In Russian) [Google Scholar] [CrossRef]
- Gobyzov, O.A.; Ryabov, M.N.; Bilsky, A.V. Study of Deformation and Breakup of Submillimeter Droplets’ Spray in a Supersonic Nozzle Flow. Appl. Sci. 2020, 10, 6149. [Google Scholar] [CrossRef]
- Gelfand, B. Droplet breakup phenomena in flows with velocity lag. Prog. Energy Combust. Sci. 1996, 22, 201–265. [Google Scholar] [CrossRef]
- Guildenbecher, D.R.; López-Rivera, C.; Sojka, P.E. Secondary atomization. Exp. Fluids 2009, 46, 371–402. [Google Scholar] [CrossRef]
- Pilch, M.; Erdman, C.A. Use of breakup time data and velocity history data to predict the maximum size of stable fragments for acceleration-induced breakup of a liquid drop. Int. J. Multiph. Flow 1987, 13, 741–757. [Google Scholar] [CrossRef]
- Sichani, A.B.; Emami, M.D. A droplet deformation and breakup model based on virtual work principle. Phys. Fluids 2015, 27, 32103. [Google Scholar] [CrossRef]
- Liu, N.; Wang, Z.; Sun, M.; Wang, H.; Wang, B. Numerical simulation of liquid droplet breakup in supersonic flows. Acta Astronaut. 2018, 145, 116–130. [Google Scholar] [CrossRef]
- Arefyev, K.Y.; Voronetsky, A.V. Modelling of the process of fragmentation and vaporization of non-reacting liquid droplets in high-enthalpy gas flows. Thermophys. Aeromech. 2015, 22, 585–596. [Google Scholar] [CrossRef]
- Voronetsky, A.V.; Suchkov, S.A.; Filimonov, L.A. Peculiarities of high-temperature two-phase flow of combustion products in channels with an intentionally structured system of shock-waves. Thermophys. Aeromech. 2007, 14, 201–210. [Google Scholar] [CrossRef]
- Abramzo, В.; Sirignano, W.A. Droplet vaporization model for spray combustion calculations. Int. J. Heat Mass Trans. 1989, 32, 1605–1618. [Google Scholar] [CrossRef]
- Sula, C.; Grosshans, H.; Papalexandris, M.V. Assessment of Droplet Breakup Models for Spray Flow Simulations. Flow Turbul. Combust. 2020, 105, 889–914. [Google Scholar] [CrossRef]
- Kucharika, М.; Shashkov, M. Conservative multi-material remap for staggered multi-material Arbitrary Lagrangian—Eulerian methods. J. Comput. Phys. 2014, 258, 268–304. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Chang, C.H. On the computation of multiphase interactions in transonic and supersonic flows. In Proceedings of the AIAA-2008 Conference, Reno, NV, USA, 7–10 January 2008; p. 1233. [Google Scholar]
- Arefiev, K.Y.; Voronetsky, A.V.; Suchkov, S.A.; Ilchenko, M.A. Computational and experimental study of two-phase mixture formation in a gas-dynamic ignition system. Thermophys. Aeromech. 2017, 24, 225–237. [Google Scholar] [CrossRef]
- Betelin, V.B.; Smirnov, N.N.; Nikitin, V.F.; Dushin, V.R.; Kushnirenko, A.G.; Nerchenko, V.A. Evaporation and ignition of droplets in combustion chambers modeling and simulation. Acta Astronaut. 2012, 70, 23–35. [Google Scholar] [CrossRef]
- Li, P.; Wang, Z.; Sun, M.; Wang, H. Numerical simulation of the gas-liquid interaction of a liquid jet in supersonic crossflow. Acta Astronaut. 2017, 134, 333–344. [Google Scholar] [CrossRef]
- Reinecke, W.G.; Waldman, G.D. Shock layer shattering of cloud drops in reentry flight. AIAA Pap. 1975, 152, 22. [Google Scholar]
- Arefyev, K.Y.; Prokhorov, A.N.; Saveliev, A.S. Study of the breakup of liquid droplets in the vortex wake behind pylon at high airspeeds. Thermophys. Aeromech. 2018, 25, 55–66. [Google Scholar] [CrossRef]
- Arefyev, K.Y.; Guskov, O.V.; Prokhorov, A.N.; Saveliev, A.S.; Son, E.E.; Gauthame, K.; Same, D.; Sonu, K.T.; Muruganandame, T.M. Experimental research of gasdynamic liquid drops breakup in the supersonic flow with the oblique shock wave. High Temp. 2020, 58, 884–892. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Scarano, F.; Kähler, C.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Settles, G.S. Schliren and Shadowgraph Techniques, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Liou, M.S.; Steffen, C.J. A New Flux Splitting Scheme; Academic Press Professional Inc.: Cambridge, MA, USA, 1993. [Google Scholar]
- Pavlenko, I.; Sklabinskyi, V.; Doligalski, M.; Ochowiak, M.; Mrugalski, M.; Liaposhchenko, O.; Skydanenko, M.; Ivanov, V.; Włodarczak, S.; Woziwodzki, S.; et al. The Mathematical Model for the Secondary Breakup of Dropping Liquid. Energies 2020, 13, 6078. [Google Scholar] [CrossRef]
- Huang, X.; Liu, J.; Liao, S.; Wu, J. Experimental investigation of the deformation and breakup of a droplet in high-speed flow. Sci. Sin. Phys. Mech. Astron. 2018, 48, 054701. [Google Scholar] [CrossRef]
- Han, J.; Tryggvason, G. Secondary breakup of axisymmetric liquid drops. I. Acceleration by a constant body force. Phys. Fluids 1999, 11, 3650–3667. [Google Scholar] [CrossRef]
- Han, J.; Tryggvason, G. Secondary breakup of axisymmetric liquid drops. II. Impulsive acceleration. Phys. Fluids 2001, 13, 1554–1565. [Google Scholar] [CrossRef]
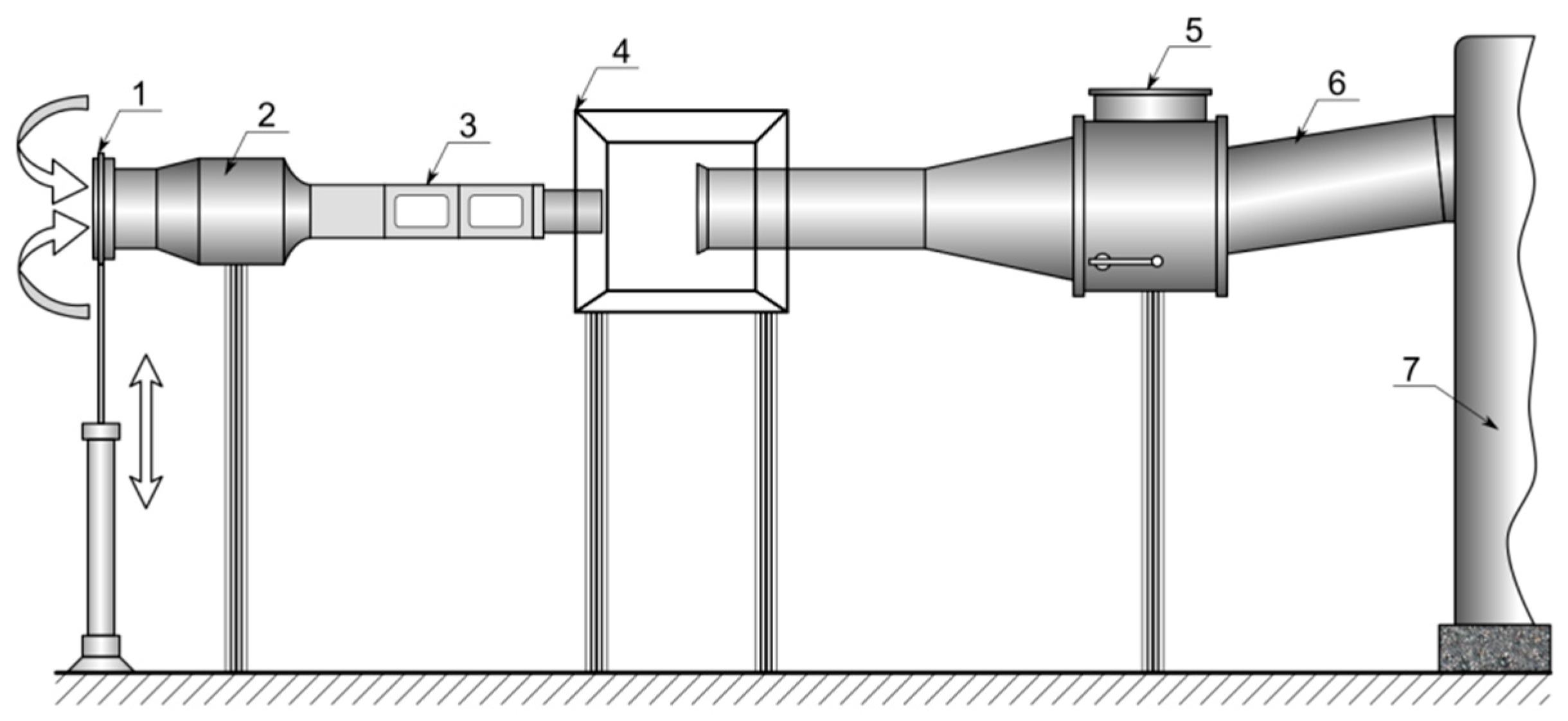
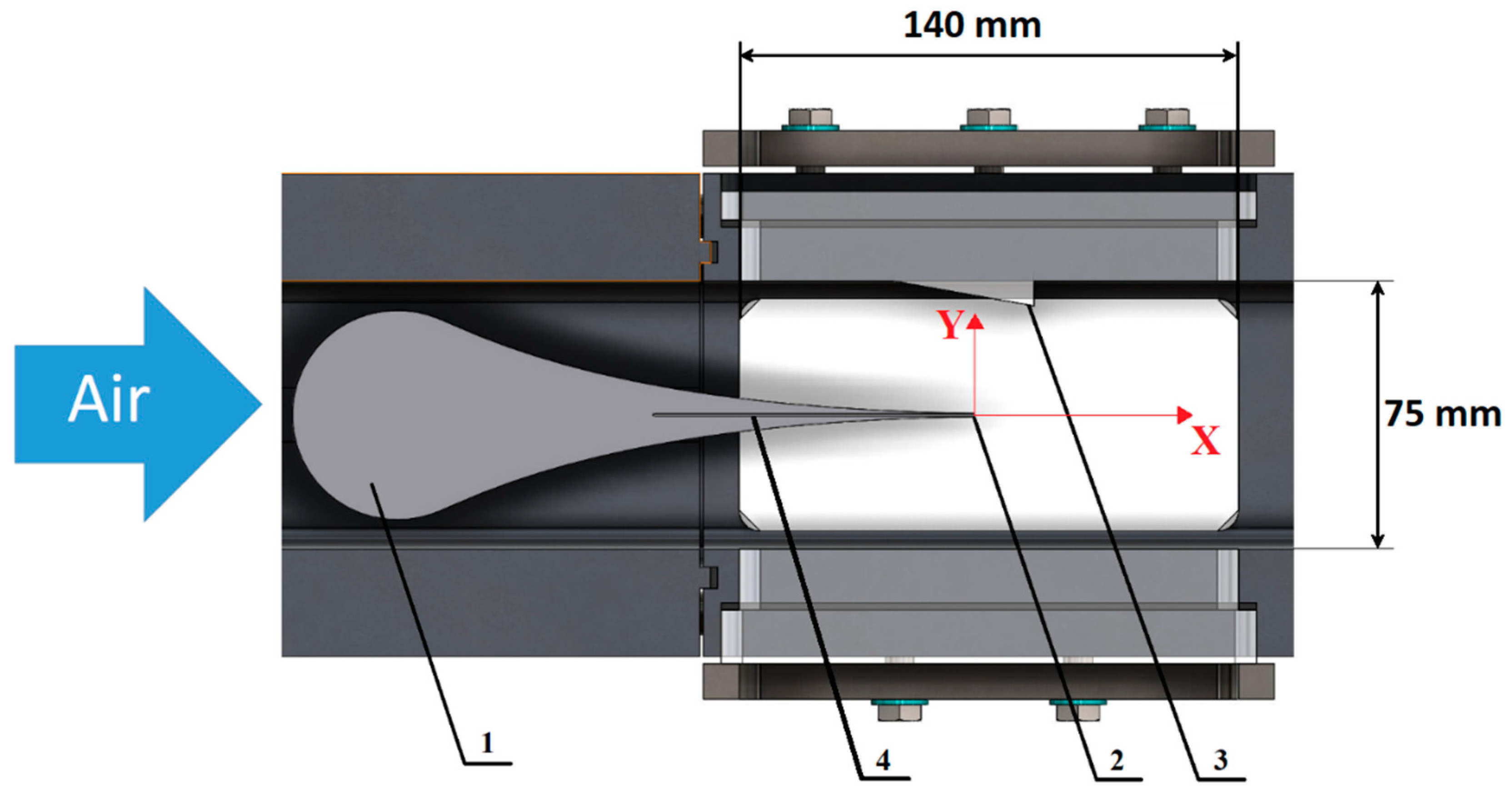
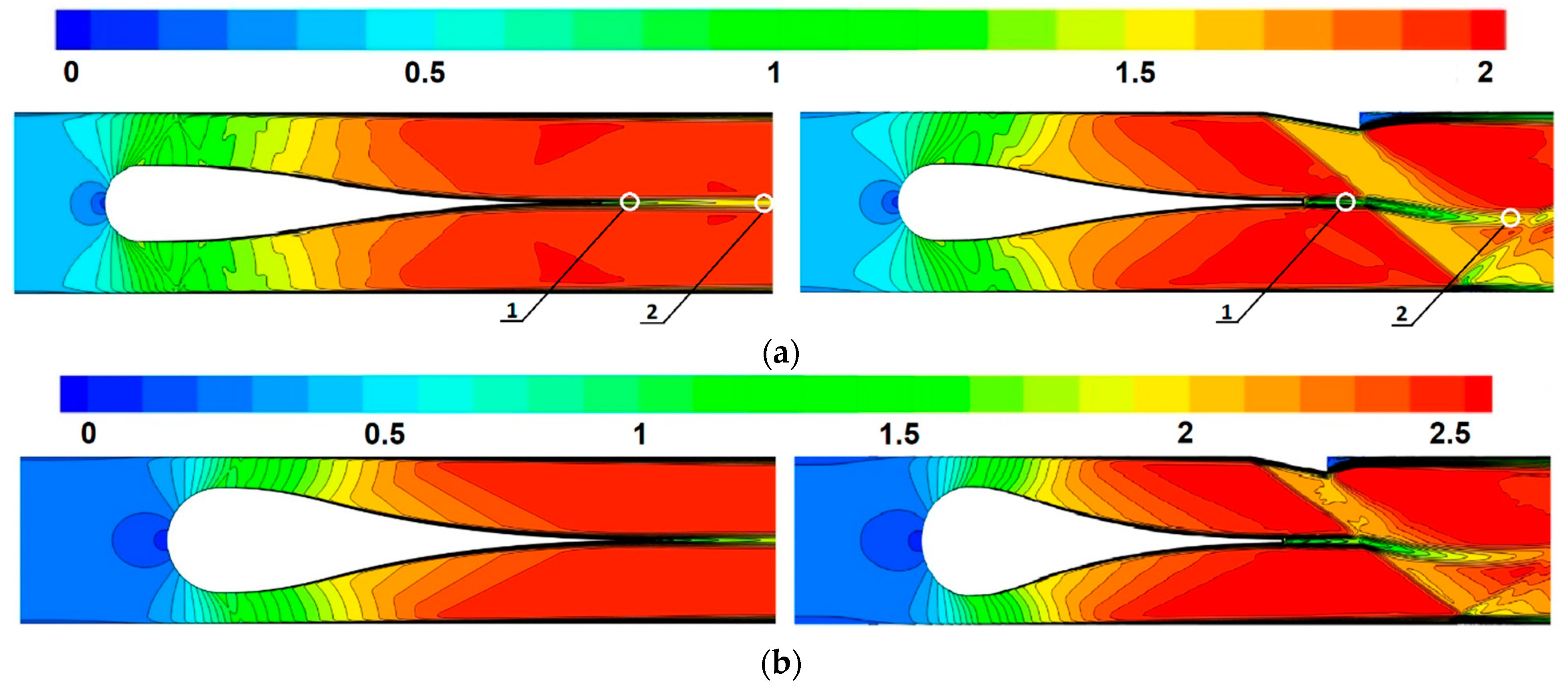

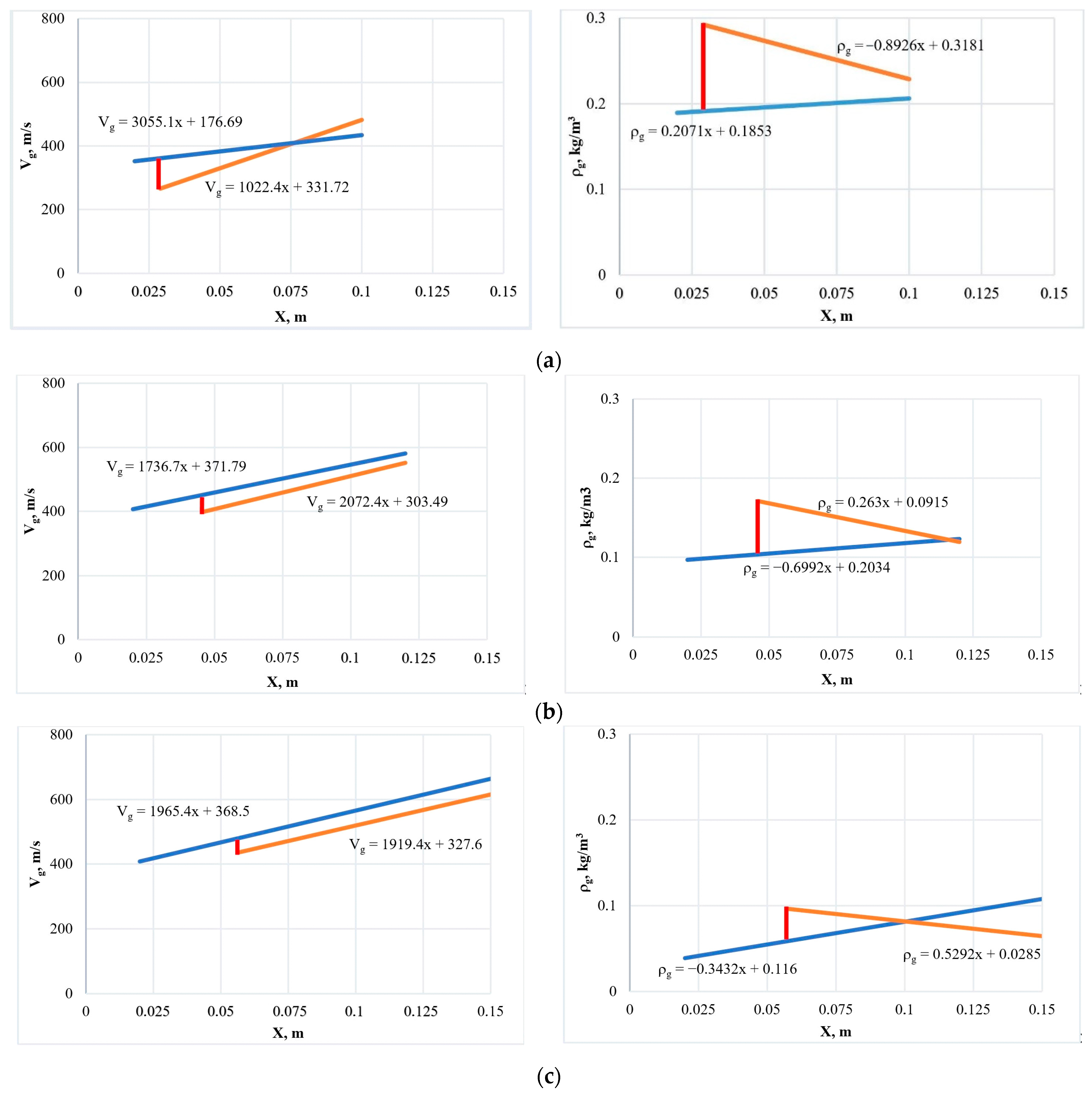
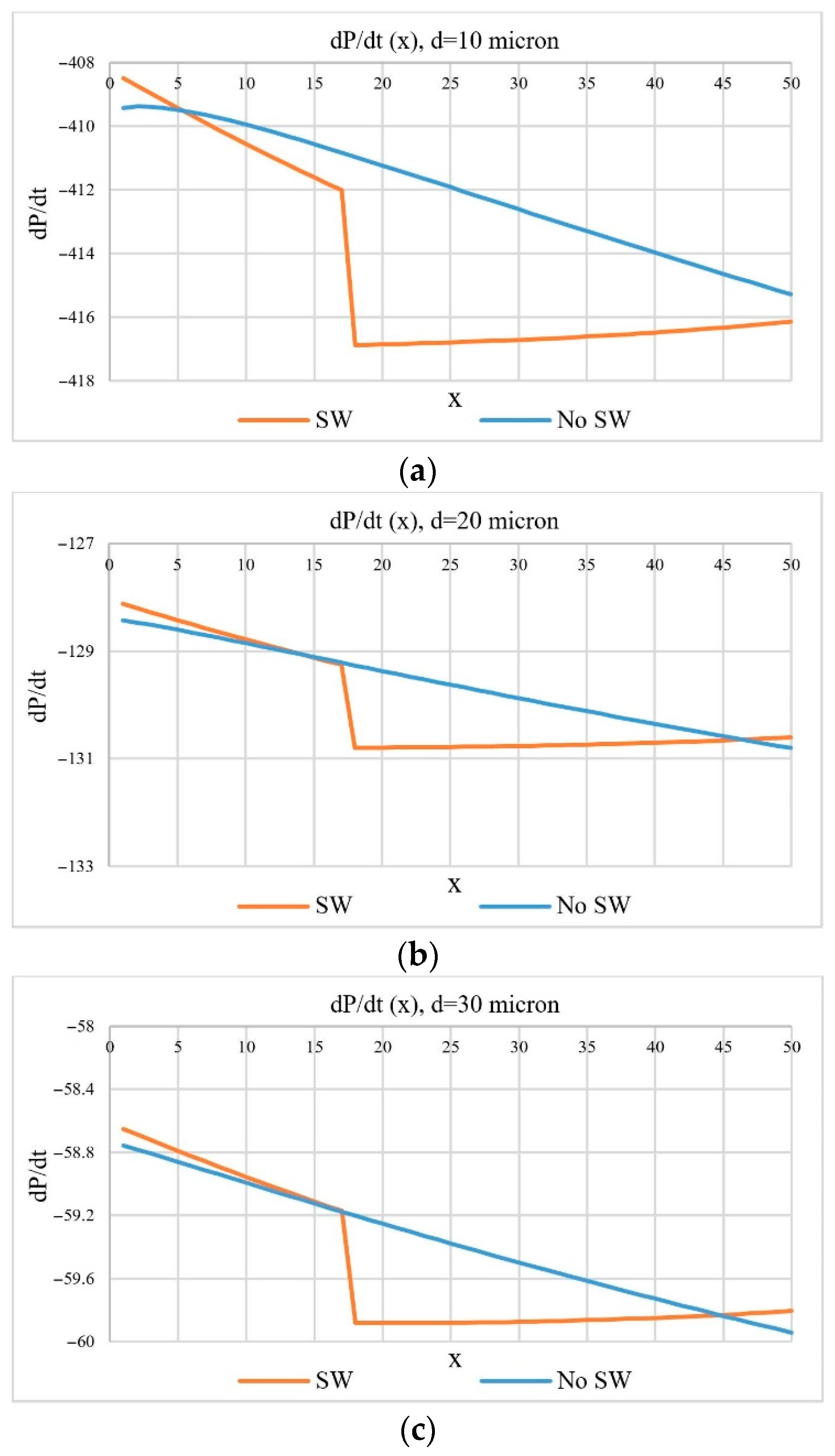
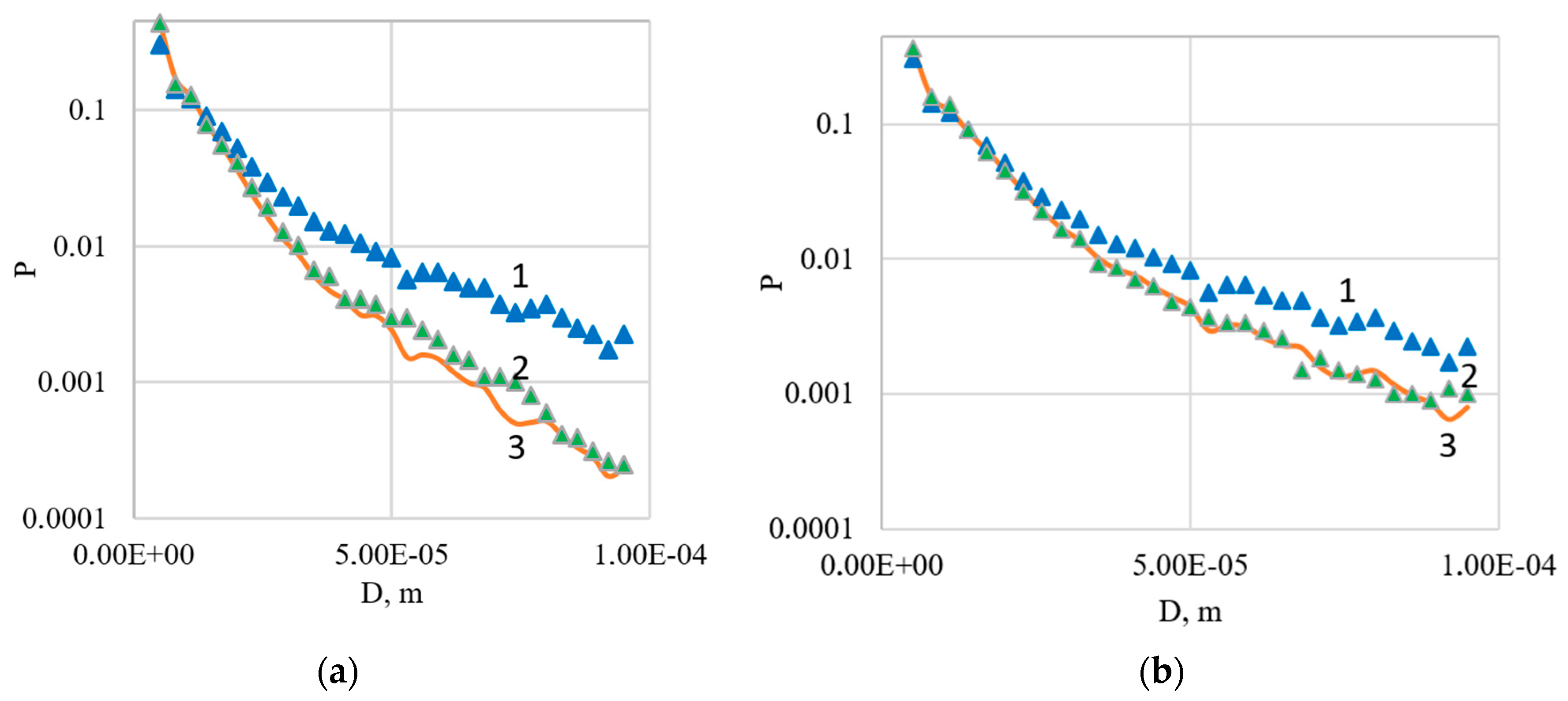
| Nozzle | 1 | 2 | 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mach Number | 2 | 2.5 | 3 | ||||||
| Measurement Area | 1 | 2 | 1 | 2 | 1 | 2 | |||
| After Shock Wave | Without Shock Wave | After Shock Wave | Without Shock Wave | After Shock Wave | Without Shock Wave | ||||
| X, mm | 20 | 100 | 100 | 20 | 120 | 120 | 20 | 130 | 130 |
| Y, mm | −0.5 | −3.2 | −0.5 | −0.5 | −4.0 | −0.5 | 0 | −2.5 | 0 |
| pl, MPa | Shock Wave | , 1/с | Er, % | Re | |
|---|---|---|---|---|---|
| 0.6 | + | 5000 | 0.27 | 2.8 | 140 |
| 1.1 | + | 4400 | 0.2 | 0.8 | 149 |
| 1.7 | + | 3400 | 0.15 | 1.6 | 182 |
| 0.6 | − | 3800 | 0.25 | 2.3 | 158 |
| 1.1 | − | 3500 | 0.22 | 2.0 | 162 |
| 1.7 | − | 3200 | 0.2 | 3.6 | 176 |
| pl, MPa | Shock Wave | , 1/s | Er, % | Re | |
|---|---|---|---|---|---|
| 0.6 | + | 2400 | 0.22 | 1.0 | 76 |
| 1.1 | + | 1250 | 0.2 | 0.8 | 87 |
| 1.7 | + | 600 | 0.15 | 1.5 | 110 |
| 0.6 | − | 800 | 0.22 | 1.2 | 96 |
| 1.1 | − | 600 | 0.2 | 0.5 | 103 |
| 1.7 | − | 400 | 0.18 | 1.1 | 116 |
| pl, MPa | Shock Wave | , 1/s | Er, % | Re | |
|---|---|---|---|---|---|
| 0.6 | + | 1500 | 0.23 | 1.0 | 49 |
| 1.1 | + | 1100 | 0.19 | 0.8 | 53.7 |
| 1.7 | + | 850 | 0.13 | 0.9 | 69 |
| 0.6 | − | 600 | 0.29 | 0.7 | 60.2 |
| 1.1 | − | 400 | 0.25 | 0.9 | 64.7 |
| 1.7 | − | 300 | 0.21 | 1.0 | 75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minko, A.; Guskov, O.; Arefyev, K.; Saveliev, A. Physical and Mathematical Modeling of the Interaction of Water Droplets and High-Speed Gas Flow. Appl. Sci. 2021, 11, 11146. https://doi.org/10.3390/app112311146
Minko A, Guskov O, Arefyev K, Saveliev A. Physical and Mathematical Modeling of the Interaction of Water Droplets and High-Speed Gas Flow. Applied Sciences. 2021; 11(23):11146. https://doi.org/10.3390/app112311146
Chicago/Turabian StyleMinko, Aleksandr, Oleg Guskov, Konstantin Arefyev, and Andrey Saveliev. 2021. "Physical and Mathematical Modeling of the Interaction of Water Droplets and High-Speed Gas Flow" Applied Sciences 11, no. 23: 11146. https://doi.org/10.3390/app112311146





