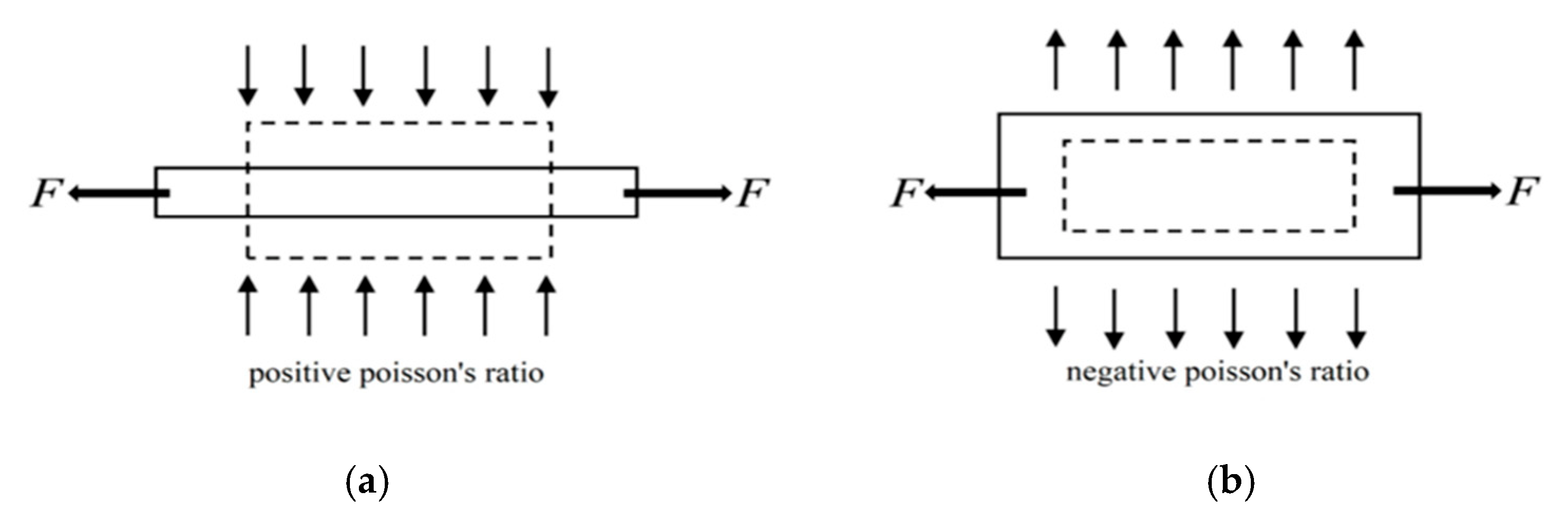
Figure 1.
Deformation diagram of positive and negative Poisson’s ratio structure under lateral hand tension is given, (a) positive Poisson’s ratio structure, (b) negative Poisson’s ratio structure.
Figure 1.
Deformation diagram of positive and negative Poisson’s ratio structure under lateral hand tension is given, (a) positive Poisson’s ratio structure, (b) negative Poisson’s ratio structure.
Figure 2.
The re-entrant hexagonal structure with negative Poisson’s ratio is given, (a) a simple schematic diagram of the honeycomb base is shown, (b) re-entrant hexagonal honeycomb cell.
Figure 2.
The re-entrant hexagonal structure with negative Poisson’s ratio is given, (a) a simple schematic diagram of the honeycomb base is shown, (b) re-entrant hexagonal honeycomb cell.
Figure 3.
Schematic diagram of re-entrant hexagonal honeycomb cell is given.
Figure 3.
Schematic diagram of re-entrant hexagonal honeycomb cell is given.
Figure 4.
Tenth order natural frequency band diagram of a single cell structure is given, (a) the single cell’s side thickness: , its angle , thus, its Poisson’s ratio is deduced: ; (b) the single cell’s side thickness: , its angle , thus, its Poisson’s ratio is deduced: .
Figure 4.
Tenth order natural frequency band diagram of a single cell structure is given, (a) the single cell’s side thickness: , its angle , thus, its Poisson’s ratio is deduced: ; (b) the single cell’s side thickness: , its angle , thus, its Poisson’s ratio is deduced: .
Figure 5.
Tenth order natural frequency band diagram of a single cell structure is given, (a) the single cell’s side thickness: , its angle , thus, its Poisson’s ratio is deduced: ; (b) the single cell’s side thickness: , its angle , thus, its Poisson’s ratio is deduced: .
Figure 5.
Tenth order natural frequency band diagram of a single cell structure is given, (a) the single cell’s side thickness: , its angle , thus, its Poisson’s ratio is deduced: ; (b) the single cell’s side thickness: , its angle , thus, its Poisson’s ratio is deduced: .
Figure 6.
(a) Traditional cellular structure of honeycomb base is given; (b) Tenth order natural frequency band diagram of traditional cellular structure of honeycomb base is given; (c) the diagram honeycomb base of traditional cellular structure; (d) the frequency response curve of the honeycomb base.
Figure 6.
(a) Traditional cellular structure of honeycomb base is given; (b) Tenth order natural frequency band diagram of traditional cellular structure of honeycomb base is given; (c) the diagram honeycomb base of traditional cellular structure; (d) the frequency response curve of the honeycomb base.
Figure 7.
The base diagram of re-entrant structure is given, (a) the diagram of honeycomb base, the Poisson’s ratio of the re-entrant hexagonal elements that make up the honeycomb base is ; (b) a fixed displacement 1 m upper plane of the base; (c) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is ; (d) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is .
Figure 7.
The base diagram of re-entrant structure is given, (a) the diagram of honeycomb base, the Poisson’s ratio of the re-entrant hexagonal elements that make up the honeycomb base is ; (b) a fixed displacement 1 m upper plane of the base; (c) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is ; (d) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is .
Figure 8.
(a) the diagram of honeycomb base, the Poisson’s ratio of the re-entrant hexagonal elements that make up the honeycomb base is ; (b) a fixed displacement 1 m upper plane of the base; (c) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is ; (d) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is .
Figure 8.
(a) the diagram of honeycomb base, the Poisson’s ratio of the re-entrant hexagonal elements that make up the honeycomb base is ; (b) a fixed displacement 1 m upper plane of the base; (c) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is ; (d) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is .
Figure 9.
(a) the diagram of honeycomb base made up by different Poisson’s ratio of the re-entrant hexagonal elements, the Poisson’s ratio of its above three layers is: , the following three layers is ; (b) a fixed displacement 1 m upper plane of the base; (c) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is ; (d) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is .
Figure 9.
(a) the diagram of honeycomb base made up by different Poisson’s ratio of the re-entrant hexagonal elements, the Poisson’s ratio of its above three layers is: , the following three layers is ; (b) a fixed displacement 1 m upper plane of the base; (c) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is ; (d) the side thickness of the re-entrant hexagonal elements that make up the honeycomb base is .
Figure 10.
Heteromorphic negative Poisson’s ratio cell structure: (a) The inner Angle plus radius is r mass block; (b) The inner and outer Angle plus radius is r mass block.
Figure 10.
Heteromorphic negative Poisson’s ratio cell structure: (a) The inner Angle plus radius is r mass block; (b) The inner and outer Angle plus radius is r mass block.
Figure 11.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.1272 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 11.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.1272 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 12.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.1272 cm, around the corner circle radius: 0.15 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 12.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.1272 cm, around the corner circle radius: 0.15 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 13.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.25 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 13.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.25 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 14.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.25 cm, around the corner circle radius: 1.25 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 14.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.25 cm, around the corner circle radius: 1.25 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 15.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 2 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 15.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 2 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 16.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 2 cm, around the corner circle radius: 2 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 16.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 2 cm, around the corner circle radius: 2 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 17.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.1528 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 17.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.1528 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 18.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.1528 cm, around the corner circle radius: 0.1528 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 18.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.1528 cm, around the corner circle radius: 0.1528 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 19.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 19.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 20.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1 cm, around the corner circle radius: 1 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 20.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1 cm, around the corner circle radius: 1 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Possion’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 21.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.75 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 21.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.75 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 22.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.75 cm, around the corner circle radius: 1.75 cm; (b) tenth order natural frequency band diagram of a single cell structure. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 22.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.75 cm, around the corner circle radius: 1.75 cm; (b) tenth order natural frequency band diagram of a single cell structure. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 23.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.2543 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 23.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.2543 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 24.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.2543 cm, around the corner circle radius: 0.5 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 24.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.2543 cm, around the corner circle radius: 0.5 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 25.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.25 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 25.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.25 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 26.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.25 cm; around the corner circle radius: 1.25 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 26.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.25 cm; around the corner circle radius: 1.25 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 27.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 2 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 27.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 2 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 28.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 2 cm, around the corner circle radius: 2 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 28.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 2 cm, around the corner circle radius: 2 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 29.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.3055 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 29.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.3055 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 30.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.3055 cm, around the corner circle radius: 0.4 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 30.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.3055 cm, around the corner circle radius: 0.4 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 31.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.75 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 31.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.75 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio:. (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 32.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.75 cm, around the corner circle radius: 0.75 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 32.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 0.75 cm, around the corner circle radius: 0.75 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 33.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.5 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 33.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.5 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 34.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.5 cm; around the corner circle radius: 1.5 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.
Figure 34.
The diagram of the cell structure and the analysis curve is given, (a) the heteromorphic negative Poisson’s ratio cell structure added circular mass blocks to the inner circle radius: 1.5 cm; around the corner circle radius: 1.5 cm; (b) tenth order natural frequency band diagram of a single cell structure, side thickness: , Poisson’s ratio: . (c) a fixed displacement 1 m upper plane of the base. (d) frequency response curve of the honeycomb base.