Combinational Optimization of the WRF Physical Parameterization Schemes to Improve Numerical Sea Breeze Prediction Using Micro-Genetic Algorithm
Abstract
:1. Introduction
2. Data and Sea Breeze Cases
3. Methods
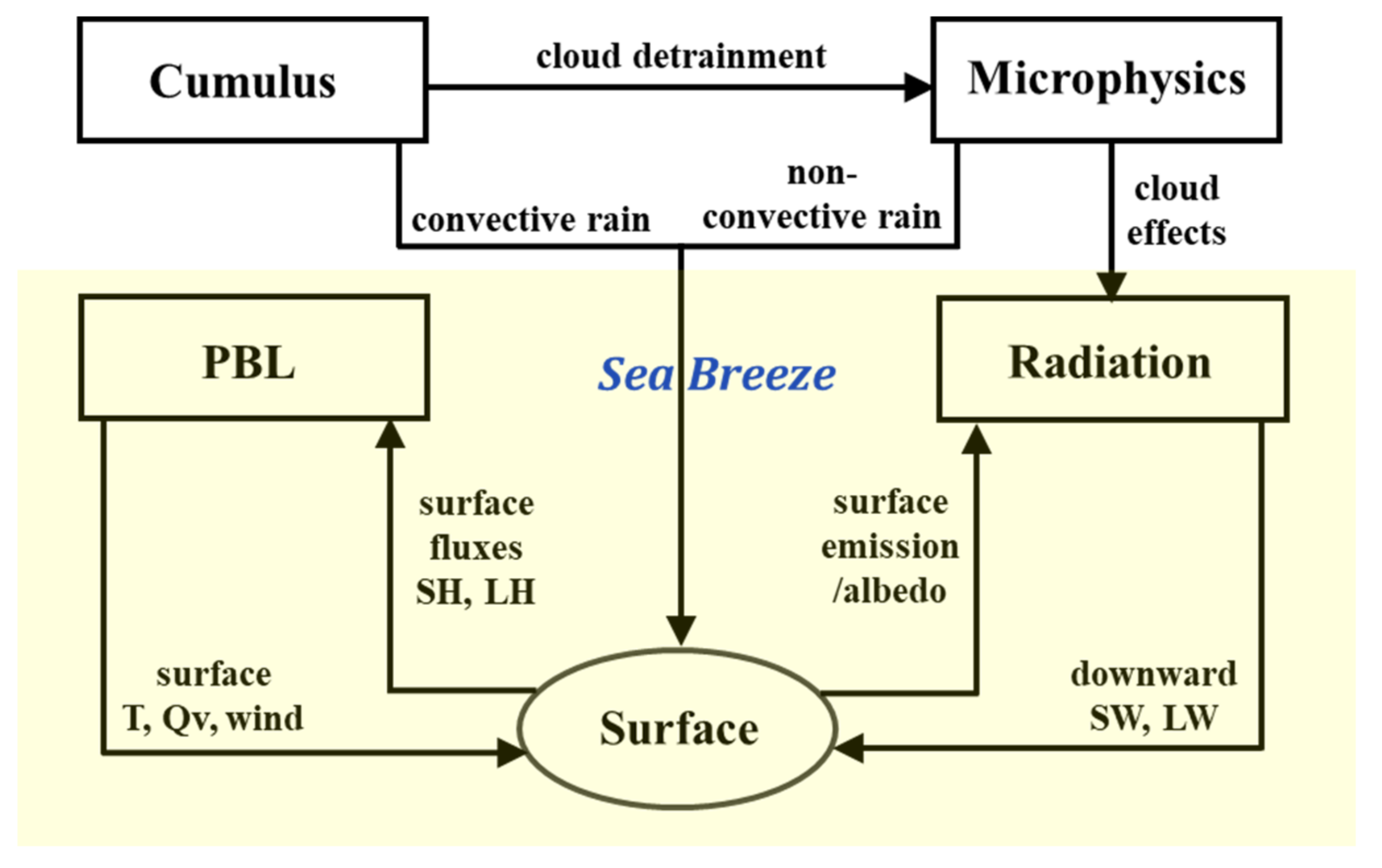
3.1. WRF Physical Parameterization Schemes
3.1.1. Planetary Boundary Layer Scheme
3.1.2. Land Surface Scheme
3.1.3. Radiation Scheme
3.2. Micro-Genetic Algorithm
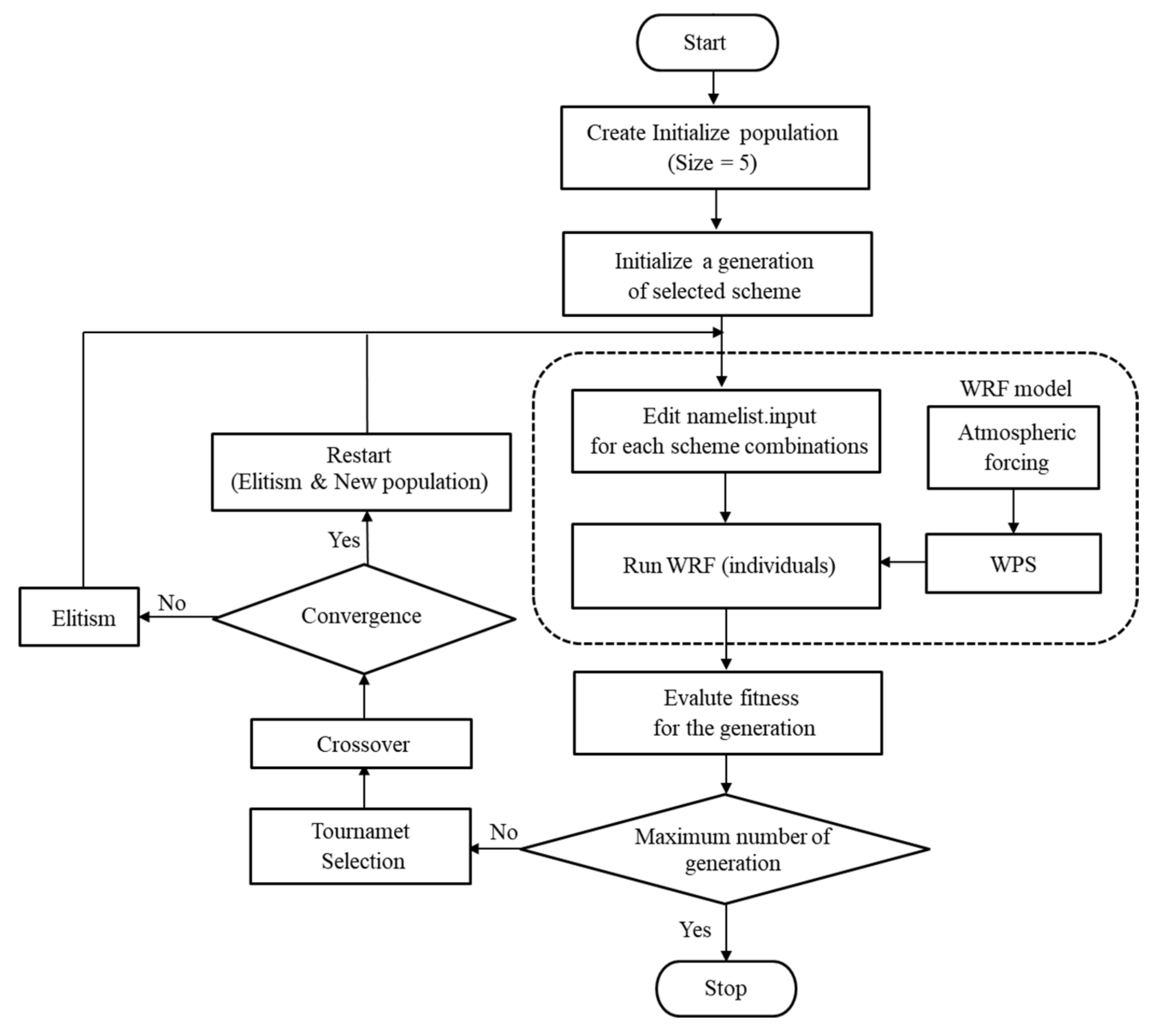
3.2.1. WRF-μGA System
3.2.2. Fitness Function
4. Experimental Designs
4.1. WRF Model
4.2. Optimization
5. Results and Discussion
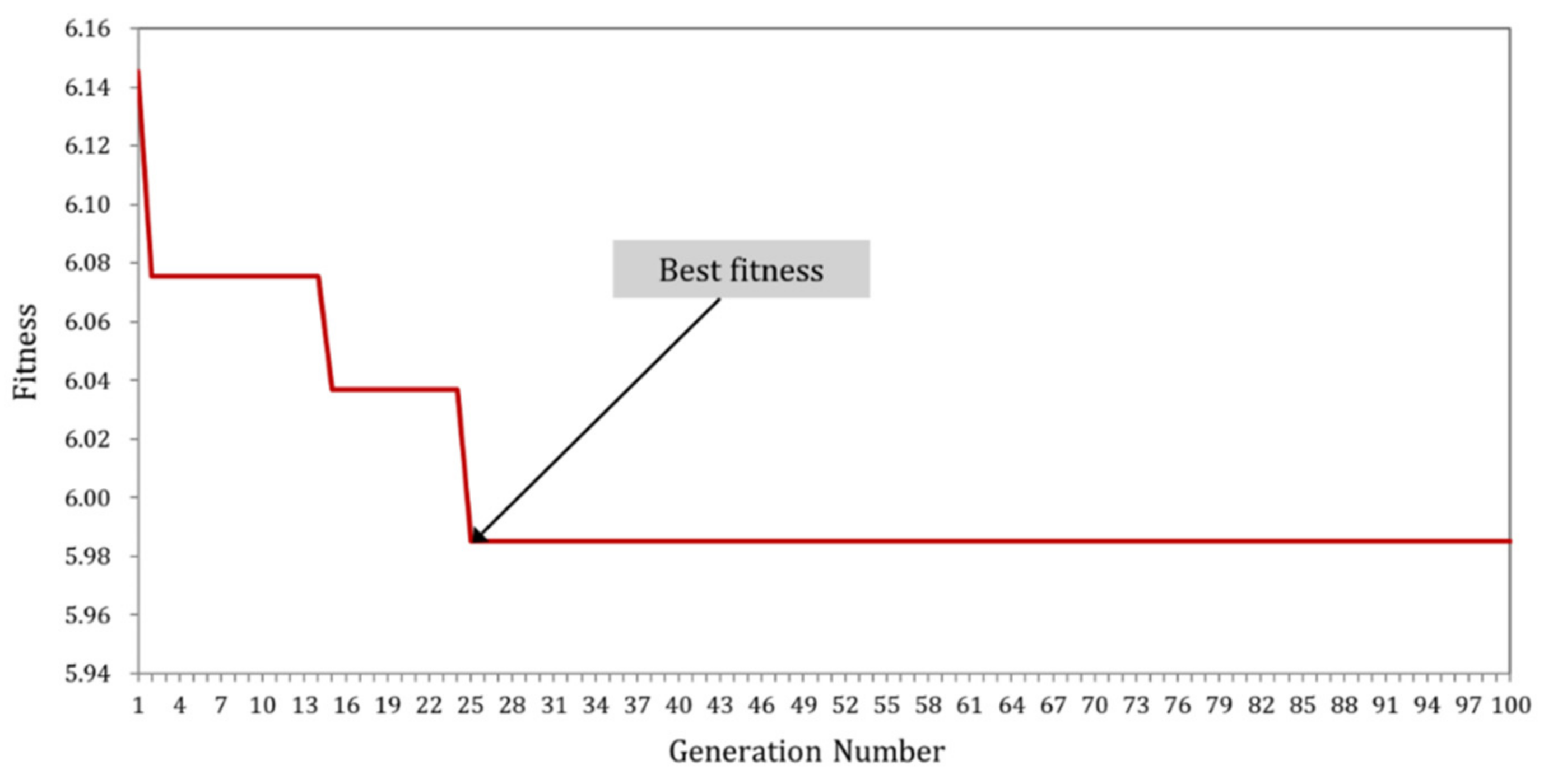
5.1. Applications of WRF-μGA System
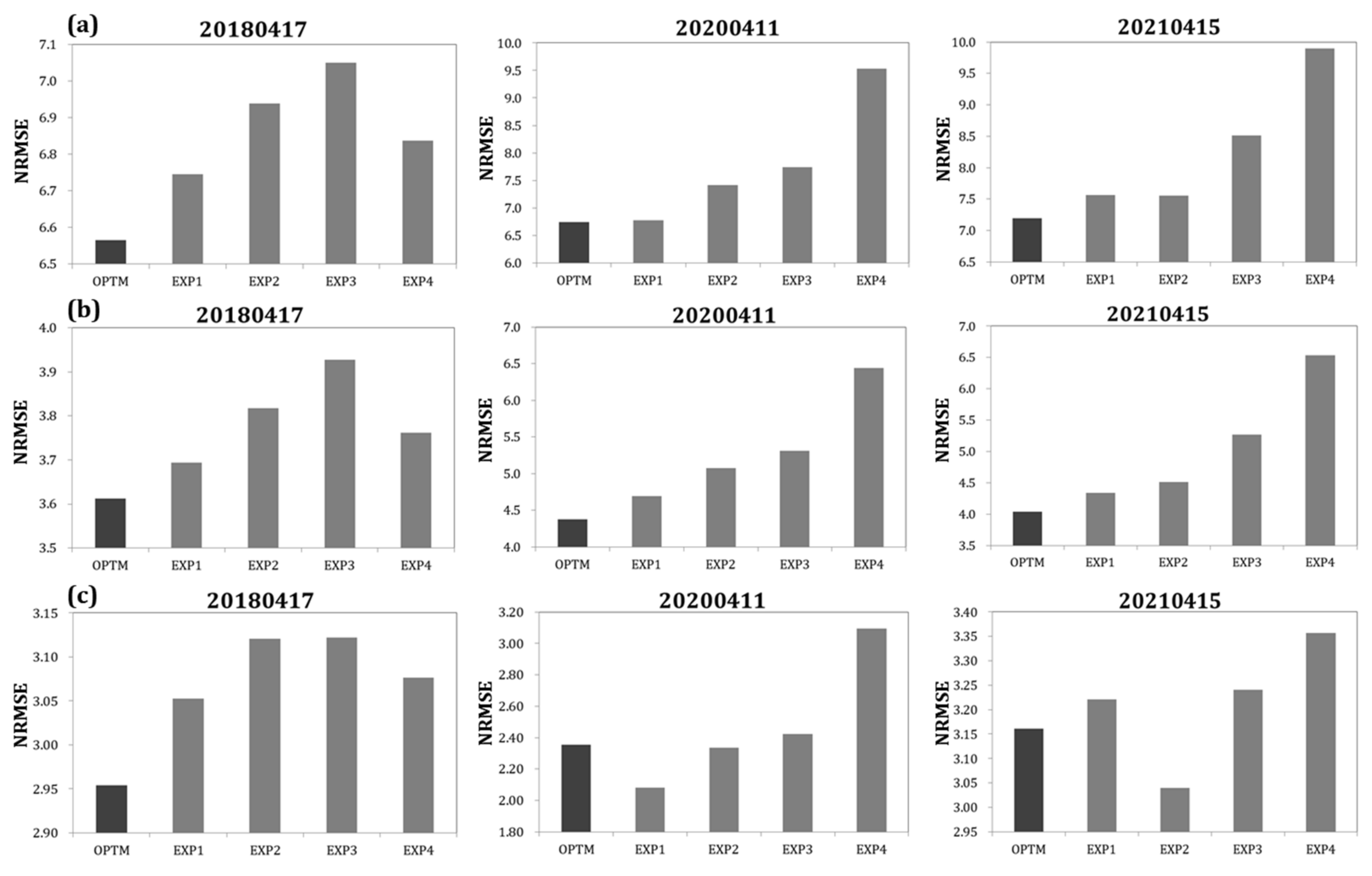
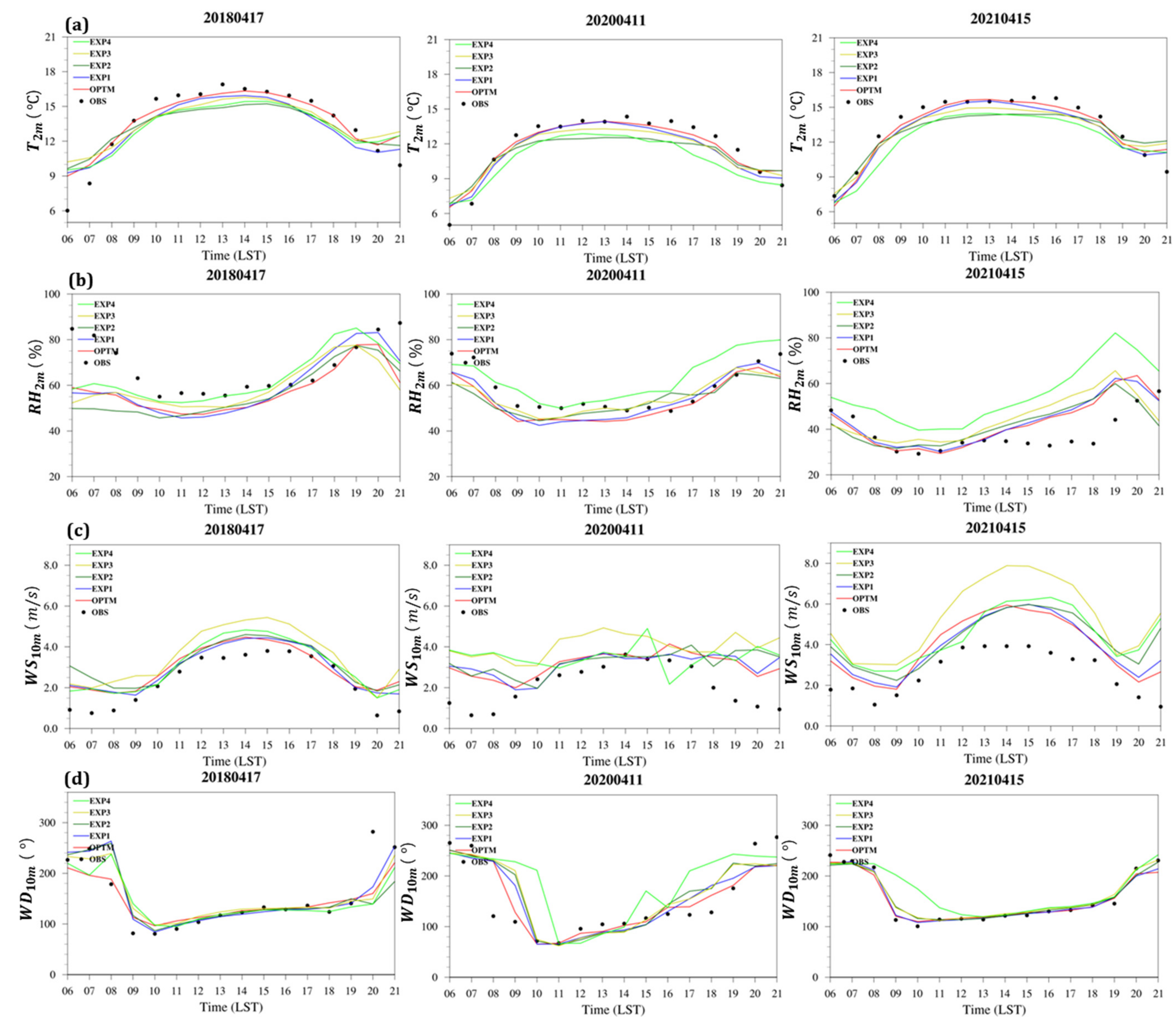
5.2. Validation
5.3. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Simpson, J.E. Sea Breeze and Local Winds; Cambridge University Press: Cambridge, UK, 1994; 234p. [Google Scholar]
- Miller, S.T.K.; Keim, B.D.; Talbot, R.W.; Mao, H. Sea breeze: Structure, forecasting, and impacts. Rev. Geophys. 2003, 41, 31. [Google Scholar] [CrossRef] [Green Version]
- Bhate, J.; Kesarkar, A.P.; Karipot, A.; Subrahamanyam, D.B.; Rajasekhar, M.; Sathiyamoorthy, V.; Kishtawal, C.M. A sea breeze induced thunderstorm over an inland station over Indian South Peninsula—A case study. J. Atmos. Sol. Terr. Phys. 2016, 148, 96–111. [Google Scholar] [CrossRef]
- Lee, D.-I.; Han, Y.-H. Vertical distribution of aerosol concentrations in the boundary layer observed by a tethered balloon: Part II: Distributions of aerosol concentrations in relation to the sea breeze front. J. Korean Meteor. Soc. 1992, 28, 497–507. [Google Scholar]
- Salvador, N.; Loriato, A.G.; Santiago, A.; Albuquerque, T.T.A.; Reis, N.C., Jr.; Santos, J.M.; Landulfo, E.; Moreira, G.; Lopes, F.; Held, G. Study of the thermal internal boundary layer in sea breeze conditions using different parameterizations: Application of the WRF model in the Greater Vitória region. Rev. Bras. Meteorol. 2016, 31, 593–609. [Google Scholar] [CrossRef] [Green Version]
- Nam, H.G.; Kim, B.G.; Han, S.O.; Lee, C.K.; Lee, S.S. Characteristics of easterly-induced snowfall in Yeongdong and its relationship to air-sea temperature difference. Asia Pac. J. Atmos. Sci. 2014, 50, 541–552. [Google Scholar] [CrossRef]
- Park, M.-S.; Chae, J.-H. Features of sea–land-breeze circulation over the Seoul metropolitan area. Geosci. Lett. 2018, 5, 28. [Google Scholar] [CrossRef] [Green Version]
- Lim, H.-J.; Lee, Y.-H. Characteristics of sea breezes at coastal area in Boseong. Atmosphere 2019, 29, 41–51, (In Korean with English abstract). [Google Scholar]
- Park, S.K.; Park, S. On a flood-producing coastal mesoscale convective storm associated with the Kor’easterlies: Multi-data analyses using remote sensing, in-situ observations and storm-scale model simulations. Remote Sens. 2020, 12, 1532. [Google Scholar] [CrossRef]
- Lee, J.G.; Lee, J.S. A numerical study of Yeongdong heavy snowfall events associated with easterly. J. Korean Meteor. Soc. 2003, 39, 475–490, (In Korean with English abstract). [Google Scholar]
- Park, S.K.; Lee, E. Synoptic features of orographically enhanced heavy rainfall on the east coast of Korea associated with Typhoon Rusa (2002). Geophys. Res. Lett. 2007, 34, L02803. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.G.; Kim, Y.J. A numerical simulation study using WRF of a heavy snowfall event in the Yeongdong coastal area in relation to the northeasterly. Atmosphere 2008, 18, 339–354, (In Korean with English abstract). [Google Scholar]
- Tsai, C.-L.; Kim, K.; Liou, Y.-C.; Lee, G.; Yu, C.-K. Impacts of topography on airflow and precipitation in the Pyeongchang area seen from multiple-Doppler radar observations. Mon. Wea. Rev. 2018, 146, 3401–3424. [Google Scholar] [CrossRef]
- Hwang, H.W.; Eun, S.H.; Kim, B.G.; Park, S.J.; Park, G.M. Occurrence characteristics of sea breeze in the Gangneung region for 2009~2018. Atmosphere 2020, 30, 221–236, (In Korean with English abstract). [Google Scholar]
- Srinivas, C.V.; Venkatesan, R.; Singh, A.B. Sensitivity of mesoscale simulations of land–sea breeze to boundary layer turbulence parameterization. Atmos. Environ. 2007, 41, 2534–2548. [Google Scholar] [CrossRef]
- Steele, C.J.; Dorling, S.R.; von Glasow, R.; Bacon, J. Idealized WRF model sensitivity simulations of sea breeze types and their effects on offshore windfields. Atmos. Chem. Phys. 2013, 13, 443–461. [Google Scholar] [CrossRef] [Green Version]
- Reddy, B.R.; Srinivas, C.V.; Shekhar, S.S.; Baskaran, R.; Venkatraman, B. Impact of land surface physics in WRF on the simulation of sea breeze circulation over southeast coast of India. Meteorol. Atmos. Phys. 2020, 132, 925–943. [Google Scholar] [CrossRef]
- Salvador, N.; Reis, N.C., Jr.; Santos, J.M.; Albuquerque, T.T.A.; Loriato, A.G.; Delbarre, H.; Augustin, P.; Sokolov, A.; Moreira, D.M. Evaluation of Weather Research and Forecasting model parameterizations under sea-breeze conditions in a North Sea coastal environment. J. Meteorol. Res. 2016, 30, 998–1018. [Google Scholar] [CrossRef]
- Hock, N.; Pu, Z. Numerical simulations of the Florida sea breeze and its associated convection with the WRF model. In Proceedings of the 28th Conference on Weather Analysis and Forecasting/24th Conference on Numerical Weather Prediction, Seattle, WA, USA, 25 January 2017; American Meteorological Society: Boston, MA, USA, 2017; p. 1181. [Google Scholar]
- Lee, Y.H.; Park, S.K.; Chang, D.-E. Parameter estimation using the genetic algorithm and its impact on quantitative precipitation forecast. Ann. Geophys. 2006, 24, 3185–3189. [Google Scholar] [CrossRef]
- Yu, X.; Park, S.K.; Lee, Y.H.; Choi, Y.-S. Quantitative precipitation forecast of a tropical cyclone through optimal parameter estimation in a convective parameterization. SOLA 2013, 9, 36–39. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; Yu, X.; Park, S.K.; Choi, Y.-S.; Myoung, B. Assessing optimal set of implemented physical parameterization schemes in a multi-physics land surface model using genetic algorithm. Geosci. Model. Dev. 2014, 7, 2517–2529. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; Park, S.K.; Yu, X. Scheme-based optimization of land surface model using a micro-genetic algorithm: Assessment of its performance and usability for regional applications. SOLA 2015, 11, 129–133. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Park, S.K. A micro-genetic algorithm (GA v1.7.1 a) for combinatorial optimization of physics parameterizations in the Weather Research and Forecasting model (v4.0.3) for quantitative precipitation forecast in Korea. Geosci. Model. Dev. 2021, 14, 6241–6255. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial System: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975; 183p. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning, 13th ed.; Addison-Wesely Publishing Company: Reading, MA, USA, 1989; 412p. [Google Scholar]
- Hu, Y.M.; Ding, Y.H.; Shen, T.L. Validation of a receptor/dispersion model coupled with a genetic algorithm using synthetic data. J. Appl. Meteorol. Climatol. 2006, 45, 476–490. [Google Scholar]
- Bastani, M.; Kholghi, M.; Rakhshandehroo, G.R. Inverse modeling of variable-density groundwater flow in a semi-arid area in Iran using a genetic algorithm. Hydrogeol. J. 2010, 18, 1191–1203. [Google Scholar] [CrossRef]
- Krishnakumar, K. Micro-genetic algorithms for stationary and non-stationary function optimization. In Intelligent Control and Adaptive Systems, Proceedings of SPIE 1196, 1989 Symposium on Visual Communications, Image Processing, and Intelligent Robotics Systems, Philadelphia, PA, USA, 1–3 November 1989; International Society for Optical Engineering: Bellingham, WA, USA, 1990; pp. 289–296. [Google Scholar]
- Dudhia, J. A history of mesoscale model development. Asia-Pac. J. Atmos. Sci. 2014, 50, 121–131. [Google Scholar] [CrossRef]
- Banks, R.F.; Tiana-Alsina, J.; Rocadenbosch, F.; Baldasano, J.M. Performance evaluation of the boundary-layer height from lidar and the Weather Research and Forecasting model at an urban coastal site in the north-east Iberian Peninsula. Bound. Layer Meteorol. 2015, 157, 265–292. [Google Scholar] [CrossRef] [Green Version]
- Banks, R.F.; Tiana-Alsina, J.; Baldasano, J.M.; Rocadenbosch, F.; Papayannis, A.; Solomos, S.; Tzanis, C.G. Sensitivity of boundary-layer variables to PBL schemes in the WRF model based on surface meteorological observations, lidar, and radiosondes during the HygrA-CD campaign. Atmos. Res. 2016, 176, 185–201. [Google Scholar] [CrossRef]
- Avolio, E.; Federico, S.; Miglietta, M.M.; Feudo, T.L.; Calidonna, C.R.; Sempreviva, A.M. Sensitivity analysis of WRF model PBL schemes in simulating boundary-layer variables in southern Italy: An experimental campaign. Atmos. Res. 2017, 192, 58–71. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Wea. Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Pleim, J.E. A combined local and nonlocal closure model for the atmospheric boundary layer. Part I: Model description and testing. J. Appl. Meteorol. Climatol. 2007, 46, 1383–1395. [Google Scholar]
- Angevine, H.J.; Mauritsen, T. Performance of an eddy diffusivity-mass flux scheme for shallow cumulus boundary layers. Mon. Wea. Rev. 2010, 138, 2895–2912. [Google Scholar] [CrossRef] [Green Version]
- Janjić, Z.I. Nonsingular Implementation of the Mellor-Yamada Level 2.5 Scheme in the NCEP Meso Model. NCEP Office Note 437; National Centers for Environmental Prediction: College Park, MD, USA, 2002; 61p. [Google Scholar]
- Sukoriansky, S.; Galperin, B.; Perov, V. Application of a new spectral theory of stably stratified turbulence to the atmospheric boundary layer over sea ice. Bound. Layer Meteorol. 2005, 117, 231–257. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An improved Mellor–Yamada level-3 model: Its numerical stability and application to a regional prediction of advection fog. Bound. Layer Meteorol. 2006, 119, 397–407. [Google Scholar] [CrossRef]
- Bougeault, P.; Lacarrere, P. Parameterization of orography-induced turbulence in a mesobeta–scale model. Mon. Wea. Rev. 1989, 117, 1872–1890. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Park, S. A new moist turbulence parameterization in the Community Atmosphere Model. J. Clim. 2009, 22, 3422–3448. [Google Scholar] [CrossRef]
- Martilli, A.; Clappier, A.; Rotach, M.W. An urban surface exchange parameterisation for mesoscale models. Bound. Layer Meteorol. 2002, 104, 261–304. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Holland, M.M.; Gent, P.R.; Ghan, S.; Kay, J.E.; Kushner, P.J.; Marshall, S. The Community Earth System Model: A framework for collaborative research. Bull. Am. Meteorol. Soc. 2013, 94, 1339–1360. [Google Scholar] [CrossRef]
- Dudhia, J. A multi-layer soil temperature model for MM5. In Proceedings of the Sixth PSU/NCAR Mesoscale Model Users’ Workshop, Boulder, CO, USA, 22–24 July 1996; pp. 22–24. [Google Scholar]
- Benjamin, S.G.; Grell, G.A.; Brown, J.M.; Smirnova, T.G.; Bleck, R. Mesoscale weather prediction with the RUC hybrid isentropic-terrain-following coordinate model. Mon. Wea. Rev. 2004, 132, 473–494. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface–hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Wea. Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef] [Green Version]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. Atmos. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Xia, Y. The community Noah land surface model with multi-parameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, D12109. [Google Scholar] [CrossRef] [Green Version]
- Smirnova, T.G.; Brown, J.M.; Benjamin, S.G.; Kenyon, J.S. Modifications to the Rapid Update Cycle Land Surface Model (RUC LSM) available in the Weather Research and Forecast (WRF) model. Mon. Wea. Rev. 2016, 144, 1851–1865. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Collins, W.D.; Rasch, P.J.; Boville, B.A.; Hack, J.J.; McCaa, J.R.; Williamson, D.L.; Kiehl, J.T.; Briegleb, B. Description of the NCAR Community Atmosphere Model (CAM 3.0); NCAR Technical Note, NCAR/TN-464+STR; Technical Report; NCAR: Boulder, CO, USA, 2004. [Google Scholar]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the long-wave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
- Jiménez, P.A.; Dudhia, J. Improving the representation of resolved and unresolved topographic effects on surface wind in the WRF model. J. Appl. Meteorol. Climatol. 2012, 51, 300–316. [Google Scholar] [CrossRef] [Green Version]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. Climatol. 2004, 43, 170–181. [Google Scholar] [CrossRef] [Green Version]
- Lim, K.-S.S.; Hong, S.-Y. Development of an effective double-moment cloud microphysics scheme with prognostic Cloud Condensation Nuclei (CCN) for weather and climate models. Mon. Wea. Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Shu, J.; Yu, X. Improvement of typhoon rainfall prediction based on optimization of the Kain-Fritsch convection parameterization scheme using a micro-genetic algorithm. Front. Earth Sci. 2019, 13, 721–732. [Google Scholar] [CrossRef]
- Rajeswari, J.R.; Srinivas, C.V.; Rao, T.N.; Venkatraman, B. Impact of land surface physics on the simulation of boundary layer characteristics at a tropical coastal station. Atmos. Res. 2020, 238, 104888. [Google Scholar] [CrossRef]
- Lombardo, K.; Colle, B.A. Processes controlling the structure and longevity of two quasi-linear convective systems crossing the southern New England coast. Mon. Wea. Rev. 2013, 141, 3710–3734. [Google Scholar] [CrossRef] [Green Version]
- Tyagi, B.; Magliulo, V.; Finardi, S.; Gasbarra, D.; Carlucci, P.; Toscano, P.; Gioli, B. Performance analysis of planetary boundary layer parameterization schemes in WRF modeling set up over southern Italy. Atmosphere 2018, 9, 272. [Google Scholar] [CrossRef] [Green Version]
- Hariprasad, K.B.R.R.; Srinivas, C.V.; Singh, A.B.; Rao, S.V.B.; Baskaran, R.; Venkatraman, B. Numerical simulation and intercomparison of boundary layer structure with different PBL schemes in WRF using experimental observations at a tropical site. Atmos. Res. 2014, 145, 27–44. [Google Scholar] [CrossRef]
- Dewi, D.P.R.; Fatmasari, D.; Gustari, I. Simulation of sea breeze events in gulf of Jakarta under different synoptic condition: An application of WRF model. In IOP Conf. Ser.: Earth Environ. Sci., Proceedings of the International Conference on Tropical Meteorology and Atmospheric Sciences, Bandung, Indonesia, 19–20 September 2018; IOP publishing: Bristol, UK, 2019; Volume 303, p. 012045. [Google Scholar] [CrossRef] [Green Version]
- Papanastasiou, D.K.; Melas, D.; Lissaridis, I. Study of wind field under sea breeze conditions; an application of WRF model. Atmos. Res. 2010, 98, 102–117. [Google Scholar] [CrossRef]
- Yerramilli, A.; Challa, V.S.; Dodla, V.B.R.; Dasari, H.P.; Young, J.H.; Patrick, C.; Swanier, S.J. Simulation of surface ozone pollution in the central gulf coast region using WRF/Chem Model: Sensitivity to PBL and Land Surface Physics. Adv. Meteorol. 2010, 2010, 319138. [Google Scholar] [CrossRef] [Green Version]
- Jain, S. WRF model analysis of land-surface processes over Jaipur Region. Int. J. Sci. Eng. Technol. 2015, 6, 1276–1284. [Google Scholar]
- Miao, J.-F.; Wyser, K.; Chen, D.; Ritchie, H. Impacts of boundary layer turbulence and land surface process parameterizations on simulated sea breeze characteristics. Ann. Geophys. 2009, 27, 2303–2320. [Google Scholar] [CrossRef]
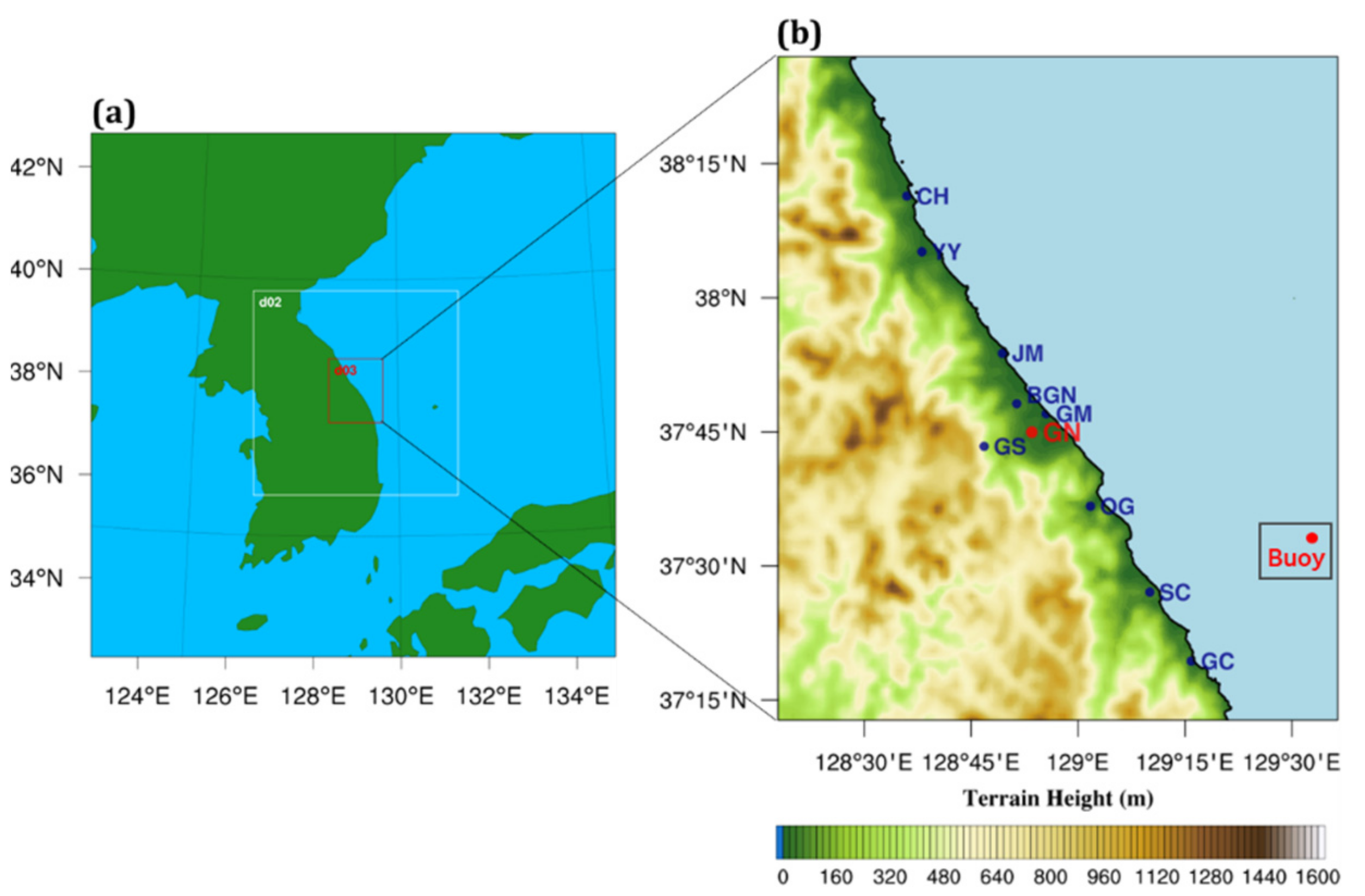
| Station | Latitude (°N) | Longitude (°E) | Altitude (m) |
|---|---|---|---|
| CheongHo (CH) | 38.19 | 128.60 | 3.65 |
| YangYang (YY) | 38.09 | 128.63 | 4.31 |
| JuMunjin (JM) | 37.90 | 128.82 | 8.94 |
| GangMun (GM) | 37.79 | 128.93 | 6.61 |
| Gangneung-Seongsan (GS) | 37.73 | 128.78 | 455.97 |
| OkGye (OG) | 37.61 | 129.03 | 58.41 |
| SamCheok (SC) | 37.45 | 129.17 | 68.48 |
| GungChon (GC) | 37.33 | 129.27 | 14.07 |
| BukGangNeung (BGN) | 37.81 | 128.86 | 75.24 |
| PBL Schemes | Land Surface Schemes | Radiation Schemes | ||||
|---|---|---|---|---|---|---|
| Option | Scheme | Surface Layer Scheme | Option | Scheme | Option | Shortwave |
| 1 | YSU | MM5 similarity | 1 | TD | 1 | Dudhia |
| 2 | MYJ | ETA similarity | 2 | Noah | 3 | CAM |
| 4 | QNSE | QNSE | 3 | RUC | 4 | RRTMG |
| 5 | MYNN2 | MYNN | 4 | Noah-MP | Option | Longwave |
| 7 | ACM2 | MM5 similarity | 1 | RRTM | ||
| 8 | BouLac | MM5 similarity | 3 | CAM | ||
| 9 | UW | MM5 similarity | 4 | RRTMG | ||
| 10 | TEMP | TEMF | ||||
| Domain 1 | Domain 2 | Domain 3 | |
|---|---|---|---|
| Horizontal resolution | 9 km × 9 km | 3 km × 3 km | 1 km × 1 km |
| Vertical layers | 45 eta levels | ||
| Cumulus physics | Kain-Fritsch | Kain-Fritsch | - |
| Microphysics | WDM 5 | WDM 5 | WDM 5 |
| Initial and Boundary conditions | NCEP FNL Global Analysis Data (0.25° × 0.25°) | ||
| Initial time | 2018/04/15 1800UTC | 2019/04/11 1800UTC | 2019/05/02 1800UTC |
| Forecast time | 18 h (6 h spin-up) | ||
| Land Surface Scheme | PBL Scheme | Shortwave Radiation Scheme | Longwave Radiation Scheme | References | |
|---|---|---|---|---|---|
| OPTM | Noah-MP | MYNN2 | RRTMG | RRTMG | - |
| EXP1 | Noah-MP | YSU | Dudhia | RRTM | [58] |
| EXP2 | Noah | YSU | Dudhia | RRTM | [62] |
| EXP3 | Noah | MYJ | Dudhia | RRTM | [18] |
| EXP4 | TD | MYJ | Dudhia | RRTM | [63] |
| OPTM | EXP1 | EXP2 | EXP3 | EXP4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | RMSE | PCC | Bias | RMSE | PCC | Bias | RMSE | PCC | Bias | RMSE | PCC | Bias | RMSE | PCC | ||
| 20180417 | ||||||||||||||||
| sfc | (°C) | −0.37 | 1.20 | 0.76 | −0.97 | 1.48 | 0.78 | −1.21 | 1.63 | 0.77 | −0.97 | 1.47 | 0.77 | −1.20 | 1.66 | 0.75 |
| −5.68 | 12.34 | 0.59 | −3.99 | 13.02 | 0.56 | −4.90 | 13.00 | 0.53 | −1.53 | 11.37 | 0.58 | 1.44 | 11.99 | 0.58 | ||
(m/s) | 0.40 | 1.23 | 0.53 | 0.39 | 1.17 | 0.62 | 0.50 | 1.18 | 0.64 | 1.12 | 1.66 | 0.63 | 0.61 | 1.32 | 0.63 | |
| (°) | 8.58 | 37.85 | 0.44 | 0.56 | 34.27 | 0.56 | 3.55 | 35.62 | 0.54 | 8.39 | 33.19 | 0.55 | 1.15 | 31.48 | 0.57 | |
| ver | (m/s) | −2.07 | 2.82 | 0.20 | −2.17 | 2.92 | 0.12 | −2.20 | 2.92 | 0.16 | −1.97 | 2.82 | 0.13 | −2.04 | 2.88 | 0.19 |
| (°) | −1.67 | 80.39 | 0.50 | −13.83 | 82.91 | 0.37 | −0.31 | 86.78 | 0.49 | 0.38 | 90.07 | 0.32 | 4.5 | 88.64 | 0.14 | |
| 20200411 | ||||||||||||||||
| sfc | (°C) | −0.86 | 1.29 | 0.80 | −1.10 | 1.55 | 0.79 | −1.71 | 1.95 | 0.75 | −1.35 | 1.70 | 0.77 | −2.06 | 2.36 | 0.74 |
| −2.50 | 11.69 | 0.36 | −1.46 | 12.71 | 0.34 | −0.09 | 11.24 | 0.34 | 1.30 | 12.83 | 0.25 | 7.81 | 15.82 | 0.22 | ||
(m/s) | 0.52 | 1.58 | 0.25 | 0.39 | 1.54 | 0.22 | 0.49 | 1.62 | 0.23 | 1.30 | 2.04 | 0.27 | 0.63 | 1.99 | 0.16 | |
| (°) | 8.24 | 55.74 | 0.35 | 8.74 | 58.61 | 0.33 | 15.15 | 66.61 | 0.26 | 11.23 | 64.62 | 0.29 | 13.93 | 83.79 | 0.23 | |
| ver | (m/s) | −0.51 | 1.73 | 0.45 | −0.49 | 1.62 | 0.56 | −0.99 | 1.98 | 0.35 | −0.10 | 1.87 | 0.45 | −1.28 | 2.37 | −0.01 |
| (°) | 16.64 | 76.16 | 0.50 | 6.28 | 64.30 | 0.48 | 12.05 | 66.54 | 0.61 | 18.39 | 75.21 | 0.41 | 42.18 | 96.63 | 0.33 | |
| 20210415 | ||||||||||||||||
| sfc | (°C) | −0.55 | 1.10 | 0.76 | −0.85 | 1.31 | 0.74 | −1.31 | 1.63 | 0.72 | −1.06 | 1.43 | 0.73 | −1.62 | 1.98 | 0.62 |
| 5.91 | 12.36 | 0.46 | 6.96 | 13.51 | 0.35 | 8.07 | 13.64 | 0.35 | 10.71 | 15.98 | 0.37 | 19.89 | 25.14 | 0.19 | ||
(m/s) | 0.87 | 2.03 | 0.39 | 0.78 | 1.93 | 0.41 | 0.91 | 1.86 | 0.48 | 2.21 | 2.83 | 0.57 | 1.12 | 2.038 | 0.49 | |
| (°) | 1.04 | 20.83 | 0.72 | 0.03 | 23.73 | 0.70 | 3.03 | 22.94 | 0.69 | 4.85 | 24.29 | 0.67 | 13.41 | 36.21 | 0.48 | |
| ver | (m/s) | −1.52 | 3.32 | −0.25 | −1.35 | 3.11 | −0.20 | −1.11 | 2.92 | −0.17 | −1.14 | 3.35 | −0.23 | −1.44 | 3.15 | −0.19 |
| (°) | 1.60 | 61.71 | 0.47 | 15.00 | 67.26 | 0.43 | 16.35 | 63.65 | 0.40 | 7.14 | 64.16 | 0.44 | 22.80 | 71.53 | 0.25 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, J.W.; Lim, S.; Park, S.K. Combinational Optimization of the WRF Physical Parameterization Schemes to Improve Numerical Sea Breeze Prediction Using Micro-Genetic Algorithm. Appl. Sci. 2021, 11, 11221. https://doi.org/10.3390/app112311221
Yoon JW, Lim S, Park SK. Combinational Optimization of the WRF Physical Parameterization Schemes to Improve Numerical Sea Breeze Prediction Using Micro-Genetic Algorithm. Applied Sciences. 2021; 11(23):11221. https://doi.org/10.3390/app112311221
Chicago/Turabian StyleYoon, Ji Won, Sujeong Lim, and Seon Ki Park. 2021. "Combinational Optimization of the WRF Physical Parameterization Schemes to Improve Numerical Sea Breeze Prediction Using Micro-Genetic Algorithm" Applied Sciences 11, no. 23: 11221. https://doi.org/10.3390/app112311221
APA StyleYoon, J. W., Lim, S., & Park, S. K. (2021). Combinational Optimization of the WRF Physical Parameterization Schemes to Improve Numerical Sea Breeze Prediction Using Micro-Genetic Algorithm. Applied Sciences, 11(23), 11221. https://doi.org/10.3390/app112311221







