Numerical Simulation of Dynamic Response and Evaluation of Flexural Damage of RC Columns under Horizontal Impact Load
Abstract
:1. Introduction
2. FE Model Validation
2.1. Test Overview
2.2. Numerical Model
2.2.1. Geometric Model
2.2.2. Material Model
- (1)
- Concrete
- (2)
- Rebar
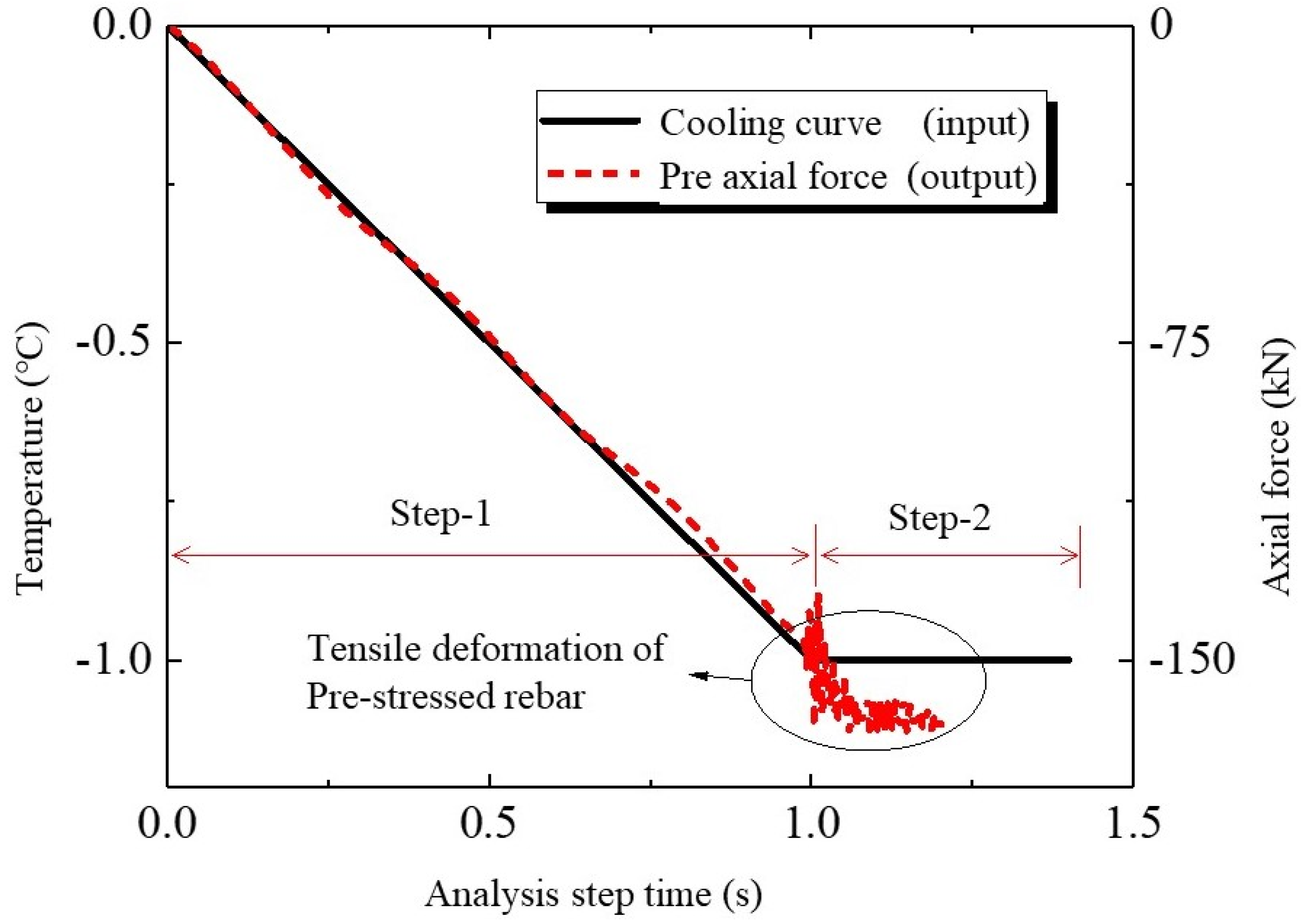
2.2.3. Application of the Axial Compression
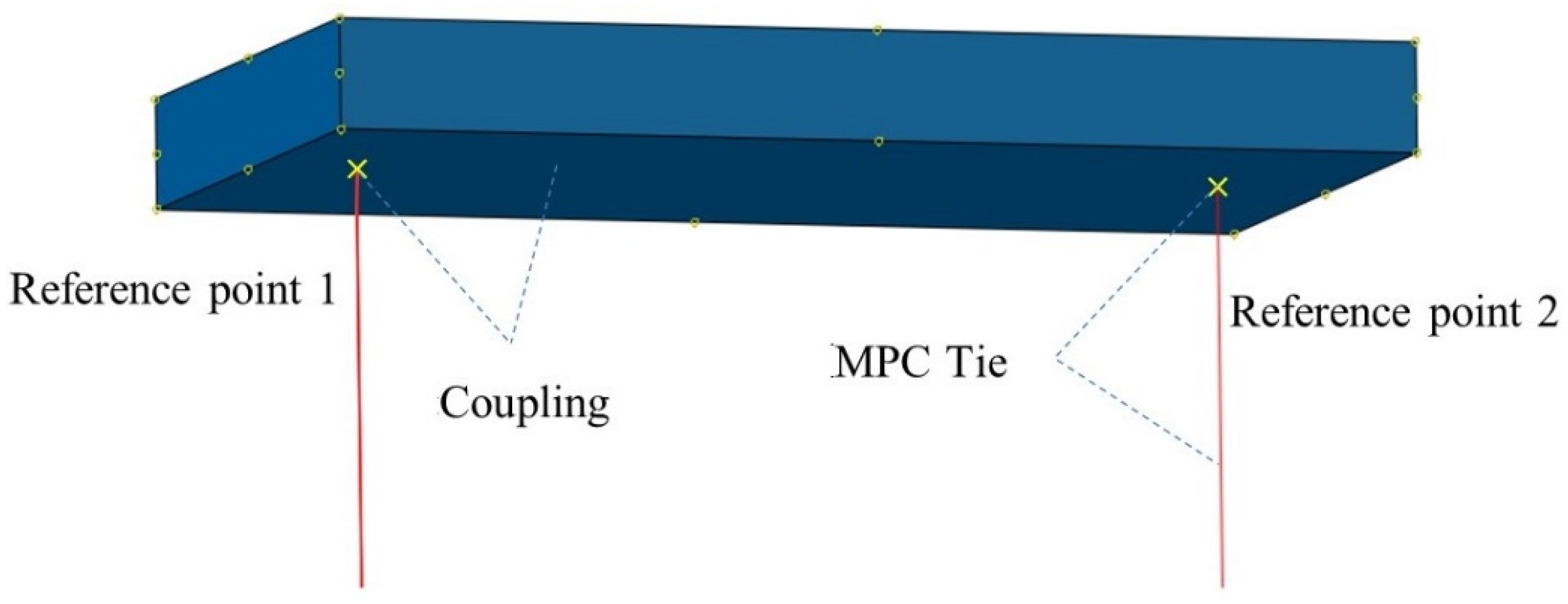
2.2.4. Contact and Boundary Conditions
2.2.5. Analysis Method
2.2.6. Mesh Size Sensitivity
2.3. Comparison of the Simulation and Test Results under Static Load
2.4. Comparison of the Simulation and Test Results under a Horizontal Impact
3. Load-Bearing Analysis of Columns under Impact Load
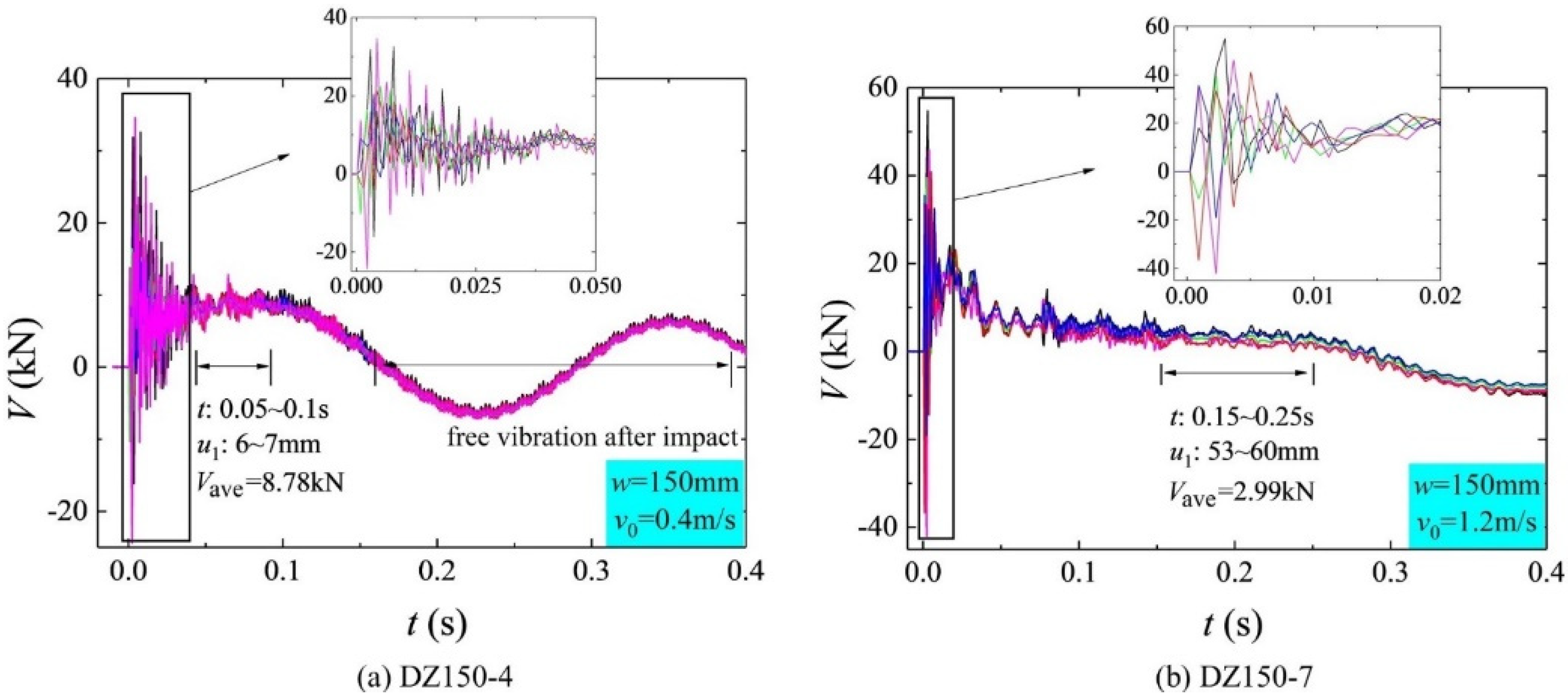
3.1. Cross-Sectional Shear V
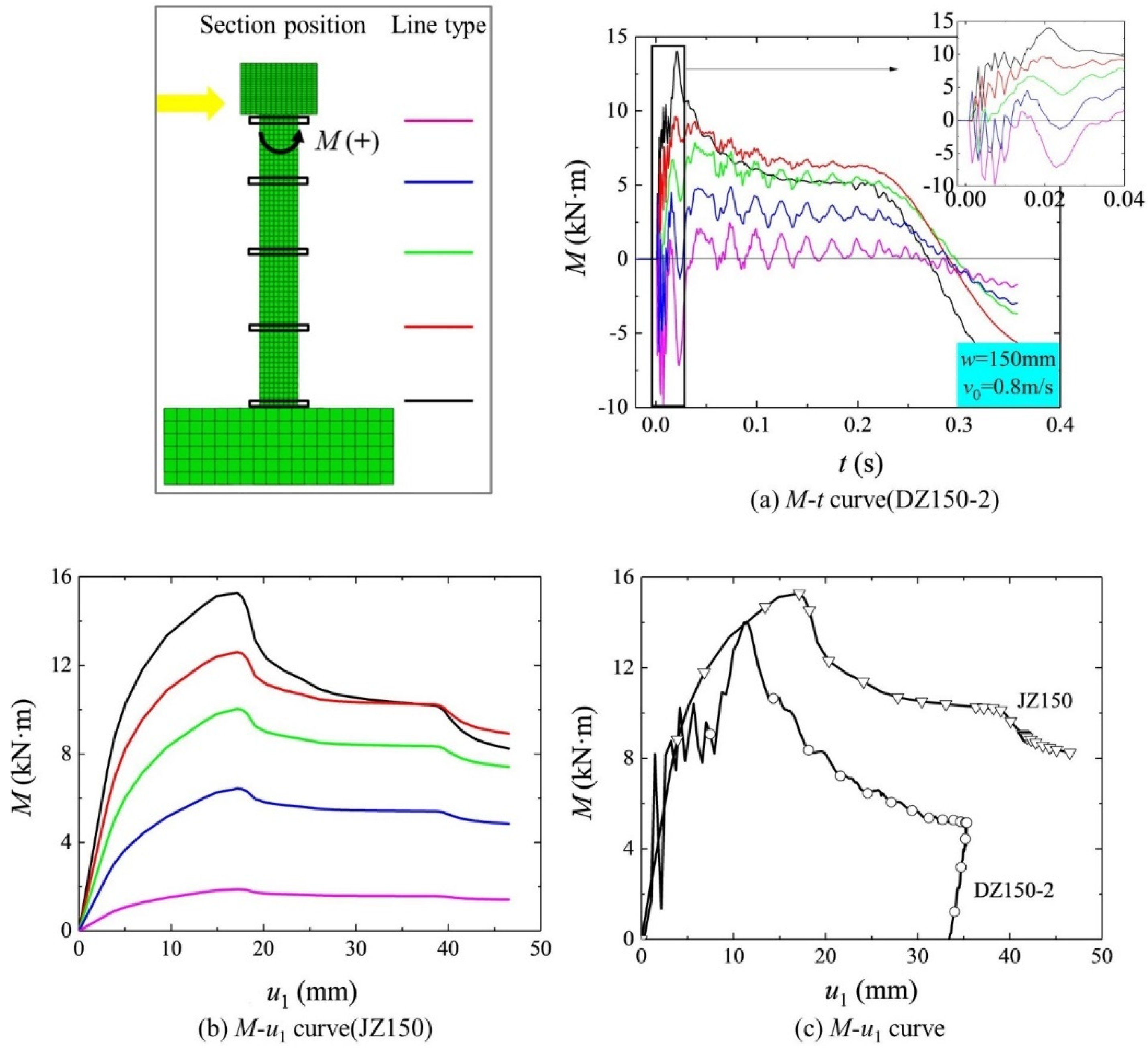
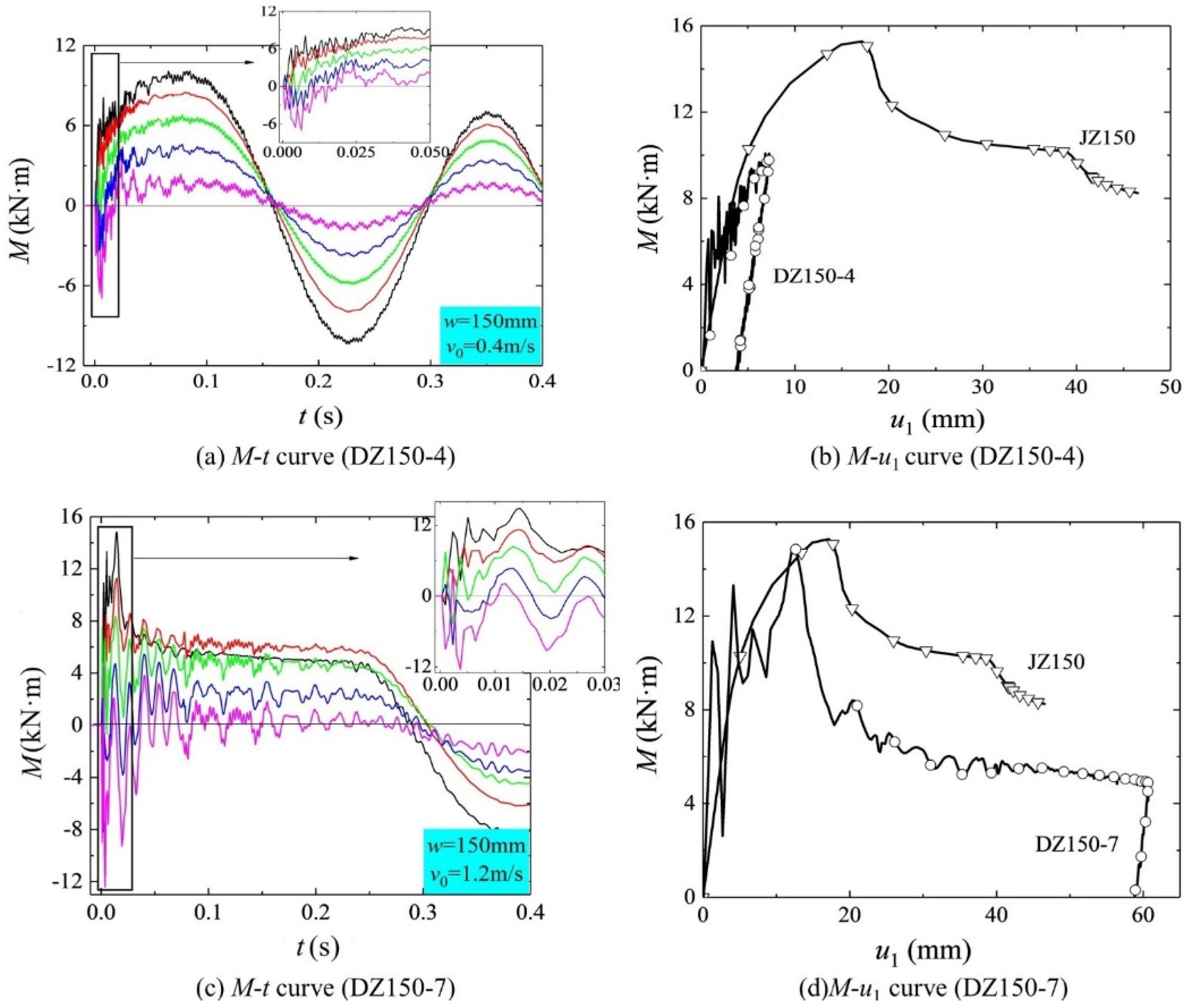
3.2. Cross-Sectional Bending Moment M
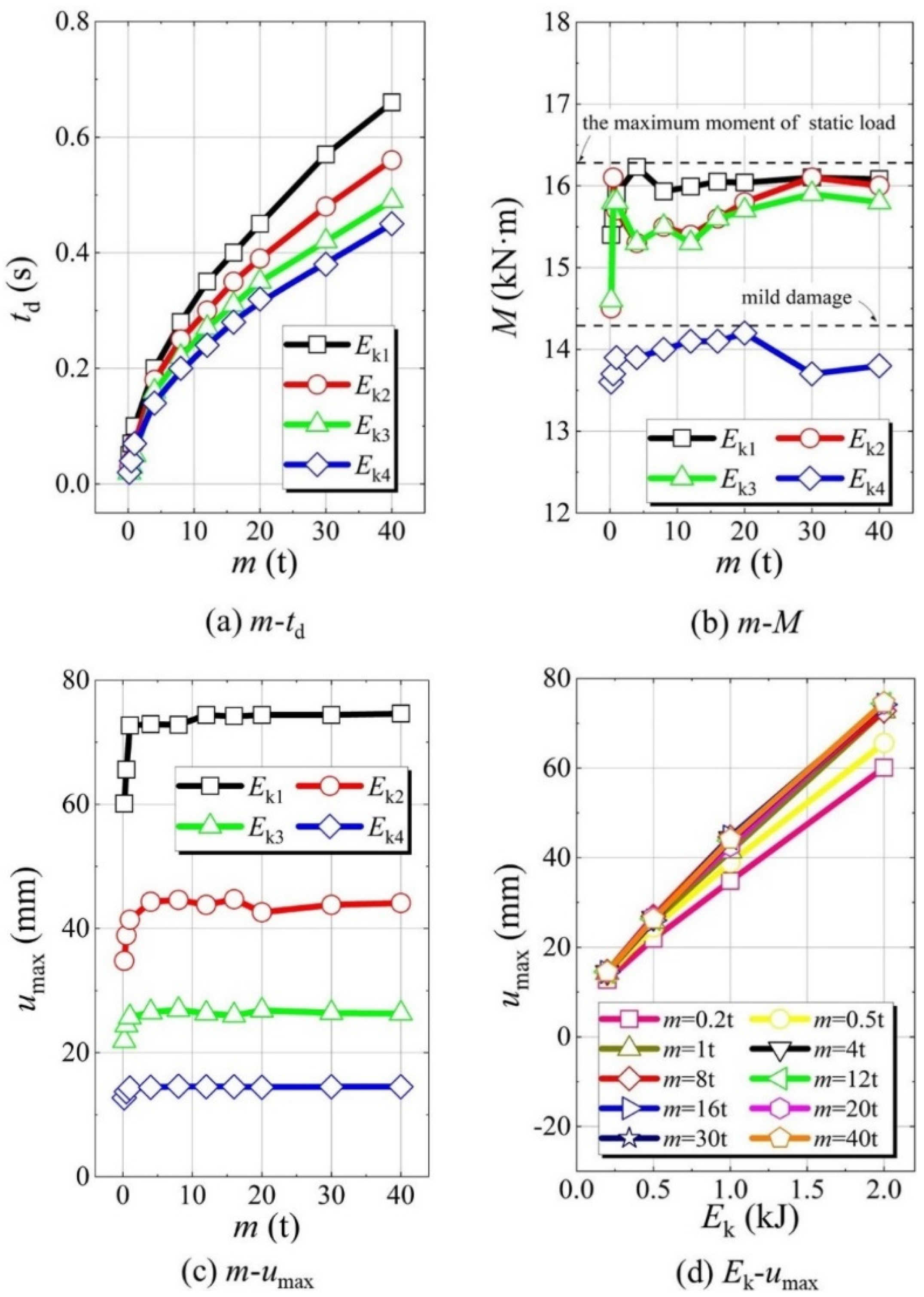
4. Effect of Different Combinations of m and v0 on the Dynamic Response of the Column with the Same Ek
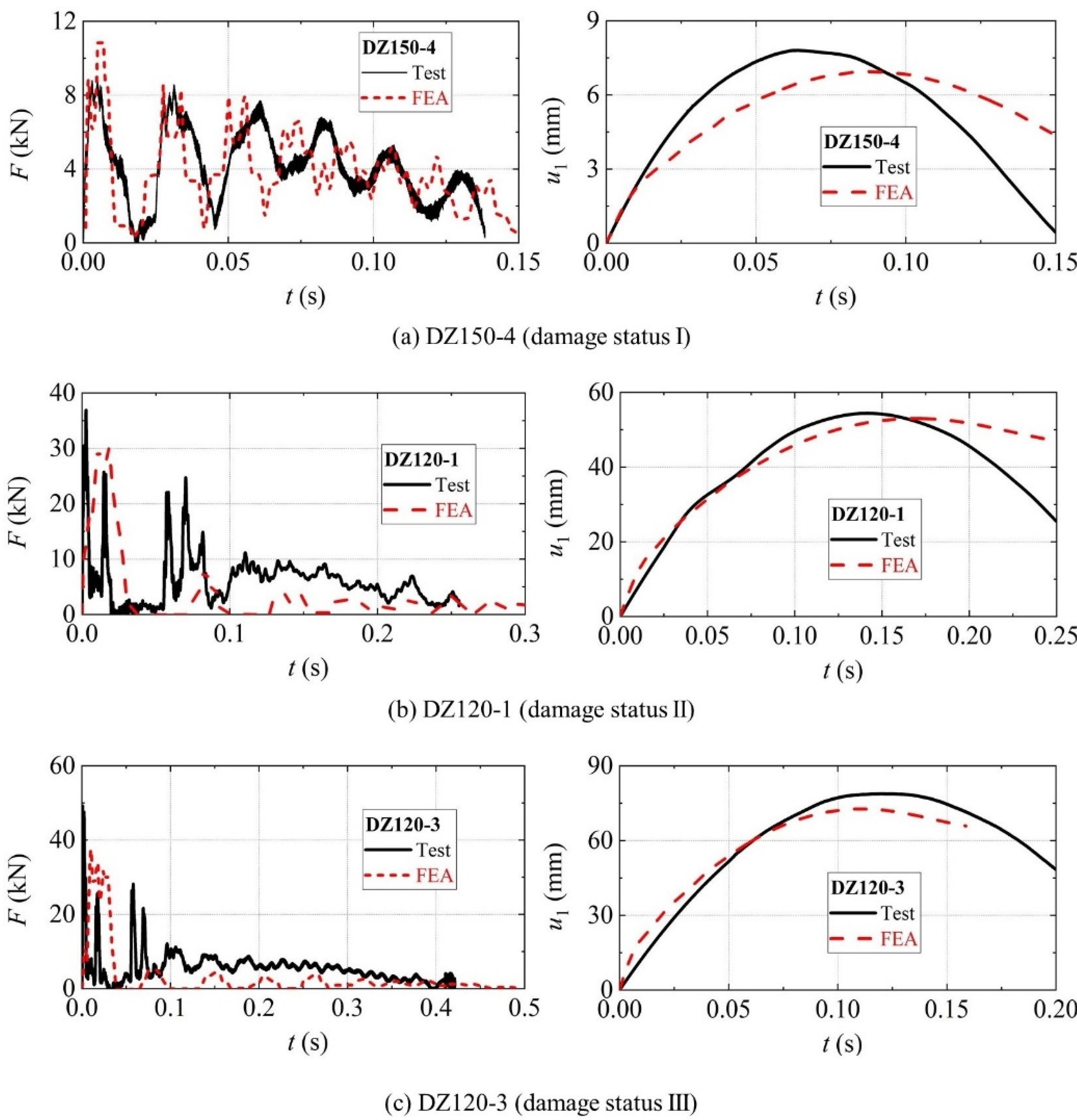
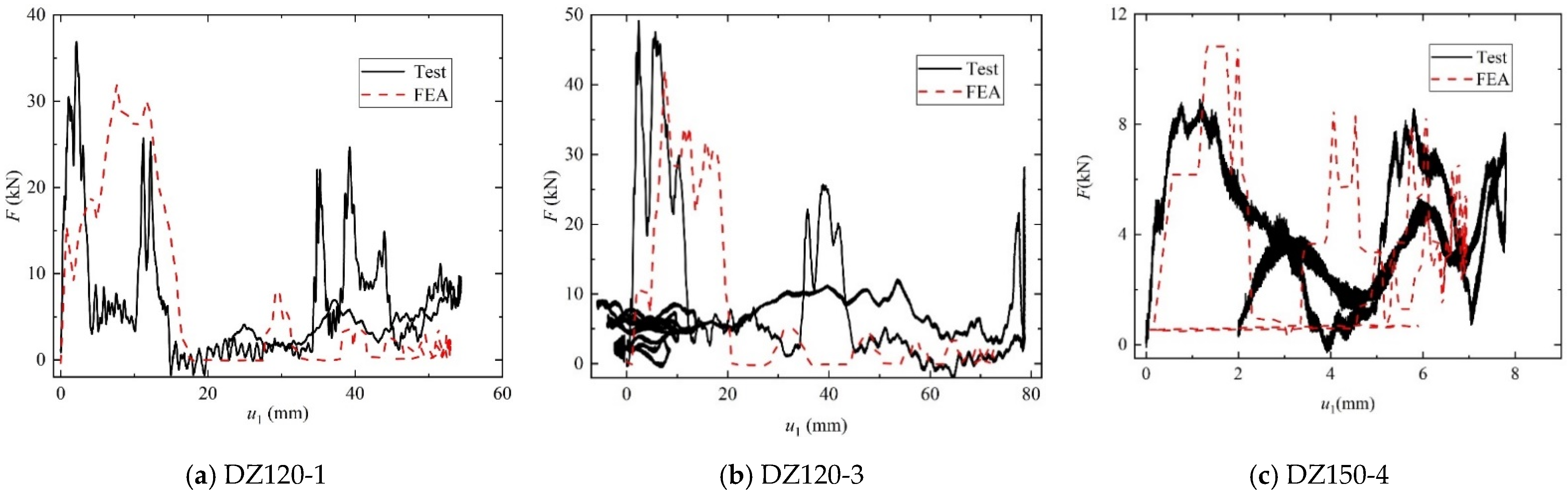
5. Damage State Evaluation of RC Columns
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kishi, N.; Sato, M.; Mikama, H.; Matsuoka, K.I. Impact behavior of full-scale of RC beams. In Proceedings of the 6th ASEC, Taipei, Taiwan, 16 February 1998; pp. 973–978. [Google Scholar]
- Saatci, S.; Vecchio, F.J. Effects of shear mechanisms on impact behavior of reinforced concrete beams. ACI Struct. J. 2009, 106, 78–86. [Google Scholar]
- Xu, B.; Zeng, X. Experimental study on reinforcement concrete beams under impact loadings. China Civil. Eng. J. 2014, 47, 41–51. (In Chinese) [Google Scholar]
- Liu, B.; Fan, W.; Guo, W.; Chen, B.; Liu, R. Experimental investigation and improved FE modeling of axially-loaded circular RC column under lateral impact loading. Eng. Struct. 2017, 152, 619–642. [Google Scholar] [CrossRef]
- Fan, W.; Shen, D.; Yang, T.; Shao, X. Experimental and numerical study on low-velocity lateral impact behaviors of RC, UHPFRC and UHPFRC-strengthened columns. Eng. Struct. 2019, 191, 509–525. [Google Scholar] [CrossRef]
- Liu, B.; Fan, W.; Huang, X.; Shao, X.; Kang, L. A simplified method to predict damage of axially-Loaded circular RC Columns under Lateral Impact Loading. Int. J. Concr. Struct. M 2020, 14, 1–24. [Google Scholar] [CrossRef]
- Sha, Y.; Hao, H. Laboratory tests and numerical simulations of barge impact on circular reinforced concrete piers. Eng. Struct. 2013, 46, 593–605. [Google Scholar] [CrossRef]
- Sha, Y.; Hao, H. Laboratory tests and numerical simulations of CFRP Strengthened RC pier subjected to barge impact load. Inter. J. Struct. Stab. Dyn. 2015, 15, 1–33. [Google Scholar] [CrossRef]
- Demartino, C.; Wu, J.G.; Xiao, Y. Response of shear-deficient reinforced circular RC columns under lateral impact loading. Inter. J. Impact Eng. 2017, 109, 196–213. [Google Scholar] [CrossRef]
- Adachi, T.; Tanaka, T.; Sastranegara, A.; Yamaji, A.; Kim, S.-K.; Yang, I.-Y. Effect of transverse impact on buckling behavior of a column under static axial compressive force. Inter. J. Impact Eng. 2004, 30, 465–475. [Google Scholar] [CrossRef]
- Staszak, N.; Garbowski, T.; Szymczak-Graczyk, A. Solid Truss to Shell Numerical Homogenization of Prefabricated Composite Slabs. Materials 2021, 14, 4120. [Google Scholar] [CrossRef] [PubMed]
- Zeinoddini, M.; Parke, G.A.R.; Harding, J.E. Axially pre-loaded steel tubes subjected to lateral impacts: An experimental study. Int. J. Impact Eng. 2002, 27, 669–690. [Google Scholar] [CrossRef]
- Zeinoddini, M.; Harding, J.E.; Parke, G.A.R. Axially pre-loaded steel tubes subjected to lateral impacts (a numerical simulation). Int. J. Impact Eng. 2008, 35, 1267–1279. [Google Scholar] [CrossRef]
- Al-Thairy, H.; Wang, Y.C. A numerical study of the behaviour and failure modes of axially compressed steel columns subjected to transverse impact. Int. J. Impact Eng. 2011, 38, 732–744. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.F.; Chen, W.S.; Hao, H.; Wang, Z. Numerical study of low-speed impact response of sandwich panel with tube filled honeycomb core. Compos. Struct. 2019, 220, 736–748. [Google Scholar] [CrossRef]
- Ye, J.-B.; Cai, J.; Chen, Q.-J.; Liu, X.; Tang, X.-L.; Zuo, Z.-L. Experimental Investigation of slender RC columns under horizontal static and impact loads. Structures 2020, 24, 499–513. [Google Scholar] [CrossRef]
- Code for Design of Concrete Structure (GB50010-2010); Architecture Industry Press: Beijing, China, 2010. (In Chinese)
- Szymczak-Graczyk, A.; Ksit, B.; Laks, I. Operational problems in structural nodes of reinforced concrete constructions. IOP Conference Series. Mater. Sci. Eng. 2019, 603, 032096. [Google Scholar] [CrossRef]
- CEB. Concrete Structures under Impact and Impulsive Loading; Committee Euro-International du Beton: Lausanne, Switzerland, 1998. [Google Scholar]
- Malvar, L.J.; Crawford, J.E. Dynamic Increase Factors for Steel Reinforcing Bar. In Proceedings of the 28th DDESB Seminar, Orlando, FL, USA, 18 August 1998. [Google Scholar]
- Malvar, L.J.; Ross, C.A. A review of strain rate effects for concrete in tensions. ACI Mater. J. 1998, 95, 735–739. [Google Scholar]
- Cowper, G.R.; Symonds, P.S. Strain-Hardening and Strain-Rate Effects in the Impact Loading of Cantilever Beams; Report; Brown University: Providence, RI, USA, 1957. [Google Scholar]
- Guo, J.L.; Cai, J.; Chen, W.S. Inertial effect on RC beam subjected to impact loads. Int. J. Struct. Stab. Dy. 2017, 17, 1750053. [Google Scholar] [CrossRef]
- Zhao, D.B.; Yi, W.J.; Kunnath, S.K. Shear mechanism in reinforced concrete beams under impact loading. J. Struct. Eng. 2017, 143, 04107089. [Google Scholar] [CrossRef]
- Fujikake, K.; Li, B.; Soeun, S. Impact response of reinforced concrete beam and its analytical evaluation. J. Struct. Eng. 2009, 135, 938–950. [Google Scholar] [CrossRef]
- Tachibana, S.; Masuya, H.; Nakamura, S. Performance based design of reinforced concrete beams under impact. Nat. Hazards Earth Syst. Sci. 2010, 10, 1069–1078. [Google Scholar] [CrossRef] [Green Version]
- Kishi, N.; Mikami, H.; Matsuoka, K.G.; Ando, T. Impact behavior of shear-failure-type RC beams without shear rebar. Inter. J. Impact Eng. 2002, 27, 955–968. [Google Scholar] [CrossRef]
- Kishi, N.; Mikami, H. Empirical formulas for designing reinforced concrete beams under impact loading. ACI Struct. J. 2012, 109, 509–519. [Google Scholar]
- Adhikary, S.D.; Li, B.; Fujikake, K. State-of the art review on low-velocity impact response of reinforced concrete beams. Mag. Concr. Res. 2015, 68, 701–723. [Google Scholar] [CrossRef]
- Cai, J.; Ye, J.-B.; Chen, Q.-J.; Liu, X.; Wang, Y. Dynamic behaviour of axially-loaded RC columns under horizontal impact loading. Eng. Struct. 2018, 168, 684–697. [Google Scholar] [CrossRef]
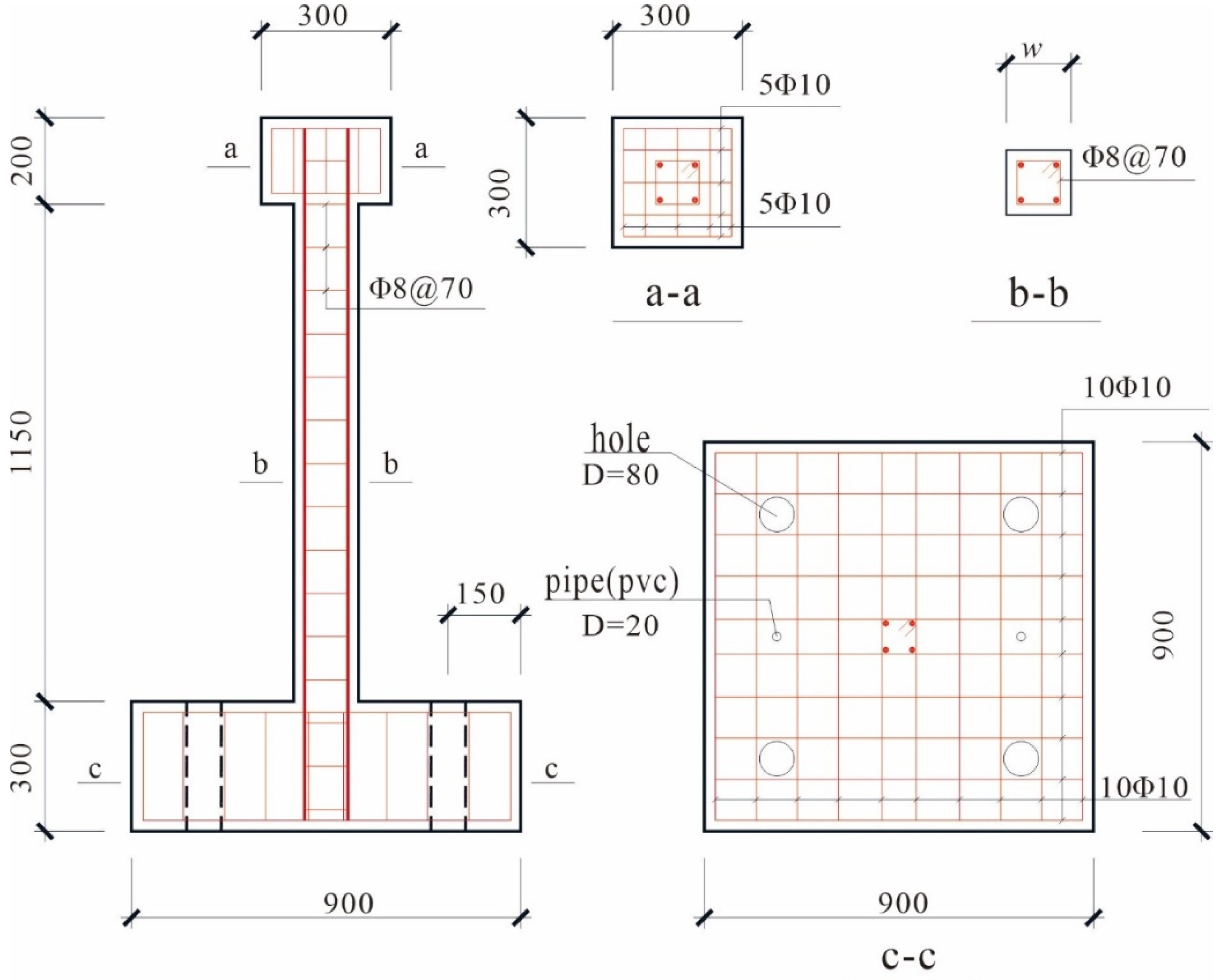

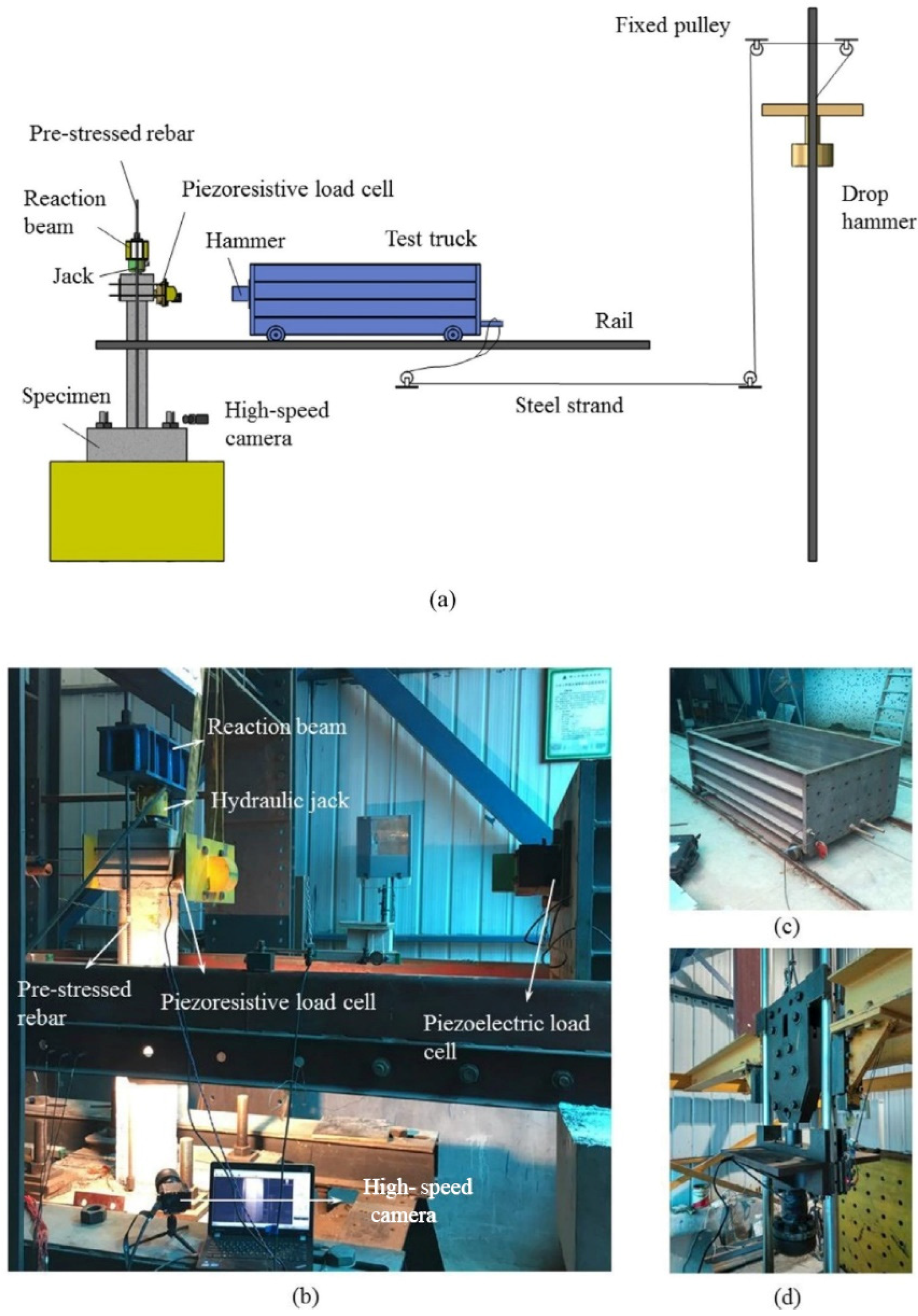
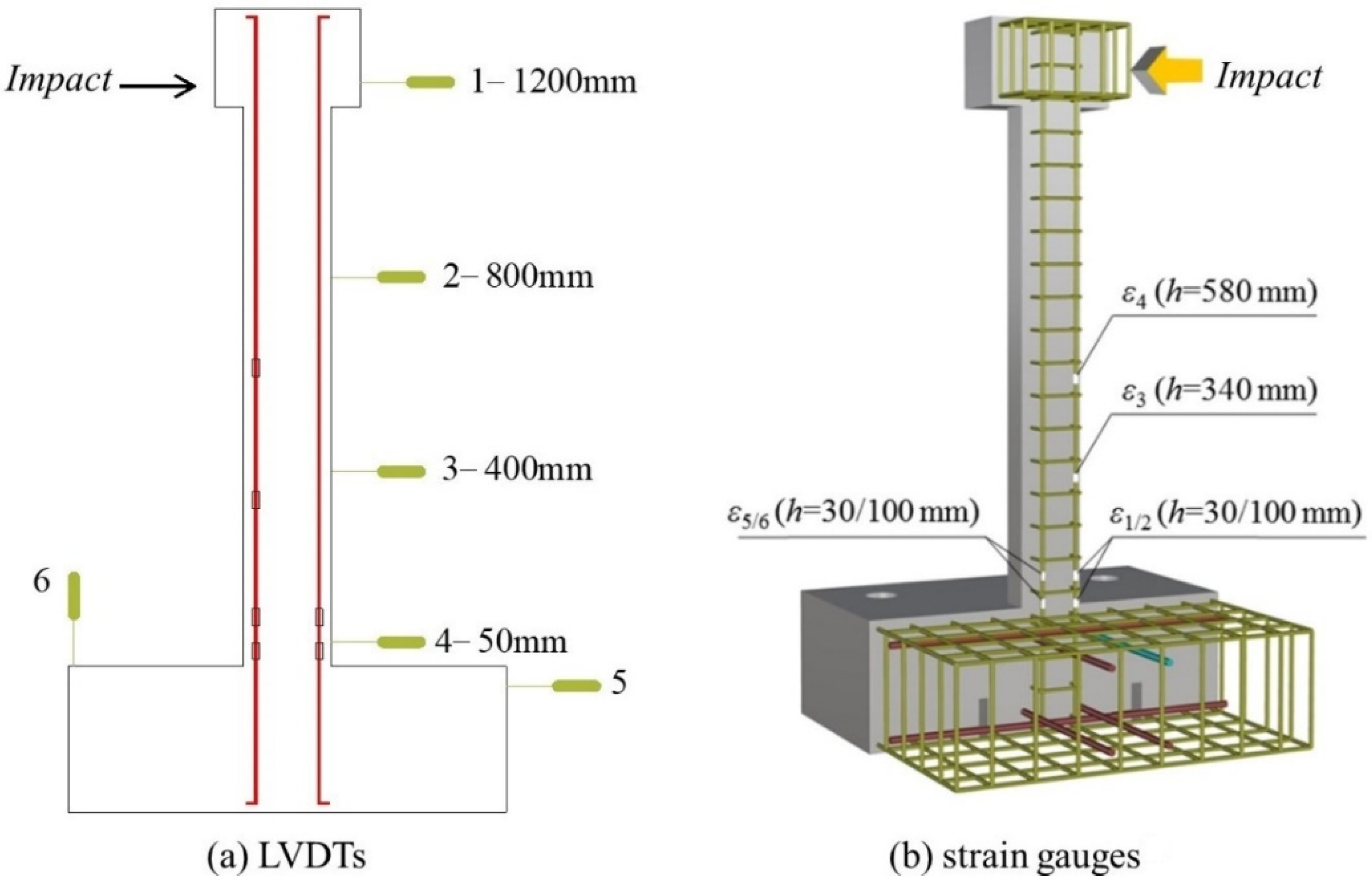
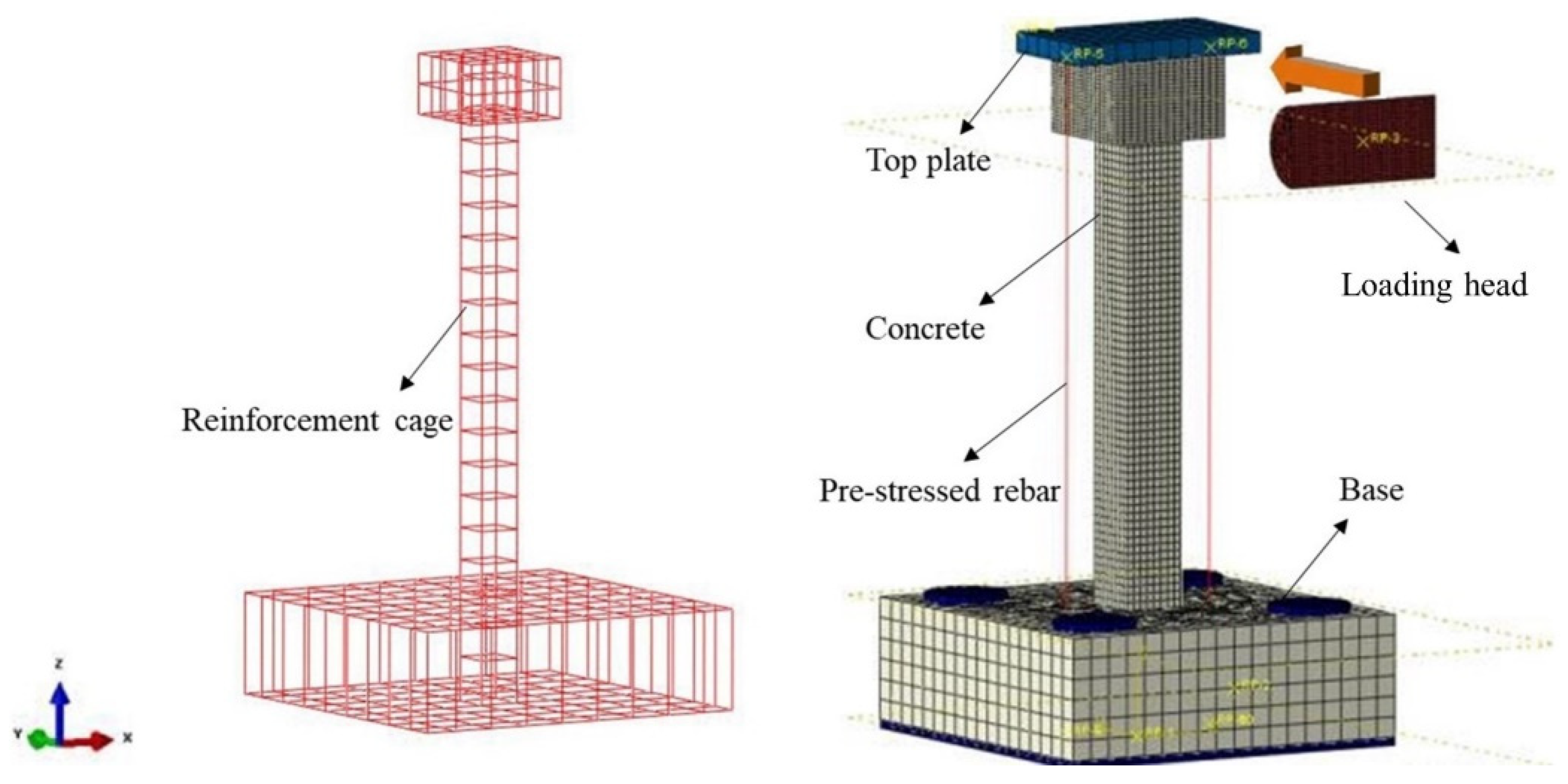




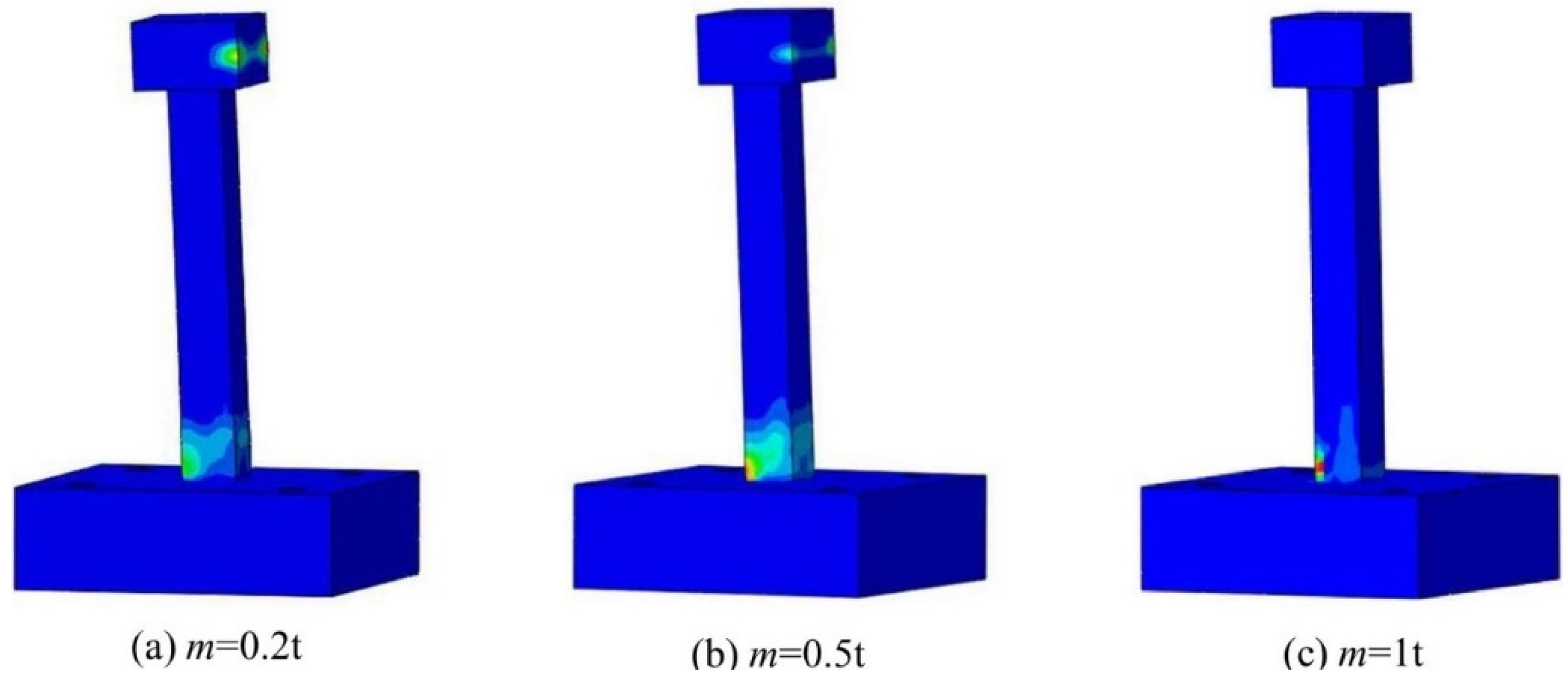

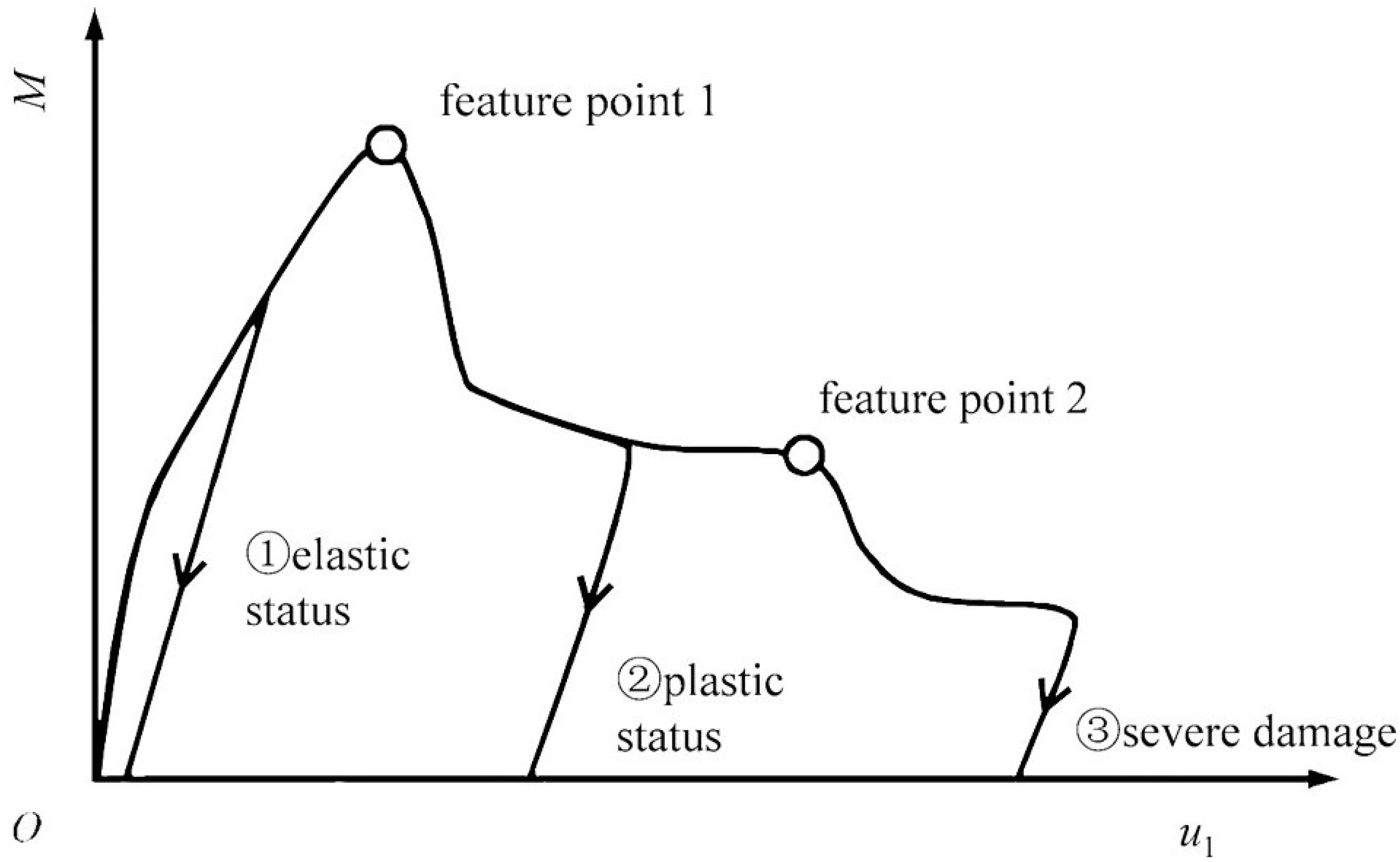
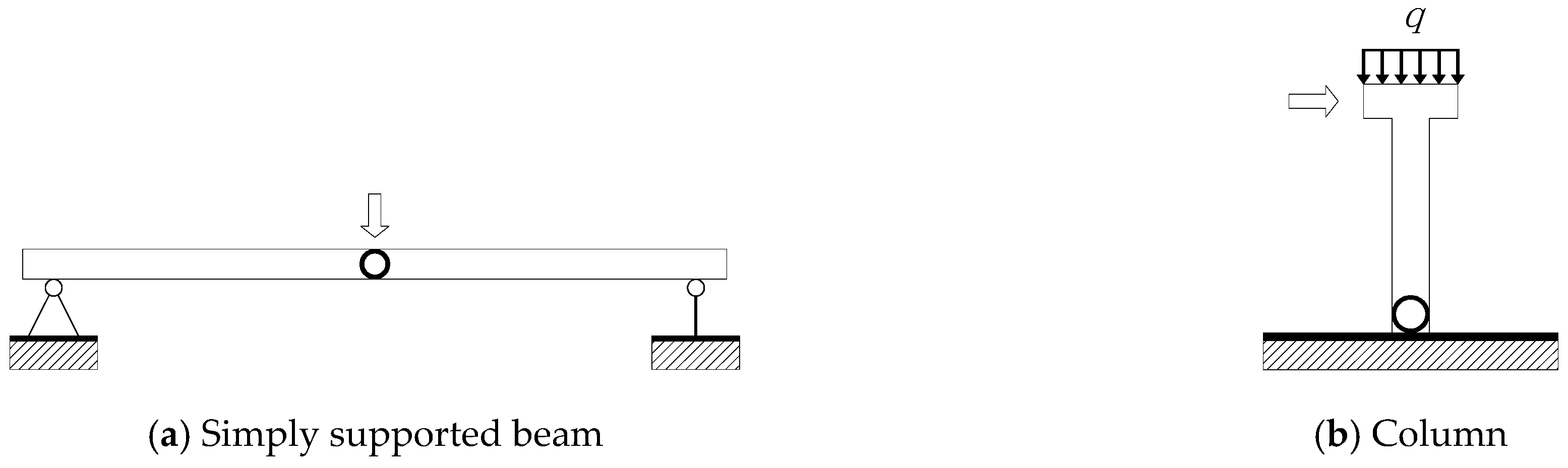

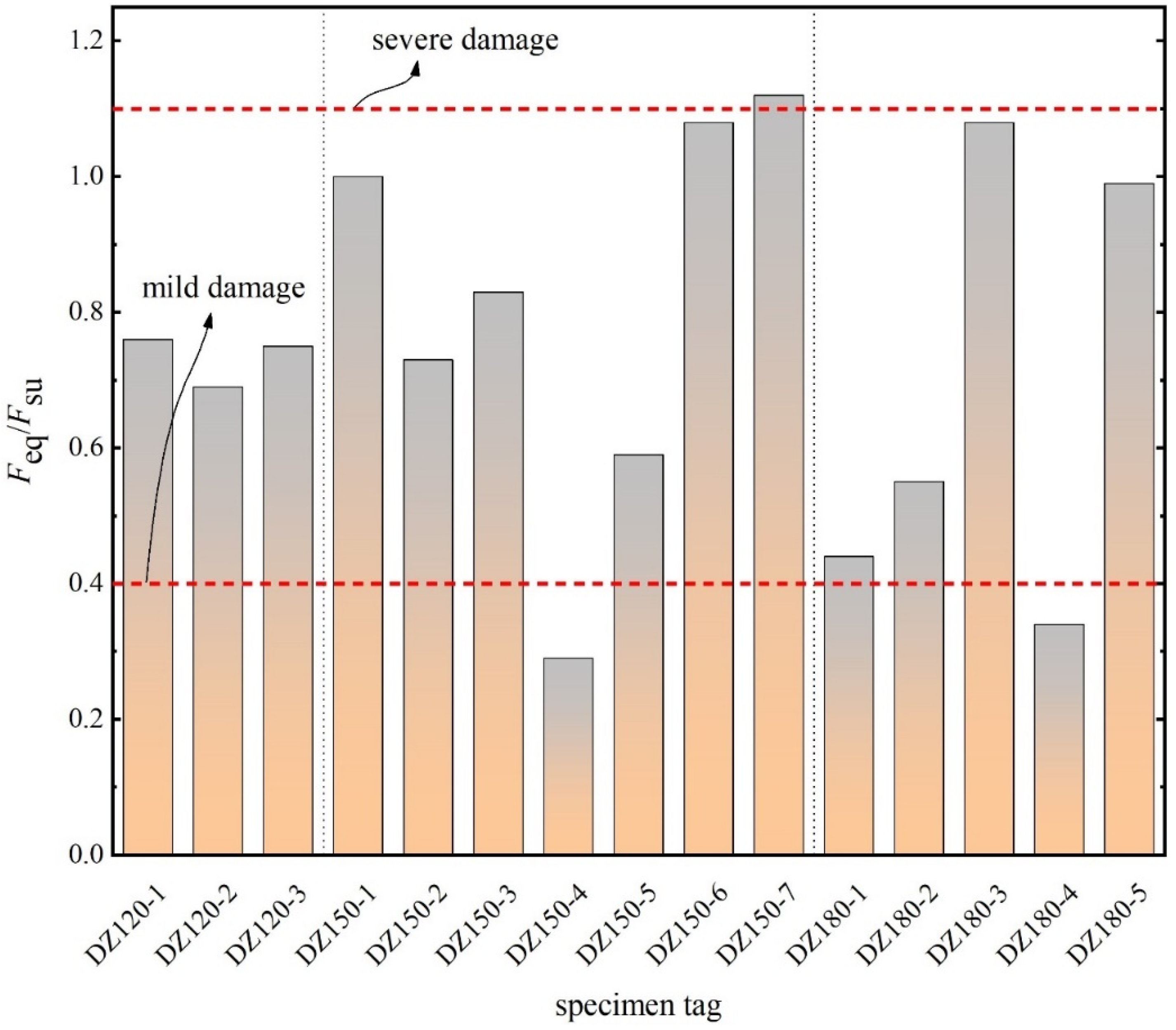
| v | ρ/(kg·m−3) | Ea/GPa | e | αf | Kε | μ | ψ/(°) |
|---|---|---|---|---|---|---|---|
| 0.2 | 2500 | 36.2 | 0.1 | 1.16 | 0.6667 | 0.00001 | 38 |
| ρ/(t/mm3) | E/MPa | v | εu | fy/(MPa) | fu/(MPa) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Φ8 | Φ10 | Φ12 | Φ8 | Φ10 | Φ12 | ||||
| 7.8 × 10−9 | 2.1 × 105 | 0.3 | 0.2 | 408.8 | 424.6 | 470.4 | 541.1 | 642.3 | 685.7 |
| Mesh size | 40 mm | 25 mm | 10 mm |
| Number of concrete | 7140 | 16,520 | 60,765 |
| Number of reinforcement | 1848 | 2136 | 3328 |
| Calculation time | 3 h 57 min | 7 h 15 min | Error report after 39 h 11 min (excessive mesh deformation) |
| Ek (kJ) | Specimen Number | m (t) | v0 (m/s) | td (s) | umax (mm) | Mmax (kN·m) |
|---|---|---|---|---|---|---|
| 2 | DZ150-Ek1-0.2 | 0.2 | 4.47 | 0.05 | 60.1 | 15.4 |
| DZ150-Ek1-0.5 | 0.5 | 2.83 | 0.07 | 65.6 | 15.6 | |
| DZ150-Ek1-1 | 1 | 2.00 | 0.1 | 72.7 | 15.9 | |
| DZ150-Ek1-4 | 4 | 1.00 | 0.2 | 72.9 | 16.23 | |
| DZ150-Ek1-8 | 8 | 0.71 | 0.28 | 72.8 | 15.93 | |
| DZ150-Ek1-12 | 12 | 0.58 | 0.35 | 74.4 | 15.99 | |
| DZ150-Ek1-16 | 16 | 0.50 | 0.4 | 74.2 | 16.05 | |
| DZ150-Ek1-20 | 20 | 0.45 | 0.45 | 74.4 | 16.04 | |
| DZ150-Ek1-30 | 30 | 0.36 | 0.57 | 74.4 | 16.1 | |
| DZ150-Ek1-40 | 40 | 0.32 | 0.66 | 74.6 | 16.08 | |
| 1 | DZ150-Ek2-0.2 | 0.2 | 3.16 | 0.03 | 34.8 | 14.5 |
| DZ150-Ek2-0.5 | 0.5 | 2.00 | 0.04 | 38.9 | 16.1 | |
| DZ150-Ek2-1 | 1 | 1.41 | 0.07 | 41.4 | 15.7 | |
| DZ150-Ek2-4 | 4 | 0.71 | 0.18 | 44.3 | 15.3 | |
| DZ150-Ek2-8 | 8 | 0.50 | 0.25 | 44.6 | 15.5 | |
| DZ150-Ek2-12 | 12 | 0.41 | 0.3 | 43.8 | 15.4 | |
| DZ150-Ek2-16 | 16 | 0.35 | 0.35 | 44.7 | 15.6 | |
| DZ150-Ek2-20 | 20 | 0.32 | 0.39 | 42.6 | 15.8 | |
| DZ150-Ek2-30 | 30 | 0.26 | 0.48 | 43.8 | 16.1 | |
| DZ150-Ek2-40 | 40 | 0.22 | 0.56 | 44.1 | 16.0 | |
| 0.5 | DZ150-Ek3-0.2 | 0.2 | 2.24 | 0.02 | 21.9 | 14.6 |
| DZ150-Ek3-0.5 | 0.5 | 1.41 | 0.03 | 24.4 | 15.8 | |
| DZ150-Ek3-1 | 1 | 1.00 | 0.05 | 25.7 | 15.8 | |
| DZ150-Ek3-4 | 4 | 0.50 | 0.16 | 26.5 | 15.3 | |
| DZ150-Ek3-8 | 8 | 0.35 | 0.22 | 26.9 | 15.5 | |
| DZ150-Ek3-12 | 12 | 0.29 | 0.27 | 26.3 | 15.3 | |
| DZ150-Ek3-16 | 16 | 0.25 | 0.31 | 26.0 | 15.6 | |
| DZ150-Ek3-20 | 20 | 0.22 | 0.35 | 26.8 | 15.7 | |
| DZ150-Ek3-30 | 30 | 0.18 | 0.42 | 26.4 | 15.9 | |
| DZ150-Ek3-40 | 40 | 0.16 | 0.49 | 26.3 | 15.8 | |
| 0.2 | DZ150-Ek4-0.2 | 0.2 | 1.41 | 0.02 | 12.7 | 13.6 |
| DZ150-Ek4-0.5 | 0.5 | 0.89 | 0.04 | 13.7 | 13.7 | |
| DZ150-Ek4-1 | 1 | 0.63 | 0.07 | 14.3 | 13.9 | |
| DZ150-Ek4-4 | 4 | 0.32 | 0.14 | 14.4 | 13.9 | |
| DZ150-Ek4-8 | 8 | 0.22 | 0.2 | 14.6 | 14.0 | |
| DZ150-Ek4-12 | 12 | 0.18 | 0.24 | 14.5 | 14.1 | |
| DZ150-Ek4-16 | 16 | 0.16 | 0.28 | 14.5 | 14.1 | |
| DZ150-Ek4-20 | 20 | 0.14 | 0.32 | 14.4 | 14.2 | |
| DZ150-Ek4-30 | 30 | 0.12 | 0.38 | 14.5 | 13.7 | |
| DZ150-Ek4-40 | 40 | 0.10 | 0.45 | 14.5 | 13.8 |
| Specimen Type | Specimen Tag | m (t) | v0 (m/s) | Eab (kJ) | umax (mm) | Feq/Fsu |
|---|---|---|---|---|---|---|
| w = 120 mm | DZ120-1 | 1.2 | 0.802 | 0.383 | 52.98 | 0.76 |
| DZ120-2 | 1.5 | 0.794 | 0.463 | 69.75 | 0.69 | |
| DZ120-3 | 1.8 | 0.869 | 0.520 | 72.66 | 0.75 | |
| w = 150 mm | DZ150-1 | 1.2 | 1.083 | 0.753 | 44.90 | 1.00 |
| DZ150-2 | 1.5 | 0.767 | 0.430 | 35.31 | 0.73 | |
| DZ150-3 | 1.8 | 0.891 | 0.705 | 50.41 | 0.83 | |
| DZ150-4 | 1.5 | 0.329 | 0.034 | 6.94 | 0.29 | |
| DZ150-5 | 0.592 | 0.208 | 20.86 | 0.59 | ||
| DZ150-6 | 0.935 | 0.866 | 47.80 | 1.08 | ||
| DZ150-7 | 1.191 | 1.138 | 60.62 | 1.12 | ||
| w = 180 mm | DZ180-1 | 1.2 | 0.791 | 0.158 | 13.42 | 0.44 |
| DZ180-2 | 1.5 | 0.743 | 0.257 | 17.61 | 0.55 | |
| DZ180-3 | 1.8 | 0.907 | 0.907 | 31.12 | 1.08 | |
| DZ180-4 | 1.5 | 0.503 | 0.082 | 9.11 | 0.34 | |
| DZ180-5 | 1.291 | 1.230 | 46.04 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Cai, J.; Ye, J. Numerical Simulation of Dynamic Response and Evaluation of Flexural Damage of RC Columns under Horizontal Impact Load. Appl. Sci. 2021, 11, 11223. https://doi.org/10.3390/app112311223
Hu B, Cai J, Ye J. Numerical Simulation of Dynamic Response and Evaluation of Flexural Damage of RC Columns under Horizontal Impact Load. Applied Sciences. 2021; 11(23):11223. https://doi.org/10.3390/app112311223
Chicago/Turabian StyleHu, Bin, Jian Cai, and Jiabin Ye. 2021. "Numerical Simulation of Dynamic Response and Evaluation of Flexural Damage of RC Columns under Horizontal Impact Load" Applied Sciences 11, no. 23: 11223. https://doi.org/10.3390/app112311223
APA StyleHu, B., Cai, J., & Ye, J. (2021). Numerical Simulation of Dynamic Response and Evaluation of Flexural Damage of RC Columns under Horizontal Impact Load. Applied Sciences, 11(23), 11223. https://doi.org/10.3390/app112311223





