Accounting for Interelement Interferences in Atomic Emission Spectroscopy: A Nonlinear Theory

Abstract

The article describes a nonlinear theory of how the presence of third elements affects the results of analyzing the elemental composition of substances by means of atomic emission spectroscopy. The theory is based on the assumption that there is an arbitrary relationship between the intensity of the analytical line of the analyte and the concentration of impurities and alloying elements. The theory has been tested on a simulation problem using commercially available equipment (the SPAS-05 spark spectrometer). By comparing the proposed algorithm with the traditional one, which assumes that there is a linear relationship between the intensity of the analytical line of the analyte and the intensities of the spectral lines (or concentrations) in the substance, it was revealed that there is a severalfold decrease in the deviations of nominal impurity concentrations from the measured ones. The results of this study allow for reducing the number of analytical procedures used in analyzing materials that have different compositions and the same matrix element. For instance, it becomes possible to determine the composition of iron-based alloys (low-alloy and carbon steels; high-speed steels; high-alloy, and heat-resistant steels) using one calibration curve within the framework of a universal analytical method.

1. Introduction

Atomic emission spectroscopy (AES) is one of the most common methods for determining the elemental composition of materials, which largely influences their physicochemical properties, and accordingly, their performance characteristics [1,2,3,4,5].

The basic principle of AES consists of atomizing the substance being analyzed by one method or another and promoting the resulting atoms (or ions) to an excited state. Then, by measuring the intensities of the spectral lines of various elements, one can find their concentrations in the substance. As a rule, the relative intensity of the analytical line is determined to eliminate the effect of the variability in the parameters of the spectrometer system on measurements. That is, the intensity is determined in relation to that of a specifically selected line (reference line) in the spectrum of the principal component of the substance.

To conduct spectroscopy analysis, various types of atomic emission spectrometers have been developed and are commercially available. They differ in terms of:

• the state of matter and the type of substances to be analyzed (gases, liquids, and solids);
• the atomization method (flame atomization; electrothermal atomization in graphite furnaces; laser ablation);
• the method of optical excitation (excitation of atoms and ions in different types of plasma; selective excitation by light sources);
• the type of system for recording light emission produced by the excited atoms and (or) ions of the substance being analyzed (photomultiplier tubes; photodiodes; charge-coupled devices).

However, whatever the type of the spectrometer, it is often found that when determining the elemental composition of a material, the analytical signal depends on the concentration of other elements in it [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Four causes of this can be distinguished [25,26]:

(1)

changes in the concentration of the principal component at different concentrations, the impurities being determined when working with relative intensities (see above);

(2)

superposition of the spectral line of the analyte and that of another element on the focal surface of the spectrometer;

(3)

changes in the physicochemical properties (atomic structure, crystal structure, melting point, evaporation temperature, etc.) of the substance when the concentration of the influencing element changes, causing the rate at which the atoms of the substance enter the optical excitation zone to change;

(4)

changes in the parameters of the optical excitation system due to the presence of atoms of influencing elements in the excitation zone (for example, changes in the temperature of plasma electrons when using arc discharge or other discharge methods).

It should be noted that, as a rule, the first and second causes can be eliminated by carefully choosing the analytical line of the analyte and accurately calculating the concentration of base atoms by measuring the relative intensities of the impurities and alloying elements, respectively.

The third and fourth causes directly affect how atoms enter the active zone and become optically excited. In what follows, it is these causes of the dependence of the analytical signal on the content of elements in the substance that we deal with when discussing the problem of effects caused by third elements.

Examples of such effects in non-ferrous alloys are the influence that Zn and Si concentrations have on the results of analyzing copper-based alloys by means of spark spectrometers [15,16,17,18,19,20,21,22,23,24,27,28,29] and the effect of Cu content on the determination of the quantities of Zn, Fe, Mg, and Mn [26,30,31] in aluminum alloys. Similarly, when analyzing ferrous alloys, a number of elements significantly affect the results of emission analysis due to the third and fourth causes [32,33,34,35,36,37,38,39,40]. When analyzing substances using the method of evaporation from a graphite electrode, there is an effect on elements with a boiling point lower than that of carbon on the intensity of analytical lines of other impurities, which is caused by a decrease in the rate of entry of sample atoms into the discharge zone [41,42] with an increase in the concentration of such elements.

To factor in the influence of third elements on experimental data, various methods are used [43]:

• mathematical methods for calculating corrections;
• methods that adjust the procedure of measuring the analytical signal;
• methods optimizing the process of measuring the analytical signal;
• spectrum transformation methods (Fourier transform, the differentiation of spectra, etc.).

Calculating corrections is the most convenient method that does not involve making changes to the sample preparation procedure, experimental conditions, the optical arrangement of the equipment, or optical materials. However, the existing mathematical methods have a number of disadvantages. The biggest one is that the relationship between the corresponding correction and the concentration (or, in other modifications, the intensity of the analytical line) of the influencing element and the analyte (see Formula (A4) in Appendix A) [44,45,46,47,48] is assumed to be linear. When considering the complexity of the physicochemical processes that occur during the emission of impurity and alloying element atoms from the substance being analyzed (crystal structure rearrangement, diffusion, melting, evaporation, explosive emission, etc.), and the complexity of the processes that determine the dependence of plasma parameters (if plasma is used for optical excitation) on the composition of the plasma gas, it becomes obvious that the assumed linear relationship does not correspond to the real one and, in the general case, can only give a qualitative (and only to some extent quantitative) description of the observed effects caused by third elements. In [49], it is noted that today the problem of factoring in the effects produced by third elements has no solution in the general case.

The above means that when calibrating spectrometers for analyzing substances that contain impurities and alloying elements whose concentrations fluctuate over a wide range (two to four orders of magnitude), it is necessary to set different excitation and atomization parameters, i.e., to develop analytical techniques specifically for relatively small groups of alloys. For example, when analyzing low-alloy, high-speed, and high-alloy steels by means of spark spectrometers, it is necessary to adjust the parameters of the spark generator and the registration system and use different analytical and reference lines. However, when the effects caused by third elements are adequately corrected for, only one technique can be used. This obviously saves time and material resources in the production of spectrometers.

Thus, it is of importance to develop a method for factoring in the effects caused by third elements that will adequately describe their influence on the results of AES experiments.

2. Materials and Methods

Derivation of the basic formulas. Appendix A describes the traditional method for factoring in the effects caused by third elements. Some of the formulas within its framework will be used in the Discussion section.

We will assume that we have $M$ reference standards, in each of which $N$ elements are known. Let us imagine a situation in which the concentration of the i-th element ($C_i$), determined by the analytical method, depends not only on the intensity of its analytical line but also on the concentrations (and hence on the intensities of the analytical lines) of other elements. Let us assume that the number of these elements $V<N$ and number them from $m$ to $m+V-1$. It is obvious that:

$$m+s\ne i,\hspace{1em}\mathrm{where}\hspace{1em}s=0,\dots ,V-1.$$

(1)

Let us also assume that the relationship between the i-th element being determined and the intensities of the analytical lines of the analyte $I_i$ and the influencing elements $I_m, \dots ,I_{m+V-1}$ has the form:

$$C_i={\mathsf{\Phi }}_i\left(I_i+{\displaystyle \sum }_{k=m}^{m+V-1}{d}_{ik}{I}_k,I_m, \dots ,I_{m+V-1}\right)$$

(2)

where $d_{ik}$ are yet unknown dimensionless numerical coefficients, and the relationship between ${\mathsf{\Phi }}_i\left(I_i+{{\displaystyle \sum }}_{k=m}^{m+V-1}{d}_{ik}{I}_k,I_m, \dots ,I_{m+V-1}\right)$ and the arguments $I_m, \dots ,I_{m+V-1}$ has not yet been determined. The form of the first argument of the function on the right side of (2) $I_i+{{\displaystyle \sum }}_{k=m}^{m+V-1}{d}_{ik}{I}_k$ has a simple physical meaning. It takes into account possible spectral line interferences and the dependence of the background where the analytical line of the analyte is located on the presence of influencing elements in the plasma. For simplicity, we have taken this relationship to be linear depending on the intensity of the influencing elements $I_k$. In modern optical emission spectrometers, when there are interferences of the lines of elements that affect the intensity of the line of the analyte, the real relationship is apparently close to linear.

On the contrary, the relationship between the intensity of the plasma background and the intensities of the lines of the influencing elements (which are determined by their concentrations) is more complex. We will assume that this relationship can be expanded in a Taylor series at $I_k=0$; thus, (2) takes into account the first term of this series. Strictly speaking, it is possible that the coefficient of a linear Taylor series in the $I_k$ term is zero, and this series begins with $I_k{}^2$.

If there are no line interferences and the background of the analytical line of analyte does not depend on the concentration of the influencing elements in the plasma, $d_{ik}\equiv 0$ and ${\mathsf{\Phi }}_i\left(I_i,I_k\right)$ should be written in (2).

It is quite obvious that the identity holds:

$${\mathsf{\Phi }}_i{\left(I_i+{\displaystyle \sum }_{k=m}^{m+V-1}{d}_{ik}{I}_k,I_m, \dots ,I_{m+V-1}\right)}_{I_k=0,k=m\dots m+V-1}\equiv F_i\left(I_i\right).$$

(3)

That is, $F_i\left(I_i\right)$ represents the dependence of the concentration of the i-th element on the intensity of its analytical line if there are no effects caused by third elements. Let us suppose that these effects are additive and consider first the case of one influencing element with number $k$ ($m\le k\le m+V-1$):

$$C_i={\mathsf{\Phi }}_i\left(I_i+d_{ik}{I}_k,I_k\right).$$

(4)

Note that, as a rule, the function $F_i\left(I_i\right)$ is represented in AES as a polynomial of degree $N_0\le 4$.

Let us expand the function (4) of two variables ${\mathsf{\Phi }}_i\left(Y_{ik},I_k\right)$, where $Y_{ik}=I_i+d_{ik}{I}_k$, in a double Taylor series at a point $I_k=0; Y_{ik}=I_i$. By expanding ${\mathsf{\Phi }}_i\left(Y_{ik},I_k\right)$ at a constant value $Y_{ik}$, we have:

$${\mathsf{\Phi }}_i\left(Y_{ik},I_k\right)={\displaystyle \sum }_{l=0}^{\infty }\frac{1}{l!}{\frac{{\partial }^l{\mathsf{\Phi }}_i\left(Y_{ik},I_k\right)}{\partial I_k{}^l}}_{I_k=0}{I}_k{}^l.$$

(5)

Now let us consider the function ${\psi }_{lik}={\frac{{\partial }^l{\mathsf{\Phi }}_i\left(Y_{ik},I_k\right)}{\partial I_k{}^l}}_{I_k=0}$ and expand it in a Taylor series at $Y_{ik}=I_i$. Then we get:

$${\psi }_{lik}={\displaystyle \sum }_{n=0}^{\infty }\frac{1}{n!}{\frac{{\partial }^n{\psi }_{lik}\left(x\right)}{\partial x^n}}_{x=I_i}{\left(Y_{ik}-I_i\right)}^n.$$

(6)

Taking (6) into account, after changing the order of summation, (5) takes the following form:

$${\mathsf{\Phi }}_i\left(Y_{ik},I_k\right)={\displaystyle \sum }_{n=0}^{\infty }{\displaystyle \sum }_{l=0}^{\infty }\frac{1}{n!}\frac{1}{l!}{\frac{{\partial }^{n+l}{\mathsf{\Phi }}_i\left(I_i,I_k\right)}{\partial I_i{}^n\partial I_k{}^l}}_{I_k=0}{\left(Y_{ik}-I_i\right)}^n{I}_k{}^l.$$

(7)

Let us consider an arbitrary term ${\psi }_n\left(Y_{ik},I_k\right)$ in the outer sum (7):

$${\psi }_n\left(Y_{ik},I_k\right)=\frac{{\left(Y_{ik}-I_i\right)}^n}{n!}\frac{{\partial }^n}{\partial I_i{}^n}\left\{F_i\left(I_i\right)+{\displaystyle \sum }_{l=1}^{\infty }\frac{1}{l!}{\frac{{\partial }^l{\mathsf{\Phi }}_i\left(I_i,I_k\right)}{\partial I_k{}^l}}_{I_k=0}{I}_k{}^l\right\}.$$

(8)

Let $F_i\left(I_i\right)$ be a polynomial of degree $N_0$. Suppose that for any concentration of influencing elements, the dependence of ${\mathsf{\Phi }}_i\left(Y_{ik},I_k\right)$ on $Y_{ik}$ is also described by a polynomial of degree $N_0$. This means that the following holds:

$${\mathsf{\Phi }}_i\left(I_i,I_k\right)={\displaystyle \sum }_{r=0}^{N_0}{a}_r{}^{\left(ik\right)}\left(I_k\right)I_i{}^r,$$

(9)

where $a_r{}^{\left(ik\right)}\left(I_k\right)$ are functions of the intensity of $I_k$, and $a_r{}^{\left(ik\right)}\left(0\right)=a_l.$ Note that the real form of the functions $a_r{}^{\left(ik\right)}\left(I_k\right)$ are shaped by the dependence between the rate constants of the processes occurring when the atoms of the analyte are emitted from the sample into the plasma, as well as by the conditions in the plasma that determine how line emission is generated and transferred. Suppose these functions can be expanded in Taylor series at $I_k=0$. As we are discussing the concentrations of the analyte and the influencing elements, which are relatively small, we will expand it into $I_k$ and limit by $M_0$, that is:

$$a_r{}^{\left(ik\right)}\left(I_k\right)={\displaystyle \sum }_{q=0}^{M_0}\frac{1}{q!}{A}_q{}^{\left(ikr\right)}{I}_k{}^q,$$

(10)

where $A_r{}^{\left(ikl\right)}$ are constants; $M_0$ is a yet undefined integer. Using (9) and (10), and taking into account $Y_{ik}-I_i=d_{ik}{I}_k$, we can rewrite (8) in the following form:

$${\psi }_n\left(Y_{ik},I_k\right)=\frac{{\left(d_{ik}{I}_k\right)}^n}{n!}\frac{{\partial }^n}{\partial I_i{}^n}\left\{F_i\left(I_i\right)+{\displaystyle \sum }_{r=0}^{N_0}{\displaystyle \sum }_{l=1}^{M_0}\frac{A_l{}^{\left(ikr\right)}{I}_k{}^l{I}_i{}^r}{l!}\right\},$$

(11)

and (7) can be rewritten as follows:

$${\mathsf{\Phi }}_i\left(Y_{ik},I_k\right)={\displaystyle \sum }_{n=0}^{N_0}{\left(d_{ik}{I}_k\right)}^n\left\{\frac{1}{n!}\frac{{\partial }^n{F}_i\left(I_i\right)}{\partial I_i{}^n}+{\displaystyle \sum }_{r=n}^{N_0}{\displaystyle \sum }_{l=1}^{M_0}\frac{A_l{}^{\left(ikr\right)}{I}_k{}^l}{l!}\frac{I_i{}^{r-n}}{\left(n-r\right)!}\right\}.$$

(12)

Remember that (7) is valid for an arbitrary dependence of ${\mathsf{\Phi }}_i\left(Y_{ik},I_k\right)$ on the arguments $Y_{ik},I_k$, and (12) is valid when (9) and (10) are satisfied.

In what follows, all formulas assume that $F_i\left(I_i\right)$ is a polynomial of $N_0$ degree and relations (9) and (10) are satisfied. Then the analog of formula (A4) (the linear algorithm for taking into account the effects caused by third elements) for the influencing element under the number $k=m+s$ and the analyte under the number $i$ has the form:

$${\varphi }_i^s\left(I_i,I_k\right)={\mathsf{\Phi }}_i\left(Y_{ik},I_k\right)-F_i\left(I_i\right)={\displaystyle \sum }_{n=1}^{N_0}{d}_{ik}{}^n\left\{\frac{I_k{}^n}{n!}\frac{{\partial }^n{F}_i\left(I_i\right)}{\partial I_i{}^n}+{\displaystyle \sum }_{r=n}^{N_0}{\displaystyle \sum }_{l=1}^{M_0}\frac{A_l{}^{\left(ikr\right)}{I}_k{}^{l+n}}{l!}\frac{I_i{}^{r-n}}{\left(r-n\right)!}\right\}+{\displaystyle \sum }_{l=1}^{M_0}\frac{A_l{}^{\left(ik0\right)}{I}_k{}^l}{l!}.$$

(13)

Thus, in the situation being discussed, the analogue of (A4) contains $M_0·\left(N_0+1\right)+1$ constants:

$$d_{ik}, A_1{}^{\left(ik0\right)},\dots A_{M_0}{}^{\left(ik0\right)}; A_1{}^{\left(ik1\right)},\dots A_{M_0}{}^{\left(ik1\right)};\dots ;A_1{}^{\left(ik{N}_0\right)},\dots ,A_{M_0}{}^{\left(ik{N}_0\right)}.$$

(14)

To find them, it is necessary, as in the linear case, to minimize a functional similar to that defined by (A5). Let us first introduce some corrections to (A5). When applying these results to specific methods for determining the elemental composition of substances (for example, to AES methods), the concentrations of the analyte can be of the third or fourth order of magnitude. In this case, the terms of the sum in (A5) that are related to the lower values of the concentrations will make almost no contribution to the functional $S_i$ being minimized. Therefore, we introduce a modified functional $S_i{}^k$:

$$S_i{}^k={\displaystyle \sum }_{j=1}^M\frac{{\left[C_i{}^{\left(j\right)}-{\mathsf{\Phi }}_i\left(Y_{ik}{}^{\left(j\right)},I_k{}^{\left(j\right)}\right)\right]}^2}{C_i{{}^{\left(j\right)}}^2}\frac{1}{W_{ij}},$$

(15)

It represents the sum of squares of the relative deviation of the calculated concentrations from their nominal values. In contrast to $S_i$, which represents the sum of squares of absolute deviations taking into account the statistical weights of points, the biggest contribution of $S_i{}^k$ is made by the points with the maximum systematic relative error regardless of the absolute value of the concentration of the analyte at a given point, which, in our opinion, is methodologically correct. The system of equations for minimizing the functional $S_i{}^k$ are:

$$\frac{\partial S_i{}^k}{\partial A_l{}^{\left(ikr\right)}}=0;l=1, \dots N_0;r=1\dots M_0$$

(16)

$$\frac{\partial S_i{}^k}{\partial d_{ik}}=0$$

takes the form of:

$${\displaystyle \sum }_{j=1}^M\frac{\left[{\mathsf{\Phi }}_i\left(Y_{ik}{}^{\left(j\right)},I_k{}^{\left(j\right)}\right)-C_i{}^{\left(j\right)}\right]}{C_i{{}^{\left(j\right)}}^2}\frac{I_k{{}^{\left(j\right)}}^l}{l!W_{ij}};l=1, \dots M_0$$

(17)

$${\displaystyle \sum }_{j=1}^M\frac{\left[{\mathsf{\Phi }}_i\left(Y_{ik}{}^{\left(j\right)},I_k{}^{\left(j\right)}\right)-C_i{}^{\left(j\right)}\right]}{C_i{{}^{\left(j\right)}}^2}{\displaystyle \sum }_{n=1}^r{d}_{ik}{}^n\frac{I_k{{}^{\left(j\right)}}^{l+n}}{l!}\frac{I_i{{}^{\left(j\right)}}^{r-n}}{\left(r-n\right)!};l=1, \dots M_0;r=1, \dots N_0$$

$${\displaystyle \sum }_{j=1}^M\frac{\left[{\mathsf{\Phi }}_i\left(Y_{ik}{}^{\left(j\right)},I_k{}^{\left(j\right)}\right)-C_i{}^{\left(j\right)}\right]}{C_i{{}^{\left(j\right)}}^2{W}_{ij}}{\displaystyle \sum }_{n=1}^{N_0}\frac{1}{\left(n-1\right)!}{\frac{{\partial }^n{F}_i\left(I_i\right)}{\partial I_i{}^n}}_{I_i=I_i{}^{\left(j\right)}}{d}_{ik}{}^{n-1}{I}_k{{}^{\left(j\right)}}^n,$$

and consists, as mentioned above, of $M_0·\left(N_0+1\right)+1$ nonlinear algebraic equations. In this case, the following is satisfied:

$${\mathsf{\Phi }}_i\left(Y_{ik}{}^{\left(j\right)},I_k{}^{\left(j\right)}\right)-C_i{}^{\left(j\right)}={\varphi }_i^s\left(I_i{}^{\left(j\right)},I_k{}^{\left(j\right)}\right)+F_i\left(I_i{}^{\left(j\right)}\right)-C_i{}^{\left(j\right)},$$

(18)

${\varphi }_i^s\left(I_i{}^{\left(j\right)},I_k{}^{\left(j\right)}\right)$ is defined by (13). Recall that the indices $i,k,j$ refer to the analyte, the influencing element, and the number of the reference standard, respectively.

The constants $d_{ik}, A_l{}^{\left(ikr\right)}$ found from (17) give the solution to the problem posed.

Note that at $N_0>0 \mathrm{t}$, this system is nonlinear due to the presence of $d_{ik}$. In this case, only its numerical solution is possible.

To conclude this section, let us formulate considerations for choosing $M_0.$ Recall that this is the degree of the term with the highest intensity of the influencing element in the expansion of the parameters $a_r{}^{\left(ik\right)}\left(I_k\right)$ in powers $I_k$ (see (10)). This series is assumed to converge. In the case of a sequence with constant signs $A_l{}^{\left(ikr\right)}$, this means that these coefficients will decrease with an increase in $l$ as $o\left(\frac{1}{l}\right)$, where:

$${\frac{o\left(x\right)}{x}}_{x\to 0}\to 0.$$

Recall that growth in $M_0$ means an increase in the number of parameters to be determined. With a fixed number of reference standards, this means that for one coefficient being determined, there are fewer and fewer experimental points, i.e., less physically significant information. If random error is zero when measuring $I_i, I_k, C_i$, the maximum number of parameters can be quite large (and equal to the number of reference standards). In reality, the relative error in measuring the relative intensities in AES experiments on metals and alloys ranges from several tenths of a percent to 50%, depending on the concentration. Numerous calculations show that with an increase in the relative error for a fixed number of parameters, their uncertainty increases. If we generate intensity arrays using a random number generator with a certain variance, and, by solving (17), find the parameters $d_{ik}, A_l{}^{\left(ikr\right)}$, the spread in the values of the same parameter grows with an increase in this variance. In order for the maximum relative error to not exceed 5%, it is sufficient that the number of parameters $L_0$ and the number of samples $M$ are connected by an empirical relationship:

$$K\left(\left|\frac{∆I_i}{I_i}\right|\right)·\left(1+L_0\right)\le M,$$

(19)

where $\left|\frac{∆I_{i,k}}{I_{i,k}}\right|$ is the maximum relative error in measuring the intensities $I_i, I_k$. Here, the following is satisfied:

$$K\left(0.05\right)\approx 6; K\left(0\right)=\frac{1}{1+\frac{1}{L_0}}.$$

It is easy to show that the average values of the parameters found by means of (17) are obtained by using the average intensity values from the results of parallel measurements.

Let us discuss in more detail some of the differences between the universal approach and the traditional (empirical) one, which is presented in the first section of the article. When using the empirical approach, the function ${\varphi }_i^s\left(I_i,I_k\right)$ is linear in intensity $I_k$ and product $I_i·I_k$. Using the universal approach, the maximum degrees of $I_k$ and $I_i$, on which this function depends, depend on $N_0$ and $M_0$ discussed above. The maximum degree of intensity $I_k$ is $N_0+M_0$, therefore, cannot be less than 2, and $I_i$ is equal to $N_0$. Therefore, for $N_0=3$ and $M_0=2$ we get the degree of $I_k$ equal to 5 and the degree of $I_i$ equal to 3, respectively. This is a fundamental difference between the two approaches. In addition, in the empirical approach, there are two constants (for any degree of the polynomial $F_i\left(I_i\right)$), which need to be found from the condition for minimizing the functional (A5). In the universal approach, the number of constants to be determined from system (17) depends on the degree of the polynomial $F_i\left(I_i\right)$ and is equal to $M_0·\left(N_0+1\right)+1$. Thus, the minimum number of constants in this case is attained at $N_0=M_0=1$ and is equal to three. In practice, when analyzing the elemental composition of substances by means of atomic emission spectroscopy, it is usually (with the exception of analysis using a discharge with inductively coupled plasma in argon) the case that $N_0\ge 2$, consequently, at $M_0=1$ we have at least four constants. In this case, one should expect better results of factoring in interelement effects with an increase in $M_0$ if there is a corresponding increase in the number of reference standards.

Finally, let us pay attention to the difference between the functionals being minimized in the empirical and universal approaches (formulas (A1) and (15), respectively). As noted, the difference lies in the fact that the former is the sum of the absolute squares overall reference standards, and the latter is the sum of relative deviations of the calculated concentrations of the analyte from nominal ones that take into account the statistical weights of the points $W_{ij}$ (see (A1)). Thus, with a decrease in the concentration being analyzed in the standards, their contribution to the functional (A1) decreases (which enhances the effect of the growing statistical weight with a decrease in concentration due to an increase in the random relative measurement error). Consequently, the points with the minimum concentrations of the analyte have little effect on the values of the constants in (A4). On the contrary, the contribution to the functional (17) of points with different concentrations of the analyte does not depend on the value of this concentration, which means that all points with the same relative error have the same effect on the constants being determined (see (14)).

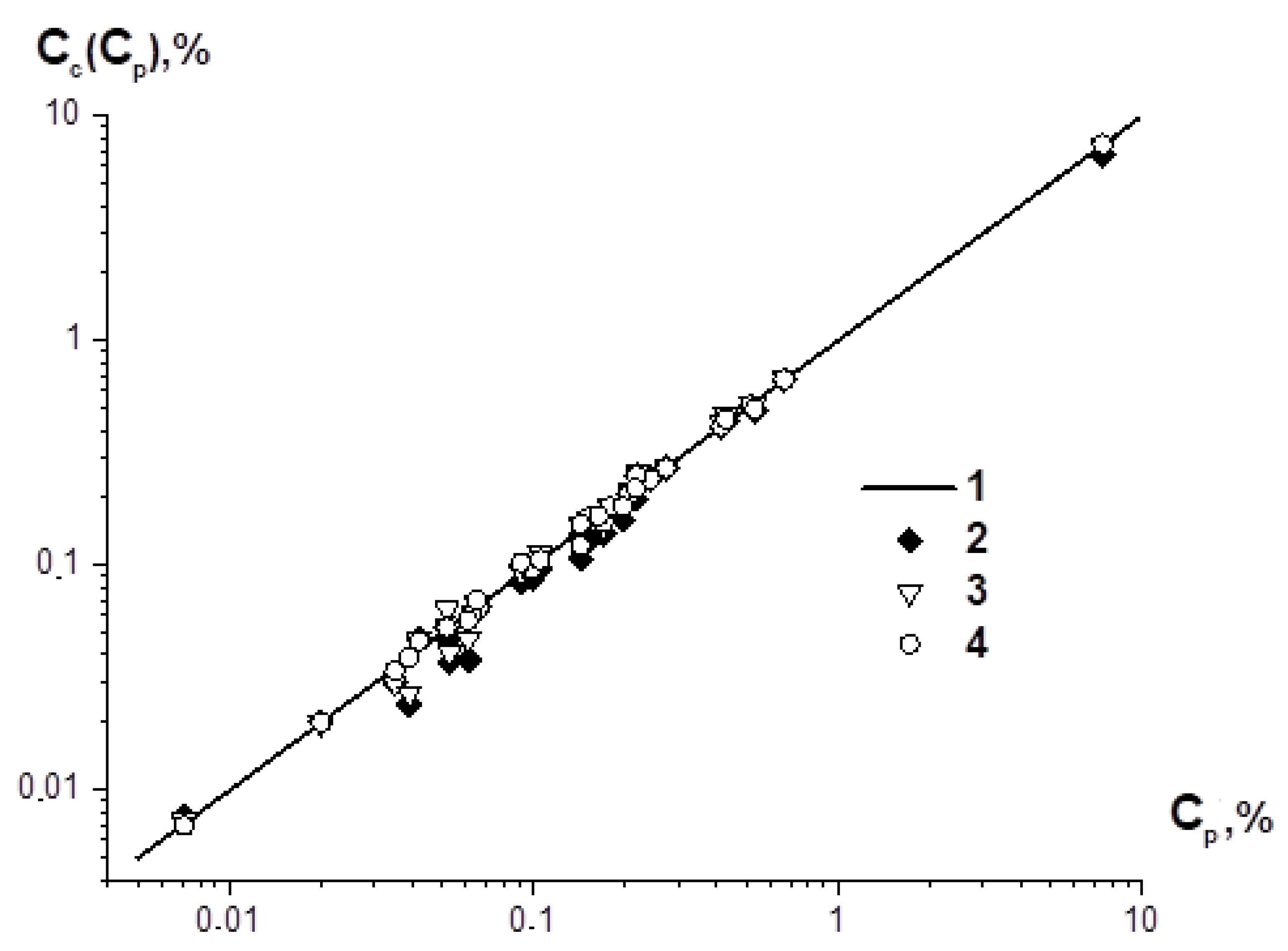
3. Discussion

The proposed theory can be verified using a simulation problem, testing its applicability to analyzing steels, and comparing the results with those produced by the empirical theory. Let us consider how the proposed universal approach can be applied to AES experiments in which the results of determining the concentration of a certain element are affected by the presence of other elements. We verified the proposed method by using a simulation problem, software, and test results produced by commercially available optical emission spectrometers.

We will start by discussing the results of solving the simulation problem. Appendix B gives a detailed description of the algorithm. It was assumed that there are three elements affecting the results of measuring the concentration of the analyte. It was also assumed that the relationship between the effects produced by these elements and the intensities of their analytical lines could be described as a Gaussian function (see Appendix B). The problem consisted in finding whether it is possible to compensate for these effects with the help of the proposed algorithm if there are significant systematic errors (with maximum values approaching 100%) caused by these effects.

Figure 1 shows the results of simulating the process of measuring the relative concentration of the i-th element in a set of 37 reference standards depending on the intensity $I_i^j$, as well as the model function $F_i\left(I_i\right)=F_{im}\left(I_i\right),$ which is defined by (A12). The simulation parameters are given in the figure caption. It can be seen that in this simulation, the effects caused by the three elements are manifested at different intensities, that is, when different standards are used. The effects are significant and reach a value of 100% in relation to the concentration.

Next, we tested the algorithm described above for $N_0=3;M_0=1$ and tried to describe the complex effects introduced in the simulation by means of (12). The results are presented in Figure 2 and Figure 3. Figure 2 show the data on the relationship between the estimated concentration $C_{ic}$ and the observed one $C_{ie}$. Figure 3 demonstrate their values $D_i$ и $F{d}_i$ and the relative differences $C_{ic}$ and $C_{ie}$ when factoring in the effects and without doing it, respectively. It can be seen that $C_{ic}$ and $C_{ie}$ are so close that $D_i$ turns out to be of the order of the variance of $C_{ie}$, which is 5% in this example. At the same time, $F{d}_i$ reaches 200% (at low concentrations).

Next, we tested the proposed algorithm using analytical techniques realized in a commercially available optic emission spectrometer. As an example, we determined Cu and Al concentrations in steels. We used SPAS-02 and SPAS-05 optical emission spectrometers and sets of state standard reference samples of steels: UG0k–UG9k (low-alloy and medium-alloy steels); RG10–RG18 (high-speed steels); LG57, LG32–LG36, LG60–LG65 (high-alloy steels). The function $F_i\left(I_i\right)$ for the analytical line of Cu was found as a third-degree polynomial using the UG0k–UG9k set (see Figure 4).

Cu I 219.958 nm and Al I 394.401 nm analytical lines were used with Fe I 219.604 nm and Fe I 389.566 nm comparison lines, respectively. To determine the arrays of intensities and the corresponding mean square root errors necessary to implement the above-described algorithm accounting for the effect of the third elements, the spectra of each of the standards were taken three times. After the measurements were completed, the specified arrays were uploaded from the service libraries of the spectrometer software.

A low-voltage spark in an argon atmosphere was used in the SPAS-5 spectrometer. The exposure was roughly 4 s at a sparking time of 7 s. The CCD signal accumulation time was 16 ms, and the number of frames was 200. Spectrum excitation source parameters: voltage on the discharge interval at discharge pulse start at a sparking and exposure of 400 V and pulse frequency of 400 Hz. Ar purge speed is 7 L/min.

Figure 5 shows the relationship $C_c\left(C_p\right)$, where $C_c, C_p$ are the measured and nominal concentrations of copper in UG0k–UG9k, respectively. When interelement interferences were taken into account, the effects produced by Ni, W, Cr, and V were analyzed as high-speed steels. High W and V concentrations and high-alloy steels are rich in Ni and Cr. The figure demonstrates that the proposed universal theory significantly reduces the error in determining Cu content in steel. The root-mean-square deviation of the measured concentration from the nominal one decreases by a factor of 2.41 (from 14.1 to 5.8%). For a set of low-alloy and medium-alloy steels (where no third-element effects are observed), i.e., at $C_c\left(I_i\right)=F_i\left(I_i\right)$, the root-mean-square deviation is equal to 5.6%, i.e., the results are almost equal.

This shows that in the case under consideration, the proposed theory adequately takes into account the effects caused by third elements. It should be noted that when these effects are described by means of the empirical theory, the root-mean-square deviation of the measured concentration from the nominal one is 11%, which is almost twice as much as the result produced by the universal theory.

It is interesting to note that the range of Cu concentrations for which the relationship $C_c\left(I_i\right)=F_i\left(I_i\right)$ was plotted (0.0993 to 0.25%) does not exceed one order of magnitude, while the results of analyzing the effects produced by third elements in the determination of Cu content (0.007 to 8%, as can be seen from Figure 4) cover more than three orders of magnitude. The range of the concentrations of influencing elements varies from hundredths to tens of a percent, covering more than two orders of magnitude.

Figure 6 shows data similar to those presented in Figure 5 for Al as an impurity in the same sets of steels. By applying the proposed universal theory, it becomes possible to reduce the root-mean-square relative deviation by a factor of 2.9 (from 25.5 to 8.8%). The use of the empirical method results in a twofold decrease in this value to 12.5%. In the absence of third-element effects when using the UG0k–UG9k set, the value is equal to 4.2%. As can be seen, the difference between the results produced by both theories is not as great as in the case of Cu as an impurity. Apparently, this can be explained by the fact that for a number of reasons (uneven distribution over the sample, etc.), Al content in steels is determined with large random errors.Therefore, while the random error at a Cu concentration of about 0.01% is approximately 5%, the same concentration of Al will generate a random error of roughly 10%. It is for this reason that the deviation of Al concentration from nominal values in the corresponding standard steels is also roughly 10% (for example, in the UG3k sample, the concentration is 0.015% with an error of 0.0015%). Thus, the root-mean-square relative deviation of $C_c$ from $C_p$ for Al obtained when applying the universal theory is due, for the most part, to a random error in the process of concentration measurement rather than to unaccounted effects caused by third elements.

4. Conclusions

In conclusion, we will once again formulate the key physical ideas that shaped the foundation for the proposed theory:

• Third-element effects are additive. This assumption is justified by the fact that we considered a case of samples with small amounts of impurities, which makes it possible to neglect so-called effects superimposed on other effects.
• The main causes of third-element effects on the results of determining impurity content in the sample are: (1) changes in the conditions for the emission of impurity atoms from the sample to the plasma zone and the dependence of the plasma parameters (in particular, the excitation temperature) on the concentrations of the third elements in the sample; (2) changes in the registered signal of the analyte due to spectral line interferences and the dependence of the background plasma radiation on the concentrations of the third elements in the sample. This makes it possible to represent the relationship between the measured impurity concentration and the intensities of the analytical lines in the form of (4).
• As a rule, the concentrations of impurities are small, which makes it possible to use expansions in series of the type (10).
• When there are third-element effects, the relationship between the concentration of the analyte and the intensity of its analytical line can be represented as a polynomial of some degree $N_0$ that coincides with the degree of the corresponding polynomial in the absence of third-element effects. When they are present, the coefficients of this polynomial depend on the intensities of the analytical lines $I_k$ of the influencing elements and, at $I_k=0$, are equal to the corresponding coefficients in the absence of third-element effects.

As a result of the study, a new theory on the influence of third elements on the results of AES experiments has been developed and tested. As the proposed algorithm implies using only data arrays on the intensities of analytical lines of both the analyte and influencing elements, it makes it possible to avoid the use of successive approximation methods that slow down the operation of the spectrometer. However, the use of such methods is necessary when the algorithm accounting for the effects caused by third elements uses data on the concentrations of elements.