K-Means-Based Nature-Inspired Metaheuristic Algorithms for Automatic Data Clustering Problems: Recent Advances and Future Directions
Abstract
:1. Introduction
2. Scientific Background
2.1. Nature-Inspired Metaheuristics for Automatic Clustering Problems
2.2. Review Methodology
2.2.1. Research Questions
- RQ1: What are the various nature-inspired meta-heuristics techniques that have been hybridized with the K-means clustering algorithm?
- RQ2: Which of the reported hybridization of nature-inspired meta-heuristics techniques with K-means clustering algorithm handled automatic clustering problems?
- RQ3: What various automatic clustering approaches were adopted in the reported hybridization?
- RQ4: What contributions were made to improve the performance of the K-means clustering algorithm in handling automatic clustering problems?
- RQ5: What is the rate of publication of hybridization of K-means with nature-inspired meta-heuristic algorithms for automatic clustering?
2.3. Adopted Strategy for Article Selection
3. Data Synthesis and Analysis
3.1. RQ1. What Are the Various Nature-Inspired Meta-Heuristics Techniques That Have Been Hybridized with the K-Means Clustering Algorithm?
3.1.1. Genetic Algorithm
3.1.2. Particle Swarm Optimization
3.1.3. Firefly Algorithm
3.1.4. Bat Algorithm
3.1.5. Flower Pollination Algorithm
3.1.6. Artificial Bee Colony
3.1.7. Grey Wolf Optimizer
3.1.8. Sine–Cosine Algorithm
3.1.9. Cuckoo Search Algorithm
3.1.10. Differential Evolution
3.1.11. Invasive Weed Optimization
3.1.12. Imperialist Competitive Algorithm
3.1.13. Harmony Search
3.1.14. Blackhole Algorithm
3.1.15. Membrane Computing
3.1.16. Dragonfly Algorithm
3.1.17. Ant Lion Optimizer
3.1.18. Social Spider Algorithm
3.1.19. Fruit Fly Optimization
3.1.20. Bees Swarm Optimization
3.1.21. Bacterial Colony Optimization
3.1.22. Stochastic Diffusion Search
3.1.23. Honey Bee Mating Optimization
3.1.24. Cockroach Swarm Optimization
3.1.25. Glowworm Swarm Optimization
3.1.26. Bee Colony Optimization
3.1.27. Symbiotic Organism Search
3.2. RQ2. Which of the Reported Hybridization of Nature-Inspired Meta-Heuristics Techniques with K-Means Clustering Algorithm Handled Automatic Clustering Problems?
3.3. RQ3. What Were the Various Automatic Clustering Approaches Adopted in the Reported Hybridization?
3.4. RQ4. What Were the Contributions Made to Improve the Performance of the K-Means Clustering Algorithm in Handling Automatic Clustering Problems?
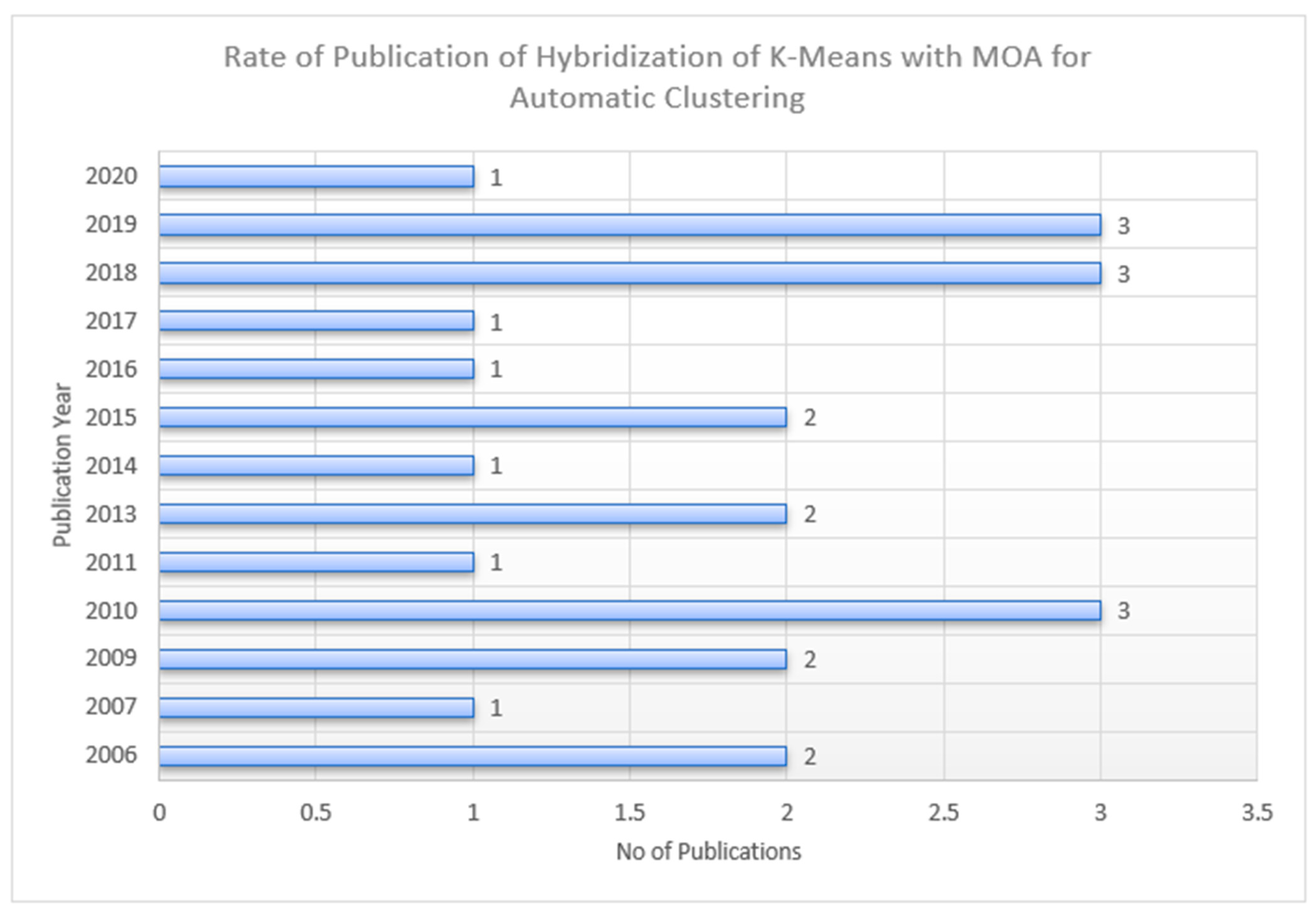
3.5. RQ5. What Is the Rate of Publication of Hybridization of K-Means with Nature-Inspired Meta-Heuristic Algorithms for Automatic Clustering?
Publications Trend of K-Means Hybridization with MOA
4. Results and Discussions
4.1. Metrics
4.2. Strength of This Study
4.3. Weakness of This Study
4.4. Hybridization of K-Means with MOA
4.5. Impact of Automatic Hybridized K-Means with MOA
4.6. Trending Areas of Application of Hybridized K-Means with MOA
4.7. Research Implication and Future Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABC | Artificial Bee Colony |
| ABC-KM | Artificial Bee Colony K-Means |
| ABDWT-FCM | Artificial Bee Colony based discrete wavelet transform with fuzzy c-mean |
| AC | Accuracy of Clustering |
| ACA-AL | Agglomerative clustering algorithm with average link |
| ACA-CL | Agglomerative clustering algorithm with complete link |
| ACA-SL | Agglomerative clustering algorithm with single link |
| ACDE-K-means | Automatic Clustering-based differential Evolution algorithm with K-Means |
| ACN | Average Correct Number |
| ACO | Ant Colony Optimization |
| ACO-SA | Ant Colony Optimization with Simulated Annealing |
| AGCUK | Automatic Genetic Clustering for Unknown K |
| AGWDWT-FCM | Adaptive Grey Wolf-based Discrete Wavelet Transform with Fuzzy C-mean |
| ALO | Ant Lion Optimizer |
| ALO-K | Ant Lion Optimizer with K-Means |
| ALPSOC | Ant Lion Particle Swarm Optimization |
| ANFIS | Adaptive Network based Fuzzy Inference System |
| ANOVA | Analysis of Variance |
| AR | Accuracy Rate |
| ARI | Adjusted Rand Index |
| ARMIR | Association Rule Mining for Information Retrieval |
| BBBC | Big Bang Big Crunch |
| BCO | Bacterial Colony Optimization |
| BCO+KM | Bacterial Colony Optimization with K-Means |
| BFCA | Bacterial Foraging Clustering Algorithm |
| BFGSA | Bird Flock Gravitational Search Algorithm |
| BFO | Bacterial foraging Optimization |
| BGLL | A modularity-based algorithm by Blondel, Guillaume, Lambiotte, and Lefebvre |
| BH | Black Hole |
| BH-BK | Black Hole and Bisecting K-means |
| BKBA | K-Means Binary Bat Algorithm |
| BPN | Back Propagation Network |
| BPZ | Bavarian Postal Zones Data |
| BSO | Bees Swarm Optimization |
| BSO-CLARA | Bees Swarm Optimization Clustering Large Dataset |
| BSOGD1 | Bees Swarm Optimization Guided by Decomposition |
| BTD | British Town Data |
| C4.5 | Tree-induction algorithm for Classification problems |
| CAABC | Chaotic Adaptive Artificial Bee Colony Algorithm |
| CAABC-K | Chaotic Adaptive Artificial Bee Colony Algorithm with K-Means |
| CABC | Chaotic Artificial Bee Colony |
| CCI | Correctly Classified Instance |
| CCIA | Cluster Centre Initialization Algorithm |
| CDE | Clustering Based Differential Evolution |
| CFA | Chaos-based Firefly Algorithm |
| CGABC | Chaotic Gradient Artificial Bee Colony |
| CIEFA | Compound Inward Intensified Exploration Firefly Algorithm |
| CLARA | Clustering Large Applications |
| CLARANS | Clustering Algorithm based on Randomized Search |
| CMC | Contraceptive Method Choice |
| CMIWO K-Means | Cloud model-based Invasive weed Optimization |
| CMIWOKM | Combining Invasive weed optimization and K-means |
| COA | Cuckoo Optimization Algorithm |
| COFS | Cuckoo Optimization for Feature Selection |
| CPU | Central Processing Unit |
| CRC | Chinese Restaurant Clustering |
| CRPSO | Craziness based Particle Swarm Optimization |
| CS | Cuckoo Search |
| CSA | Cuckoo Search Algorithm |
| CS-K-means | Cuckoo Search K-Means |
| CSO | Cockroach Swarm Optimization |
| CSOAKM | Cockroach Swarm Optimization and K-Means |
| CSOS | Clustering based Symbiotic Organism Search |
| DA | Dragonfly Algorithm |
| DADWT-FCM | Dragonfly Algorithm based discrete wavelet transform with fuzzy c-mean |
| DBI | Davies-Bouldin Index |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| DCPSO | Dynamic Clustering Particle Swarm Optimization |
| DDI | Dunn-Dunn Index |
| DE | Differential Evolution |
| DEA-based K-means | Data Envelopment Analysis based K-Means |
| DE-AKO | Differential Evolution with K-Means Operation |
| DE-ANS-AKO | Differential Evolution with adaptive niching and K-Means Operation |
| DEFOA-K-means | Differential Evolution Fruit Fly Optimization Algorithm with K-means |
| DE-KM | Differential Evolution and K-Means |
| DE-SVR | Differential Evolution -Support Vector Regression |
| DFBPKBA | Dynamic frequency-based parallel K-Bat Algorithm |
| DFSABCelite | ABC with depth-first search framework and elite-guided search equation |
| DMOZ | A dataset |
| DNA | Deoxyribonucleic Acid |
| DR | Detection Rate |
| DWT-FCM | Discrete wavelets transform with fuzzy c-mean |
| EABC | Enhanced Artificial Bee Colony |
| EABCK | Enhanced Artificial Bee Colony K-Means |
| EBA | Enhanced Bat Algorithm |
| ECOA | Extended Cuckoo Optimization Algorithm |
| ECOA-K | Extended Cuckoo Optimization Algorithm K-means |
| EFC | Entropy-based Fuzzy Clustering |
| EPSONS | PSO based on new neighborhood search strategy with diversity mechanism and Cauchy mutation operator |
| ER | Error Rate |
| ESA | Elephant Search Algorithm |
| EShBAT | Enhanced Shuffled Bat Algorithm |
| FA | Firefly Algorithm |
| FACTS | Flexible AC Transmission Systems |
| FA-K | Firefly-based K-Means Algorithm |
| FA-K-Means | Firefly K-Means |
| FAPSO-ACO-K | Fuzzy adaptive Particle Swarm Optimization with Ant Colony Optimization and K-Means |
| FA-SVR | Firefly Algorithm based Support Vector Regression |
| FBCO | Fuzzy Bacterial Colony Optimization |
| FBFO | Fractional Bacterial Foraging Optimization |
| FCM | Fuzzy C-Means |
| FCM-FA | Fuzzy C-Means Firefly Algorithm |
| FCMGWO | Fuzzy C-means Grey Wolf Optimization |
| FCSA | Fuzzy Cuckoo Search Algorithm |
| FFA-KELM | Firefly Algorithm based Kernel Extreme Learning Machine |
| FFO | Fruit Fly Optimization |
| FGKA | Fast Genetic K-means Algorithm |
| FI | F-Measure |
| FKM | Fuzzy K-Means |
| FM | F-Measure |
| FN | A modularity-based algorithm by Newman |
| FOAKFCM | Kernel-based Fuzzy C-Mean clustering based on Fruitfly Algorithm |
| FPA | Flower Pollination Algorithm |
| FPAGA | Flower Pollination Algorithm and Genetic Algorithm |
| FPAKM | Flower Pollination Algorithm K-Means |
| FPR | False Positive Rate |
| FPSO | Fuzzy Particle Swarm Optimization |
| FSDP | Fast Search for Density Peaks |
| GA | Genetic Algorithm |
| GABEEC | Genetic Algorithm Based Energy-efficient Clusters |
| GADWT | Genetic Algorithm Discrete Wavelength Transform |
| GAEEP | Genetic Algorithm Based Energy Efficient adaptive clustering hierarchy Protocol |
| GAGR | Genetic Algorithm with Gene Rearrangement |
| GAK | Genetic K-Means Algorithm |
| GAS3 | Genetic Algorithm with Species and Sexual Selection |
| GAS3KM | Modifying Genetic Algorithm with species and sexual selection using K-Means |
| GA-SVR | Genetic Algorithm based Support Vector Regression |
| GCUK | Genetic Clustering for unknown K |
| GENCLUST | Genetic Clustering |
| GENCLUST-F | Genetic Clustering variant |
| GENCLUST-H | Genetic Clustering variant |
| GGA | Genetically Guided Algorithm |
| GKA | Genetic K-Means Algorithm |
| GKM | Genetic K-Means Membranes |
| GKMC | Genetic K-Means Clustering |
| GM | Gaussian Mixture |
| GN | A modularity-based algorithm by Girvan and Newman |
| GP | Genetic Programming |
| GPS | Global Position System |
| GSI | Geological Survey of Iran |
| GSO | Glowworm Swarm Optimization |
| GSOKHM | Glowworm Swarm Optimization |
| GTD | Global Terrorist Dataset |
| GWDWT-FCM | Grey Wolf-based Discrete Wavelength Transform with Fuzzy C-Means |
| GWO | Grey wolf optimizer |
| GWO-K-Means | Grey wolf optimizer K-means |
| HABC | Hybrid Artificial Bee Colony |
| HBMO | Honeybees Mating Optimization |
| HCSPSO | Hybrid Cuckoo Search with Particle Swarm Optimization and K-Means |
| HESB | Hybrid Enhanced Shuffled Bat Algorithm |
| HFCA | Hybrid Fuzzy Clustering Algorithm |
| HHMA | Hybrid Heuristic Mathematics Algorithm |
| HKA | Harmony K-Means Algorithm |
| HS | Harmony Search |
| HSA | Harmony Search Algorithm |
| HSCDA | Hybrid Self-adaptive Community Detection algorithms |
| HSCLUST | Harmony Search clustering |
| HSKH | Harmony Search K-Means Hybrid |
| HS-K-means | Harmony Search K-Means |
| IABC | Improved Artificial Bee Colony |
| IBCOCLUST | Improved Bee Colony Optimization Clustering |
| ICA | Imperialist Competitive Algorithm |
| ICAFKM | Imperialist Competitive Algorithm with Fuzzy K Means |
| ICAKHM | Imperial Competitive Algorithm with K-Harmonic Mean |
| ICAKM | Imperial Competitive Algorithm with K-Mean |
| ICGSO | Image Clustering Glowworm Swarm Optimization |
| ICMPKHM | Improved Cuckoo Search with Modified Particle Swarm Optimization and K-Harmonic Mean |
| ICS | Improved Cuckoo Search |
| ICS-K-means | Improved Cuckoo Search K-Means |
| ICV | Intracluster Variation |
| IFCM | Interactive Fuzzy C-Means |
| IGBHSK | Global Best Harmony Search K-Means |
| IGNB | Information Gain-Naïve Bayes |
| IIEFA | Inward Intensified Exploration Firefly Algorithm |
| IPSO | Improved Particle Swarm Optimization |
| IPSO-K-Means | Improved Particle swarm Optimization with K-Means |
| IWO | Invasive weed optimization |
| IWO-K-Means | Invasive weed Optimization K-means |
| kABC | K-Means Artificial Bee Colony |
| KBat | Bat Algorithm with K-Means Clustering |
| KCPSO | K-Means and Combinatorial Particle Swarm Optimization |
| K-FA | K-Means Firefly Algorithm |
| KFCFA | K-member Fuzzy Clustering and Firefly Algorithm |
| KFCM | Kernel-based Fuzzy C-Mean Algorithm |
| KGA | K-Means Genetic Algorithm |
| K-GWO | Grey wolf optimizer with traditional K-Means |
| KHM | K-Harmonic Means |
| K-HS | Harmony K-Means Algorithm |
| KIBCLUST | K-Means with Improved bee colony |
| KMBA | K-Means Bat Algorithm |
| KMCLUST | K-Means Modified Bee Colony K-means |
| K-Means FFO | K-Means Fruit fly Optimization |
| KMeans-ALO | K-Means with Ant Lion Optimization |
| K-Means-FFA-KELM | Kernel Extreme Learning Machine Model coupled with K-means clustering and Firefly algorithm |
| KMGWO | K-Means Grey wolf optimizer |
| K-MICA | K-Means Modified Imperialist Competitive Algorithm |
| KMQGA | Quantum-inspired Genetic Algorithm for K-Means Algorithm |
| KMVGA | K-Means clustering algorithm based on Variable string length Genetic Algorithm |
| K-NM-PSO | K-Means Nelder–Mead Particle Swarm Optimization |
| KNNIR | K-Nearest Neighbors for Information Retrieval |
| KPA | K-means with Flower pollination algorithm |
| KPSO | K-means with Particle Swarm Optimization |
| KSRPSO | K-Means selective regeneration Particle Swarm Optimization |
| LEACH | Low-Energy Adaptive Clustering Hierarchy |
| MABC-K | Modified Artificial Bee Colony |
| MAE | Mean Absolute Error |
| MAX-SAT | Maximum satisfiability problem |
| MBCO | Modified Bee Colony K-means |
| MC | Membrane Computing |
| MCSO | Modified Cockroach Swarm Optimization |
| MEQPSO | Multi-Elitist Quantum-behaved Particle Swarm Optimization |
| MFA | Modified Firefly Algorithm |
| MFOA | Modified Fruit Fly Optimization Algorithm |
| MfPSO | Modified Particle Swarm Optimization |
| MICA | Modified Imperialist Competitive Algorithm |
| MKCLUST | Modified Bee Colony K-means Clustering |
| MKF-Cuckoo | Multiple Kernel-Based Fuzzy C-Means with Cuckoo Search |
| MN | Multimodal Nonseparable function |
| MOA | Meta-heuristic Optimization Algorithm |
| MPKM | Modified Point symmetry-based K-Means |
| MSE | Mean Square Error |
| MTSP | Multiple Traveling Salesman Problem |
| NaFA | Firefly Algorithm with neighborhood attraction |
| NGA | Niche Genetic Algorithm |
| NGKA | Niching Genetic K-means Algorithm |
| NM-PSO | Nelder–Mead simplex search with Particle Swarm Optimization |
| NNGA | Novel Niching Genetic Algorithm |
| Noiseclust | Noise clustering |
| NR-ELM | Neighborhood-based ratio (NR) and Extreme Learning Machine (ELM) |
| NSE | Nash-Sutcliffe Efficiency |
| NSL-KDD | NSL Knowledge Discovery and Data Mining |
| PAM | Partitioning Around Medoids |
| PCA | Principal component analysis |
| PCA-GAKM | Principal Component Analysis with Genetic Algorithm and K-means |
| PCAK | Principal Component Analysis K-means |
| PCA-SOM | Principal Component Analysis and Self-Organizing Map |
| PCAWK | Principal component analysis |
| PGAClust | Parallel Genetic Algorithm Clustering |
| PGKA | Prototypes-embedded Genetic K-means Algorithm |
| P-HS | Progressive Harmony Search |
| P-HS-K | Progressive Harmony Search with K-means |
| PIMA | Indian diabetic dataset |
| PNSR | Peak Signal to Noise Ratio |
| PR | Precision-Recall |
| PSC-RCE | Particle Swarm Clustering with Rapid Centroid Estimation |
| PSDWT-FCM | Particle Swarm based Discrete Wavelength Transform with Fuzzy C-Means |
| PSNR | Peak Signal-to-Noise Ratio |
| PSO | Particle Swarm Optimization |
| PSO-ACO | Particle Swarm Optimization and Ant Colony Optimization |
| PSO-FCM | Particle Swarm Optimization with Fuzzy C-Means |
| PSOFKM | Particle Swarm Optimization with Fuzzy K-means |
| PSOK | Particle Swarm Optimization with K-Means based clustering |
| PSOKHM | Particle Swarm Optimization with K-Harmonic Mean |
| PSO-KM | PSO-based K-Means clustering algorithm |
| PSOLF-KHM | Particle Swarm Optimization with Levy Flight and K-Harmonic Mean Algorithm |
| PSOM | Particle Swarm optimization with mutation operation |
| PSO-SA | Particle Swarm Optimization with Simulated Annealing |
| PSO-SVR | Particle Swarm Optimization based Support Vector Regression |
| PTM | Pattern Taxonomy Mining |
| QALO-K | Quantum Ant Lion Optimizer with K-Means |
| rCMA-ES | restart Covariance Matrix Adaptation Evolution Strategy |
| RMSE | Root Mean Square Error |
| ROC | Receive Operating Characteristics |
| RSC | Relevant Set Correlation clustering model |
| RVPSO-K | K-Means cluster algorithm based on Improved velocity of Particle Swarm Optimization cluster algorithm |
| RWFOA | Fruit Fly Optimization based on Stochastic Inertia Weight |
| SA | Simulated Annealing |
| SaNSDE | Self-adaptive Differential Evolution with Neighborhood Search |
| SAR | Synthetic Aperture Radar |
| SCA | Sine-Cosine Algorithm |
| SCAK-Means | Sine-Cosine Algorithm with K-means |
| SD | Standard Deviation |
| SDM | Sexual Determination Method |
| SDME | Second Derivative-like Measure of Enhancements |
| SDN | Software defined Network |
| SDS | Stochastic Diffusion Search |
| SFLA-CQ | Shuffled frog leaping algorithm for Color quantization |
| SHADE | Success-History based Adaptive Differential Evolution |
| SI | Scatter Index |
| SI | Silhouette Index |
| SIM dataset | Simulated dataset |
| SMEER | Secure multi-tier energy-efficient routing protocol |
| SOM | Self-Organizing Feature Maps |
| SOM+K | Self-Organizing Feature Maps neural networks with K-Means |
| SRPSO | Selective Regeneration Particle Swarm Optimization |
| SSB | Sum of Square Between |
| SSE | Sum of Square Error |
| SSIM | Structural Similarity |
| SS-KMeans | Scattering search K-Means |
| SSO | Social Spider Optimization |
| SSOKC | Social Spider Optimization with K-Means Clustering |
| SSW | Sum of Square within |
| SVC | Support Vector Clustering |
| SVM+GA | Support Vector Machine with Genetic Algorithm |
| SVMIR | Support Vector Machine for Information Retrieval |
| TCSC | Thyristor Controlled Series Compensator |
| TKMC | Traditional K-means Clustering |
| TP | True Positivity Rate |
| TPR | True Positivity Rate |
| TREC | Text Retrieval Conference dataset |
| TS | Tabu Search |
| TSMPSO | Two-Stage diversity mechanism in Multiobjective Particle Swarm Optimization |
| TSP-LIB-1600 | dataset for Travelling Salesman Problem |
| TSP-LIB-3038 | dataset for Travelling Salesman Problem |
| UCC | U-Control Chart |
| UCI | University of California Irvine |
| UN | Unimodal Nonseparable function |
| UPFC | Unified Power Flow Controller |
| US | Unimodal Separable function |
| VGA | Variable string length Genetic Algorithm |
| VSGSO-D K-means | Variable Step-size glowworm swarm optimization |
| VSSFA | Variable Step size firefly Algorithm |
| WDBC | Wisconsin Diagnostic Breast Cancer |
| WHDA-FCM | Wolf hunting based dragonfly with Fuzzy C-Means |
| WK-Means | Weight-based K-Means |
| WOA | Whale Optimization Algorithm |
| WOA-BAT | Whale Optimization Algorithm with Bat Algorithm |
| WSN | Wireless Sensor Networks |
References
- Ezugwu, A.E. Nature-inspired metaheuristic techniques for automatic clustering: A survey and performance study. SN Appl. Sci. 2020, 2, 273. [Google Scholar] [CrossRef] [Green Version]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. Am. J. Hum. Genet. 1969, 21, 407–408. [Google Scholar]
- Kapil, S.; Chawla, M.; Ansari, M.D. On K-Means Data Clustering Algorithm with Genetic Algorithm. In Proceedings of the 2016 Fourth International Conference on Parallel, Distributed and Grid Computing (PDGC), Solan, India, 22–24 December 2016; pp. 202–206. [Google Scholar]
- Ezugwu, A.E.-S.; Agbaje, M.B.; Aljojo, N.; Els, R.; Chiroma, H.; Elaziz, M.A. A Comparative Performance Study of Hybrid Firefly Algorithms for Automatic Data Clustering. IEEE Access 2020, 8, 121089–121118. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Shukla, A.K.; Agbaje, M.B.; Oyelade, O.N.; José-García, A.; Agushaka, J.O. Automatic clustering algorithms: A systematic review and bibliometric analysis of relevant literature. Neural Comput. Appl. 2020, 33, 6247–6306. [Google Scholar] [CrossRef]
- José-García, A.; Gómez-Flores, W. Automatic clustering using nature-inspired metaheuristics: A survey. Appl. Soft Comput. 2016, 41, 192–213. [Google Scholar] [CrossRef]
- Hruschka, E.; Campello, R.J.G.B.; Freitas, A.A.; de Carvalho, A. A Survey of Evolutionary Algorithms for Clustering. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2009, 39, 133–155. [Google Scholar] [CrossRef] [Green Version]
- Ezugwu, A.E.; Shukla, A.K.; Nath, R.; Akinyelu, A.A.; Agushaka, J.O.; Chiroma, H.; Muhuri, P.K. Metaheuristics: A comprehensive overview and classification along with bibliometric analysis. Artif. Intell. Rev. 2021, 54, 4237–4316. [Google Scholar] [CrossRef]
- Rana, S.; Jasola, S.; Kumar, R. A review on particle swarm optimization algorithms and their applications to data clustering. Artif. Intell. Rev. 2010, 35, 211–222. [Google Scholar] [CrossRef]
- Nanda, S.J.; Panda, G. A survey on nature inspired metaheuristic algorithms for partitional clustering. Swarm Evol. Comput. 2014, 16, 1–18. [Google Scholar] [CrossRef]
- Alam, S.; Dobbie, G.; Koh, Y.S.; Riddle, P.; Rehman, S.U. Research on particle swarm optimization based clustering: A systematic review of literature and techniques. Swarm Evol. Comput. 2014, 17, 1–13. [Google Scholar] [CrossRef]
- Mane, S.U.; Gaikwad, P.G. Nature Inspired Techniques for Data Clustering. In Proceedings of the 2014 International Conference on Circuits, Systems, Communication and Information Technology Applications (CSCITA), Mumbai, India, 4–5 April 2014; pp. 419–424. [Google Scholar]
- Falkenauer, E. Genetic Algorithms and Grouping Problems; John Wiley & Sons, Inc.: London, UK, 1998. [Google Scholar]
- Cowgill, M.; Harvey, R.; Watson, L. A genetic algorithm approach to cluster analysis. Comput. Math. Appl. 1999, 37, 99–108. [Google Scholar] [CrossRef] [Green Version]
- Okwu, M.O.; Tartibu, L.K. Metaheuristic Optimization: Nature-Inspired Algorithms Swarm and Computational Intelligence, Theory and Applications; Springer Nature: Berlin/Heidelberg, Germany, 2020; Volume 927. [Google Scholar]
- Malik, K.; Tayal, A. Comparison of Nature Inspired Metaheuristic Algorithms. Int. J. Electron. Electr. Eng. 2014, 7, 799–802. [Google Scholar]
- Engelbrecht, A.P. Computational Intelligence: An Introduction; John Wiley & Sons: London, UK, 2007. [Google Scholar]
- Agbaje, M.B.; Ezugwu, A.E.; Els, R. Automatic Data Clustering Using Hybrid Firefly Particle Swarm Optimization Algorithm. IEEE Access 2019, 7, 184963–184984. [Google Scholar] [CrossRef]
- Rajakumar, R.; Dhavachelvan, P.; Vengattaraman, T. A Survey on Nature Inspired Meta-Heuristic Algorithms with its Domain Specifications. In Proceedings of the 2016 International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 21–26 October 2016; pp. 1–6. [Google Scholar]
- Ezugwu, A.E. Advanced discrete firefly algorithm with adaptive mutation–based neighborhood search for scheduling unrelated parallel machines with sequence–dependent setup times. Int. J. Intell. Syst. 2021, 1–42. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Sivanandam, S.N.; Deepa, S.N. Genetic algorithms. In Introduction to Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; pp. 15–37. [Google Scholar]
- Krishna, K.; Murty, M.N. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. Part B 1999, 29, 433–439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bandyopadhyay, S.; Maulik, U. An evolutionary technique based on K-means algorithm for optimal clustering in RN. Inf. Sci. 2002, 146, 221–237. [Google Scholar] [CrossRef]
- Cheng, S.S.; Chao, Y.H.; Wang, H.M.; Fu, H.C. A prototypes-embedded genetic k-means algorithm. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, China, 20–24 August 2006; Volume 2, pp. 724–727. [Google Scholar]
- Laszlo, M.; Mukherjee, S. A genetic algorithm using hyper-quadtrees for low-dimensional k-means clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 533–543. [Google Scholar] [CrossRef] [PubMed]
- Laszlo, M.; Mukherjee, S. A genetic algorithm that exchanges neighboring centers for k-means clustering. Pattern Recognit. Lett. 2007, 28, 2359–2366. [Google Scholar] [CrossRef]
- Dai, W.; Jiao, C.; He, T. Research of K-Means Clustering Method based on Parallel Genetic Algorithm. In Proceedings of the Third International Conference on Intelligent Information Hiding and Multimedia Signal. Processing (IIH-MSP 2007), Kaohsiung, Taiwan, 26–28 November 2007; Volume 2, pp. 158–161. [Google Scholar]
- Chang, D.-X.; Zhang, X.-D.; Zheng, C.-W. A genetic algorithm with gene rearrangement for K-means clustering. Pattern Recognit. 2009, 42, 1210–1222. [Google Scholar] [CrossRef]
- Sheng, W.; Tucker, A.; Liu, X. A niching genetic k-means algorithm and its applications to gene expression data. Soft Comput. 2008, 14, 9–19. [Google Scholar] [CrossRef]
- Xiao, J.; Yan, Y.; Zhang, J.; Tang, Y. A quantum-inspired genetic algorithm for k-means clustering. Expert Syst. Appl. 2010, 37, 4966–4973. [Google Scholar] [CrossRef]
- Rahman, M.A.; Islam, M.Z. A hybrid clustering technique combining a novel genetic algorithm with K-Means. Knowl.-Based Syst. 2014, 71, 345–365. [Google Scholar] [CrossRef]
- Sinha, A.; Jana, P.K. A Hybrid MapReduce-based k-Means Clustering using Genetic Algorithm for Distributed Datasets. J. Supercomput. 2018, 74, 1562–1579. [Google Scholar] [CrossRef]
- Islam, M.Z.; Estivill-Castro, V.; Rahman, M.A.; Bossomaier, T. Combining K-Means and a genetic algorithm through a novel arrangement of genetic operators for high quality clustering. Expert Syst. Appl. 2018, 91, 402–417. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, X. A Novel Clustering Algorithm Combining Niche Genetic Algorithm with Canopy and K-Means. In Proceedings of the 2018 International Conference on Artificial Intelligence and Big Data (ICAIBD), Chengdu, China, 26–28 May 2018; pp. 26–32. [Google Scholar]
- Mustafi, D.; Sahoo, G. A hybrid approach using genetic algorithm and the differential evolution heuristic for enhanced initialization of the k-means algorithm with applications in text clustering. Soft Comput. 2019, 23, 6361–6378. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Ayoub, A.Y.; Mousa, A.A.; El-Desoky, I.M. An enhanced genetic algorithm with new mutation for cluster analysis. Comput. Stat. 2019, 34, 1355–1392. [Google Scholar] [CrossRef]
- Ghezelbash, R.; Maghsoudi, A.; Carranza, E.J.M. Optimization of geochemical anomaly detection using a novel genetic K-means clustering (GKMC) algorithm. Comput. Geosci. 2019, 134, 104335. [Google Scholar] [CrossRef]
- Kuo, R.; An, Y.; Wang, H.; Chung, W. Integration of self-organizing feature maps neural network and genetic K-means algorithm for market segmentation. Expert Syst. Appl. 2006, 30, 313–324. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Li, Y.; Wang, Z. An Improved k-Means Clustering Algorithm Combined with the Genetic Algorithm. In Proceedings of the 6th International Conference on Digital Content, Multimedia Technology and Its Applications, Seoul, Korea, 16–18 August 2010; pp. 121–124. [Google Scholar]
- Karegowda, A.G.; Vidya, T.; Jayaram, M.A.; Manjunath, A.S. Improving Performance of k-Means Clustering by Initializing Cluster Centers using Genetic Algorithm and Entropy based Fuzzy Clustering for Categorization of Diabetic Patients. In Proceedings of International Conference on Advances in Computing; Springer: New Delhi, India, 2013; pp. 899–904. [Google Scholar]
- Eshlaghy, A.T.; Razi, F.F. A hybrid grey-based k-means and genetic algorithm for project selection. Int. J. Bus. Inf. Syst. 2015, 18, 141. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, K.; He, J.; Niu, Y. Applying k-Means Clustering and Genetic Algorithm for Solving MTSP. In International Conference on Bio-Inspired Computing: Theories and Applications; Springer: Singapore, 2016; pp. 278–284. [Google Scholar]
- Barekatain, B.; Dehghani, S.; Pourzaferani, M. An Energy-Aware Routing Protocol for Wireless Sensor Networks Based on New Combination of Genetic Algorithm & k-means. Procedia Comput. Sci. 2015, 72, 552–560. [Google Scholar]
- Zhou, X.; Gu, J.; Shen, S.; Ma, H.; Miao, F.; Zhang, H.; Gong, H. An Automatic K-Means Clustering Algorithm of GPS Data Combining a Novel Niche Genetic Algorithm with Noise and Density. ISPRS Int. J. Geo-Inf. 2017, 6, 392. [Google Scholar] [CrossRef] [Green Version]
- Mohammadrezapour, O.; Kisi, O.; Pourahmad, F. Fuzzy c-means and K-means clustering with genetic algorithm for identification of homogeneous regions of groundwater quality. Neural Comput. Appl. 2018, 32, 3763–3775. [Google Scholar] [CrossRef]
- Esmin, A.A.A.; Coelho, R.A.; Matwin, S. A review on particle swarm optimization algorithm and its variants to clustering high-dimensional data. Artif. Intell. Rev. 2013, 44, 23–45. [Google Scholar] [CrossRef]
- Niu, B.; Duan, Q.; Liu, J.; Tan, L.; Liu, Y. A population-based clustering technique using particle swarm optimization and k-means. Nat. Comput. 2016, 16, 45–59. [Google Scholar] [CrossRef]
- Van der Merwe, D.W.; Engelbrecht, A.P. Data Clustering using Particle Swarm Optimization. In Proceedings of the 2003 Congress on Evolutionary Computation, CEC’03, Canberra, Australia, 8–12 December 2003; Volume 1, pp. 215–220. [Google Scholar]
- Omran, M.G.H.; Salman, A.; Engelbrecht, A.P. Dynamic clustering using particle swarm optimization with application in image segmentation. Pattern Anal. Appl. 2005, 8, 332–344. [Google Scholar] [CrossRef]
- Alam, S.; Dobbie, G.; Riddle, P. An Evolutionary Particle Swarm Optimization Algorithm for Data Clustering. In Proceedings of the 2008 IEEE Swarm Intelligence Symposium, St. Louis, MO, USA, 21–23 September 2008; pp. 1–7. [Google Scholar]
- Kao, I.W.; Tsai, C.Y.; Wang, Y.C. An effective particle swarm optimization method for data clustering. In Proceedings of the 2007 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 2 December 2007; pp. 548–552. [Google Scholar]
- Niknam, T.; Amiri, B. An efficient hybrid approach based on PSO, ACO and k-means for cluster analysis. Appl. Soft Comput. 2010, 10, 183–197. [Google Scholar] [CrossRef]
- Thangaraj, R.; Pant, M.; Abraham, A.; Bouvry, P. Particle swarm optimization: Hybridization perspectives and experimental illustrations. Appl. Math. Comput. 2011, 217, 5208–5226. [Google Scholar] [CrossRef]
- Chuang, L.-Y.; Hsiao, C.-J.; Yang, C.-H. Chaotic particle swarm optimization for data clustering. Expert Syst. Appl. 2011, 38, 14555–14563. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Ye, F. Particle Swarm Optimization Algorithm and its Application to Clustering Analysis. In Proceedings of the 17th Conference on Electrical Power Distribution, Tehran, Iran, 2–3 May 2012; pp. 789–794. [Google Scholar]
- Yuwono, M.; Su, S.W.; Moulton, B.D.; Nguyen, H.T. Data clustering using variants of rapid centroid estimation. IEEE Trans. Evol. Comput. 2013, 18, 366–377. [Google Scholar] [CrossRef]
- Omran, M.; Engelbrecht, A.P.; Salman, A. Particle swarm optimization method for image clustering. Int. J. Pattern Recognit. Artif. Intell. 2005, 19, 297–321. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, H. Research on Application of Clustering Algorithm based on PSO for the Web Usage Pattern. In Proceedings of the 2007 International Conference on Wireless Communications, Networking and Mobile Computing, Honolulu, HI, USA, 21–25 September 2007; pp. 3705–3708. [Google Scholar]
- Kao, Y.-T.; Zahara, E.; Kao, I.-W. A hybridized approach to data clustering. Expert Syst. Appl. 2008, 34, 1754–1762. [Google Scholar] [CrossRef]
- Kao, Y.; Lee, S.Y. Combining K-Means and Particle Swarm Optimization for Dynamic Data Clustering Problems. In Proceedings of the 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems, Shanghai, China, 20–22 November 2009; Volume 1, pp. 757–761. [Google Scholar]
- Yang, F.; Sun, T.; Zhang, C. An efficient hybrid data clustering method based on K-harmonic means and Particle Swarm Optimization. Expert Syst. Appl. 2009, 36, 9847–9852. [Google Scholar] [CrossRef]
- Tsai, C.-Y.; Kao, I.-W. Particle swarm optimization with selective particle regeneration for data clustering. Expert Syst. Appl. 2011, 38, 6565–6576. [Google Scholar] [CrossRef]
- Prabha, K.A.; Visalakshi, N.K. Improved Particle Swarm Optimization based k-Means Clustering. In Proceedings of the 2014 International Conference on Intelligent Computing Applications, Coimbatore, India, 6–7 March 2014; pp. 59–63. [Google Scholar]
- Emami, H.; Derakhshan, F. Integrating Fuzzy K-Means, Particle Swarm Optimization, and Imperialist Competitive Algorithm for Data Clustering. Arab. J. Sci. Eng. 2015, 40, 3545–3554. [Google Scholar] [CrossRef]
- Nayak, S.; Panda, C.; Xalxo, Z.; Behera, H.S. An Integrated Clustering Framework Using Optimized K-means with Firefly and Canopies. In Computational Intelligence in Data Mining-Volume 2; Springer: New Delhi, India, 2015; pp. 333–343. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Ratanavilisagul, C. A Novel Modified Particle Swarm Optimization Algorithm with Mutation for Data Clustering Problem. In Proceedings of the 5th International Conference on Computational Intelligence and Applications (ICCIA), Beijing, China, 19–21 June 2020; pp. 55–59. [Google Scholar]
- Paul, S.; De, S.; Dey, S. A Novel Approach of Data Clustering Using An Improved Particle Swarm Optimization Based K–Means Clustering Algorithm. In Proceedings of the 2020 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Virtual, 2–4 July 2020; pp. 1–6. [Google Scholar]
- Jie, Y.; Yibo, S. The Study for Data Mining of Distribution Network Based on Particle Swarm Optimization with Clustering Algorithm Method. In Proceedings of the 2019 4th International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 21–23 September 2019; pp. 81–85. [Google Scholar]
- Chen, X.; Miao, P.; Bu, Q. Image Segmentation Algorithm Based on Particle Swarm Optimization with K-means Optimization. In Proceedings of the 2019 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 12–14 July 2019; pp. 156–159. [Google Scholar]
- Yang, X.S. Firefly Algorithms for Multimodal Optimization. In Proceedings of the International Symposium on Stochastic Algorithms, Sapporo, Japan, 26–28 October 2009; pp. 169–178. [Google Scholar]
- Xie, H.; Zhang, L.; Lim, C.P.; Yu, Y.; Liu, C.; Liu, H.; Walters, J. Improving K-means clustering with enhanced Firefly Algorithms. Appl. Soft Comput. 2019, 84, 105763. [Google Scholar] [CrossRef]
- Hassanzadeh, T.; Meybodi, M.R. A New Hybrid Approach for Data Clustering using Firefly Algorithm and K-Means. In Proceedings of the 16th CSI c (AISP 2012), Fars, Iran, 2–3 May 2012; pp. 007–011. [Google Scholar]
- Mathew, J.; Vijayakumar, R. Scalable Parallel Clustering Approach for Large Data using Parallel K Means and Firefly Algorithms. In Proceedings of the 2014 International Conference on High. Performance Computing and Applications (ICHPCA), Bhubaneswar, India, 22–24 December 2014; pp. 1–8. [Google Scholar]
- Nayak, J.; Kanungo, D.P.; Naik, B.; Behera, H.S. Evolutionary Improved Swarm-based Hybrid K-Means Algorithm for Cluster Analysis. In Proceedings of the Second International Conference on Computer and Communication Technologies; Springer: New Delhi, India, 2017; Volume 556, pp. 343–352. [Google Scholar]
- Behera, H.S.; Nayak, J.; Nanda, M.; Nayak, K. A novel hybrid approach for real world data clustering algorithm based on fuzzy C-means and firefly algorithm. Int. J. Fuzzy Comput. Model. 2015, 1, 431. [Google Scholar] [CrossRef]
- Nayak, J.; Naik, B.; Behera, H.S. Cluster Analysis Using Firefly-Based K-means Algorithm: A Combined Approach. In Computational Intelligence in Data Mining. Advances in Intelligent Systems and Computing; Behera, H., Mohapatra, D., Eds.; Springer: Singapore, 2017; Volume 556. [Google Scholar]
- Jitpakdee, P.; Aimmanee, P.; Uyyanonvara, B. A hybrid approach for color image quantization using k-means and firefly algorithms. World Acad. Sci. Eng. Technol. 2013, 77, 138–145. [Google Scholar]
- Kuo, R.; Li, P. Taiwanese export trade forecasting using firefly algorithm based K-means algorithm and SVR with wavelet transform. Comput. Ind. Eng. 2016, 99, 153–161. [Google Scholar] [CrossRef]
- Kaur, A.; Pal, S.K.; Singh, A.P. Hybridization of K-Means and Firefly Algorithm for intrusion detection system. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 901–910. [Google Scholar] [CrossRef]
- Langari, R.K.; Sardar, S.; Mousavi, S.A.A.; Radfar, R. Combined fuzzy clustering and firefly algorithm for privacy preserving in social networks. Expert Syst. Appl. 2019, 141, 112968. [Google Scholar] [CrossRef]
- HimaBindu, G.; Kumar, C.R.; Hemanand, C.; Krishna, N.R. Hybrid clustering algorithm to process big data using firefly optimization mechanism. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Wu, L.; Peng, Y.; Fan, J.; Wang, Y.; Huang, G. A novel kernel extreme learning machine model coupled with K-means clustering and firefly algorithm for estimating monthly reference evapotranspiration in parallel computation. Agric. Water Manag. 2020, 245, 106624. [Google Scholar] [CrossRef]
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef] [Green Version]
- Sood, M.; Bansal, S. K-medoids clustering technique using bat algorithm. Int. J. Appl. Inf. Syst. 2013, 5, 20–22. [Google Scholar] [CrossRef]
- Tripathi, A.; Sharma, K.; Bala, M. Dynamic frequency based parallel k-bat algorithm for massive data clustering (DFBPKBA). Int. J. Syst. Assur. Eng. Manag. 2017, 9, 866–874. [Google Scholar] [CrossRef]
- Pavez, L.; Altimiras, F.; Villavicencio, G. A K-means Bat Algorithm Applied to the Knapsack Problem. In Proceedings of the Computational Methods in Systems and Software; Springer: Cham, Switzerland, 2020; pp. 612–621. [Google Scholar]
- Gan, J.E.; Lai, W.K. Automated Grading of Edible Birds Nest Using Hybrid Bat Algorithm Clustering Based on K-Means. In Proceedings of the 2019 IEEE International Conference on Automatic Control. and Intelligent Systems (I2CACIS), Kuala Lumpur, Malaysia, 19 June 2019; pp. 73–78. [Google Scholar]
- Chaudhary, R.; Banati, H. Hybrid enhanced shuffled bat algorithm for data clustering. Int. J. Adv. Intell. Paradig. 2020, 17, 323–341. [Google Scholar] [CrossRef]
- Yang, X.S. Flower pollination algorithm for global optimization. In Proceedings of the International Conference on Unconventional Computing and Natural Computation; Springer: Berlin/Heidelberg, Germany, 2012; pp. 240–249. [Google Scholar]
- Jensi, R.; Jiji, G.W. Hybrid data clustering approach using k-means and flower pollination algorithm. arXiv 2015, arXiv:1505.03236. [Google Scholar]
- Kumari, G.V.; Rao, G.S.; Rao, B.P. Flower pollination-based K-means algorithm for medical image compression. Int. J. Adv. Intell. Paradig. 2021, 18, 171–192. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-tr06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turcia, 2005. [Google Scholar]
- Armano, G.; Farmani, M.R. Clustering Analysis with Combination of Artificial Bee Colony Algorithm and k-Means Technique. Int. J. Comput. Theory Eng. 2014, 6, 141–145. [Google Scholar] [CrossRef] [Green Version]
- Tran, D.C.; Wu, Z.; Wang, Z.; Deng, C. A Novel Hybrid Data Clustering Algorithm Based on Artificial Bee Colony Algorithm and K-Means. Chin. J. Electron. 2015, 24, 694–701. [Google Scholar] [CrossRef]
- Bonab, M.B.; Hashim, S.Z.M.; Alsaedi, A.K.Z.; Hashim, U.R. Modified K-Means Combined with Artificial Bee Colony Algorithm and Differential Evolution for Color Image Segmentation. In Computational Intelligence in Information Systems; Springer: Cham, Switzerland, 2015; pp. 221–231. [Google Scholar]
- Jin, Q.; Lin, N.; Zhang, Y. K-Means Clustering Algorithm Based on Chaotic Adaptive Artificial Bee Colony. Algorithms 2021, 14, 53. [Google Scholar] [CrossRef]
- Dasu, M.V.; Reddy, P.V.N.; Reddy, S.C.M. Classification of Remote Sensing Images Based on K-Means Clustering and Artificial Bee Colony Optimization. In Advances in Cybernetics, Cognition, and Machine Learning for Communication Technologies; Springer: Singapore, 2020; pp. 57–65. [Google Scholar]
- Huang, S.C. Color Image Quantization Based on the Artificial Bee Colony and Accelerated K-means Algorithms. Symmetry 2020, 12, 1222. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Lin, Y.; Zhang, Z.; Gong, X. Dynamic Equivalent Modeling for Wind Farms with DFIGs Using the Artificial Bee Colony With K-Means Algorithm. IEEE Access 2020, 8, 173723–173731. [Google Scholar] [CrossRef]
- Cao, L.; Xue, D. Research on modified artificial bee colony clustering algorithm. In Proceedings of the 2015 International Conference on Network and Information Systems for Computers, Wuhan, China, 13–25 January 2015; pp. 231–235. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Soft. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Katarya, R.; Verma, O.P. Recommender system with grey wolf optimizer and FCM. Neural Comput. Appl. 2016, 30, 1679–1687. [Google Scholar] [CrossRef]
- Korayem, L.; Khorsid, M.; Kassem, S. A Hybrid K-Means Metaheuristic Algorithm to Solve a Class of Vehicle Routing Problems. Adv. Sci. Lett. 2015, 21, 3720–3722. [Google Scholar] [CrossRef]
- Pambudi, E.A.; Badharudin, A.Y.; Wicaksono, A.P. Enhanced K-Means by Using Grey Wolf Optimizer for Brain MRI Segmentation. ICTACT J. Soft Comput. 2021, 11, 2353–2358. [Google Scholar]
- Mohammed, H.M.; Abdul, Z.K.; Rashid, T.A.; Alsadoon, A.; Bacanin, N. A new K-means gray wolf algorithm for engineering problems. World J. Eng. 2021. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Moorthy, R.S.; Pabitha, P. A Novel Resource Discovery Mechanism using Sine Cosine Optimization Algorithm in Cloud. In Proceedings of the 4th International Conference on Intelligent Computing and Control. Systems (ICICCS), Madurai, India, 13–15 May 2020; pp. 742–746. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy Flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Ye, S.; Huang, X.; Teng, Y.; Li, Y. K-Means Clustering Algorithm based on Improved Cuckoo Search Algorithm and its Application. In Proceedings of the 2018 IEEE 3rd International Conference on Big Data Analysis (ICBDA), Shanghai, China, 9–12 March 2018; pp. 422–426. [Google Scholar]
- Saida, I.B.; Kamel, N.; Omar, B. A New Hybrid Algorithm for Document Clustering based on Cuckoo Search and K-Means. In Recent Advances on Soft Computing and Data Mining; Springer: Cham, Swizterland, 2014; pp. 59–68. [Google Scholar]
- Girsang, A.S.; Yunanto, A.; Aslamiah, A.H. A Hybrid Cuckoo Search and K-Means for Clustering Problem. In Proceedings of the 2017 International Conference on Electrical Engineering and Computer Science (ICECOS), Palembang, Indonesia, 22–23 August 2017; pp. 120–124. [Google Scholar]
- Zeng, L.; Xie, X. Collaborative Filtering Recommendation Based On CS-Kmeans Optimization Clustering. In Proceedings of the 2019 4th International Conference on Intelligent Information Processing, Wuhan, China, 16–17 November 2019; pp. 334–340. [Google Scholar]
- Tarkhaneh, O.; Isazadeh, A.; Khamnei, H.J. A new hybrid strategy for data clustering using cuckoo search based on Mantegna levy distribution, PSO and k-means. Int. J. Comput. Appl. Technol. 2018, 58, 137–149. [Google Scholar] [CrossRef]
- Singh, S.P.; Solanki, S. A Movie Recommender System Using Modified Cuckoo Search. In Emerging Research in Electronics, Computer Science and Technology; Springer: Singapore, 2019; pp. 471–482. [Google Scholar]
- Arjmand, A.; Meshgini, S.; Afrouzian, R.; Farzamnia, A. Breast Tumor Segmentation Using K-Means Clustering and Cuckoo Search Optimization. In Proceedings of the 9th International Conference on Computer and Knowledge Engineering (ICCKE), Virtual, 24–25 October 2019; pp. 305–308. [Google Scholar]
- García, J.; Yepes, V.; Martí, J.V. A Hybrid k-Means Cuckoo Search Algorithm Applied to the Counterfort Retaining Walls Problem. Mathematics 2020, 8, 555. [Google Scholar] [CrossRef]
- Binu, D.; Selvi, M.; George, A. MKF-Cuckoo: Hybridization of Cuckoo Search and Multiple Kernel-based Fuzzy C-means Algorithm. AASRI Procedia 2013, 4, 243–249. [Google Scholar] [CrossRef]
- Manju, V.N.; Fred, A.L. An efficient multi balanced cuckoo search K-means technique for segmentation and compression of compound images. Multimed. Tools Appl. 2019, 78, 14897–14915. [Google Scholar] [CrossRef]
- Deepa, M.; Sumitra, P. Intrusion Detection System Using K-Means Based on Cuckoo Search Optimization. IOP Conf. Ser. Mater. Sci. Eng. 2020, 993, 012049. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Brest, J.; Maučec, M.S. Population size reduction for the differential evolution algorithm. Appl. Intell. 2007, 29, 228–247. [Google Scholar] [CrossRef]
- Kwedlo, W. A clustering method combining differential evolution with the K-means algorithm. Pattern Recognit. Lett. 2011, 32, 1613–1621. [Google Scholar] [CrossRef]
- Cai, Z.; Gong, W.; Ling, C.X.; Zhang, H. A clustering-based differential evolution for global optimization. Appl. Soft Comput. 2011, 11, 1363–1379. [Google Scholar] [CrossRef]
- Kuo, R.J.; Suryani, E.; Yasid, A. Automatic clustering combining differential evolution algorithm and k-means algorithm. In Proceedings of the Institute of Industrial Engineers Asian Conference 2013; Springer: Singapore, 2013; pp. 1207–1215. [Google Scholar]
- Sierra, L.M.; Cobos, C.; Corrales, J.C. Continuous Optimization based on a Hybridization of Differential Evolution with K-Means. In IBERO-American Conference on Artificial Intelligence; Springer: Cham, Switzerland, 2014; pp. 381–392. [Google Scholar]
- Hu, J.; Wang, C.; Liu, C.; Ye, Z. Improved K-Means Algorithm based on Hybrid Fruit Fly Optimization and Differential Evolution. In Proceedings of the 12th International Conference on Computer Science and Education (ICCSE), Houston, TX, USA, 22–25 August 2017; pp. 464–467. [Google Scholar]
- Wang, F. A Weighted K-Means Algorithm based on Differential Evolution. In Proceedings of the 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control. Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 1–2274. [Google Scholar]
- Silva, J.; Lezama, O.B.P.; Varela, N.; Guiliany, J.G.; Sanabria, E.S.; Otero, M.S.; Rojas, V. U-Control Chart Based Differential Evolution Clustering for Determining the Number of Cluster in k-Means. In International Conference on Green, Pervasive, and Cloud Computing; Springer: Cham, Switzerland, 2019; pp. 31–41. [Google Scholar]
- Sheng, W.; Wang, X.; Wang, Z.; Li, Q.; Zheng, Y.; Chen, S. A Differential Evolution Algorithm with Adaptive Niching and K-Means Operation for Data Clustering. IEEE Trans. Cybern. 2020, 1–15. [Google Scholar] [CrossRef]
- Mustafi, D.; Mustafi, A.; Sahoo, G. A novel approach to text clustering using genetic algorithm based on the nearest neighbour heuristic. Int. J. Comput. Appl. 2020, 1–13. [Google Scholar] [CrossRef]
- Mehrabian, A.; Lucas, C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar] [CrossRef]
- Fan, C.; Zhang, T.; Yang, Z.; Wang, L. A Text Clustering Algorithm Hybriding Invasive Weed Optimization with K-Means. In Proceedings of the 12th International Conference on Autonomic and Trusted Computing and 2015 IEEE 15th International Conference on Scalable Computing and Communications and Its Associated Workshops (UIC-ATC-ScalCom), Beijing, China, 10–14 August 2015; pp. 1333–1338. [Google Scholar] [CrossRef]
- Pan, G.; Li, K.; Ouyang, A.; Zhou, X.; Xu, Y. A hybrid clustering algorithm combining cloud model IWO and k-means. Int. J. Pattern Recogn. Artif. Intell. 2014, 28, 1450015. [Google Scholar] [CrossRef]
- Boobord, F.; Othman, Z.; Abubakar, A. PCAWK: A Hybridized Clustering Algorithm Based on PCA and WK-means for Large Size of Dataset. Int. J. Adv. Soft Comput. Appl. 2015, 7, 3. [Google Scholar]
- Razi, F.F. A hybrid DEA-based K-means and invasive weed optimization for facility location problem. J. Ind. Eng. Int. 2018, 15, 499–511. [Google Scholar] [CrossRef] [Green Version]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist Competitive Algorithm: An Algorithm for Optimization Inspired by Imperialistic Competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007. [Google Scholar]
- Niknam, T.; Fard, E.T.; Pourjafarian, N.; Rousta, A. An efficient hybrid algorithm based on modified imperialist competitive algorithm and K-means for data clustering. Eng. Appl. Artif. Intell. 2011, 24, 306–317. [Google Scholar] [CrossRef]
- Abdeyazdan, M. Data clustering based on hybrid K-harmonic means and modifier imperialist competitive algorithm. J. Supercomput. 2014, 68, 574–598. [Google Scholar] [CrossRef]
- Forsati, R.; Meybodi, M.; Mahdavi, M.; Neiat, A. Hybridization of K-Means and Harmony Search Methods for Web Page Clustering. In Proceedings of the 2008 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology, Melbourne, Australia, 14–17 December 2020; Volume 1, pp. 329–335. [Google Scholar]
- Mahdavi, M.; Abolhassani, H. Harmony K-means algorithm for document clustering. Data Min. Knowl. Discov. 2008, 18, 370–391. [Google Scholar] [CrossRef]
- Cobos, C.; Andrade, J.; Constain, W.; Mendoza, M.; León, E. Web document clustering based on Global-Best Harmony Search, K-means, Frequent Term Sets and Bayesian Information Criterion. In Proceedings of the IEEE Congress on Evolutionary Computation, New Orleans, LA, USA, 5–8 June 2011; pp. 1–8. [Google Scholar]
- Chandran, L.P.; Nazeer, K.A.A. An improved clustering algorithm based on K-means and harmony search optimization. In Proceedings of the 2011 IEEE Recent Advances in Intelligent Computational Systems, Trivandrum, India, 22–24 September 2011; pp. 447–450. [Google Scholar]
- Nazeer, K.A.; Sebastian, M.; Kumar, S.M. A novel harmony search-K means hybrid algorithm for clustering gene expression data. Bioinformation 2013, 9, 84–88. [Google Scholar] [CrossRef] [PubMed]
- Raval, D.; Raval, G.; Valiveti, S. Optimization of Clustering Process for WSN with Hybrid Harmony Search and K-Means Algorithm. In Proceedings of the 2016 International Conference on Recent Trends in Information Technology (ICRTIT), Chennai, India, 8–9 April 2016; pp. 1–6. [Google Scholar]
- Kim, S.; Ebay, S.K.; Lee, B.; Kim, K.; Youn, H.Y. Load Balancing for Distributed SDN with Harmony Search. In Proceedings of the 2019 16th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 11–14 January 2019; pp. 1–2. [Google Scholar]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Tsai, C.W.; Hsieh, C.H.; Chiang, M.C. Parallel Black Hole Clustering based on MapReduce. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 2543–2548. [Google Scholar]
- Abdulwahab, H.A.; Noraziah, A.; Alsewari, A.A.; Salih, S.Q. An Enhanced Version of Black Hole Algorithm via Levy Flight for Optimization and Data Clustering Problems. IEEE Access 2019, 7, 142085–142096. [Google Scholar] [CrossRef]
- Eskandarzadehalamdary, M.; Masoumi, B.; Sojodishijani, O. A New Hybrid Algorithm based on Black Hole Optimization and Bisecting K-Means for Cluster Analysis. In Proceedings of the 22nd Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 20–22 May 2014; pp. 1075–1079. [Google Scholar]
- Pal, S.S.; Pal, S. Black Hole and k-Means Hybrid Clustering Algorithm. In Computational Intelligence in Data Mining; Springer: Singapore, 2020; pp. 403–413. [Google Scholar]
- Feng, L.; Wang, X.; Chen, D. Image Classification Based on Improved Spatial Pyramid Matching Model. In International Conference on Intelligent Computing; Springer: Cham, Switzerland, 2018; pp. 153–164. [Google Scholar]
- Jiang, Y.; Peng, H.; Huang, X.; Zhang, J.; Shi, P. A novel clustering algorithm based on P systems. Int. J. Innov. Comput. Inf. Control 2014, 10, 753–765. [Google Scholar]
- Jiang, Z.; Zang, W.; Liu, X. Research of K-Means Clustering Method based on DNA Genetic Algorithm and P System. In International Conference on Human Centered Computing; Springer: Cham, Switzerland, 2016; pp. 193–203. [Google Scholar]
- Zhao, D.; Liu, X. A Genetic K-means Membrane Algorithm for Multi-relational Data Clustering. In Proceedings of the International Conference on Human Centered Computing, Colombo, Sri Lanka, 7–9 January 2016; pp. 954–959. [Google Scholar]
- Xiang, W.; Liu, X. A New P System with Hybrid MDE-k-Means Algorithm for Data Clustering. 2016. Available online: http://www.wseas.us/journal/pdf/computers/2016/a145805-1077.pdf (accessed on 21 October 2021).
- Zhao, Y.; Liu, X.; Zhang, H. The K-Medoids Clustering Algorithm with Membrane Computing. TELKOMNIKA Indones. J. Electr. Eng. 2013, 11, 2050–2057. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, L.; Liu, X. A Hybrid Approach Optimized by Tissue-Like P System for Clustering. In International Conference on Intelligent Science and Big Data Engineering; Springer: Cham, Switzerland, 2018; pp. 423–432. [Google Scholar]
- Wang, S.; Liu, X.; Xiang, L. An improved initialisation method for K-means algorithm optimised by Tissue-like P system. Int. J. Parallel Emergent Distrib. Syst. 2019, 36, 3–10. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Angelin, B. A Roc Curve Based K-Means Clustering for Outlier Detection Using Dragon Fly Optimization. Turk. J. Compu. Math. Educ. 2021, 12, 467–476. [Google Scholar]
- Kumar, J.T.; Reddy, Y.M.; Rao, B.P. WHDA-FCM: Wolf Hunting-Based Dragonfly With Fuzzy C-Mean Clustering for Change Detection in SAR Images. Comput. J. 2019, 63, 308–321. [Google Scholar] [CrossRef]
- Majhi, S.K.; Biswal, S. Optimal cluster analysis using hybrid K-Means and Ant Lion Optimizer. Karbala Int. J. Mod. Sci. 2018, 4, 347–360. [Google Scholar] [CrossRef]
- Chen, J.; Qi, X.; Chen, L.; Chen, F.; Cheng, G. Quantum-inspired ant lion optimized hybrid k-means for cluster analysis and intrusion detection. Knowl.-Based Syst. 2020, 203, 106167. [Google Scholar] [CrossRef]
- Murugan, T.M.; Baburaj, E. Alpsoc Ant Lion*: Particle Swarm Optimized Hybrid K-Medoid Clustering. In Proceedings of the 2020 International Conference on Smart Technologies in Computing, Electrical and Electronics (ICSTCEE), Bengaluru, India, 9–10 October 2020; pp. 145–150. [Google Scholar]
- Naem, A.A.; Ghali, N.I. Optimizing community detection in social networks using antlion and K-median. Bull. Electr. Eng. Inform. 2019, 8, 1433–1440. [Google Scholar] [CrossRef]
- Dhand, G.; Sheoran, K. Protocols SMEER (Secure Multitier Energy Efficient Routing Protocol) and SCOR (Secure Elliptic curve based Chaotic key Galois Cryptography on Opportunistic Routing). Mater. Today Proc. 2020, 37, 1324–1327. [Google Scholar] [CrossRef]
- Cuevas, E.; Cienfuegos, M.; Zaldívar, D.; Pérez-Cisneros, M. A swarm optimization algorithm inspired in the behavior of the social-spider. Expert Syst. Appl. 2013, 40, 6374–6384. [Google Scholar] [CrossRef] [Green Version]
- Chandran, T.R.; Reddy, A.V.; Janet, B. Performance Comparison of Social Spider Optimization for Data Clustering with Other Clustering Methods. In Proceedings of the 2018 Second International Conference on Intelligent Computing and Control. Systems (ICICCS), Madurai, India, 14–15 June 2018; pp. 1119–1125. [Google Scholar]
- Thiruvenkatasuresh, M.P.; Venkatachalam, V. Analysis and evaluation of classification and segmentation of brain tumour images. Int. J. Biomed. Eng. Technol. 2019, 30, 153–178. [Google Scholar] [CrossRef]
- Xing, B.; Gao, W.J. Fruit fly optimization algorithm. In Innovative Computational Intelligence: A Rough Guide to 134 Clever Algorithms; Springer: Cham, Switzerland, 2014; pp. 167–170. [Google Scholar]
- Sharma, V.K.; Patel, R. Unstructured Data Clustering using Hybrid K-Means and Fruit Fly Optimization (KMeans-FFO) algorithm. Int. J. Comput. Sci. Inf. Secur. (IJCSIS) 2020, 18. [Google Scholar]
- Jiang, X.Y.; Pa, N.Y.; Wang, W.C.; Yang, T.T.; Pan, W.T. Site Selection and Layout of Earthquake Rescue Center Based on K-Means Clustering and Fruit Fly Optimization Algorithm. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 27–29 June 2020; pp. 1381–1389. [Google Scholar]
- Gowdham, D.; Thangavel, K.; Kumar, E.S. Fruit Fly K-Means Clustering Algorithm. Int. J. Scient. Res. Sci. Eng. Technol. 2016, 2, 156–159. [Google Scholar]
- Wang, Q.; Zhang, Y.; Xiao, Y.; Li, J. Kernel-based Fuzzy C-Means Clustering based on Fruit Fly Optimization Algorithm. In Proceedings of the 2017 International Conference on Grey Systems and Intelligent Services (GSIS), Stockholm, Sweden, 8–11 August 2017; pp. 251–256. [Google Scholar]
- Drias, H.; Sadeg, S.; Yahi, S. Cooperative Bees Swarm for Solving the Maximum Weighted Satisfiability Problem. In International Work-Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 2005; pp. 318–325. [Google Scholar]
- Djenouri, Y.; Belhadi, A.; Belkebir, R. Bees swarm optimization guided by data mining techniques for document information retrieval. Expert Syst. Appl. 2018, 94, 126–136. [Google Scholar] [CrossRef]
- Aboubi, Y.; Drias, H.; Kamel, N. BSO-CLARA: Bees Swarm Optimization for Clustering Large Applications. In International Conference on Mining Intelligence and Knowledge Exploration; Springer: Cham, Switzerland, 2015; pp. 170–183. [Google Scholar]
- Djenouri, Y.; Habbas, Z.; Aggoune-Mtalaa, W. Bees Swarm Optimization Metaheuristic Guided by Decomposition for Solving MAX-SAT. ICAART 2016, 2, 472–479. [Google Scholar]
- Li, M.; Yang, C.W. Bacterial colony optimization algorithm. Control Theory Appl. 2011, 28, 223–228. [Google Scholar]
- Revathi, J.; Eswaramurthy, V.P.; Padmavathi, P. Hybrid data clustering approaches using bacterial colony optimization and k-means. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1070, 012064. [Google Scholar] [CrossRef]
- Vijayakumari, K.; Deepa, V.B. Hybridization of Fuzzy C-Means with Bacterial Colony Optimization. 2019. Available online: http://infokara.com/gallery/118-dec-3416.pdf (accessed on 18 September 2021).
- Al-Rifaie, M.M.; Bishop, J.M. Stochastic Diffusion Search Review. Paladyn J. Behav. Robot. 2013, 4, 155–173. [Google Scholar] [CrossRef] [Green Version]
- Karthik, J.; Tamizhazhagan, V.; Narayana, S. Data leak identification using scattering search K Means in social networks. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Fathian, M.; Amiri, B.; Maroosi, A. Application of honey-bee mating optimization algorithm on clustering. Appl. Math. Comput. 2007, 190, 1502–1513. [Google Scholar] [CrossRef]
- Teimoury, E.; Gholamian, M.R.; Masoum, B.; Ghanavati, M. An optimized clustering algorithm based on K-means using Honey Bee Mating algorithm. Sensors 2016, 16, 1–19. [Google Scholar]
- Aghaebrahimi, M.R.; Golkhandan, R.K.; Ahmadnia, S. Localization and Sizing of FACTS Devices for Optimal Power Flow in a System Consisting Wind Power using HBMO. In Proceedings of the 18th Mediterranean Electrotechnical Conference (MELECON), Athens, Greece, 18–20 April 2016; pp. 1–7. [Google Scholar]
- Obagbuwa, I.C.; Adewumi, A. An Improved Cockroach Swarm Optimization. Sci. World J. 2014, 2014, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Senthilkumar, G.; Chitra, M.P. A Novel Hybrid Heuristic-Metaheuristic Load Balancing Algorithm for Resource Allocationin IaaS-Cloud Computing. In Proceedings of the Third International Conference on Smart Systems and Inventive Technology, Tirunelveli, India, 20–22 August 2020; pp. 351–358. [Google Scholar]
- Aljarah, I.; Ludwig, S.A. A New Clustering Approach based on Glowworm Swarm Optimization. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2642–2649. [Google Scholar]
- Zhou, Y.; Ouyang, Z.; Liu, J.; Sang, G. A novel K-means image clustering algorithm based on glowworm swarm optimization. Przegląd Elektrotechniczny 2012, 266–270. Available online: http://pe.org.pl/articles/2012/8/66.pdf (accessed on 11 July 2021).
- Onan, A.; Korukoglu, S. Improving Performance of Glowworm Swarm Optimization Algorithm for Cluster Analysis using K-Means. In International Symposium on Computing in Science & Engineering Proceedings; GEDIZ University, Engineering and Architecture Faculty: Ankara, Turkey, 2013; p. 291. [Google Scholar]
- Tang, Y.; Wang, N.; Lin, J.; Liu, X. Using Improved Glowworm Swarm Optimization Algorithm for Clustering Analysis. In Proceedings of the 18th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), Wuhan, China, 8–10 November 2019; pp. 190–194. [Google Scholar]
- Teodorović, D. Bee colony optimization (BCO). In Innovations in Swarm Intelligence; Springer: Berlin/Heidelberg, Germany, 2009; pp. 39–60. [Google Scholar]
- Das, P.; Das, D.K.; Dey, S. A modified Bee Colony Optimization (MBCO) and its hybridization with k-means for an application to data clustering. Appl. Soft Comput. 2018, 70, 590–603. [Google Scholar] [CrossRef]
- Forsati, R.; Keikha, A.; Shamsfard, M. An improved bee colony optimization algorithm with an application to document clustering. Neurocomputing 2015, 159, 9–26. [Google Scholar] [CrossRef]
- Yang, C.-L.; Sutrisno, H. A clustering-based symbiotic organisms search algorithm for high-dimensional optimization problems. Appl. Soft Comput. 2020, 97, 106722. [Google Scholar] [CrossRef]
- Zhang, D.; Leung, S.C.; Ye, Z. A Decision Tree Scoring Model based on Genetic Algorithm and k-Means Algorithm. In Proceedings of the Third International Conference on Convergence and Hybrid Information Technology, Busan, Korea, 11–13 November 2008; Volume 1, pp. 1043–1047. [Google Scholar]
- Patel, R.; Raghuwanshi, M.M.; Jaiswal, A.N. Modifying Genetic Algorithm with Species and Sexual Selection by using K-Means Algorithm. In Proceedings of the 2009 IEEE International Advance Computing Conference, Patiala, India, 6–7 March 2009; pp. 114–119. [Google Scholar]
- Niu, B.; Duan, Q.; Liang, J. Hybrid Bacterial Foraging Algorithm for Data Clustering. In International Conference on Intelligent Data Engineering and Automated Learning; Springer: Berlin/Heidelberg, Germany, 2013; pp. 577–584. [Google Scholar]
- Karimkashi, S.; Kishk, A.A. Invasive Weed Optimization and its Features in Electromagnetics. IEEE Trans. Antennas Propag. 2010, 58, 1269–1278. [Google Scholar] [CrossRef]
- Charon, I.; Hudry, O. The noising method: A new method for combinatorial optimization. Oper. Res. Lett. 1993, 14, 133–137. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007. [Google Scholar]
- Pykett, C. Improving the efficiency of Sammon’s nonlinear mapping by using clustering archetypes. Electron. Lett. 1978, 14, 799–800. [Google Scholar] [CrossRef]
- Lee, R.C.T.; Slagle, J.R.; Blum, H. A triangulation method for the sequential mapping of points from N-space to two-space. IEEE Trans. Comput. 1977, 26, 288–292. [Google Scholar] [CrossRef]
- McCallum, A.; Nigam, K.; Ungar, L.H. Efficient clustering of high-dimensional data sets with application to reference matching. In Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, MA, USA, 1 August 2000; pp. 169–178. [Google Scholar]
- Wikaisuksakul, S. A multi-objective genetic algorithm with fuzzy c-means for automatic data clustering. Appl. Soft Comput. 2014, 24, 679–691. [Google Scholar] [CrossRef]
- Neath, A.A.; Cavanaugh, J.E. The Bayesian information criterion: Background, derivation, and applications. Wiley Interdiscip. Rev. Comput. Stat. 2012, 4, 199–203. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 224–227. [Google Scholar] [CrossRef]


| Metaheuristic Algorithm | Objective | Application | Method for Automatic Clustering | MOA Role | K-Means Role | Dataset Used for Testing | Compared with | Performance Measure | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Genetic Algorithm (GA) | |||||||||||
| 1 | Zhou et al., [45]-NoiseClust | Niche Genetic Algorithm (NGA) and K-means++ | Automatic | Global Positioning System | Density-Based Method | Adaptive probabilities of crossover and mutation | |||||
| 2 | Dai, Jiao & He, [28]-PGAClust | Parallel Genetic Algorithm (PGA) and K-means | Automatic | Dynamic mining of cluster number | |||||||
| 3 | Li et al. [40] | GA and K-means | Automatic | Adopting a k-value learning algorithm using GA | |||||||
| 4 | Kuo et al. [39]-SOM+GKA | SOM and Modified GKA | Automatic | Market Segmentation in Electronic Commerce | Self-Organizing Feature Maps (SOM) neural networks | SOM+K, K-means | Within Cluster Variations (SSW) and number of misclassifications | ||||
| 5 | Eshlaghy & Razi [42] | Grey-based K-means and GA | Non-Automatic | Research and Project selection and management | Project allocation selection | clustering of different projects | SSE | ||||
| 6 | Sheng, Tucker & Liu [30]-NGKA | Niche Genetic Algorithm (NGA) + one step of K-means | Improving GA optimization procedure for general clustering | Non-Automatic | Gene Expression | Gene Expression Data (Subcellcycle_384 subcellcycle_2945 data, Serum data Subcancer data | GGA and GKA | Sum of Square Error (SSE) | |||
| 7 | Karegowda et al. [41] | K-means + GA | Avoidance of random selection of cluster centers | Non-Automatic | Medical Data Mining | initial cluster center assignment | Clustering of dataset | PIMA Indian diabetic dataset | Classification error and execution time | ||
| 8 | Bandyopadhyay & Maulik [24]-KGA | GA + K-means | Escape from local optimum convergence | Non-Automatic | Satellite image classification | GA perturb the system to avoid local convergence | determining new cluster center for each generation | Artificial Data Real-life data sets (Vowel data, iris data, Crude oil data) | K-means and GA-Clustering | ||
| 9 | Cheng et al. [25]-PGKA | Prototype Embedded GA + K-Means | Encoding Cluster prototypes for general GA clustering | Non-Automatic | SKY testing data | K-Means, GKA and FGKA | Ga based criteria | ||||
| 10 | Zhang & Zhou [35]-Nclust | novel niching genetic algorithm (NNGA) + K-means | Finding better cluster number automatically | Automatic | General Cluster Analysis | Improved canopy and K-means ++ | UCI dataset | GAK and GenClust | SSE, DBIPBM, COSEC, ARI and SC | ||
| 11 | Ghezelbash, Maghsoudi & Carranza [38] -Hybrid GKMC | Genetic K-means clustering + Traditional K-means algorithm | General Improvement of K-Means | Non-Automatic | Geochemical Anomaly Detection from stream sediments | Determining cluster center locations | General Clustering | GSI Analytical Data | Traditional K-Means Clustering (TKMC) | Prediction rate curve based on a defined fitness function | |
| 12 | Mohammadrezapou, Kisi & Pourahmadm [46] | K-means + Genetic Algorithm and Fuzzy C-Means + Genetic Algorithm | Avoidance of random selection of cluster centers | Automatic | Homogeneous regions of groundwater quality identification | GA method | Determining the optimum number of clusters | General Clustering | Av. Silhouette width Index; Levene’s homogeneity test; Schuler & Wilcox classification; Piper’s diagram | ||
| 13 | El-Shorbagy et al. [37] | K-means + GA | Combining the advantages of K-means and GA in general clustering | Non-Automatic | Electrical Distribution system | GA Clustering with a new mutation | GA population Initialization for best cluster centers | UCI dataset | K-means Clustering and GA-Clustering | ||
| 14 | Barekatain, Dehghani & Pourzaferani [44] | K-means + Improved GA | New cluster-based routing protocols | Automatic | Energy Reduction and Extension of network Lifetime | Determine the optimum number of clusters | Dynamic clustering of the network | Ns2Network (Fedora10) | Other network routing protocols, i.e., LEACH, GABEEC and GAEEP. | ||
| 15 | Lu et al. [43] | K-means + GA | Combining the advantages of the two algorithms | Non-Automatic | Multiple Travelling Salesman Problem | ||||||
| 16 | Sinha & Jana [33] | GA with Mahalanobis distance + K-Means with K-means++ Initialization | clustering algorithm for distributed dataset | Automatic | GA method | Initial clustering using GA method | Fine-tuning the result obtained from GA clustering | Breast Cancer Iris Glass Yeast) | Map Reduced-based Algorithms, MRk-means, parallel K-means and scaling GA | Davies-Bouldin index, Fisher’s discriminant ratio, Sum of the squared differences | |
| 17 | Laszlo & Mukherjee [26] | GA + K-means | improving GA-based clustering method | Non-Automatic | Evolving initial cluster centers using hyper-quad tree | To return the fitness value of a chromosome | GTD, BTD, BPZ, TSP-LIB-1060 TSP-LIB-3038; Simulated dataset | GA-based clustering, J-Means | |||
| 18 | Zhang, Leung & Ye [199] | GA + K-means | Improving accuracy | Non-Automatic | Credit Scoring | Reduce data attribute’s redundancy | Removal of noise data | German credit dataset Australian credit dataset | C4.5, BPN, GP, SVM+GA and RSC | ||
| 19 | Kapil, Chawla & Ansari [3] | K-means + GA | Optimizing the K-means | Automatic | General Cluster Analysis | GA method | Generating initial cluster centers | Basic K-means clustering | Online User dataset | K-means | SSE |
| 20 | Rahman & Islam [32]-GENCLUST | GA + K-means | Finds cluster number with high-quality centers | Automatic | General Cluster Analysis | Deterministic selection of Initial Genes | Generating initial cluster centers | Basic K-means clustering | UCI dataset | RUDAW, AGCUK, GAGR, GFCM and SABC | Xie-Beni Index, SSE, COSEC, F-Measure, Entropy, and Purity |
| 21 | Islam et al. [34] GENCLUST++ | GA + K-means | Computational complexity reduction | Automatic | General Cluster Analysis | GA method | Generating initial cluster centers | Basic K-means clustering | UCI dataset | GENCLUST-H, GENCLUST-F, AGCUK, GAGR, K-Means | GA Performance Measure |
| 22 | Mustafi & Sahoo [36] | GA + DE + K-means | Choice of initial centroid | Automatic | Clustering Text Document | Using DE | Generating initial cluster centers | Basic K-means clustering | Corpus | K-Means | Standard clustering validity parameters |
| 23 | Laszlo & Mukherjee [27] | GA + K-means | Superior Partitioning | Non-Automatic | German credit dataset Australian credit dataset | ||||||
| 24 | Patel, Raghuwanshi & Jaiswal [200]-GAS3KM | GAS3 + K-means | Improving the performance of GAS3 | Automatic | GA method | Generating initial cluster centers | Basic K-means clustering | Unconstrained unimodal and multi-modal functions with or without epistasis among n-variables. | GAS3 | GA Performance Measure | |
| 25 | Xiao, Yan, Zhang, & Tang [31]-KMQGA | K-means + QGA | Quantum inspired GA for K-means | Automatic | GA method | Generating initial cluster centers | Basic K-means clustering | Simulated datasets Glass, Wine, SPECTF-Heart, Iris | KMVGA (Variable String Length Genetic Algorithm) | Davies–Bouldin rule index | |
| Particle Swarm Optimisation (PSO) | |||||||||||
| 26 | Jie and Yibo [70] | PSO + K-means | Outlier detection | Non-Automatic | Distribution Network Sorting | Optimizing the clustering center | Determining the optimal number of Clusters | Simulated datasets | K-Means | SSE | |
| 27 | Tsai & Kao [63]-KSRPSO | Selective Regeneration PSO + K-means | SRPSO Performance improvement | Non-Automatic | Global optimal convergence | Basic K-means clustering | Artificial datasets, Iris, Crude oil, Cancer, Vowel, CMC, Wine, and Glass | SRPSO, PSO and K-Means | Sum of intra-cluster distances and Error Rate (ER) | ||
| 28 | Paul, De & Dey, [69]-MfPSO based K-Means | MfPSO + K-Means | Improved multidimensional data clustering | Non-Automatic | Cluster center generation | Basic K-Means clustering | Iris, Wine, Seeds, and Abalone | K-Means and Chaotic Inertia weight PSO | DBI, SI, Means, SD and computational time, ANOVA test and a two-tailed t-test conducted at 5% significance | ||
| 29 | Prabha & Visalakshi [64]-PSO-K-Means | PSO + Normalisation + K-Means | Improving performance using normalization | Non-Automatic | Global optimal convergence | Basic K-means clustering | Australian, Wine, Bupa, Mammography, Sattelite Image, and Pima Indian Diabetes | PSO-KM, K-Means | Rand Index, FMeasure, Entropy, and Jacquard Index | ||
| 30 | Ratanavilisagul [69]-PSOM | PSO + K-Means + mutation operations applied with particles | Avoidance of getting entrapped in local optima | Non-Automatic | Global optimal convergence | Basic K-means clustering | (Iris, Wine, Glass, Heart, Cancer, E.coli, Credit, Yeast | Standard PSO, PSOFKM, PSOLF-KHM | F-Measure (FM), Average correct Number (ACN), and Standard Deviation (SD)of FM. | ||
| 31 | Nayak et al. [66] | Improved PSO + K-Means | optimal cluster centers for non-globular clusters | Non-Automatic | Global optimal convergence | Basic K-means clustering | K-Means, GA-K-Means, and PSO-K-Means | ||||
| 32 | Emami, & Derakhshan [65]-SOFKM | PSO + FKM | Escape from local optimum with increased convergence speed | Non-Automatic | Global optimal convergence | Fuzzy K-means clustering | FKM, ICA, PSO, PSOKHM, and HABC algorithms | Sample, Iris, Glass, Wine, and Contraceptive Method Choice (indicated as CMC) | F-Measure (FM) and Runtime Metrics | ||
| 33 | Chen, Miao & Bu [71] | PSO + K-Means | Solving initial center selection problem and escape from local optimal | Non-Automatic | Image Segmentation | Global optimal convergence | Dynamic clustering using k-means algorithm | Lena, Tree and Flower images from the Matlab Environment | K-Means PSOK | Sphere function and Griewank function | |
| 34 | Niu et al. [48] | Six different PSOs with different social communications + K-means | Escape from local optimum convergence with accelerated convergence speed | Non-Automatic | Global optimal convergence | Refining partitioning results for accelerating convergence | Iris, Wine, Coil2, Breast Cancer, German Credit, Optdigits, Musk, Magic 04, and Road Network with synthetic datasets | PSC-RCE, MacQueens K-Means, ACA-SL, ACA-CL, ACA-AL and Lloyd’s K-means | Mean squared error (MSE—sum of intra-cluster distances) | ||
| 35 | Yang, Sun & Zhang [62]-PSOKHM | PSO + KHM | Combining the merits of PSO and KHM | Non-Automatic | Global optimal convergence | Refining cluster center and KHM clustering | Artificial datasets, Wine, Glass, Iris, breast-cancer-Wisconsin, and Contraceptive Method Choice. | KHM, PSO | Objective function of KHM and F-Measure | ||
| 36 | Chen & Zhang [59]-RVPSO-K | PSO + K-means | Improved stability, precision, and convergence speed. | Non-Automatic | Web Usage Pattern Clustering | A parallel search for optimal clustering | Refining cluster center and K-means clustering | Two-day Web log of a university website | PSO-K | Fitness Measure and Run-time | |
| 37 | Niknam, & Amiri, [53]-APSO-ACO-K | Fuzzy Adaptive PSO + ACO + K-means | Solving non-linear partitioning clustering problem | Non-Automatic | Provide Initial state for K-means algorithm | Basic K-means clustering | Artificial datasets, Iris, Wine, Vowel, Contraceptive Method Choice (CMC), Wisconsin breast cancer, and Ripley’s glass | PSO, ACO, SA, PSO–SA, ACO–SA, PSO–ACO, GA, TS, HBMO, and K-means | Total mean-square quantization error and F-Measure | ||
| 38 | Kao, Zahara & Kao [60]-K-NM-PSO | K-means + + PSO | Effective global convergence | Non-Automatic | Providing more accurate clustering | Provide initial seedling | Artificial datasets, Vowel, Iris, Crude-oil, CMC, Cancer, Glass, and Wine | PSO, NM–PSO, K–PSO, and K-means | Sum of the intra-cluster distances and the Error Rate | ||
| 39 | Omran, Salman & Engelbrecht [58]-DCPSO | Dynamic Clustering PSO + K-means | An automatic clustering with reduced effect of initial conditions | Automatic | Image Segmentation | Binary PSO optimization | Basic PSO clustering | Refine cluster center | Lenna, mandrill, jet, peppers, one MRI, and one satellite image of Lake Tahoe | GA and Random Search dynamic Clustering | Dunn’s index, Validity index proposed by Turi, S_Dbw validity index |
| 40 | Van der Merwe & Engelbrecht [49] | PSO + K-means | Improving the performance of PSO | Non-Automatic | PSO clustering | Initial Seedling for PSO | Artificial datasets Iris, Wine, Breast cancer, and Automotives | K-Means and PSO | The Quantization error, the intra-cluster distances and the inter-cluster distances | ||
| 41 | Kao & Lee [61]-KCPSO | Combinatorial PSO + K-means | Automatic | Discrete PSO to optimize cluster numbers | Optimizing the number of clusters | Basic K-means clustering | Artificial datasets, Iris, and Breast Cancer | DCPSO and GCUK | DB index | ||
| Firefly Algorithm (FA) | |||||||||||
| 42 | Mathew & Vijayakumar [75]-MPKM | K-means + Firefly | Parallelization of K-Means | Non-Automatic | Initial optimal cluster centroid | Refine optimized centroid | Wisconsin diagnostic breast cancer, Wine, Glass, and Credit data | Parallel K-means | Accuracy, SSW, SSB, DBI, DDI and SC. | ||
| 43 | Jitpakdee, Aimmanee & Uyyanonvara [79]- FA-K | K-means + Firefly | Hybrid-clustering-based color quantization | Non-Automatic | Colour Image Quantization | Initial cluster centroids and Global optimal convergence | Refine initial centroids | Three images from USC-SIPI Image Database (Lena, Peppers, and Mandrill) | FA and K-Means | Mean Square Error (MSE) and Peak Signal-to-Noise Ratio (PSNR) | |
| 44 | Kuo & Li [80] | Wavelet Transform + FA based K-Means + F A based SVR | Forecasting model with wavelet transform | Non-Automatic | Export Trade Forecasting | Noise detection and Normalisation | Basic clustering | GA-SVR, PSO-SVR, FA-SVR and DE-SVR | Mean Square Error (MSE) | ||
| 45 | HimaBindu et al. [83] | Firefly + K-Means | Improved Big Data Clustering | Non-Automatic | Generate initial cluster centroids | Basic K-means clustering | Iris Plants database, Glass, Wine, two microarray information indexes and Artificial datasets. | K-Means, K-Means++ | Total computation time, centroid selection time and accuracy | ||
| 46 | Langari et al. [82]-KFCFA | K-member Fuzzy clustering + FA | A combined anonymizing algorithm | Non-Automatic | Social Network Privacy Preservation | Optimizing the primary clusters | The use of the K-member version of fuzzy c-means | Social network databases from Facebook, Twitter, Google + and YouTube | |||
| 47 | Kaur, Pal & Singh [81] | K-means + Firefly | IDS training model for data classification | Non-Automatic | Intrusion Detection | Initialize method for the K-Means | Clustering for Classification | NSL-KDD dataset | K-Means + Bat K-Means + Cuckoo, K-Means++, K-Means, Farthest First and Canopy | CCI, TP, FP Precision, Recall, F-Measure, ROC and Time to build training model. | |
| 48 | Nayak et al. [77] | Optimized K-means with firefly and Canopies | A hybrid algorithm for classification | Non-Automatic | Pre-clustering | Basic Clustering | Haberman’s survival dataset | K-means algorithm | Classification accuracy | ||
| 49 | Xie et al. [74]-IIEFA and CIEFA | K-means + Improved Firefly | resolve initialization sensitivity and local optimal traps | Non-Automatic | FA Clustering | Generate Initial Cluster Models as seed solution | ALL-IDB2 database Sonar, Ozone, Wbc1, Wbc2 Wine, Iris, Balance, Thyroid, and E. coli | GA, ACO, K-means, FA, DA, SCA, CFA, CFA2, NaFA, VSSFA, and MFA | Sum of intra-cluster distances Av.accuracy Av.sensitivity, Av.specificity & macro-average F-score | ||
| 50 | Wu et al. [84]-Kmeans-FFA-KELM | K-means + FFA + Kernel Extreme Learning Machine Model | Non-Automatic | Evapotranspiration Estimation | Building various sub-models | Decomposition of training dataset into multiple subsets | meteorological data (Tave, Tmax, and Tmin), wind speed, relative humidity and sunshine | FFA-KELM | Coefficient of determination, RMSE, MAE, SI and NSE | ||
| 51 | Behera et al. [77] -FCM-FA | Fuzzy C-Means + FireFly Algorithm | tackles Fuzzy C-Means problems | Non-Automatic | |||||||
| 52 | Nayak, Naik & Behera [79]-FA-K-means | Firefly + K-means | global search capacity for K-means | Non-Automatic | |||||||
| 53 | Hassanzadeh & Meybodi [74]-K-FA | K-means + Firefly | Finding initial centroids | Non-Automatic | Finding initial centroids | Refining the centroids | Standard data set from UCI (Iris, WDBC, Sonar, Glass, and Wine) | K-means, PSO, KPSO | Intra-cluster distance and clustering error | ||
| Bat Algorithm (BAT) | |||||||||||
| 54 | Tripathi, Sharma & Bala [87]-DBPKBA | Bat algorithm + K-means | the parallelized approach in a distributed environment | Non-Automatic | Obtaining global optimum convergence | better population initialization | Wine, Magic, Poker hand and Replicated wine | K-means, PSO, and Bat Algorithm | Best and Average intra-cluster distance | ||
| 55 | Chaudhary & Banati [90]-HESB | EShBAT + K-medoids + K-means | Leveraging optimisation capabilities | Non-Automatic | Dividing populations into groups | starting population and refining solutions | BA, EShBAT, K-means, K-Medoids | ||||
| 56 | Gan, & Lai [89]-KMBA | K-means + Bat Algorithm | Classification of EBN | Non-Automatic | EBN Classification | Basic Bat Algorithm Clustering | Initiating Initial points for BA | Three classes of data (Grades AA, A, and B) | Classification Accuracy | ||
| 57 | Pavez, Altimiras, & Villavicencio [88] | K-means + Binary Bat Algorithm | demonstrate K-means technique utility in binarization | Non-Automatic | Multidimensional Backpack Problem | ||||||
| 58 | Sood & Bansal [86] | K-Medoids + Bat Algorithm | Automatic | Generating initial cluster center for K-Medoids | K-Medoids clustering | K-Medoids | |||||
| Flower Pollination Algorithm (FPA) | |||||||||||
| 59 | Jensi & Jiji [92]-FPAKM | K-means + FPA | Combining the advantages of the two algorithms | Non-Automatic | Provide Initial seedlings for K-means | K-means Clustering | Artificial dataset iris, thyroid, wine, CMC, crude oil, and glass | FPA, K-means | Mean-square quantization error (MSE) | ||
| 60 | Kumari, Rao & Rao [93] | K-means + FPA | optimum solutions in Image compression | Image Compression | Peak signal to noise ratio (PSNR), mean square error (MSE) and fitness function. | ||||||
| Artificial Bee Colony (ABC) | |||||||||||
| 61 | Armano & Farmani [95]-kABC | K-means + ABC | finding a global optimum solution | Non-Automatic | ABC Clustering | Use K-means for initial seedlings | Iris, Wine, and Contraceptive Method Choice (CMC) | K-means | Distortion Criterion, Computational Cost, SD and F-Measure | ||
| 62 | Cao & Xue [102]-MABC-K-means | Modified ABC + K-means | hybridized framework for cluster analysis. | Non-Automatic | Customer Relationship Management | Provide initial cluster center | Basic K-means Clustering | Simple dataset of customers and their orders of an e-commerce platform in the first quarter. | Differential Evolution algorithm (DEA), standard Genetic algorithm (GA) and standard Artificial Bee Colony algorithm (ABC) | The mean and variance of Griewank, Rastrigin, Rosenbrock, Ackley and Schwefel functions. | |
| 63 | Wang et al. [101]-ABC-KM | ABC + K-means | Improving the effectiveness of Wind farm clustering | Non-Automatic | Modeling of Farms with DFIGs | Provide initial cluster center | Basic K-means Clustering | MW DFIG | K-means | Wind speed disturbances and short-circuit faults | |
| 64 | Huang [100] | ABC + Accelerated K-means | Non-Automatic | Colour Image Quantization | Provide initial cluster center | Basic K-means Clustering | Lena, Baboon, Lake, Peppers, and Airplane with a size of 512 × 512 | SFLA-CQ | Average mean square, error, the standard deviation, and average computation time. | ||
| 65 | Tran et al. [96] -EABCK | Enhanced ABC + K-means | improvement for K-means algorithm | Non-Automatic | Generate initial cluster center | Basic K-means Clustering | Artificial datasets (Iris, Wine, Glass, E.coli, Liver disorder, Vowel, Pima, WDBC, and CMC | ABC, CABC, K-means, HABC, K-means++ and FAPSO-ACO-K | Mean square error (MSE) and Euclidean distance. | ||
| 66 | Bonab et al. [97] | Modified K-means + ABC + DE | escape from local optimum | Non-Automatic | |||||||
| 67 | Jin, Lin & Zhang [98]-CAABC-K-means. | CAABC + K-means | for optimal clustering | Non-Automatic | Generate initial points for K-means | clustering | Iris, Balance-Scale, Wine, E.coli, Glass, Abalone, Musk, Pendigits, Skin Seg, CMC, and Cancer | ABC, IABC, HABC, CAABC, DFSABCelite and PSO+K-means | Sphere, Rosenbrock, Rastrigin, Alpine and Ackley | ||
| 68 | Dasu, Reddy & Reddy [99] | K-means + ABC | Satellite Image Classification | Non-Automatic | Image Classification | Classification | Segmentation | Remote sensing Images | PSO | Sensitivity, Specificity, Overall accuracy and Kappa Coefficient. | |
| Grey Wolf Optimization (GWO) | |||||||||||
| 69 | Pambudi, Badharudin & Wicaksono [106]-GWO-K-means | GWO + K-means | Optimizing the weakness of K-means through GWO | Non-Automatic | Image Segmentation | Generate initial points for K-means | initial centroid refinements, final optimal solution | Brain MRI | K-means | Sum of Square Error (SSE) | |
| 70 | Korayem, Khorsid & Kassem [105]-K-GWO | K-means + GWO | cluster analysis performance improvement | Non-Automatic | Capacitated vehicle routing Problem | Generate initial points for K-means | K-means clustering | Benchmark problems downloaded from the web http://www.branchandcut.org/ accessed on 17 October 2021. | Compared three different versions of the proposed algorithm | Total distance travelled | |
| 71 | Katarya & Verma [104] | Fuzzy-C-Means + GWO | Non-Automatic | Recommender System | Generating Initial Clusters and initial clusters centroids | Classification by similarity of user ratings | Movie lens dataset | PCA, PCA-SOM, K-means, PCA-K-means, K-means improved, SOM-Cluster, FCM, KM-PSO-FCM, PCA-GAKM and GAKM-Cluster | Mean absolute error, standard deviation, precision and recall | ||
| 72 | Mohammed et al. [107]-KMGWO | K-means + GWO | Performance Enhancement of GWO using K-means | Classical Engineering problem | CEC2019 benchmark test functions | GWO, CSO, WOA-BAT, WOA | |||||
| Sine-Cosine Algorithm (SCA) | |||||||||||
| 73 | Moorthy & Pabitha [109]-SCAK-means | SCA + K-means | resource discovering for cloud resources | Non-Automatic | Cloud computing | Updating initial centroid position | Generate initial clusters | Cloud resources | K-means | Intra Cluster similarity, Inter-Cluster similarity, the similarity of cloud resources, and convergence rate | |
| Cuckoo Search Algorithm (CSA)/Cuckoo Search Optimizatin (CSO) | |||||||||||
| 74 | García, Yepes & Martí [118] | CSO + K-means | solving combinatorial optimization problems | Non-Automatic | Design of counterfort retaining walls | Production of new solution in continuous space | Generate initial solution (Discretization) | The emission and cost values obtained from [34,66] | K-means, HS | Wilcoxon signed-rank; the Shapiro–Wilk or Kolmogorov—Smirnov-Lilliefors normality test | |
| 75 | Manju & Fred [120] | CSO + K-means | Optimization-based segmentation and compression | Compound images segmentation &compression | |||||||
| 76 | Deepa, & Sumitra [121]-CSOAKM | CSO + K-means | optimal global solution | Non-Automatic | Intrusion Detection System | Generate initial cluster centroid | NSL-KDD dataset | IGNB chi square selection, and COFS | Image quality index, PSNR, RMSE, SSIM and SDME | ||
| 77 | Arjmand et al. [117] | an automatic tumor segmentation algorithm | Non-Automatic | Breast tumor segmentation | Generate initial Centroids for K-means algorithm | Clustering for segmentation | RIDER breast dataset | K-means and Fuzzy C-Means | |||
| 78 | Binu, Selvi & George [119]-MKF-Cuckoo | Cuckoo Search Algorithm + Multiple Kernel-based Fuzzy C-Means | Searching for the best cluster centroids | Non-Automatic | Iris and wine datasets | Cluster accuracy, rand coefficient, jacquard coefficient and computational time. | |||||
| 79 | Girsang, Yunanto & Aslamiah [113]-FCSA | Cuckoo search algorithm + K-means | faster cluster analysis | Non-Automatic | Exploration | Convergence | Iris, Wine, Yeast, Abalone, Breast cancer, Glass, E.coli, Haberman, Sonar, and Parkinson | K-means | Mean and Standard Deviation | ||
| 80 | Tarkhaneh, Isazadeh & Khamenei [115]-HCSPSO | CS + PSO + K-means | More optimized cluster result | Non-Automatic | Clustering | PSO and K-means produces new nest for CS | Standard benchmark datasets | CS, k-means, PSO, Improved Cuckoo Search ICS, ESA), BFGSAand EBA | |||
| 81 | Ye et al. [111]-ICS-Kmeans | Improved Cuckoo search + K-means | Better clustering, accuracy, and faster convergence rate | Non-Automatic | initial centroids for K-means algorithm | Basic K-means Clustering | UCI standard dataset (Iris, Wine, Seeds, and Haberman) | CS-Kmeans, K-Means, PSO-Kmeans | Sum of Square Error (SSE) | ||
| 82 | Lanying & Xiaolan [114] | Cuckoo Search + K-means | Optimization of cluster center in K-Means | Non-Automatic | Recommender System | Optimizing the clustering center | Basic K-Means Clustering | Movie Lens dataset | K-Means, PSO-Kmeans and GA-Kmeans | Clustering accuracy and convergence speed | |
| 83 | Saida, Kamel & Omar [112] | Cuckoo Search + K-Means | Reduction of the number of CS iteration | Non-Automatic | Document clustering | Clustering | Generate Initial Cluster Centroids | Reuters 21578 Text Categorization Dataset and the UCI Dataset | F-Measure | ||
| 84 | Singh & Solanki [116] | K-means + Modified Cuckoo Search | Global optimum convergence | Non-Automatic | Initial centroids for K-means algorithm | K-means clustering | Sum of Square Error (SSE) | ||||
| Differential Evolution (DE) | |||||||||||
| 85 | Kwedlo [124]-DE-KM | DE + K-means | High-quality clustering solutions. | Non-Automatic | Production of candidate solutions | initial centroids fine-tuning solution | UCI dataset, TSPLIB library, USC-SIPI repository | Global K-means, DE, two K-means variants algorithm Genetic K-means algorithm | Sum of Square Errors (SSE) | ||
| 86 | Wang [129] | DE + K-means | Non-Automatic | Determine the initial cluster centers | Clustering using weighted K-means algorithm | Iris, Wine, Seed, and Page Blocks | |||||
| 87 | Silva et al. [130] | ACDE + K-means | Automatically determine k activation threshold | Automatic | DE approach | Automatic determination of cluster number | Basic K-means clustering | UCI standard dataset | Davies Bouldin Index (DBI) and Cosine Similarity (CS) measure | ||
| 88 | Cai et al. [125]-CDE | DE + one-step K-means | Improvement of DE | Automatic | DE approach | Clustering | multi-parent crossover operator | unconstrained single-objective benchmark functions with different characteristic | DE | Number of fitness function evaluations (NFFEs) and quality of the final solutions. | |
| 89 | Mustafi & Sahoo [36] | GA + DE + K-means | To improve the initial cluster centroids | Automatic | Text Document Clustering | DE approach | Generating improving cluster centers | Basic K-means clustering | Basic implementations of K-Means | ||
| 90 | Bonab et al. [97] | ABC + DE + Modified K-means | To solve initialization problems | initial cluster centers, find global solution | Clustering | Standard UCI dataset | |||||
| 91 | Sierra, Cobos, & Corrales [127] | DE + K-Means | A hybrid for continuous optimization | Non-Automatic | DE clustering | Generation of initial groups for DE | A large set of test functions | DE and PSO | Fitness function value reached, av. number of fitness function evaluation to obtain optimal value. Friedman and Wilcoxon signed test, with a 95% significance. | ||
| 92 | Sheng et al. [131]-DE-ANS-AKO | DE + Adaptive niching + K-means | Dynamic adjustment of niche size to prevent premature convergence | Non-Automatic | DE clustering | Use of one iteration of k-means for fine-tuning the initial solution | Synthetic datasets, Letter, Connectionist, Shuttle, MFCCs, Isolet1, Isolet2, HARs Flowers17, Mnist, Cancer728, Yeast2945 | DE-AKO, DE-ANS-KO, GKA, MEQPSO, EPSONS, PSOKM, CGABC, SHADE, TSMPSO, ICMPKHM, FPAGA | Mean ICV Mean ARI Mean AC, Mean runtimes and Wilcoxon’s rank-sum tests. | ||
| 93 | Kuo, Suryani & Yasid [126]-CDE-K-Means | ACDE + K-means | An Automatic clustering algorithm | Automatic | Clustering | Tuning cluster centroids to improve performance | Iris and Wine | DE | |||
| 94 | Hu et al. [128] | DEFOA + K-means | Improving K-means | Non-Automatic | Sales database | K-Means | the error sum of squares criterion function as fitness function | ||||
| Invasive Weed Optimisation (IWO) | |||||||||||
| 95 | Fan et al. [134]-IWO-KMEANS | IWO + K-means | Improve global optimization while utilizing local optimization power | Non-Automatic | Text Clustering | Selection of initial cluster center | Basic K-means clustering | Chinese documents (history, transportation, medical, and sports) from the corpus of Fudan University | K-Means, DE-K-Means | F-Measure | |
| 96 | Pan et al. [135]-CMIWO K-Means | IWO + K-means | Overcome the drawbacks of K-Means | Non-Automatic | Direct K-means search for definite evolution direction | Clustering | |||||
| 97 | Razi [137] | DEA based K-means + IWO | Clustering algorithm for better facility location | Non-Automatic | Facility Location problem | Determining the Pareto solution for the bi-objective model | Clustering | ||||
| 98 | Boobord, Othman, & Abubakar [136]-PCAWK | PCA + IWO + K-means | Non-Automatic | PCA for dimensionality reduction | WK-means for clustering | Wine, Cancer, USCensus90, SPECTF Heart and Musk2000 | PCAK | Sum of Square Error (Best, Average, Worst and Standard deviation) | |||
| Imperialist Competition Algorithm (ICA) | |||||||||||
| 99 | Emami & Derakhshan [65]-ICAFKM | ICA + Fuzzy K-means | Escape from local optimal and increased convergence speed | Non-Automatic | Clustering in an alternate manner with the FKM | Clustering in an alternate manner with the ICA | Iris, Glass, Sample, Contraceptive Method Choice (CMC), and Wine | ICA, PSOKHM, PSO, FKM and HABC | F-measure and runtime metrics | ||
| 100 | Abdeyazdan [140]-ICAKHM | Modifier ICA + K-Harmonic means | Compensate existing problems in cluster analysis | Non-Automatic | Milling Machines classification | generates the initial population and empires | Generates initial empires for the modified ICA | Iris, Glass, Contraceptive Method Choice, and Wine | ICAKM, KHM, GSOKHM and PSOKHM methods. | F-measure, KHM (X, C), Runtime (s) | |
| 101 | Niknam et al. [139]-K-MICA | K-means + Modified Imperial Competitive Algorithm | Optimum clustering | Non-Automatic | Generates population and forms the initial empire | Improve empires’ colonies & imperialists position | Iris, Vowels, Wine and Contraceptive method choice | ACO, MICA, SA, PSO, GA, HBMO, TS and K-Means | The best, average, worst of the fitness function and Standard deviation of the fitness function. | ||
| Harmony Search (HS) | |||||||||||
| 102 | Nazeer, Sebastian & Kumar [145]-HSKH | Harmony Search + K-Means | Better cluster accuracy | Non-Automatic | Clustering Gene expression Data | Determining the initial cluster centroids | Clustering | Human Fibroblast Serum data and the Rat CNS data | K-Means, SOM, IFCM, VGA, CRC | Silhouette Index | |
| 103 | Forsati et al. [141]-HSCLUST | Harmony Search + K-Means | Less dependent on initial parameters | Non-Automatic | Document Clustering | Initial centroids | Obtain the best vector from the HS | K-Means, HSCLUST | F measure | ||
| 104 | Chandran & Nazeer [144] | Enhanced K-Means + Harmony Search | Better cluster solution | Non-Automatic | Determining the initial cluster centroids | Clustering | UCI Machine Learning Repository dataset (Iris, New-Thyroid and Breast Cancer) | K-Means, HS-K-means | Cluster Purity metric. | ||
| 105 | Raval, Raval & Valiveti [146] | Harmony Search + K-Means | Cluster Analysis Optimization | Non-Automatic | Sensor Network Energy Utilization | Finding initial cluster centers called Clustering Hierarchy (CH) | Fine-tuning the initial CH obtained from HS | Dataset simulation using NS2 simulator | K-Means, HSA | Energy dissipation, Total data transfer in number of packets | |
| 106 | Cobos et al. [143]-IGBHSK | Global best Harmony Search + K-Means | Hybridizing Global best Harmony Search with K-Means | Automatic | Web document clustering | Using BIC or Davies-Bouldin index | Providing global search strategy in the solution space | Finds the optimum value in a local search space | Datasets based on Reuters-21578 and DMOZ | Carrot2 | BIC, Precision, Recall, F-measure, NRL, OTC |
| 107 | Mahdavi & Abolhassani [142]-HKA | K-means + Harmony Search | An algorithm based on HS optimization | Non-Automatic | Web document clustering | Global search for optimum solutions | Localize search in the proximity of the obtained global solution | TREC-5, TREC-6, TREC-7, DMOZ, and 20 Newsgroup | K-Means, GA, PSO AND GM | Quality and speed of convergence, F-Measure | |
| 108 | Kim et al. [147] | Harmony Search + K-means | Clustering-based SDN load balancing scheme | Non-Automatic | SDN load balancing | Fine-tuning the solution from K-means clustering | Basic clustering | 100 to 1000 switches and 10 to 100 controllers are randomly placed in an area of 100 × 100 | HS, P-HS, and P-HS-K. | Measure of accuracy | |
| Black Hole (BH) Algorithm | |||||||||||
| 109 | Eskandarzadehalamdary, Masoumi, & Sojodishijani [151]-BH-BK | Black Hole + Bisecting K-means | Improve performance of bisecting K-means | Non-Automatic | Generates initial cluster centroids for BK-means | Basic clustering and refinement | Iris, Glass, Vowel, and Contraceptive Method Choice (CMC) | Bisecting K-Means, BH, PSO | Sum of intra-cluster distances and Error Rate (ER) | ||
| 110 | Feng, Wang & Chen [153] | Black Hole + K-means | Initial cluster centers for K-means | Non-Automatic | Image Classification | Determining the initial cluster center for K-means | Basic clustering and refinement | ||||
| 111 | Pal & Pal [152] | Black Hole + K-means | Improved cluster analysis | Non-Automatic | Clustering | Partly generates initial cluster center | K-Means | ||||
| Membrane Computing (P System) | |||||||||||
| 112 | Jiang, Zang & Liu [155] | K-means + DNA genetic Algorithm + P system | K-means based on DNA genetic algorithm and P system | Non-Automatic | Analyze the initial cluster center with P system | Randomly generated dataset | Convergence rate, Measure of accuracy and intra cluster distance | ||||
| 113 | Wang, Xiang & Liu [159] | K-means + K-medoids + Tissue-like P system | Handling noises and outliers | Non-Automatic | Tissue-like P system to present parallel operation | optimizing the result with K-medoids | UCI dataset | K-means and K-medoids | |||
| 114 | Zhao, Liu & Zhang [158] | P system + K-medoids | Using P system to realize K-medoids algorithm | Non-Automatic | Provide parallel operation for lower time complexity | Clustering | |||||
| 115 | Weisun & Liu [157] | MDE K-means + P system | Improved initial cluster center for K-means | Non-Automatic | Evolve the objects with MDE | Clustering | Artificial data sets, the iris, wine | K-means algorithm and DE -K-means algorithm | Cluster validity index, Xie-Beni index, the PBMF index | ||
| 116 | Zhao & Liu [156]-GKM | K-Means + GA + Tissue-like P system | Improved initial cluster center for K-means | Non-Automatic | P system for parallelism and GA for good convergence | Clustering | |||||
| 117 | Wang, Liu & Xiang [160] | K-means + Tissue-like P system | Improved initial cluster center for K-means | Non-Automatic | Selection of initial cluster centers | Clustering | UCI datasets -Wine, Glass, Haberman, Soybean-small, and Zoo | K-means, CCIA, kd-tree, K-means++, FSDP, Bai’s, Khan’s | No of initialisation cells | ||
| Dragonfly Algorithm (DA) | |||||||||||
| 118 | Angelin [162] | K-means + Dragonfly | Outlier detection | Non-Automatic | Optimizing the generated clusters | Initial cluster generation | Arrhythmia, Diabetics and Epileptic seizure | K-means and K-median | Detection rate, ROC as objective function | ||
| 119 | Kumar, Reddy,& Rao [164]-WHDA-FCM | Wolf hunting-based dragonfly + Fuzzy C-means | SAR Images change detection | Non-Automatic | SAR Image Change detection | Selection of optimal coefficients (cluster center) | Clustering | SAR Images | DWT-FCM, NR-ELM, GADWT-FCM, ABDWT-FCM, PSDWT-FCM, FFDWT-FCM, GWDWT-FCM, AGWDWT-FCM and DADWT-FCM | accuracy, specificity, sensitivity, precision, negative predictive value, F1 score and Matthew’s correlation coefficient. False positive rate, false negative rate and false discovery rate | |
| Ant Lion Optimizer (ALO) | |||||||||||
| 120 | Chen et al. [165]-QALO-K | Quantum-inspired ant lion optimizer + K-Means | An efficient algorithm for intrusion detection | Non-Automatic | Intrusion detection | Generate initial cluster center for K-means | Clustering | KDD Cup datasets and Iris, Glass, Wine, Cancer, Vowel, CMC and Vehicle | GA, ACO, MBCO, MKCLUST and ALO-K | Accuracy rate (AR), Detection Rate (DR), False positive rate (FPR) and F-measure (F1) | |
| 121 | Murugan & Baburaj [166]-ALPSOC | Improved K-medoids + Ant lion + PSO | Computational efficiency and better performance | Non-Automatic | Optimized the generated initial clusters | Generate initial clusters | UCI datasets—Glass, Leaf, Seeds, Soybean and Ionosphere | K-Means, K-Means -FA, KMeans—PSO | Intra-cluster distance, F-measure, Rand Index, Adjusted Rand Index, Entropy and Normalized Mutual Information | ||
| 122 | Dhand & Sheoran [168] | Ant Lion Optimizer + K-Means algorithm | Energy-efficient routing protocol | Non-Automatic | Energy-efficient routing protocol | Clustering | |||||
| 123 | Majhi & Biswal [164] | K-Means + Ant Lion Optimizer | Optimal cluster analysis | Non-Automatic | Optimized the generated clusters | Generate initial clusters | Glass, vowel, ionosphere, leaf, gene expression cancer RNA-seq, waveform database generator (version 2), immunotherapy, and soybean | K-Means, KMeans-PSO, KMeans-FA, DBSCAN and Revised DBSCAN | Sum of intra-cluster distances and F-measure. | ||
| 124 | Naem & Ghali [167]-K-median Modularity ALO | K-Median + Ant Lion Optimizer | Social network community detection | Non-Automatic | Social Networks community detection | Optimized the generated clusters | Generate initial clusters | Zachary karate Club, Bottlenose Dolphins network, American College football network, Polbooks network | K-means Modularity PSO, K-means Modularity Bat optimization, K-means Modularity CSO, K-median Modularity PSO, K-median Modularity Bat optimization, K-median Modularity CSO, GN, FN, BGLL, HSCDA. | Normalized Mutual Information (NMI), Measure of Modularity for community quality | |
| Social Spider Algorithm (SSO) | |||||||||||
| 125 | Thiruvenkatasuresh & Venkatachalam [171] | Social Spider Algorithm + Fuzzy C-means | classify and segment Brain tumor images | Non-Automatic | Tumor detection in Brain images | Optimizing Centroid | Clustering | ANFIS and FCMGWO | |||
| 126 | Chandran, Reddy, & Janet [170]-SSOKC | Balance local and global searches with improved convergence speed. | Non-Automatic | To find the vicinity of optimal solution | initial centroid refinements and final optimal solution | UCI datasets (Iris, Glass, Vowel, Wine, Ruspini, and Cancer) | Kbat, KFA, KPA, | CPU Elapse Time | |||
| Fruit Fly Optimization (FFO) | |||||||||||
| 127 | Sharma & Patel [173]-K-Means-FFO | K-means + FFO | Optimal clustering quality | Non-Automatic | Optimize initial Clusters | Generate initial clusters | 20NewsGroup, Reuters-21578, and Classic4 dataset | K-means, K-means-PSO and K-means-ALO | Intra-cluster distance, Purity Index, F-Measure and Standard Deviation | ||
| 128 | Jiang et al. [174] | K-means + FOA | Optimal clustering quality | Non-Automatic | Earthquake Rescue center Site Selection and Layout | Optimize initial Clusters | Generate initial clusters | Integrated data of affected areas | RWFOA and MFOA | Weighted sum of construction costs, transportation costs and penalty costs of emergency rescue centers | |
| 129 | Wang et al. [176]-FOAKFCM | Kernel-based Fuzzy C-means + FOA | Integrating kernel-based fuzzy c-means and FOA | Non-Automatic | Initialize initial cluster centroids | Classifying/Clustering the data | Iris, Glass, and Seeds | FCM, KFCM | Classification evaluation index (XB index | ||
| 130 | Hu et al. [128] | DEFOA + K-means | Improving K-means for universal continuous optimization | Non-Automatic | Generate initial cluster centroids | Optimize the initial clustering | Sales database | K-means | Convergence performance | ||
| Bees Swarm Optimization (BSO) | |||||||||||
| 131 | Aboubi, Drias & Kamel [179]-BSO-CLARA | BSO + K-medoids | Effective and efficient algorithm | Non-Automatic | PAM, CLARA and CLARANS | ||||||
| 132 | Djenouri, Habbas & Aggoune-Mtalaa [180] | Using K-means as decomposition | Non-Automatic | Clustering | DIMACS | ||||||
| 133 | Djenouri, Belhadi & Belkebir [178] | BSO + K-means | Document Information Retrieval Problem | Document Information Retrieval | Exploration of already created clusters | Clustering | CACM collection, TREC, Webdocs and Wikilinks | PTM, SVMIR, KNNIR and ARMIR | F-measure, Runtime | ||
| Bacterial Colony Optimization (BCO) | |||||||||||
| 134 | Revathi, Eswaramurthy, & Padmavathi [182]-BCO + KM | BCO + K-means | Reduced computational cost | Non-Automatic | Selection of initial cluster centroids | Optimizing the initial clusters for optimal solution | 2 Artificial datasets; UCI datasets (CMC, Glass WBC, Heart, Iris, Wine, Vowel, Balance) | K-means, PSO, BFO and BCO | Sum of Square Errors (SSE) | ||
| 135 | Vijayakumari & Deepa [183]-HFCA | FCM + Fuzzy BCO | High efficiency | Non-Automatic | Selection of initial cluster centroids | Optimizing the initial clusters for optimal solution | Iris, WBC, Glass, Wine, Vowel, and CMC | FBFO, FBCO, FCM AND FPSO | IntraCluster distance | ||
| Stochastic Diffusion Search (SDS) | |||||||||||
| 136 | Karthik, Tamizhazhagan, & Narayana [185]-SS-KMeans | SDS + K-means | Finding optimal clustering points | Non-Automatic | Data Leak Prevention in Social Medial | Select initial centroid for clustering | Clustering | S | True Positive Rate (TPR) | ||
| Modified Honey Bees Mating Optimization (HBMO) | |||||||||||
| 137 | Teimoury et al. [187]-HMBK | HBMO + KMeans | An optimized hybrid clustering algorithm | Non-Automatic | Selection of Initial Cluster centroids | Clustering | Wine, Iris and B.C | SA, PSO, TS, ACO, GA, K-means | Sum of Square Error (SSE) | ||
| 138 | Aghaebrahimi, Golkhandan & Ahmadnia [188] | HBMO + KMeans | Localization and sizing of flexible AC transmission system | Non-Automatic | Localization and sizing of Flexible AC Transmission System | Determining the best fitness function | Data Classification—Clustering | TCSC, UPFC AND SVC | Average Installation Cost, total generation cost and cost of power transmission losses | ||
| Cockroach Swarm Optimization (CSO) | |||||||||||
| 139 | Senthilkumar & Chitra [190]-HHMA | MCSO + K-means | Load balance in cloud networks | Non-Automatic | Measuring the load ratio | Clustering | Overall Response time and Processing time | ||||
| Glowworm Swarm Optimization (GSO) | |||||||||||
| 140 | Onan & Korukoglu [193] | K-means + GSO | An efficient and effective hybrid algorithm | Non-Automatic | Find initial Cluster Centroids | Clustering | Iris, Breast Cancer, E.coli, Diabetes, Haberman’s survival data | K-means, Fuzzy C-Means, GSO | F-measure and Rand Index | ||
| 141 | Tang et al. [194]-VSGSO-D KMeans | Improved GSO + K-means | Multi-modal optimization for optimal cluster analysis | Non-Automatic | Generates the initial cluster center | Clustering | Iris dataset | K-means, K-means++, K-means||, GSO + K-means, | Run time, minimum number of iterations, SSE, NMI, Purity and Rand Index | ||
| 142 | Zhou et al. [192] | GSO + K-means | Avoid the effect of the initial condition | Non-Automatic | Image Classification | Generates the initial cluster center | Clustering | Pepper, Lena, and Mandrill | K-means, Fuzzy C-Means | Quantization error, the maximum intra-distance, the minimum inter-distance | |
| Bee Colony Optimization (Bee) | |||||||||||
| 143 | Das, Das & Dey [196]-MKCLUST & KMCLUST | MBCO + K-means | Faster convergence | Non-Automatic | Either generate initial centroids or does the clustering | Either generate initial centroids or does the clustering | Glass, Wine, Vowel, CMC, Cancer, HV, Iris | MBCO, K-NM-PSO, K-PSO, K-HS, KIBCLUST, IBCOCLUST, PSO | Percentage Error (PE) | ||
| 144 | Forsati, Keikha & Shamsfard [197] | Improved BCO + K-means | An efficient algorithm for large and high dimensional dataset | Non-Automatic | Document Clustering | Generates initial cluster centroids | Clustering | Wine, Iris, Glass, Vowel, Cancer Document dataset (Politics, TREC, DMOZ, 20 Newsgroup and Web Ace) | GA, ACO, K-means, PSO, CABC, IBCOCLUST, HSCLUST, K-NM-PSO, K-PSO, K-GA, K-HS, K-ABC | Cluster Quality and Rate of Convergence | |
| Bacteria Foraging Optimization (BFO) | |||||||||||
| 145 | Niu, Duan & Liang [201]-BFCA | BFO + K-means | Efficient algorithm with global and parallel search capacities | Non-Automatic | Generates initial cluster centroids | Clustering | |||||
| Cuckoo Optimization Algorithm (COA) | |||||||||||
| 146 | Lashkari & Moattar [202]-ECOA-K | ECOA + K-means | Fast convergence algorithm with intelligent operators | Non-Automatic | Generate initial cluster centroids | Clustering | UCI dataset (CMC, Iris, and Wine) | BH, Big Bang Big Crunch (BBBC), CSA, COA, K-means | Purity Index, Convergence rate, Coefficient of Variance, time complexity | ||
| Symbiotic Optimization Search (SOS) | |||||||||||
| 147 | Yang, & Sutrisno [198]-CSOS | SOS + K-means | An automatic hybrid clustering algorithm | Automatic | Assigning half the population size as the number of clusters | Clustering | Generate initial cluster centroids automatically | 28 benchmark functions, | CRPS, SaNSDE, rCMA-ES, GA, SOS and GWO | Number of successful runs, Average computational time, and Average number of evaluations | |
| S/N | Authors | Adopted Automatic Clustering Approach |
|---|---|---|
| 1 | Zhou et al. [45] | Noise method combined with K-means++ |
| 2 | Dai, Jiao and He [28] | Dynamic optimization through heredity, mutation with parallel evolution, and community intermarriage |
| 3 | Li et al. [40] | Determined optimal number of k from the initial seed of chromosomes ranging between 1 and MaxClassVal, |
| 4 | Kuo et al. [39] | Self-organizing feature map (SOM) neural network method |
| 5 | Zhang & Zhou [35] | An improved canopy with K-means++ |
| 6 | Mohammadrezapour, Kisi and Pourahmad [46] | Optimizing a uniform distribution over a specified range of values |
| 7 | Patel, Raghuwanshi and Jaiswal [200] | Sex determination method |
| 8 | Barekatain, Dehghani & Pourzaferani [44] | Segmented into nonequivalent cells and selection of nodes whose residual energy is more than the cell’s average |
| 9 | Sinha & Jana [33] | The use of Mahalanobis distance and MapReduce framework |
| 10 | Kapil, Chawla & Ansari [3] | Executing GA operators on data objects as candidates for cluster centroids to find the fittest instance |
| 11 | Rahman and Islam [32] | Selecting a fixed number of chromosomes (half selected deterministically and the other half randomly) as the initial population for the GA process to obtain the fittest instances |
| 12 | Islam et al. [34] | Allocating a range of values for k (between 2 and 10) and selecting the best value that produced the optimal solution |
| 13 | Mustafi and Sahoo [36] | Combining GA framework with differential evolution |
| 14 | Xiao et al. [31] | Employing GA-based method that adopts Q-bit representation for dataset pattern with a single run of the conventional K-means on each chromosome |
| 15 | Omran, Salman and Engelbrecht [58] | Using PSO to find the best set of cluster centroids among the existing data objects |
| 16 | Kao and Lee [61] | Using discrete PSO in optimizing the number of clusters |
| 17 | Sood and Bansal [86] | Using Bat algorithm to optimize the initial representative objects for each cluster |
| 18 | Silva et al. [130] | Using a manual strategy to find activation threshold by DE |
| 19 | Cai et al. [125] | Random generation of value as = rndint [2] where NP is the population size and rndint is a random integer number |
| 20 | Kuo, Suryani and Yasid [126] | DE approach in obtaining the number of clusters |
| 21 | Cobos et al. [143] | Optimizing Bayesian information criterion (BIC) or the Davies–Bouldin index (BDI) |
| 22 | Yang and Sutrisno [198] | Specifying the initial number of clusters as half of ecosize generated as sub-ecosystems which CSOS then optimizes |
| MOA | 2002 | 2003 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | Total | Norm. Ra |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ALO (2015) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 | 1 | 2 | 1 | 5 | 0.83 |
| ABC (2005) | - | - | - | - | - | - | - | - | - | - | 1 | 3 | - | - | - | - | 3 | 1 | 8 | 0.50 |
| BAT (2010) | - | - | - | - | - | - | - | - | - | 1 | - | - | - | - | 1 | 1 | 2 | - | 5 | 0.45 |
| Bacterial CO (2012) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 | - | 1 | 2 | 0.22 |
| BFO (2000) | - | - | - | - | - | - | - | - | - | 1 | - | - | - | - | - | - | - | - | 1 | 0.05 |
| BCO (2012) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 | - | 1 | 2 | 0.22 |
| BSO (2012) | - | - | - | - | - | - | - | - | - | - | 1 | 1 | - | 1 | - | - | - | 3 | 0.33 | |
| BH (2013) | - | - | - | - | - | - | - | - | - | - | 1 | - | - | 1 | - | 1 | - | 3 | 0.38 | |
| CS (2009) | - | - | - | - | - | - | - | - | - | 1 | 1 | - | - | 3 | 4 | 2 | - | 11 | 0.92 | |
| Cockroach SO (2010) | - | - | - | - | - | - | - | - | - | - | - | - | 1 | - | 1 | 0.09 | ||||
| DE (2013) | - | - | - | - | - | - | - | 2 | - | 1 | 1 | 1 | - | 1 | 1 | 2 | 1 | - | 10 | 1.25 |
| DA (2015) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 | 1 | 2 | 0.33 |
| COA (2011) | - | - | - | - | - | - | - | - | - | - | - | - | 1 | - | - | - | 1 | 0.10 | ||
| FFA (2008) | - | - | - | - | - | - | - | - | 1 | - | 1 | 2 | 2 | 1 | 1 | 1 | 2 | 1 | 12 | 0.92 |
| FFO ((2000) | - | - | - | - | - | - | - | - | - | - | - | - | 2 | - | - | 2 | - | 4 | 0.19 | |
| FPA (2012) | - | - | - | - | - | - | - | - | - | - | - | 1 | - | - | - | - | - | 1 | 2 | 0.22 |
| GA (1988) | 1 | 3 | 2 | 1 | 1 | 3 | - | - | 1 | 1 | 2 | 2 | 1 | 3 | 2 | 2 | - | 25 | 0.76 | |
| GSO (2009) | - | - | - | - | - | - | - | - | 1 | 1 | - | - | - | - | - | 1 | - | - | 3 | 0.25 |
| GWO (2014) | - | - | - | - | - | - | - | - | - | - | - | 1 | - | - | 1 | - | - | 2 | 4 | 0.57 |
| HS (2001) | 1 | 1 | 1 | 1 | - | 1 | - | - | 1 | - | - | 1 | - | - | 7 | 0.35 | ||||
| ICA 92007) | - | - | - | - | - | - | - | 1 | - | - | 1 | 1 | - | - | - | - | - | 3 | 0.21 | |
| IWO (2010) | - | - | - | - | - | - | - | - | - | - | 1 | 2 | - | - | - | 1 | - | - | 4 | 0.36 |
| MC (1998) | - | - | - | - | - | - | - | - | - | 1 | 3 | - | - | - | 1 | - | 1 | 4 | 0.20 | |
| HBMO (2011) | - | - | - | - | - | - | - | - | - | - | - | - | 2 | - | - | - | - | - | 2 | 0.20 |
| PSO (1995) | 1 | 1 | 1 | 1 | 2 | 1 | - | - | - | 1 | 1 | 2 | 1 | - | 2 | 2 | - | 16 | 0.62 | |
| SCA (2016) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 | - | 1 | 0.20 |
| SDS (2011) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 | 1 | 0.10 |
| SOS (2014) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 | - | 1 | 0.14 |
| Social Spider O (2015) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 | 1 | - | - | 2 | 0.33 |
| Total/Year | 1 | 1 | 4 | 3 | 3 | 4 | 5 | 4 | 2 | 8 | 12 | 15 | 10 | 7 | 15 | 19 | 22 | 11 | 147 |
| Authors | Publishers | Journal/Conference | Indexing | Citation | Impact Factor | ||||
|---|---|---|---|---|---|---|---|---|---|
| SCI | WOS | Scopus | Google Scholar | DBLP | |||||
| Abdeyazdan [140] | Springer | Journal of Supercomputing | √ | √ | √ | √ | 15 | 2.474 | |
| Aboubi, Drias & Kamel [179] | Springer | Conf | 2 | ||||||
| Aghaebrahimi, Golkh&an & Ahmadnia [188] | IEEE | Conf | 8 | ||||||
| Angelin, B. [162] | Turkish Journal of Computer & Mathematics Education | √ | √ | 0 | 0.33 | ||||
| Arjmand et al. [117] | IEEE | Conf | √ | 5 | |||||
| Armano & Farmani [95] | IRIS | Int’l Journal of Computer Theory & Engineering | √ | 36 | |||||
| Bandyopadhyay & Maulik [24] | Elsevier | Information Sciences | √ | √ | √ | √ | 465 | 6.795 | |
| Barekatain, Dehghani & Pourzaferani [44] | Elsevier | Procedia Computer Science | √ | 38 | 2.09 | ||||
| Behera et al. [77] | Inderscience | Int’l Journal of Fuzzy Computation & Modelling | √ | 2 | |||||
| Binu, Selvi & George [119] | Elsevier | AASRI Procedia | √ | √ | 17 | ||||
| Bonab et al. [97] | Springer | Computational Intelligence in Information Systems | 12 | ||||||
| Boobord, Othman, & Abubakar [136] | i-csrs.org | Intl. Journal of Advance Soft Computer Appl | √ | 1 | 0.79 | ||||
| Cai et al. [125] | Elsevier | Applied Soft Computing | √ | √ | 120 | 6.725 | |||
| Cao & Xue [102] | IEEE | Int’l Conf on Network & Information Systems for Computers | 4 | ||||||
| Chandran & Nazeer [144] | IEEE | Recent Adv. in Intelligent Computational Systems | √ | √ | 13 | ||||
| Chandran, Reddy, & Janet [170] | IEEE | Second Int’l Conf on Intelligent Computing & Control Systems | 1 | ||||||
| Chaudhary & Banati [90] | Inderscience | Int’l Journal of Advanced Intelligence Paradigms | √ | √ | √ | 0 | 0.63 | ||
| Chen & Zhang [59] | IEEE | Int’l Conf on Wireless Comms, Networking & Mobile Computing | 31 | ||||||
| Chen et al. [166] | Elsevier | Knowledge-Based Systems | √ | √ | √ | √ | 13 | ||
| Chen, Miao & Bu [72] | IEEE | Int’l Conf on Power, Intelligent Computing & Systems | 2 | ||||||
| Cheng et al. [25] | IEEE | Int’l Conf on Pattern Recognition (ICPR’06) | 23 | ||||||
| Cobos et al. [143] | IEEE | IEEE congress on evolutionary computation | 13 | ||||||
| Dai, Jiao & He [28] | IEEE | Int’l Conf on Intelligent Information Hiding & Multimedia Signal Proc | 10 | ||||||
| Das, Das & Dey [196] | Elsevier | Applied Soft Computing | √ | √ | 25 | 6.725 | |||
| Dasu, Reddy & Reddy [99] | Springer | Adv. in Cybernetics, Cognition, & Machine Learning for Comm Tech | 1 | ||||||
| Deepa, & Sumitra [121] | IOPScience | Int’l Conf on Mechanical, Electronics & Computer Engineering | √ | 0 | |||||
| Dhand & Sheoran [168] | Elsevier | Materials Today: Conf Proceeding | √ | √ | 4 | 31.04 | |||
| Djenouri, Belhadi & Belkebir [178] | Elsevier | Expert Systems with Appl | √ | √ | √ | √ | 48 | 6.954 | |
| Djenouri, Habbas & Aggoune-Mtalaa [180] | SCITEPRESS | Int’l Conf on Agents & Artificial Intelligence | 5 | ||||||
| El-Shorbagy et al. [37] | Springer | Computational Statistics | √ | √ | √ | √ | √ | 14 | 1 |
| Emami & Derakhshan [65] | Springer | Arabian Journal of Science & Engineering | √ | √ | √ | 28 | 2.334 | ||
| Eshlaghy & Razi [42] | Inderscience | Int’l Journal of Business Systems | √ | √ | 15 | 0.53 | |||
| Eskandarzadehalamdary, Masoumi, & Sojodishijani [151] | IEEE | Iranian Conf on Elect Engineering | 11 | ||||||
| Fan et al. [134] | IEEE | Int’l Conf on Autonomic & Trusted Computing | 2 | ||||||
| Feng, Wang & Chen [154] | Springer | International Conf on Scalable Computing & Comms | 0 | ||||||
| Forsati et al. [141] | Elsevier | Neurocomputing | √ | √ | √ | 60 | 5.719 | ||
| Forsati, Keikha & Shamsfard [197] | IEEE | IEEE/WIC/ACM Int’l Conf on Web Intelligence & Intelligent Agent Tech | 69 | ||||||
| Gan, & Lai [89] | IEEE | Int’l Conf on Automatic Control & Intelligent Systems (I2CACIS) | 3 | ||||||
| García, Yepes & Martí [118] | MDPI | Mathematics | √ | √ | √ | 21 | 2.258 | ||
| Ghezelbash, Maghsoudi & Carranza [38] | Elsevier | Computer & Geoscience | √ | √ | √ | 23 | 3.372 | ||
| Girsang, Yunanto & Aslamiah [113] | IEEE | Int’l Conf on Elect Engineering & Computer Science | 6 | ||||||
| Hassanzadeh & Meybodi [74] | IEEE | Int’l Conf on Elect Engineering & Computer Science | 99 | ||||||
| HimaBindu et al. [83] | Elsevier | Materials Today: Conf Proceeding | √ | √ | 0 | 31.04 | |||
| Hu et al. [128] | IEEE | Int’l Conf on Computer Science & Education (ICCSE) | 11 | ||||||
| Huang [100] | MDPI | Symmetry | √ | √ | √ | √ | 1 | 2.713 | |
| Islam et al. [34] | Elsevier | Expert Systems with Appl | √ | √ | √ | √ | 2 | 6.954 | |
| Jensi & Jiji [92] | arXiv Cornell Univerity | Advanced Computational Intelligence | √ | 37 | |||||
| Jiang et al. [174] | IEEE | IEEE Int’l Conf on Artificial Intelligence & Computer Appl | 0 | ||||||
| Jiang, Zang & Liu [155] | Springer | In Int’l Conf on Human Centered Computing | 2 | ||||||
| Jie & Yibo [71] | IEEE | Int’l Conf on Power & Renewable Energy | 0 | ||||||
| Jin, Lin & Zhang [98] | MDPI | Algorithms | √ | √ | √ | √ | 0 | 2.27 | |
| Jitpakdee, Aimmanee & Uyyanonvara [79] | World Academy of Science, Engineering & Tech | Int’l Journal of Computer & Information Engineering | 7 | ||||||
| Kao & Lee [61] | Elsevier | Expert Systems with Appl | √ | √ | √ | √ | 53 | 6.954 | |
| Kao, Zahara & Kao [60] | IEEE | Int’l Conf on Intelligent Computing & Intelligent Systems | 400 | ||||||
| Kapil, Chawla & Ansari [3] | IEEE | Int’l Conf on Parallel, Distributed & Grid Computing | 67 | ||||||
| Karegowda et al. [41] | Springer | Int’l Conf on Adv. in Computing | 16 | ||||||
| Karthik, Tamizhazhagan, & Narayana [185] | Elsevier | Materials Today: Conf Proceeding | √ | √ | 0 | 31.04 | |||
| Katarya & Verma [104] | Springer | Neural Computer & Appl | √ | √ | √ | √ | 58 | 5.606 | |
| Kaur, Pal & Singh [81] | Springer | Int’l Journal of System Assurance Engineering & Mgt | √ | √ | √ | 15 | 1.72 | ||
| Kim et al. [147] | IEEE | IEEE Annual Consumer Comms & Networking Conf | 3 | ||||||
| Korayem, Khorsid & Kassem [105] | IOP Publishing | IOP Conf series: materials science & engineering | 44 | 0.51 | |||||
| Kumar, Reddy & Rao [164] | Elsevier | Journal of Computational Design & Engineering | 4 | 6.6 | |||||
| Kumari, Rao & Rao [93] | Inderscience | Int’l Journal of Advanced Intelligence Paradigms | √ | √ | √ | 0 | 0.63 | ||
| Kuo & Li [80] | Elsevier | Computers & Industrial Engineering | √ | √ | √ | 28 | 5.431 | ||
| Kuo et al. [39] | Elsevier | Expert Systems with Appl | √ | √ | √ | √ | 120 | 6.954 | |
| Kuo, Suryani & Yasid [126] | Springer | Institute of Industrial Engineers Asian Conf | 16 | ||||||
| Kwedlo [124] | Elsevier | Pattern Recognition Letters | √ | √ | √ | √ | 128 | 3.756 | |
| Langari et al. [82] | Elsevier | Expert Systems with Appl | √ | √ | √ | √ | 17 | 6.954 | |
| Lanying & Xiaolan [115] | ACM | Int’l Conf on Intelligent Information Proc | 0 | ||||||
| Lashkari & Moattar [202] | Iran Journals | Journal of AI & Data Mining | √ | 5 | 0.127 | ||||
| Laszlo & Mukherjee, [26] | IEEE | Transactions on pattern analysis & machine intelligence | 153 | ||||||
| Laszlo & Mukherjee, [27] | Elsevier | Pattern Recognition Letters | √ | √ | √ | √ | 192 | ||
| Li et al. [40] | IEEE | Int’l Conf on Digital Content, Multimedia Tech & its Appl | 153 | ||||||
| Lu et al. [43] | Springer | Int’l Conf on Bio-Inspired Computing: Theories & Appl | 11 | ||||||
| Mahdavi & Abolhassani [142] | Springer | Data Mining & Knowledge Discovery | √ | √ | √ | √ | √ | 168 | 3.67 |
| Majhi & Biswal [164] | Elsevier | Karbala Int’l Journal of Modern Science | 44 | 2.93 | |||||
| Manju & Fred [120] | Springer | Multimedia Tools & Appl | √ | √ | √ | √ | 1 | 2.757 | |
| Mathew & Vijayakumar [75] | IEEE | Int’l Conf on High Performance Computing & Appl | 15 | ||||||
| Mohammadrezapou, Kisi & Pourahmadm [46] | Springer | Neural Computer & Appl | √ | √ | √ | √ | 12 | 5.606 | |
| Mohammed et al. [107] | Emerald Publishing | World Journal of Engineering | √ | 0 | 1.2 | ||||
| Moorthy & Pabitha [109] | IEEE | Int’l Conf on High Performance Computing & Appl | 3 | ||||||
| Murugan & Baburaj [166] | IEEE | Int’l Conf on Smart Tech in Computing, Elect & Electronics | 0 | ||||||
| Mustafi & Sahoo [36] | Springer | Soft Computing | √ | √ | √ | √ | 15 | 3.643 | |
| Naem & Ghali [167] | BEEI | Indonesia Journal | √ | √ | 2 | ||||
| Nayak et al. [66] | Springer | Int’l Conf on Computer & Comm Tech | 20 | ||||||
| Nayak et al. [77] | Springer | Computational Intelligence in Data Mining | 1 | ||||||
| Nayak, Naik & Behera [79] | Springer | Adv. in Intelligent Systems & Computing | 4 | ||||||
| Nazeer, Sebastian & Kumar [145] | PMC | Bioinformatics | √ | √ | √ | 8 | 3.242 | ||
| Niknam et al. [139] | Elsevier | Engineering Appl | √ | √ | √ | 244 | 6.212 | ||
| Niknam, & Amiri [53] | Elsevier | Applied Soft Computing | √ | √ | 476 | 6.725 | |||
| Niu et al. [48] | Elsevier | Engineering Appl | √ | √ | √ | 22 | 6.212 | ||
| Niu, Duan & Liang [201] | Springer | Int’l Conf on Intelligent Data Engineering & AutoLearning | 6 | ||||||
| Omran, Salman & Engelbrecht [58] | Springer | Pattern Analysis & Appl | √ | √ | √ | √ | 325 | 2.58 | |
| Onan & Korukoglu [193] | ProQuest | Int’l Symposium on Computing in Science & Engineering | 1 | ||||||
| Pal & Pal [152] | Springer | Computational Intelligence in Data Mining | 3 | ||||||
| Pambudi, Badharudin & Wicaksono [106] | ICTACT | Journal on Soft computing | 0 | 0.787 | |||||
| Pan et al. [135] | World Scientific | Int’l Journal of Pattern Recognition & Artificial Intelligence | √ | √ | √ | 18 | 1.375 | ||
| Patel, Raghuwanshi & Jaiswal [200] | IEEE | IEEE Int’l Advance Computing Conf | 13 | ||||||
| Paul, De & Dey [70] | IEEE | Int’l Conf on Electronics, Computing & Comm Tech | 11 | ||||||
| Pavez, Altimiras, & Villavicencio [88] | Springer | Proc of the Computational Methods in Systems & Software | |||||||
| Prabha & Visalakshi [64] | IEEE | Int’l Conf on Intelligent Computing Appl | 26 | ||||||
| Rahman & Islam [32] | Elsevier | Knowledge-Based Systems | √ | √ | √ | √ | 52 | 8.038 | |
| Ratanavilisagul [69] | IEEE | Int’l Conf on Computational Intelligence & Appl | 1 | ||||||
| Raval, Raval & Valiveti [146] | IEEE | Int’l Conf on Recent Trends in Information Tech | 0 | ||||||
| Razi [137] | Springer | Journal of Industrial Engineering Int’l | 5 | 2.02 | |||||
| Revathi, Eswaramurthy, & Padmavathi [182] | IOP Publishing | In IOP Conf Series: Materials Science & Engineering | 0 | 0.51 | |||||
| Saida, Kamel & Omar [112] | Springer | Recent Adv. on Soft Computing & Data Mining | 11 | ||||||
| Senthilkumar & Chitra [190] | IEEE | Int’l Conf on Smart Systems & Inventive Tech | 0 | ||||||
| Sharma & Patel [173] | ACADEMIA | Int’l Journal of Computer Science & Information Security (IJCSIS) | √ | √ | √ | 0 | 0.702 | ||
| Sheng et al. [131] | IEEE | Transactions on Cybernetics | 3 | 11.45 | |||||
| Sheng, Tucker & Liu, [30] | Springer | Soft Computing | √ | √ | √ | √ | 2 | 3.643 | |
| Sierra, Cobos, & Corrales [127] | Springer | Ibero-American Conf on Artificial Intelligence | 6 | ||||||
| Silva et al. [130] | Springer | Int’l Conf on Green, Pervasive, & Cloud Computing | 4 | ||||||
| Singh & Solanki [116] | Springer | Emerging Research in Electronics, Computer Science & Tech | 8 | ||||||
| Sinha & Jana [33] | Springer | Journal of Supercomputing | √ | √ | √ | √ | 21 | 2.474 | |
| Sood & Bansal [86] | Citeseer | Int’l Journal of Applied Information Systems | √ | 21 | |||||
| Tang et al. [194] | IEEE | Int’l Symposium on Distributed Computing & Appl | 1 | ||||||
| Tarkhaneh, Isazadeh & Khamnei [115] | Inderscience | Int’l Journal of Computer Appl | √ | √ | √ | 11 | 1.55 | ||
| Teimoury et al. [187] | MDPI | Sensors | √ | √ | √ | √ | 4 | 3.576 | |
| Thiruvenkatasuresh & Venkatachalam [171] | Inderscience | Int’l Journal of Biomedical Engineering & Tech | √ | √ | 1 | 1.01 | |||
| Tran et al. [96] | IEEE | Chinese Journal of Electronics | √ | √ | √ | √ | 38 | 0.941 | |
| Tripathi, Sharma & Bala [87] | Springer | Int’l Journal of System Assurance Engineering & Mgt | √ | √ | √ | 32 | 1.72 | ||
| Tsai & Kao [63] | IEEE | Int’l Conf on Systems, Man, & Cybernetics | 91 | ||||||
| Van der Merwe & Engelbrecht [49] | IEEE | Congress on Evolutionary Computation | 953 | ||||||
| Vijayakumari & Deepa [183] | Infokara | 0 | |||||||
| Wang et al. [101] | IEEE | Access | 2 | 3.367 | |||||
| Wang et al. [176] | IEEE | Int’l Conf on Grey Systems & Intelligent Services | 5 | ||||||
| Wang [129] | IEEE | Adv. Infor Mgt, Comm, Electronic & Auto Control Conf | 3 | ||||||
| Wang, Liu & Xiang [160] | Taylor & Francis | Int’l Journal of Parallel, Emergent & Distributed Systems | √ | √ | √ | √ | 2 | 1.51 | |
| Wang, Xiang & Liu [159] | IEEE | Int’l Conf on Intelligent Science & Big Data Engineering | 0 | ||||||
| Weisun & Liu [157] | WSEAS | 0 | |||||||
| Wu et al. [84] | Elsevier | Agricultural Water Mgt | √ | √ | 6 | 4.516 | |||
| Xiao, Yan, Zhang, & Tang [31] | Elsevier | Expert Systems with Appl | √ | √ | √ | √ | 108 | 6.954 | |
| Xie et al. [74] | Elsevier | Applied Soft Computing | √ | √ | 40 | 6.725 | |||
| Yang, Sun & Zhang [62] | Elsevier | Expert Systems with Appl | √ | √ | √ | √ | 228 | 6.954 | |
| Yang, & Sutrisno [198] | Elsevier | Applied Soft Computing | √ | √ | 1 | 6.725 | |||
| Ye et al. [111] | IEEE | Int’l Conf on Convergence & Hybrid Information Tech | 10 | ||||||
| Zhang & Zhou [35] | IEEE | Int’l Conf on Artificial Intelligence & Big Data | 11 | ||||||
| Zhang, Leung & Ye [199] | IEEE | Int’l Conf on Convergence & Hybrid Information Tech | 26 | ||||||
| Zhao & Liu [156] | Springer | Int’l Conf on Human Centered Computing | 0 | ||||||
| Zhao, Liu & Zhang [158] | TELKOMNIKA | Indonesian Journal of Elect Engineering, | 5 | ||||||
| Zhou et al. [192] | Guangxi Key Laboratory | 19 | |||||||
| Zhou et al. [45] | MDPI | ISPRS Int’l Journal of Geo-Information | √ | √ | √ | √ | 20 | 2.899 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ikotun, A.M.; Almutari, M.S.; Ezugwu, A.E. K-Means-Based Nature-Inspired Metaheuristic Algorithms for Automatic Data Clustering Problems: Recent Advances and Future Directions. Appl. Sci. 2021, 11, 11246. https://doi.org/10.3390/app112311246
Ikotun AM, Almutari MS, Ezugwu AE. K-Means-Based Nature-Inspired Metaheuristic Algorithms for Automatic Data Clustering Problems: Recent Advances and Future Directions. Applied Sciences. 2021; 11(23):11246. https://doi.org/10.3390/app112311246
Chicago/Turabian StyleIkotun, Abiodun M., Mubarak S. Almutari, and Absalom E. Ezugwu. 2021. "K-Means-Based Nature-Inspired Metaheuristic Algorithms for Automatic Data Clustering Problems: Recent Advances and Future Directions" Applied Sciences 11, no. 23: 11246. https://doi.org/10.3390/app112311246
APA StyleIkotun, A. M., Almutari, M. S., & Ezugwu, A. E. (2021). K-Means-Based Nature-Inspired Metaheuristic Algorithms for Automatic Data Clustering Problems: Recent Advances and Future Directions. Applied Sciences, 11(23), 11246. https://doi.org/10.3390/app112311246







