Noiseless Attenuation for Continuous-Variable Quantum Key Distribution over Ground-Satellite Uplink
Abstract
:1. Introduction
2. Uplink CV-QKD
| Variable | Value | Description | Reference |
|---|---|---|---|
| 0–60 | Zenith angle | ||
| a | 1 m | Receiver telescope radius | [21] |
| f/2a | 1 | Focal ratio | [33] |
| 10 | Fiber core diameter | [33] | |
| 80 mm | Intial beam radius | [33] | |
| 4 SNU | Modulation variance | [34] | |
| 800 nm | Wavelength | [21] | |
| Reconciliation efficiency | [21] | ||
| 0.01 SNU | Excess noise | [35] | |
| × | Refraction index structure parameter | [17] | |
| 0.61 | Mean number of scatterer particles | [17] |
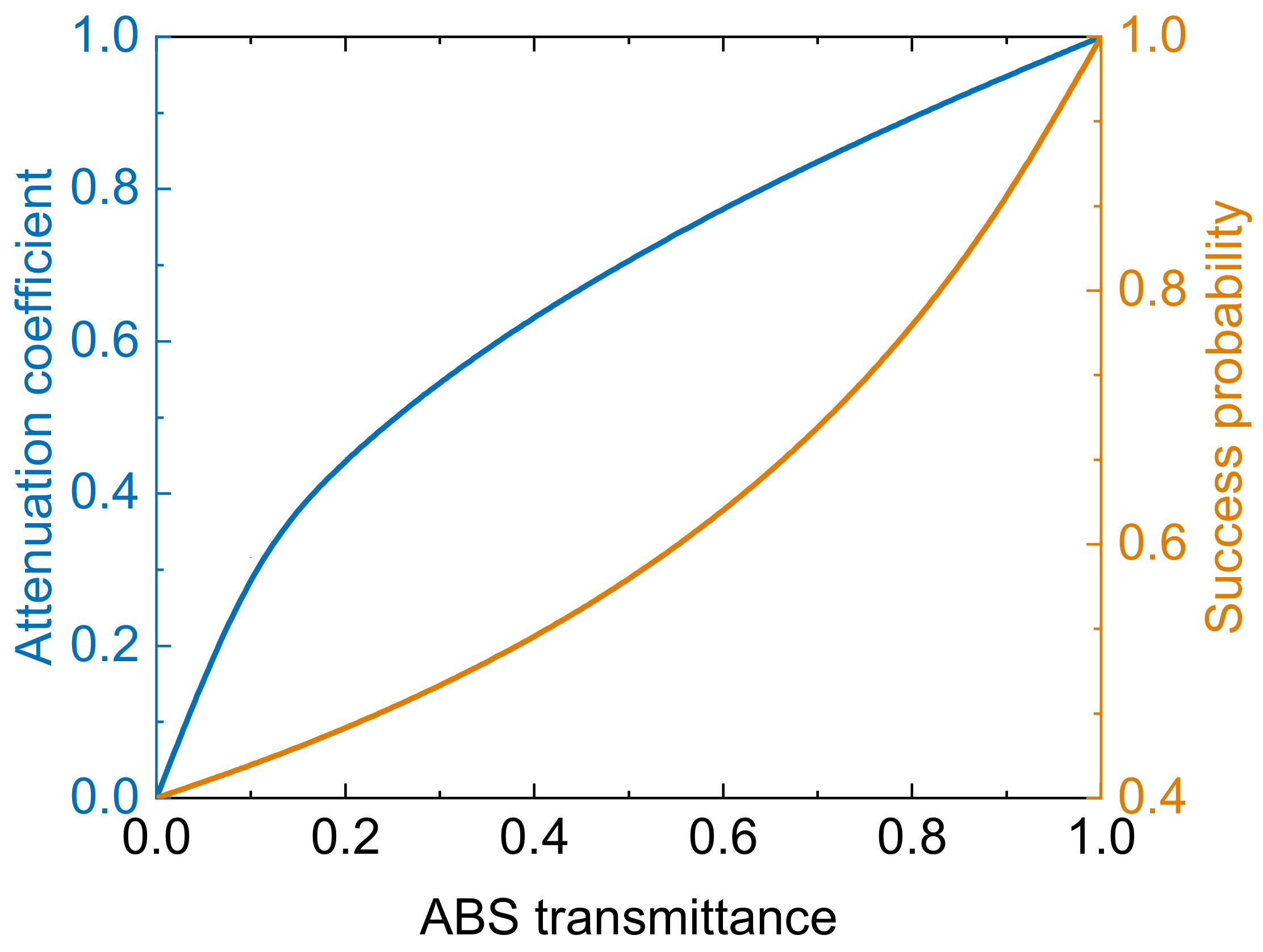
3. Modified Protocol with Noiseless Attenuation
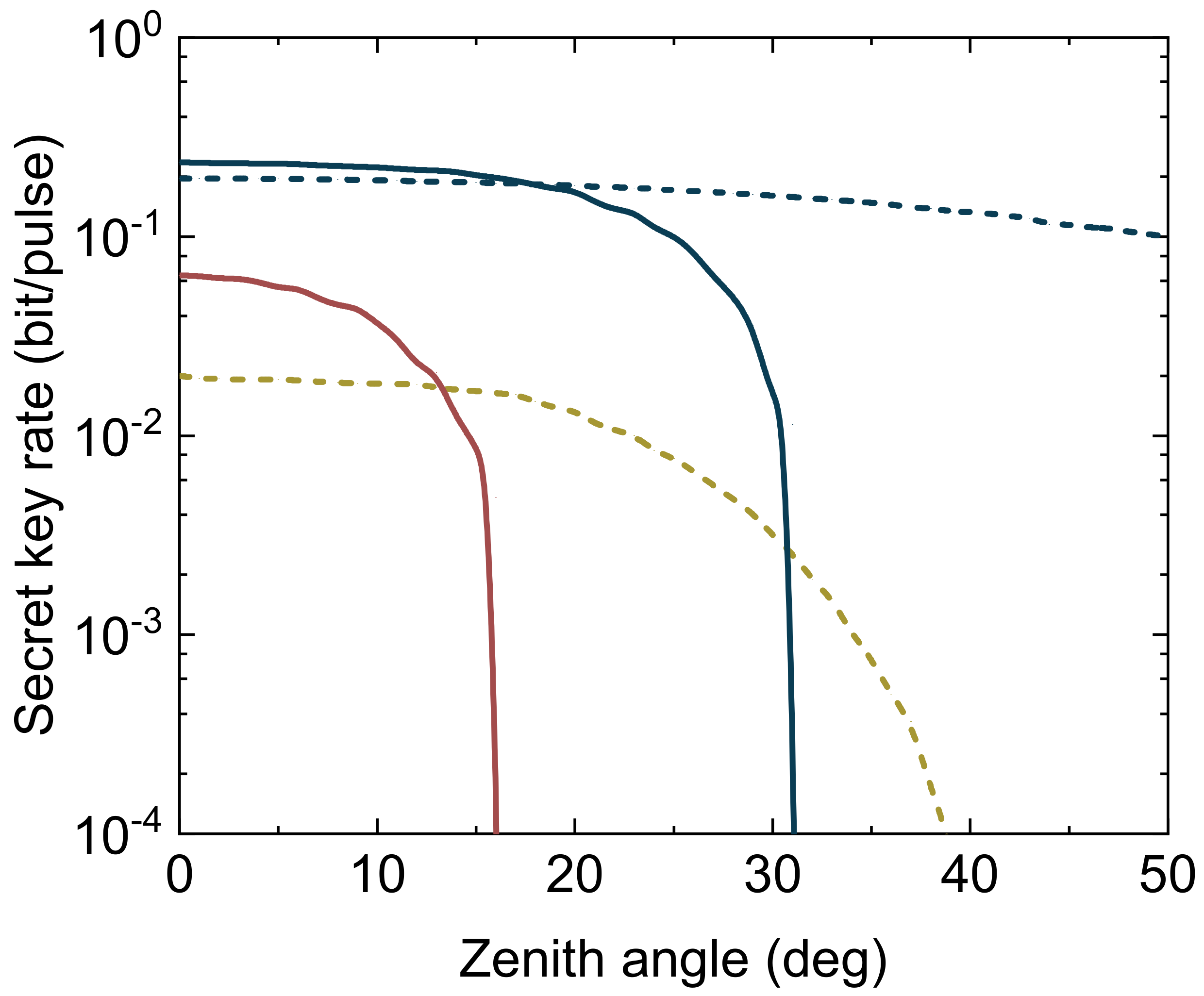
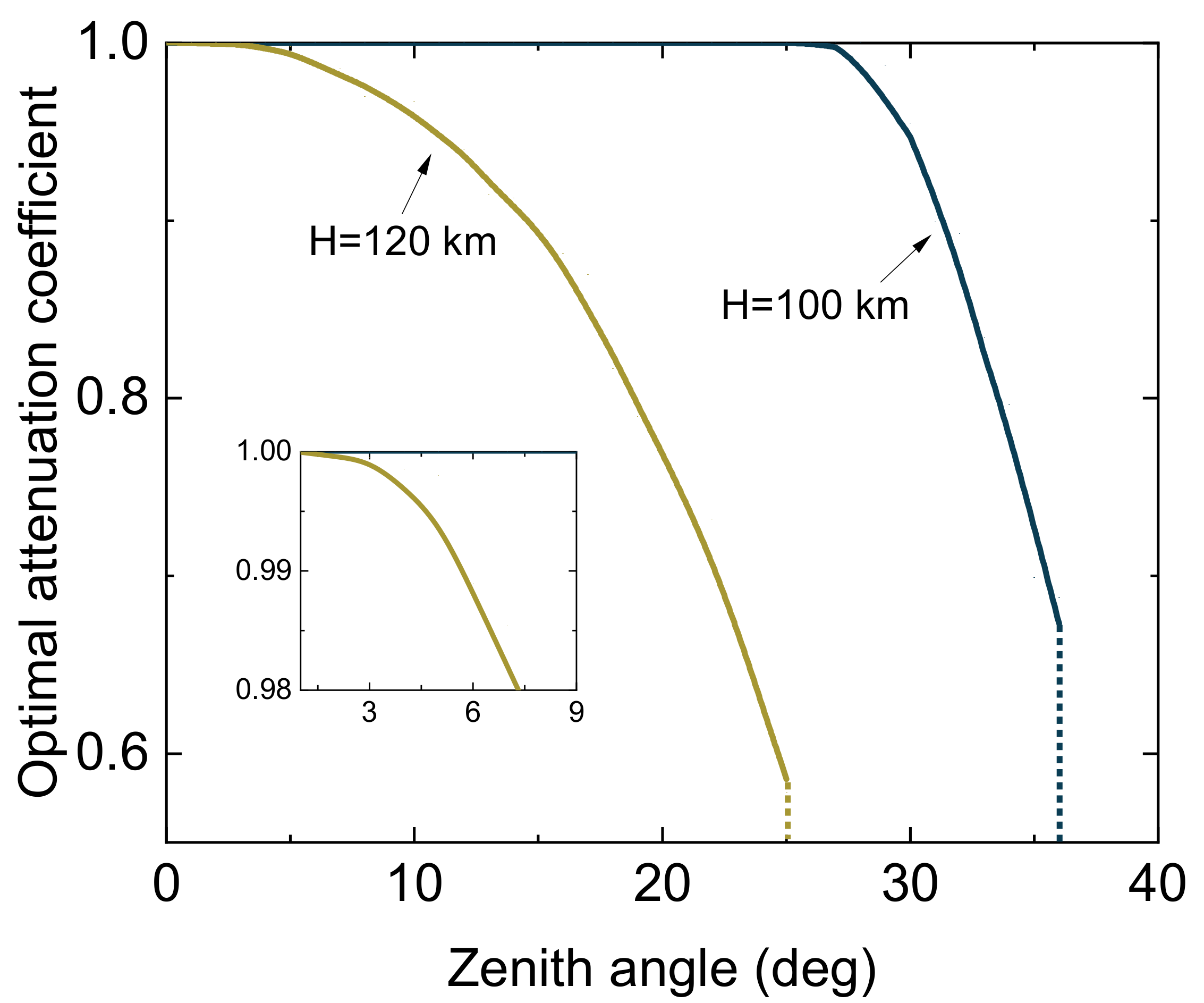
4. Performance Analysis
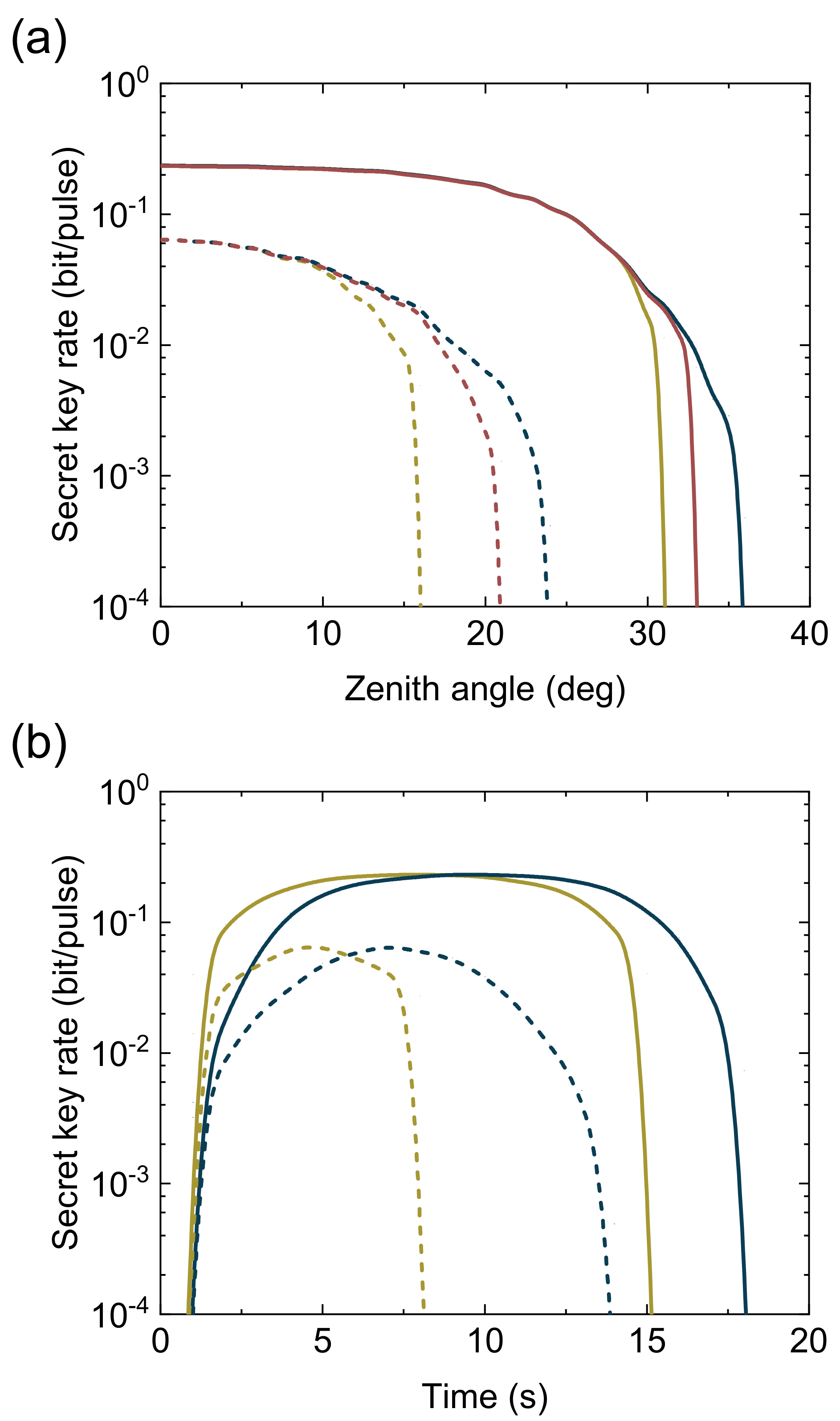
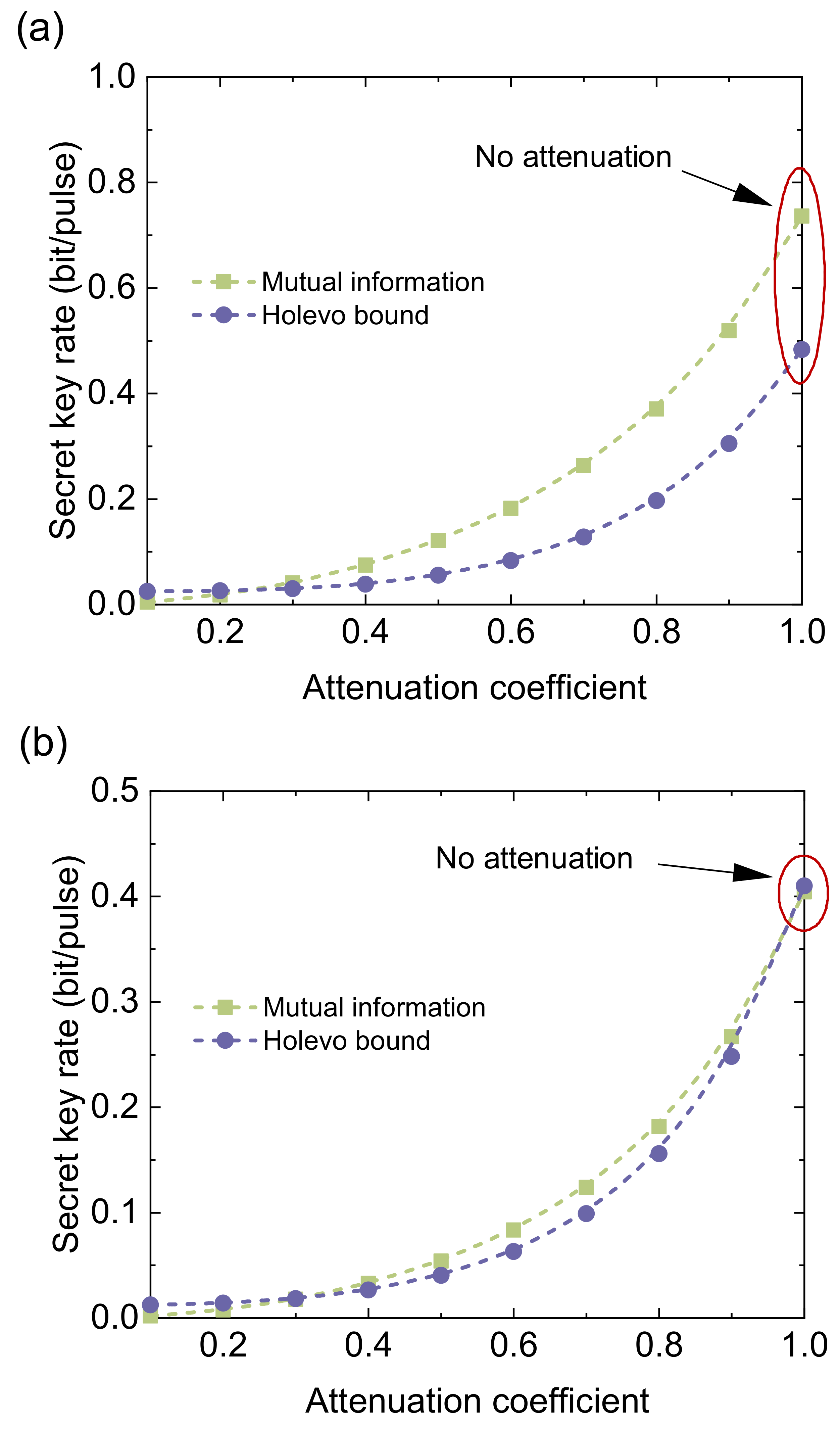
4.1. Asymptotic Analysis
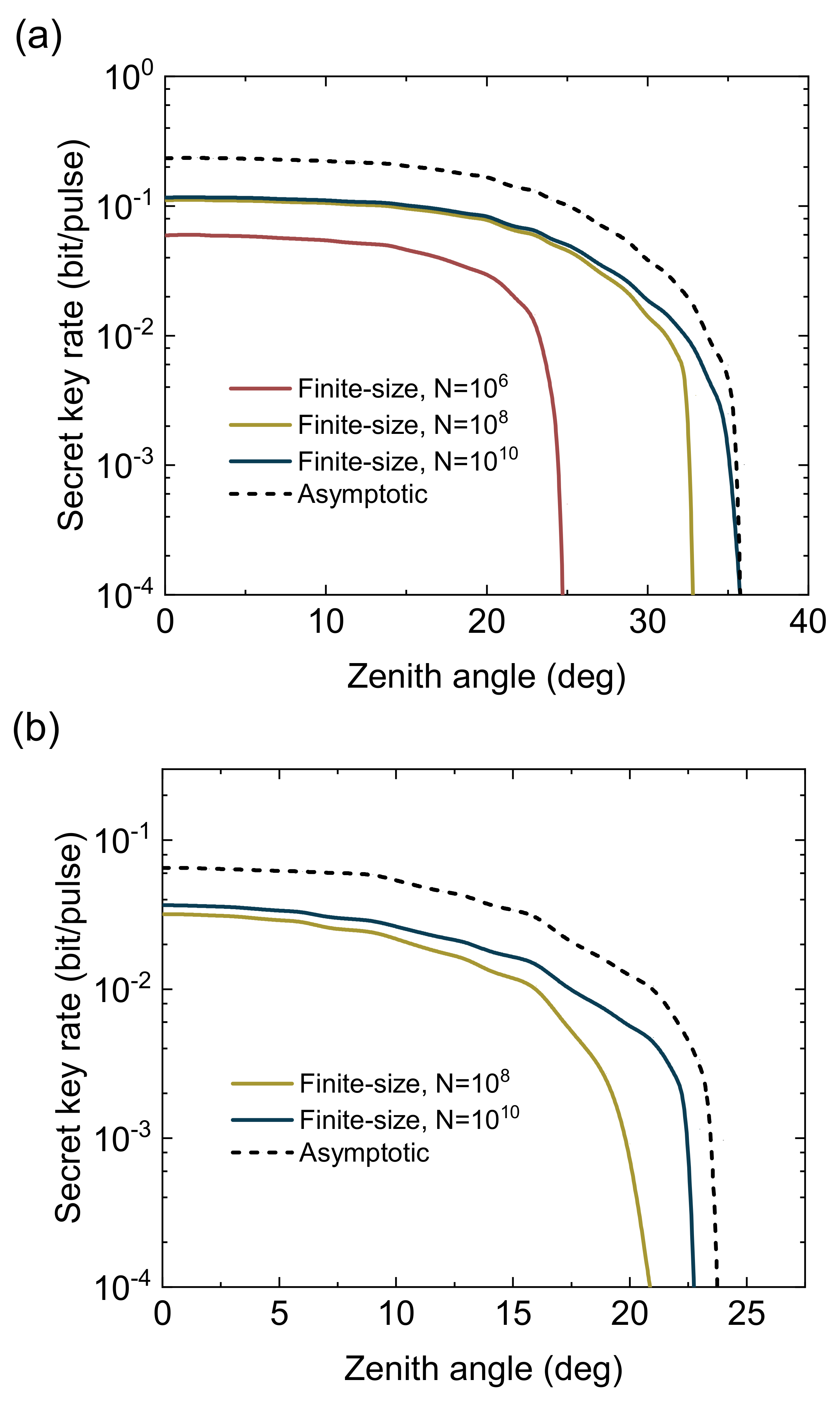
4.2. Finite-Size Regime
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| QKD | Quantum key distribution |
| DV | Discrete-variable |
| CV | Continuous-variable |
| NA | Noiseless attenuation |
| ZPC | Zero-photon catalysis |
| EB | Entanglement-based |
| TMSV | Two-mode squeezed vacuum |
| BS | Beam splitter |
| PDT | Probability distribution of transmittance |
| ABS | Asymmetrical beam splitter |
| PNRD | Photon number resolving detector |
| CF | Characteristic function |
Appendix A. The Elements of μ and Σ in Equation (4)
Appendix B. The Calculations of IAB and χE
Appendix C. Details of 〈〉 in Uplink Case
Appendix D. Derivation of γAB1
References
- Luo, Y.H.; Chen, M.-C.; Erhard, M.; Zhong, H.; Wu, D. Quantum teleportation of physical qubits into logical code spaces. Proc. Natl. Acad. Sci. USA 2021, 118, 1–5. [Google Scholar] [CrossRef]
- Ahmed, A.H.M.; Zakaria, M.N.; Metwally, N. Teleportation in the presence of technical defects in transmission stations. Appl. Math. Inf. Sci. 2012, 6, 781. [Google Scholar]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, M.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photonics 2020, 12, 1012–1236. [Google Scholar] [CrossRef] [Green Version]
- Hillery, M.; Bužek, V.; Berthiaume, A.; Gisin, N. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Wang, Y.; Huang, D. Passive continuous-variable quantum secret sharing using a thermal source. Phys. Rev. A 2020, 101, 022301. [Google Scholar] [CrossRef]
- Liao, Q.; Liu, H.; Zhu, L.; Guo, Y. Quantum secret sharing using discretely modulated coherent states. Phys. Rev. A 2021, 103, 032410. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Cheong, L.Y.; Zakaria, N.; Metwally, N. Dynamics of Information Coded in a Single Cooper Pair Box. Int. J. Theor. Phys. 2013, 52, 1979–1988. [Google Scholar] [CrossRef]
- Sridevi, R.; Philominathan, P. Quantum Colour Image Encryption Algorithm Based on DNA and Unified Logistic Tent Map. Inf. Sci. Lett. 2020, 9, 9. [Google Scholar]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [Green Version]
- Grosshans, F.; Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scarani, V.; Acin, A.; Ribordy, G.; Gisin, N. Quantum cryptography protocols robust against photon number splitting attacks for weak laser pulse implementations. Phys. Rev. Lett. 2004, 92, 057901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A.; Grangier, P.; Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photon. 2013, 7, 378–381. [Google Scholar] [CrossRef]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.K.; Pan, J.W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Liao, Q.; Xiao, G.; Zhong, H.; Guo, Y. Multi-label learning for improving discretely-modulated continuous-variable quantum key distribution. New J. Phys. 2020, 22, 083086. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Sidhu, J.S.; Siddarth, K.J.; Mustafa, G.; Thomas, B.; David, L.; Luca, M.; Markus, K.; Sonali, M.; Daniele, D.; Giuseppe, V.; et al. Advances in Space Quantum Communications. arXiv 2021, arXiv:2103.12749. [Google Scholar] [CrossRef]
- Liorni, C.; Kampermann, H.; Bruß, D. Satellite-based links for quantum key distribution: Beam effects and weather dependence. New J. Phys. 2019, 21, 093055. [Google Scholar] [CrossRef] [Green Version]
- Vasylyev, D.; Vogel, W.; Moll, F. Satellite-mediated quantum atmospheric links. Phys. Rev. A 2019, 99, 053830. [Google Scholar] [CrossRef] [Green Version]
- Bourgoin, J.P.; Meyer-Scot, E.; Higgins, B.L.; Erven, C.; Hube, H.; Kumar, H.; Hudson, D.; D’Souza, I.; Girard, R.; Laflamme, R.; et al. A comprehensive design and performance analysis of low Earth orbit satellite quantum communication. New J. Phys. 2013, 15, 023006. [Google Scholar] [CrossRef]
- Pirandola, S. Satellite quantum communications: Fundamental bounds and practical security. Phys. Rev. Res. 2021, 3, 023130. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, Y.; Huang, D.; Guo, Y. Atmospheric effects on satellite-mediated continuous-variable quantum key distribution. J. Phys. A Math. Theor. 2020, 53, 465302. [Google Scholar] [CrossRef]
- Mičuda, M.; Straka, I.; Miková, M.; Dušek, M.; Cerf, N.J.; Fiurášek, J.; Ježek, M. Noiseless loss suppression in quantum optical communication. Phys. Rev. Lett. 2012, 109, 180503. [Google Scholar] [CrossRef]
- Fiurášek, J.; Cerf, N.J. Gaussian postselection and virtual noiseless amplification in continuous-variable quantum key distribution. Phys. Rev. A 2012, 86, 060302. [Google Scholar] [CrossRef] [Green Version]
- Meng, G.; Yang, S.; Zou, X.; Zhang, S.; Shi, B.; Guo, G. Noiseless suppression of losses in optical quantum communication with conventional on-off photon detectors. Phys. Rev. A 2012, 86, 042305. [Google Scholar] [CrossRef]
- Blandino, R.; Walk, N.; Lund, A.P.; Ralph, T.C. Channel purification via continuous-variable quantum teleportation with Gaussian postselection. Phys. Rev. A 2016, 93, 012326. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Zhang, X. Photon catalysis acting as noiseless linear amplification and its application in coherence enhancement. Phys. Rev. A 2018, 97, 043830. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621. [Google Scholar] [CrossRef]
- Usenko, V.C.; Heim, B.; Peuntinger, C.; Wittmann, C.; Marquardt, C.; Leuchs, G.; Filip, R. Entanglement of Gaussian states and the applicability to quantum key distribution over fading channels. New J. Phys. 2012, 14, 093048. [Google Scholar] [CrossRef]
- Vasylyev, D.; Semenov, A.A.; Vogel, W. Atmospheric quantum channels with weak and strong turbulence. Phys. Rev. Lett. 2016, 117, 090501. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, Y.; Mao, Y.; Ruan, X.; Guo, Y. Security of quantum communications in oceanic turbulence. Phys. Rev. A 2021, 104, 052613. [Google Scholar] [CrossRef]
- Grosshans, F.; Van Assche, G.; Wenger, J.; Brouri, R.; Cerf, N.J.; Grangier, P. Quantum key distribution using gaussian-modulated coherent states. Nature 2003, 421, 238–241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellingham, WA, USA, 2005; pp. 199–201. [Google Scholar]
- Wang, S.; Huang, P.; Wang, T.; Zeng, G. Atmospheric effects on continuous-variable quantum key distribution. New J. Phys. 2018, 20, 083037. [Google Scholar] [CrossRef] [Green Version]
- Zuo, Z.; Wang, Y.; Mao, Y.; Ye, W.; Hu, L.; Huang, D.; Guo, Y. Quantum catalysis-assisted attenuation for improving free-space continuous-variable quantum key distribution. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 185501. [Google Scholar] [CrossRef]
- Qi, B.; Zhu, W.; Qian, L.; Lo, H.K. Feasibility of quantum key distribution through a dense wavelength division multiplexing network. New J. Phys. 2010, 12, 103042. [Google Scholar] [CrossRef]
- Wang, S.; Huang, P.; Wang, T.; Zeng, G. Feasibility of All-Day Quantum Communication with Coherent Detection. Phys. Rev. Appl. 2019, 12, 024041. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, Y.; Liao, Q.; Guo, Y. Overcoming the uplink limit of satellite-based quantum communication with deterministic quantum teleportation. Phys. Rev. A 2021, 104, 022615. [Google Scholar] [CrossRef]
- Leverrier, A.; Grosshans, F.; Grangier, P. Finite-size analysis of a continuous-variable quantum key distribution. Phys. Rev. A 2010, 81, 062343. [Google Scholar] [CrossRef] [Green Version]
- Pirandola, S. Limits and security of free-space quantum communications. Phys. Rev. Res. 2021, 3, 013279. [Google Scholar] [CrossRef]
- Liao, Q.; Xiao, G.; Xu, C.G.; Xu, Y.; Guo, Y. Discretely modulated continuous-variable quantum key distribution with an untrusted entanglement source. Phys. Rev. A 2020, 102, 032604. [Google Scholar] [CrossRef]
- Ruppert, L.; Peuntinger, C.; Heim, B.; Günthner, K.; Usenko, V.C. Fading channel estimation for free-space continuous-variable secure quantum communication. New J. Phys. 2019, 21, 123036. [Google Scholar] [CrossRef]
- Vasylyev, D.; Semenov, A.A.; Vogel, W.; Günthner, K.; Thurn, A.; Bayraktar, Ö.; Marquardt, C. Free-space quantum links under diverse weather conditions. Phys. Rev. A 2017, 96, 043856. [Google Scholar] [CrossRef] [Green Version]
- Hulst, H.C.; van de Hulst, H.C. Light Scattering by Small Particles, 1st ed.; Dover: New York, NY, USA, 1981. [Google Scholar]
- Xiang, Y.; Wang, Y.; Ruan, X.; Zuo, Z.; Guo, Y. Improving the discretely modulated underwater continuous-variable quantum key distribution with heralded hybrid linear amplifier. Phys. Scr. 2021, 96, 065103. [Google Scholar] [CrossRef]
- Holevo, A.S.; Werner, R.F. Evaluating capacities of bosonic Gaussian channels. Phys. Rev. A 2001, 63, 032312. [Google Scholar] [CrossRef] [Green Version]
- Hu, L.; Al-amri, M.; Liao, Z.; Zubairy, M.S. Continuous-variable quantum key distribution with non-Gaussian operations. Phys. Rev. A 2020, 102, 012608. [Google Scholar] [CrossRef]
- Maniscalco, S.; Piilo, J.; Intravaia, F.; Petruccione, F.; Messina, A. Lindblad-and non-Lindblad-type dynamics of a quantum Brownian particle. Phys. Rev. A 2004, 70, 032113. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Li, Y.; Wang, Y.; Mao, Y.; Zuo, Z.; Ruan, X.; Guo, Y. Noiseless Attenuation for Continuous-Variable Quantum Key Distribution over Ground-Satellite Uplink. Appl. Sci. 2021, 11, 11289. https://doi.org/10.3390/app112311289
Xu S, Li Y, Wang Y, Mao Y, Zuo Z, Ruan X, Guo Y. Noiseless Attenuation for Continuous-Variable Quantum Key Distribution over Ground-Satellite Uplink. Applied Sciences. 2021; 11(23):11289. https://doi.org/10.3390/app112311289
Chicago/Turabian StyleXu, Shengjie, Yin Li, Yijun Wang, Yun Mao, Zhiyue Zuo, Xinchao Ruan, and Ying Guo. 2021. "Noiseless Attenuation for Continuous-Variable Quantum Key Distribution over Ground-Satellite Uplink" Applied Sciences 11, no. 23: 11289. https://doi.org/10.3390/app112311289
APA StyleXu, S., Li, Y., Wang, Y., Mao, Y., Zuo, Z., Ruan, X., & Guo, Y. (2021). Noiseless Attenuation for Continuous-Variable Quantum Key Distribution over Ground-Satellite Uplink. Applied Sciences, 11(23), 11289. https://doi.org/10.3390/app112311289






