Optimization of Carsharing Fleet Placement in Round-Trip Carsharing Service
Abstract
:1. Introduction
- Developing a concept of station and their locations that maximize user coverage while giving a certain degree of flexibility when returning a car;
- Maintaining the right balance between user coverage and ease of access to the service;
- Considering or designing a suitable metric which can be used to determine the ease of access for users at a global scale.
2. Related Work
2.1. Fleet Placement and Location Problems
2.2. Shared Fleet Placement
2.3. Existing Resolution Approaches
3. Optimization Model
- Utilizing graph theory to implement graph model representing a street network
- Multiobjective Optimization model with two objectives, maximizing user coverage and minimizing global walking distance between cars and users
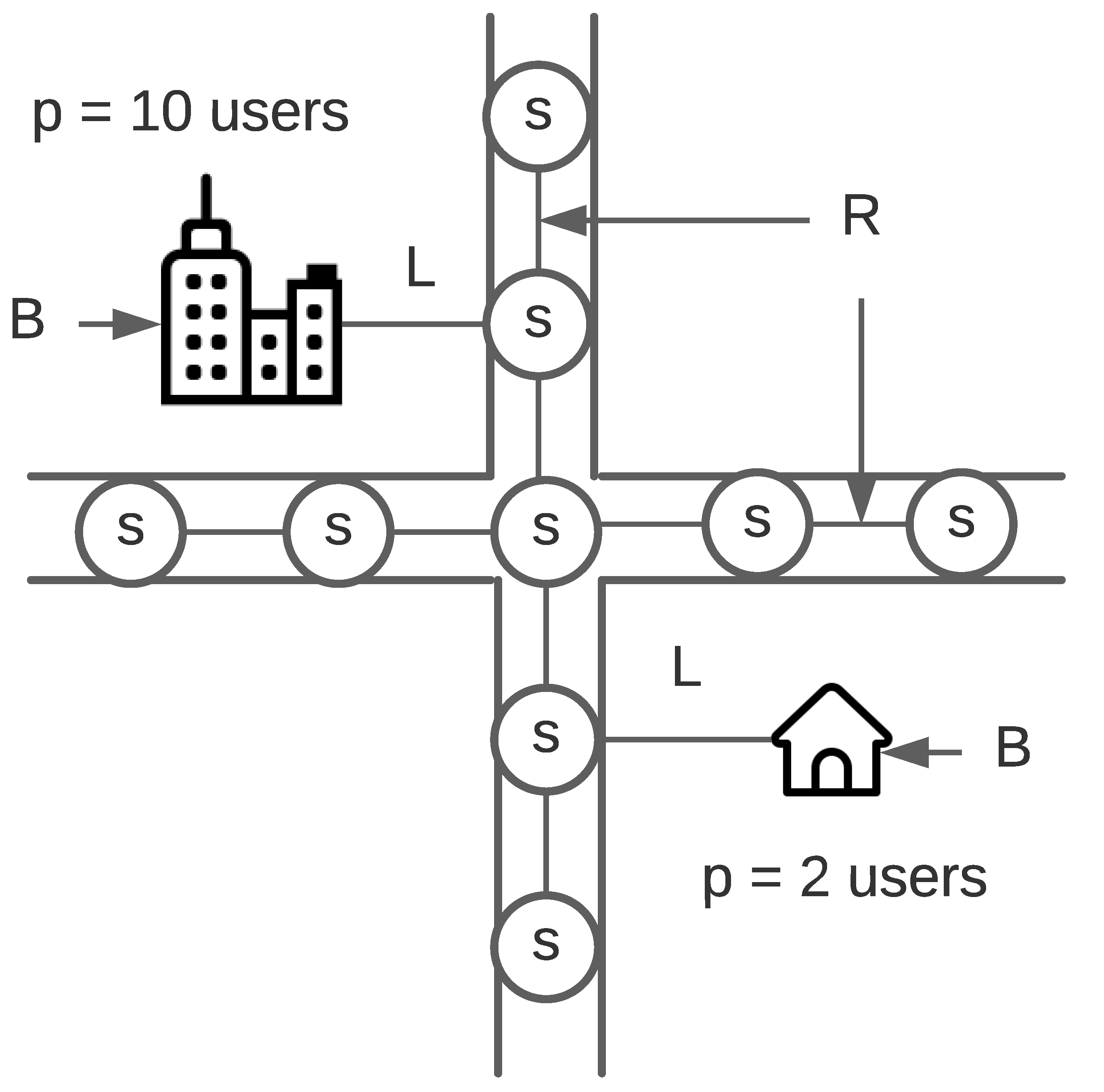
3.1. Graph Instance Definition
3.2. Fleet Placement Problem
3.2.1. FPP Parameters
3.2.2. FPP Variables
3.2.3. FPP Objectives
3.3. NP-Hardness Proof
4. Optimization Methods
4.1. PolySCIP
4.2. Heuristic Algorithms
| Algorithm 1: Greedy search algorithm |
 |
| Algorithm 2: Iterative search algorithm |
 |
- Coverage-focused greedy algorithm;
- Distance-focused greedy algorithm;
- Bi-objective-focused greedy algorithm;
- Coverage-focused iterative algorithm;
- Distance-focused iterative algorithm;
- Bi-objective-focused iterative algorithm.
4.3. Non-Dominated Sorting Genetic Algorithm-II (NSGA-II)
| Algorithm 3: Nondominated Sorting Genetic Algorithm (NSGA-II) |
 |
4.4. Multi-Objective Performance Metrics
5. Execution of the Proposed Model
5.1. Building Graph Instances
5.2. Problem Instances
5.3. Algorithms Implementation and Parameters
6. Results
6.1. Result of LU1 Instance
6.2. Result of LU2 Instance
6.3. Result of MU1 Instance
6.4. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- CarsharingNews. Carsharing Anbieter. 2019. Available online: https://www.carsharing-news.de/carsharing-anbieter/ (accessed on 3 April 2019).
- Deloitte. Car Sharing in Europe: Business Models, National Variations and Upcoming Disruptions. 2017. Available online: https://www2.deloitte.com/content/dam/Deloitte/de/Documents/consumer-industrial-products/CIP-Automotive-Car-Sharing-in-Europe.pdf (accessed on 29 August 2017).
- Luè, A.; Colorni, A.; Nocerino, R.; Paruscio, V. Green move: An innovative electric vehicle-sharing system. Procedia-Soc. Behav. Sci. 2012, 48, 2978–2987. [Google Scholar] [CrossRef] [Green Version]
- Reichert, A.; Holz-Rau, C. Mode use in long-distance travel. J. Transp. Land Use 2015, 8, 87–105. [Google Scholar] [CrossRef] [Green Version]
- Church, R.; ReVelle, C. The maximal covering location problem. In Papers of the Regional Science Association; Springer: Berlin/Heidelberg, Germany, 1974; Volume 32, pp. 101–118. [Google Scholar]
- Megiddo, N.; Supowit, K.J. On the complexity of some common geometric location problems. SIAM J. Comput. 1984, 13, 182–196. [Google Scholar] [CrossRef]
- Seargeant, D.B. The Maximal Covering Location Problem: An Application in Reproductive Health Services. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 2012. [Google Scholar]
- Schmid, V.; Doerner, K.F. Ambulance location and relocation problems with time-dependent travel times. Eur. J. Oper. Res. 2010, 207, 1293–1303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghaffarinasab, N.; Motallebzadeh, A. Hub interdiction problem variants: Models and metaheuristic solution algorithms. Eur. J. Oper. Res. 2018, 267, 496–512. [Google Scholar] [CrossRef]
- Xiao, N.; Bennett, D.A.; Armstrong, M.P. Using evolutionary algorithms to generate alternatives for multiobjective site-search problems. Environ. Plan. A 2002, 34, 639–656. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Murray, A.T. Enhancing spatial representation in primary and secondary coverage location modeling. J. Reg. Sci. 2008, 48, 745–768. [Google Scholar] [CrossRef]
- Malekpoor, H.; Chalvatzis, K.; Mishra, N.; Ramudhin, A. A hybrid approach of vikor and bi-objective integer linear programming for electrification planning in a disaster relief camp. Ann. Oper. Res. 2018, 283, 443–469. [Google Scholar] [CrossRef] [Green Version]
- Megiddo, N.; Tamir, A. On the complexity of locating linear facilities in the plane. Oper. Res. Lett. 1982, 1, 194–197. [Google Scholar] [CrossRef]
- Laporte, G.; Nickel, S.; da Gama, F.S. Location Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 528. [Google Scholar]
- Sakai, T.; Kawamura, K.; Hyodo, T. The relationship between commodity types, spatial characteristics, and distance optimality of logistics facilities. J. Transp. Land Use 2018, 11, 575–591. [Google Scholar] [CrossRef] [Green Version]
- Razi, N.; Karatas, M. A multi-objective model for locating search and rescue boats. Eur. J. Oper. Res. 2016, 254, 279–293. [Google Scholar] [CrossRef]
- Raisanen, L.; Whitaker, R.M. Comparison and evaluation of multiple objective genetic algorithms for the antenna placement problem. Mob. Netw. Appl. 2005, 10, 79–88. [Google Scholar] [CrossRef]
- Vasquez, M.; Hao, J.K. A heuristic approach for antenna positioning in cellular networks. J. Heuristics 2001, 7, 443–472. [Google Scholar] [CrossRef] [Green Version]
- Awasthi, A.; Breuil, D.; Chauhan, S.S.; Parent, M.; Reveillere, T. A multicriteria decision making approach for carsharing stations selection. J. Decis. Syst. 2007, 16, 57–78. [Google Scholar] [CrossRef]
- Kumar, P.; Bierlaire, M. Optimizing locations for a vehicle sharing system. In Proceedings of the Swiss Transport Research Conference, Number EPFL-CONF-195890, Ascona, Switzerland, 2–4 May 2012. [Google Scholar]
- Boyacı, B.; Zografos, K.G.; Geroliminis, N. An optimization framework for the development of efficient one-way car-sharing systems. Eur. J. Oper. Res. 2015, 240, 718–733. [Google Scholar] [CrossRef] [Green Version]
- Lage, M.; Machado, C.; Berssaneti, F.; Quintanilha, J. A method to define the spatial stations location in a carsharing system in São Paulo–Brazil. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-4/W11, 27–32. [Google Scholar] [CrossRef] [Green Version]
- Schwer, J.; Timpf, S. Local-Level Site-Selection Model for Integrated Carsharing Services. GI_Forum 2016, 4, 243–249. [Google Scholar] [CrossRef] [Green Version]
- Calık, H.; Fortz, B. Location of stations in a one-way electric car sharing system. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; pp. 134–139. [Google Scholar]
- Jiao, Z.; Ran, L.; Chen, J.; Meng, H.; Li, C. Data-driven approach to operation and location considering range anxiety of one-way electric vehicles sharing system. Energy Procedia 2017, 105, 2287–2294. [Google Scholar] [CrossRef]
- Brandstätter, G.; Kahr, M.; Leitner, M. Determining optimal locations for charging stations of electric car-sharing systems under stochastic demand. Transp. Res. Part B Methodol. 2017, 104, 17–35. [Google Scholar] [CrossRef]
- Yıldız, B.; Olcaytu, E.; Şen, A. The urban recharging infrastructure design problem with stochastic demands and capacitated charging stations. Transp. Res. Part B Methodol. 2019, 119, 22–44. [Google Scholar] [CrossRef]
- Datner, S.; Raviv, T.; Tzur, M.; Chemla, D. Setting inventory levels in a bike sharing network. Transp. Sci. 2017, 53, 62–76. [Google Scholar] [CrossRef] [Green Version]
- García-Palomares, J.C.; Gutiérrez, J.; Latorre, M. Optimizing the location of stations in bike-sharing programs: A GIS approach. Appl. Geogr. 2012, 35, 235–246. [Google Scholar] [CrossRef]
- Liu, J.; Li, Q.; Qu, M.; Chen, W.; Yang, J.; Xiong, H.; Zhong, H.; Fu, Y. Station site optimization in bike sharing systems. In Proceedings of the 2015 IEEE International Conference on Data Mining, Atlantic City, NJ, USA, 14–17 November 2015; pp. 883–888. [Google Scholar]
- Raviv, T.; Tzur, M.; Forma, I.A. Static repositioning in a bike-sharing system: Models and solution approaches. EURO J. Transp. Logist. 2013, 2, 187–229. [Google Scholar] [CrossRef] [Green Version]
- Romero, J.P.; Ibeas, A.; Moura, J.L.; Benavente, J.; Alonso, B. A simulation-optimization approach to design efficient systems of bike-sharing. Procedia-Soc. Behav. Sci. 2012, 54, 646–655. [Google Scholar] [CrossRef] [Green Version]
- Talbi, E.G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 74. [Google Scholar]
- Efroymson, M.; Ray, T. A branch-bound algorithm for plant location. Oper. Res. 1966, 14, 361–368. [Google Scholar] [CrossRef]
- Manopiniwes, W.; Irohara, T. Stochastic optimisation model for integrated decisions on relief supply chains: Preparedness for disaster response. Int. J. Prod. Res. 2017, 55, 979–996. [Google Scholar] [CrossRef]
- Zarandi, M.F.; Davari, S.; Sisakht, S.H. The large scale maximal covering location problem. Sci. Iran. 2011, 18, 1564–1570. [Google Scholar] [CrossRef]
- CPLEX, I.I. V12. 1: User’s Manual for CPLEX. Int. Bus. Mach. Corp. 2009, 46, 157. [Google Scholar]
- Galvão, R.D.; ReVelle, C. A Lagrangean heuristic for the maximal covering location problem. Eur. J. Oper. Res. 1996, 88, 114–123. [Google Scholar] [CrossRef]
- Gendron, B.; Khuong, P.V.; Semet, F. A Lagrangian-based branch-and-bound algorithm for the two-level uncapacitated facility location problem with single-assignment constraints. Transp. Sci. 2016, 50, 1286–1299. [Google Scholar] [CrossRef] [Green Version]
- Gendreau, M.; Laporte, G.; Semet, F. Solving an ambulance location model by tabu search. Locat. Sci. 1997, 5, 75–88. [Google Scholar] [CrossRef]
- Murray, A.T.; Church, R.L. Applying simulated annealing to location-planning models. J. Heuristics 1996, 2, 31–53. [Google Scholar] [CrossRef]
- Ho, S.C. An iterated tabu search heuristic for the single source capacitated facility location problem. Appl. Soft Comput. 2015, 27, 169–178. [Google Scholar] [CrossRef]
- Ye, F.; Zhao, Q.; Xi, M.; Dessouky, M. Chinese National Emergency Warehouse Location Research based on VNS Algorithm. Electron. Notes Discret. Math. 2015, 47, 61–68. [Google Scholar] [CrossRef]
- Karasakal, E.; Silav, A. A multi-objective genetic algorithm for a bi-objective facility location problem with partial coverage. Top 2016, 24, 206–232. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef] [Green Version]
- RanjbarTezenji, F.; Mohammadi, M.; Pasandideh, S.H.R. Bi-objective location-allocation-inventory-network design in a two-echelon supply chain using de novo programming, NSGA-II and NRGA. Int. J. Logist. Syst. Manag. 2017, 28, 308–337. [Google Scholar] [CrossRef]
- de Almeida Correia, G.H.; Antunes, A.P. Optimization approach to depot location and trip selection in one-way carsharing systems. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 233–247. [Google Scholar] [CrossRef]
- Asamer, J.; Reinthaler, M.; Ruthmair, M.; Straub, M.; Puchinger, J. Optimizing charging station locations for urban taxi providers. Transp. Res. Part A Policy Pract. 2016, 85, 233–246. [Google Scholar] [CrossRef] [Green Version]
- Mourad, A.; Puchinger, J.; Chu, C. A survey of models and algorithms for optimizing shared mobility. Transp. Res. Part B Methodol. 2019, 123, 323–346. [Google Scholar] [CrossRef]
- Barth, M.; Todd, M. Simulation model performance analysis of a multiple station shared vehicle system. Transp. Res. Part C Emerg. Technol. 1999, 7, 237–259. [Google Scholar] [CrossRef]
- Ströhle, P.; Flath, C.M.; Gärttner, J. Leveraging customer flexibility for car-sharing fleet optimization. Transp. Sci. 2018, 53, 42–61. [Google Scholar] [CrossRef]
- Daniels, R.; Mulley, C. Explaining walking distance to public transport: The dominance of public transport supply. J. Transp. Land Use 2013, 6, 5–20. [Google Scholar] [CrossRef]
- Luxen, D.; Vetter, C. Real-time routing with OpenStreetMap data. In Proceedings of the 19th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, GIS ’11, Chicago, IL, USA, 1–4 November 2011; pp. 513–516. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W. H. Freeman & Co.: New York, NY, USA, 1979. [Google Scholar]
- Karp, R.M. Reducibility among combinatorial problems. In Complexity of Computer Computations; Springer: Berlin/Heidelberg, Germany, 1972; pp. 85–103. [Google Scholar]
- Raz, R.; Safra, S. A Sub-constant Error-probability Low-degree Test, and a Sub-constant Error-probability PCP Characterization of NP. In Proceedings of the Twenty-Ninth Annual ACM Symposium on Theory of Computing, STOC ’97, El Paso, TX, USA, 4–6 May 1997; ACM: New York, NY, USA, 1997; pp. 475–484. [Google Scholar] [CrossRef]
- Borndörfer, R.; Schenker, S.; Skutella, M.; Strunk, T. PolySCIP. In International Congress on Mathematical Software; Springer: Berlin/Heidelberg, Germany, 2016; pp. 259–264. [Google Scholar]
- Fourer, R.; Gay, D.M.; Kernighan, B. Ampl; Boyd & Fraser: Danvers, MA, USA, 1993; Volume 117. [Google Scholar]
- Laumanns, M.; Thiele, L.; Zitzler, E. Running time analysis of evolutionary algorithms on a simplified multiobjective knapsack problem. Nat. Comput. 2004, 3, 37–51. [Google Scholar] [CrossRef]
- Corne, D.W.; Knowles, J.D.; Oates, M.J. The Pareto envelope-based selection algorithm for multiobjective optimization. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 839–848. [Google Scholar]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Van Veldhuizen, D.A. Multiobjective Evolutionary Algorithms: Classifications, Analyses, and New Innovations. Ph.D. Thesis, Wright Patterson AFB, Montgomery County, OH, USA, 1999. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective Evolutionary Algorithms: A Comparative Case Study and the Strength Pareto Approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef] [Green Version]
- OpenStreetMap Contributors. Luxembourg City and Munich City Dump. 2017. Available online: https://www.openstreetmap.org (accessed on 28 June 2018).
- Boeing, G. OSMnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef] [Green Version]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conference (SciPy2008), Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- Frost and Sullivan. Future of Carsharing Market to 2025. 2016. Available online: https://store.frost.com/future-of-carsharing-market-to-2025.html (accessed on 29 August 2017).
- La Ville de Luxembourg. Etat de la Population 2019. 2016. Available online: https://statistiques.public.lu/stat/ReportFolders/ReportFolder.aspx?IF_Language=fra&MainTheme=2&FldrName=1 (accessed on 15 August 2017).
- Fortin, F.A.; De Rainville, F.M.; Gardner, M.A.; Parizeau, M.; Gagné, C. DEAP: Evolutionary Algorithms Made Easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]












| Input Parameters | Description | Type |
|---|---|---|
| f | Maximum number of desired fleet stations. | |
| w | Maximum walking distance allowed. | |
| r | Station area radius. | , |
| Instance Parameters | Description | Type |
|---|---|---|
| n | Number of street nodes. | |
| m | Number of buildings. | |
| i | Index for street nodes | |
| j | Index for buildings | |
| S | Set of street nodes (potential stations) | |
| B | Set of buildings (housing users) | |
| P | Set of population of buildings | . |
| D | Set of walking distances between street nodes and buildings. | |
| Decision Variables | Description | Type |
|---|---|---|
| C | Set of state of buildings | |
| Set of state of street nodes | ||
| z | maximum global walking distance |
| LU1 | LU2 | MU1 | |
|---|---|---|---|
| City | Luxembourg | Luxembourg | Munich |
| Population | 561 | 11,439 | 17,486 |
| Number of carsharing stations (f) | 4 | 10 | 10,072 |
| Number of street nodes | 63 | 2026 | 16,075 |
| Number of residential buildings | 47 | 1063 | 21,816 |
| Maximum walking distance (w) | 150 m | 500 m | 500 m |
| Carsharing station area radius (r) | 0 m | 100 m | 100 m |
| LU1 Instance | LU2 Instance | MU1 Instance | |
|---|---|---|---|
| Number of generations | 400 | 400 | 400 |
| Population size | 20 | 50 | 100 |
| Selection process | Tournament | Tournament | Tournament |
| Crossover method | 2-point crossover | 2-point crossover | 2-point crossover |
| Crossover rate | 0.8 | 0.9 | 0.9 |
| Mutation rate | 0.01 |
| Covered Users | Maximum Walking Distance (Meters) | |
|---|---|---|
| PolySCIP (Best coverage) | 391 | 149.528 |
| PolySCIP (Best distance) | 108 | 93.546 |
| NSGA-II (Best coverage) | 391 | 149.528 |
| NSGA-II (Best distance) | 203 | 106.4 |
| Coverage Heuristic | 348 | 148.491 |
| Distance Heuristic | 187 | 112.398 |
| Bi-objective Heuristic | 333 | 144.515 |
| Coverage Iterative Heuristic | 391 | 149.528 |
| Distance Iterative Heuristic | 87 | 106.4 |
| Bi-objective Iterative Heuristic | 358 | 144.401 |
| IGD | Spread | HV | |
|---|---|---|---|
| Exact method | True Pareto front | 0.488 | 0.449 |
| NSGA-II | 3.02 | 0.525 | 0.351 |
| Algorithm | Coverage Oriented | Distance Oriented | ||
|---|---|---|---|---|
| Covered Users | Walking Distance | Covered Users | Walking Distance | |
| Simple Heuristic | 2100 | 399.8 | 47 | 135.7 |
| Iterative Heuristic | 47 | 135.7 | 231 | 300 |
| NSGA-II | 8421 | 399.8 | 47 | 135.7 |
| Algorithm | Execution Time |
|---|---|
| NSGA-II | 26 min |
| Coverage Heuristic | 7 min |
| Distance Heuristic | 7 min |
| Bi-objective Heuristic | 7 min |
| Coverage Iterative Heuristic | 17 h |
| Distance Iterative Heuristic | 17 h |
| Bi-objective Iterative Heuristic | 17 h |
| Instance | Algorithm | Coverage Oriented | Distance Oriented | ||
|---|---|---|---|---|---|
| Covered Users | Walking Distance | Covered Users | Access Distance | ||
| Simulation | Simple Heuristic | 3421 | 399.4 | 1091 | 378.6 |
| Iterative Heuristic | 14,892 | 399.8 | 1214 | 376.1 | |
| NSGA-II | 14,892 | 399.8 | 1256 | 375.2 | |
| Real-world | Simple Heuristic | 2291 | 399.8 | 1124 | 375.9 |
| Iterative Heuristic | 13,224 | 399.8 | 986 | 374.2 | |
| NSGA-II | 13,224 | 399.8 | 986 | 374.2 | |
| Manual Allocation | 7864 | 399.8 | 7864 | 399.8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Changaival, B.; Lavangnananda, K.; Danoy, G.; Kliazovich, D.; Guinand, F.; Brust, M.; Musial, J.; Bouvry, P. Optimization of Carsharing Fleet Placement in Round-Trip Carsharing Service. Appl. Sci. 2021, 11, 11393. https://doi.org/10.3390/app112311393
Changaival B, Lavangnananda K, Danoy G, Kliazovich D, Guinand F, Brust M, Musial J, Bouvry P. Optimization of Carsharing Fleet Placement in Round-Trip Carsharing Service. Applied Sciences. 2021; 11(23):11393. https://doi.org/10.3390/app112311393
Chicago/Turabian StyleChangaival, Boonyarit, Kittichai Lavangnananda, Grégoire Danoy, Dzmitry Kliazovich, Frédéric Guinand, Matthias Brust, Jedrzej Musial, and Pascal Bouvry. 2021. "Optimization of Carsharing Fleet Placement in Round-Trip Carsharing Service" Applied Sciences 11, no. 23: 11393. https://doi.org/10.3390/app112311393
APA StyleChangaival, B., Lavangnananda, K., Danoy, G., Kliazovich, D., Guinand, F., Brust, M., Musial, J., & Bouvry, P. (2021). Optimization of Carsharing Fleet Placement in Round-Trip Carsharing Service. Applied Sciences, 11(23), 11393. https://doi.org/10.3390/app112311393









