Analysis of Interference-Fit Joints
Abstract
:1. Introduction
2. Materials and Methods
3. Results of Numerical Calculations and Experimental Studies
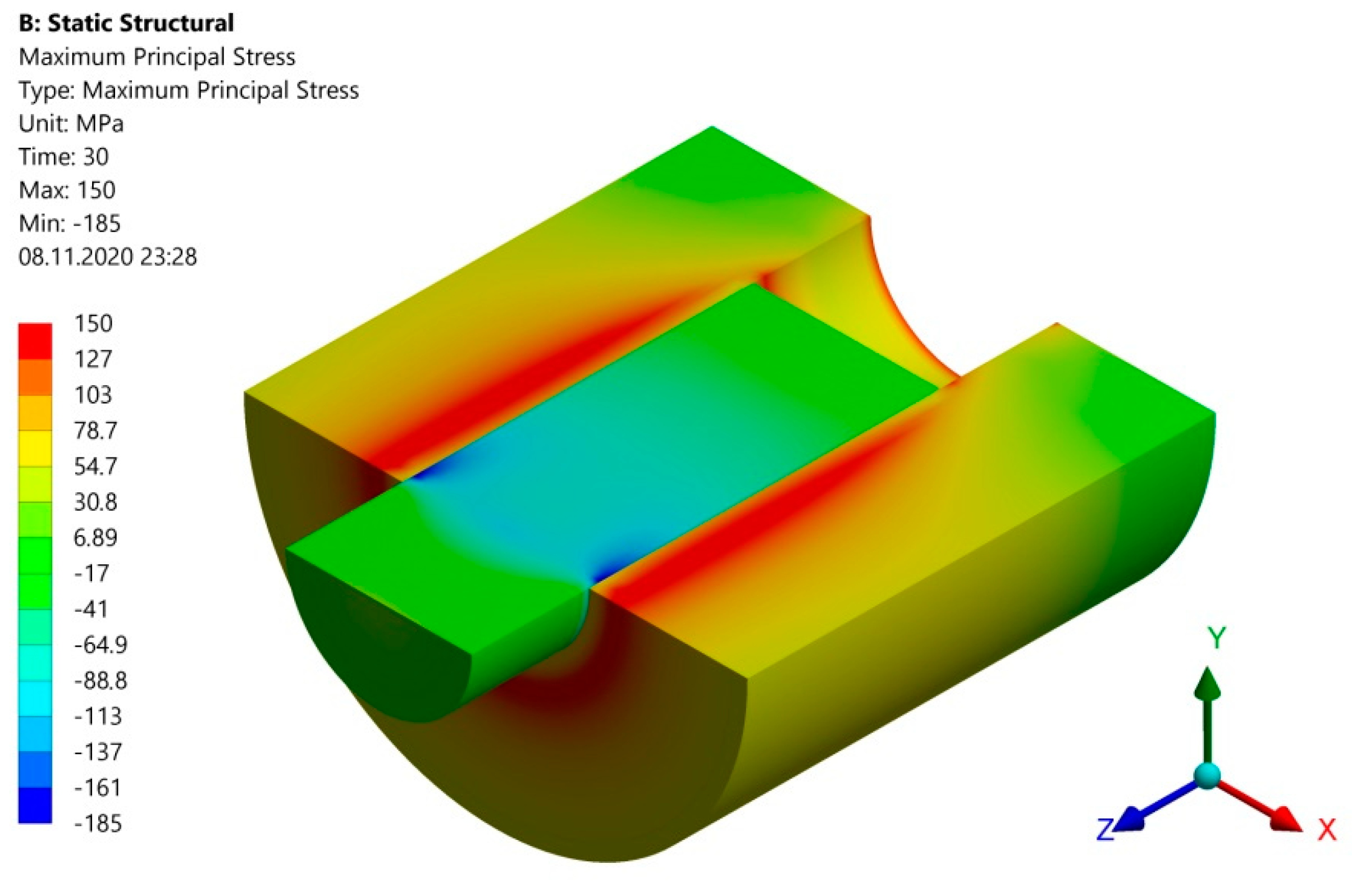
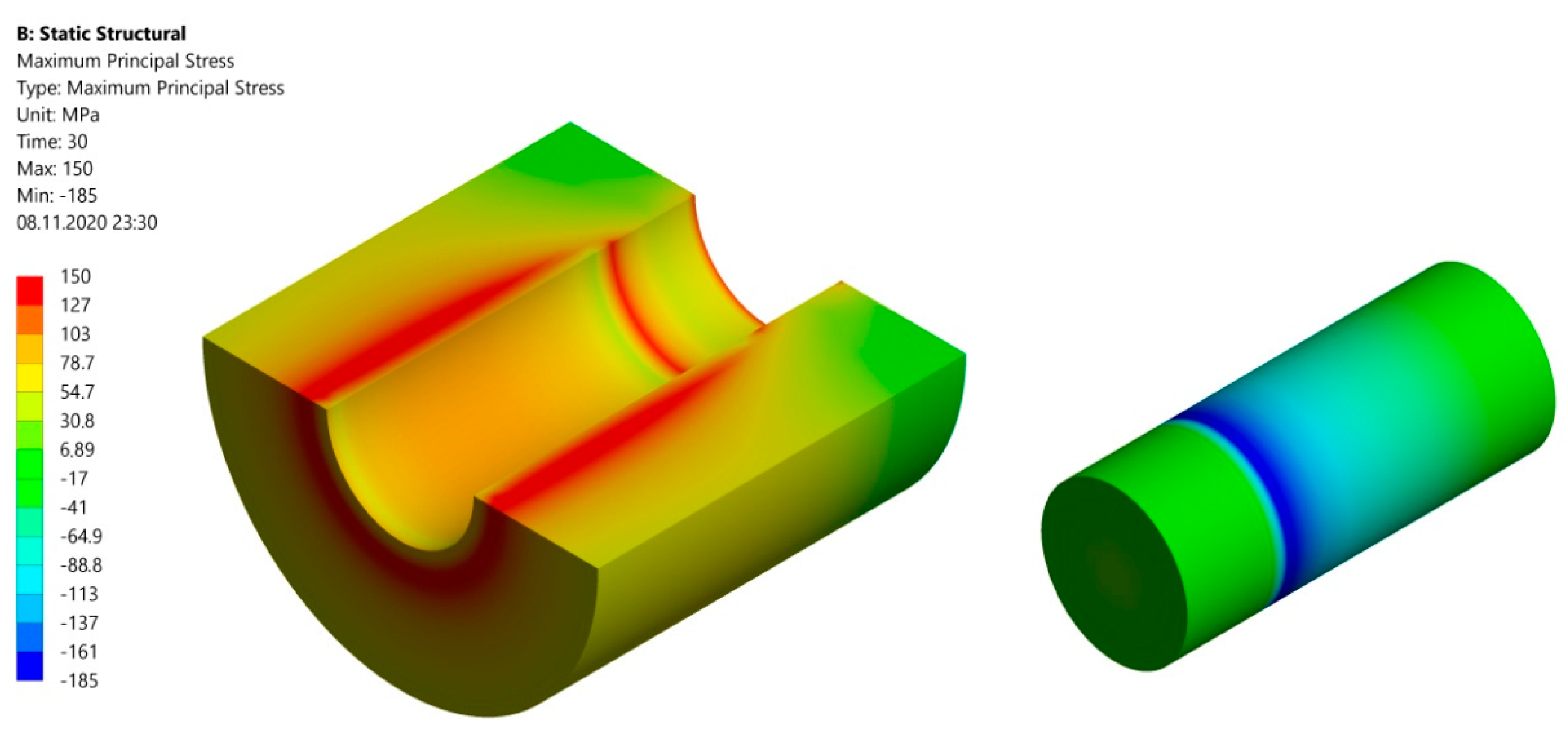
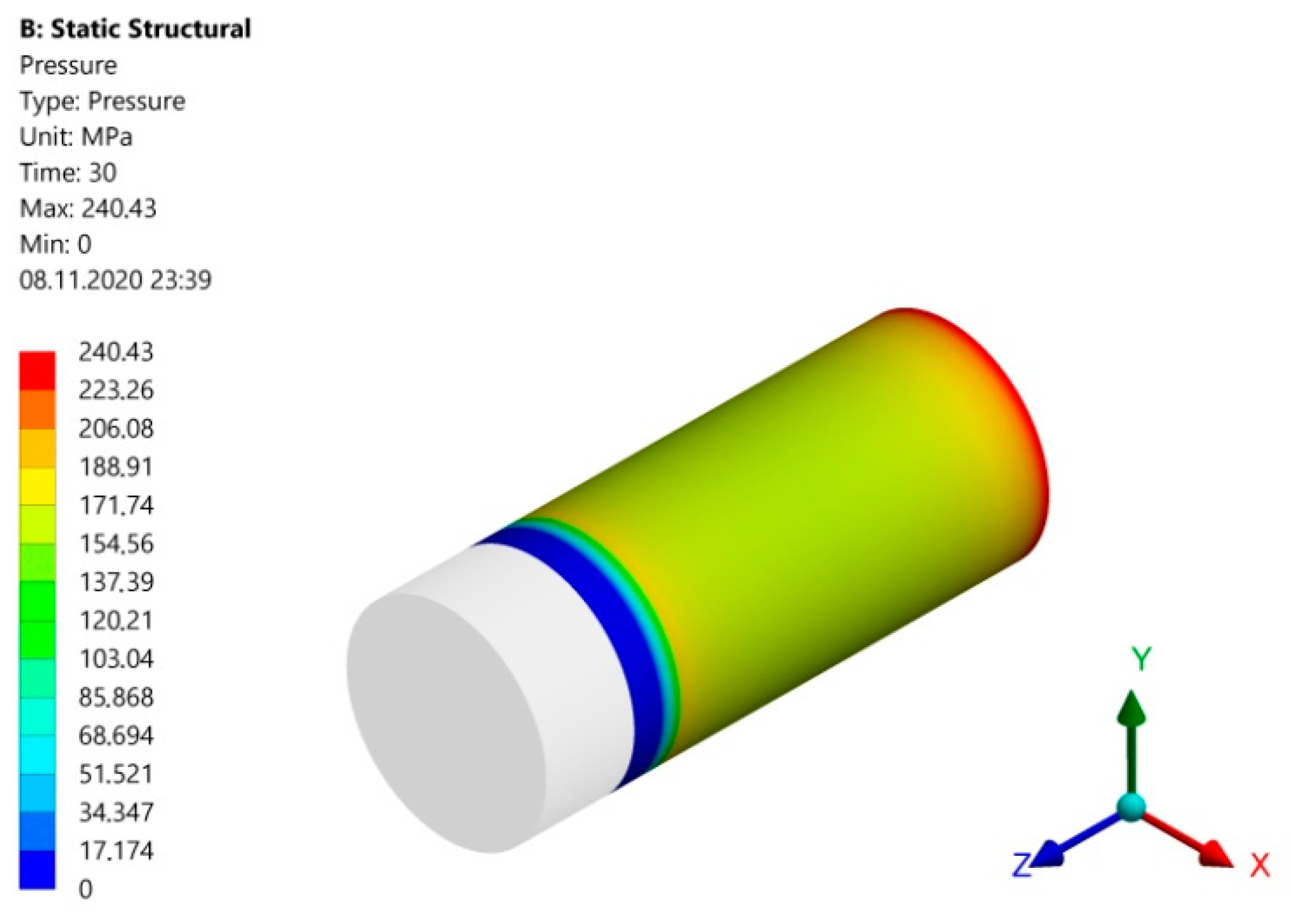
3.1. Numerical Simulation of the Pressing Process
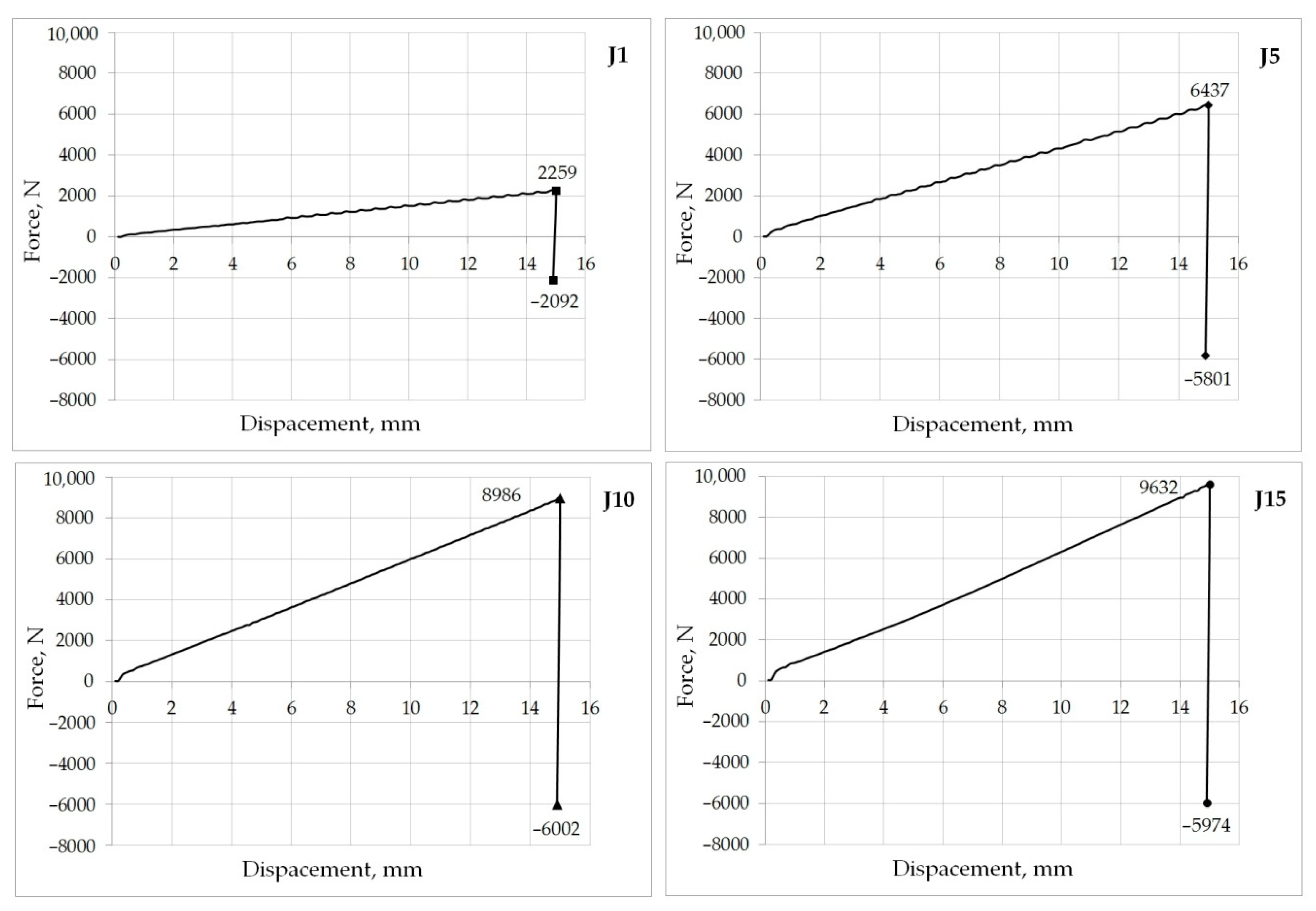
3.2. Experimental Verification
4. Conclusions
- A large convergence of breaking force value obtained from the numerical simulation with the mean value of this force obtained from experimental tests confirmed the correctness of the numerical model.
- Even though in J1 and J2 joint the pressures in the contact zone are in the elastic range (no plastic strain), the difference between the value of the force breaking the joint calculated from formulas (2 and 4) and the value of the force obtained from numerical simulations is 1707 N (for J2 3137−1430 = 1707 N), which gives a relative percentage error of 54%.
- As shown by numerical simulations in J3-J15 joints, surface pressures exceeding the value of the yield point appear in contact zones. This is accompanied by the formation of plastic strains, which leads to the conclusion that the load capacity of the joint cannot be determined from Formula (2) based on the solution of the linear-elastic Lame’s problem.
- As results from numerical simulations for J3–J15 joints, increasing interference increases the value of the assembly force of the joint, but does not significantly increase the value of the joint breaking force. The observation is in line with those in the paper [10]. This is due to the plasticization of the entire contact surface occurring along the entire length of the joint and continuing deeper into the joined elements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, G.M.; Coquille, J.C.; Fontaine, J.F.; Lambertin, M. Contact pressure between two rough surfaces of a cylindrical fit. J. Mater. Process. Technol. 2002, 123, 490–497. [Google Scholar] [CrossRef]
- Wang, X.; Lou, Z.; Wang, X.; Xua, C. A new analytical method for press-fit curve prediction of interference fitting parts. J. Mater. Process. Technol. 2017, 250, 16–24. [Google Scholar] [CrossRef]
- Lewis, R.; Marshall, M.B.; Dwyer-Joyce, R.S. Measurement of interface pressure in interference fits. J. Mech. Eng. Sci. 2005, 219, 127–139. [Google Scholar] [CrossRef] [Green Version]
- Shigley, J.E.; Mischke, C.R. Standard Handbook of Machine Design, 2nd ed.; McGraw-Hill: New York, NY, USA, 1996; pp. 607–619. ISBN 0-07-056958-4. [Google Scholar]
- Lanoue, F.; Vadean, A.; Sanschagrin, B. Finite element analysis and contact modeling considerations of interference fits for fretting fatigue strength calculations. Simul. Model. Pract. Theory 2009, 17, 1587–1602. [Google Scholar] [CrossRef]
- Meerkamm, H. Schaeffler Technical Pocket Guide, 1st ed.; Schaeffler Technologies GmbH & Co. KG: Herzogenaurach, Germany, 2014; pp. 432–433. [Google Scholar]
- Cajuhi, A.J.; Pepe, I.M.; Moreno, D.M. Using finite element analysis and strain gauge experimental data to evaluate stress concentration factor on press-fit assembly. In Proceedings of the 20th International Congress of Mechanical Engineering, Gramado, Brazil, 15–20 November 2009; pp. 15–20. [Google Scholar]
- Croccolo, D.; Vincenzi, N. Stress concentration factors in compression–fit couplings. J. Mech. Eng. Sci. 2010, 224, 1143–1152. [Google Scholar] [CrossRef]
- Gallio, G.; Marcuccio, G.; Bonisoli, E.; Tornincasa, S.; Pezzini, D.; Ugues, D.; Lombardi, M.; Rovarino, D.; Fino, P.; Montanaro, L. Study of the interference contribution on the performance of an adhesive bonded press-fitted cylindrical joint. Int. J. Adhes. Adhes. 2014, 53, 89–96. [Google Scholar] [CrossRef]
- Hüyük, H.; Music, O.; Koç, A.; Karadogan, C.; Bayram, Ç. Analysis of elastic-plastic interference-fit joints. In Proceedings of the 11th International Conference on Technology of Plasticity, Nagoya, Japan, 19–24 October 2014; pp. 2030–2035. [Google Scholar]
- Sinitsyna, V.; Sinitsyn, A. Finite-Element Analysis of Parts Stress State of Tight Joint Assembled by Press Fitting. Mod. Mech. Eng. 2014, 4, 198–206. [Google Scholar] [CrossRef] [Green Version]
- McMillan, M.; Booker, J.; Smith, D. Simulation of interference fitted joint strength as used in hot rolling work rolls. In Experimental and Applied Mechanics; Ventura, C.E., Crone, W.C., Furlong, C., Eds.; Springer: New York, NY, USA, 2013; pp. 319–326. ISBN 978-1-4614-4225-7. [Google Scholar]
- Croccolo, D.; De Agostinis, M.; Olmi, G. Fatigue Life Characterisation of Interference Fitted Joints. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition. Volume 2B: Advanced Manufacturing, San Diego, CA, USA, 15–21 November 2013. [Google Scholar] [CrossRef]
- Strozzi, A.; Bertocchi, E.; Baldini, A.; Mantovani, S. Normalization of the stress concentrations at the rounded edges of an interference fit between a solid shaft subjected to bending and a hub. Mech. Based Des. Struct. Mach. 2015, 44, 405–425. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Fini, S.; Olmi, G.; Paiardini, L.; Robusto, F. Influence of the interference level and of the assembly process on the shear strength of loctite 648 anaerobic adhesive. J. Adhes. 2020, 96, 90–112. [Google Scholar] [CrossRef]
- Jakubiec, W.; Płowucha, W.; Rosner, P. Uncertainty of measurement for design engineers. Procedia CIRP 2016, 43, 309–314. [Google Scholar] [CrossRef] [Green Version]
- European Standard: ISO 286-1: 2011—Geometrical Product Specifications (GPS)—ISO Linear Tolerance System—Part 1: Fundamentals of Tolerances, Deviations and Fits. Available online: https://www.iso.org/obp/ui/#iso:std:iso:286:-1:en (accessed on 15 August 2020).
- ANSYS Inc. PDF Documentation for Release 2020 R1. Available online: https://d.shikey.com/down/Ansys.Products.2020.R1.x64/install_docs/Ansys.Products.PDF.Docs.2020R1/readme.html (accessed on 15 August 2020).
- Hirmand, M.; Vahab, M.; Khoei, A.R. An augmented Lagrangian contact formulation for frictional discontinuities with the extended finite element method. Finite Elem. Anal. Des. 2015, 107, 28–43. [Google Scholar] [CrossRef]
- Santos, D.B.V.; Bandeira, A.A. Numerical modeling of contact problems with the finite element method utilizing a B-Spline surface for contact surface smoothing. Lat. Am. J. Solids Struct. 2018, 15, 1–23. [Google Scholar] [CrossRef]
- Gardoń, A. Rozkład statystyki t-Studenta przy danej wariancji z próby o rozkładzie normalnym. Didact. Math. 2011, 12, 17–30. [Google Scholar]
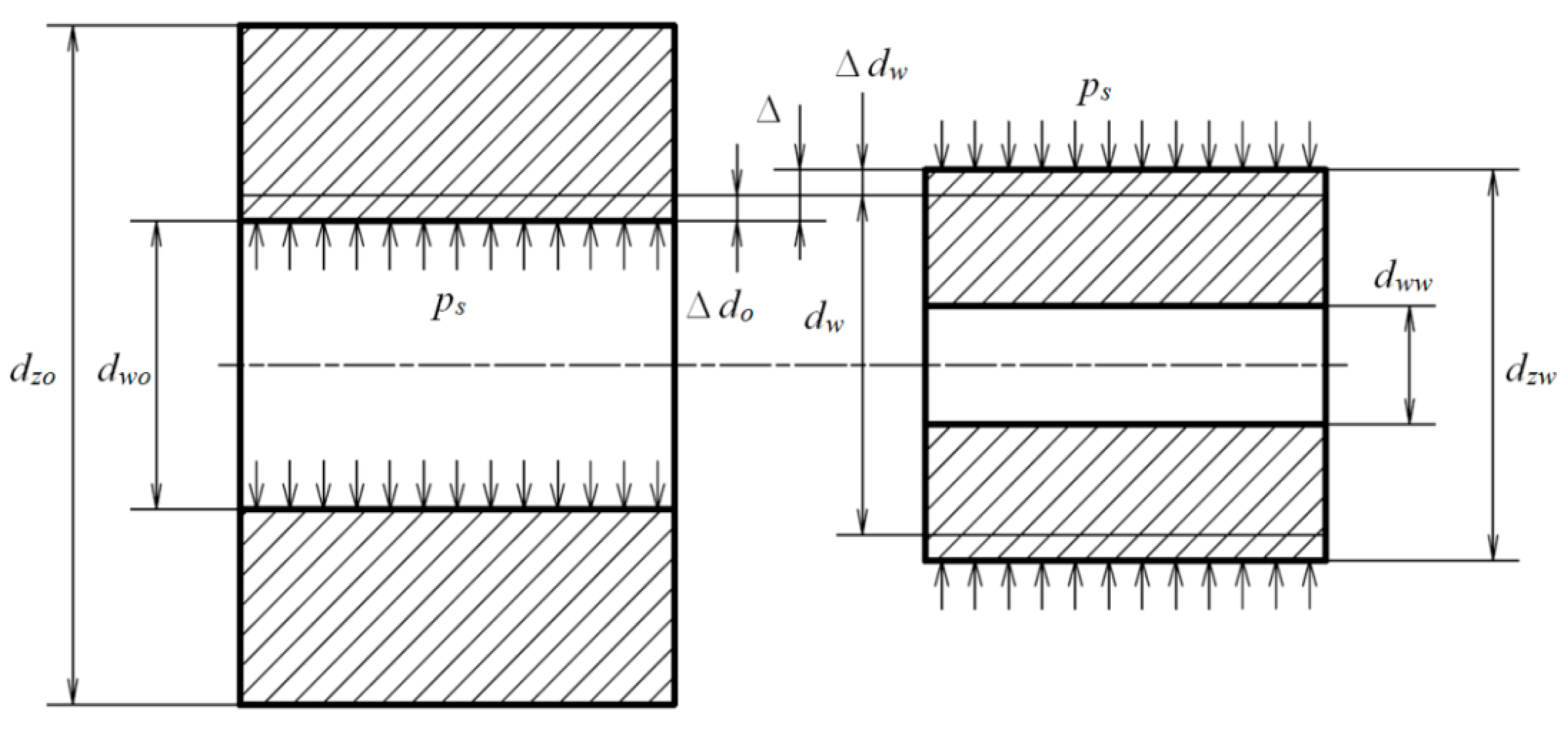
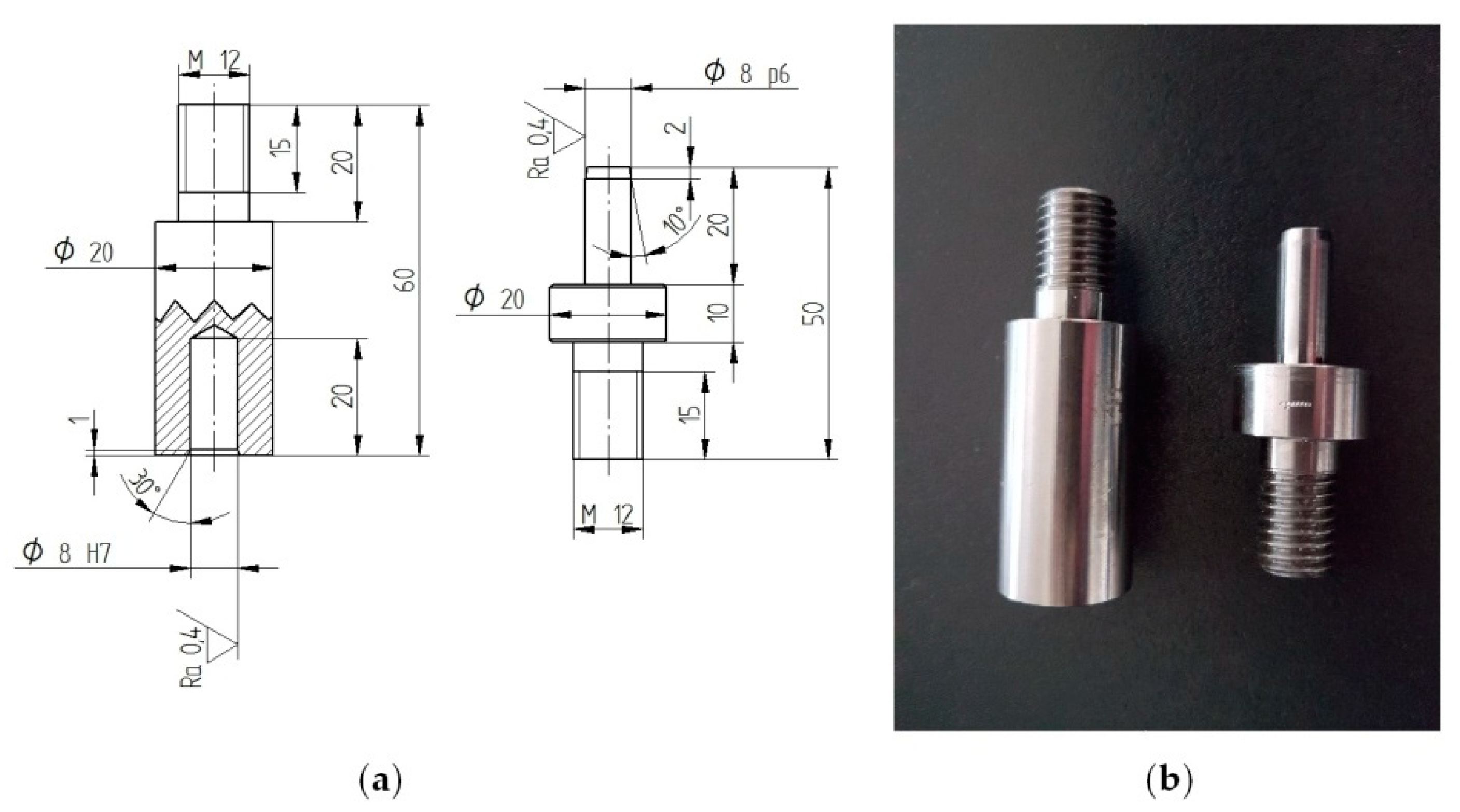

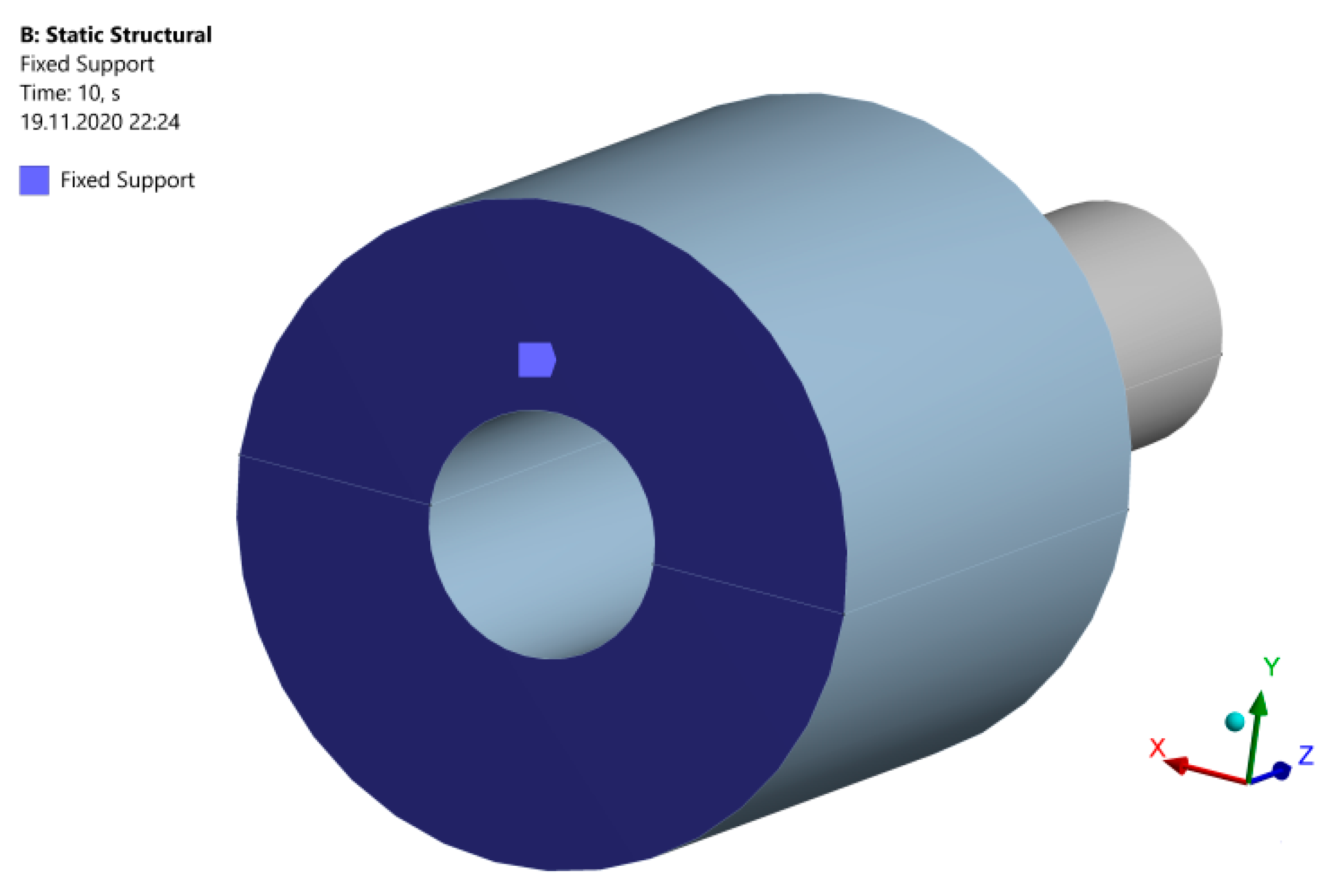






| Joint Symbol | Nominal Diameter of the Joint | Fit | Interference Δ, mm | Type of Fit |
|---|---|---|---|---|
| J1 | ø 8 | H7/k6 | 0.004 | Locational transition fit |
| J2 | 0.006 | |||
| J3 | 0.008 | |||
| J4 | 0.010 | |||
| J5 | H7/p6 | 0.012 | Locational interference fit | |
| J6 | 0.014 | |||
| J7 | 0.016 | |||
| J8 | 0.018 | |||
| J9 | 0.020 | |||
| J10 | H7/s6 | 0.022 | Medium drive fit | |
| J11 | 0.024 | |||
| J12 | 0.026 | |||
| J13 | 0.028 | |||
| J14 | H7/u6 | 0.030 | Force fit | |
| J15 | 0.032 |
| Joint Symbol | Surface Pressure acc. (1), MPa | Breaking Force acc. (2), N | Surface Pressure acc. (4), MPa | Breaking Force acc. (2), N |
|---|---|---|---|---|
| J1 | 44.10 | 1663 | 15.88 | 599 |
| J2 | 66.15 | 2494 | 37.93 | 1430 |
| J3 | 88.20 | 3325 | 59.98 | 2261 |
| J4 | 110.25 | 4156 | 82.03 | 3092 |
| J5 | 132.30 | 4988 | 104.08 | 3924 |
| J6 | 154.35 | 5819 | 126.13 | 4755 |
| J7 | 176.40 | 6650 | 148.18 | 5586 |
| J8 | 198.45 | 7481 | 170.23 | 6417 |
| J9 | 220.50 | 8313 | 192.28 | 7249 |
| J10 | 242.55 | 9144 | 214.33 | 8080 |
| J11 | 264.60 | 9975 | 236.38 | 8911 |
| J12 | 286.65 | 10,806 | 258.43 | 9742 |
| J13 | 308.70 | 11,638 | 280.48 | 10,574 |
| J14 | 330.75 | 12,469 | 302.53 | 11,405 |
| J15 | 352.80 | 13,300 | 324.58 | 12,236 |
| Joint Symbol | Surface Pressure, MPa | Maximum Plastic Strain, mm/mm |
|---|---|---|
| J1 | 81 | 0 |
| J2 | 122 | 0 |
| J3 | 162 | 9.05 × 10–4 |
| J4 | 202 | 4.95 × 10–3 |
| J5 | 240 | 1.09 × 10–2 |
| J6 | 236 | 1.71 × 10–2 |
| J7 | 253 | 2.34 × 10–2 |
| J8 | 263 | 2.97 × 10–2 |
| J9 | 272 | 3.62 × 10–2 |
| J10 | 277 | 4.22 × 10–2 |
| J11 | 277 | 4.91 × 10–2 |
| J12 | 270 | 5.26 × 10–2 |
| J13 | 274 | 5.77 × 10–2 |
| J14 | 283 | 6.05 × 10–2 |
| J15 | 293 | 6.39 × 10–2 |
| Joint Symbol | Interference Δ, mm | FEM Analysis | Lame’s Formula | ||
|---|---|---|---|---|---|
| Assembly Force, N | Breaking Force, N | Breaking Force acc. (1 and 2), N | Breaking Force acc. (4 and 2), N | ||
| J1 | 0.004 | 2293 | 2092 | 1663 | 599 |
| J2 | 0.006 | 3438 | 3137 | 2494 | 1430 |
| J3 | 0.008 | 4516 | 4220 | 3325 | 2261 |
| J4 | 0.010 | 5549 | 5125 | 4156 | 3092 |
| J5 | 0.012 | 6437 | 5801 | 4988 | 3924 |
| J6 | 0.014 | 7174 | 6006 | 5819 | 4755 |
| J7 | 0.016 | 7784 | 6004 | 6650 | 5586 |
| J8 | 0.018 | 8285 | 6010 | 7481 | 6417 |
| J9 | 0.020 | 8682 | 6010 | 8313 | 7249 |
| J10 | 0.022 | 8986 | 6002 | 9144 | 8080 |
| J11 | 0.024 | 9209 | 5999 | 9975 | 8911 |
| J12 | 0.026 | 9373 | 6001 | 10,806 | 9742 |
| J13 | 0.028 | 9474 | 5999 | 11,638 | 10,574 |
| J14 | 0.030 | 9560 | 5960 | 12,469 | 11,405 |
| J15 | 0.032 | 9632 | 5974 | 13,300 | 12,236 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madej, J.; Śliwka, M. Analysis of Interference-Fit Joints. Appl. Sci. 2021, 11, 11428. https://doi.org/10.3390/app112311428
Madej J, Śliwka M. Analysis of Interference-Fit Joints. Applied Sciences. 2021; 11(23):11428. https://doi.org/10.3390/app112311428
Chicago/Turabian StyleMadej, Jerzy, and Mateusz Śliwka. 2021. "Analysis of Interference-Fit Joints" Applied Sciences 11, no. 23: 11428. https://doi.org/10.3390/app112311428
APA StyleMadej, J., & Śliwka, M. (2021). Analysis of Interference-Fit Joints. Applied Sciences, 11(23), 11428. https://doi.org/10.3390/app112311428