Theoretical Analysis for Stability Evaluation of Rock Mass Engineering Structure under Combined Compression-Shear Loading: A Case Study of Inclined Pillar
Abstract
:1. Introduction
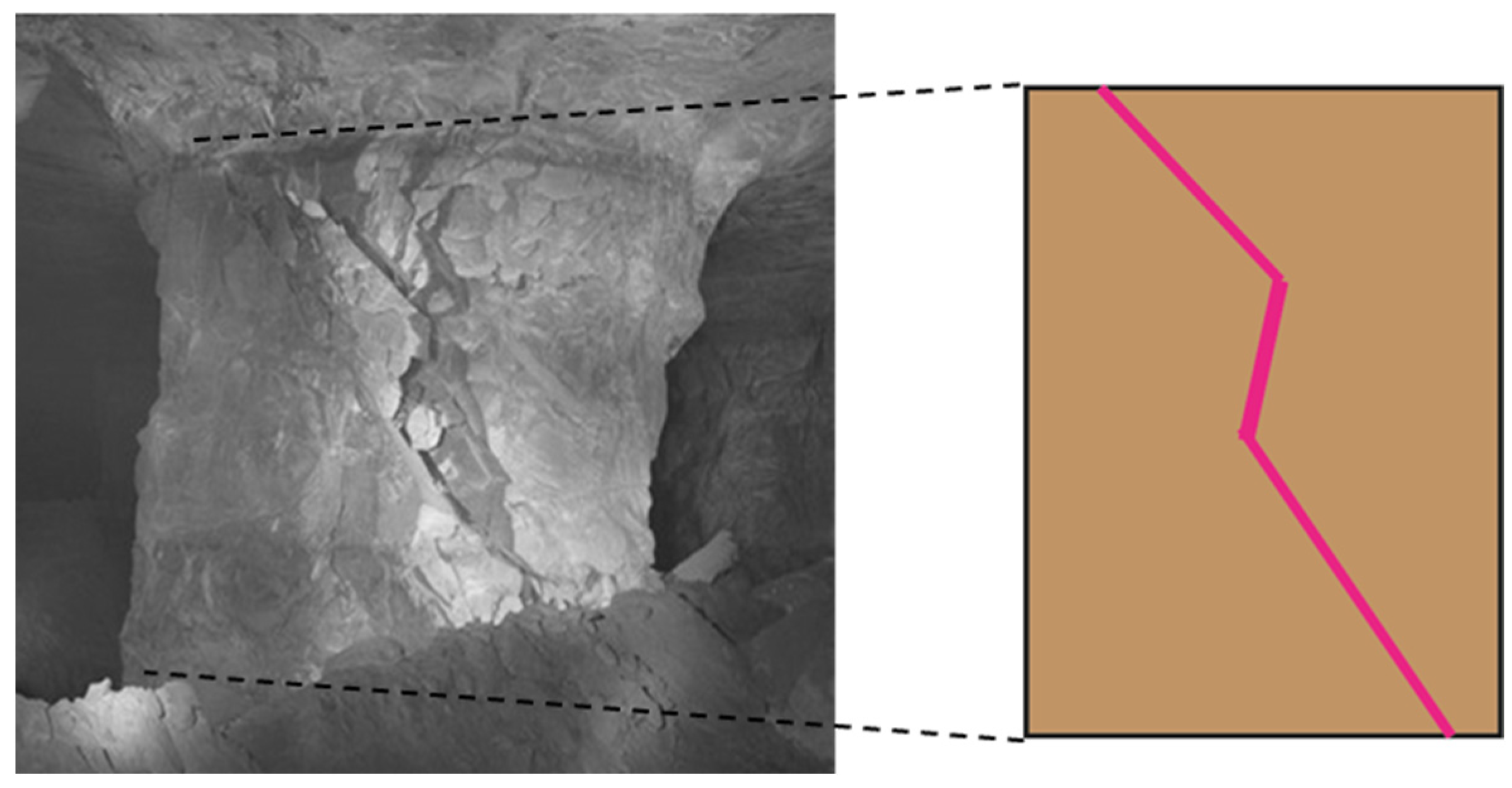
2. Stress State of Inclined Pillar
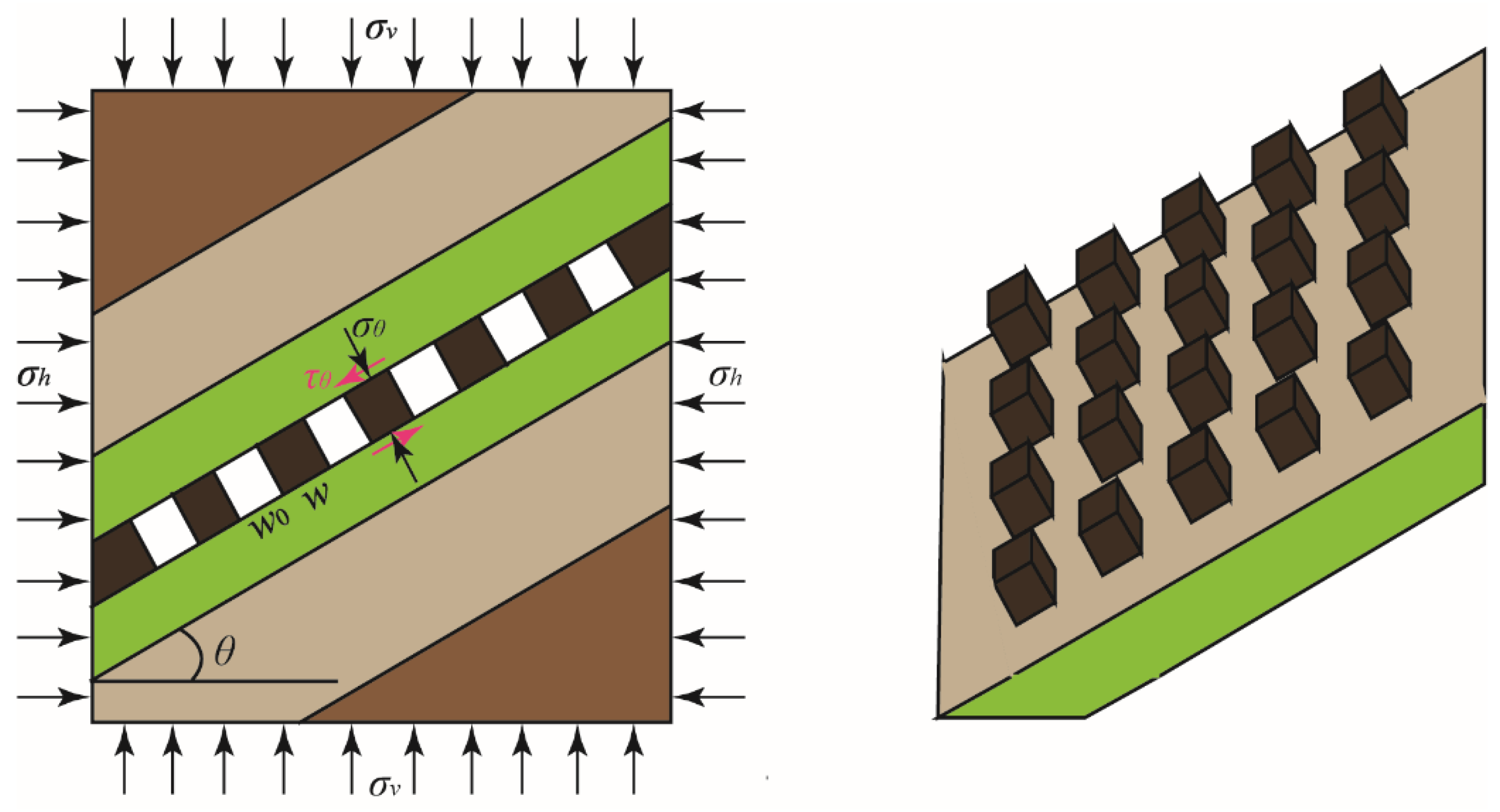
2.1. Load Calculation of Inclined Pillar
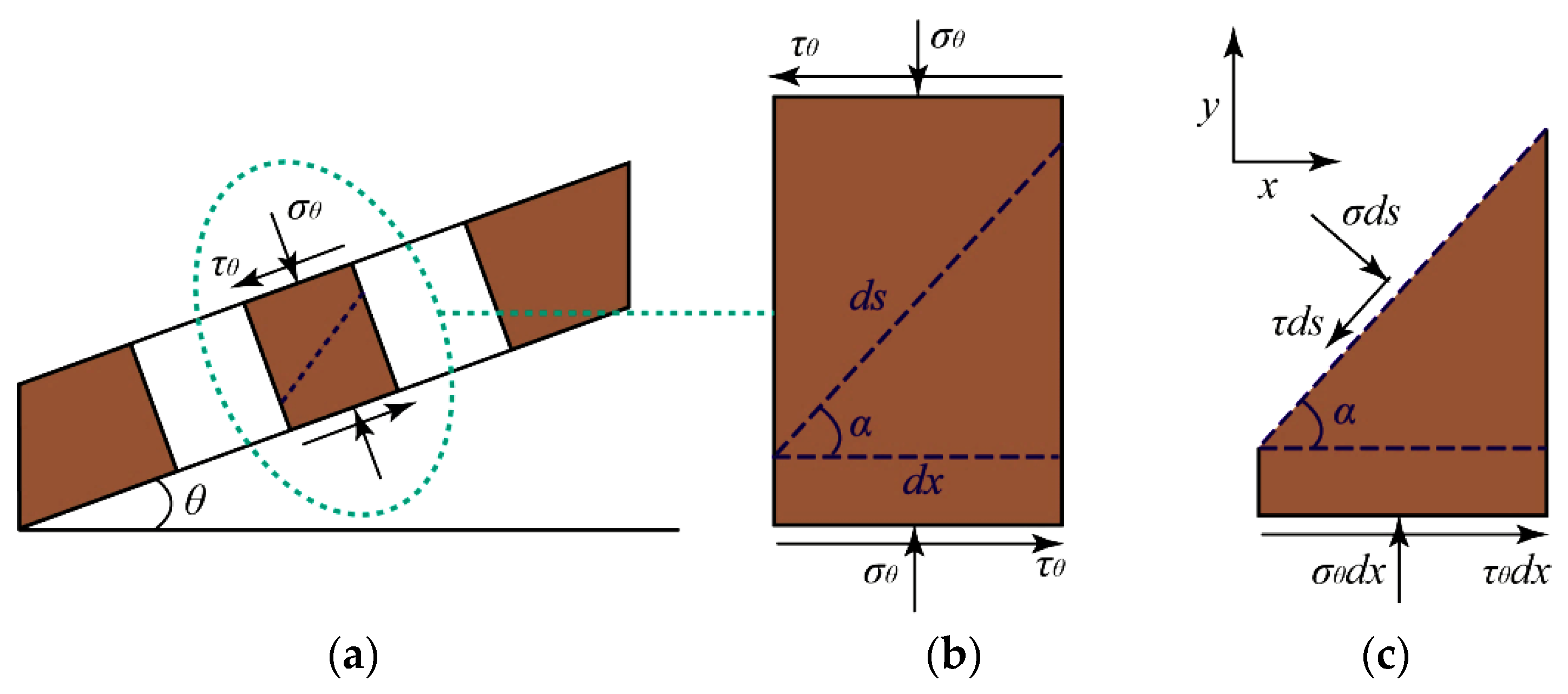
2.2. Stress State Equation of Inclined Pillar
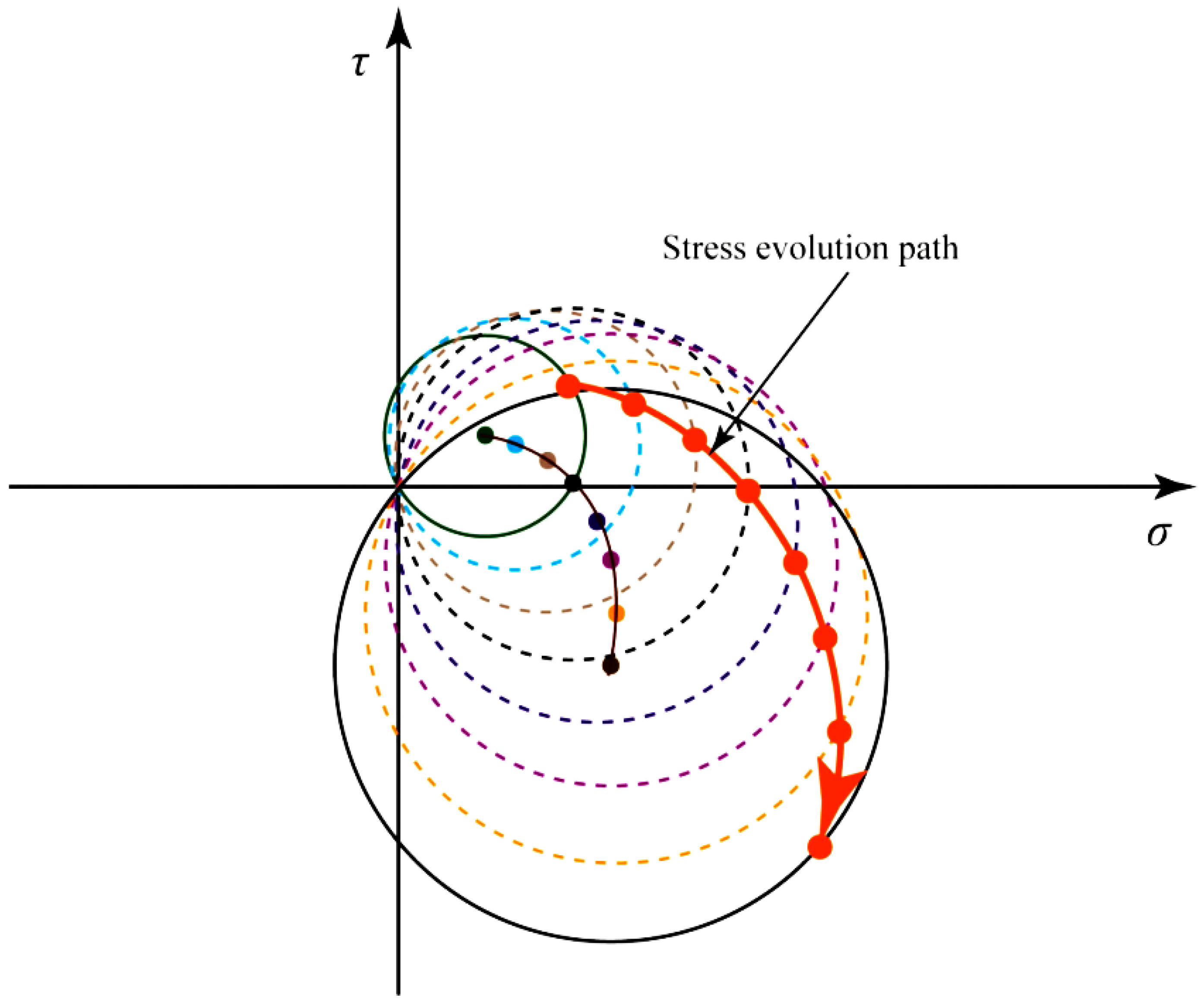
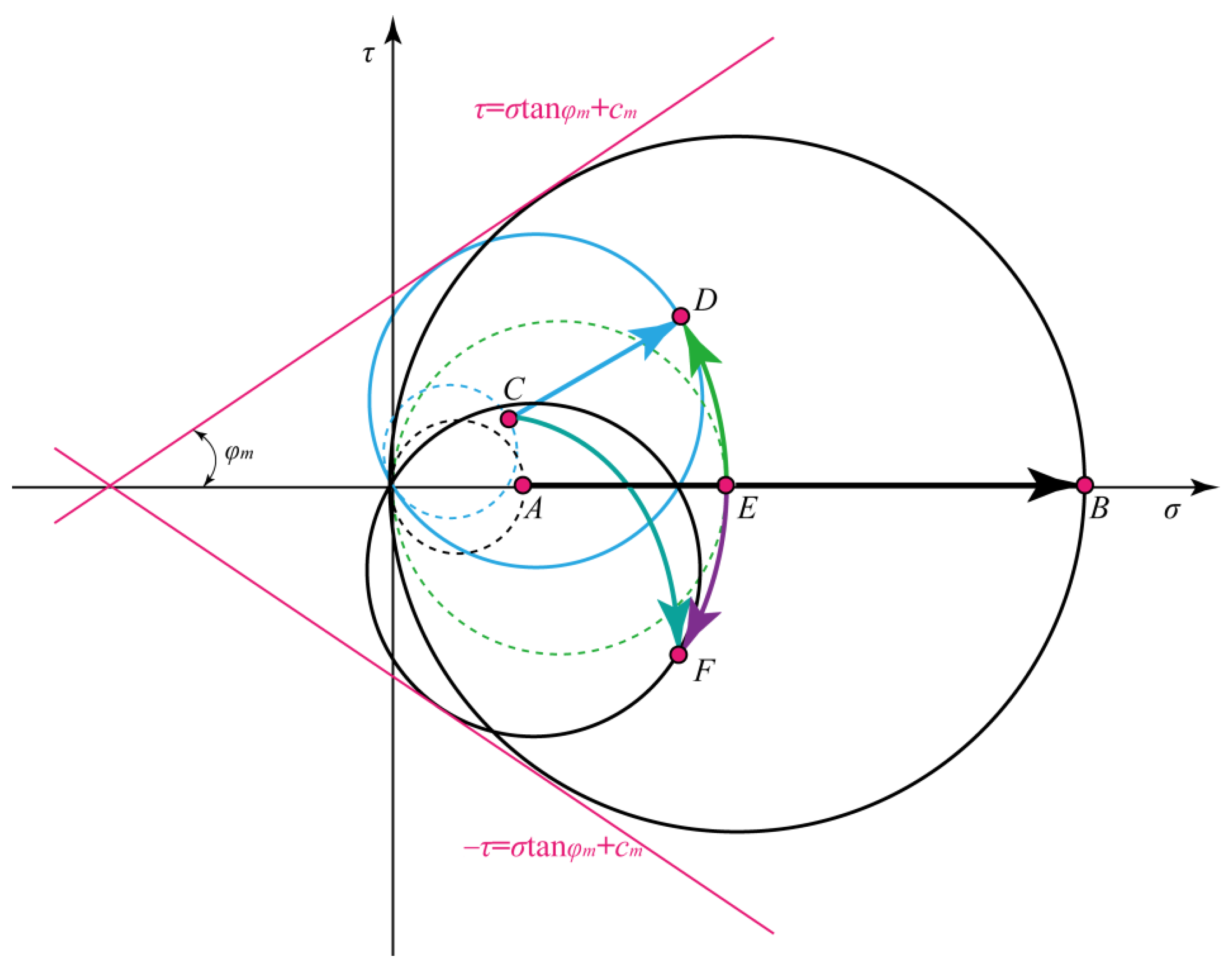
3. Stress Evolution Path of Inclined Pillar
3.1. Stress Path Controlled by Area Extraction Ratio
3.2. Stress Path Controlled by Dip Angle
3.3. Stress Path Controlled by In-Situ Stress Ratio
4. Strength Model of Inclined Pillar
4.1. Establishment of the Strength Model of Inclined Pillar
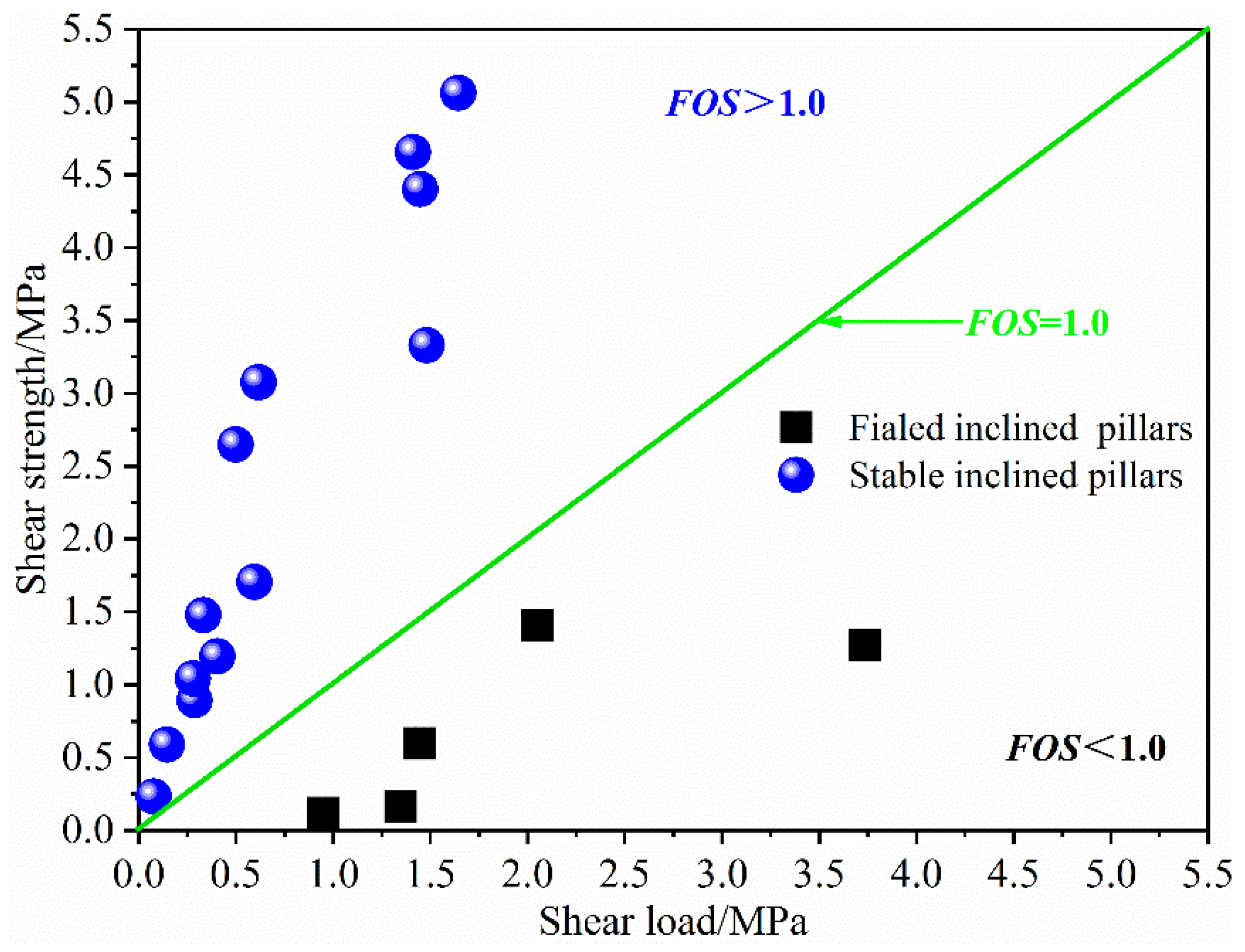
4.2. Verification of Inclined Pillar Shear Strength Model
5. Analysis of Factors Affecting Bearing Capacity of Inclined Pillar
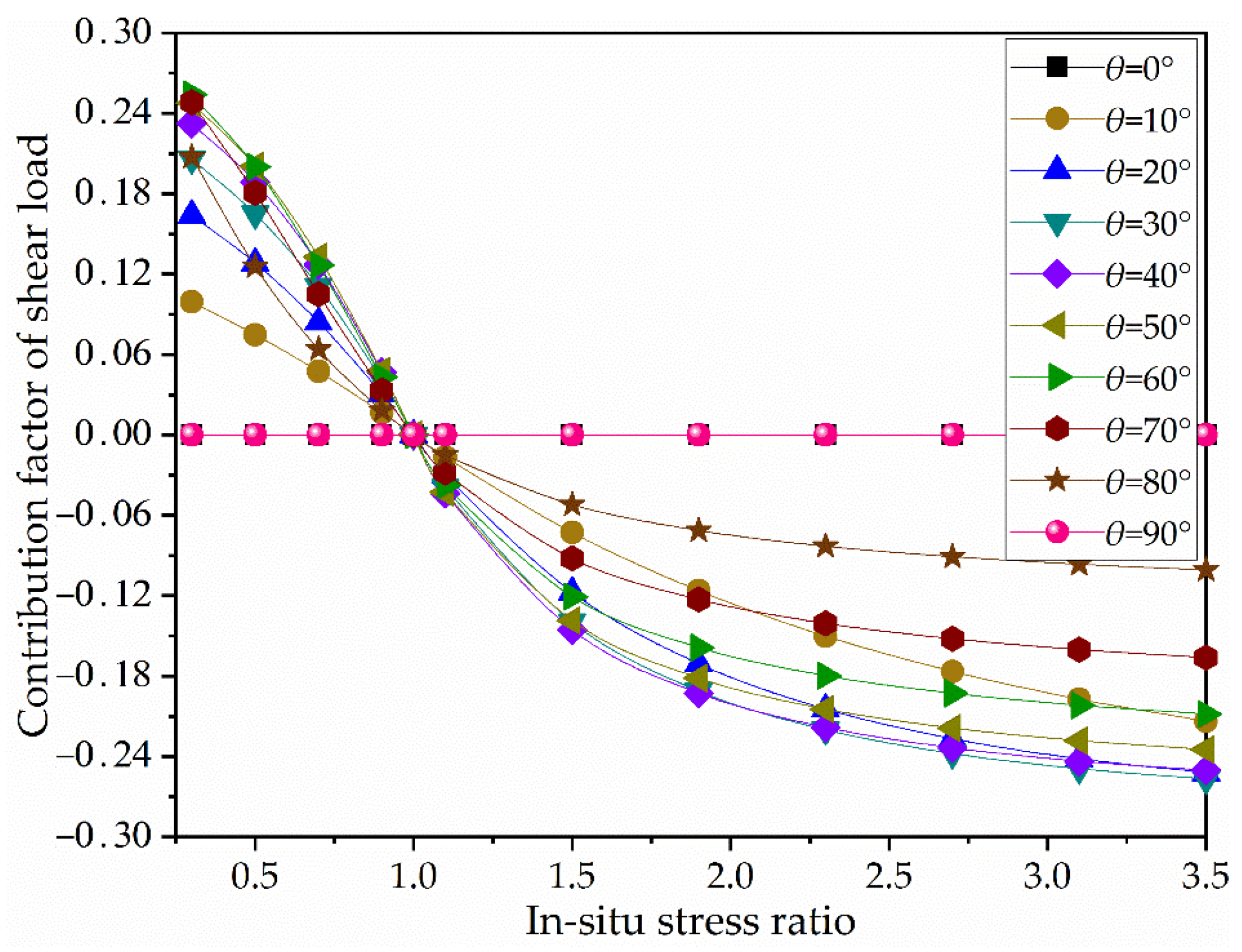
5.1. Stress Path Effect on the Bearing Capacity of Pillar
5.2. Stress Path Effect on the Bearing Capacity of Pillar
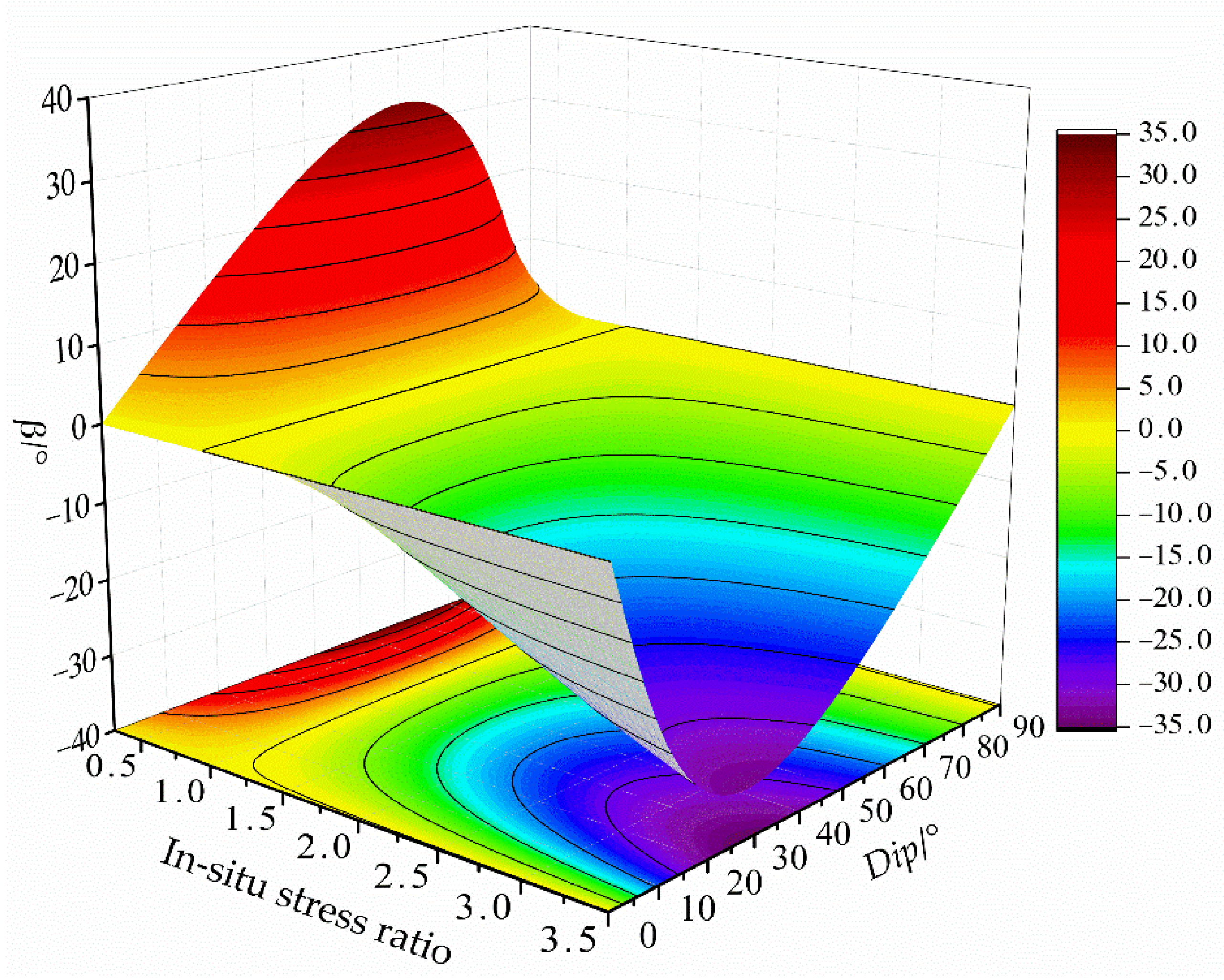
5.3. In-Situ Stress Ratio Effect on the Bearing Capacity of Pillar
5.4. Dip Effect on the Bearing Capacity of Pillar
6. Conclusions
- (1)
- There are three kinds of stress evolution paths of an inclined pillar, which are the stress paths controlled by the area extraction ratio, inclination, and the in-situ stress ratio; the stress paths controlled by the three factors satisfy a straight line, an arc, and a curve, respectively.
- (2)
- The change of load property of an inclined pillar is the essence of the dip effect on strength. With the increase of inclination angle, the compressive load is transformed into a shear load. As a result, the bearing capacity of the pillar is reduced and the risk of instability is increased.
- (3)
- A shear strength model was proposed to evaluate the bearing capacity of inclined pillars. The model is multiplied by a vertical pillar strength model and a dimensionless coefficient that is named the contribution factor of the shear load. The model was used to evaluate the bearing capacity of some inclined failed and stable pillars, and the results are consistent with the actual situation.
- (4)
- The bearing capacity of an inclined pillar is affected by the in-situ stress ratio and dip angle; when the dip angle θ∈(0°, 90°) and the in-situ stress ratio is less than 1.0, the larger the in-situ stress ratio, the greater the pillar bearing capacity. When the in-situ stress ratio is greater than 1.0, the larger the in-situ stress ratio, the smaller the pillar bearing capacity. In giving an in-situ stress ratio, the bearing capacity of the pillar decreases firstly and then increases with the increase of dip angle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ching, J.; Yang, Z.; Shiau, J.; Chen, C. Estimation of rock pressure during an excavation/cut in sedimentary rocks with inclined bedding planes. Struct. Saf. 2013, 41, 11–19. [Google Scholar] [CrossRef]
- Liu, S.; Jia, F.; Shen, C.; Weng, L.P. Strength characteristics of soilbags under inclined loads. Geotext. Geomembr. 2018, 46, 1–10. [Google Scholar] [CrossRef]
- Zhang, W.; Li, B.; Hwang, H.J.; Weng, L. Punching shear strength of reinforced concrete column footings under eccentric compression: Experiment and analysis. Eng. Struct. 2019, 198, 109509. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A.; Vena, M. Behaviour of flexible piles subjected to inclined loads. Comput. Geotech. 2015, 69, 199–209. [Google Scholar] [CrossRef]
- Sohrabi, S.; Banan, M.; Banan, M.R.; Zamiri, A. A new procedure for determination of lateral in-plane failure modes of reinforced concrete squat shear walls. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 1047–1056. [Google Scholar] [CrossRef]
- Preciado, A.; Sperbeck, S.T. Failure analysis and performance of compact and slender carved stone walls under compression and seismic loading by the FEM approach. Eng. Fail. Anal. 2019, 96, 508–524. [Google Scholar] [CrossRef]
- Mohan, G.M.; Sheorey, P.R.; Kushwaha, A. Numerical estimation of pillar strength in coal mines. Int. J. Rock Mech. Min. Sci. 2001, 38, 1185–1192. [Google Scholar] [CrossRef]
- Brady, B.H.G.; Brown, E.T. Rock Mechanics for Underground Mining; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Peng, S.S. Topical areas of research needs in ground control—A state of the art review on coal mine ground control. Int. J. Min. Sci. Technol. 2015, 25, 1–6. [Google Scholar] [CrossRef]
- Yao, Q.; Li, X.; Sun, B.; Ju, M.; Chen, T.; Zhou, J.; Liang, S.; Qu, Q. Numerical investigation of the effects of coal seam dip angle on coal wall stability. Int. J. Rock Mech. Min. Sci. 2017, 100, 298–309. [Google Scholar] [CrossRef]
- Pariseau, W.G. Design Analysis in Rock Mechanics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Luo, B.; Ye, Y.; Li, Y.; Luo, J.; Chen, H. Safety factor method for stability of inclined pillars under Mohr-Coulomb criterion. J. China Coal Soc. 2018, 43, 2408–2415. (in Chinese). [Google Scholar]
- Esterhuizen, G.S.; Dolinar, D.R.; Ellenberger, J.L. Pillar strength in underground stone mines in the United States. Int. J. Rock Mech. Min. Sci. 2011, 48, 42–50. [Google Scholar] [CrossRef]
- Ma, H.; Wang, J.; Wang, Y. Study on mechanics and domino effect of large-scale goaf cave-in. Saf. Sci. 2012, 50, 689–694. [Google Scholar] [CrossRef]
- Li, C.; Xu, J.; Wang, Z.; Qin, S. Domino instability effect of surrounding rock-coal pillars in a room-and-pillar gob. Int. J. Min. Sci. Technol. 2013, 23, 913–918. [Google Scholar] [CrossRef]
- Suorineni, F.T.; Kaiser, P.K.; Mgumbwa, J.J.; Thibodeau, D. Mining of orebodies under shear loading Part 1—Case histories. Trans. Inst. Min. Metall. Sect. A Min. Technol. 2011, 120, 137–145. [Google Scholar] [CrossRef]
- Kvapil, R.L.; Beaza, J.R.; Flores, G. Block caving at EI Teniente Mine, Chile. Trans. Inst. Min. Metall. Sect. A Min. Technol. 1989, 98, 43–56. [Google Scholar]
- Wang, J.; Shang, X.; Ma, H. Investigation of catastrophic ground collapse in Xingtai gypsum mines in China. Int. J. Rock Mech. Min. Sci. 2008, 45, 1480–1499. [Google Scholar] [CrossRef]
- Alvarez-Garcia, I.N.; Ramos-Lopez, F.L.; Gonzalez-Nicieza, C.; Alvarez-Fernandez, M.I.; Alvarez-Vigilet, A.E. The mine collapse at Lo Tacón (Murcia, Spain), possible cause of the Torre Pacheco earthquake (2nd May 1998, SE Spain). Eng. Fail. Anal. 2013, 28, 115–133. [Google Scholar] [CrossRef]
- Mark, C.; Agioutantis, Z. Analysis of coal pillar stability (ACPS): A new generation of pillar design software. Int. J. Min. Sci. Technol. 2019, 29, 87–91. [Google Scholar] [CrossRef]
- Jessu, K.V.; Spearing, A.J.S.; Sharifzadeh, M. Laboratory and numerical investigation on strength performance of inclined pillars. Energies 2018, 11, 3229. [Google Scholar] [CrossRef] [Green Version]
- He, Q.; Li, Y.; She, S. Mechanical properties of basalt specimens under combined compression and shear loading at low strain rates. Rock Mech. Rock Eng. 2019, 52, 4101–4112. [Google Scholar] [CrossRef]
- He, Q.; Li, Y.; Xu, J.; Zhang, C. Prediction of mechanical properties of igneous rocks under combined compression and shear loading through statistical analysis. Rock Mech. Rock Eng. 2020, 53, 841–859. [Google Scholar] [CrossRef]
- Xu, S.; Huang, J.; Wang, P.; Zhang, C.; Zhou, L.; Hu, S. Investigation of rock material under combined compression and shear dynamic loading: An experimental technique. Int. J. Impact Eng. 2015, 86, 206–222. [Google Scholar] [CrossRef]
- Luo, B.; Ye, Y.; Hu, N.; Wang, W. Investigation of dip effect on uniaxial compressive strength of inclined rock sample by experimental and theoretical models. Rock Mech. Rock Eng. 2020, 53, 5659–5675. [Google Scholar] [CrossRef]
- Jessu, K.V.; Spearing, A.J.S. Effect of dip on pillar strength. J. S. Afr. Inst. Min. Metall. 2018, 118, 765–776. [Google Scholar] [CrossRef]
- Lorig, L.J.; Cabrera, A. Pillar strength estimates for foliated and inclined pillars in schistose material. In Proceedings of the 3rd International FLAC/DEM Symposium, Hangzhou, China, 22–24 October 2013; pp. 1–7. [Google Scholar]
- Ma, T.; Wang, L.; Suorineni, F.T.; Tang, C. Numerical analysis on failure modes and mechanisms of mine pillars under shear loading. Shock Vib. 2016, 1, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Garza-Cruz, T.; Pierce, M.; Board, M. Effect of shear stresses on pillar stability: A back analysis of the troy mine experience to predict pillar performance at montanore mine. Rock Mech. Rock Eng. 2019, 52, 4979–4996. [Google Scholar] [CrossRef]
- Suorineni, F.T.; Mgumbwa, J.J.; Kaiser, P.K.; Thibodeau, D. Mining of orebodies under shear loading Part 2—Failure modes and mechanisms. Trans. Inst. Min. Metall. Sect. A Min. Technol. 2014, 123, 240–249. [Google Scholar] [CrossRef] [Green Version]
- Das, A.J.; Mandal, P.K.; Bhattacharjee, R.; Tiwari, S.; Kushwaha, A.; Roy, L.B. Evaluation of stability of underground workings for exploitation of an inclined coal seam by the ubiquitous joint model. Int. J. Rock Mech. Min. Sci. 2017, 93, 101–114. [Google Scholar] [CrossRef]
- Das, A.J.; Mandal, P.K.; Paul, P.S.; Sinha, R.K.; Tewari, S. Assessment of the strength of inclined coal pillars through numerical modelling based on the ubiquitous joint model. Rock Mech. Rock Eng. 2019, 52, 3691–3717. [Google Scholar] [CrossRef]
- Das, A.J.; Mandal, P.K.; Paul, P.S.; Sinha, R.K. Generalised analytical models for the strength of the inclined as well as the flat coal pillars using rock mass failure criterion. Rock Mech. Rock Eng. 2020, 52, 3921–3946. [Google Scholar] [CrossRef]
- Zhu, D.; Tu, S. Mechanisms of support failure induced by repeated mining under gobs created by two-seam room mining and prevention measures. Eng. Fail. Anal. 2017, 82, 161–178. [Google Scholar] [CrossRef]
- Pariseau, W.G. A symmetry requirement for failure criteria. Int. J. Rock Mech. Min. Sci. 2012, 52, 46–49. [Google Scholar] [CrossRef]
- Salamon, M.D.G.; Munro, A.H. A study of the strength of coal pillars. J. S. Afr. Inst. Min. Metall. 1967, 68, 55–67. [Google Scholar]
- Prassetyo, S.H.; Irnawan, M.A.; Simangunsong, G.M. New coal pillar strength formulae considering the effect of interface friction. Int. J. Rock Mech. Min. Sci. 2019, 123, 104102. [Google Scholar] [CrossRef]
- Sheorey, P.R. Pillar strength considering in-situ stress. In Proceedings of the Workshop on Coal Pillar Mechanics and Design; USBM IC 9315; Iannacchione, A.T., Mark, C., Repsher, R.C., Tuchman, R.J., Jones, C.C., Eds.; United States Department of the Interior: Santa Fe, NM, USA, 1992; pp. 122–127. [Google Scholar]
- Hedley, D.G.F.; Grant, F. Stope-and-pillar design for the Elliot Lake Uranium Mines. Bull. Can. Inst. Min. Metall. 1972, 63, 37–44. [Google Scholar]
- Potvin, Y.; Hudyma, M.R.; Miller, H.D.S. Design guidelines for open stope support. CIM Bull. 1989, 82, 53–62. [Google Scholar]




| Pillar Case Number | Depth/m | Pillar Height/m | Pillar Width/m | Dip/Degree | In-Situ Stress Ratio (k) | Roadway Width/m | UCS of Intact Ore-Body/MPa |
|---|---|---|---|---|---|---|---|
| 1 | 95 | 2.0 | 3.0 × 7.15 | 22.0 | 2.10 | 4.2 | 27.6 |
| 2 | 103 | 1.8 | 2.0 × 7.15 | 18.3 | 1.33 | 4.2 | 8.3 |
| 3 | 73 | 1.8 | 2.0 × 7.15 | 18.3 | 1.71 | 4.2 | 44.7 |
| 4 | 65 | 1.8 | 2.0 × 9.20 | 14.0 | 1.90 | 3.6 | 18.3 |
| 5 | 235 | 1.5 | 2.5 × 13.15 | 12.4 | 0.81 | 4.5 | 8.1 |
| Pillar Case Number | Depth/m | Pillar Height/m | Pillar Width/m | Dip/Degree | In-Situ Stress Ratio (k) | Roadway Width/m | UCS of Intact Ore-Body/MPa |
|---|---|---|---|---|---|---|---|
| 1 | 95 | 2.0 | 18.3 × 18.3 | 22.0 | 2.10 | 4.2 | 27.60 |
| 2 | 103 | 1.8 | 20.8 × 18.3 | 18.3 | 1.33 | 4.2 | 8.30 |
| 3 | 73 | 1.8 | 20.8 × 18.3 | 18.3 | 1.71 | 4.2 | 44.70 |
| 4 | 65 | 1.8 | 22.4 × 22.4 | 14.0 | 1.90 | 3.6 | 18.30 |
| 5 | 129 | 3.0 | 25.0 × 35.0 | 14.0 | 1.14 | 4.5 | 16.45 |
| 6 | 380 | 3.4 | 53.6 × 53.6 | 12.4 | 1.11 | 5.5 | 18.90 |
| 7 | 380 | 3.4 | 62.8 × 62.8 | 12.4 | 1.11 | 5.5 | 18.90 |
| 8 | 457 | 3.0 | 53.8 × 53.8 | 15.6 | 0.61 | 4.2 | 14.92 |
| 9 | 445.3 | 2.8 | 53.8 × 53.8 | 15.6 | 0.61 | 4.2 | 15.34 |
| 10 | 235 | 1.5 | 30.5 × 30.5 | 12.4 | 0.81 | 4.5 | 8.10 |
| 11 | 240 | 2.5 | 30.0 × 30.0 | 22.0 | 0.80 | 4.5 | 28.00 |
| 12 | 400 | 2.5 | 43.5 × 43.5 | 22.0 | 0.64 | 4.5 | 28.00 |
| 13 | 315 | 3.0 | 40.8 × 40.8 | 10.9 | 0.96 | 4.2 | 17.79 |
| No. | Author | Formula | Sl | Remarks | Eq. |
|---|---|---|---|---|---|
| 1 | Salamon et al. [36] | 7.2 | Coal pillar | (19) | |
| 2 | Prassetyo et al. [37] | 2.7 | Coal pillar | (20) | |
| 3 | Sheorey et al. [7,38] | 0.27σ0 | Coal pillar | (21) | |
| 4 | Hedley et al. [39] | 132.9 | Hard rock pillar | (22) | |
| 5 | Potvin et al. [40] | 0.42σ0 | Hard rock pillar | (23) | |
| 6 | Esterhuizen et al. [13] | LDF∈(0, 1) | 0.65σ0 | Hard rock pillar | (24) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Ye, Y.; Luo, B.; Hu, N.; Li, P. Theoretical Analysis for Stability Evaluation of Rock Mass Engineering Structure under Combined Compression-Shear Loading: A Case Study of Inclined Pillar. Appl. Sci. 2021, 11, 11439. https://doi.org/10.3390/app112311439
Sun L, Ye Y, Luo B, Hu N, Li P. Theoretical Analysis for Stability Evaluation of Rock Mass Engineering Structure under Combined Compression-Shear Loading: A Case Study of Inclined Pillar. Applied Sciences. 2021; 11(23):11439. https://doi.org/10.3390/app112311439
Chicago/Turabian StyleSun, Lijun, Yicheng Ye, Binyu Luo, Nanyan Hu, and Pengcheng Li. 2021. "Theoretical Analysis for Stability Evaluation of Rock Mass Engineering Structure under Combined Compression-Shear Loading: A Case Study of Inclined Pillar" Applied Sciences 11, no. 23: 11439. https://doi.org/10.3390/app112311439
APA StyleSun, L., Ye, Y., Luo, B., Hu, N., & Li, P. (2021). Theoretical Analysis for Stability Evaluation of Rock Mass Engineering Structure under Combined Compression-Shear Loading: A Case Study of Inclined Pillar. Applied Sciences, 11(23), 11439. https://doi.org/10.3390/app112311439





