Automated Diagnosis of Childhood Pneumonia in Chest Radiographs Using Modified Densely Residual Bottleneck-Layer Features

Abstract

Pneumonia is a severe infection that affects the lungs due to viral or bacterial infections such as the novel COVID-19 virus resulting in mild to critical health conditions. One way to diagnose pneumonia is to screen prospective patient’s lungs using either a Computed Tomography (CT) scan or chest X-ray. To help radiologists in processing a large amount of data especially during pandemics, and to overcome some limitations in deep learning approaches, this paper introduces a new approach that utilizes a few light-weighted densely connected bottleneck residual block features to extract rich spatial information. Then, shrinking data batches into a single vector using four efficient methods. Next, an adaptive weight setup is proposed utilizing Adaboost ensemble learning which adaptively sets weight for each classifier depending on the scores generated to achieve the highest true positive rates while maintaining low negative rates. The proposed method is evaluated using the Kaggle chest X-ray public dataset and attained an accuracy of 99.6% showing superiority to other deep networks-based pneumonia diagnosis methods.

1. Introduction

Pneumonia is mainly caused by virus pathogens or bacteria pathogens that infect the balloon-shaped air sacks in the human lungs causing inflammation in these sacks and serious implications on patient health. Pneumonia according to the Health World Organization (WHO) [1,2] is the main cause of death in young children under 5 years old, recording an 18% death rate. Furthermore, one of the devastating viruses that affect the lungs and cause pneumonia at an advanced stage is the novel COVID-19 virus which was declared as a global pandemic by WHO in March 2020 [3]. In particular, the new variant of the virus has been shown to affect young children. Some of the common symptoms of bacterial and viral pneumonia include fever, cough, increased breathing rate, and breathing difficulty. However, while bacterial pneumonia can be treated using special antibiotics, viral pneumonia is still challenging. Thus, further diagnosis and supporting techniques are necessary such as radiography imaging. Radiographic images are one of the effective diagnostic methods which are captured by either using Chest X-ray (CXR) radiography or Computed Tomography (CT). Although these images can help radiologists in their diagnosis, however in some viral, bacterial, or other inflammatory lung diseases, CXR images might show similar blurry white areas thus making the diagnosis task rather challenging [4]. Examples of healthy and infected lungs in CXR images are shown in Figure 1.

Nowadays, Artificial Intelligence (AI) techniques such as Deep learning Convolutional Neural Network (CNN) techniques have emerged as a supporting tool for distinguishing various features of lung infections as these networks have achieved an outstanding efficiency for feature extraction through representation learning and classification. In essence, these techniques have also made a huge step in the development of disease diagnosis systems via processing an immense number of clinical digital images and interpreting the spatial information of these images, which are prone to various types of noise. However, as these networks went deeper going from few layers such as AlexNet [5] to hundreds such as ResNet [6] as the demand to boost accuracy leading to deeper networks resulting in higher complexity cost and inflated number of parameters [7].

One answer to the aforementioned issues is transfer learning. Transfer learning is the strength of a learning algorithm to utilize similarities between various learning tasks such as similar image representations sharing statistical power and transfer learning information over other tasks. Using these representations has been motivated by the fact that they tend to describe many general priors that are not task-specific but would be beneficial for a machine to solve feature learning tasks [5]. Hence, the power of representation learning through utilizing pre-trained deep networks appears because these networks promote ease of feature reuse and extract more abstract features at higher layers which tend to be invariant to most local changes of the input images [8]. In general, deep-learning networks consist of multiple layers employed to progressively extract high-level features from raw data. The strength of transfer learning feature for medical data is demonstrated for instance through breast cancer classification using histopathology biopsy images [9] and brain tumor semantic segmentation [10]. Yet, there are still challenges that accompany the transfer learning process particularly the negative transfer and task-mapping automation [11]. Hence, a different approach for exploiting transfer learning is necessary to mitigate the aforementioned issues [12].

1.1. Related Work

There has been extensive research on detecting pneumonia using deep learning techniques. As a case in point, Chowdhury et al. [4] tested four different pre-trained deep networks for detecting pneumonia in CXR images through transfer learning and concluded that SqueezeNet [13] outperformed the other three networks. On the other hand, a fine-tuned version of a typical off-the-shelf deep network has been utilized in [14] to automatically classify pneumonia binary images. A CNN network with 10 layers was used by Saraiva et al. [15] to detect infant pneumonia using CXR images. Furthermore, Apostolopoulos and Mpesiana [16] have used transfer learning techniques with a CNN such as VGG19 [17] and MobileNet v2 to classify CXR lung images with pneumonia. Moreover, VGG16 [17], DenseNet [18], Xception [19], and Inception networks [20] along with transfer learning are utilized in [21]. Abdullah et al. [10] proposed a method a method for brain tumor segmentation using CNN and transfer learning. Kermany et al. [22], have investigated medical diagnosis on treatable diseases such as pneumonia in CXR images utilizing transfer learning with pre-trained deep networks. Togacar et al. [23] on the other hand have extracted features from deep layers using Alexnet, VGG16, and VGG19 deep networks and applied the minimum Redundancy Maximum Relevance (mRMR) algorithm for feature reduction.

Rajpurkar et al. [24] developed a deep network named CheXNet which is a 121-layer Dense network applied on the ChestX-ray14 dataset [25]. A contrastive learning with supervised fine tuning was used in the RSNA Kaggle Pneumonia challenge [26,27] and achieved 88% accuracy. Chouhan et al. [28] utilized transfer learning for extracting features from five pre-trained deep networks stated as AlexNet, GoogleNet [29], Inception V3, ResNet18, and DenseNet121. Whereas in [30], four deep pre-trained networks were compared and showed that DenseNet201 outperforms AlexNet, ResNet18, and SqueezeNet in terms of accuracy. Zhang et al. [31] formulated the detection of a viral infection in the lungs as a one-class classification-based anomaly detection problem where an anomaly score is measured for each CXR image and a decision is made based on a threshold. Ayan et al. [32] proposed using transfer learning with seven pre-trained famous deep networks such as VGG16, ResNet50, and SqueezeNet along with an ensemble method based on probabilistic voting to diagnose CXR images. A CNN with Extreme Machine Learning (EML) and Principal Component Analysis (PCA) are utilized in [33] after enhancing the contrast of CXR images using Contrast Limited Adaptive Histogram Equalisation (CLAHE) to diagnose pneumonia. Finally, Gour and Jain [34] proposed Uncertainty-Aware Convolutional neural Network (UA-ConvNet) which is based on the fine-tuned EfficientNet-B3 model for CXR images.

1.2. Limitations and Proposed Work

Although deep learning networks have achieved an efficient disease diagnosis accuracy, their performance has shown some drawback which can be summarized as: (1) increasing network depth does not ensure higher diagnosis accuracy as simply stacking layers together might cause the training error to be higher [35] on top of increasing complexity and computational cost; (2) deep networks are hard to train because of the vanishing gradient problem as the gradient is back-propagated to more initial layers [35]. As a result, when training deep networks, their performance becomes saturated or even begins to degrade rapidly; (3) transfer learning has some problems related to negative learning and the automation of task mapping; (4) features extracted from deep layers lose important spatial information in the CXR images as these deep layers are either identity mappings or copies of the early layers; (5) depending on single descriptor may introduce more classification errors; and (6) most recent work has evaluated their prediction models in only healthy lung vs. either bacterial or viral infected lung CXR images.

Therefore in this paper, our contributions can be summarized as (1) instead of using a complete deep network, we propose a light-weighted bottleneck layer feature descriptors exploiting the residual building blocks suggested in [6] and dense blocks suggested in [18] for building an improved feature descriptor which introduces no extra parameters thereby achieving low training errors and time; (2) the extracted features are reduced based on an efficient method for feature reduction, wherein 3D map of features generated for each image are shrunk into one vector using four methods; (3) adaptive score fusion with learned weights is performed using Adaboost ensemble learning that for each iteration, the decision power for prediction model weights is altered; and (4) the proposed model is examined in three scenarios which are: Normal vs. infected lungs and normal vs. bacterial vs. viral infected lungs.

The organization of this paper is as follows: The proposed method including feature extraction and reduction, the prediction model, and the adaptive score fusion are explained in Section 2. Results and discussion are discussed in Section 3 whereas we draw our conclusion and feature work in Section 4.

2. Proposed Method

2.1. Feature Extraction and Reduction

In general, auto-encoders converts higher dimensional input data into lower dimensional more abstract information through encoding data into another form. Then, the encoded data can be reconstructed to an approximate shape of the original input data depending on the reconstruction error [8,36]. In our work, we utilize the encoding process only and apply post-processing steps to increase the diagnosis accuracy. To avoid learning everything from scratch, we propose an efficient method through feature reuse to extract high spatial information characteristics deduced through abstract features utilizing ResNet auto-encoder bottleneck layers. ResNet has shown exceptional performance in several challenging classification task competitions such as the competition on ImageNet dataset [37].

The encoding process can be defined as a feature-extraction function denoted as ${\xi }_{\varphi }$ applied on training data $\left\{{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_N\right\}$ as:

$$\begin{array}{c}\hfill {\xi }_{\varphi }\left({\mathbf{x}}_n\right)=\sigma \left(\mathbf{W}{\mathbf{x}}_n+\mathbf{b}\right),\end{array}$$

(1)

where $\mathbf{x}$ represents the input image data vector and N is the number of images producing ${\mathbf{c}}_n={\xi }_{\varphi }\left({\mathbf{x}}_n\right)$ which is the first coded representation of the n input image. The parameters $\mathbf{b}$ and $\mathbf{W}$ are the encoder bias vector and weights matrices, respectively, whereas $\sigma$ is the activation function which typically is either sigmoid or Rectified Linear Unit (RELU) function.

Given that a CXR image has a size of $a\times b$, the image is first resized to the size of the ResNet input image layer, i.e., $224\times 224$, and is then passed to the building blocks of the ResNet network to extract the raw features from that image. Each block, which is denoted as ${ϝ}_l\left({\mathbf{c}}_n\right)$ where l is the number of bottleneck blocks, consists of 3 weighted convolution layers with Batch Normalization (BN) and RELU as shown in Figure 2. Since a skip connection has some advantages such as no extra parameters, proven to improve deep network performance [6], and can smooth information propagation, therefore, we propose adding more skip connections in a dense-fashion way [18] which allow feature reuse and leading to more accurate and compact learning.

Thus, we can define the resulted code for one image after ${ϝ}_l$ blocks with skip connections known as identity mapping from previous blocks as:

$$\begin{array}{c}\hfill {\mathbf{c}}_{n,l}=\sum _{i=2}^l\left(h\left({\mathbf{c}}_{n,1:i-1}\right),{ϝ}_i\left({\mathbf{c}}_n\right)\right),\end{array}$$

(2)

where $h\left({\mathbf{c}}_n\right)$ represents the identity mapping. As depicted in Figure 3, each residual block has an identity mapping as shown in sub-Figure 3a and each layer in the dense block is fed with information from all previous layers as shown in sub-Figure 3b, whereas the proposed feature extraction descriptor takes advantage of both paradigms where each residual block is fed with information from previous blocks through skip connections as shown in sub-Figure 3c. For instance, ${\mathbf{c}}_{n,3}$ is the sum of $h\left({\mathbf{c}}_{n,1}\right)$, $h\left({\mathbf{c}}_{n,2}\right)$, and ${ϝ}_2\left({\mathbf{c}}_n\right)$.

As a consequence of many input images being processed through the ResNet layers each having different convolution and batch size, stride, and padding, leading to a higher data dimensionality. To alleviate this problem, feature reduction techniques are performed on each slide of the 3D data resulting in reduced feature points for each input image. These techniques include calculating one point for each slide based on four rules, i.e., $\{min,max,\sigma ,\mu \}$, where $\mu$ is the mean and $\sigma$ is the standard deviation. This will result in four feature vectors of size $1\times h$, i.e., ${\mathbf{c}}_{n_{max}},{\mathbf{c}}_{n_{min}},{\mathbf{c}}_{n_{\sigma }},$ and ${\mathbf{c}}_{n_{\mu }}$ where h represents the feature vector length.

2.2. Prediction Model

Next for classification, each matrix (i.e., ${\mathbf{C}}_{N_{max}},{\mathbf{C}}_{N_{min}},{\mathbf{C}}_{N_{\sigma }},$ and ${\mathbf{C}}_{N_{\mu }}$) is divided into training and testing observations and utilized to create a prediction model based on Support Vector Machine (SVM). SVM has proven to perform well in many classification tasks although its hyper-parameters and regularization term must be tuned carefully during the training process to achieve the highest accuracy resulting in high computational cost [38]. Therefore, Bayesian optimization is used to find the best hyper-parameters and thus improving the prediction model [39].

Given N observations ${\{{\mathbf{c}}_n,{\mathbf{y}}_n\}}_{n=1}^N$ where ${\mathbf{c}}_n\in {\mathbb{R}}^N$ and ${\mathbf{y}}_n$ is the corresponding category vector for each ${\mathbf{c}}_n$, the optimal score function f is found by SVM through solving the regularized risk minimization objective using hinge loss [40,41] as an optimization problem such:

$$\begin{array}{c}\hfill arg\underset{f\left(x\right)}{min}\sum _{n=1}^{N}max\left(0,1-{\mathbf{y}}_{n}f\left({\mathbf{c}}_n\right)\right)+\gamma R\left(f\right)\end{array}$$

(3)

where $max\left(0,1-{\mathbf{y}}_{n}f\left({\mathbf{c}}_n\right)\right)$ is the hinge loss for the classification function $f\left({\mathbf{c}}_n\right)$, $\gamma$ is the hyper-parameter to fine-tune f training error versus complexity, and R is the regularize function. For nonlinear classifier, a kernel method is used in SVM which transform $f\left({\mathbf{c}}_n\right)$ into higher transformed data-point function $\phi \left({\mathbf{c}}_n\right)$ using a kernel function $k\left({\mathbf{c}}_n,{\mathbf{c}}_m\right)=\phi \left({\mathbf{c}}_n\right).\phi \left({\mathbf{c}}_m\right)$. The hyper-parameters are obtained by maximizing:

$$\begin{array}{c}\hfill \underset{{\alpha }_n=1:N}{max}=\sum _{n=1}^N{\alpha }_n-\frac{1}{2}\sum _{m=1}^N{\mathbf{c}}_n{\mathbf{y}}_{n}k\left({\mathbf{c}}_n,{\mathbf{c}}_m\right){\mathbf{c}}_m{y}_m.\end{array}$$

(4)

Various kernel functions, scales, and constrained are examined such as linear, quadratic, cubic, and Gaussian kernels.

2.3. Adaptive Score Fusion

To make the final prediction, an adaptive score fusion technique is proposed based on Adaboost ensemble learning [42] where the weights for each classifier are updated based on previous errors made by these classifiers. This is shown in Algorithm 1. First, each classifier is given a weight equally. Second, for several iterations, each classifier is trained and classification error is calculated, and based on that error, each classifier weight is updated where the higher the weighted error, the less the decision power is given to the corresponding classifier. Finally, a weighted sum rule is exploited where the final score is determined via summing the four scores such that:

$$\begin{array}{c}\hfill S_f=\sum _{i=1}^4{S}_i.\widehat{w_i},\end{array}$$

(5)

where $S_f$ is the final score, $S_i$ is the binary score generated from one of the four prediction models where the value 1 refers to positive pneumonia diagnosis.

Algorithm 1: Adaboost ensemble weights learning.

initialize classifier weights as $w_i=\frac{1}{No.ofclassifiers}$;

3. Results and Discussion

The proposed method is evaluated using a publicly available dataset named Kaggle collected and labeled by Kermany et al. [22,43]. The dataset includes 5232 CXR images collected from a cohort of pediatric patients of age from one to five years old. Image resolution varies from 400 to 2000 pixels with common noise factors introduced in the CXR imaging such as the position of the patient during image capture, the screening device, medical sensors and tools fixed on the patient while screening, and other inherited health conditions. In particular, the dataset consists of 3883 pneumonia-diagnosed CXR images including bacterial and viral infection and 1349 normal CXR images. As shwon in

Table 1. Training, Validation, and testing CXR image number using Kaggle CXR dataset.

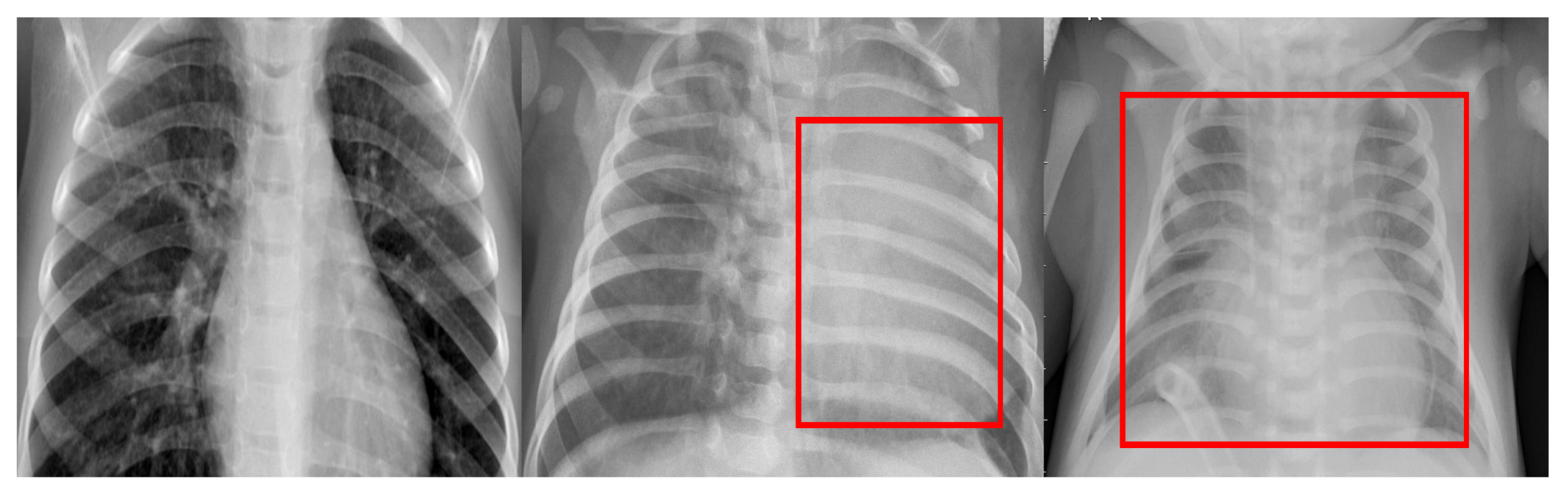
Category	No. of Images	Training	Testing
Normal	1349	1012	337
Bacterial	2538	1903	635
Viral	1345	1008	337
Total	5232	3922	1309

, we trained the proposed system utilizing 75% of the dataset with 10-K fold validation to avoid over-fitting achieving a training time of 96.57 s whereas the rest of the data are used for testing with image augmentation including rotation, scaling, and translation.

The experiment is conducted on a PC with core i7 and 16 GB of RAM under the Matlab 2020b environment and we utilized ResNet50 as the backbone network which was modified using Matlab Deep Learning Design Application. The input size of each image is changed to $224\times 224$ as the ResNet50 input layer with batch normalization utilized before the activation layer and before the convolution layer. The list of layers before the $l=5$ residual bottle-neck building blocks depicted in Figure 2 can be listed as the first convolution layer with 64 ($7\times 7$) filters with stride = 2, batch normalization, RELU, and $3\times 3$ max pooling. Stochastic Gradient Descent (SGD) with a mini-batch size of 256 is used. The learning rate is set to 0.1 and is divided by 10 when the error is high whereas the weight decay is set to 0.0001 and a momentum of 0.9.

For evaluating the proposed method, three metrics are employed namely: sensitivity, F1 score, and accuracy. These metrics can be defined as:

$$\begin{array}{c}\hfill sensitivity=\frac{TP}{TP+FN}\end{array}$$

(6)

$$\begin{array}{c}\hfill F1score=\frac{2TP}{2TP+FP+FN}\end{array}$$

(7)

$$\begin{array}{c}\hfill accuracy=\frac{TP+TN}{TP+FP+TN+FN}\end{array}$$

(8)

where $TP$ and $TN$ are the true positives and negatives, respectively, and $FP$ and $FN$ are the false positives and negatives consequently. As shown in

Table 2. Performance of the number of modified ResNet bottleneck layers.

Number of Bottleneck Blocks	Accuracy	Number of Features
1	95.6	1 × 256
2	96.2	1 × 256
3	96.8	1 × 256
4	96.8	1 × 512
5	99.6	1 × 512
6	97.6	1 × 512
7	97.2	1 × 512

, only $l=5$ bottleneck blocks are needed, which is neither deep nor early layers to achieve the best performance $(99.6\%)$ as the accuracy degraded after $l=6$ although the number of features is the same from $l=4$. This is an evidence that going deeper using CNN can complicate the classification system while degrading its accuracy.

3.1. SVM Optimization Using Bayesian Optimization

First, 50 iterations were set for the Bayesian optimizer of the SVM classifier as shown in Figure 4 where minimum classification error is plotted at each iteration. Figure 4 depicts the optimized hyper-parameters for the SVM including kernel function, kernel scale, and box constraint level. As shown in sub-Figure 4b, the optimization needed only 4 iterations to achieve the optimal SVM hyper-parameters achieving lower than $1\%$ of minimum classification error. In comparison, the random search optimization of the SVM reached higher than $9\%$ of the minimum classification error as shown in sub-Figure 4a.

Then, for weight learning using Adaboost, we set the number of trials of testing to 20 and the weights for each classifier is set equally for the $S_i\left(\mu \right),S_i\left(\sigma \right),S_i(max)$, and $S_i(min)$, respectively, where Algorithm 1 is used to obtain the optimum final score $S_f$. We plotted the ROC curve for each sub-classifier $(min,max,\sigma ,\mu )$ compared to $S_F$ as shown in Figure 5. The feature reduction techniques using mean and standard deviation for each batch have achieved the highest weights, subsequently these two feature vectors contribute in $75\%$ of the decision power. The $S_f$ performed better than other classifiers achieving an area under the curve of 99.6% supporting that the proposed method has significance in terms of adaptive weight setting over a single decision process.

3.2. Normal vs. Bacterial vs. Viral Pneumonia Infected Lungs

The most challenging scenario is when testing the prediction model utilizing bacterial vs. viral CXR lung images. According to a study conducted by Swingler [44] on the differentiation between viral and bacterial pneumonia in children using CXR images, many radiologists have agreed on distinguishing bacterial cases in an accuracy ranging from 26% to 70%. The review findings raise intriguing questions regarding the accuracy of lung pneumonia diagnosis and highlighted the complexity of deciding by either a human expert or a prediction model. This is evident in the feature space shown in sub-Figure 6a where the feature points of the viral and bacterial lung infections are overlapping. Next, a similar procedure, where SVM with Bayesian optimization and adaptive score fusion, is applied as shown in sub-Figure 4, Figure 7 and in Figure 8. The minimum classification error plot shows that even after 50 iterations, the classification error has not improved reaching 9%. In addition, the confusion matrix in Figure 8 shows that the prediction model has performed better in detecting viral pneumonia. Nevertheless, the overall prediction model accuracy is lower when classifying normal vs. viral and bacterial pneumonia compared to healthy vs. infected lung CXR images scoring 89.5% yet higher when compared to deep features.

3.3. Normal vs. Pneumonia Infected Lungs

The first scenario conducted is to test the proposed algorithm in a normal vs. infected lungs fashion including a mix of bacterial and viral infection CXR images. First, the confusion matrix of the proposed feature extraction method compared to deep-layer features is shown in Figure 7. The sensitivity, F1 score and accuracy are (99.4%, 99.2%, and 99.6% respectively compared to features extracted from deap bottleneck layers, i.e., when l is larger than 5. It is evident that in our case, going deeper in some applications and in particular using medical images for diagnosis could have a negative impact on system performance. Additionally, to illustrate the advantage of using the modified residual building blocks as an efficient feature extractor, we conducted the same experiment on most off-the-shelve deep networks as shown in

Table 3. Comparison of early-layer and deep-layer accuracy for pneumonia diagnosis using most off-the-shelf deep networks vs. proposed densely-connected residual blocks.

Deep Network	Number of Layers	Accuracy (%)
		Deep Layer Features	Early Layer Features
AlexNet [5]	8	96.0	97.3
VGG [17]	19	96.8	98.4
SqueezeNet [13]	14	96.7	96.0
GoogleNet [29]	27	96.2	97.7
ShuffleNet [45]	20	96.5	96.8
NASNetMobile [46]	913	95.8	96.9
DenseNet [18]	201	98.0	98.4
Xception [19]	36	96.4	98.4
ResNet [6]	50	97.6	97.1
Proposed method	35	na	99.6

. We extracted low-layer features from these networks and our proposed method has the upper hand in terms of accuracy achieving 99.6%.

Next, we compared our work with recent state-of-the-art methods for pneumonia diagnosis using CXR images as shown in

Table 4. Comparison of proposed pneumonia diagnosis system with recent state-of-the-art methods.

Pneumonia Diagnosis Method	Deep Learning Technique	Accuracy (%)
Chowdhury et al. [4]	Transfer Learning with SqueezeNet	99.00
Asnaoui et al. [14]	Transfer Learning with ResNet50	96.61
Saraiva et al. [15]	CNN 10 Layers	95.30
Apostolopoulos et al. [16]	Transfer Learning with MobileNetv2	96.78
Liang and Zheng [21]	CNN with 49 Residual Blocks	95.30
Kermany et al. [22]	Transfer Learning with AlexNet	92.80
Toğaçar et al. [23]	Deep Features Fused from AlexNet, VGG16, and VGG19	99.41
Rajpurkar et al. [24]	Transfer Learning with ChexNet	82.83
Han et al. [26]	Contrastive Learning with ResNetAttention	88.00
Chouhan et al. [28]	Transfer Learning with 5 Deep Networks	96.40
Rahman et al. [30]	Transfer Learning with DenseNet201	98.00
Zhang et al. [31]	One-Class Classification Based Anomaly Detection	83.61
Ayan et al. [32]	Transfer Learning with Ensemble Voting	95.21
Nahiduzzaman et al. [33]	CNN with EML and PCA	99.83
Gour and Jain [34]	fine-tuned EfficientNet-B3	99.83
Proposed Method	Bottleneck Layer Features with 5 Densely-Connected Residual Building Blocks	99.60

. It is evident that the proposed method has outperformed recent transfer learning methods in terms of accuracy, training time, and complexity as only a few modified residual blocks are needed and trained to achieve higher accuracy on a simple PC providing a feasible solution. It is worth pointing out that our proposed method is slightly better than the work in [23] by only $0.02\%$ and lower than the work in [33] by only $0.04\%$, our proposed method however utilizes only five residual building blocks densely connected to extract features. Whereas the method in [23] involves transfer learning and re-train three different deep networks extracting an abundance amount of features; the classification method in [33] uses mix of various algorithms such as PCA, CNN, CLAHE, and EML. As a consequence, more complex feature reduction and more processing time are required which subsequently increase system complexity. Besides, our proposed method uses an adaptive weight setting method to assign the decision power effectively to the best feature descriptor.

3.4. Discussion

This work set out with the aim of assessing the importance of utilizing features extracted from modified deep network layers to detect viral and bacterial pneumonia in CXR lung images. A light-weighted bottleneck layer feature descriptors with an adaptive score fusion with learned weights are applied in two scenarios which are: Normal vs. infected lungs and normal vs. bacterial vs. viral infected lungs.

One interesting finding is only four iterations were required to optimize the hyperparameters of the SVM classification utilizing Bayesian optimization and achieving a classification error lower than $0.1\%$ as shown in Figure 4 compared to Random search optimization in terms of performance and processing time. Furthermore, the proposed weight learning method as depicted in Algorithm 1 has showed a significant benefit of score fusion of four descriptors as $S_f$ achieved $99.6\%$ of area under the curve in Figure 5 compared to scores acquired individually (i.e.,) $S_i\left(\mu \right),S_i\left(\sigma \right),S_i(max)$, and $S_i(min)$.

Another interesting finding for normal vs. infected lungs fashion including a mix of bacterial and viral infection CXR images scenario was that going deeper in some classification tasks could have a negative impact on accuracy. This is evident in Table 2 when the value of $l>5$, the accuracy starts degrading as well as the complexity increases as more layers are used to extract features. Nevertheless, the proposed method has the upper hand compared to recent state-of-the-art methods shown in Table 3 and Table 4.

Despite these promising results, questions remain. For instance, the accuracy of determining viral or bacterial pneumonia by either human experts or prediction models and how the process is prone to errors affecting patients’ health. For instance, the observed results when viral vs. bacterial vs. normal lung CXR images are used confirm the challenging task as the overall accuracy degraded to $89.5\%$. We recommend more future studies on the aforementioned issue.

4. Conclusions

We proposed an efficient method for pneumonia diagnosis using features extracted from bottleneck layers using modified densely-connected residual building blocks. Four types of features using four feature descriptors were extracted for each CXR image and the adaptive score fusion with Adaboost ensemble learning weight set-up was employed for selecting the best weight for each descriptor. The proposed method was evaluated using Kaggle’s chest X-ray public dataset which contains more than 5000 images using two scenarios. The achieved accuracy compared to deep-layer features extracted from the most famous deep networks using state-of-the-art methods was promising to reach 99.6% and 90.2% for healthy vs. infected lungs classification scenario and bacterial vs. viral infected lungs classification scenario, respectively.

Furthermore, this work proposed a feasible pneumonia approach that can be utilized for COVID-19 chest X-ray images where the viral infection is present, we have not used images of real COVID-19 cases as to our knowledge, there is no sufficient public dataset for COVID-19 chest X-ray or CT images. Nevertheless, this case will be tested in our future work as soon as it becomes available.