Tip and Torque Accuracy According to the ISO 27020:2019 Norm in Currently Available Pre-Adjusted Orthodontic Brackets
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Sample
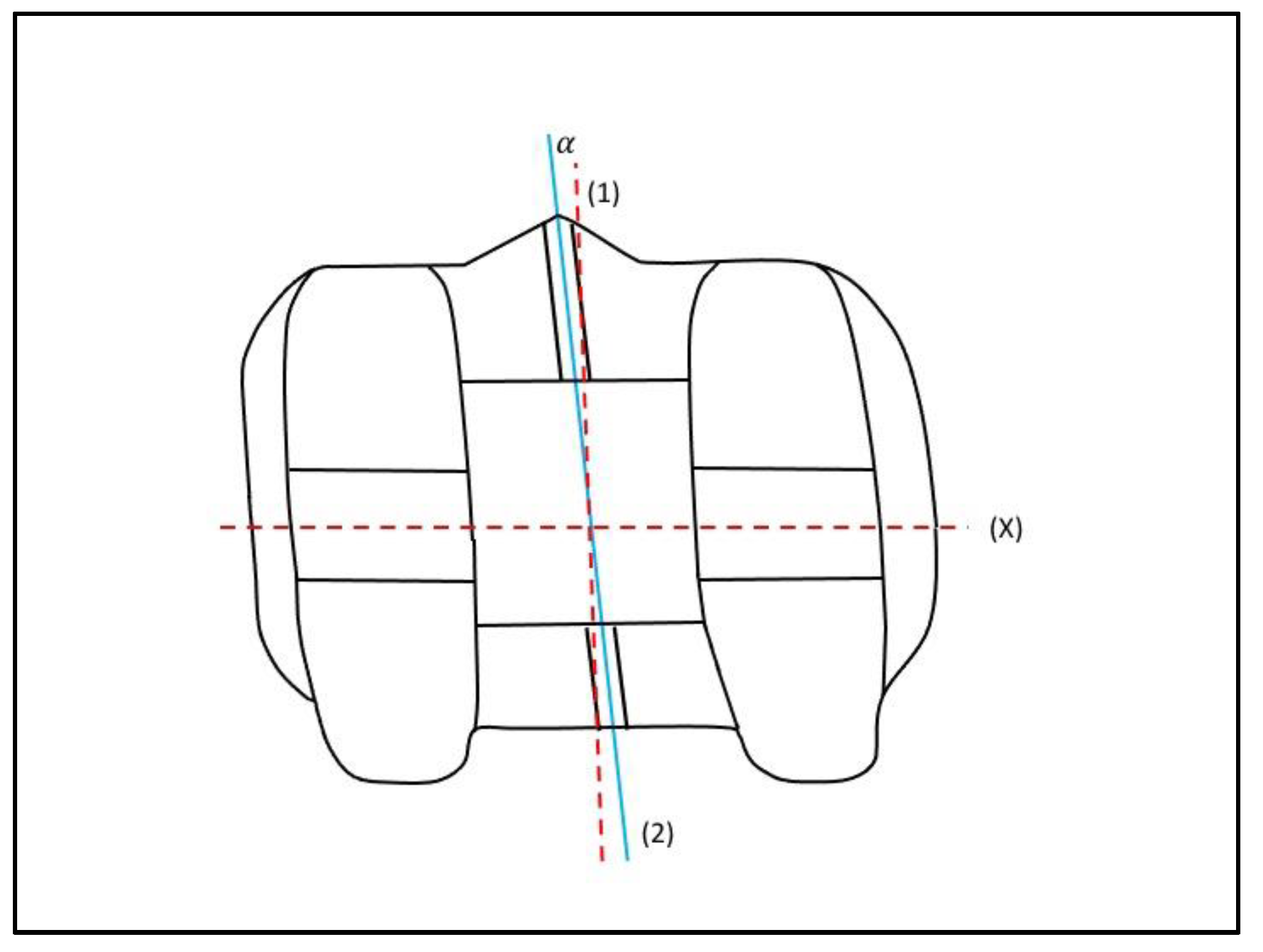
2.2. Measurement Protocol
2.3. Statistical Analysis
3. Results
3.1. Intra- and Inter-Operator Reliability
3.2. Torque Assessment
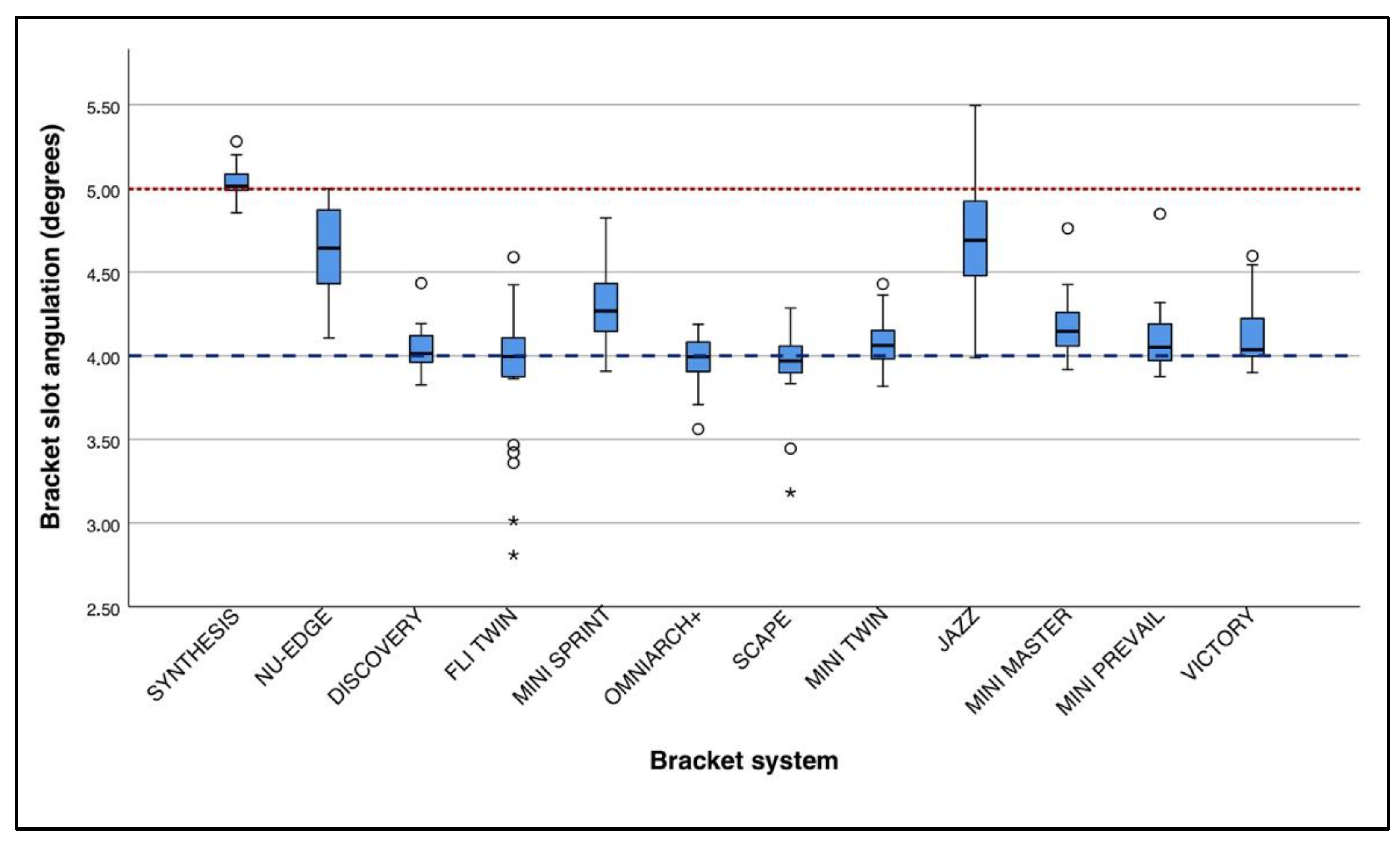
3.3. Tip Assessment
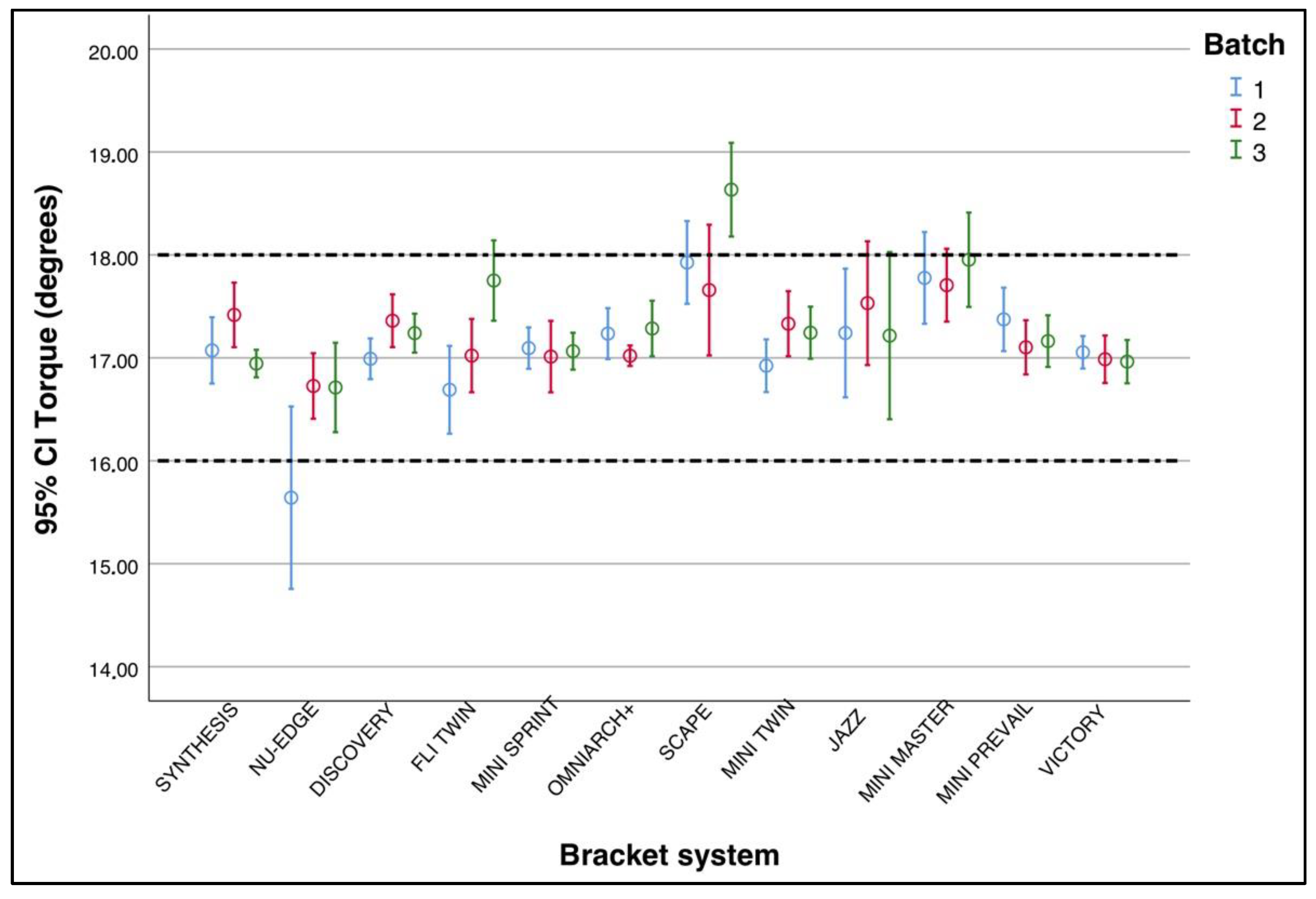
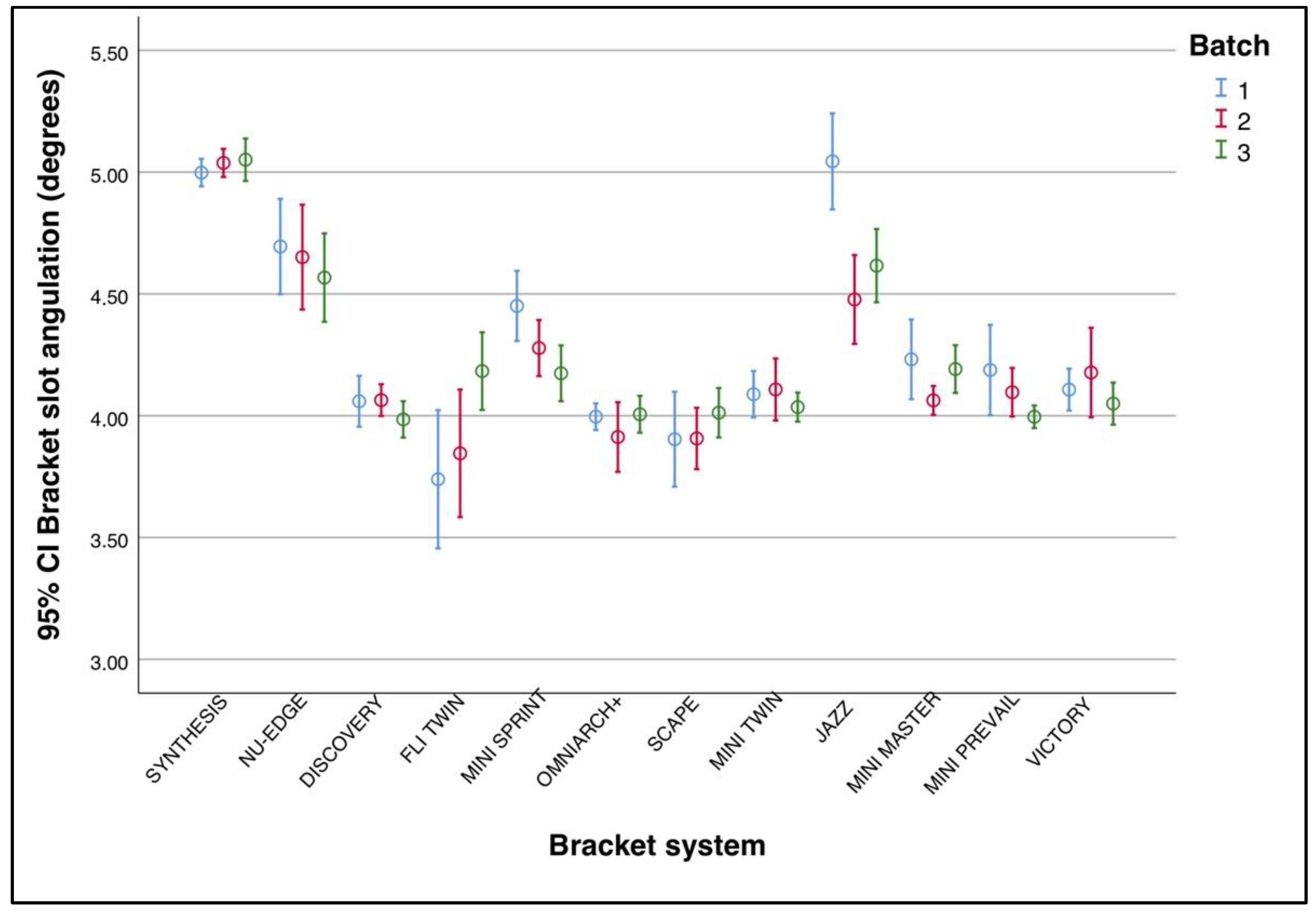
3.4. Inter-Batch Variability
4. Discussion
4.1. Torque
4.2. Tip
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Awasthi, E.; Sharma, N.; Shrivastav, S.; Kamble, R. Evaluation and Comparison of Various Prescription Specifications and Slot Distortion of Pre-Adjusted Edgewise Brackets Manufactured By Different Companies Available in India. Int. J. Curr. Res. Rev. 2015, 7, 44–51. [Google Scholar]
- Plaza, S.P.; Barrera, J.P.; Leon, M.; Pinilla, S.E.; Peñaranda, L.; Zamora, J.A. Variación de torque y angulación de brackets de prescripción MBT de cuatro casas comerciales. Rev. CES Odontol. 2010, 23, 9–16. [Google Scholar] [CrossRef]
- Alavi, S.; Tajmirriahi, F. Assessment of dimensional accuracy of pre-adjusted metal injection molding orthodontic brackets. Dent. Res. J. 2016, 13, 440–445. [Google Scholar]
- Mendonca, M.R.; Verri, A.C.G.; Fabre, A.F.; Cuoghi, O.A. Analysis of mesiodistal angulations of pre-adjusted brackets. Braz. Oral Res. 2014, 28, S1806-83242014000100247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anjos, A.D.; Pompeo, D.D.; Gilson, J.; Anjos, E.D.; Oliveira, G.M.S.; Rosário, H.D. Assessment of torque angle of brackets from different brands. Brazilian J. Oral Sci. 2015, 14, 66–70. [Google Scholar] [CrossRef]
- Streva, A.M.; Cotrim-Ferreira, F.A.; Garib, D.G.; Carvalho, P.E.G. Are torque values of pre-adjusted brackets precise? J. Appl. Oral Sci. 2011, 19, 313–317. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martínez, L.B.; Garcovich, D.; Pamplona, P.E.; Martín, M.A.A.; Lorenzo, A.A. Compliance with the ISO 27020:2019 norm of a sample of currently available pre-adjusted Orthodontic bracket systems. Are the actual dimensions as expected? Head Face Med. 2021, 17, 1–10. [Google Scholar] [CrossRef]
- Dalstra, M.; Eriksen, H.; Bergamini, C.; Melsen, B. Actual versus theoretical torsional play in conventional and self-ligating bracket systems. J. Orthod. 2015, 42, 103–113. [Google Scholar] [CrossRef] [PubMed]
- Andrews, L.F. The six keys to normal occlusion. Am. J. Orthod. 1972, 62, 296–309. [Google Scholar] [CrossRef]
- Sernetz, F. Standardization of orthodontic products--does it make sense? J. Orofac. Orthop. 2005, 66, 307–318. [Google Scholar] [CrossRef] [PubMed]
- Archambault, A.; Lacoursiere, R.; Badawi, H.; Major, P.W.; Carey, J.; Flores-Mir, C. Torque expression in stainless steel orthodontic brackets. Angle Orthod. 2010, 80, 201–210. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, D.-Y.; Kim, Y.-J.R. Dimensional accuracy of ceramic self-ligating brackets and estimates of theoretical torsional play. Angle Orthod. 2016, 86, 804–809. [Google Scholar] [CrossRef] [Green Version]
- Joch, A.; Pichelmayer, M.; Weiland, F. Bracket slot and archwire dimensions: Manufacturing precision and third order clearance. J. Orthod. 2010, 37, 241–249. [Google Scholar] [CrossRef] [PubMed]
- Eliades, T.; Zinelis, S.; Bourauel, C.; Eliades, G. Manufacturing of Orthodontic Brackets: A Review of Metallurgical Perspectives and Applications. Recent Patents Mater. Sci. 2010, 1, 135–139. [Google Scholar] [CrossRef]
- Schmidli, H.; Grize, Y.-L. Quantification of batch homogeneity. Qual. Eng. 1997, 10, 359–364. [Google Scholar] [CrossRef]
- Tepedino, M.; Paiella, G.; Potrubacz, M.I.; Monaco, A.; Gatto, R.; Chimenti, C. Dimensional variability of orthodontic slots and archwires: An analysis of torque expression and clinical implications. Prog. Orthod. 2020, 21, 32. [Google Scholar] [CrossRef] [PubMed]
- Arreghini, A.; Lombardo, L.; Mollica, F.; Siciliani, G. Torque expression capacity of 0.018 and 0.022 bracket slots by changing archwire material and cross section. Prog. Orthod. 2014, 15, 53. [Google Scholar] [CrossRef] [Green Version]
- Castro, I.O.; Gribel, B.F.; Alencar, A.H.G.; Valladares-Neto, J.; Estrela, C. Evaluation of crown inclination and angulation after orthodontic treatment using digital models: Comparison to the prescription of the brackets used. J. Orofac. Orthop. 2018, 79, 227–234. [Google Scholar] [CrossRef] [PubMed]
- Pereira, D.V.; Cavalcante, R.T.; Silva, L.H.; Maeda, F.A.; Torres, F.C.; Carvalho, P.E.G. Torque value accuracy of pre-adjusted metal brackets for upper and lower incisors. Minerva Stomatol. 2019, 68, 31–35. [Google Scholar] [CrossRef]



| Bracket System | N | Mean (±SD) | Min | Max | MD | ZW | p |
|---|---|---|---|---|---|---|---|
| SYNTHESIS | 30 | 17.14 (±0.418) | 16.25 | 18.38 | 0.145 | −1.903 | 0.057 |
| NU-EDGE | 30 | 16.36 (±0.959) | 13.15 | 17.55 | −0.640 | −3.723 | <0.001 *** |
| DISCOVERY | 30 | 17.20 (±0.331) | 16.35 | 18.18 | 0.197 | −2.993 | 0.003 ** |
| FLI TWIN | 30 | 17.15 (±0.695) | 15.32 | 18.78 | 0.154 | −1.286 | 0.199 |
| MINI SPRINT | 30 | 17.06 (±0.344) | 16.06 | 17.72 | 0.057 | −1.255 | 0.210 |
| OMNIARCH+ | 30 | 17.18 (±0.318) | 16.53 | 17.73 | 0.180 | −2.581 | 0.010 ** |
| SCAPE | 30 | 18.07 (±0.802) | 15.37 | 19.52 | 1.070 | −4.268 | <0.001 *** |
| MINI-TWIN | 30 | 17.17 (±0.414) | 16.53 | 18.16 | 0.166 | −1.923 | 0.054 |
| JAZZ | 30 | 17.33 (±0.937) | 15.11 | 19.32 | 0.329 | −2.026 | 0.043 * |
| MINI MASTER | 30 | 17.81 (±0.579) | 16.98 | 19.17 | 0.812 | −4.741 | <0.001 *** |
| MINIPREVAIL | 30 | 17.21 (±0.390) | 16.36 | 18.20 | 0.213 | −2.777 | 0.005 ** |
| VICTORY | 30 | 17.05 (±0.275) | 16.35 | 17.60 | 0.051 | −0.309 | 0.758 |
| Bracket System | N | Mean (±SD) | Min | Max | MD | ZW | p |
|---|---|---|---|---|---|---|---|
| SYNTHESIS | 30 | 5.03 (±0.095) | 4.85 | 5.28 | 0.029 | −1.611 | 0.107 |
| NU-EDGE | 30 | 4.64 (±0.272) | 4.11 | 5.00 | −0.363 | −4.782 | <0.001 *** |
| DISCOVERY | 30 | 4.04 (±0.118) | 3.83 | 4.43 | 0.036 | −1.525 | 0.127 |
| FLI TWIN | 30 | 3.92 (±0.378) | 2.81 | 4.59 | −0.078 | −0.422 | 0.673 |
| MINI SPRINT | 30 | 4.30 (±0.205) | 3.91 | 4.82 | 0.301 | −4.680 | <0.001 *** |
| OMNIARCH + | 30 | 3.97 (±0.139) | 3.56 | 4.19 | −0.029 | −0.782 | 0.434 |
| SCAPE | 30 | 3.94 (±0.204) | 3.18 | 4.29 | −0.060 | −1.718 | 0.086 |
| MINI-TWIN | 30 | 4.08 (±0.136) | 3.82 | 4.43 | 0.077 | −2.478 | 0.013 * |
| JAZZ | 30 | 4.71 (±0.343) | 3.99 | 5.50 | 0.712 | −4.762 | <0.001 *** |
| MINI MASTER | 30 | 4.16 (±0.172) | 3.92 | 4.76 | 0.162 | −4.247 | <0.001 *** |
| MINIPREVAIL | 30 | 4.09 (±0.186) | 3.88 | 4.85 | 0.093 | −2.509 | 0.012 * |
| VICTORY | 30 | 4.11 (±0.180) | 3.90 | 4.60 | 0.110 | −2.887 | 0.004 ** |
| Bracket System | Batch 1 | Batch 2 | Batch 3 | ||||
|---|---|---|---|---|---|---|---|
| N | Mean (±SD) | N | Mean (± SD) | N | Mean (±SD) | p | |
| SYNTHESIS | 10 | 17.07 (±0.45) | 10 | 17.42 (±0.44) | 10 | 16.94 (±0.19) | 0.026 * |
| NU-EDGE | 10 | 15.64 (±1.24) | 10 | 16.73 (±0.44) | 10 | 16.71 (±0.61) | 0.019 * |
| DISCOVERY | 10 | 17.00 (±0.28) | 10 | 17.36 (±0.36) | 10 | 17.24 (±0.26) | 0.051 |
| FLI TWIN | 10 | 16.69 (±0.60) | 10 | 17.02 (±0.50) | 10 | 17.75 (±0.55) | 0.001 ** |
| MINI SPRINT | 10 | 17.09 (±0.28) | 10 | 17.01 (±0.48) | 10 | 17.06 (±0.25) | 0.870 |
| OMNIARCH+ | 10 | 17.24 (±0.35) | 10 | 17.02 (±0.14) | 10 | 17.29 (±0.38) | 0.140 |
| SCAPE | 10 | 17.93 (±0.56) | 10 | 17.66 (±0.89) | 10 | 18.63 (±0.64) | 0.014 * |
| MINI-TWIN | 10 | 16.92 (±0.36) | 10 | 17.33 (±0.44) | 10 | 17.24 (±0.35) | 0.062 |
| JAZZ | 10 | 17.24 (±0.87) | 10 | 17.53 (±0.84) | 10 | 17.22 (±1.14) | 0.719 |
| MINI MASTER | 10 | 17.78 (±0.62) | 10 | 17.71 (±0.49) | 10 | 17.95 (±0.64) | 0.632 |
| MINIPREVAIL | 10 | 17.37 (±0.43) | 10 | 17.10 (±0.37) | 10 | 17.16 (±0.35) | 0.271 |
| VICTORY | 10 | 17.05 (±0.22) | 10 | 16.99 (±0.32) | 10 | 16.96 (±0.29) | 0.758 |
| Bracket System | Batch 1 | Batch 2 | Batch 3 | ||||
|---|---|---|---|---|---|---|---|
| N | Mean (±SD) | N | Mean (±SD) | N | Mean (±SD) | p | |
| SYNTHESIS | 10 | 5.00 (±0.08) | 10 | 5.04 (±0.08) | 10 | 5.05 (±0.12) | 0.492 |
| NU-EDGE | 10 | 4.69 (±0.27) | 10 | 4.65 (±0.30) | 10 | 4.57 (±0.25) | 0.584 |
| DISCOVERY | 10 | 4.06 (±0.15) | 10 | 4.06 (±0.09) | 10 | 3.98 (±0.10) | 0.224 |
| FLI TWIN | 10 | 3.74 (±0.40) | 10 | 3.85 (±0.37) | 10 | 4.18 (±0.22) | 0.006 ** |
| MINI SPRINT | 10 | 4.45 (±0.20) | 10 | 4.28 (±0.16) | 10 | 4.17 (±0.16) | 0.005 ** |
| OMNIARCH+ | 10 | 4.00 (±0.08) | 10 | 3.91 (±0.20) | 10 | 4.01 (±0.11) | 0.266 |
| SCAPE | 10 | 3.90 (±0.27) | 10 | 3.90 (±0.18) | 10 | 4.01 (±0.14) | 0.596 |
| MINI-TWIN | 10 | 4.09 (±0.13) | 10 | 4.11 (±0.18) | 10 | 4.04 (±0.08) | 0.484 |
| JAZZ | 10 | 5.04 (±0.28) | 10 | 4.48 (±0.25) | 10 | 4.62 (±0.21) | <0.001 *** |
| MINI MASTER | 10 | 4.23 (±0.23) | 10 | 4.06 (±0.08) | 10 | 4.19 (±0.14) | 0.067 |
| MINIPREVAIL | 10 | 4.19 (±0.26) | 10 | 4.10 (±0.14) | 10 | 4.00 (±0.06) | 0.064 |
| VICTORY | 10 | 4.11 (±0.12) | 10 | 4.18 (±0.26) | 10 | 4.05 (±0.12) | 0.290 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernes Martinez, L.; Garcovich, D.; Alvarado Lorenzo, A.; Zhou Wu, A.; Aiuto, R.; Adobes Martin, M. Tip and Torque Accuracy According to the ISO 27020:2019 Norm in Currently Available Pre-Adjusted Orthodontic Brackets. Appl. Sci. 2021, 11, 11657. https://doi.org/10.3390/app112411657
Bernes Martinez L, Garcovich D, Alvarado Lorenzo A, Zhou Wu A, Aiuto R, Adobes Martin M. Tip and Torque Accuracy According to the ISO 27020:2019 Norm in Currently Available Pre-Adjusted Orthodontic Brackets. Applied Sciences. 2021; 11(24):11657. https://doi.org/10.3390/app112411657
Chicago/Turabian StyleBernes Martinez, Laura, Daniele Garcovich, Alfonso Alvarado Lorenzo, Angel Zhou Wu, Riccardo Aiuto, and Milagros Adobes Martin. 2021. "Tip and Torque Accuracy According to the ISO 27020:2019 Norm in Currently Available Pre-Adjusted Orthodontic Brackets" Applied Sciences 11, no. 24: 11657. https://doi.org/10.3390/app112411657
APA StyleBernes Martinez, L., Garcovich, D., Alvarado Lorenzo, A., Zhou Wu, A., Aiuto, R., & Adobes Martin, M. (2021). Tip and Torque Accuracy According to the ISO 27020:2019 Norm in Currently Available Pre-Adjusted Orthodontic Brackets. Applied Sciences, 11(24), 11657. https://doi.org/10.3390/app112411657










