Robust Control for Non-Minimum Phase Systems with Actuator Faults: Application to Aircraft Longitudinal Flight Control
Abstract
:1. Introduction
- 1.
- Compared with the input state FBL method, which is based on adding hard constraints such as the second-order Lyapunov constraint to ensure the closed-loop stability in the case of NMP dynamics [19], the proposed method ensures a robust and stable closed-loop for the NMP dynamics with actuator faults without any additional constraints.
- 2.
- In contrast with the real-zero elimination, which can be applied only with MIMO systems [10], the proposed method is appropriate for both MIMO and SISO systems without necessitating to reach all the internal states.
- 1.
- In the proposed approach, the fractional-order integral controller (FIC) is augmented with an LQR as a pre-compensator to cope with the non-minimum phase problem.
- 2.
- The implementation of non-integer order derivatives and integrals in the closed-loop to function as a pre-compensator extends the LQR optimal problem from optimizing just the states of the system to optimizing the new augmented dynamics, whereas, in the literature, for example, the integrator is added to the LQR controller loop as an error tracker.
- 3.
- The proposed controller exhibits superior performance even in fault cases that are considered one of the challenges in practical applications.
- 4.
- The fractional-order integral control (FIC) is compared with a fractional-order derivative control (FDC) in terms of internal stability and closed-loop stability.
- 5.
- The feedback controller and the pre-compensator, i.e., feedforward controller parameters are calculated simultaneously to create a more flexible and robust control system.
2. Problem Description, the Proposed Approach, and Aircraft Dynamics
2.1. Non-Minimum Phase Problem
2.2. Proposed Solution
2.3. Aircraft Dynamics
3. Preliminaries
3.1. Fractional-Order Integral Definition
3.2. Fractional-Order Approximation
3.3. Particle Swarm Optimization Algorithm (PSO)
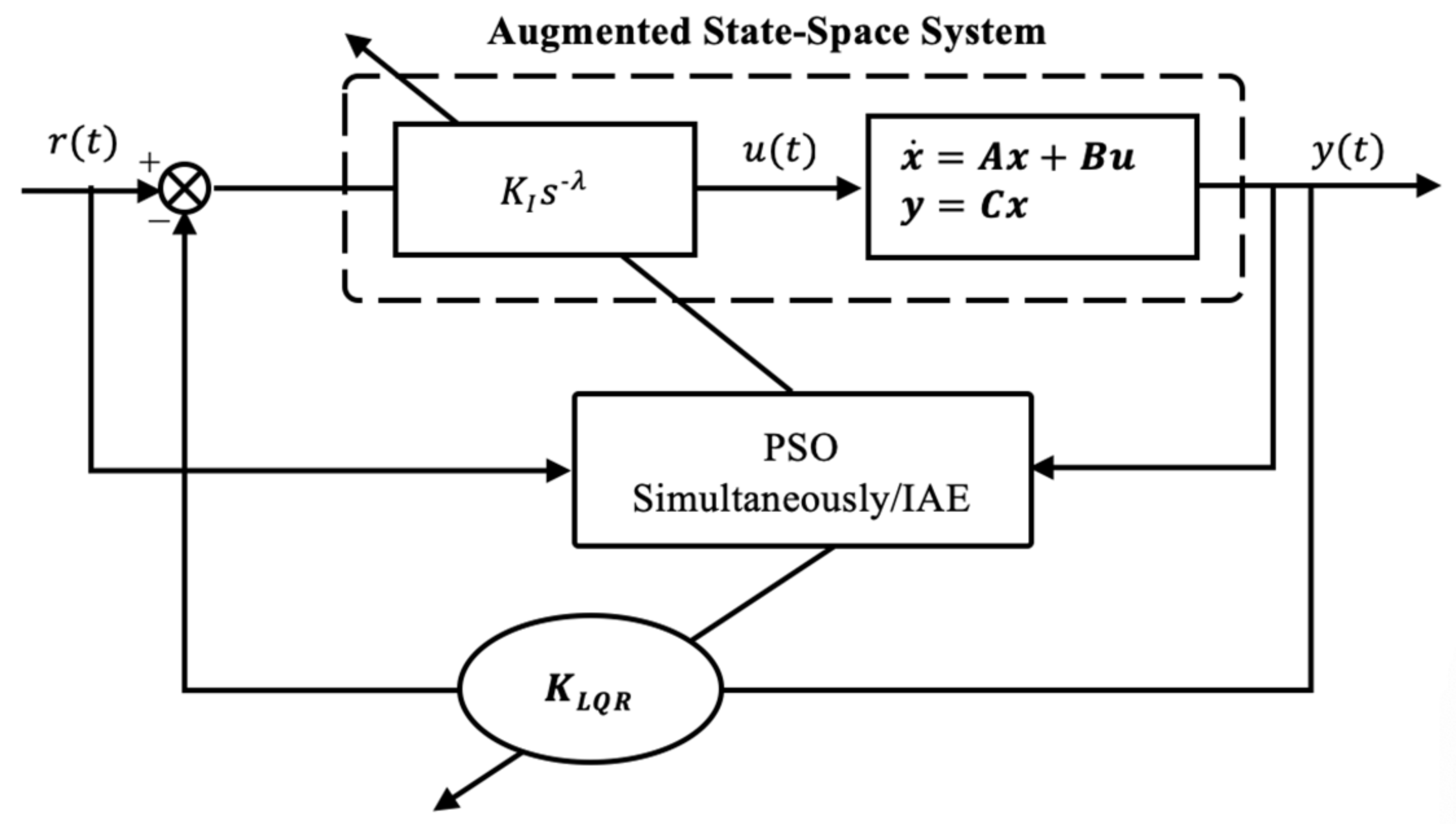
4. Proposed Adaptive Linear Quadratic Regulator with Fractional Integral (LQR-FI) Control Structure
4.1. Augmented State-Space Model
4.2. Mathematical Model and Constraints of the Proposed Controller Based on PSO Optimization
- (1)
- Calculate the real value of eigenvalue of the closed-loop system according to the equation,
- (2)
- Then, according to the obtained eigenvalues in step one, the PSO particles are updated along with position and velocity values with or without constraints as follows: if the position of the pole stays on the right half of the -plane, the objective function, IAE, is allocated to to force the algorithm to find a better solution in the next election. If not, the obtained IAE value is carried out for the next selection.
5. Results and Discussions
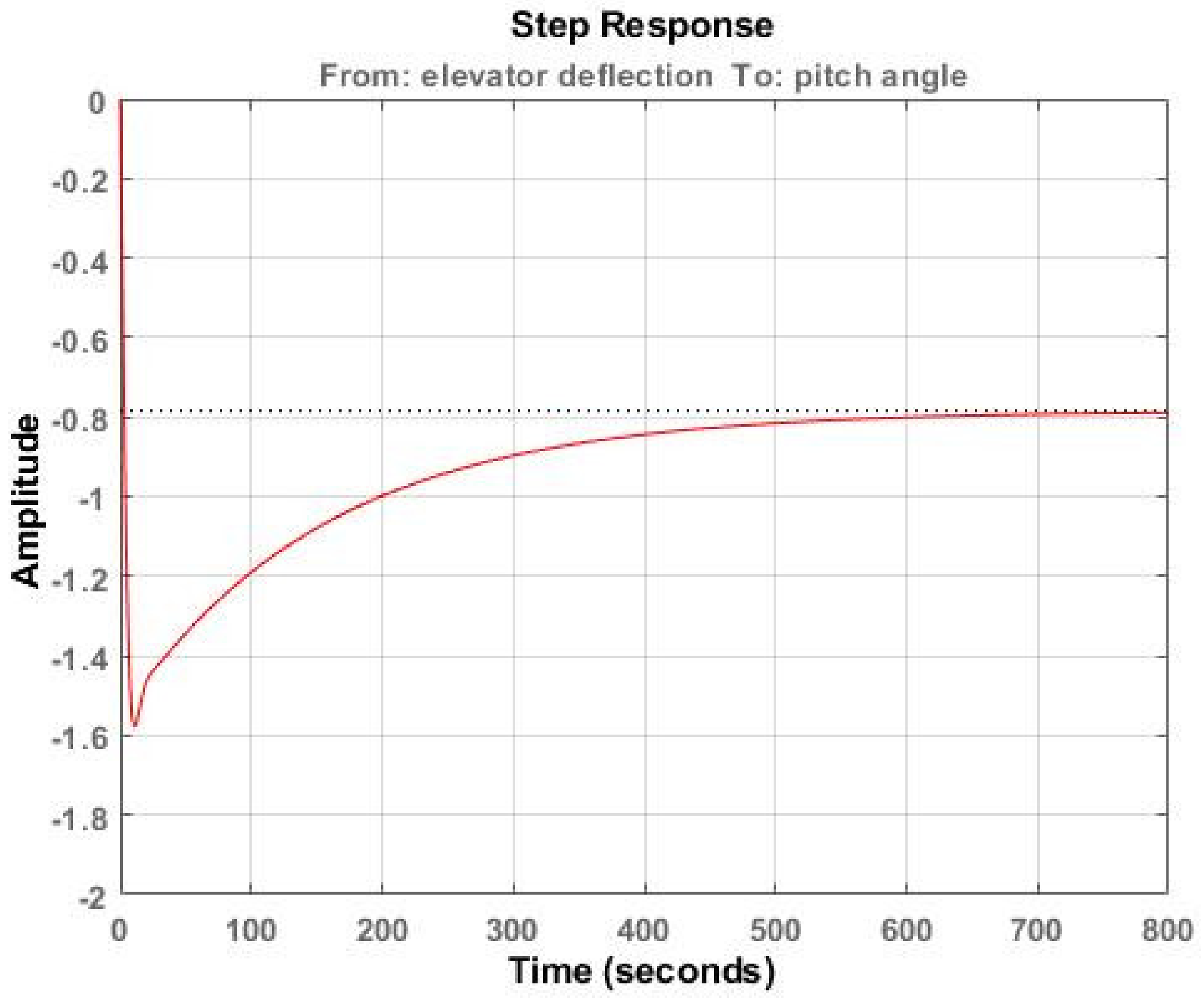
5.1. Open-Loop Step Response: Augmented Dynamics
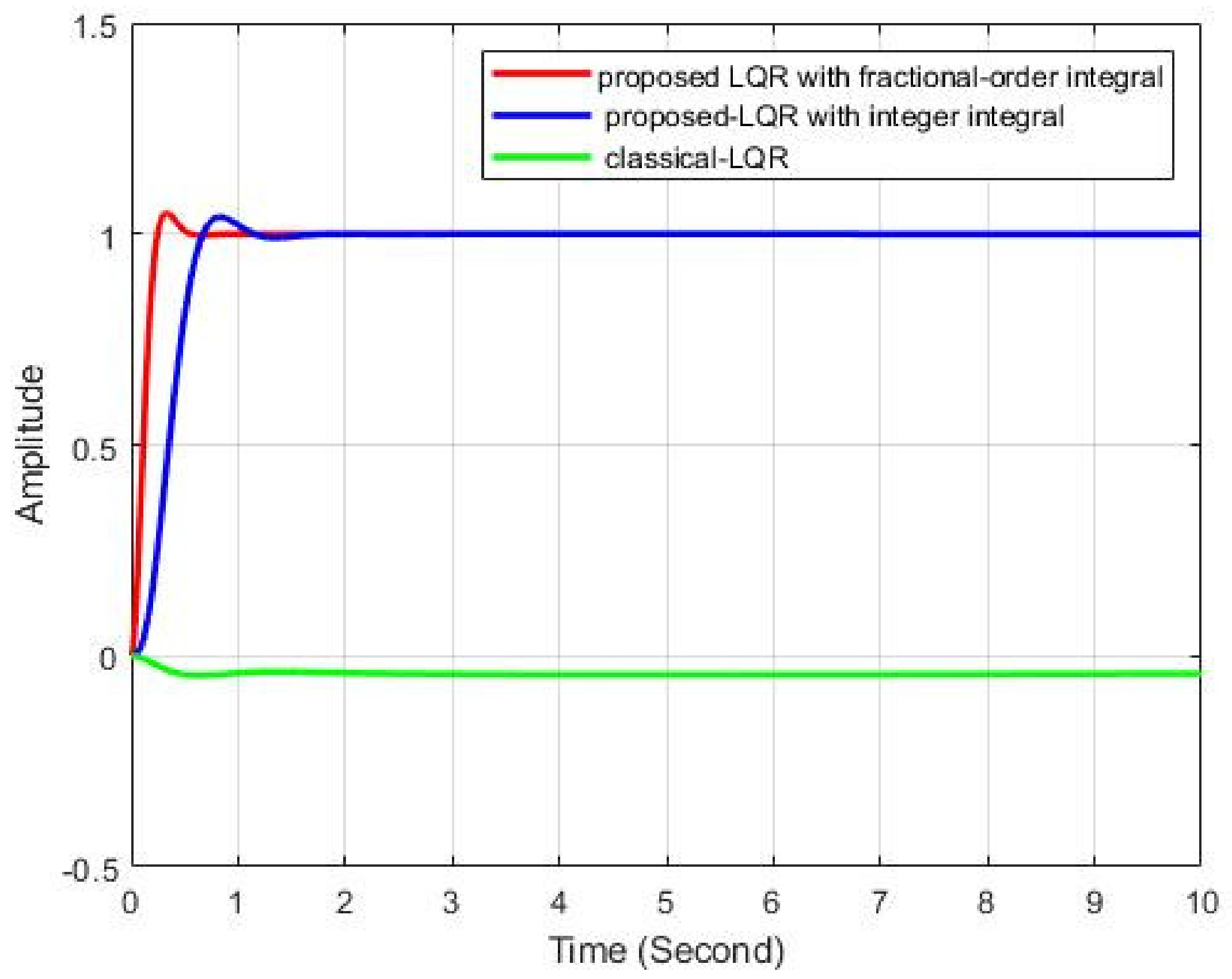
5.2. Closed-Loop Step Response: Proposed LQR-FIC Controller
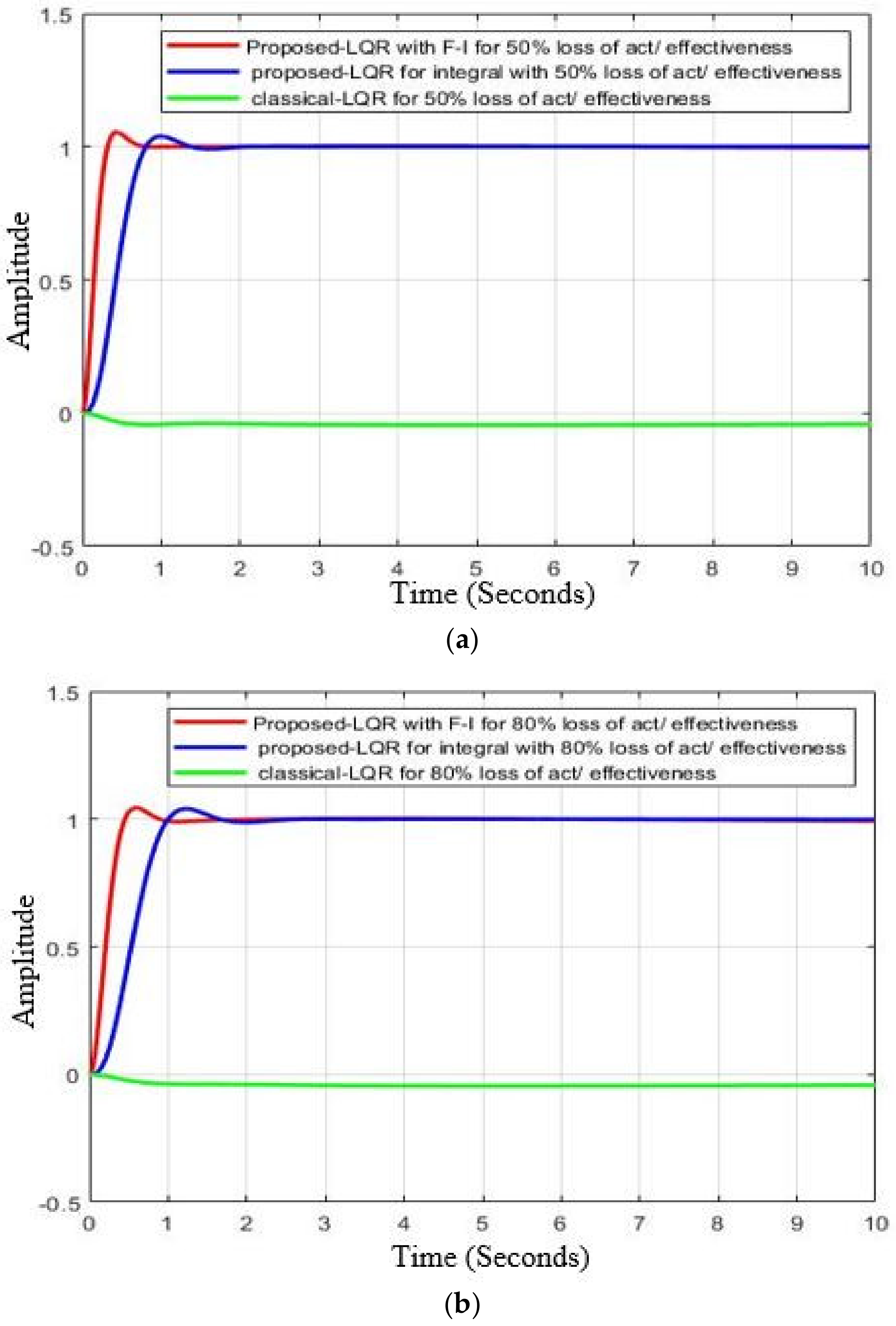
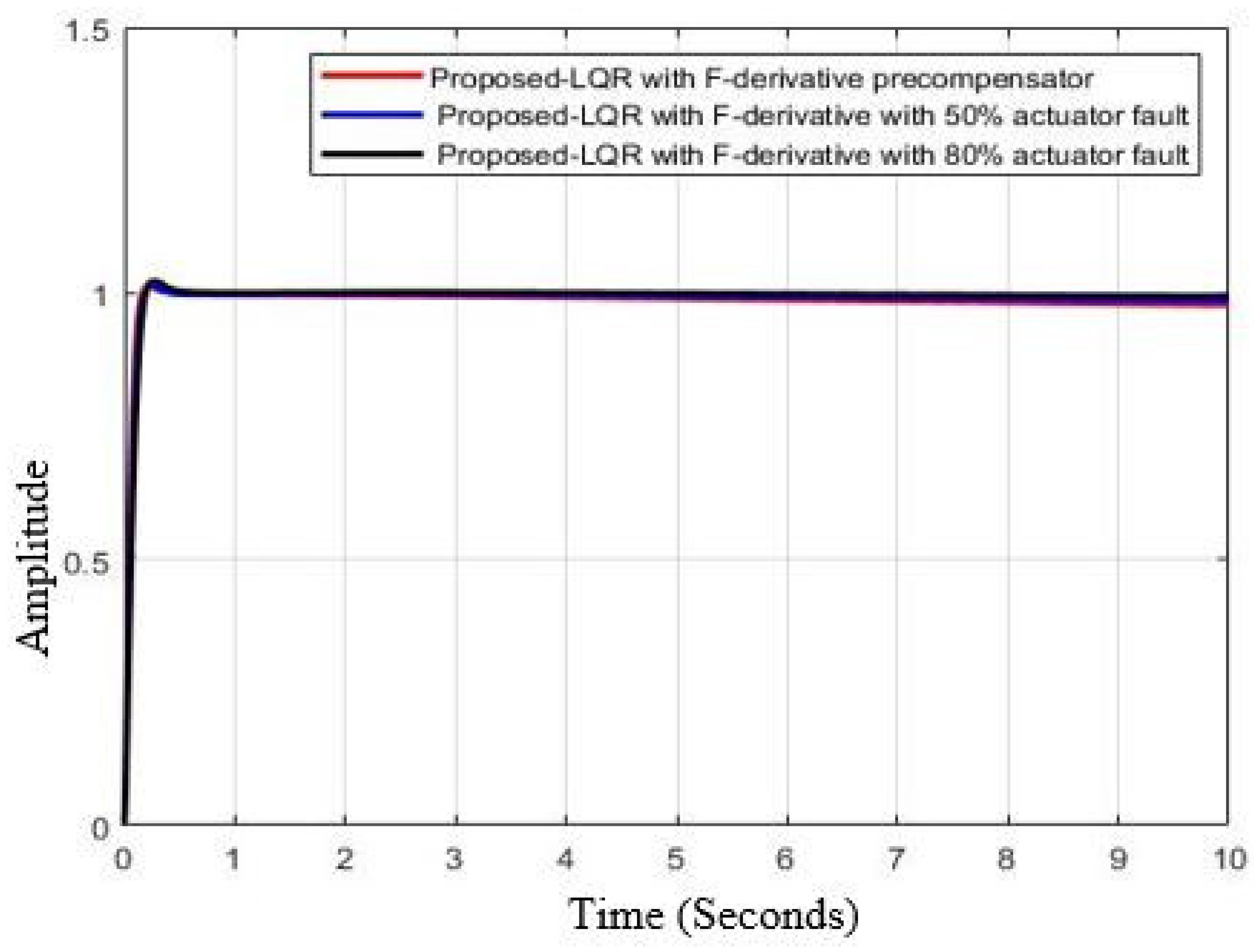
5.3. Proposed LQR-FI Pitch Angle Controller under Fault Flight Condition
5.4. Proposed Structure with FD Pre-Compensator (LQR-FDC): Fault-Free and Fault Flight Conditions
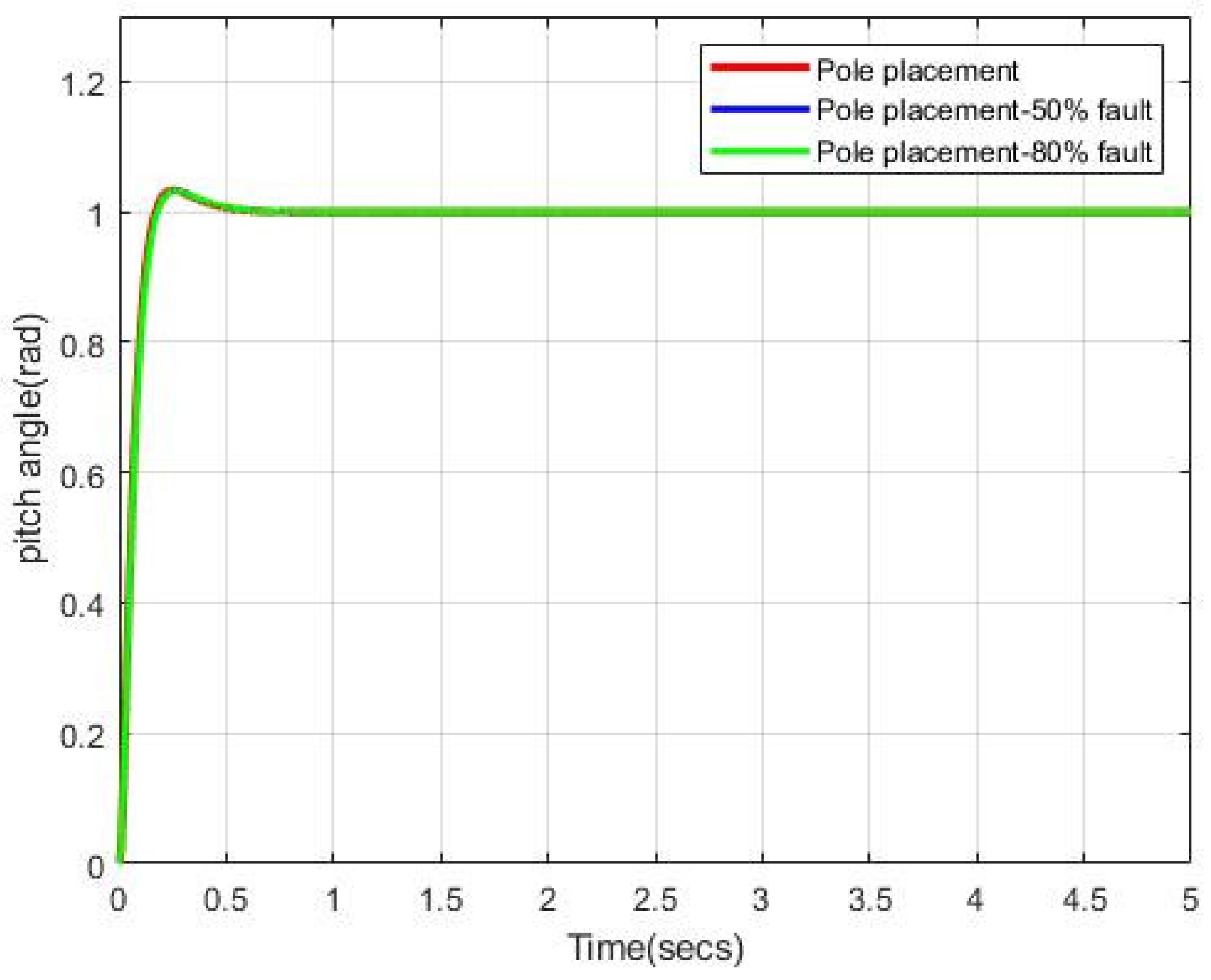
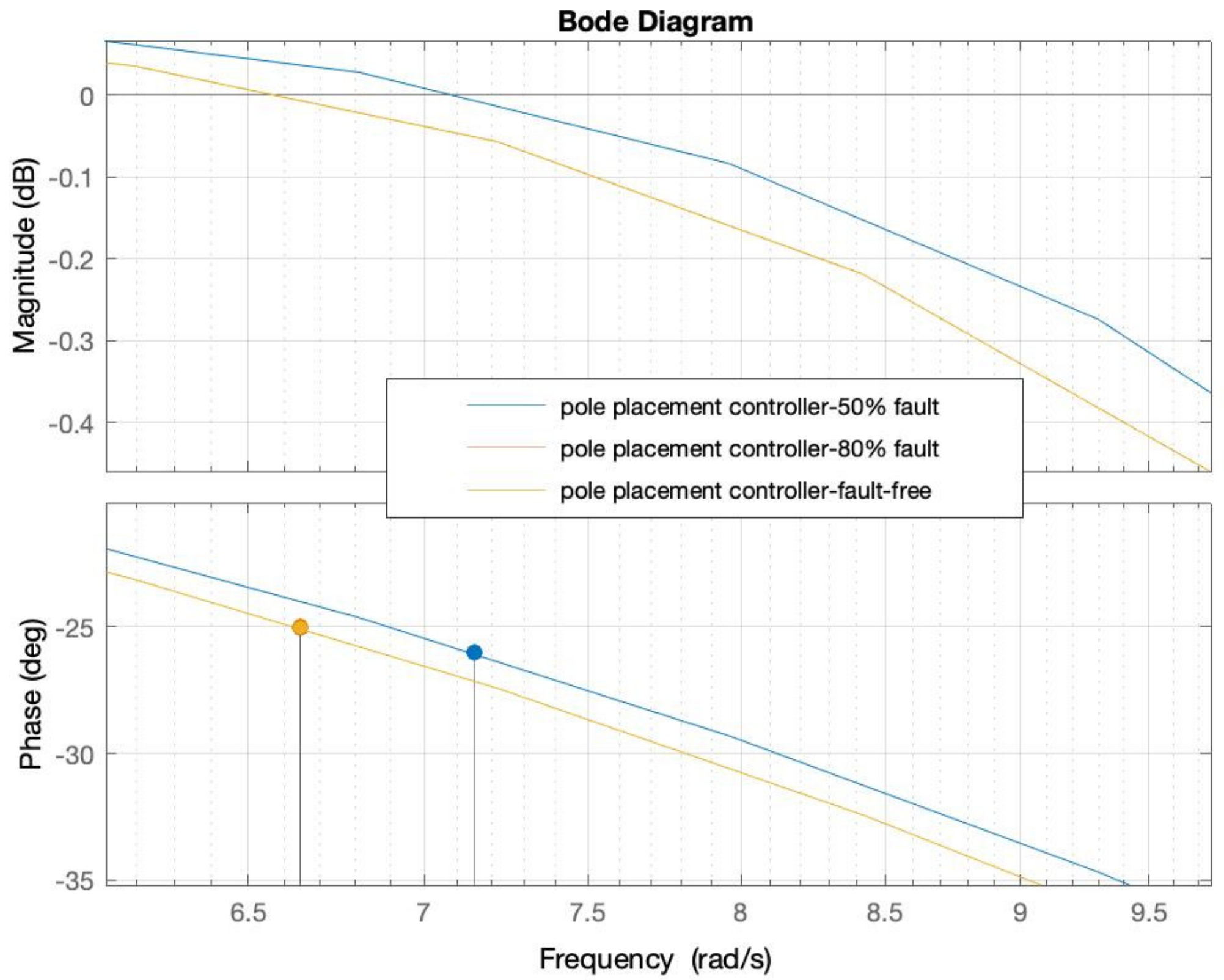
5.5. Proposed LQR-FIC Controller against Pole Placement Controller
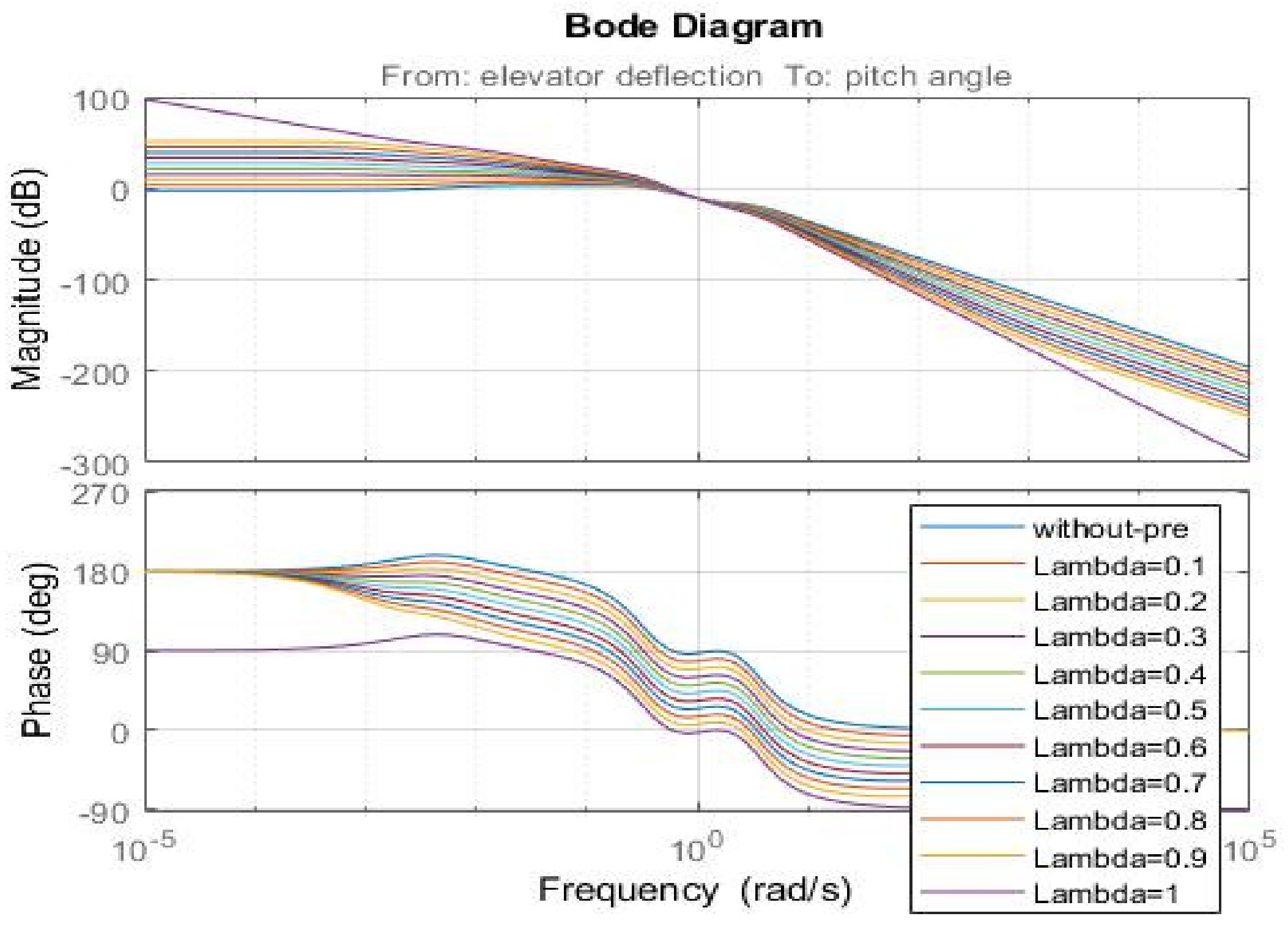
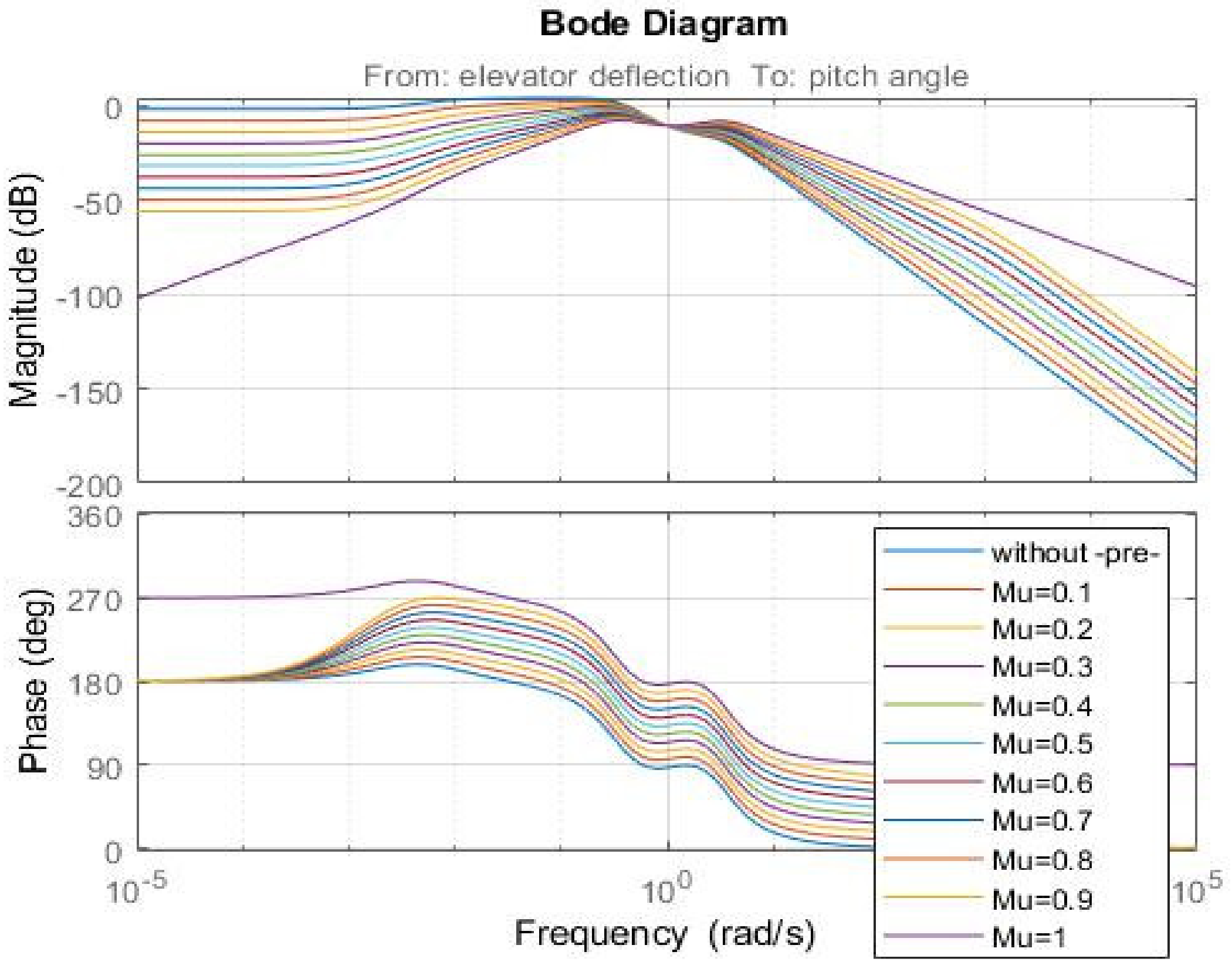
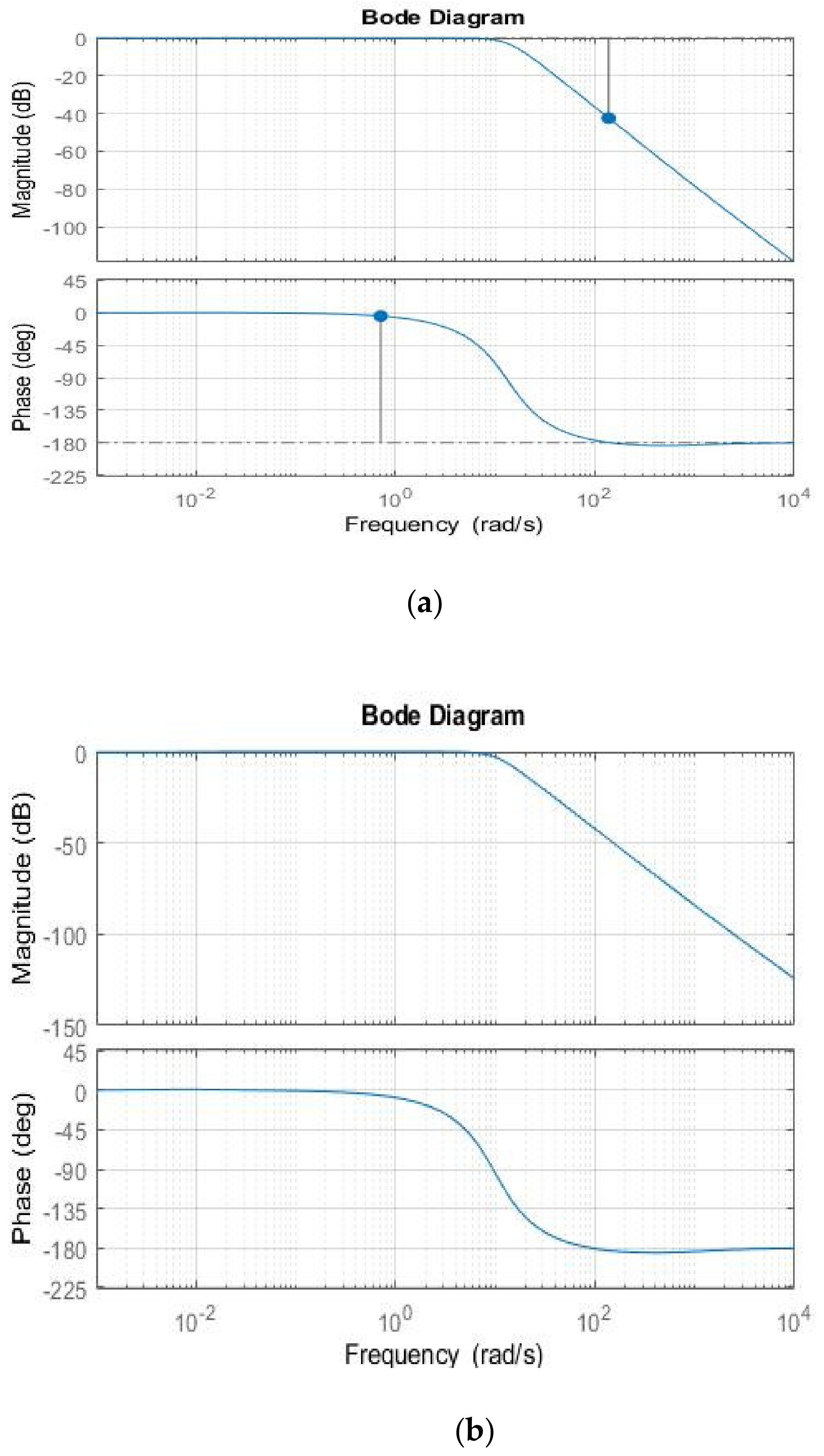
5.6. Effect of Fractional-Order-Based Pre-Compensators on the Phase and Gain Margins of Open- and Closed-Loop Systems
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Approximation of the Fractional-Order Integrator using the Oustaloup Method | |
| Approximation of the fractional−order integrator using Oustaloup method | |
Appendix B
References
- Boeing Commercial Airplanes. Statistical Summary of Commercial Jet Airplane Accidents; Boeing Commercial Airplanes: Seattle, WA, USA, 2015; p. 24. [Google Scholar]
- Boeing Operations. Statistical Summary of Commercial Jet Airplane Accidents Worldwide Operations|1959–2016; Boeing Commercial Airplanes: Seattle, WA, USA, 2017. [Google Scholar]
- Airbus. A Statistical Analysis of Commercial Aviation Accidents 1958–2019; Airbus: Blagnac, France, 2020; p. 22. [Google Scholar]
- Liao, Y.K.; Liao, Y.K. Limitations of non-minimum-phase feedback systems. Int. J. Control 1984, 40, 1003–1013. [Google Scholar] [CrossRef]
- Sidi, M. Gain–bandwidth limitations of feedback systems with non-minimum-phase plants. Int. J. Control 1997, 67, 731–744. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control—Analysis and Design. IEEE Control Syst. 2007, 27, 80–81. [Google Scholar] [CrossRef]
- Estrada, M. Toward the Control of Non-Linear, Non-Minimum Phase Systems via Feedback Linearization and Reinforcement Learning. Master’s Thesis, University of California, Berkeley, CA, USA, 2021. [Google Scholar]
- Benvenuti, L.; di Benedetto, M.D.; Grizzle, J.W. Approximate output tracking for nonlinear non-minimum phase systems with an application to flight control. Int. J. Robust Nonlinear Control 1994, 4, 397–414. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, D. A finite energy property of stable inversion to nonminimum phase nonlinear systems. IEEE Trans. Autom. Control 1998, 43, 1170–1174. [Google Scholar] [CrossRef]
- Rajput, J.; Weiguo, Z. Fundamental methodologies for control of nonlinear non minimum-phase systems: An overview. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2014, 228, 553–564. [Google Scholar] [CrossRef]
- Chen, D.; Paden, B. Stable inversion of nonlinear non-minimum phase systems. Int. J. Control 1996, 64, 81–97. [Google Scholar] [CrossRef]
- Zhou, S.; Helwa, M.K.; Schoellig, A.P. An Inversion-Based Learning Approach for Improving Impromptu Trajectory Tracking of Robots with Non-Minimum Phase Dynamics. IEEE Robot. Autom. Lett. 2018, 3, 1663–1670. [Google Scholar] [CrossRef] [Green Version]
- Guardabassi, G.O.; Savaresi, S.M. Approximate linearization via feedback—An overview. Automatica 2001, 37, 1–15. [Google Scholar] [CrossRef]
- Zietkiewicz, J. Non-minimum phase properties and feedback linearization control of nonlinear chemical reaction. In Proceedings of the 20th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 24–27 August 2015. [Google Scholar] [CrossRef]
- Zhao, S. Practical Solutions to the Non-Minimum Phase and Vibration Problems under the Disturbance Rejection Paradigm. Ph.D. Thesis, Cleveland State University, Cleveland, OH, USA, 2012. [Google Scholar]
- Lee, H.P.; Clemens, J.W.; Youssef, H.M. Dynamic Inversion Flight Control Design for Aircraft with Non-Minimum Phase Response; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2011. [Google Scholar] [CrossRef]
- Hoagg, J.B.; Bernstein, D.S. Nonminimum-phase zeros-much to do about nothing-classical control-revisited part II. IEEE Control Syst. 2007, 27, 45–57. [Google Scholar] [CrossRef]
- Patrick, M.J.; Ishak, N.; Rahiman, M.H.F.; Tajjudin, M.; Adnan, R. Modeling and controller design for non-minimum phase system with application to XY-table. In Proceedings of the 2011 IEEE Control and System Graduate Research Colloquium, Shah Alam, Malaysia, 27–28 June 2011. [Google Scholar]
- Panjapornpon, C.; Soroush, M. Control of non-minimum-phase nonlinear systems through constrained input-output linearization. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar] [CrossRef]
- Terra, M.H.; Cerri, J.P.; Ishihara, J.Y. Optimal robust linear quadratic regulator for systems subject to uncertainties. IEEE Trans. Autom. Control 2014, 59, 2586–2591. [Google Scholar] [CrossRef]
- Tanaka, R.; Koga, T. An approach to linear active disturbance rejection controller design with a linear quadratic regulator for a non-minimum phase system. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; Volume 2019, pp. 250–255. [Google Scholar] [CrossRef]
- Benosman, M.; Le Vey, G. Control of flexible manipulators: A survey. Robotica 2004, 22, 533–545. [Google Scholar] [CrossRef]
- Ghazali, R.; Sam, Y.M.; Rahmat, M.F.A. Point-to-point trajectory tracking with two-degree-of-freedom robust control for a non-minimum phase electro-hydraulic system. In Proceedings of the 10th World Congress on Intelligent Control and Automation, Beijing, China, 6–8 July 2012; pp. 2661–2668. [Google Scholar] [CrossRef]
- Klemm, V.; Morra, A.; Gulich, L.; Mannhart, D.; Rohr, D.; Kamel, M.; de Viragh, Y.; Siegwart, R. LQR-Assisted Whole-Body Control of a Wheeled Bipedal Robot with Kinematic Loops. IEEE Robot. Autom. Lett. 2020, 5, 3745–3752. [Google Scholar] [CrossRef]
- Blight, J.D.; Dailey, R.L.; Gangsaas, D. Practical control law design for aircraft using multivariable techniques. Int. J. Control 1994, 59, 93–137. [Google Scholar] [CrossRef]
- Balas, G.J. Flight control law design: An industry perspective. Eur. J. Control 2003, 9, 207–226. [Google Scholar] [CrossRef]
- Peng, C.; Ma, J. Adaptive Online Data-Driven Tracking Control for Highly Flexible Aircrafts with Partial Observability. IEEE Access 2020, 8, 192844–192856. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, W.; Liu, H. Robust Controller Design of Non-minimum Phase Hypersonic Aircrafts Model based on Quantitative Feedback Theory. J. Astronaut. Sci. 2020, 67, 137–163. [Google Scholar] [CrossRef]
- Al-Hiddabi, S.A.; McClamroch, N.H. Output tracking for nonlinear non-minimum phase VTOL aircraft. In Proceedings of the 37th IEEE Conference on Decision and Control (Cat. No.98CH36171), Tampa, FL, USA, 18 December 1998; Volume 4, pp. 4573–4577. [Google Scholar] [CrossRef]
- Kim, S.; Horspool, K.R. Nonlinear controller design for non-minimum phase flight system enhanced by adaptive elevator algorithm. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; Volume 1, pp. 1–24. [Google Scholar] [CrossRef]
- Tomlin, C.; Lygeros, J.; Benvenuti, L. Output tracking for a non-minimum phase dynamic CTOL aircraft model. In Proceedings of the 34th IEEE Conference on Decision and Control, New Orleans, LA, USA, 13–15 December 1995. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Hu, X.; Wang, X.; Guo, Y. Robust Adaptive Control for Uncertain Input Delay MIMO Nonlinear Non-Minimum Phase System: A Fuzzy Approach. IEEE Access 2020, 8, 154143–154152. [Google Scholar] [CrossRef]
- Ahmadi, A.; Mohammadi-Ivatloo, B.; Anvari-Moghaddam, A.; Marzband, M. Optimal robust LQI controller design for Z-source inverters. Appl. Sci. 2020, 10, 7260. [Google Scholar] [CrossRef]
- Souza, D.A.; de Mesquita, V.A.; Reis, L.L.N.; Silva, W.A.; Batista, J.G. Optimal LQI and PID Synthesis for Speed Control of Switched Reluctance Motor Using Metaheuristic Techniques. Int. J. Control Autom. Syst. 2021, 19, 221–229. [Google Scholar] [CrossRef]
- Birs, I.; Nascu, I.; Ionescu, C.; Muresan, C. Event-based fractional order control. J. Adv. Res. 2020, 25, 191–203. [Google Scholar] [CrossRef] [PubMed]
- De Almeida, A.M.; Lenzi, M.K.; Lenzi, E.K. A survey of fractional order calculus applications of multiple-input, multiple-output (Mimo) process control. Fractal Fract. 2020, 4, 22. [Google Scholar] [CrossRef]
- Shi, X.; Cheng, Y.; Yin, C.; Zhong, S.; Huang, X.; Chen, K.; Qiu, G. Adaptive Fractional-Order SMC Controller Design for Unmanned Quadrotor Helicopter under Actuator Fault and Disturbances. IEEE Access 2020, 8, 103792–103802. [Google Scholar] [CrossRef]
- Cieslak, J.; Henry, D.; Zolghadri, A. Fault tolerant flight control: From theory to piloted flight simulator experiments. IET Control Theory Appl. 2010, 4, 1451–1464. [Google Scholar] [CrossRef]
- Nie, C. Observer-Based Robust Fault Estimation For Fault-Tolerant Control. Ph.D. Thesis, Department of Engineering, The University of Hull, Hull, UK, 2012. [Google Scholar]
- Liu, Y.; Dong, X.; Ren, Z.; Cooper, J. Fault-tolerant control for commercial aircraft with actuator faults and constraints. J. Frankl. Inst. 2019, 356, 3849–3868. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Jiang, J. Bibliographical review on reconfigurable fault-tolerant control systems. Annu. Rev. Control 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Xingjian, W.; Shaoping, W.; Zhongwei, Y.; Chao, Z. Active fault-tolerant control strategy of large civil aircraft under elevator failures. Chin. J. Aeronaut. 2015, 28, 1658–1666. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Wang, J. Passive Actuator Fault-Tolerant Control for a Class of Overactuated Nonlinear Systems and Applications to Electric Vehicles. IEEE Trans. Veh. Technol. 2013, 62, 972–985. [Google Scholar] [CrossRef]
- Mirshams, M.; Khosrojerdi, M.; Hasani, M. Passive fault-tolerant sliding mode attitude control for flexible spacecraft with faulty thrusters. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 2343–2357. [Google Scholar] [CrossRef]
- Ijaz, S.; Hamayun, M.T.; Yan, L.; Shi, C. Active fault-tolerant control for vertical tail damaged aircraft with dissimilar redundant actuation system using integral sliding mode control. J. Mech. Eng. Sci. 2018, 29, 1–18. [Google Scholar] [CrossRef]
- Abbaspour, A.; Yen, K.K.; Forouzannezhad, P.; Sargolzaei, A. A Neural Adaptive Approach for Active Fault-Tolerant Control Design in UAV. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 3401–3411. [Google Scholar] [CrossRef]
- Sun, X.; Wang, X.; Zhou, Z.; Zhou, Z. Active Fault-Tolerant Control Strategy for More Electric Aircraft under Actuation System Failure. J. Actuators 2020, 9, 122. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Jiang, J. Issues on integration of fault diagnosis and reconfigurable control in active fault-tolerant control systems. IFAC Proc. 2006, 39, 1437–1448. [Google Scholar] [CrossRef]
- Lee, T.H.; Lim, C.P.; Nahavandi, S.; Roberts, R.G. Observer-Based H_inf Fault-Tolerant Control for Linear Systems with Sensor and Actuator Faults. IEEE Syst.J. 2019, 13, 1981–1990. [Google Scholar] [CrossRef]
- Ru, J.; Li, X.R. Variable-Structure Multiple-Model Approach to Fault Detection, Identification, and Estimation. IEEE Trans. Control Syst. Technol. 2008, 16, 1029–1038. [Google Scholar] [CrossRef]
- Sweilam, N.H.; AL-Mekhlafi, S.M.; Baleanu, D. A hybrid fractional optimal control for a novel Coronavirus (2019-nCov) mathematical model. J. Adv. Res. 2020, 32, 149–160. [Google Scholar] [CrossRef]
- Esteban, A.M. Aircraft Applications of Fault Detection and Isolation Techniques. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2004. [Google Scholar]
- Matychyn, I.; Onyshchenko, V. Optimal control of linear systems of arbitrary fractional order. Fract. Calculus Appl. Anal. 2019, 22, 170–179. [Google Scholar] [CrossRef]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB; Advances in Industrial Control; Grimble, M.J., Johnson, M.A., Eds.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; ISSN 1430-9491. [Google Scholar]
- Viaro, U. On the rational approximation of fractional order systems. In Proceedings of the 2011 16th International Conference on Methods & Models in Automation & Robotics, Miedzyzdroje, Poland, 22–25 August 2011; pp. 132–136. [Google Scholar]
- Ranaee, V.; Ebrahimzadeh, A.; Ghaderi, R. Application of the PSO–SVM model for recognition of control chart patterns. J. ISA Trans. 2010, 49, 577–586. [Google Scholar] [CrossRef]
- Barbieri, R.; Barbieri, N.; De Lima, K.F. Some applications of the PSO for optimization of acoustic filters. J. Appl. Acoust. 2015, 89, 62–70. [Google Scholar] [CrossRef]
- Doctor, S.; Venayagamoorthy, G.K.; Gudise, V.G. Optimal PSO for collective robotic search applications. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No. 04TH8753), Portland, OR, USA, 19–23 June 2004; pp. 1390–1395. [Google Scholar]
- Guo, W. Gain Scheduling for a Passengeraircraft Control System to Satisfy Handling Qualities; Cranfield University: Silsoe, UK, 2010. [Google Scholar]
- Qian, Z.Z.; Zhai, X.H. Flight Control Law Design via Pole Placement. Adv. Mater. Res. 2012, 466–467, 1202–1206. [Google Scholar] [CrossRef]
- Andrade, J.P.P.; Campos, V.A.F. Robust Control of a Dynamic Model of an F-16 Aircraft with Improved Damping through Linear Matrix Inequalities. World Acad. Sci. Eng. Technol. Int. J. Comput. Inf. Eng. 2017, 11, 230–236. [Google Scholar]
- Wahab, A.A.; Mamat, R.; Shamsudin, S.S. The Effectiveness of Pole Placement Method in Control System Design for an Autonomous Helicopter Model in Hovering Flight. Int. J. Integr. Eng. 2009, 1, 33–46. [Google Scholar]


| Parameters | LQR-FIC and LQR-IC | LQR-FDC | Classical-LQR | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fault-Free | 50% Fault | 80% Fault | Fault-Free | 50% Fault | 80% Fault | Fault-Free | 50% Fault | 80% Fault | ||||
| LQR-FIC | LQR-IC | LQR-FIC | LQR-IC | LQR-FIC | LQR-IC | LQR-FDC | LQR-FDC | LQR-FDC | LQR | LQR | LQR | |
| IAE | 0.0138 | 0.0386 | 0.0183 | 0.0453 | 0.0255 | 0.0568 | 0.0043 | 0.0061 | 0.0101 | 1.0436 | 1.0416 | 1.0428 |
| −149.9 | −150 | −150 | −149.9 | −150 | −150 | −150 | −149.99 | −150 | - | - | ||
| 0.1 | 1 | 0.1 | 1 | 0.1 | 1 | 0.6 | 0.6 | 0.5 | - | - | ||
| 0.01 | 0.01 | 0.01 | 1.2887 | 0.0105 | 0.8077 | 0.01 | 0.01 | 0.01 | 10 | 10 | 10 | |
| 0.0409 | 0.01 | 0.0358 | 0.0419 | 0.01 | 0.0248 | 0.01 | 0.01 | 0.01 | 10 | 10 | 10 | |
| 0.4453 | 0.8318 | 0.3258 | 0.5953 | 0.5015 | 0.4684 | 0.18 | 0.8237 | 0.01 | 10 | 10 | 10 | |
| 89.4723 | 96.1881 | 69.48 | 87.986 | 87.745 | 92.616 | 788.72 | 974.16 | 984.8474 | 1000 | 1000 | 1000 | |
| 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 10 | 10 | 10 | |
| 99.873 | 100 | 79 | 98 | 92 | 99.4215 | 797.77 | 986.24 | 999.9998 | 10 | 10 | 10 | |
| Controller | IAE | P1 | P2 | P3 | P4 | P5 | Forward Negative Scaling Factor |
|---|---|---|---|---|---|---|---|
| Pole placement-Fault free | 0.0704 | −50.117 | −10.420 | −14.27 | −14.200 | −1.26 | −627.4238 |
| Pole placement-50% Fault free | 0.0728 | −50.117 | −47.777 | −9.29 | −14.274 | −1.21 | −599.9231 |
| Pole placement-80% Fault free | 0.0728 | −50.117 | −47.769 | −9.29 | −14.274 | −1.21 | −599.9041 |
| Adaptive Fractional Integral Pre-Compensator (AFI) | Adaptive Fractional Derivative Pre-Compensator (AFD) | Pole Placement Controller | |
|---|---|---|---|
| Gain Margin (dB) | 42.4 | 34.8 | Inf |
| Phase Margin (deg) | 175 | 171 | 155 |
| Delay margin (second) | 4.3 | 0.419 | 0.472 |
| 50% loss of actuator effectiveness | |||
| Gain Margin (dB) | 51.2 | 48.2 | Inf |
| Phase Margin (deg) | 162 | 162 | 154 |
| Delay margin (sec) | 1.85 | 0.71 | 0.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sir Elkhatem, A.; Engin, S.N.; Pasha, A.A.; Rahman, M.M.; Pillai, S.N. Robust Control for Non-Minimum Phase Systems with Actuator Faults: Application to Aircraft Longitudinal Flight Control. Appl. Sci. 2021, 11, 11705. https://doi.org/10.3390/app112411705
Sir Elkhatem A, Engin SN, Pasha AA, Rahman MM, Pillai SN. Robust Control for Non-Minimum Phase Systems with Actuator Faults: Application to Aircraft Longitudinal Flight Control. Applied Sciences. 2021; 11(24):11705. https://doi.org/10.3390/app112411705
Chicago/Turabian StyleSir Elkhatem, Aisha, Seref Naci Engin, Amjad Ali Pasha, Mustafa Mutiur Rahman, and Subramania Nadaraja Pillai. 2021. "Robust Control for Non-Minimum Phase Systems with Actuator Faults: Application to Aircraft Longitudinal Flight Control" Applied Sciences 11, no. 24: 11705. https://doi.org/10.3390/app112411705






