Cyber-Physical LPG Debutanizer Distillation Columns: Machine-Learning-Based Soft Sensors for Product Quality Monitoring
Abstract
:Featured Application
Abstract
1. Introduction
- a machine-learning model to predict C5 content in LPG stream;
- a machine-learning model to predict if C5 content exceeds specification levels
2. Related work
2.1. Distillation Process-Related Models
2.2. Explainable Artificial Intelligence
3. Problem Statement
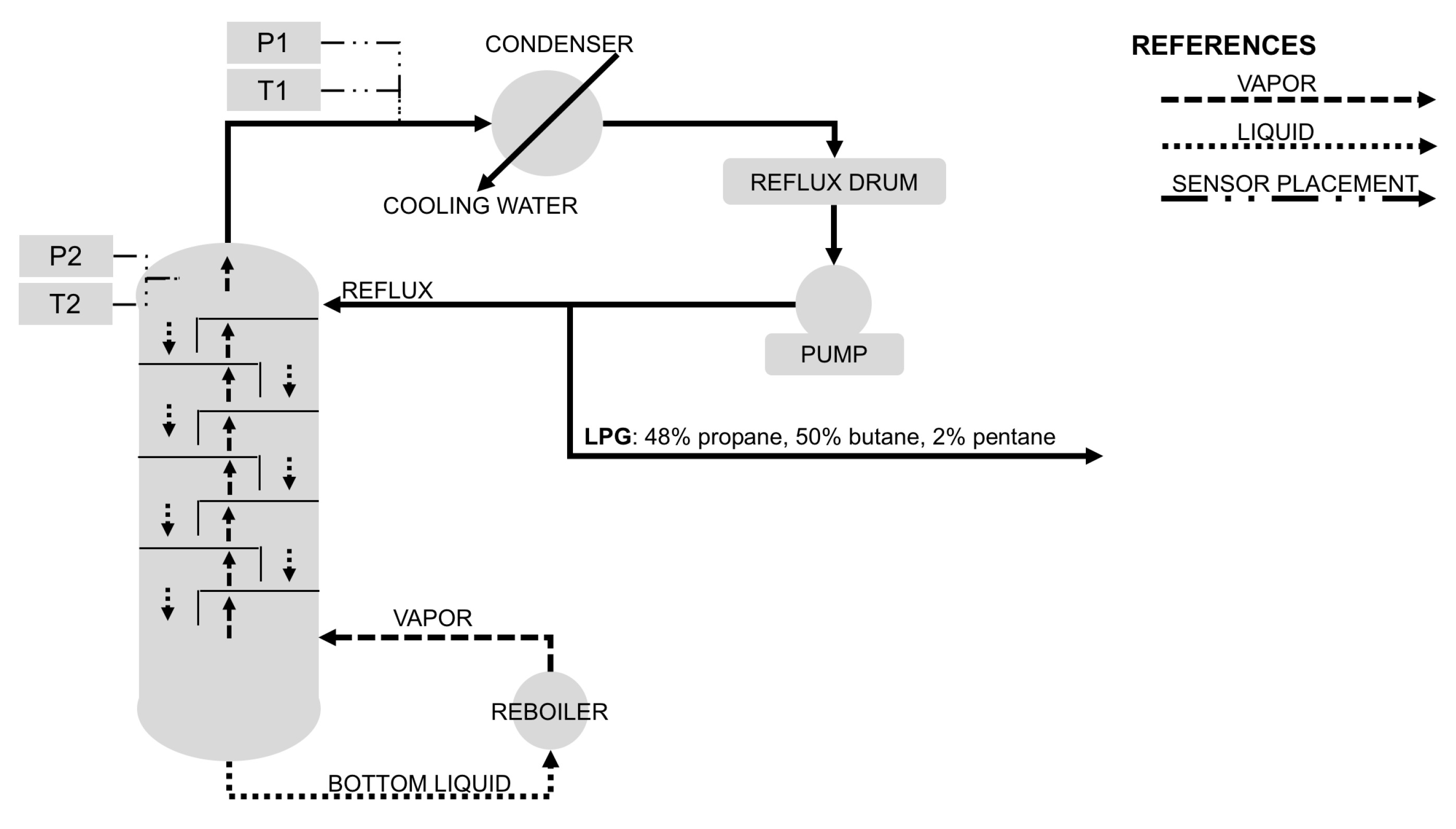
3.1. Tüpras Refinery
3.2. Debutanization Process
3.3. Relevant Physical and Chemical Principles and Laws
- Raoult’s law states that the total pressure of a component equals the vapor pressure of its pure components multiplied by their mole fraction (see Equation (1));
- Antoine’s equations provide a relationship between the vapor pressure of a pure component and three empirically measured constants at a given temperature (see Equation (2));
- Combined Gas Law states that the ratio of the product of pressure and volume and the absolute temperature of a gas equal a constant (see Equation (3));
- Clausius-Clapeyron relation describes pressure at a given temperature T2 if the enthalpy of vaporization and vapor pressure are known at some other temperature T1 (see Equation (4))
4. Methodology
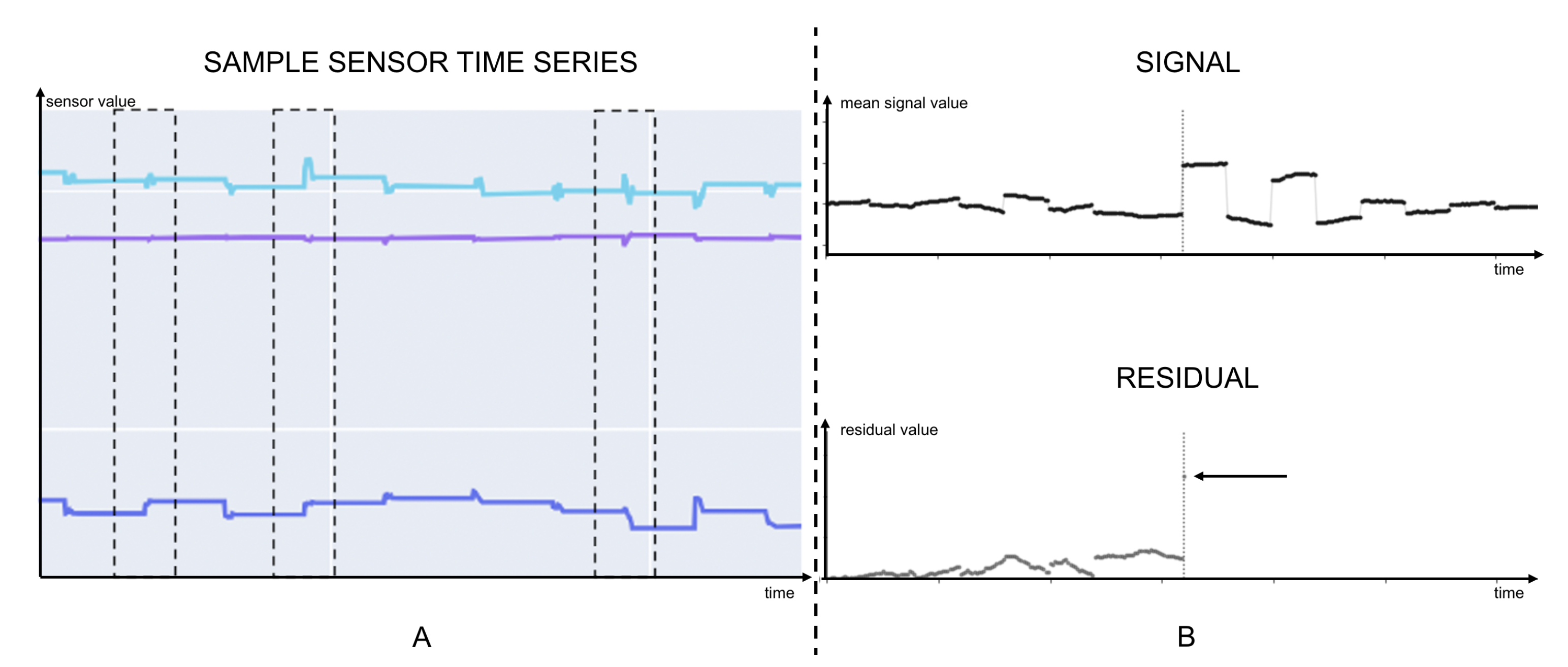
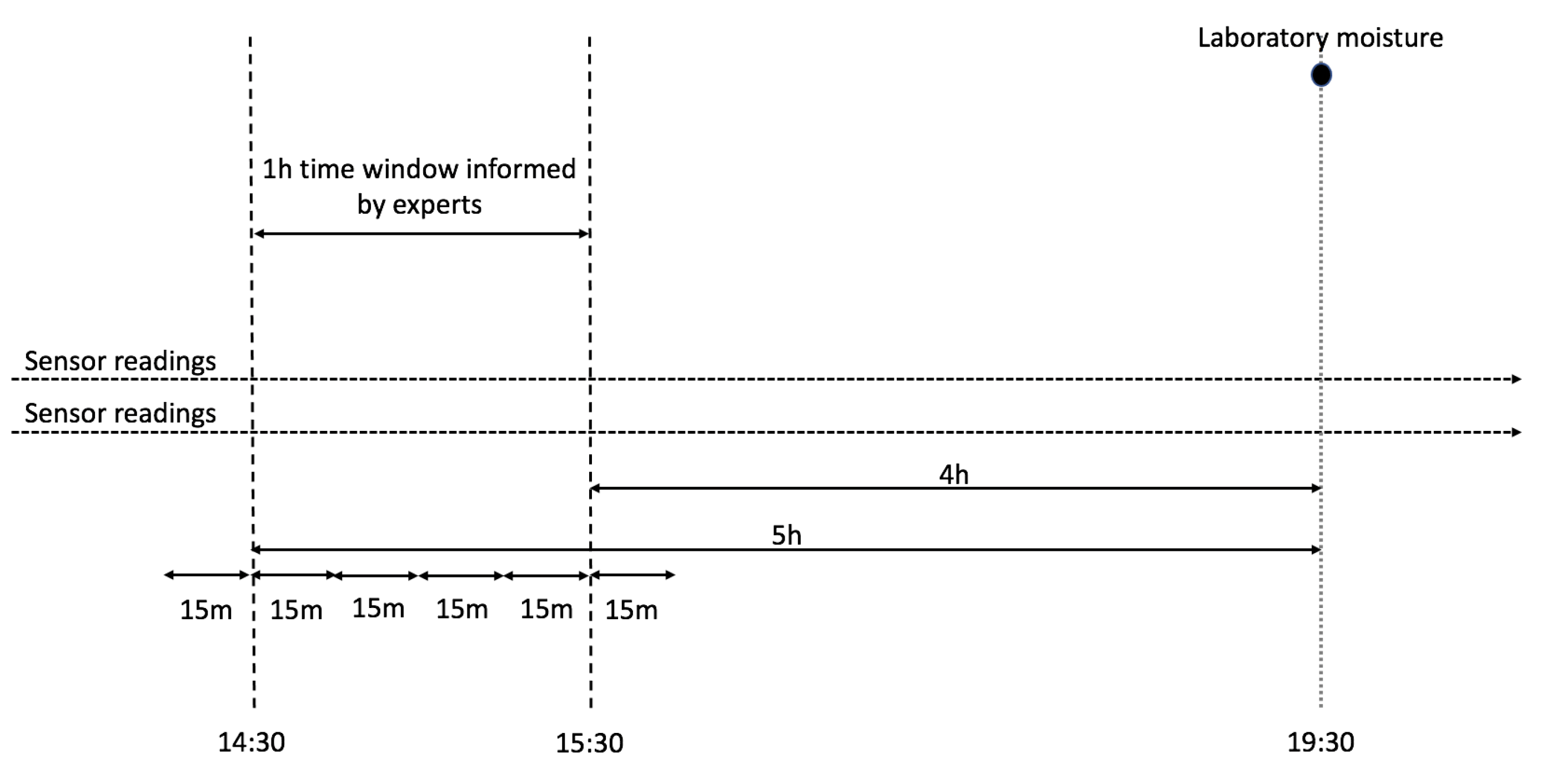
4.1. Data Preparation
4.2. Data Analysis
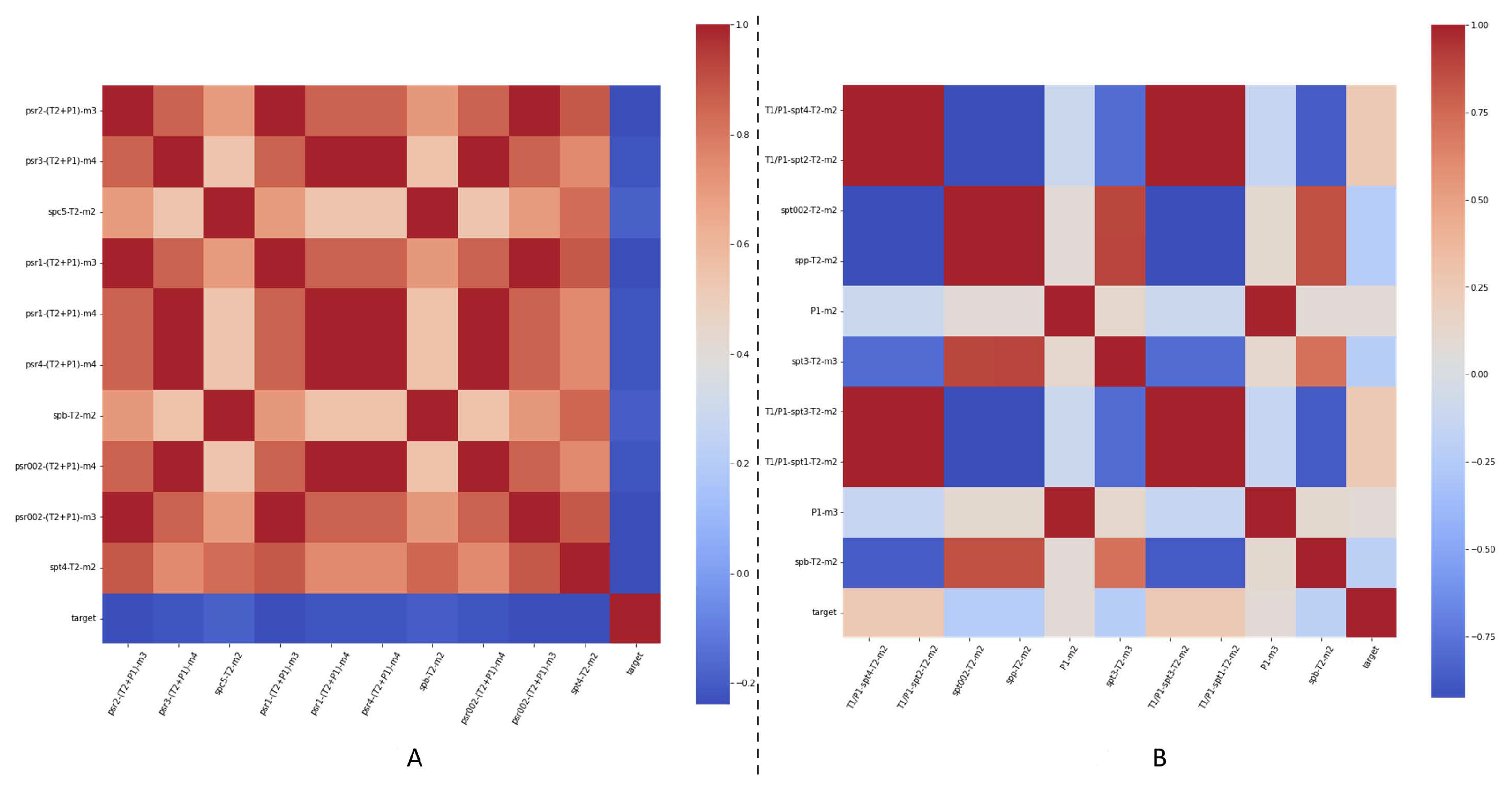
4.3. Feature Creation
4.4. Machine-Learning Model Development
4.4.1. Regression Machine Learning Models
- Baseline 1 (C5 median): our prediction is the median of C5 values observed in the data set for model training;
- Model 2 (SVR): Support Vector Regressor [84], which takes into account most relevant features assessed over all created features;
- Model 3 (MLPR): Multi-layer Perceptron regressor [85], which takes into account most relevant features assessed over all created features;
- Model 4 (VR): composite model introduced in Figure 9, and described in detail later in this section. The model takes into account most relevant features assessed over all created features.
4.4.2. Classification Machine Learning Models
- Baseline 1 (zero forecast): we predict no off-spec occurrence takes place;
- Model 2 (SVC): Support Vector Classifier [84], which takes into account most relevant features assessed over all created features;
- Model 3 (MLPC): Multi-layer Perceptron Classifier [85], which takes into account most relevant features assessed over all created features;
- Model 4 (CatBoost): a CatBoost classifier with a Focal loss [92], which provides an asymmetric penalization to training instances, focusing more on those that are misclassified. The model takes into account most relevant features assessed over all created features.
5. Experiments and Results
5.1. Regression Models
5.2. Classification Models
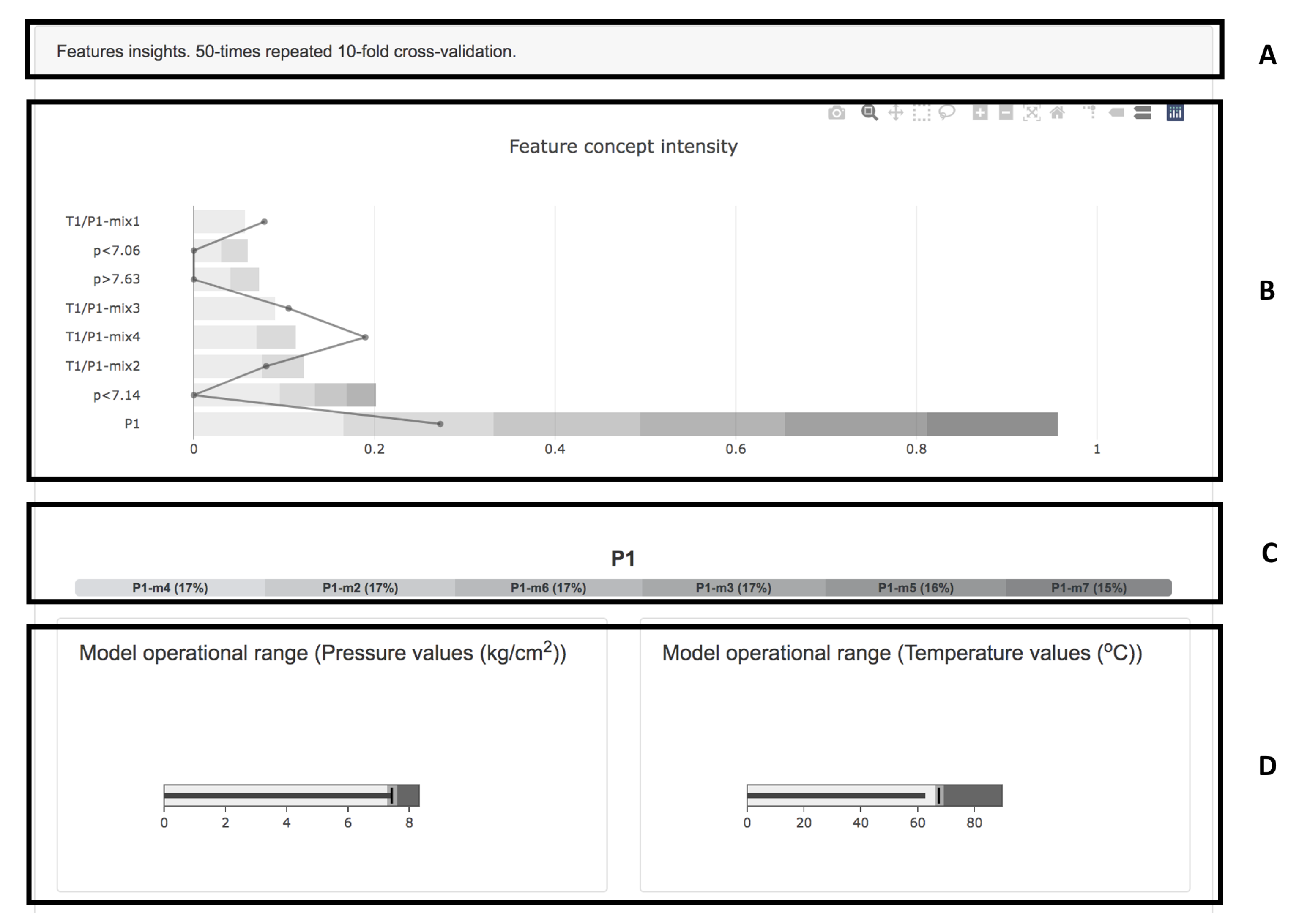
5.3. Explaining Artificial Intelligence Models
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| APC | Advanced Process Control |
| AUC ROC | Area Under the Receiver Operating Characteristic Curve |
| C1 | Molecules with a single carbon atom |
| C2 | Molecules with two carbon atoms |
| C4 | Molecules with four carbon atoms |
| C5 | Pentanes |
| CDU | Crude Distillation Unit |
| FCC | Fluid Catalytic Cracker |
| FG | Features Group |
| LgR | Logistic Regression |
| LiR | Linear Regression |
| LPG | Liquified Petroleum Gas |
| MAE | Mean Absolute Error |
| MLPC | Multi-layer Perceptron Classifier |
| MLPR | Multi-layer Perceptron regressor |
| MPC | Multivariable Model Predictive Control |
| ReLU | Rectified Linear Unit |
| RMSE | Root Mean Squared Error |
| SVC | Support Vector Classifier |
| SVR | Support Vector Regressor |
| VR | Voting Regressor |
References
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef] [Green Version]
- Ferrer-Nadal, S.; Yélamos-Ruiz, I.; Graells, M.; Puigjaner, L. On-line fault diagnosis support for real time evolution applied to multi-component distillation. In Proceedings of the European Symposium on Computer-Aided Process Engineering-15, 38th European Symposium of the Working Party on Computer Aided Process Engineering, Barcelona, Spain, 29 May–1 June; Puigjaner, L., Espuña, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 20, pp. 961–966. [Google Scholar] [CrossRef]
- Abdullah, Z.; Aziz, N.; Ahmad, Z. Nonlinear Modelling Application in Distillation Column. Chem. Prod. Process. Model. 2007, 2. [Google Scholar] [CrossRef]
- Michelsen, F.A.; Foss, B.A. A comprehensive mechanistic model of a continuous Kamyr digester. Appl. Math. Model. 1996, 20, 523–533. [Google Scholar] [CrossRef]
- Franzoi, R.E.; Menezes, B.C.; Kelly, J.D.; Gut, J.A.; Grossmann, I.E. Cutpoint Temperature Surrogate Modeling for Distillation Yields and Properties. Ind. Eng. Chem. Res. 2020, 59, 18616–18628. [Google Scholar] [CrossRef]
- Friedman, Y.; Neto, E.; Porfirio, C. First-principles distillation inference models for product quality prediction. Hydrocarb. Process. 2002, 81, 53–60. [Google Scholar]
- Garcia, A.; Loria, J.; Marin, A.; Quiroz, A. Simple multicomponent batch distillation procedure with a variable reflux policy. Braz. J. Chem. Eng. 2014, 31, 531–542. [Google Scholar] [CrossRef]
- Ryu, J.; Maravelias, C.T. Computationally efficient optimization models for preliminary distillation column design and separation energy targeting. Comput. Chem. Eng. 2020, 143, 107072. [Google Scholar] [CrossRef]
- Küsel, R.R.; Wiid, A.J.; Craig, I.K. Soft sensor design for the optimisation of parallel debutaniser columns: An industrial case study. IFAC-PapersOnLine 2020, 53, 11716–11721. [Google Scholar] [CrossRef]
- Ibrahim, D.; Jobson, M.; Guillen-Gosalbez, G. Optimization-based design of crude oil distillation units using rigorous simulation models. Ind. Eng. Chem. Res. 2017, 56, 6728–6740. [Google Scholar] [CrossRef] [Green Version]
- Schäfer, P.; Caspari, A.; Schweidtmann, A.M.; Vaupel, Y.; Mhamdi, A.; Mitsos, A. The Potential of Hybrid Mechanistic/Data-Driven Approaches for Reduced Dynamic Modeling: Application to Distillation Columns. Chem. Ing. Tech. 2020, 92, 1910–1920. [Google Scholar] [CrossRef]
- Bachnas, A.; Tóth, R.; Ludlage, J.; Mesbah, A. A review on data-driven linear parameter-varying modeling approaches: A high-purity distillation column case study. J. Process. Control 2014, 24, 272–285. [Google Scholar] [CrossRef] [Green Version]
- Eikens, B.; Karim, M.N.; Simon, L. Neural Networks and First Principle Models for Bioprocesses. IFAC Proc. Vol. 1999, 32, 6974–6979. [Google Scholar] [CrossRef]
- McBride, K.; Sanchez Medina, E.I.; Sundmacher, K. Hybrid Semi-parametric Modeling in Separation Processes: A Review. Chem. Ing. Tech. 2020, 92, 842–855. [Google Scholar] [CrossRef]
- Schweidtmann, A.M.; Bongartz, D.; Huster, W.R.; Mitsos, A. Deterministic global process optimization: Flash calculations via artificial neural networks. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2019; Volume 46, pp. 937–942. [Google Scholar]
- van Lith, P.F.; Betlem, B.H.; Roffel, B. Combining prior knowledge with data driven modeling of a batch distillation column including start-up. Comput. Chem. Eng. 2003, 27, 1021–1030. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Hontoir, Y.; Huang, D.; Zhang, J.; Morris, A. Combining first principles with black-box techniques for reaction systems. Control. Eng. Pract. 2004, 12, 819–826. [Google Scholar] [CrossRef]
- Cubillos, F.; Callejas, H.; Lima, E.; Vega, M. Adaptive control using a hybrid-neural model: Application to a polymerisation reactor. Braz. J. Chem. Eng. 2001, 18, 113–120. [Google Scholar] [CrossRef]
- Chang, J.S.; Lu, S.C.; Chiu, Y.L. Dynamic modeling of batch polymerization reactors via the hybrid neural-network rate-function approach. Chem. Eng. J. 2007, 130, 19–28. [Google Scholar] [CrossRef]
- Siddharth, K.; Pathak, A.; Pani, A. Real-time quality monitoring in debutanizer column with regression tree and ANFIS. J. Ind. Eng. Int. 2018, 15, 41–51. [Google Scholar] [CrossRef] [Green Version]
- Ochoa-Estopier, L.M.; Jobson, M. Optimization of Heat-Integrated Crude Oil Distillation Systems. Part I: The Distillation Model. Ind. Eng. Chem. Res. 2015, 54, 4988–5000. [Google Scholar] [CrossRef]
- Shang, C.; Yang, F.; Huang, D.; Lyu, W. Data-driven soft sensor development based on deep learning technique. J. Process. Control 2014, 24, 223–233. [Google Scholar] [CrossRef]
- Michalopoulos, J.; Papadokonstadakis, S.; Arampatzis, G.; Lygeros, A. Modelling of an Industrial Fluid Catalytic Cracking Unit Using Neural Networks. Chem. Eng. Res. Des. 2001, 79, 137–142. [Google Scholar] [CrossRef]
- Bollas, G.; Papadokonstadakis, S.; Michalopoulos, J.; Arampatzis, G.; Lappas, A.; Vasalos, I.; Lygeros, A. Using hybrid neural networks in scaling up an FCC model from a pilot plant to an industrial unit. Chem. Eng. Process. Process. Intensif. 2003, 42, 697–713. [Google Scholar] [CrossRef]
- Fortuna, L.; Graziani, S.; Xibilia, M. Soft sensors for product quality monitoring in debutanizer distillation columns. Control. Eng. Pract. 2005, 13, 499–508. [Google Scholar] [CrossRef]
- Pani, A.K.; Amin, K.G.; Mohanta, H.K. Soft sensing of product quality in the debutanizer column with principal component analysis and feed-forward artificial neural network. Alex. Eng. J. 2016, 55, 1667–1674. [Google Scholar] [CrossRef] [Green Version]
- Ge, Z.; Song, Z. A comparative study of just-in-time-learning based methods for online soft sensor modeling. Chemom. Intell. Lab. Syst. 2010, 104, 306–317. [Google Scholar] [CrossRef]
- Zheng, J.; Song, Z.; Ge, Z. Probabilistic learning of partial least squares regression model: Theory and industrial applications. Chemom. Intell. Lab. Syst. 2016, 158, 80–90. [Google Scholar] [CrossRef]
- Ge, Z. Active learning strategy for smart soft sensor development under a small number of labeled data samples. J. Process. Control 2014, 24, 1454–1461. [Google Scholar] [CrossRef]
- Ge, Z. Supervised Latent Factor Analysis for Process Data Regression Modeling and Soft Sensor Application. IEEE Trans. Control Syst. Technol. 2016, 24, 1004–1011. [Google Scholar] [CrossRef]
- Yao, L.; Ge, Z. Locally Weighted Prediction Methods for Latent Factor Analysis with Supervised and Semisupervised Process Data. IEEE Trans. Autom. Sci. Eng. 2017, 14, 126–138. [Google Scholar] [CrossRef]
- Yuan, X.; Ye, L.; Bao, L.; Ge, Z.; Song, Z. Nonlinear feature extraction for soft sensor modeling based on weighted probabilistic PCA. Chemom. Intell. Lab. Syst. 2015, 147, 167–175. [Google Scholar] [CrossRef]
- Bidar, B.; Sadeghi, J.; Shahraki, F.; Khalilipour, M.M. Data-driven soft sensor approach for online quality prediction using state dependent parameter models. Chemom. Intell. Lab. Syst. 2017, 162, 130–141. [Google Scholar] [CrossRef]
- Mohamed Ramli, N.; Hussain, M.; Mohamed Jan, B.; Abdullah, B. Composition Prediction of a Debutanizer Column using Equation Based Artificial Neural Network Model. Neurocomputing 2014, 131, 59–76. [Google Scholar] [CrossRef]
- Subramanian, R.; Moar, R.R.; Singh, S. White-box Machine learning approaches to identify governing equations for overall dynamics of manufacturing systems: A case study on distillation column. Mach. Learn. Appl. 2021, 3, 100014. [Google Scholar] [CrossRef]
- Shi, J.; Wan, J.; Yan, H.; Suo, H. A survey of cyber-physical systems. In Proceedings of the 2011 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 9–11 November 2011; pp. 1–6. [Google Scholar]
- Chen, H. Applications of cyber-physical system: A literature review. J. Ind. Integr. Manag. 2017, 2, 1750012. [Google Scholar] [CrossRef]
- Lu, Y. Cyber physical system (CPS)-based industry 4.0: A survey. J. Ind. Integr. Manag. 2017, 2, 1750014. [Google Scholar] [CrossRef]
- Khodabakhsh, A.; Ari, I.; Bakir, M.; Ercan, A.O. Multivariate Sensor Data Analysis for Oil Refineries and Multi-mode Identification of System Behavior in Real-time. IEEE Access 2018, 6, 64389–64405. [Google Scholar] [CrossRef]
- Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on explainable artificial intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Keller, P.; Drake, A. Exclusivity and Paternalism in the public governance of explainable AI. Comput. Law Secur. Rev. 2021, 40, 105490. [Google Scholar] [CrossRef]
- El-Assady, M.; Jentner, W.; Kehlbeck, R.; Schlegel, U.; Sevastjanova, R.; Sperrle, F.; Spinner, T.; Keim, D. Towards XAI: Structuring the Processes of Explanations. In Proceedings of the ACM Workshop on Human-Centered Machine Learning, Glasgow, UK, 4 May 2019. [Google Scholar]
- Xu, F.; Uszkoreit, H.; Du, Y.; Fan, W.; Zhao, D.; Zhu, J. Explainable AI: A brief survey on history, research areas, approaches and challenges. In Proceedings of the CCF International Conference on Natural Language Processing and Chinese Computing, Gansu, China, 9–11 October 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 563–574. [Google Scholar]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef] [Green Version]
- Loyola-Gonzalez, O. Black-box vs. white-box: Understanding their advantages and weaknesses from a practical point of view. IEEE Access 2019, 7, 154096–154113. [Google Scholar] [CrossRef]
- Das, A.; Rad, P. Opportunities and challenges in explainable artificial intelligence (xai): A survey. arXiv 2020, arXiv:2006.11371. [Google Scholar]
- Alicioglu, G.; Sun, B. A survey of visual analytics for Explainable Artificial Intelligence methods. Comput. Graph. 2021. [Google Scholar] [CrossRef]
- Messalas, A.; Kanellopoulos, Y.; Makris, C. Model-agnostic interpretability with shapley values. In Proceedings of the 2019 10th International Conference on Information, Intelligence, Systems and Applications (IISA), Patras, Greece, 15–17 July 2019; pp. 1–7. [Google Scholar]
- Frye, C.; de Mijolla, D.; Begley, T.; Cowton, L.; Stanley, M.; Feige, I. Shapley explainability on the data manifold. arXiv 2020, arXiv:2006.01272. [Google Scholar]
- Polley, S.; Koparde, R.R.; Gowri, A.B.; Perera, M.; Nuernberger, A. Towards trustworthiness in the context of explainable search. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Online, 11–15 July 2021; pp. 2580–2584. [Google Scholar]
- Chan, G.Y.Y.; Bertini, E.; Nonato, L.G.; Barr, B.; Silva, C.T. Melody: Generating and Visualizing Machine Learning Model Summary to Understand Data and Classifiers Together. arXiv 2020, arXiv:2007.10614. [Google Scholar]
- Chan, G.Y.Y.; Yuan, J.; Overton, K.; Barr, B.; Rees, K.; Nonato, L.G.; Bertini, E.; Silva, C.T. SUBPLEX: Towards a Better Understanding of Black Box Model Explanations at the Subpopulation Level. arXiv 2020, arXiv:2007.10609. [Google Scholar]
- Krause, J.; Perer, A.; Bertini, E. INFUSE: Interactive feature selection for predictive modeling of high dimensional data. IEEE Trans. Vis. Comput. Graph. 2014, 20, 1614–1623. [Google Scholar] [CrossRef] [PubMed]
- Seifert, C.; Aamir, A.; Balagopalan, A.; Jain, D.; Sharma, A.; Grottel, S.; Gumhold, S. Visualizations of deep neural networks in computer vision: A survey. In Transparent Data Mining for Big and Small Data; Springer: Berlin/Heidelberg, Germany, 2017; pp. 123–144. [Google Scholar]
- Jin, W.; Carpendale, S.; Hamarneh, G.; Gromala, D. Bridging ai developers and end users: An end-user-centred explainable ai taxonomy and visual vocabularies. In Proceedings of the IEEE Visualization, Vancouver, BC, Canada, 20–25 October 2019; pp. 20–25. [Google Scholar]
- Hudon, A.; Demazure, T.; Karran, A.; Léger, P.M.; Sénécal, S. Explainable Artificial Intelligence (XAI): How the Visualization of AI Predictions Affects User Cognitive Load and Confidence; Davis, F.D., Riedl, R., vom Brocke, J., Léger, P.-M., Randolph, A.B., Müller-Putz, G., Eds.; Springer: Cham, Switzerland, 2021; pp. 237–246. [Google Scholar]
- Joia, P.; Coimbra, D.; Cuminato, J.A.; Paulovich, F.V.; Nonato, L.G. Local affine multidimensional projection. IEEE Trans. Vis. Comput. Graph. 2011, 17, 2563–2571. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gou, L.; Zhang, W.; Yang, H.; Shen, H.W. Deepvid: Deep visual interpretation and diagnosis for image classifiers via knowledge distillation. IEEE Trans. Vis. Comput. Graph. 2019, 25, 2168–2180. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Collaris, D.; van Wijk, J.J. ExplainExplore: Visual exploration of machine learning explanations. In Proceedings of the 2020 IEEE Pacific Visualization Symposium (PacificVis), Tianjin, China, 14–17 April 2020; pp. 26–35. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Model-agnostic interpretability of machine learning. arXiv 2016, arXiv:1606.05386. [Google Scholar]
- Alvarez-Melis, D.; Jaakkola, T.S. Towards robust interpretability with self-explaining neural networks. arXiv 2018, arXiv:1806.07538. [Google Scholar]
- Viton, F.; Elbattah, M.; Guérin, J.L.; Dequen, G. Heatmaps for Visual Explainability of CNN-Based Predictions for Multivariate Time Series with Application to Healthcare. In Proceedings of the 2020 IEEE International Conference on Healthcare Informatics (ICHI), Oldenburg, Germany, 30 November–3 December 2020; pp. 1–8. [Google Scholar]
- Rožanec, J.; Trajkova, E.; Kenda, K.; Fortuna, B.; Mladenić, D. Explaining Bad Forecasts in Global Time Series Models. Appl. Sci. 2021, 11, 9243. [Google Scholar] [CrossRef]
- Greenwell, B.M. pdp: An R package for constructing partial dependence plots. R J. 2017, 9, 421. [Google Scholar] [CrossRef] [Green Version]
- Apley, D.W.; Zhu, J. Visualizing the effects of predictor variables in black box supervised learning models. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2020, 82, 1059–1086. [Google Scholar] [CrossRef]
- Council of the European Union; European Parliament. Regulation (EC) No 715/2007 of the European Parliament and of the Council; Technical report, 715/2007/EC; Official Journal of the European Union, Publications Office of the European Union: Luxembourg, 20 June 2007. [Google Scholar]
- Luyben, W.L. Distillation column pressure selection. Sep. Purif. Technol. 2016, 168, 62–67. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Jobson, M. The effect of operating pressure on distillation column throughput. Comput. Chem. Eng. 1999, 23, S831–S834. [Google Scholar] [CrossRef]
- Kister, H.Z. Distillation Operation; McGraw-Hill: New York, NY, USA, 1990. [Google Scholar]
- Mejdell, T.; Skogestad, S. Composition estimator in a pilot-plant distillation column using multiple temperatures. Ind. Eng. Chem. Res. 1991, 30, 2555–2564. [Google Scholar] [CrossRef]
- Huang, K.; Wang, S.J.; Iwakabe, K.; Shan, L.; Zhu, Q. Temperature control of an ideal heat-integrated distillation column (HIDiC). Chem. Eng. Sci. 2007, 62, 6486–6491. [Google Scholar] [CrossRef]
- Behnasr, M.; Jazayeri-Rad, H. Robust data-driven soft sensor based on iteratively weighted least squares support vector regression optimized by the cuckoo optimization algorithm. J. Nat. Gas Sci. Eng. 2015, 22, 35–41. [Google Scholar] [CrossRef]
- Aston, J.; Messerly, G. Additions and Corrections-The Heat Capacity and Entropy, Heats of Fusion and Vaporization, and the Vapor Pressure of n-Butane. J. Am. Chem. Soc. 1941, 63, 3549. [Google Scholar] [CrossRef]
- Das, T.R.; Reed Jr, C.O.; Eubank, P.T. PVT [pressure-volume-temperature] surface and thermodynamic properties of butane. J. Chem. Eng. Data 1973, 18, 244–253. [Google Scholar] [CrossRef]
- Carruth, G.F.; Kobayashi, R. Vapor pressure of normal paraffins ethane through n-decane from their triple points to about 10 mm mercury. J. Chem. Eng. Data 1973, 18, 115–126. [Google Scholar] [CrossRef]
- Kemp, J.; Egan, C.J. Hindered rotation of the methyl groups in propane. The heat capacity, vapor pressure, heats of fusion and vaporization of propane. Entropy and density of the gas. J. Am. Chem. Soc. 1938, 60, 1521–1525. [Google Scholar] [CrossRef]
- Rips, S. On a Feasible Level of Filling in of Reservoires by Liquid Hydrocarbons. Khim. Prom. (Moscow) 1963, 8, 610–613. [Google Scholar]
- Helgeson, N.; Sage, B.H. Latent heat of vaporization of propane. J. Chem. Eng. Data 1967, 12, 47–49. [Google Scholar] [CrossRef]
- Yaws, C.; Yang, H. To estimate vapor pressure easily. Hydrocarb. Process. (USA) 1989, 68. [Google Scholar]
- Osborn, A.G.; Douslin, D.R. Vapor-pressure relations for 15 hydrocarbons. J. Chem. Eng. Data 1974, 19, 114–117. [Google Scholar] [CrossRef]
- Hua, J.; Xiong, Z.; Lowey, J.; Suh, E.; Dougherty, E.R. Optimal number of features as a function of sample size for various classification rules. Bioinformatics 2005, 21, 1509–1515. [Google Scholar] [CrossRef] [Green Version]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Fukushima, K. Visual feature extraction by a multilayered network of analog threshold elements. IEEE Trans. Syst. Sci. Cybern. 1969, 5, 322–333. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- An, K.; Meng, J. Voting-averaged combination method for regressor ensemble. In Proceedings of the International Conference on Intelligent Computing, Xiamen, China, 29–31 October 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 540–546. [Google Scholar]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Aigner, D.; Lovell, C.K.; Schmidt, P. Formulation and estimation of stochastic frontier production function models. J. Econom. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Ehm, W.; Gneiting, T.; Jordan, A.; Krüger, F. Of quantiles and expectiles: Consistent scoring functions, Choquet representations and forecast rankings. J. R. Stat. Soc. Ser. Stat. Methodol. 2016, 78 Pt 3, 505–562. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Broyden, C.G. The convergence of a class of double-rank minimization algorithms 1. general considerations. IMA J. Appl. Math. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Fletcher, R. A new approach to variable metric algorithms. Comput. J. 1970, 13, 317–322. [Google Scholar] [CrossRef] [Green Version]
- Goldfarb, D. A family of variable-metric methods derived by variational means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of quasi-Newton methods for function minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Soc. Ser. B (Methodological) 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics; Springer: Berlin/Heidelberg, Germany, 1992; pp. 196–202. [Google Scholar]





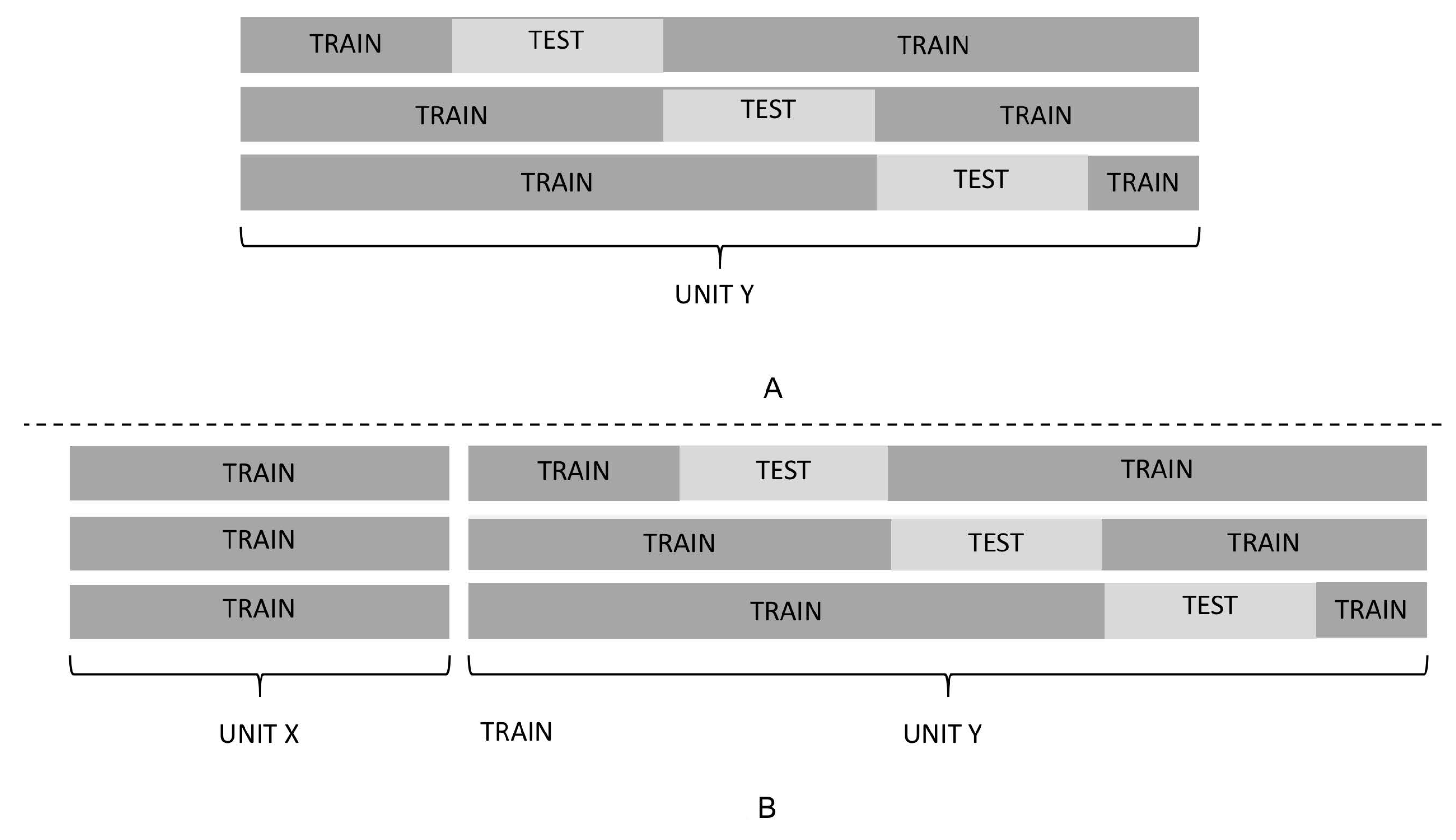

| Unit A | Unit B | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Stdev | min | 25% | 50% | 75% | Max | Mean | Stdev | min | 25% | 50% | 75% | Max | |
| P1 (kg/cm2) | 7.42 | 0.29 | 6.54 | 7.28 | 7.43 | 7.60 | 8.32 | 4.98 | 3.84 | 0.00 | 0.00 | 7.61 | 8.02 | 8.78 |
| T2 (°C) | 62.66 | 19.82 | 0.00 | 66.17 | 67.41 | 69.13 | 89.70 | 35.99 | 30.84 | 0.00 | 0.00 | 58.20 | 61.38 | 80.36 |
| C5 (%) | 0.63 | 1.15 | 0.00 | 0.02 | 0.17 | 0.70 | 6.52 | 0.04 | 0.11 | 0.00 | 0.00 | 0.00 | 0.03 | 0.74 |
| LPG Sample Mixture | C2H6S2 | C3H8 | C4H10 | C5H12 |
|---|---|---|---|---|
| 1 | 0.000 | 0.485 | 0.505 | 0.010 |
| 2 | 0.000 | 0.480 | 0.500 | 0.020 |
| 3 | 0.030 | 0.465 | 0.485 | 0.020 |
| 4 | 0.000 | 0.465 | 0.485 | 0.050 |
| 5 | 0.000 | 0.455 | 0.475 | 0.070 |
| Features Group (FG) | FG ID | Feature | Description | Type |
|---|---|---|---|---|
| Sensor reading values | 1 | P1 | Pressure measurement from sensor P1 | Real number |
| T2 | Temperature measurement from sensor T2 | Real number | ||
| Expected mixture vapor saturation pressure for temperature T2 | 2 | spt002 | Mixture #1 | Real number |
| spt0 | Mixture #2 | Real number | ||
| spt1 | Mixture #3 | Real number | ||
| spt2 | Mixture #4 | Real number | ||
| spt3 | Mixture #5 | Real number | ||
| spt4 | Mixture #6 | Real number | ||
| Pressure P1 in range | 3 | p < 7.06 | Pressure below 7.06 kg/cm2 | Boolean |
| p < 7.14 | Pressure below 7.14 kg/cm2 | Boolean | ||
| p > 7.63 | Pressure above 7.63 kg/cm2 | Boolean | ||
| Expected T1 temperature for mixture | 4 | T1-spt1 | Mixture #3 | Real number |
| T1-spt2 | Mixture #4 | Real number | ||
| T1-spt3 | Mixture #5 | Real number | ||
| T1-spt4 | Mixture #6 | Real number | ||
| Relative pressure, comparing pressure P1 and expected mixture pressure for temperature T2. | 5 | spr002 | spt002/P1 | Real number |
| spr0 | spt1/P1 | Real number | ||
| spr1 | spt2/P1 | Real number | ||
| spr2 | spt3/P1 | Real number | ||
| spr3 | spt4/P1 | Real number | ||
| spr4 | spt5/P1 | Real number | ||
| Ratio between estimated T1 temperature for mixture, and the P1 pressure. | 6 | T1/P1-spt1-T2 | Mixture #3 | Real number |
| T1/P1-spt2-T2 | Mixture #4 | Real number | ||
| T1/P1-spt3-T2 | Mixture #5 | Real number | ||
| T1/P1-spt4-T2 | Mixture #6 | Real number | ||
| Categorical feature indicating whether the relationship between estimated T1 temperature and P1 pressure is above or below the value measured from normal operating conditions, from values obtained in diagrams provided. | 7 | T1/P1-spt1.vref | Mixture #3 | Boolean |
| T1/P1-spt2.vref | Mixture #4 | Boolean | ||
| T1/P1-spt3.vref | Mixture #5 | Boolean | ||
| T1/P1-spt4.vref | Mixture #6 | Boolean |
| Model | Unit A | Unit B | ||
|---|---|---|---|---|
| RMSEmean | MAEmean | RMSEmean | MAEmean | |
| Baseline 1 (C5 median) | ** 1.1179 | * 0.6028 | 0.1174 | * 0.0853 |
| Baseline 2 (LR) | ** 1.1794 | 0.7601 | 1.4150 | 0.7248 |
| Model 1 (LR) | 1632.9693 | 560.4650 | 96826.5563 | 46730.6566 |
| Model 2 (SVR) | * 1.0754 | * 0.6087 | * 0.1240 | 0.0991 |
| Model 3 (MLPR) | * 1.0728 | 0.7122 | 0.2115 | 0.1424 |
| Model 4 | 1.0352 | * 0.6127 | * 0.1201 | * 0.0871 |
| Model | Unit A | Unit B | ||
|---|---|---|---|---|
| RMSEmean | MAEmean | RMSEmean | MAEmean | |
| Baseline 1 (C5 median) | 1.1760↓ | 0.6141↓ | 0.1152↑ | 0.0818↑ |
| Baseline 2 (LR) | 1.0603↑ | 0.7009↑ | ** 0.2126↑ | 0.1978↑ |
| Model 1 (LR) | 1198266158.9503↓ | 411001902.3054↓ | ** 0.2753↑ | 0.1900↑ |
| Model 2 (SVR) | 1.1098↓ | 0.6193↓ | * 0.1287↓ | 0.1021↓ |
| Model 3 (MLPR) | 1.0771↓ | 0.7234↓ | 0.2044↑ | 0.1581↓ |
| Model 4 | 0.9655↑ | 0.5743↑ | * 0.1270↓ | 0.0852↑ |
| Model | Experiment 1 | Experiment 2 |
|---|---|---|
| AUC ROCmean | AUC ROCmean | |
| Baseline 1 (zero forecast) | 0.5000 | * 0.5000 |
| Baseline 2 (LR) | 0.5656 | ↑0.5675 |
| Model 1 (LR) | 0.6567 | ↓0.6059 |
| Model 2 (SVC) | 0.4491 | * ↑0.4897 |
| Model 3 (MLPC) | 0.6709 | ↓0.5381 |
| Model 4 (Catboost) | 0.7359 | ↑0.7670 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rožanec, J.M.; Trajkova, E.; Lu, J.; Sarantinoudis, N.; Arampatzis, G.; Eirinakis, P.; Mourtos, I.; Onat, M.K.; Yilmaz, D.A.; Košmerlj, A.; et al. Cyber-Physical LPG Debutanizer Distillation Columns: Machine-Learning-Based Soft Sensors for Product Quality Monitoring. Appl. Sci. 2021, 11, 11790. https://doi.org/10.3390/app112411790
Rožanec JM, Trajkova E, Lu J, Sarantinoudis N, Arampatzis G, Eirinakis P, Mourtos I, Onat MK, Yilmaz DA, Košmerlj A, et al. Cyber-Physical LPG Debutanizer Distillation Columns: Machine-Learning-Based Soft Sensors for Product Quality Monitoring. Applied Sciences. 2021; 11(24):11790. https://doi.org/10.3390/app112411790
Chicago/Turabian StyleRožanec, Jože Martin, Elena Trajkova, Jinzhi Lu, Nikolaos Sarantinoudis, George Arampatzis, Pavlos Eirinakis, Ioannis Mourtos, Melike K. Onat, Deren Ataç Yilmaz, Aljaž Košmerlj, and et al. 2021. "Cyber-Physical LPG Debutanizer Distillation Columns: Machine-Learning-Based Soft Sensors for Product Quality Monitoring" Applied Sciences 11, no. 24: 11790. https://doi.org/10.3390/app112411790
APA StyleRožanec, J. M., Trajkova, E., Lu, J., Sarantinoudis, N., Arampatzis, G., Eirinakis, P., Mourtos, I., Onat, M. K., Yilmaz, D. A., Košmerlj, A., Kenda, K., Fortuna, B., & Mladenić, D. (2021). Cyber-Physical LPG Debutanizer Distillation Columns: Machine-Learning-Based Soft Sensors for Product Quality Monitoring. Applied Sciences, 11(24), 11790. https://doi.org/10.3390/app112411790










