Abstract
Correctness of networking protocols represents the principal requirement of cybersecurity. Correctness of protocols is established via the procedures of their verification. A classical communication system includes a pair of interacting systems. Recent developments of computing and communication grids for radio broadcasting, cellular networks, communication subsystems of supercomputers, specialized grids for numerical methods and networks on chips require verification of protocols for any number of devices. For analysis of computing and communication grid structures, a new class of infinite Petri nets has been introduced and studied for more than 10 years. Infinite Petri nets were also applied for simulating cellular automata. Rectangular, triangular and hexagonal grids on plane, hyper cube and hyper torus in multidimensional space have been considered. Composing and solving in parametric form infinite Diophantine systems of linear equations allowed us to prove the protocol properties for any grid size and any number of dimensions. Software generators of infinite Petri net models have been developed. Special classes of graphs, such as a graph of packet transmission directions and a graph of blockings, have been introduced and studied. Complex deadlocks have been revealed and classified. In the present paper, infinite Petri nets are divided into two following kinds: a single infinite construct and an infinite set of constructs of specified size (and number of dimensions). Finally, the paper discusses possible future work directions.
1. Introduction
Petri Nets have been applied to simulations of Networking and Communications Protocols for many years [1,2], and more recently to an understanding of Cybersecurity Threats and Defence [3,4,5]. For years, Petri nets have been used extensively in Cybersecurity domain [6,7,8,9,10,11].
In this paper we explore the growing need to extend the range of Cybersecurity simulation models to include the emerging field of Infinite Petri Nets [12,13].
During the last 25 years, computer network security has evolved from basic virus attacks to sophisticated custom Trojan attacks such as Stuxnet. More recent attacks have become global with recent cases such as the massive Distributed Denial of Service (DDoS) attack (2.3TeraBits/Sec) targeting Amazon Web Service (AWS). We have also seen “BotNet” attacks using the Internet of Things (IoT) such as the “Mirai BotNet” which infiltrated millions of insecure CCTV devices as well as frequent Ransomware attacks such as the malware family of WannaCry and Petya. Ambitious “Bad Guys” now strategically target global enterprise and government networks with a new arsenal of custom intelligent malware. Increasingly these malicious tools are being based upon machine learning algorithms and advanced concepts from artificial intelligence. Cybersecurity against such massive malware attacks requires new approaches to the design of effective cyber defence tools [14]. During the coming 5 to 10 years, we suggest that the concept of infinite Petri Nets will play a useful role in understanding innovative ways to mitigate such massive, practically infinite, attacks which propagate globally at light speed across trans-continental optical-fibre networks and ultra high-speed switches, routers and servers. We now consider specific aspects of Cybersecurity Networks that may be more effectively secured through Petri Net Models.
Many towns, cities and regional government authorities are now implementing large-scale 24/7 surveillance networks using intelligent CCTV together linked with secure access control and other forms of mobile network surveillance [15]. Such security networks pose ethical issues relating to “human rights” and “privacy” but such discussion lies beyond the scope of this paper. However, the current global COVID-19 pandemic has demonstrated the strong practical applications of such intelligent urban networks to track and trace citizens that require self-isolation or quarantine. Once again, Infinite Petri Nets may be applied to modelling the architecture, connectivity and intelligent adaptive algorithms in the design and operation of these city-wide surveillance networks which are growing ever more complex during recent years.
During the last 10 years, International Agencies, such as the UN, have supported the development of National Cybersecurity Strategies with a strong focus upon CNI in major sectors including Energy, Transportation, Defence, Education, Healthcare, Defence and Government. These are all designed and implemented to International Standards, Rules, and Protocols from Organisations such as the ISO/IEC, IEEE, NIST, and UN/ITU. Both Finite and Infinite Petri Nets will provide excellent systems support in the efficient design of emerging cybersecurity standards particularly those involving machine and deep learning algorithms [4].
Traditional ICS and SCADA (Supervisory Control and Data Acquisition) systems have been at the heart of industrial processes for decades. However, these legacy devices together with the PLCs (Programmable Logic Controllers) are now highly vulnerable to Cyber Malware including RansomWare, Custom “Bots” and Cyber Sabotage. The massive scale of Chemical, Oil/Gas and Manufacturing Enterprises makes it essential that Cyber Risks and Threats are thoroughly analysed through simulations with practical tools such as Large-Scale Petri Nets [3]. Such modelling of potential malware threats will help Cybersecurity specialists to mitigate the significant cost of possible operational and business disruption.
Corporate Business is now focused upon the practical benefits of the convergence of physical and cyber security as the foundations of Integrated Security Operations [16]. The scale and speed of Malware Attacks together with 24/7 Multi-Media Surveillance Streams is quite impossible for human operators to effectively triage in real-time. So the implementation of Integrated Real-Time Security will be dependent upon tools based upon ultra-fast Artificial Intelligence (AI) and Machine Learning Algorithms. Intelligent Analytical Cybersecurity Tools based upon Deep Learning and Recursive Bayesian Learning have now been commercially marketed for more than 5 years. Such AI-based malware techniques are already being adopted by the “Bad Guys” so it is becoming critically important to understand the impact of such intelligent adaptive attacks upon enterprise networks. Once again, Infinite Petri Nets of customised topologies may play practical roles in the more detailed modelling and simulation of adaptive malware algorithms. In the present paper, for the first time, infinite Petri nets are divided into the following two categories: a single infinite construct and an infinite set of constructs of a specified size (and number of dimensions). In particular, it is likely that Infinite Petri Nets will become particularly useful in understanding the potential for stochastic machine learning tools to be used to mitigate attacks from intelligent algorithmic “AI-Bot” attacks.
2. Modern Trends in Verification of Networking Protocols
Cybersecurity [17] rests on three pillars of communication protocol properties [18]: correctness, efficiency, and reliability. Correctness of protocols is established via procedures of their verification [19], usually based on some formal technique [20], among which Petri nets [21] occupy a leading position. A classical communication system includes a pair of interacting systems which exchange by messages, whilst both valid message sequences and formats are restricted by the corresponding protocol standard [22]. Standards of Internet protocols are maintained by The Internet Engineering Task Force (IETF) in the form of Requests for Comments (RFC). The Institute of Electrical and Electronics Engineers (IEEE) develops standards for a series of physical and data-link level protocols such as Ethernet, WiFi, WiMAX, and the corresponding documents are called IEEE Standards. The International Telecommunication Union (ITU) also issues standards, the corresponding documents are called Recommendations; X25, NGN and Future Networks are among the widely known ITU standards. There are also internal standards of companies or their consortium traditionally called a Special Interest Group (SIG). Recently it has become rather easy to drown in the vast ocean of manifold communication protocols, their families, classes, and types [19,22]. The most essential trend that completely negates the conventional techniques of communication protocols verification consists in using more than two interacting parties [23]. For some protocols, for instance Internet Open Trading Protocol (IOTP) [24], the set of parties is well defined by trading roles: Customer, Merchant, Merchant Customer Care Provider, Payment Handler, and Delivery Handler. For other protocols, for instance bus Ethernet, though there is always a restricted number of devices attached to a bus of restricted length, it is advisable to obtain results for a bus of any length and any number of attached devices. The same for tree-like structures of switched Ethernet. Even before the wide application of computing and communication grids [25,26], a strong demand has arisen for techniques which model not a given network but a given structure (topology), supplied by specific rules of communication.
3. Getting Familiar with Petri Nets
A Petri net [21,27] represents a bipartite directed graph with a dynamic process defined on it. One part of vertices, depicted as circles and called places, models conditions, the other part of vertices, depicted as rectangles (bars) and called transitions, models events. Dynamic elements, called tokens, are situated inside places and are consumed and produced by transitions as a result of firing in accordance with arcs’ weights; at a step, one transition fires. Introduced in 1962 in dissertation of Carl Petri, the nets found wide application in wide range of domains including manufacture control, transportation, and business processes management.
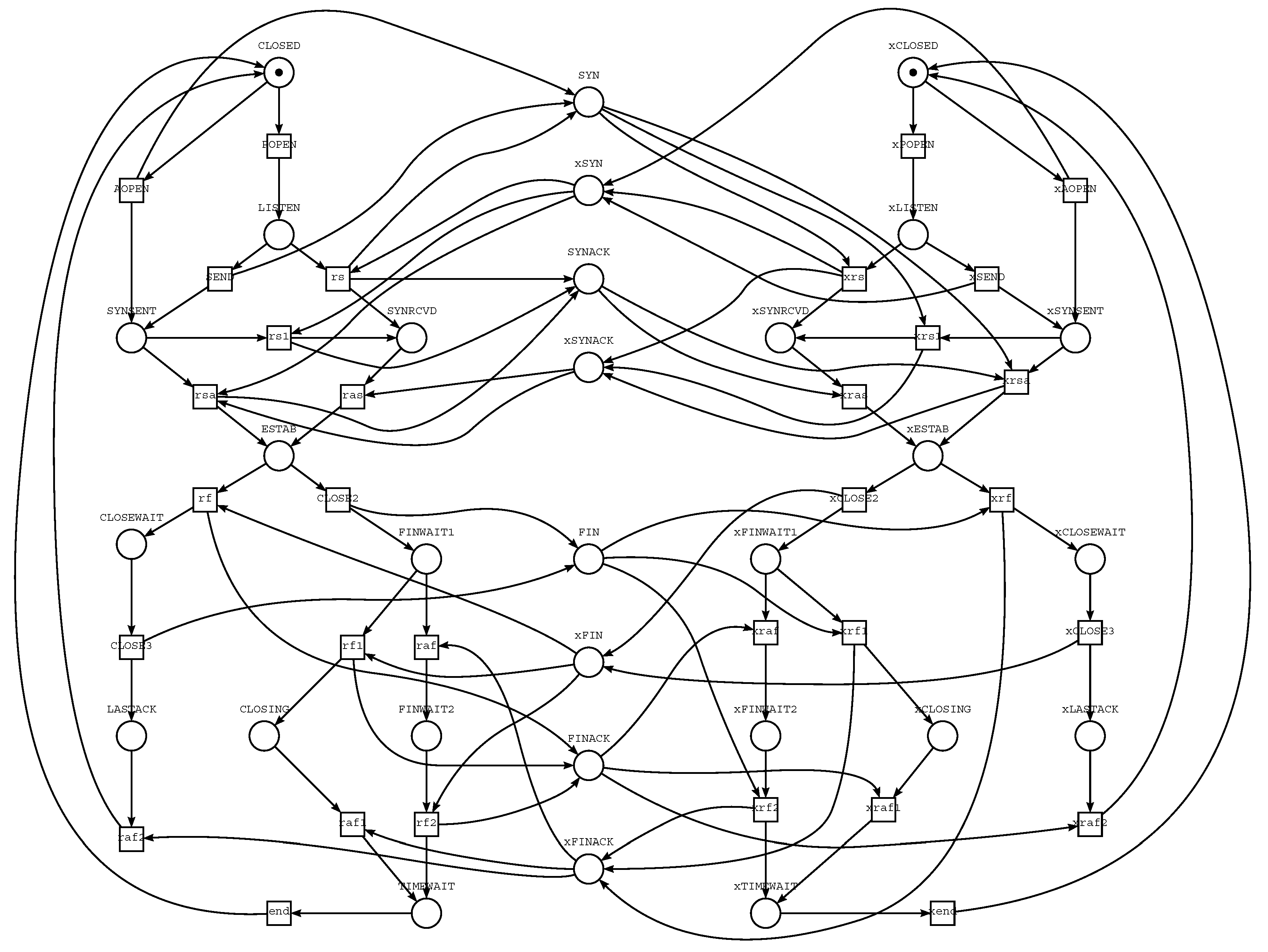
A Petri net is considered a convenient and powerful tool for verification of networking protocols [28] and correctness proof for parallel and distributed processes [27], including routing protocols [29] and mobile computing systems [30]. In Figure 1, a Petri net model of Transmission Control Protocol (TCP) [23,31]—one of the most widespread Internet protocols—is shown. It covers procedures of connection three-way-handshake and disconnection. The left and right parts model the first and the second systems while the central part represents control bites of the standard messages. The Petri net completely corresponds to the TCP Connection State Diagram and TCP Header Format; for the second system states and actions, prefix “x” is used.
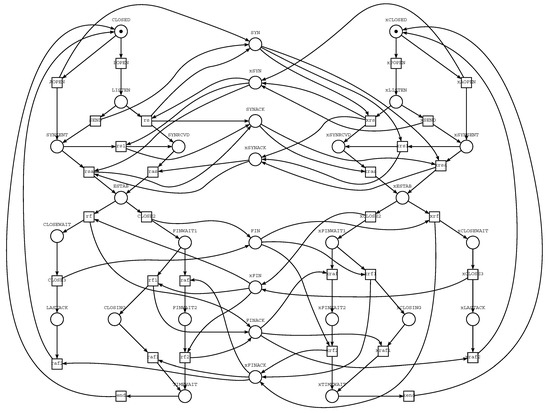
Figure 1.
Petri net model of protocol TCP (RFC793)—connection and disconnection procedures.
As an example, let us consider the tree-way-handshake procedure implementation on request of the first (left) system. AOpen transition fires modelling Active Opening of connection by the first system moving a token from place CLOSED into place SYNSENT and putting a token into place SYN that models the corresponding flag of TCP message sent from the first (left) to the second (right) system. The second system moves a token from place xCLOSED to xLISTEN by transition xPOPEN modelling Passive Opening of connection. Then it receives the message firing transition xrs that moves a token from place xLISTEN to place xSYNRCVD and putting a token into place xSYNACK that models the corresponding flag of TCP message sent from the second to the first system. Then the first system, triggered by xSYNRCVD flag of received message, moves a token from place SYNSENT to place ESTAB by transition rsa, and sends a message with flag SYNACK. From the first system point of view, a connection is established that is indicated by a token in place ESTAB. The second system receives the message containing SYNACK flag by transition xras moving a token from place xSYNRCVD to place xESTAB. Now the connection is established from the point of view of both systems.
A classical Petri net is more powerful than a finite automaton (state machine) and less powerful than a Turing machine [21]. Thus, to study a Petri net, we can apply not only simulation but formal analysis techniques as well [23,27]. Potentially infinite state space, represented with finite coverability tree, and methods of linear algebra allow us to evaluate basic properties of a Petri net such as boundedness and liveness or solve a problem of a state (marking) reachability. Among manifold tools for Petri net analysis we mention INA, Tina [32], and Snoopy.
Traditionally, finite Petri nets having finite sets of places and transitions have been studied. As a first hint to the necessity of introducing infinite Petri nets, we consider Ajmon Marsan [33] study of bus Ethernet. We can attach one, two, three, or more workstations to the bus proving properties of the protocol for each given size separately. More recently the verification of such network protocols has been extended to any number of attached workstations [23]. Then, when studying a switched Ethernet, we come to a tree-like structure and are craving for a technique to prove basic properties for any tree. The problem becomes general when considering computing and communication grids [25,26] where we come to triangular, rectangular, or hexagonal grids. Triangular grids are applied in radio broadcasting, rectangular grids—in networks on chip and in numerical difference methods, hexagonal grids—in cellular communications [34]. As a generalization of numerical methods and communication subsystems of supercomputers [35], we come to multidimensional structures such as hyper cube and hyper torus. Routing algorithms [36] are simplified within a torus that provides many alternative routes for load balancing [37]. A separate demand for infinite Petri nets arises when simulating infinite formal systems such as Turing machine or cellular automata. To answer the mentioned calls, infinite Petri nets have been introduced and studied in a series of papers cited in [12,13].
4. Infinite Petri Net of First Kind: A Single Infinite Structure
Modeling elementary Cellular Automata (CA) [38,39] and Turing Machines (TM) [40], we introduce an Infinite Petri Net (IPN) in the simplest intuitive way. We directly model each cell and connecting the cell model into an infinite net through both sides of linear structure [41,42]. The same kind of infinite structures is obtained for multidimensional cellular automata using either von Neumann or Moore, or a generalized neighborhood [43]. Recently biology inspired solutions, together with Petri nets, find their application in modeling routing protocols [29]—one of the most critical and vulnerable components of networking.
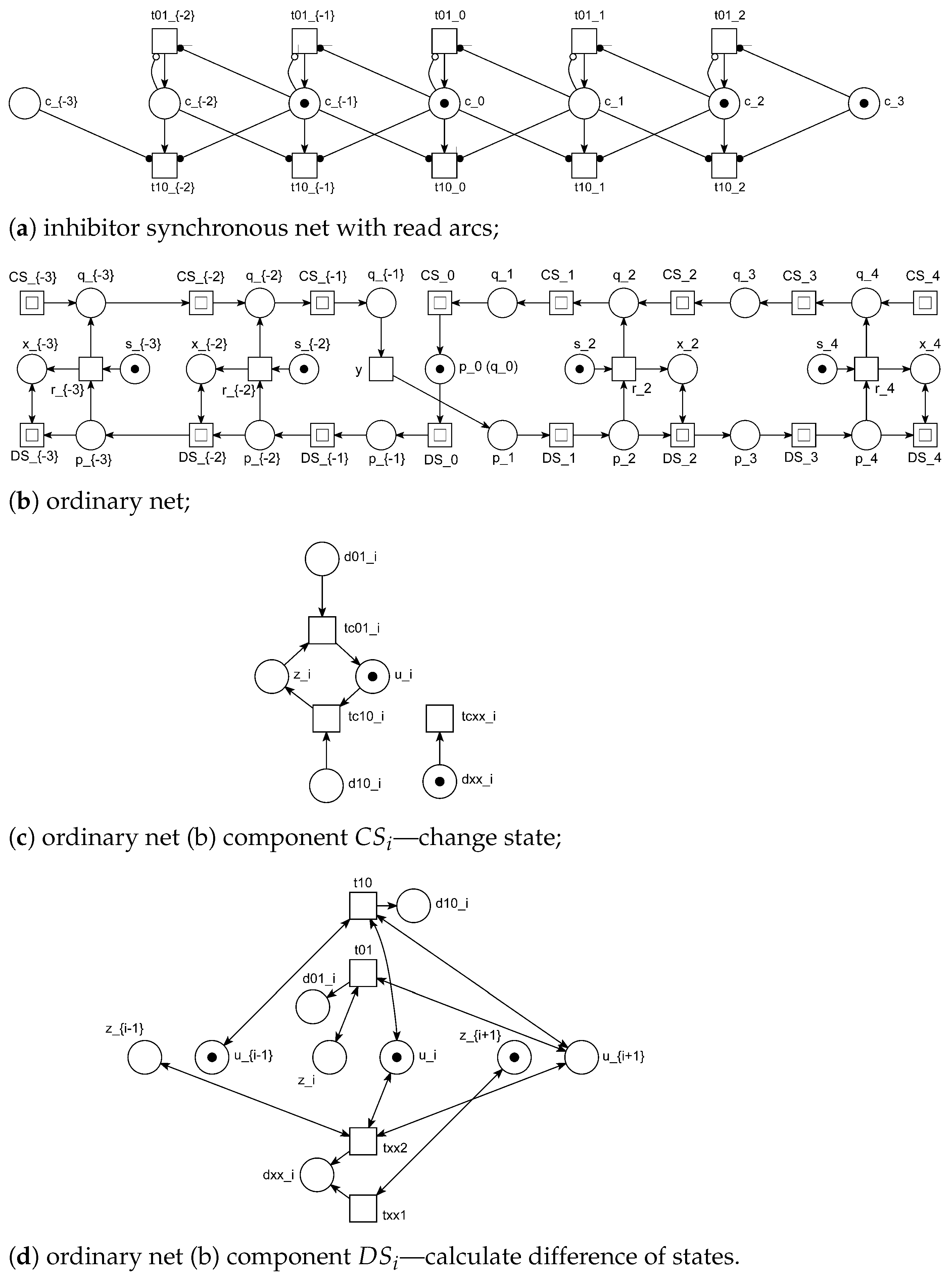
In Figure 2a, a synchronous Petri net model of elementary CA Rule 110 is shown. Elementary cellular automaton Rule 110 specified by (4) is proven a computationally universal (Turing-complete) [38]. Simulating it by a Petri net allows us to prove that an infinite Petri net is Turing-complete [41].
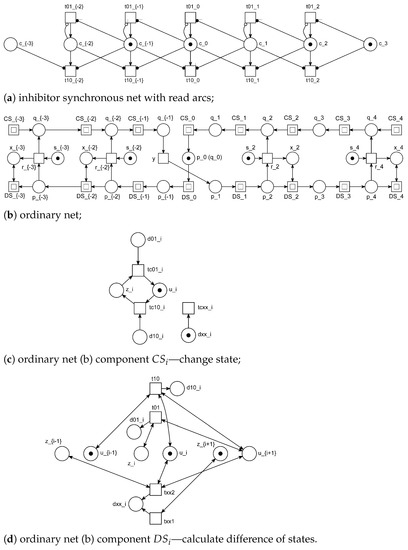
Figure 2.
Modeling elementary cellular automaton Rule 110 by infinite Petri net, seven cells fragment.
For synchronous CA, a direct way of simulation is using a synchronous Petri net based on maximal firing strategy of Burkhard-Salwicky; all the firable transitions fire simultaneously at a step simulating change of state for all the cells of CA Figure 2a. The conciseness of the construct—a cell is simulated by a place and a pair of transitions—is reached by minimizing the logical expressions which specify when to set and reset the cell value and using inhibitor and read arcs; an inhibitor arc, with a hollow circle on its end, checks whether the place value equals zero and a read arc, with a filled circle on its end, checks whether the place value is greater than zero.
At first glance, it seems that we are obliged to use a class of synchronous Petri nets. Though a technique for simulating a CA by a TM [39] suggests that it can be done via infinitely repeated traverses of the tape of cells that gives us possibility to simulate a TM by an infinite conventional (asynchronous) Petri net. In this way Turing-completeness of an infinite Petri net has been proven [41]. The corresponding Petri net shown in Figure 2b has been called “barriers and a boomerang”; note that it uses subnets , shown in Figure 2c,d, respectively, which are substituted instead of the corresponding transitions with double borders. A pair of places and represent standing and laying barrier, respectively; once overturned “barrier” remains in this state forever; a “boomerang” is repeatedly thrown to the left and to the right by someone standing in the center of coordinates.
Let us muse on an infinity of IPN modelling a CA. Using an integer parameter—the cell number, we enumerate cells and the parameter range is from minus infinity to plus infinity. The obtained construct is thought of as a single infinite structure. For this purpose a structure should not have a specific edge or bounds, the same cell model is repeated to both directions in each of dimensions. We obtain an infinite countable set of repeated connected cells forming a single construct.
5. Infinite Petri Net of Second Kind: An Infinite Set of Finite Structures
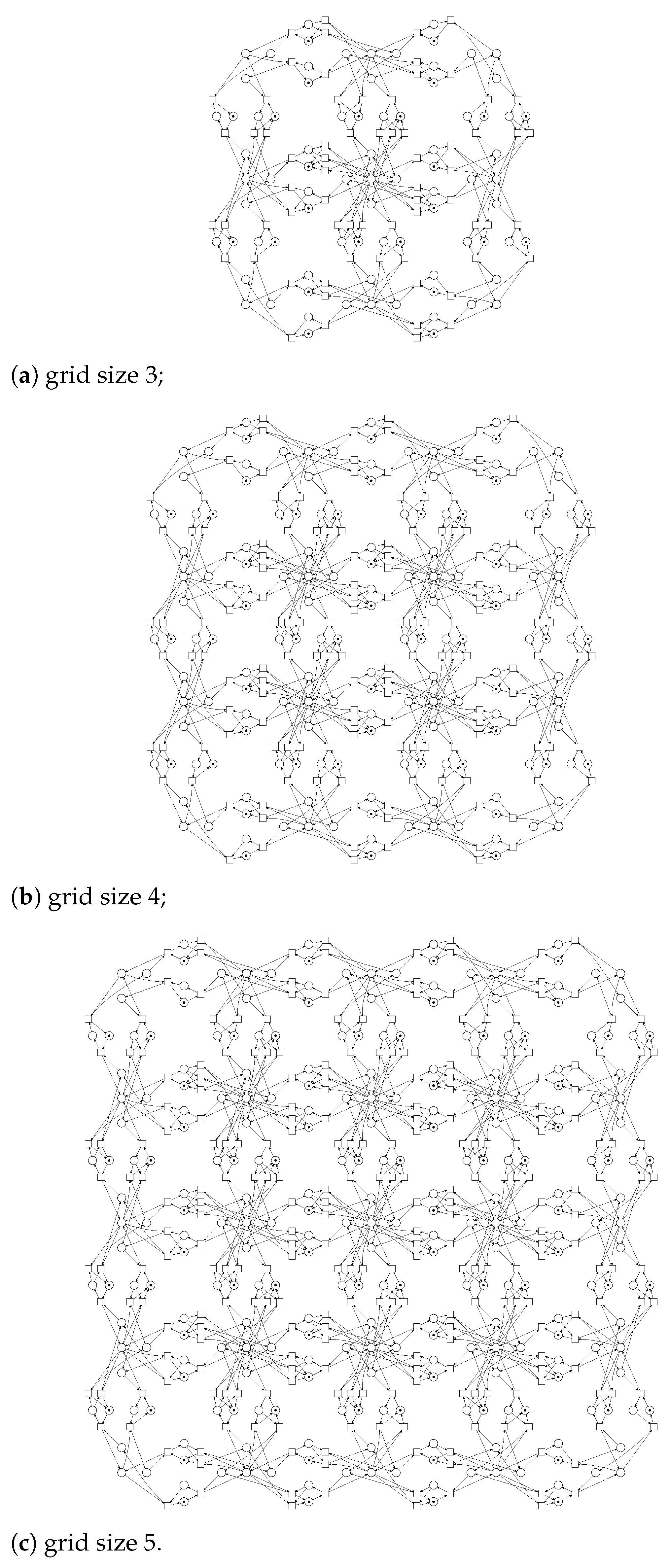
When modeling real-life computing and communication grids [25,26], we come to another kind of infinite Petri nets [12,13,44]. Here we use such parameters as the model size and the number of dimensions for multidimensional structures. Having open grids as an intermediate auxiliary construct, we specify real-life grids adding specific boundary conditions. In this way we studied three basic types of boundary conditions: connected (opposite) bounds – that makes a hyper torus from hyper cube; terminal (customer) device attached on the border; truncated communication device on the border. In each case, a closed construct of a finite size have been obtained for a given value of the model size—a parameter. In Figure 3, square 2D structures with truncated device on the edge of size 3, 4, and 5 are shown.
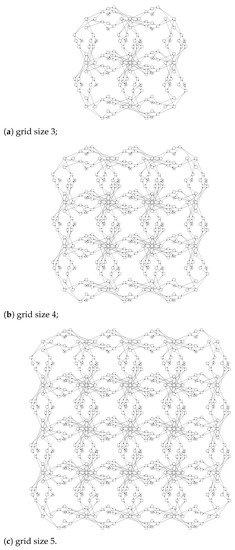
Figure 3.
Modeling square communication grid with truncated devices on edges by infinite Petri net.
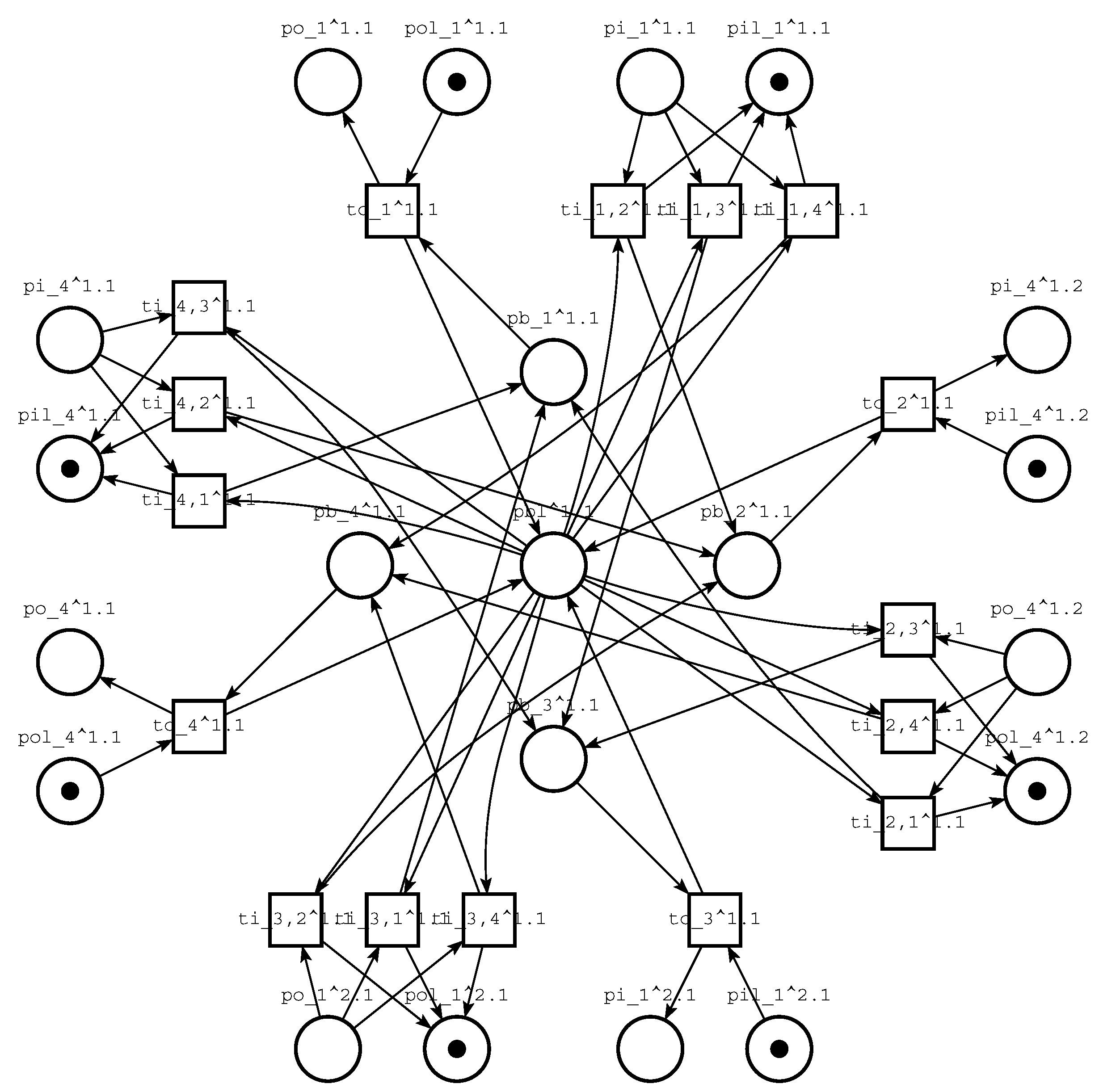
The switching device model [45] is shown in Figure 4. It represents a-state-of-art balance between simplicity and usefulness acknowledged by many papers where similar models allowed us to find deadlocks [46] in real-life grids [14,25]. The device operates in full-duplex mode having separate input and output tracts; it uses store-and-forward principle. We do not simulate a message (packet) structure, it is represented by a single token. The forwarding decision is made at the packet arrival via storing the packet within the corresponding section of the internal buffer. The internal buffer is represented by the buffer size limitation place and four places which model sections of the internal buffer corresponding to the ports. Each tract of each port is represented by a pair of places, for instance for the output tract: —a buffer; —buffer size limitation; usually the port buffer size equals unit. The packet transmission into a port is implemented by a single transition . The packet receiving from a port is modelled by three alternative transitions , each corresponding to the packet forwarding into one of three other ports j except . Transitions’ arcs keep the balance of tokens for buffers and their limitations. For instance, a transition takes a packet from place and puts a token into place because the port buffer becomes available, then it puts the packet into the internal buffer section corresponding to the port 2 and takes a token from the internal buffer limitation because available buffer size has been decreased.
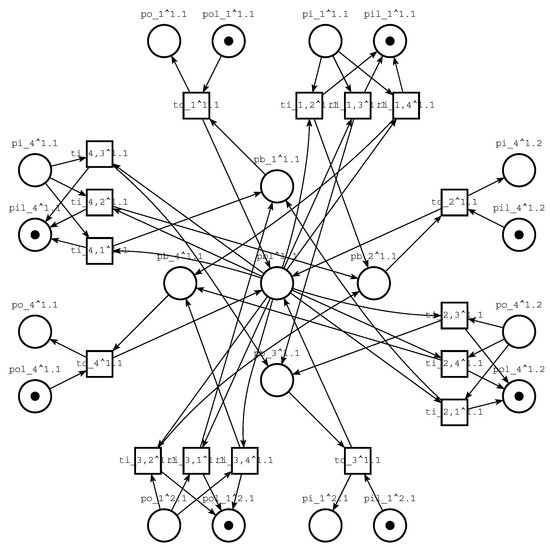
Figure 4.
Model of switching device with 4 ports situated on sides of a square—a cell model for square grids composition; upper indices specify the cell location within a grid.
Having a closed finite construct corresponding to a given value of parameter—say, the grid size as a number of cells in a dimension—and considering infinite countable set of natural values of the parameter, we come to understand the corresponding model as an infinite set of models having incremental size. In those cases in which we find out the model properties that are valid for any value of the parameter, we conclude that we have studied a given structure (topology).
6. Specifying and Analysing Infinite Petri Nets
Infinite systems having a “regular” structure are often specified in mathematics and engineering by a finite notation. Our first goal is to find a similar convenient notation that provides easiness of specification of infinite Petri nets as well as associated tasks of their analysis and synthesis.
6.1. Finite Specification of Infinite Petri Net
A finite specification of an infinite Petri net has been introduced in the form of a parametric multi-set rewriting system [47] called for brevity a parametric expression (PE). It comes from a traditional way of specifying a Petri net enumerating its transitions, a transition is specified by a pair of places’ lists, separated by “→” symbol, —for input and output places, respectively, the arc weight specified as well. A parametric expression (5) specifies the cellular automaton model [41] shown in Figure 2a. A usual arc is represented by mentioning the corresponding place name, for instance ; an inhibitor and a read arc is specified by the corresponding inequality, for instance for inhibitor arc and for read arc.
When studying computing and communication grids on plane (2D) [45], the parametric expression (6) specifies a switching device model having ports, a triangle, square, and hexagon are obtained at the parameter values , respectively. At , we obtain a formal specification of a square grid cell shown in Figure 4.
Infinitely repeating a cell model, in correspondence with a chosen lattice, and supplying it with a definite border condition, we come to the models of grid structures. To specify infinite nets, we use parameters having countable infinite range. Since our basic parameters represent the grid size and the number of dimensions, we use natural numbers in the range from unit to (plus) infinity. Let us employ the square model (6), to compose a closed infinite Petri net of the second kind [48] that represents a surface of a torus (1). Cells are connected by merging contact places; to avoid double names, for port 2 we use contact places of the neighboring cell to the right (port 4) and for port 3 we use contact places of the neighboring cell to the bottom (port 1). Actually, we connect the opposite borders using a function (7) which gives the next cell index for the inside cells and the first cell index for the border cells (to the right – port 2 and to the bottom—port 3).
In PE (1), the current cell location within the grid is specified as an upper index. According to (6), each port specification by a pair of lines (corresponding to its input and output tract, respectively) is written in an explicit form. Ports 1 (upper) and 4 (left) use elements having the same cell index. Ports 2 (right) and 3 (bottom) use names of contact places for neighboring cells, in the corresponding dimension, given by the function (7).
6.2. Solving Infinite Linear Systems in Parametric Form
To analyze the properties of infinite Petri nets, we compose and solve infinite systems of linear algebraic equations. The peculiarity of the process consists in the fact we work with Diophantine systems and it is required to solve them in non-negative numbers. For finding place invariants (p-invariants), a homogeneous system represents balance of terms corresponding to the incoming and outgoing arcs of transitions; it is constructed directly on a given parametric expression [45,48]. For example, an infinite system (2) for finding p-invariants is composed on parametric expression (1), unknowns traditionally have prefix “x”. Saying plainly, to obtain (2) from (1) we replaced commas by pluses and the arrow by equality symbol, then we moved all the variables to the left side of the system. p-invariants are applied to prove the net conservativeness and boundedness. To find transition invariants (t-invariants), a dual parametric specification, which enumerates the net places, is applied [12]. t-invariants play important role when investigating a net liveness—one of the most significant properties.
The obtained p-invariant of the infinite net is represented in parametric form by (3), only nonzero (unit) components are listed. Using it, we have proven that the net is bounded and conservative for any value of size k. Thus, properties of an infinite net are found. Considering structure of (3), we observe two kinds of parametric lines. The first five lines are of the first kind; each parametric line specifies a set of matrix lines having constant number of nonzero elements; first four parametric lines specify lines having two nonzero elements while parametric line five specifies lines having five nonzero elements. Parametric lines 6 and 7 correspond to a single line each; a line contains variable number of nonzero elements given by the index ranges. Examples of parametric p-invariant expansion on a given value of parameters are considered in [12,13]. Thus, the torus communication structure model is a bounded and conservative Petri net which are, together with liveness, basic properties of an ideal communication protocol according to seminal works of Michelle Diaz [1] and Gerard Berthelot [2].
6.3. Complex Deadlocks within Computing Grid Models
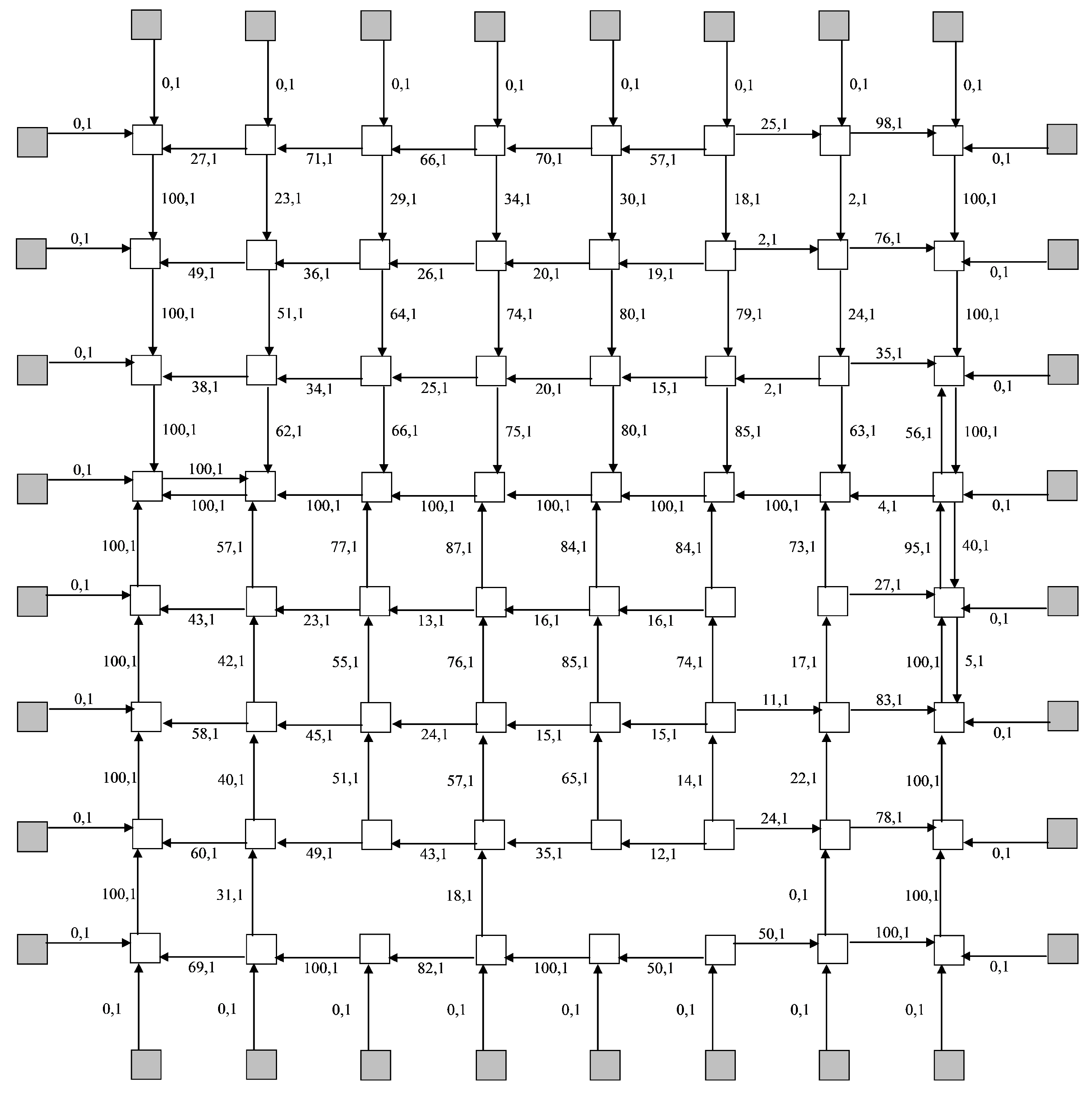
Special graphs have been introduced and studied to prove other properties of grids’ models. A graph of packet transmissions has been introduced to prove t-invariance via explicit composition of stationary repeated sequences of transitions’ firings [45]. A graph of mutual blockings have been introduced to classify complex deadlocks within grid structures, a three causes of deadlocks have been revealed: (i) a circle of blockings; (ii) a chain of blockings ending at an already blocked cell; (iii) isolation by blocked nodes. Afterwards, it has been proven that complex deadlocks can be induced by ill-intentioned traffic and appear in avalanche-like way imposing a serious thread to the grid security [49]. For this purpose colored Petri nets have been applied which allow hierarchical composition of a model and specification of timed parameters. Guns of traffic have been attached to the grid borders, the following concise and the most dangerous configurations involving two guns have been revealed: (i) a traffic duel; (ii) crossfire, and (iii) side shot. An example of a complete deadlock of an 8 × 8 grid is shown in Figure 5. Inscriptions on arcs specify the number of packets in the internal buffer, forwarded to the corresponding device, and the number of packets in the port buffer, respectively; the internal buffer size is 100 packets. Within a real-life network, a deadlock is overcome by drop packet and timeout techniques but repeated deadlicks decrease the network performance and QoS considerably.
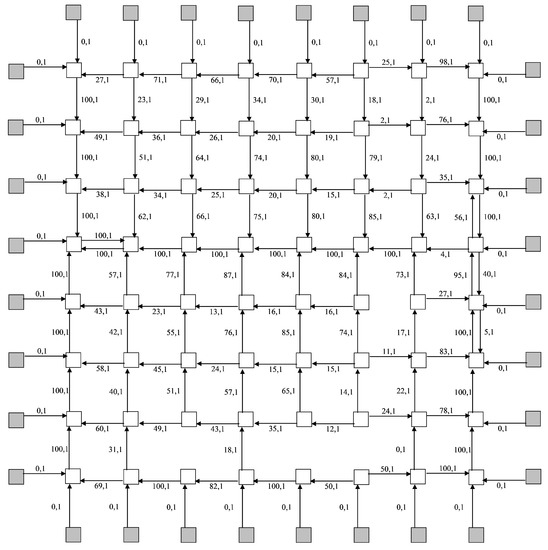
Figure 5.
A complete deadlock in an 8 × 8 communication grid.
Here we would like to note that it is not a kind of DDoS attack. We use comparably low intensity traffic that can be easily disguised say under some multimedia traffic. We call it a technique of induced (programmable) deadlocks. Arranged sources of ill-intentioned traffic can possess more sophisticated variable structure that allows disguising them even better.
6.4. Generalization of Obtained Results
The results obtained for square grids have been further generalized on triangular and hexagonal grids on plane [13,34] and hyper-cube in multidimensional space [12,50], closing opposite edges of a hyper-cube, a hyper-torus have been composed and studied [44,48,51]. Generators of the mentioned models have been programmed in C language and uploaded to GitHub [12]. An example of a generated hexagonal grid of size 6, to study cellular phone systems [34], is shown in Figure 6.

Figure 6.
Modeling hexagonal communication grid with plug devices on edges; an example of grid having size 6.
7. Open Problems
Among the exciting open problems encouraging further research, we could enumerate the following:
- A general method for solving infinite systems of Diophantine linear algebraic equations, especially in non-negative numbers.
- Methods to find siphons and traps of infinite Petri nets to solve tasks of liveness and liveness-enforcing.
- Composition methods on infinite Petri nets, say composition of clans.
- Representation and application of reachability and coverability tree for infinite Petri nets.
- Composing and analyzing infinite Petri nets built of a few repeated components.
- An algorithm of mutual transformation for direct and dual specification of infinite Petri nets.
- Recognition of disguised attacks via induced deadlocks and corresponding countermeasures.
Therefore, we hope that we have now attracted your attention through complex, whilst practical, patterns of infinite Petri nets, exciting multidimensional structures, and open problems, to apply your knowledge, experience, research skills and insights.
8. Conclusions
Petri Nets have been important tools for several decades in the simulation of system processes and communications protocols. The global scale, speed and sophistication of intelligent computer networks, grids and clouds now makes it imperative that we also integrate tools based upon Infinite Petri Nets to our process and protocol simulation toolkit. Recent worldwide DDoS, BotNet and Ransomware cyber attacks have devastated both Government and Enterprise Networks within just seconds across fibre networks at close to light speed. Further mathematical research and practical application of Infinite Petri Nets will provide network operators with effective tools to mitigate and triage future attacks.
Author Contributions
Conceptualization, D.E.P.; methodology, D.A.Z. and T.R.S.; software, D.A.Z.; validation, T.R.S. and D.E.P.; formal analysis, T.R.S.; investigation, D.A.Z.; data curation, D.E.P.; writing—original draft preparation, D.A.Z.; writing—review and editing, T.R.S. and D.E.P.; visualization, T.R.S.; supervision, D.A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Diaz, M. Modelling and Analysis of Communication and Cooperation Protocols Using Petri Net Based Model. Comput. Netw. 1982, 6, 419–441. [Google Scholar]
- Berthelot, G.; Terrat, R. Petri Nets Theory for the Correctness of Protocols. IEEE Trans. Commun. 1982, 30, 2497–2505. [Google Scholar] [CrossRef]
- Jasiul, B.; Szpyrka, M.; Śliwa, J. Detection and Modeling of Cyber Attacks with Petri Nets. Entropy 2014, 16, 6602–6623. [Google Scholar] [CrossRef] [Green Version]
- Bland, J.A.; Petty, M.D.; Whitaker, T.S.; Maxwell, K.P.; Cantrell, W.A. Machine Learning Cyberattack and Defense Strategies. Comput. Secur. 2020, 92, 101738. [Google Scholar] [CrossRef]
- Petty, M.D.; Whitaker, T.S.; Bland, J.A.; Cantrell, W.A.; Mayfield, K.P. Modeling Cyberattacks with Petri Nets: Research Program Overview and Status Report. In Proceedings of the 2019 International Conference on Modeling, Simulation, and Visualization Methods, Simulation, and Visualization Methods, Las Vegas, NV, USA, 29 July–1 August 2019; pp. 27–33. [Google Scholar]
- Sheldon, F.T.; Greiner, S.; Benzinger, M. Specification, Safety and Reliability Analysis Using Stochastic Petri Net Models. In Proceedings of the Tenth International Workshop on Software Specification and Design, San Diego, CA, USA, 7 November 2000. [Google Scholar]
- Henry, M.H.; Layer, R.M.; Snow, K.Z.; Zaret, D.R. Evaluating the risk of cyber attacks on scada systems via petri net analysis with application to hazardous liquid loading operations. In Proceedings of the 2009 IEEE Conference on Technologies for Homeland Security, HST 2009, Waltham, MA, USA, 11–12 May 2009; pp. 607–614. [Google Scholar]
- Szpyrka, M.; Jasiul, B. Evaluation of cyber security and modelling of risk propagation with Petri nets. Symmetry 2017, 9, 32. [Google Scholar] [CrossRef]
- Mayfield, K.; Petty, M. Petri Nets with Players, Strategies and Cost: A Formalism for Modelling Cyberattacks. In Proceedings of the 2018 International Conference on Security and Management, SAM’18, Las Vegas, NV, USA, 30 July–2 August 2018; pp. 237–244. [Google Scholar]
- Zhu, Q.; Qin, Y.; Zhao, Y.; Zhou, C. A hierarchical colored Petri net–based cyberattacks response strategy making approach for critical infrastructures. Int. J. Distrib. Sens. Netw. 2020, 16. [Google Scholar] [CrossRef]
- Almutairi, L.; Hong, L.; Shetty, S. Security analysis of multiple SDN controllers based on Stochastic Petri Nets. In Proceedings of the 2019 Spring Simulation Conference, SpringSim-ANSS, Tucson, AZ, USA, 29 April–2 May 2019; Volume 51. No. 1. [Google Scholar]
- Zaitsev, D.A.; Zaitsev, I.D.; Shmeleva, T.R. Infinite Petri Nets: Part 2, Modeling Triangular, Hexagonal, Hypercube and Hypertorus Structures. Complex Syst. 2017, 26, 341–371. [Google Scholar] [CrossRef] [Green Version]
- Zaitsev, D.A.; Zaitsev, I.D.; Shmeleva, T.R. Infinite Petri Nets: Part 1, Modeling Square Grid Structures. Complex Syst. 2017, 26, 157–195. [Google Scholar] [CrossRef]
- Chen, T.M.; Sanchez-Aarnoutse, J.C.; Buford, J. Petri Net Modeling of Cyber-Physical Attacks on Smart Grid. IEEE Trans. Smart Grid 2011, 2, 741–749. [Google Scholar] [CrossRef] [Green Version]
- Bhuyan, M.H.; Bhattacharyya, D.K.; Kalita, J.K. Network Traffic Anomaly Detection and Prevention: Concepts, Techniques, and Tools; Springer: Berlin/Heidelberg, Germany, 2017; 263p. [Google Scholar]
- Wang, Z.; Sun, L.; Zhu, H. Defining Social Engineering in Cybersecurity. IEEE Access 2020, 8, 85094–85115. [Google Scholar] [CrossRef]
- Blum, D. Rational Cybersecurity for Business: The Security Leaders’ Guide to Business Alignment; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Forshaw, J. Attacking Network Protocols: A Hacker’s Guide to Capture, Analysis, and Exploitation; No Starch Press: San Francisco, CA, USA, 2018. [Google Scholar]
- Lai, R.; Jirachiefpattana, A. Communication Protocol Specification and Verification; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Groote, J.F.; Mousavi, M.R. Modeling and Analysis of Communicating Systems; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Diaz, M. Petri Nets: Fundamental Models, Verification and Applications; John Wiley and Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Popovic, M. Communication Protocol Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Zaitsev, D.A. Clans of Petri Nets: Verification of Protocols and Performance Evaluation of Networks; LAP LAMBERT Academic Publishing: Chisinau, Moldova, 2013. [Google Scholar]
- Burdett, D. Internet Open Trading Protocol, Internet Standard, IETF, RFC 2801. April 2000. Available online: https://datatracker.ietf.org/doc/html/rfc2801 (accessed on 29 June 2021).
- Raj, P.; Koteeswaran, S. Novel Practices and Trends in Grid and Cloud Computing; IGI Global: Hershey, PA, USA, 2019. [Google Scholar]
- Jerger, N.E.; Krishna, T.; Peh, L.S. On-Chip Networks; Morgan & Claypool Publishers: San Rafael, CA, USA, 2017. [Google Scholar]
- Reisig, W. Understanding Petri Nets: Modeling Techniques, Analysis Methods, Case Studies; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cambronero, M.E.; Macià, H.; Valero, V.; Orozco-Barbosa, L. Modeling and Analysis of the 1-Wire Communication Protocol Using Timed Colored Petri Nets. IEEE Access 2018, 6, 27356–27372. [Google Scholar] [CrossRef]
- Kacem, I.; Sait, B.; Mekhilef, S.; Sabeur, N. A New Routing Approach for Mobile Ad Hoc Systems Based on Fuzzy Petri Nets and Ant System. IEEE Access 2018, 6, 65705–65720. [Google Scholar] [CrossRef]
- Ding, Z.; Yang, R. Modeling and Analysis for Mobile Computing Systems Based on Petri Nets: A Survey. IEEE Access 2018, 6, 68038–68056. [Google Scholar] [CrossRef]
- Postel, J. Transmission Control Protocol, Internet Standard, IETF, RFC 793. September 1981. Available online: https://datatracker.ietf.org/doc/html/rfc793 (accessed on 29 June 2021).
- Berthomieu, B.; Ribet, O.-P.; Vernadat, F. The tool TINA—Construction of abstract state space for Petri nets and Time Petri nets. Int. J. Prod. Res. 2004, 42, 2741–2756. Available online: http://www.laas.fr/tina (accessed on 15 February 2021). [CrossRef]
- Marsan, M.A.; Chiola, G.; Fumagalli, A. An accurate performance model of CSMA/CD bus LAN. In Advances in Petri Nets 1987; APN 1986; Rozenberg, G., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1987; Volume 266. [Google Scholar]
- Shmeleva, T.R. Automated Composition of Petri Net Models for Cellular Structures. In Proceedings of the Electrical and Computer Engineering (UKRCON) 2017: Transactions of IEEE First Ukraine Conference, Kyiv, Ukraine, 29 May–2 June 2017; pp. 1019–1024. [Google Scholar] [CrossRef]
- Ajima, Y.; Sumimoto, S.; Shimizu, T. Fujitsu Tofu: A 6D Mesh/Torus Interconnect for Exascale Computers. Computer 2009, 42, 36–40. [Google Scholar] [CrossRef]
- Medhi, D.; Ramasamy, K. Network Routing Algorithms, Protocols, and Architectures; Morgan Kaufmann: Burlington, MA, USA, 2018; 1018p. [Google Scholar]
- Cheng, S.; Zhong, W.; Isaacs, K.E.; Mueller, K. Visualizing the Topology and Data Traffic of Multi-Dimensional Torus Interconnect Networks. IEEE Access 2018, 6, 57191–57204. [Google Scholar] [CrossRef]
- Wolfram, S. A New Kind of Science; Wolfram Media Place: Champaign, IL, USA, 2002. [Google Scholar]
- Li, X.; Wu, J.; Li, X. Theory of Practical Cellular Automaton; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Morita, K. Theory of Reversible Computing; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Zaitsev, D.A. Simulating Cellular Automata by Infinite Petri Nets. J. Cell. Autom. 2018, 13, 121–144. [Google Scholar]
- Zaitsev, D.A. Universality in Infinite Petri Nets. In Proceedings of the 7th International Conference, MCU 2015, Famagusta, North Cyprus, 9–11 September 2015; Volume 9288, pp. 180–197. [Google Scholar]
- Zaitsev, D.A. A generalized neighborhood for cellular automata. Theor. Comput. Sci. 2017, 666, 21–35. [Google Scholar] [CrossRef]
- Zaitsev, D.A.; Shmeleva, T.R.; Groote, J.F. Verification of Hypertorus Communication Grids by Infinite Petri Nets and Process Algebra. IEEE/CAA J. Autom. Sin. 2019, 6, 733–742. [Google Scholar] [CrossRef]
- Shmeleva, T.R.; Zaitsev, D.A.; Zaitsev, I.D. Verification of square communication grid protocols via infinite Petri nets. In Proceedings of the MESM 2009—10th Middle Eastern Simulation Multiconference, Beirut, Lebanon, 27–29 September 2009; pp. 53–59. [Google Scholar]
- Chen, H.; Wu, N.; Zhou, M.C. A novel method for deadlock prevention of AMS by using resource-oriented petri nets. Inf. Sci. 2016, 363, 178–189. [Google Scholar] [CrossRef]
- Bistarelli, S.; Cervesato, I.; Gabriele, L.; Fabio, M. Relating Multiset Rewriting and Process Algebras for Security Protocol Analysis. J. Comput. Secur. 2005, 13, 3–47. [Google Scholar] [CrossRef] [Green Version]
- Zaitsev, D.A. Verification of Computing Grids with Special Edge Conditions by Infinite Petri Nets. Autom. Control Comput. Sci. 2013, 47, 403–412. [Google Scholar] [CrossRef]
- Zaitsev, D.A.; Shmeleva, T.R.; Retschitzegger, W.; Pröll, B. Security of grid structures under disguised traffic attacks. Clust. Comput. 2016, 19, 1183–1200. [Google Scholar] [CrossRef]
- Zaitsev, D.A.; Shmeleva, T.R. Verification of hypercube communication structures via parametric Petri nets. Cybern. Syst. Anal. 2010, 46, 105–114. [Google Scholar] [CrossRef]
- Shmeleva, T.R. Analysis of a Hypertorus Grid. Electronics and Nanotechnology ELNANO-2018. In Proceedings of the IEEE 38th International Conference, Kyiv, Ukraine, 24–26 April 2018; NTUU, Igor Sikorsky Kyiv Polytechnic Institute: Kyiv, Ukraine, 2018; pp. 56–59. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).