Interaction between Screw Dislocation and Interfacial Crack in Fine-Grained Piezoelectric Coatings under Steady-State Thermal Loading
Abstract
:1. Introduction
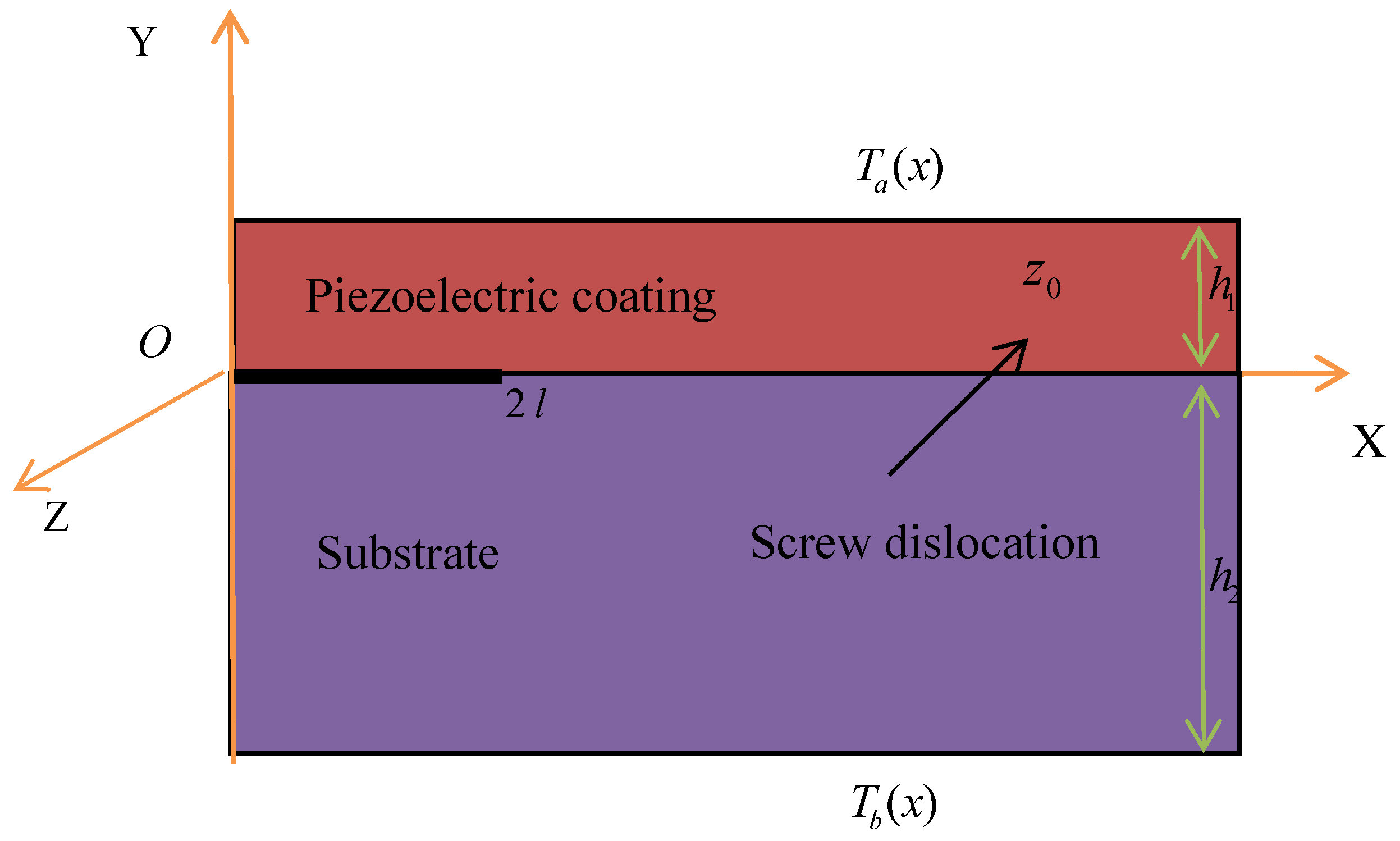
2. Problem Formulation
3. Solution to the Problem
3.1. Temperature Field
3.2. Thermal Stress and Electric Displacement Field
3.3. Image Force
4. Numerical Example
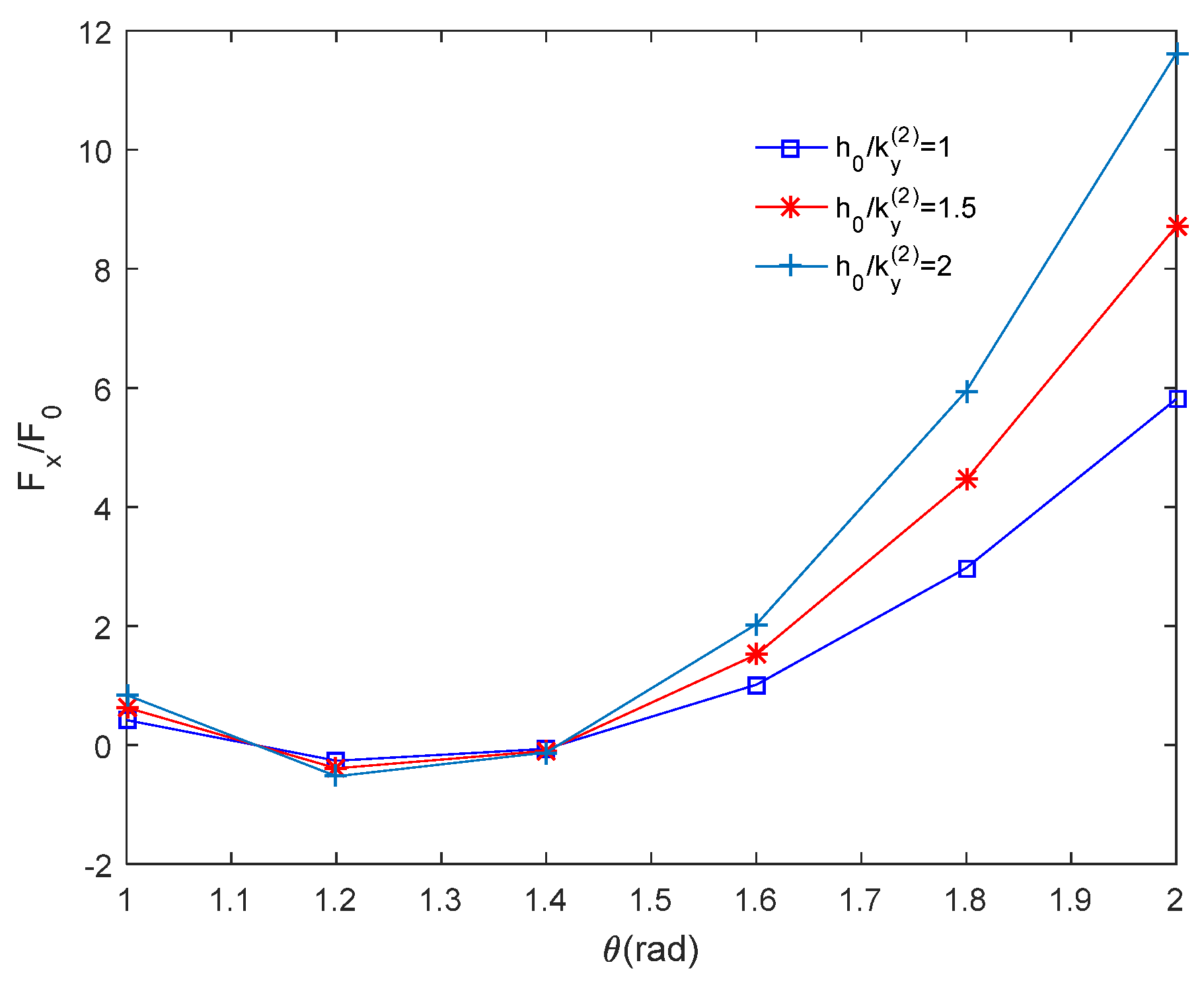
4.1. Effect of Temperature Gradient on Image Force
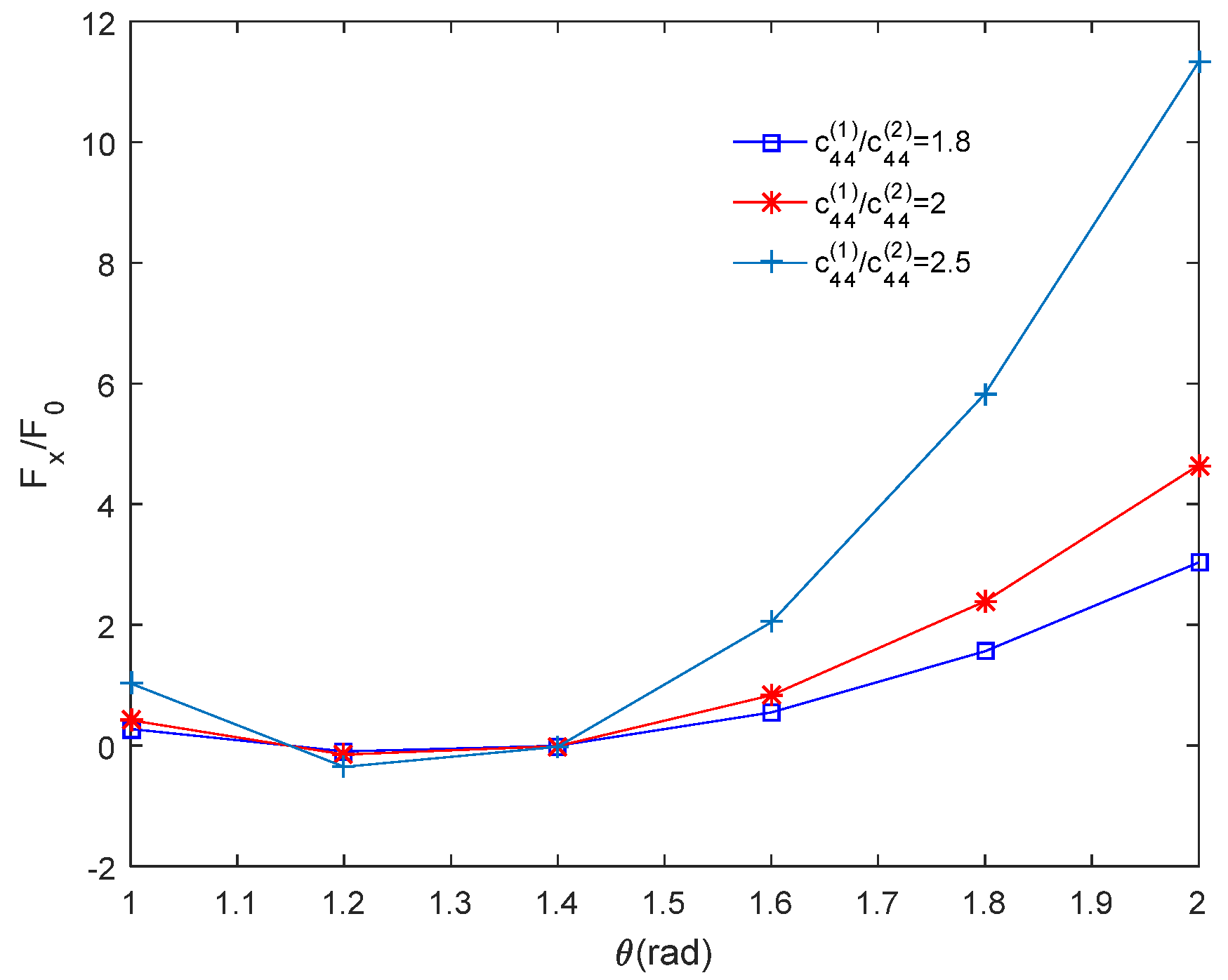
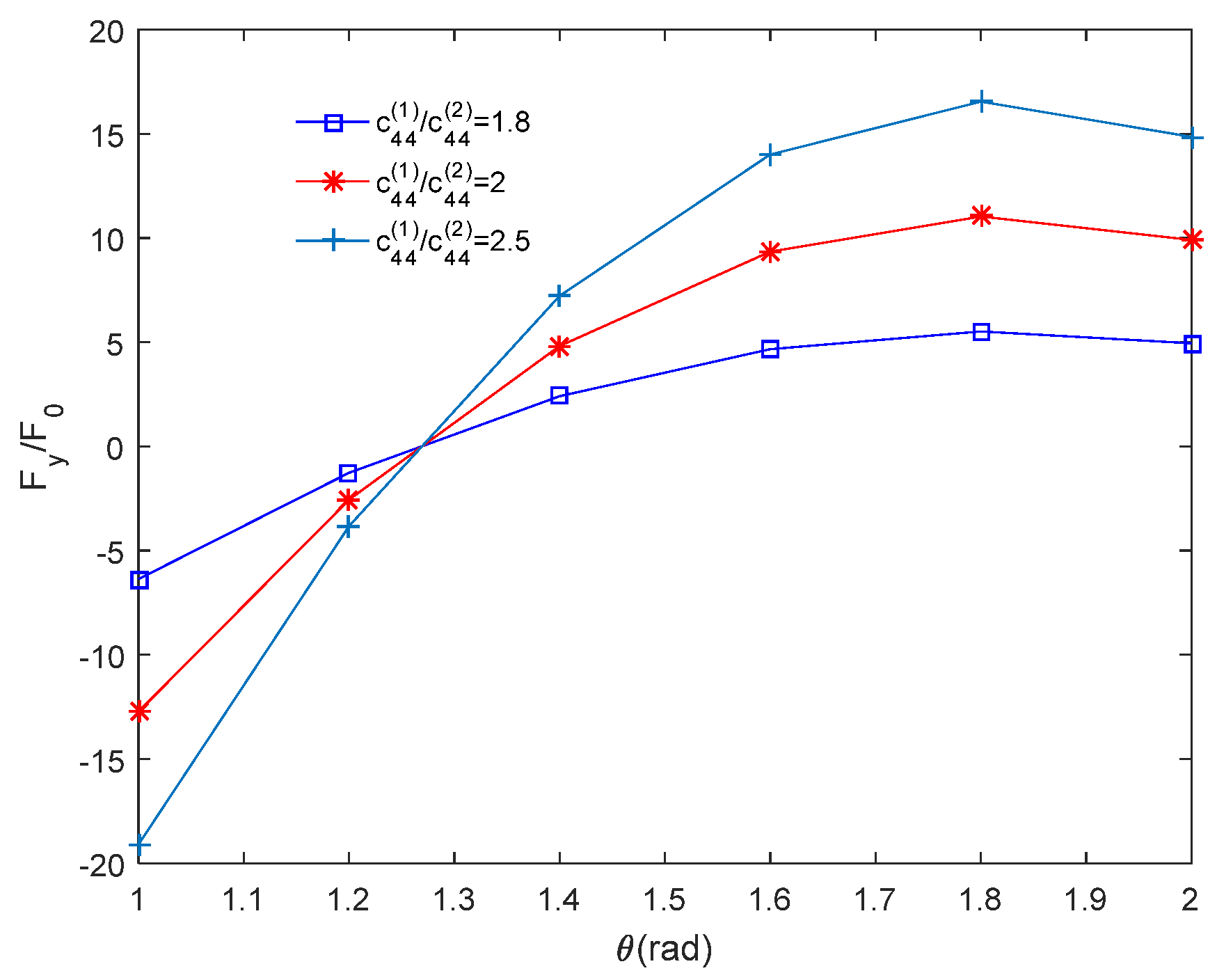
4.2. Effect of Material Elastic Modulus on Image Force
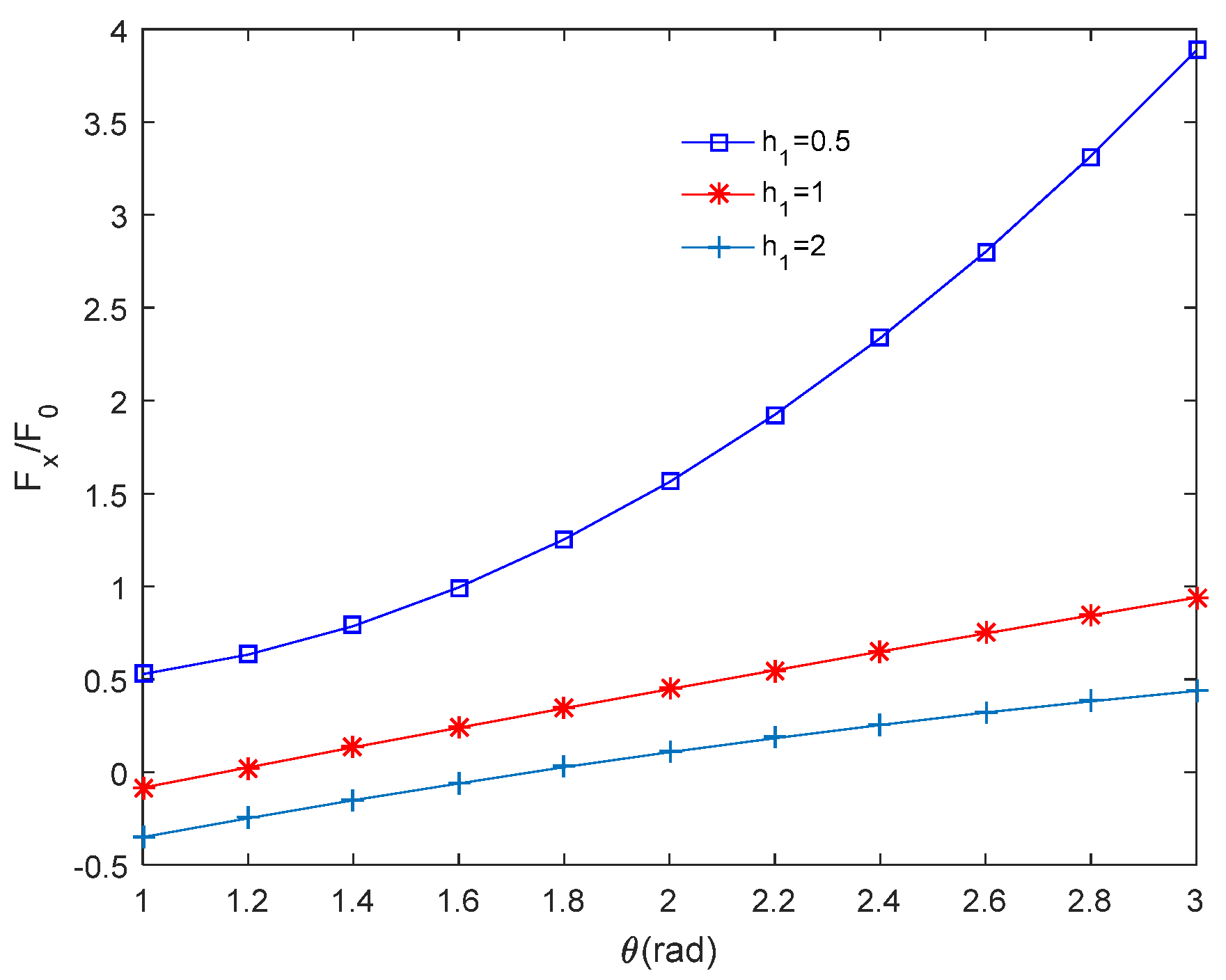
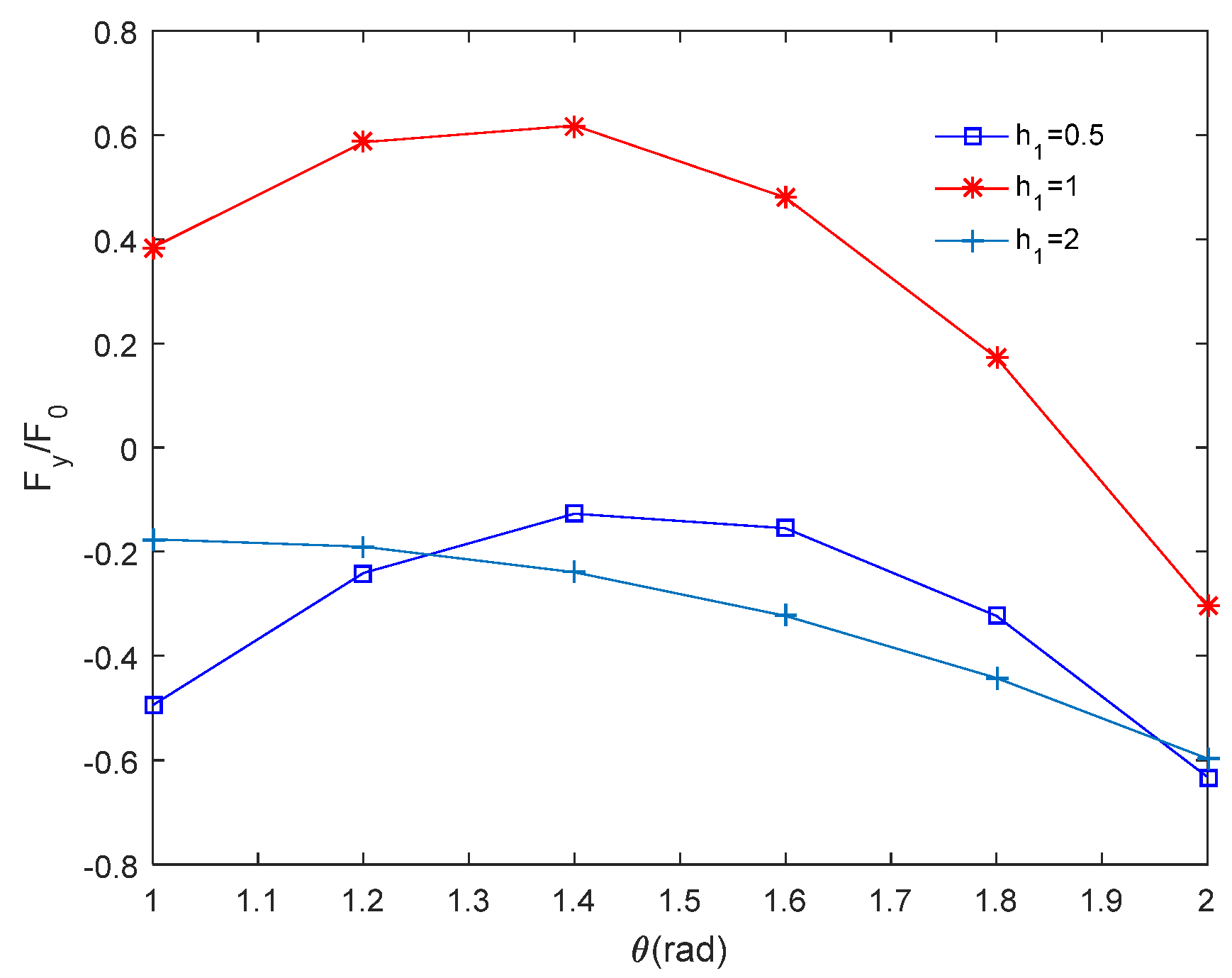
4.3. Effect of Coating Thickness on Image Force
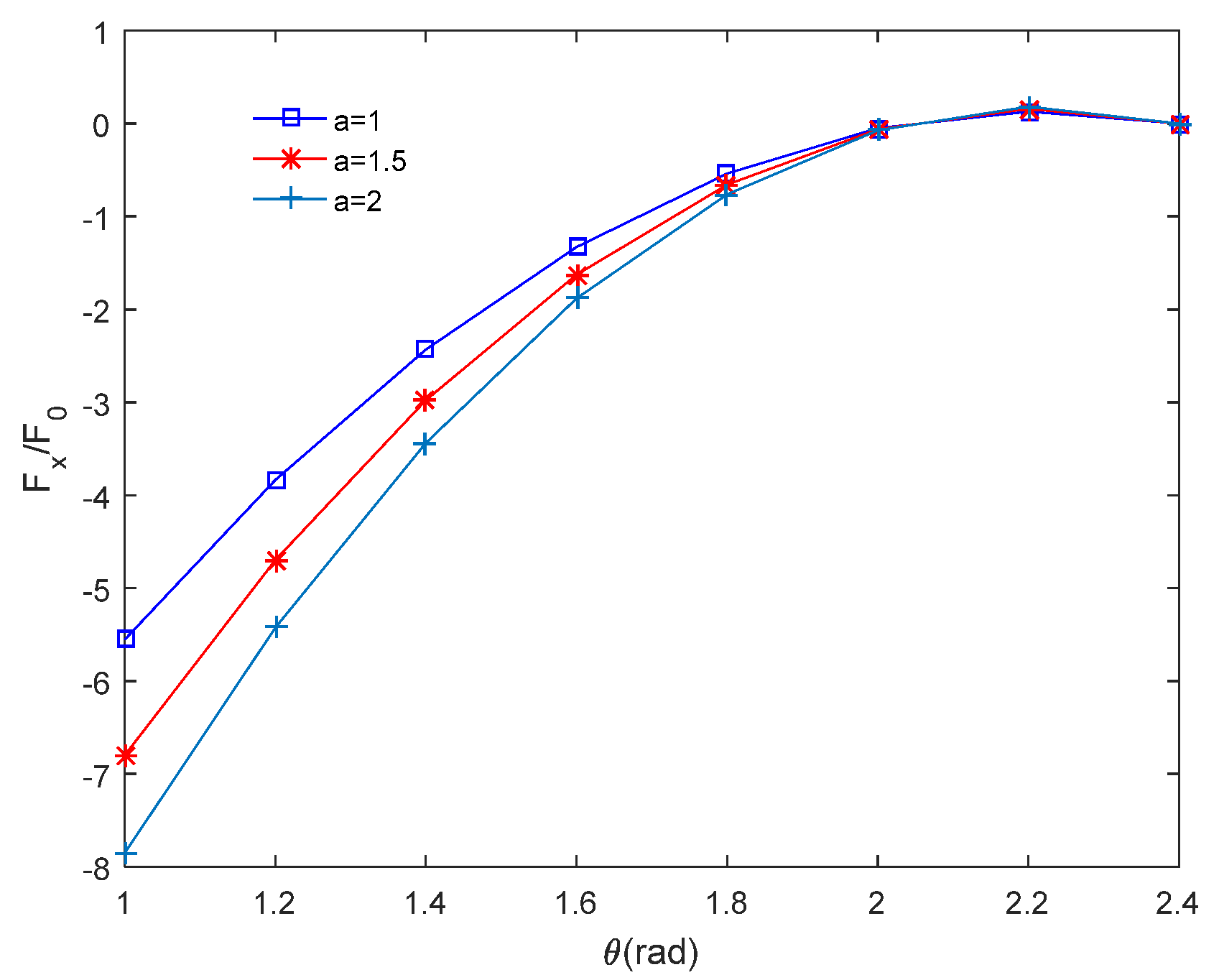
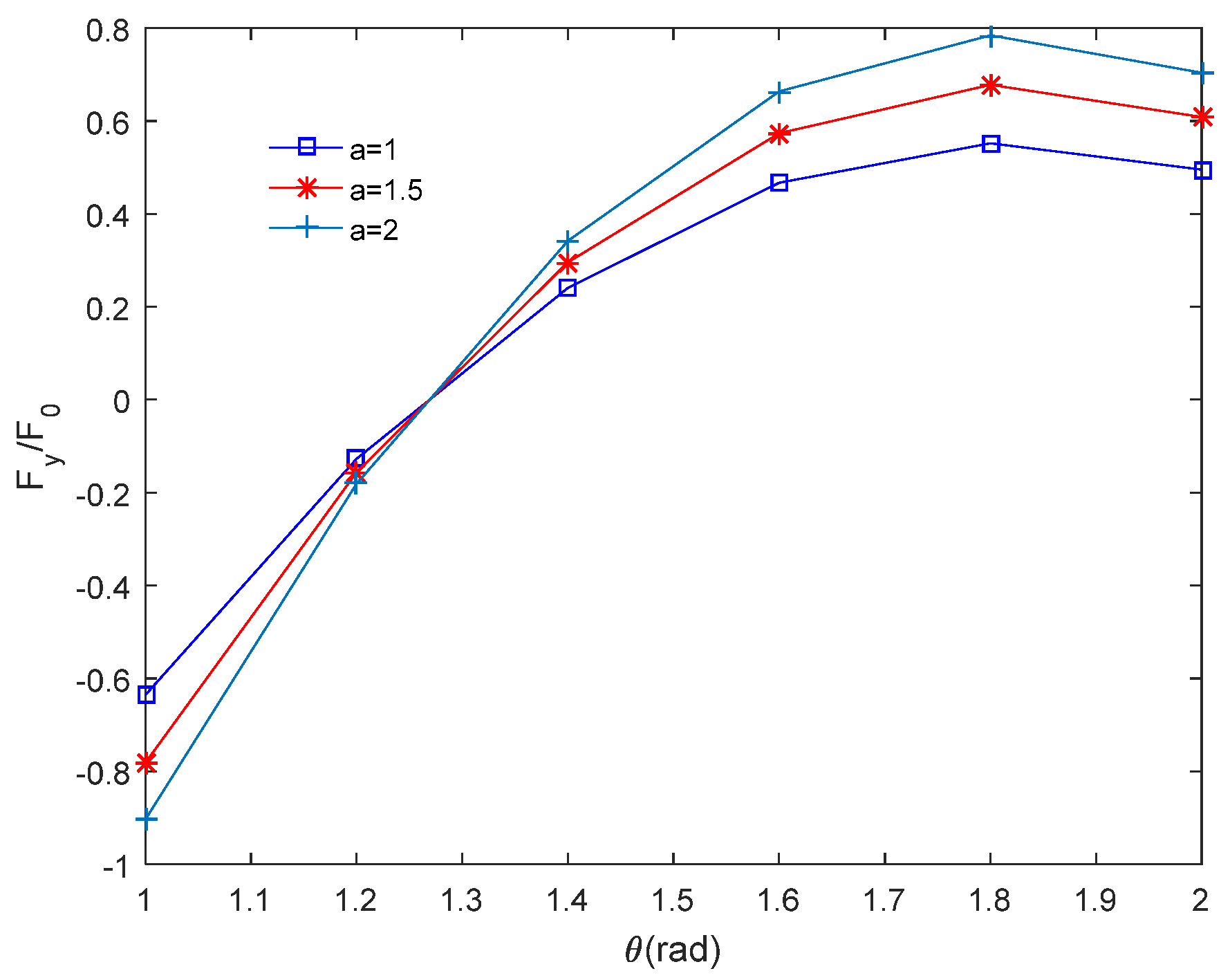
4.4. Effect of Crack Size on Image Force
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pak, Y.E. Crack extension force in a piezoelectric material. Int. J. Appl. Mech. 1990, 57, 647–653. [Google Scholar] [CrossRef]
- Pak, Y.E. Force on a Piezoelectric Screw Dislocation. Int. J. Appl. Mech. 1990, 57, 863–869. [Google Scholar] [CrossRef]
- Suo, Z.; Kuo, C.M.; Barnett, D.M. Fracture mechanics for piezoelectric ceramics. J. Mech. Phys. Solids 1990, 40, 739–765. [Google Scholar] [CrossRef]
- Park, S.; Sun, C.T. Fracture Criteria for Piezoelectric Ceramics. J. Am. Ceram. Soc. 1995, 78, 1475–1480. [Google Scholar] [CrossRef]
- Liang, J.; Han, J.; Du, S. Rigid line inclusions and cracks in anisotropic piezoelectric solids. Mech. Res. Commun. 1995, 22, 43–49. [Google Scholar] [CrossRef]
- Liu, J.X.; Lee, K.Y. Electroelastic behavior of arectangular piezoelectric ceramic with an anti-plane shear crack at arbitrary position. Eur. J. Mech. A-Solid. 2004, 23, 645–658. [Google Scholar] [CrossRef]
- Gao, C.F.; Fan, W.X. An exact solution of crack problems in piezoelectric materials. Appl. Math. Mech.-Engl. 1999, 20, 51–58. [Google Scholar] [CrossRef]
- Gao, C.F.; Fan, W.X. An interface inclusion between two dissimilar piezoelectric materials. Appl. Math. Mech.-Engl. 2001, 22, 96–104. [Google Scholar] [CrossRef]
- Xiao, W.S.; Wei, G. The Interaction between Piezoelectric Screw Dislocation and Circular Crack under Remote Uniform Heat Flux. J. Hunan Univ. 2006, 33, 97–101. [Google Scholar] [CrossRef]
- Ueda, S.; Okada, M.; Nakaue, Y. Transient thermal response of a functionally graded piezoelectric laminate with a crack normal to the bimaterial interface. J. Therm. Stresses 2017, 41, 98–118. [Google Scholar] [CrossRef]
- Jiang, L.J.; Liu, G.T. The interaction between a screw dislocation and a wedge-shaped crack in one-dimensional hexagonal piezoelectric quasicrystals. Chin. Phys. B 2017, 26, 245–251. [Google Scholar] [CrossRef]
- Lv, X.; Liu, G.T. Interaction between many parallel screw dislocations and a semi-infinite crack in a magnetoelectroelastic solid. Chin. Phys. B 2018, 27, 448–452. [Google Scholar] [CrossRef]
- Lee, K.Y.; Lee, W.G.; Pak, Y.E. Interaction Between a Semi-Infinite Crack and a Screw Dislocation in a Piezoelectric Material. J. Appl. Mech. 2000, 67, 165–170. [Google Scholar] [CrossRef]
- Gherrous, M.; Ferdjani, H. Analysis of a Griffith crack at the interface of two piezoelectric materials under anti-plane loading. Contin. Mech. Therm. 2016, 28, 1683–1704. [Google Scholar] [CrossRef]
- Bayat, J.; Ayatollahi, M.; Bagheri, R. Fracture analysis of an orthotropic strip with imperfect piezoelectric coating containing multiple defects. Theor. Appl. Fract. Mech. 2015, 77, 41–49. [Google Scholar] [CrossRef]
- Nourazar, M.; Ayatollahi, M. Analysis of an orthotropic strip containing multiple defects bonded between two piezoelectric layers. Acta Mech. 2016, 227, 1293–1306. [Google Scholar] [CrossRef]
- Viun, O.; Komarov, A.; Lapusta, Y. A polling direction influence on fracture parameters of a limited permeable interface crack in a piezoelectric bi-material. Eng. Fract. Mech. 2018, 191, 143–152. [Google Scholar] [CrossRef]
- Shen, M.H.; Hung, S.Y. Screw dislocation near a piezoelectric oblique edge crack. Meccanica 2016, 51, 1445–1456. [Google Scholar] [CrossRef]
- Mishra, R.; Burela, R.G.; Pathak, H. Crack interaction study in piezoelectric materials under thermo-electro-mechanical loading environment. Int. J. Mech. Mater. Des. 2019, 15, 379–412. [Google Scholar] [CrossRef]
- Xiao, C.J.; Li, Z.X.; Zhu, L.Y.; Zhang, H.T. Effect of grain size of BaTiO3 ceramics on thermal expansion and electrical properties. Int. J. Theor. Phys. 2014, 35, 346–351. [Google Scholar] [CrossRef]
- Shi, Y.; Pu, Y.P.; Cui, Y.F.; Luo, Y.J. Enhanced grain size effect on electrical characteristics of fine grained BaTiO3 ceramics. J. Mater. Sci.-Mater. Electron. 2017, 28, 13229–13235. [Google Scholar] [CrossRef]
- Martirena, H.T.; Burfoot, J.C. Grain-size effects on properties of some ferroelectric ceramics. J. Phys. C Solids Phys. 2001, 7, 3182–3192. [Google Scholar] [CrossRef] [Green Version]
- Bell, A.J.; Moulson, A.J. The Effect of Grain Size on the Dielectric Properties of Barium Titanate Ceramic. J. Am. Ceram. Soc. 1985, 62, 325–328. [Google Scholar]
- Lobo, R.P.S.M.; Mohallem, N.D.; Moreira, R.L. Grain size eff ect on diffuse phase transitions of sol-gel prepared barium titanate ceramics. J. Am. Ceram. Soc. 1995, 78, 1343–1346. [Google Scholar] [CrossRef]
- Hu, S.S.; Liu, J.S.; Li, J.L.; Xie, X.F. Interaction of Screw Dislocation with Edge Interfacial Crack on Fine-Grained Piezoelectric Coating/Substrate. Adv. Mater. Sci. Eng. 2019, 2019, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Shen, Y.P. A solution of the elliptical piezoelectric inclusion problem under uniform heat flux. Int. J. Solids Struct. 2001, 38, 2503–2516. [Google Scholar] [CrossRef]
- Muskhelishvili, N.L. Some Basic Problems of the Mathematical Theory of Elasticity; Noordhoff International Publishing: Gromngen, The Netherlands, 1975. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Li, J. Interaction between Screw Dislocation and Interfacial Crack in Fine-Grained Piezoelectric Coatings under Steady-State Thermal Loading. Appl. Sci. 2021, 11, 11922. https://doi.org/10.3390/app112411922
Hu S, Li J. Interaction between Screw Dislocation and Interfacial Crack in Fine-Grained Piezoelectric Coatings under Steady-State Thermal Loading. Applied Sciences. 2021; 11(24):11922. https://doi.org/10.3390/app112411922
Chicago/Turabian StyleHu, Shuaishuai, and Junlin Li. 2021. "Interaction between Screw Dislocation and Interfacial Crack in Fine-Grained Piezoelectric Coatings under Steady-State Thermal Loading" Applied Sciences 11, no. 24: 11922. https://doi.org/10.3390/app112411922




