Is Cork Growth a Reliable Proxy for Stem Diameter Growth in Cork Oak (Quercus suber L.)? Implications for Forest Management under Climate Change in Mediterranean Regions
Abstract
:1. Introduction
2. Materials and Methods
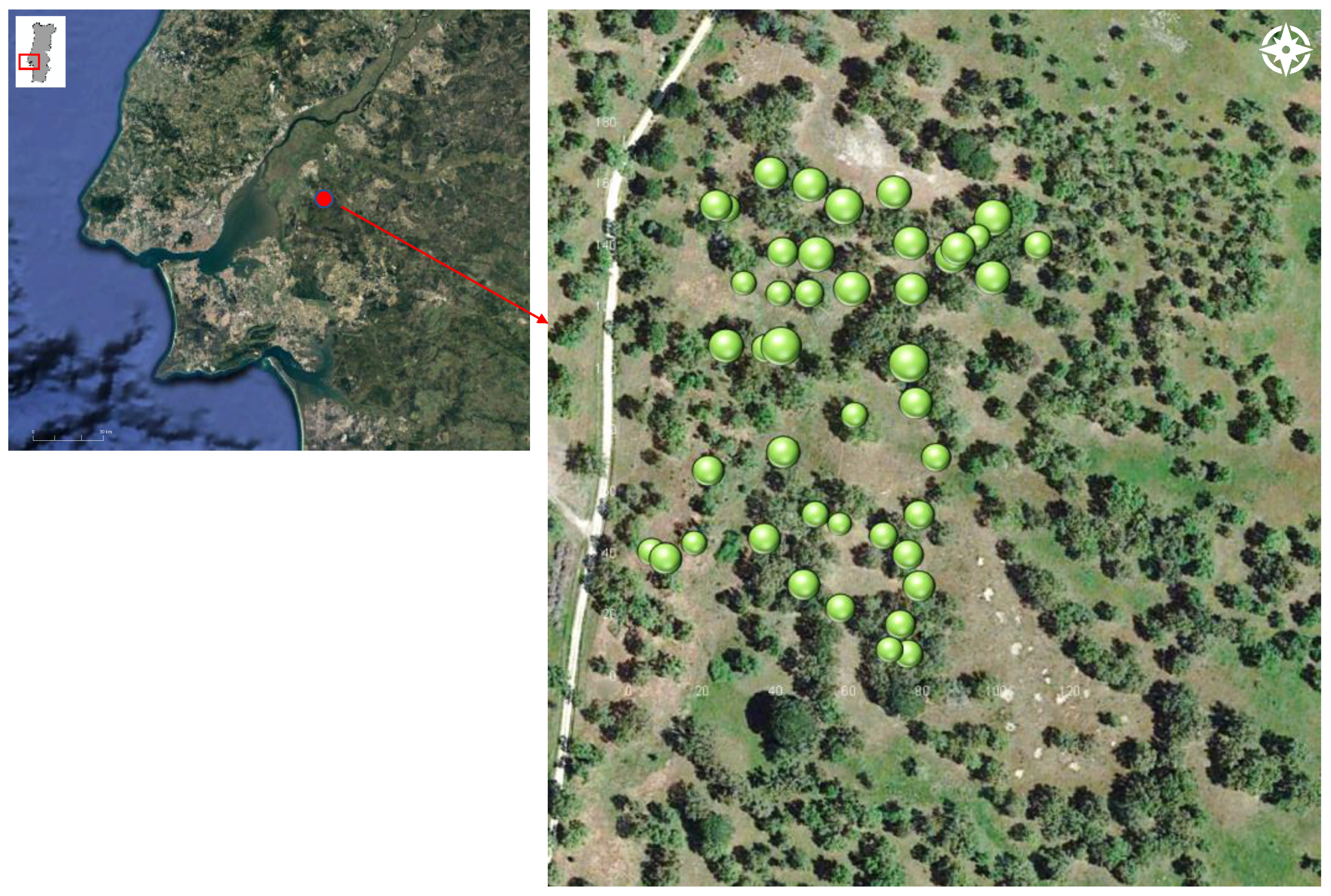
2.1. Study Area and Climate
2.2. Data Measurements
2.3. Data Analysis
3. Results
3.1. Stem Diameter and Cork Growth Chronologies
3.2. Precipitation and Temperature Relationships with Stem Diameter Growth and Cork Growth Indices
3.3. Influence of Tree Size on the Relationship between Climate and Stem Diameter Growth and Cork-Ring Width
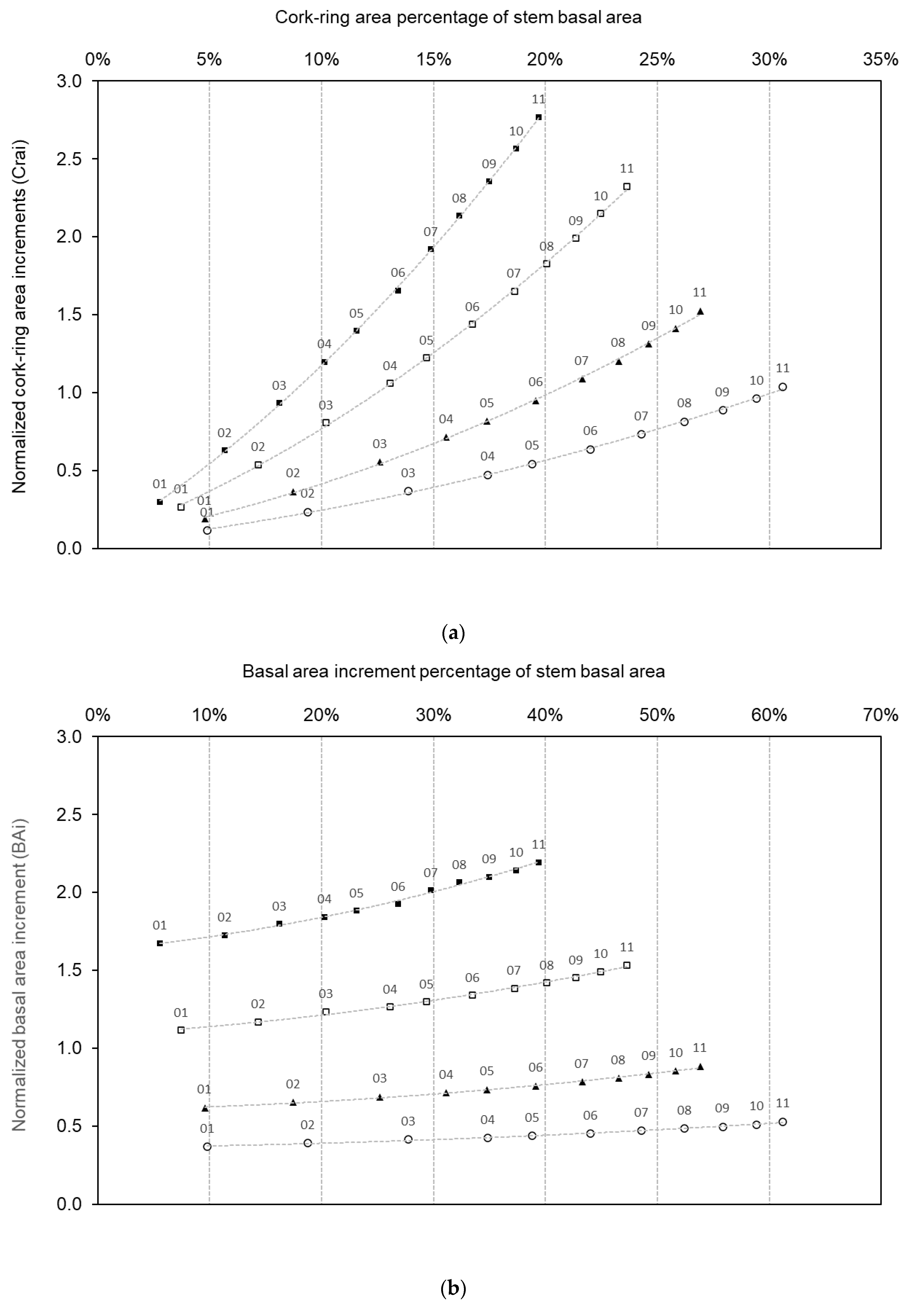
3.4. Cross-Sectional Area Increments of Cork and Stem Diameter
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lindner, M.; Maroschek, M.; Netherer, S.; Kremer, A.; Barbati, A.; Garcia-Gonzalo, J.; Seidl, R.; Delzon, S.; Corona, P.; Kolström, M.; et al. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. For. Ecol. Manag. 2010, 259, 698–709. [Google Scholar] [CrossRef]
- Garzón, M.B.; De Dios, R.S.; Ollero, H.S. Effects of climate change on the distribution of Iberian tree species. Appl. Veg. Sci. 2008, 11, 169–178. [Google Scholar] [CrossRef]
- Cherubini, P.; Gartner, B.L.; Tognetti, R.; Bräker, O.U.; Schoch, W.; Innes, J. Identification, measurement and interpretation of tree rings in woody species from mediterranean climates. Biol. Rev. 2003, 78, 119–148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kurz-Besson, C.; Otieno, D.; Vale, R.L.D.; Siegwolf, R.; Schmidt, M.; Herd, A.; Nogueira, C.; David, T.; David, J.S.; Tenhunen, J.; et al. Hydraulic Lift in Cork Oak Trees in a Savannah-Type Mediterranean Ecosystem and its Contribution to the Local Water Balance. Plant Soil 2006, 282, 361–378. [Google Scholar] [CrossRef]
- Costa, A.; Barbosa, I.; Roussado, C.; Graça, J.; Spiecker, H. Climate response of cork growth in the Mediterranean oak (Quercus suber L.) woodlands of southwestern Portugal. Dendrochronologia 2016, 38, 72–81. [Google Scholar] [CrossRef]
- Oliveira, G.; Costa, A. How resilient is Quercus suber L. to cork harvesting? A review and identification of knowledge gaps. For. Ecol. Manag. 2012, 270, 257–272. [Google Scholar] [CrossRef]
- Ghalem, A.; Barbosa, I.; Bouhroua, R.T.; Costa, A. Climate signal in cork-rings chronologies: Case-studies on southwestern Portugal and north-western Algeria. Tree Ring Res. 2017, 74, 1–14. [Google Scholar] [CrossRef]
- Costa, A.; Pereira, H.; Oliveira, Â. Influence of climate on the seasonality of radial growth of cork oak during a cork production cycle. Ann. For. Sci. 2002, 59, 429–437. [Google Scholar] [CrossRef] [Green Version]
- Leal, S.; Nunes, E.; Pereira, H. Cork oak (Quercus suber L.) wood growth and vessel characteristics variations in relation to climate and cork harvesting. Eur. J. For. Res. 2008, 127, 33–41. [Google Scholar] [CrossRef]
- Costa, A.; Pereira, H.; Oliveira, A. Variability of radial growth in cork oak adult trees under cork production. For. Ecol. Manag. 2003, 175, 239–246. [Google Scholar] [CrossRef]
- Mendes, M.P.; Cherubini, P.; Plieninger, T.; Ribeiro, L.; Costa, A. Climate effects on stem radial growth of Quercus suber L.: Does tree size matter? Forestry 2019, 92, 73–84. [Google Scholar] [CrossRef]
- Machado, D.P. Contribuição para o estudo da formação da cortiça no sobreiro. Rev. Agronómica 1935, 23, 75–104. [Google Scholar]
- Knapic, S.; Louzada, J.L.; Leal, S.; Pereira, H. Radial variation of wood density components and ring width in cork oak trees. Ann. For. Sci. 2007, 64, 211–218. [Google Scholar] [CrossRef] [Green Version]
- Almeida, C.; Mendonça, J.J.L.; Jesus, M.R.; Gomes, A.J. Sistemas Aquíferos de Portugal: Aluviões do Tejo (T7); Instituto Nacional da Água, Sistema Nacional de Informação de Recursos Hídricos: Lisbon, Portugal, 2000.
- Costa, A.; Madeira, M.; Oliveira, Â.C. The relationship between cork oak growth patterns and soil, slope and drainage in a cork oak woodland in Southern Portugal. For. Ecol. Manag. 2008, 255, 1525–1535. [Google Scholar] [CrossRef] [Green Version]
- Mendes, M.P.; Ribeiro, L.; David, T.S.; Costa, A. How dependent are cork oak (Quercus suber L.) woodlands on groundwater? A case study in southwestern Portugal. For. Ecol. Manag. 2016, 378, 122–130. [Google Scholar] [CrossRef]
- West, P.W. Use of diameter increment and basal area increment in tree growth studies. Can. J. For. Res. 1980, 10, 71–77. [Google Scholar] [CrossRef]
- Caritat, A.; Gutiérrez, E.; Molinas, M. Influence of weather on cork-ring width. Tree Physiol. 2000, 20, 893–900. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferreira, A.; Lopes, F.; Pereira, H. Caractérisation de la croissance et de la qualité du liège dans une région de production. Ann. For. Sci. 2000, 57, 187–193. [Google Scholar] [CrossRef] [Green Version]
- Natividade, J.V. Subericultura; Direcção Geral dos Serviços Florestais e Aquícolas: Lisbon, Portugal, 1950. [Google Scholar]
- Johnson, S.E.; Abrams, M.D. Age class, longevity and growth rate relationships: Protracted growth increases in old trees in the eastern United States. Tree Physiol. 2009, 29, 1317–1328. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pereira, H. Cork: Biology, Production and Uses; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Costa, A.; Nunes, L.C.; Spiecker, H.; Graça, J. Insights into the Responsiveness of Cork Oak (Quercus suber L.) to Bark Harvesting. Econ. Bot. 2015, 69, 171–184. [Google Scholar] [CrossRef]
- Seabra, L. Aspectos gerais da cicatrização no sobreiro. An. Inst. Super. Agron. 1939, X, 89–97. [Google Scholar]
- Tessier, L.; Nola, P.; Serre-Bachet, F. Deciduous Quercus in the Mediterranean region: Tree-ring/climate relationships. New Phytol. 1994, 126, 355–367. [Google Scholar] [CrossRef]
- Corcuera, L.; Camarero, J.J.; Gil-Pelegrín, E. Effects of a severe drought on Quercus ilex radial growth and xylem anatomy. Trees 2004, 18, 83–92. [Google Scholar]
- Gea-Izquierdo, G.; Martín-Benito, D.; Cherubini, P.; Cañellas, I. Climate-growth variability in Quercus ilex L. west Iberian open woodlands of different stand density. Ann. For. Sci. 2009, 66, 802. [Google Scholar] [CrossRef] [Green Version]
- Andivia, E.; Fernández, M.; Vázquez-Piqué, J.; González-Pérez, A.; Tapias, R. Nutrients return from leaves and litterfall in a mediterranean cork oak (Quercus suber L.) forest in southwestern Spain. Eur. J. For. Res. 2010, 129, 5–12. [Google Scholar] [CrossRef]
- Costa, A.; Barbosa, I.; Miguel, C.; Graça, J. Variation of cork porosity along the stem in harvested cork oak (Quercus suber L.) trees. Ann. For. Sci. 2021, 78, 52. [Google Scholar] [CrossRef]
- Costa, A.; Barbosa, I.; Pestana, M.; Miguel, C. Modelling bark thickness variation in stems of cork oak in south-western Portugal. Eur. J. For. Res. 2020, 139, 611–625. [Google Scholar] [CrossRef]
- Rozas, V. Dendrochronology of pedunculate oak (Quercus robur L.) in an old-growth pollarded woodland in northern Spain: Tree-ring growth responses to climate. Ann. For. Sci. 2005, 62, 209–218. [Google Scholar] [CrossRef] [Green Version]
- Pasho, E.; Camarero, J.J.; de Luis, M.; Vicente-Serrano, S.M. Impacts of drought at different time scales on forest growth across a wide climatic gradient in north-eastern Spain. Agric. For. Meteorol. 2011, 151, 1800–1811. [Google Scholar] [CrossRef]
- Faias, S.P.; Paulo, J.A.; Firmino, N.; Tomé, M. Drivers for annual cork growth under two understory management alternatives on a podzolic cork oak stand. Forests 2019, 10, 133. [Google Scholar] [CrossRef] [Green Version]
- Stephenson, N.L.; Das, A.J.; Condit, R.; Russo, S.E.; Baker, P.J.; Beckman, N.G.; Coomes, D.A.; Lines, E.R.; Morris, W.K.; Ruger, N.; et al. Rate of tree carbon accumulation increases continuously with tree size. Nature 2014, 507, 7490. [Google Scholar] [CrossRef] [PubMed]
- Vanoni, M.; Bugmann, H.; Nötzli, M.; Bigler, C. Quantifying the effects of drought on abrupt growth decreases of major tree species in Switzerland. Ecol. Evol. 2016, 6, 3555–3570. [Google Scholar] [CrossRef] [PubMed]



| Stem Diameter Growth (IDbh) | MODEL | Model Equation | a0 | a1 | sTreej(mj) | seij | AIC | |
|---|---|---|---|---|---|---|---|---|
| Climate Variables | ||||||||
| Precipitation | ||||||||
| June–July (CLIM0) | M0 | IDbhij = a0 + a1 CLIM0ij + mTreej + eij | 0.905 | 0.009 ** | 0.002 | 0.133 | 450.33 | |
| September-1 (CLIM1) | M1 | IDbhij = a0 + a1 CLIM1ij + mTreej + eij | 0.953 | 0.003 ** | 0.002 | 0.140 | 476.56 | |
| June (CLIM2) | M2 | IDbhij = a0 + a1 CLIM2ij + mTreej + eij | 0.933 | 0.008 ** | 0.002 | 0.134 | 453.71 | |
| June–August (CLIM3) | M3 | IDbhij = a0 + a1 CLIM3ij + mTreej + eij | 0.882 | 0.007 ** | 0.002 | 0.133 | 451.24 | |
| Temperature | ||||||||
| June (CLIM4) | M4 | IDbhij = a0 + a1 CLIM4ij + mTreej + eij | 3.388 | −0.115 ** | 0.002 | 0.133 | 448.72 | |
| October-1 (CLIM5) | M5 | IDbhij = a0 + a1 CLIM5ij + mTreej + eij | −0.811 | 0.108 ** | 0.002 | 0.139 | 473.69 | |
| February–April (CLIM6) | M6 | IDbhij = a0 + a1 CLIM6ij + mTreej + eij | −2.340 | 0.268 ** | 0.002 | 0.135 | 457.81 | |
| January–December (CLIM7) | M7 | IDbhij = a0 + a1 CLIM7ij + mTreej + eij | 5.995 | −0.316 ** | 0.002 | 0.141 | 480.44 | |
| Cork growth index (ICrw) | ||||||||
| Climate variables | ||||||||
| Precipitation | ||||||||
| August (CLIM8) | M8 | ICrwij = a0 + a1 CLIM8ij + mTreej + eij | 0.941 | 0.009 ** | 0.000 | 0.029 | −348.81 | |
| September-1 (CLIM9) | M9 | ICrwij = a0 + a1 CLIM9ij + mTreej + eij | 0.969 | 0.001 ** | 0.000 | 0.031 | −318.93 | |
| February (CLIM10) | M10 | ICrwij = a0 + a1 CLIM10ij + mTreej + eij | 0.938 | 0.001 ** | 0.000 | 0.031 | −326.74 | |
| July–August (CLIM11) | M11 | ICrwij = a0 + a1 CLIM11ij + mTreej + eij | 0.931 | 0.008 ** | 0.000 | 0.030 | −337.73 | |
| Temperature | ||||||||
| November-1–February (CLIM12) | M12 | ICrwij = a0 + a1 CLIM12ij + mTreej + eij | −0.247 | 0.120 ** | 0.000 | 0.029 | −362.80 | |
| September-1–March (CLIM13) | M13 | ICrwij = a0 + a1 CLIM13ij + mTreej + eij | −1.440 | 0.186 ** | 0.000 | 0.029 | −354.13 | |
| October-1–February (CLIM14) | M14 | ICrwij = a0 + a1 CLIM14ij + mTreej + eij | −0.491 | 0.127 ** | 0.000 | 0.029 | −352.85 | |
| November-1–March (CLIM15) | M15 | ICrwij = a0 + a1 CLIM15ij + mTreej + eij | −0.588 | 0.147 ** | 0.000 | 0.029 | −360.68 | |
| November-1–April (CLIM16) | M16 | ICrwij = a0 + a1 CLIM16ij + mTreej + eij | −0.938 | 0.168 ** | 0.000 | 0.029 | −350.33 | |
| February (CLIM17) | M17 | ICrwij = a0 + a1 CLIM17ij + mTreej + eij | 0.362 | 0.063 ** | 0.000 | 0.029 | −358.30 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, A.; Cherubini, P. Is Cork Growth a Reliable Proxy for Stem Diameter Growth in Cork Oak (Quercus suber L.)? Implications for Forest Management under Climate Change in Mediterranean Regions. Appl. Sci. 2021, 11, 11998. https://doi.org/10.3390/app112411998
Costa A, Cherubini P. Is Cork Growth a Reliable Proxy for Stem Diameter Growth in Cork Oak (Quercus suber L.)? Implications for Forest Management under Climate Change in Mediterranean Regions. Applied Sciences. 2021; 11(24):11998. https://doi.org/10.3390/app112411998
Chicago/Turabian StyleCosta, Augusta, and Paolo Cherubini. 2021. "Is Cork Growth a Reliable Proxy for Stem Diameter Growth in Cork Oak (Quercus suber L.)? Implications for Forest Management under Climate Change in Mediterranean Regions" Applied Sciences 11, no. 24: 11998. https://doi.org/10.3390/app112411998
APA StyleCosta, A., & Cherubini, P. (2021). Is Cork Growth a Reliable Proxy for Stem Diameter Growth in Cork Oak (Quercus suber L.)? Implications for Forest Management under Climate Change in Mediterranean Regions. Applied Sciences, 11(24), 11998. https://doi.org/10.3390/app112411998





