Experimental and Numerical Investigation of Contact Parameters in a Dovetail Type of Blade Root Joints
Abstract
:1. Introduction
2. Experimental Configuration
2.1. Test Bench
- The support and traction system of the blade simulacrum, shown in Figure 2. This system includes two crosspieces: a fixed piece integrated with a support of dovetail type (c); and a mobile piece connected to a hydraulic actuator that enables the traction (b).
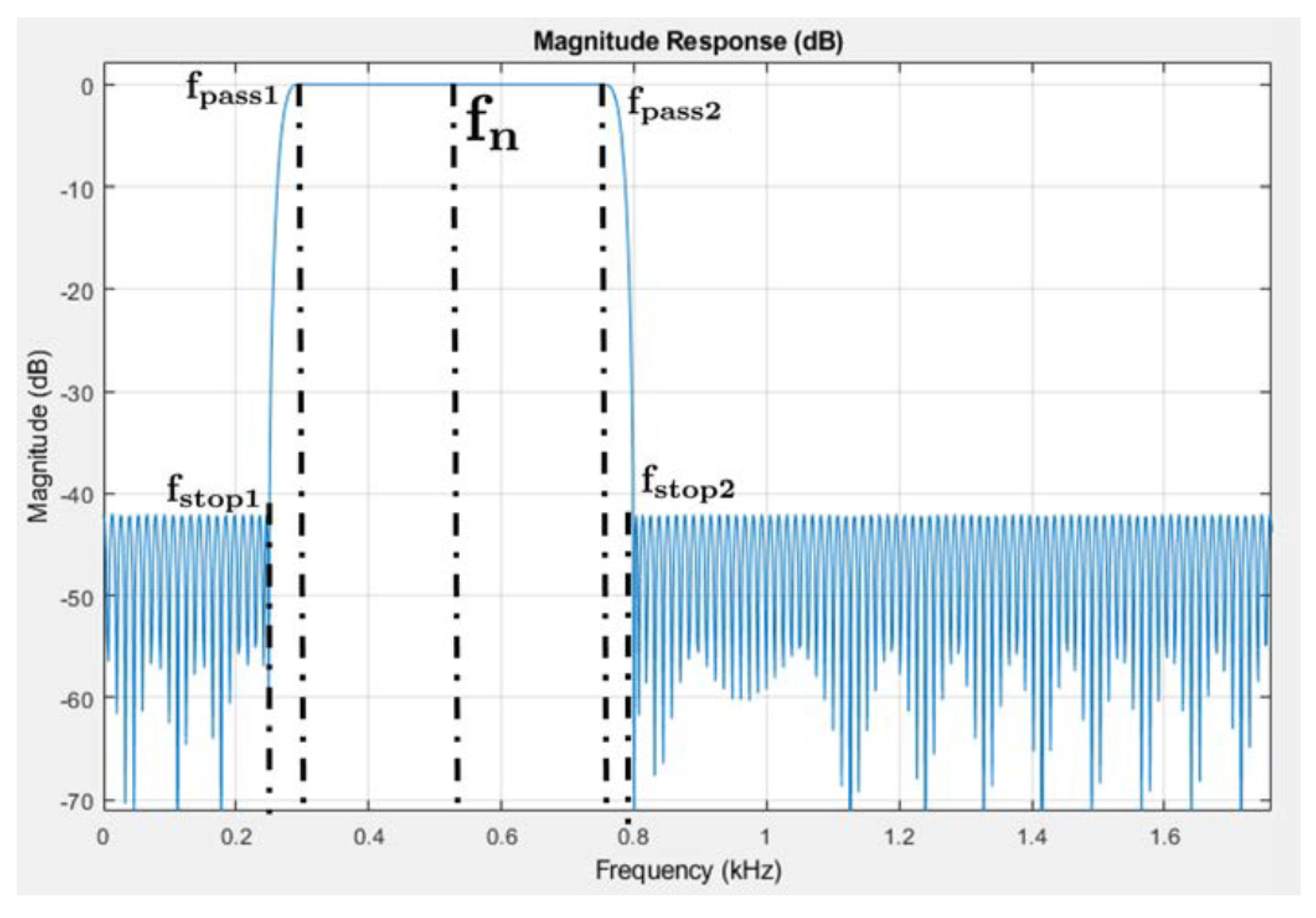
- The dynamic excitation system, which includes a signal generator, an amplifier, and a shaker. To obtain the response associated with the mode shapes, a type of input signal, shown in Figure 3, is applied. Performing excitation by the shaker was utilized for the first time in the present study unlike other contributions [6,15,16].
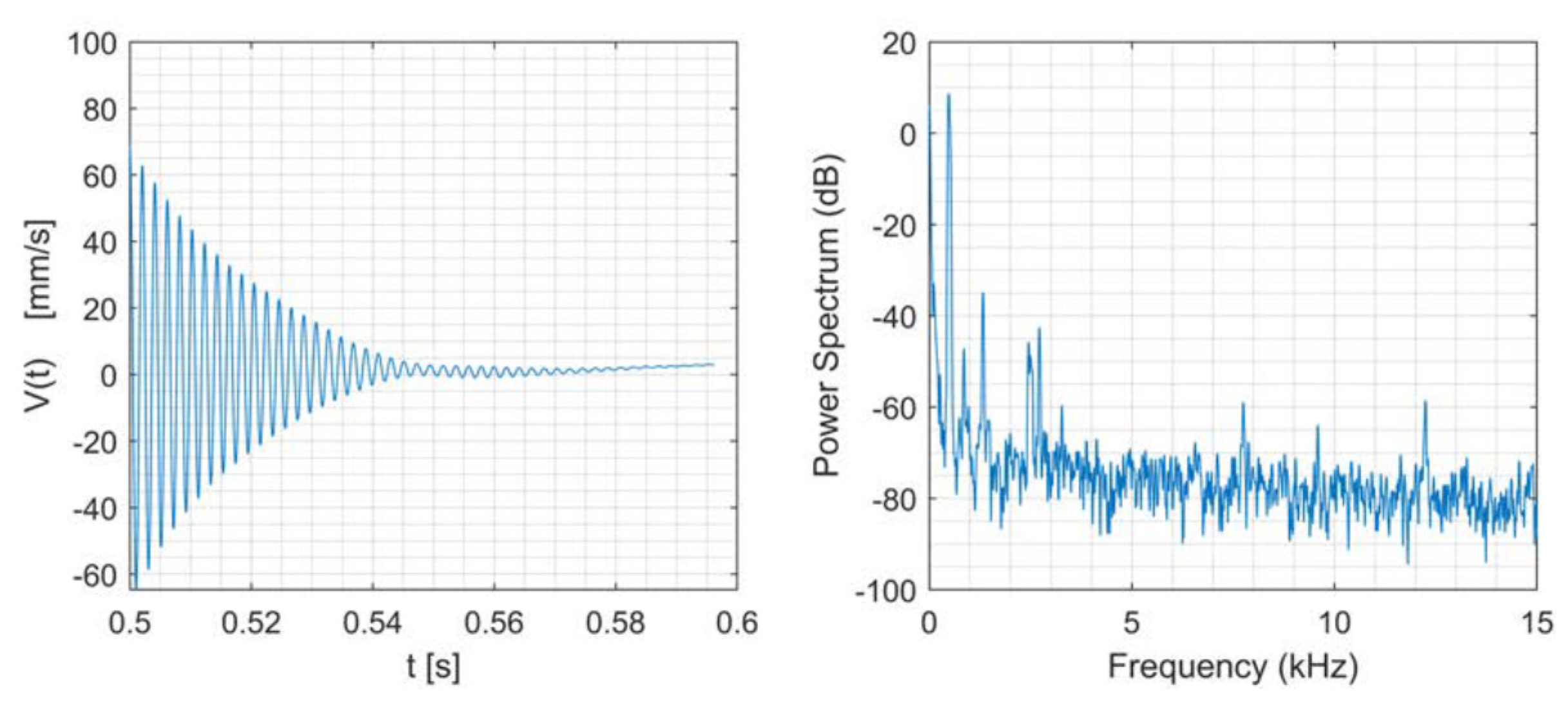
- The vibration measurement system, which consists of a laser pointer, Figure 4, and a laser controller. As the specimen were excited at frequencies close to the first and second flexural modes (1B and 2B), the laser was pointed towards the nodes of the corresponding mode shapes, where the maximum amplitude occurs.
- The traction force measurement system, incorporating two independent subsystems that allow for double checking the measurements. The first consists of a pressure gauge, providing pressure inside the hydraulic actuator. The second is composed of a Wheatstone bridge strain gauges (Figure 5) for measuring the axial deformation δ of the beam and a data acquisition system.
- The data collection and acquisition system, which collects the velocity signals measured by the laser and the strain from the gauges and the input currents of the shaker, later to be used for further analysis.
2.2. Technical Limitations
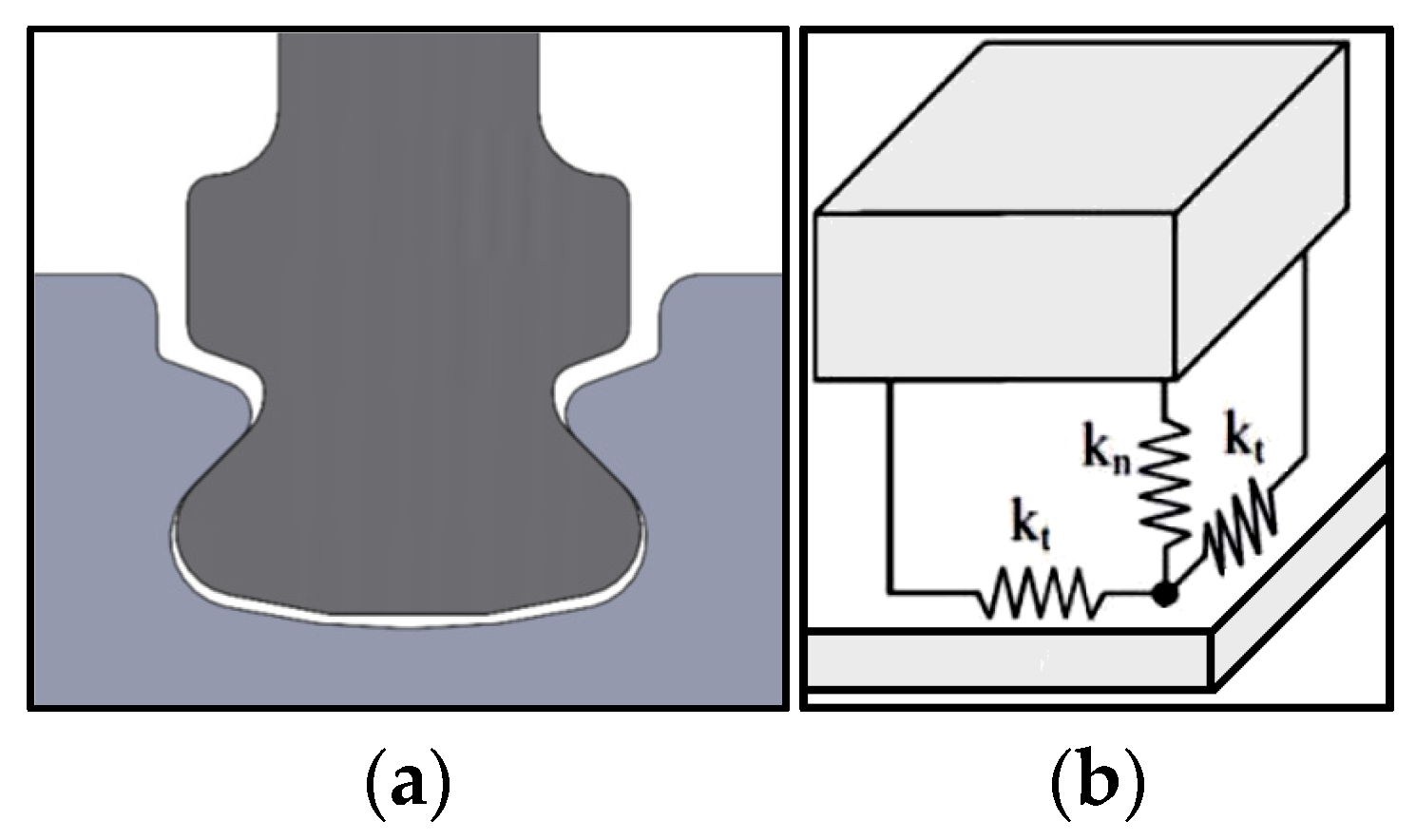
3. Contact Model
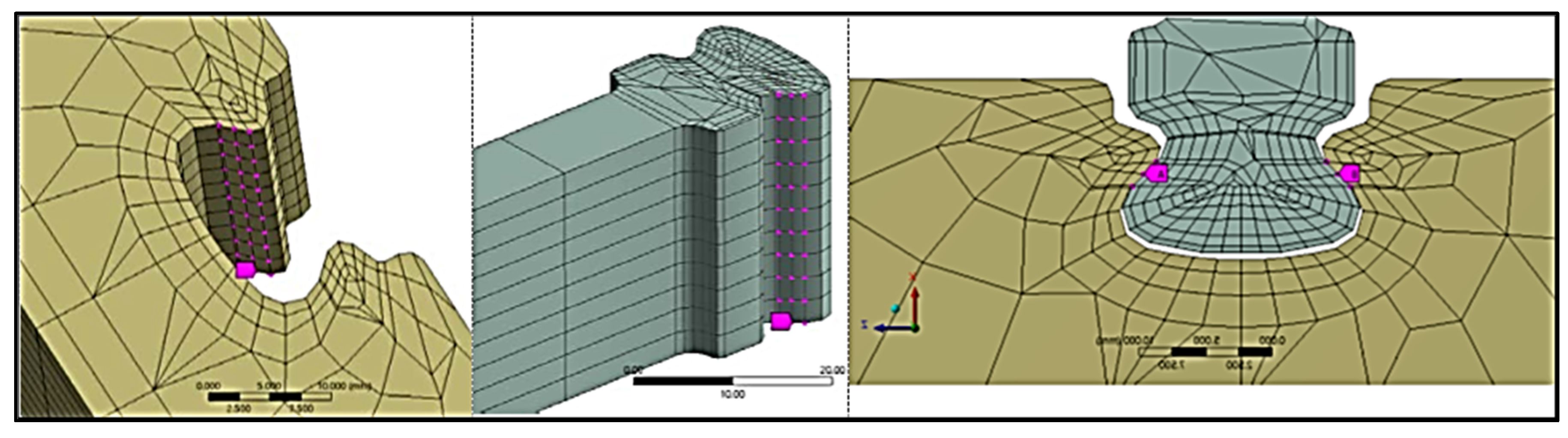
- The model of the beam with dovetail supports at both ends as well as the corresponding supports was discretized with the finite element method implemented in commercial finite element software, paying particular attention to the coincidence of the nodes in the contact interfaces.
- Nonlinear static analyses were carried out in commercial finite element software on the beam alone as the axial traction varied to discern the stiffening effect of the force on the stiffness matrices of the blade simulacrum.
- Reducing the model DOF in commercial finite element software using Craig-Bampton’s Component Mode Synthesis technique [24] and importing the reduced mass and stiffness matrices into a numeric computing environment.
- The reduced models of the blade simulacrum and supports (slots) were assembled in a numeric computing environment by introducing linear contact elements.
3.1. Finite Element Method
3.2. Reduction Technique
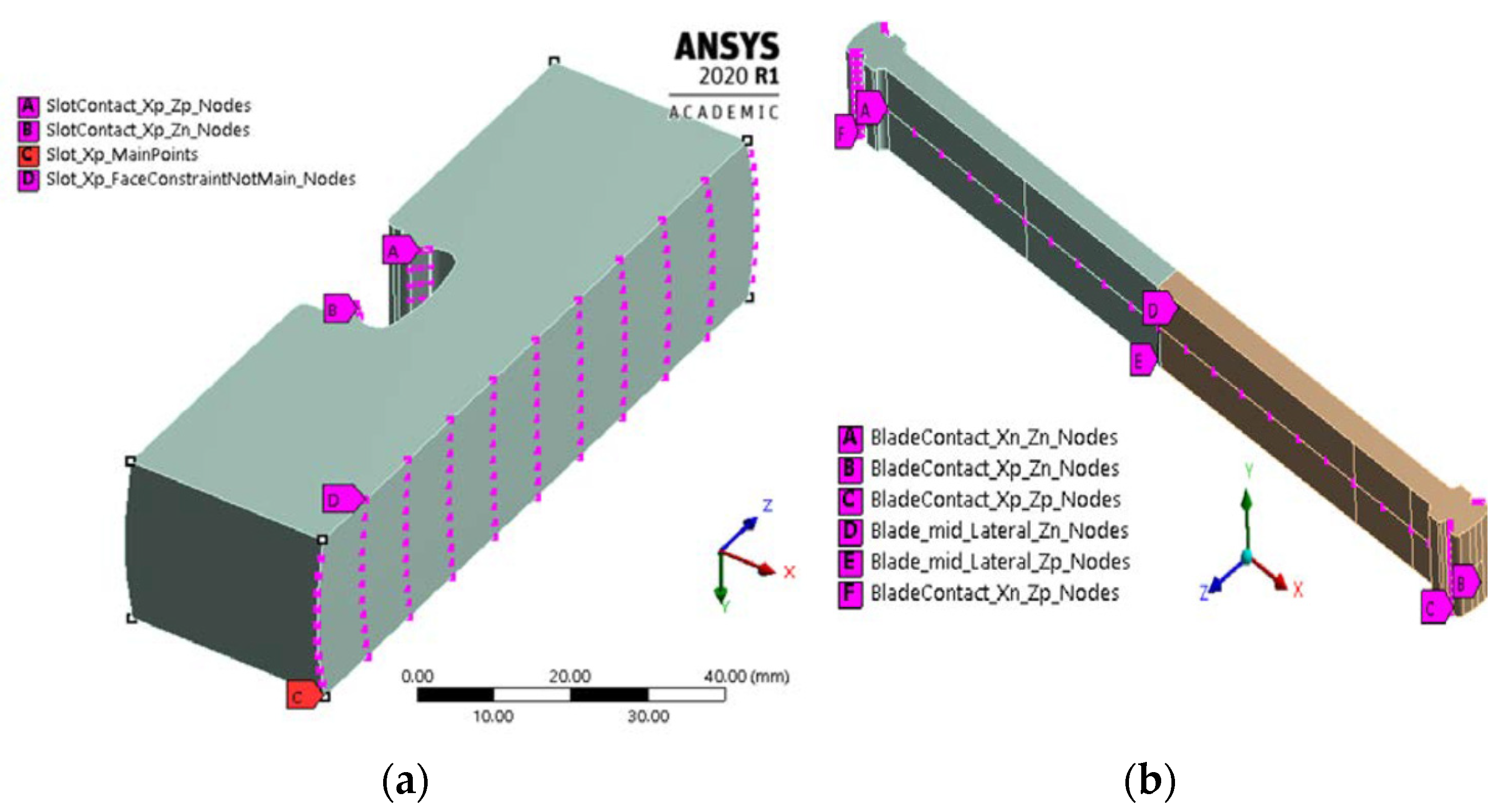
- 33 nodes for each of the four contact interfaces
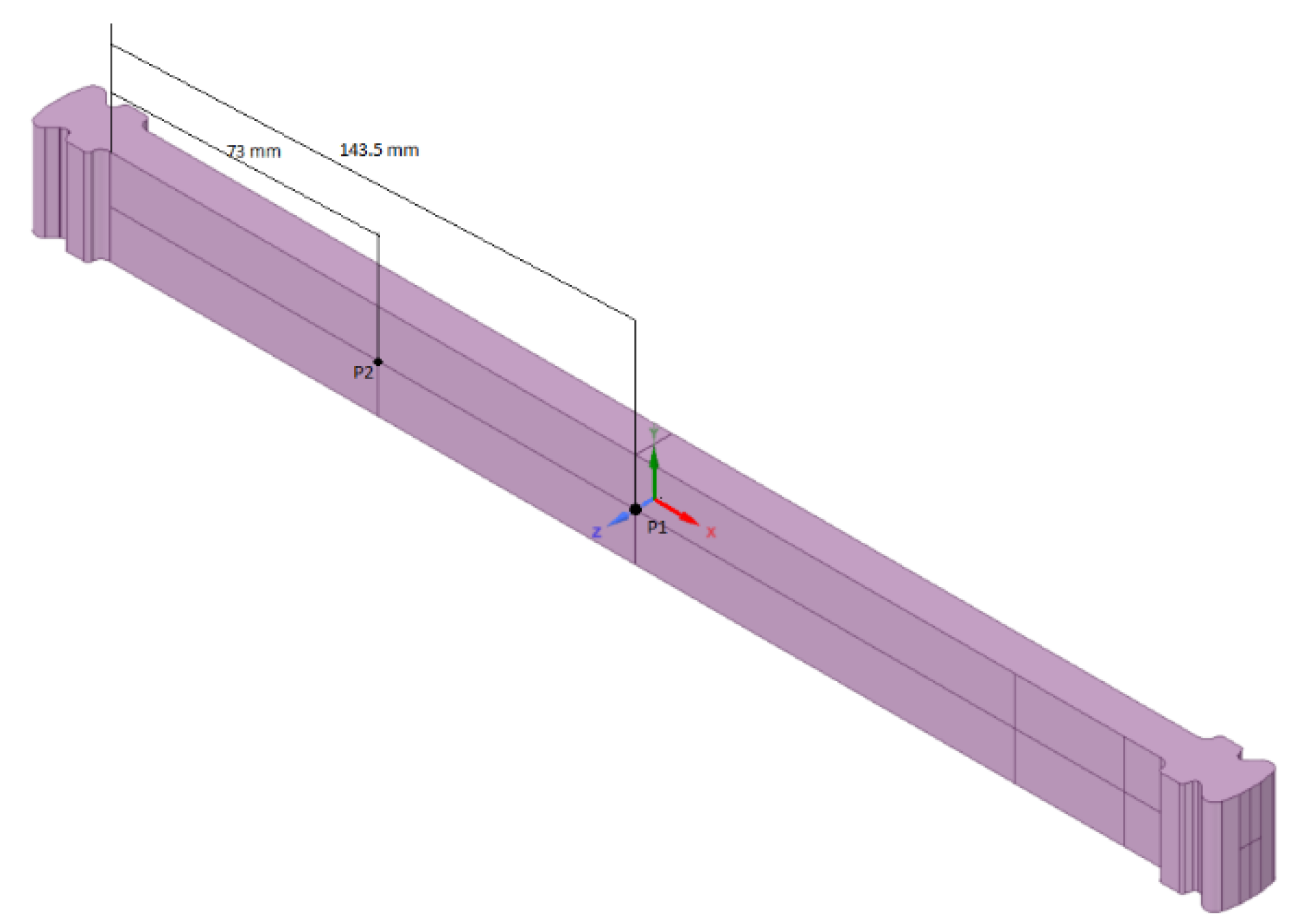
- 21 nodes along the longitudinal axis of the beam on each side, see Figure 14b, to be capable of viewing the mode shapes of the reduced model.
- 33 nodes for each of the two contact interfaces
- 8 nodes corresponding to the vertices of the support for displaying the modes.
- 117 nodes at the base of the support, see Figure 14a, to be subsequently constrained in a numeric computing environment.
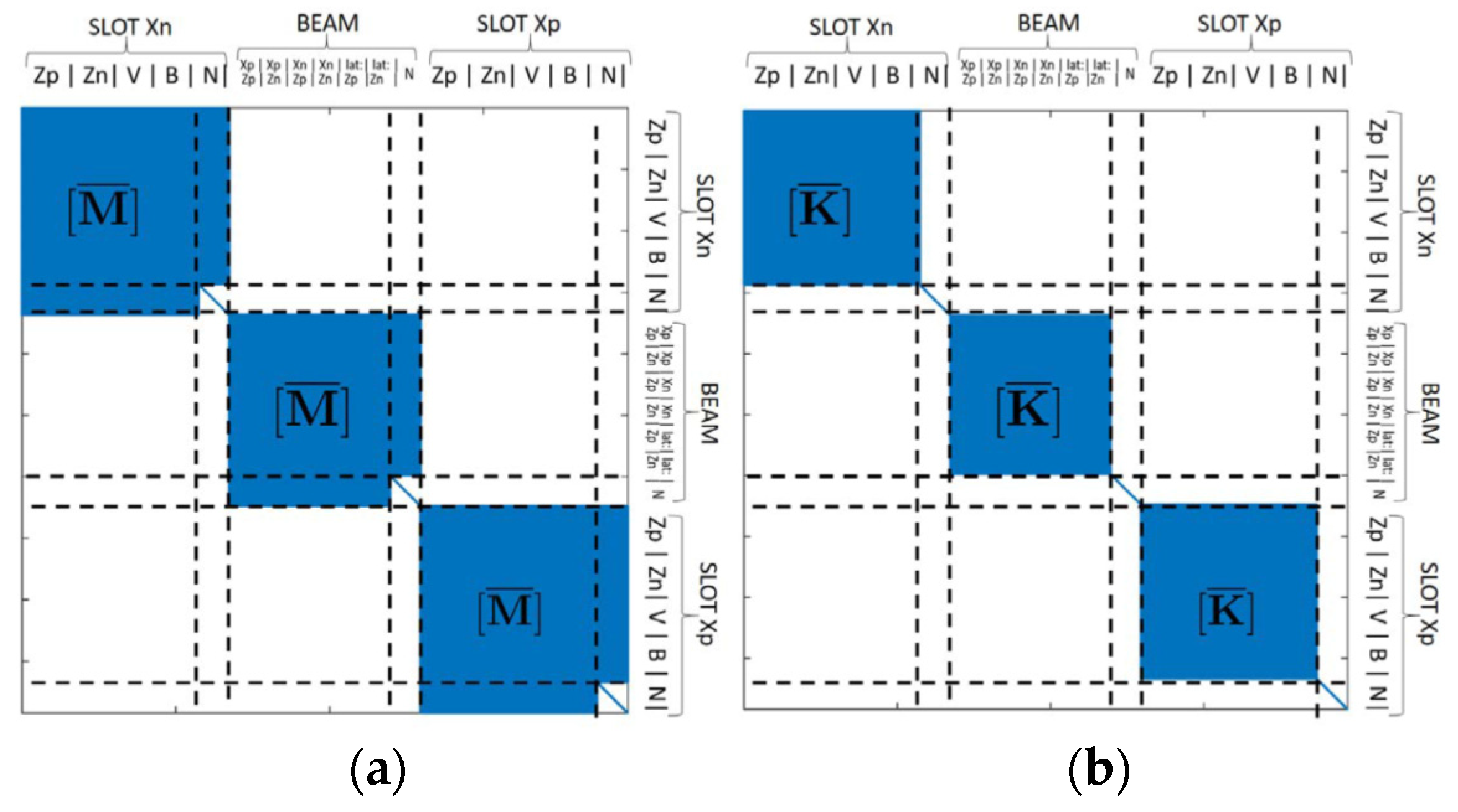
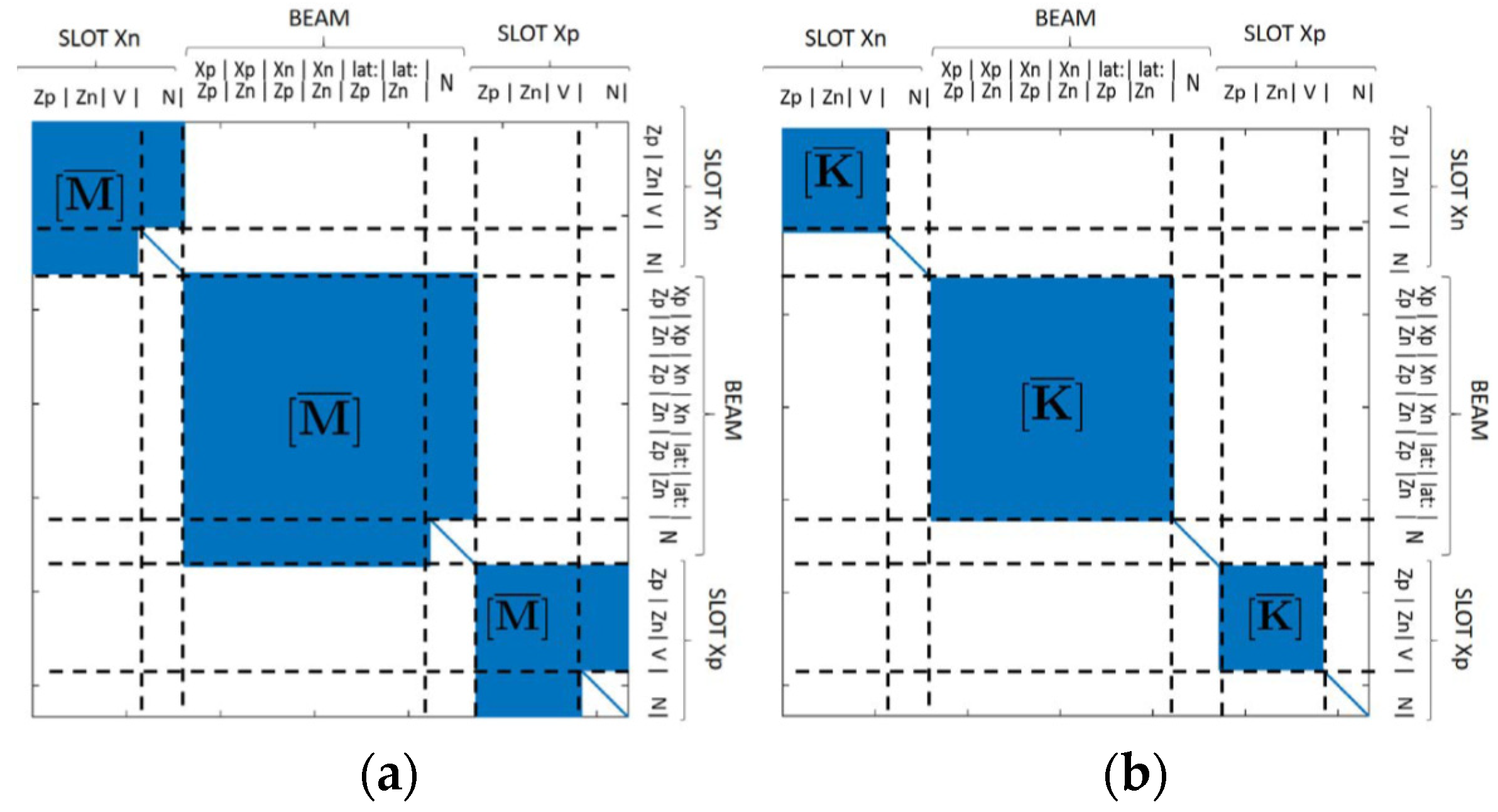
3.3. Assembly of Stiffness and Mass Matrices
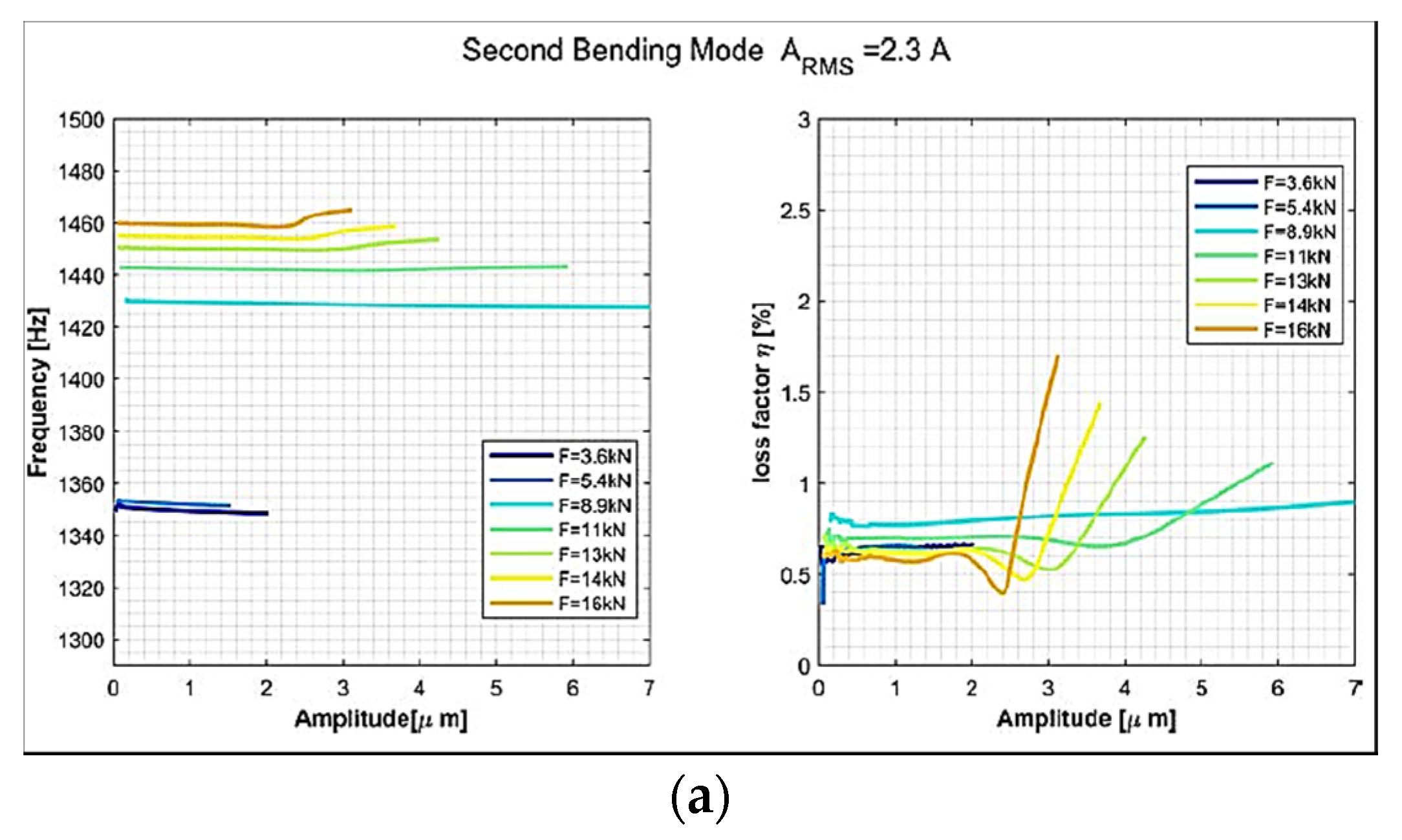
3.4. Determination of Stiffness, and
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mindlin, R.D.; Mason, W.P.; Osmer, T.F.; Deresiewicz, H. Effects of an Oscillating Tangential Force on the Contact Surfaces of Elastic Spheres. Proc. First US Natl. Congr. Appl. Mech. 1952, 1951, 203–208. [Google Scholar]
- Johnson, K.L. Surface Interaction between Elastically Loaded Bodies under Tangential Forces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 230, 531–548. [Google Scholar] [CrossRef]
- Goodman, L.E.; Brown, C.B. Energy Dissipation in Contact Friction: Constant Normal and Cyclic Tangential Loading. J. Appl. Mech. Trans. ASME 1960, 29, 17–22. [Google Scholar] [CrossRef]
- Filippi, S.; Akay, A.; Gola, M.M. Measurement of Tangential Contact Hysteresis during Microslip. J. Tribol. 2004, 126, 482–489. [Google Scholar] [CrossRef]
- Filippi, S.; Rodrigues, E.B.; Gola, M.M. Experimental Characterization of Contact Hysteresis at High Temperatures. In Proceedings of the ASME Turbo Expo, Barcelona, Spain, 19 September 2006; American Society of Mechanical Engineers Digital Collection. Volume 5, Part B. pp. 893–902. [Google Scholar]
- Lavella, M.; Botto, D.; Gola, M.M. Test Rig for Wear and Contact Parameters Extraction for Flat-on-Flat Contact Surfaces. In Proceedings of the American Society of Mechanical Engineers, Tribology Division, TRIB, Copenhagen, Denmark, 9 February 2011; American Society of Mechanical Engineers Digital Collection. pp. 307–309. [Google Scholar]
- Schwingshackl, C.W.; Petrov, E.P.; Ewins, D.J. Measured and Estimated Friction Interface Parameters in a Nonlinear Dynamic Analysis. Mech. Syst. Signal Process. 2012, 28, 574–584. [Google Scholar] [CrossRef]
- Stanbridge, A.B.; Ewins, D.J.; Sanliturk, K.Y.; Ferreira, J.V. Experimental Investigation of Dry Friction Damping and Cubic Stiffness Non-Linearity. In Proceedings of the ASME Design Engineering Technical Conference, Pittsburgh, PA, USA, 11 November 2001; American Society of Mechanical Engineers Digital Collection. Volume 6B, pp. 2141–2148. [Google Scholar]
- Afzal, M.; Arteaga, I.L.; Kari, L. An analytical calculation of the Jacobian matrix for 3D friction contact model applied to turbine blade shroud contact. J. Comput. Struct. 2006, 177, 204–217. [Google Scholar] [CrossRef] [Green Version]
- Afzal, M.; Arteaga, I.L.; Kari, L. Numerical analysis of multiple friction contacts in bladed disks. Int. J. Mech. Sci. 2018, 137, 224–237. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, D.; Xie, Y. A Nonlinear vibration analysis of forced response for a bladed-disk with dry friction dampers. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1522–1539. [Google Scholar] [CrossRef]
- She, H.; Li, C.; Tang, Q.; Wen, B. Nonlinear Vibration Analysis of a Rotating Disk-Beam System Subjected to Dry Friction. Shock Vib. 2020, 2020, 19. [Google Scholar] [CrossRef]
- Chaofeng, L.; Xiaowen, L.; Qiansheng, T.; Zilin, C. Modeling and nonlinear dynamics analysis of a rotating beam with dry friction support boundary conditions. J. Sound Vib. 2021, 498, 115978. [Google Scholar] [CrossRef]
- Goodman, L.E.; Klumpp, J.H. Analysis of Slip Damping with Reference to Turbine-Blade Vibration. J. Appl. Mech. 1956, 23, 421–429. [Google Scholar] [CrossRef]
- Allara, M.; Filippi, S.; Gola, M.M. An Experimental Method for the Measurement of Blade-Root Damping. In Proceedings of the ASME Turbo Expo, Barcelona, Spain, 19 September 2006; American Society of Mechanical Engineers Digital Collection. Volume 5, Part B. pp. 903–912. [Google Scholar]
- Firrone, C.M.; Bertino, I. Experimental Investigation on the Damping Effectiveness of Blade Root Joints. Exp. Mech. 2015, 55, 981–988. [Google Scholar] [CrossRef]
- Asai, K.; Sakurai, S.; Kudo, T.; Ozawa, N.; Ikeda, T. Evaluation of Friction Damping in Dovetail Root Joints Based on Dissipation Energy on Contact Surfaces. In Proceedings of the ASME Turbo Expo, Orlando, FL, USA, 16 February 2009; American Society of Mechanical Engineers Digital Collection. Volume 6, pp. 301–313. [Google Scholar]
- Simmons, H.R.; Iyengar, V. Effect of Non-Uniform Blade Root Friction and Sticking on Disk Stresses. In Proceedings of the ASME International Conference, Denver, CO, USA, 1 January 2011; pp. 829–838. [Google Scholar]
- Umer, M.; Botto, D. Measurement of Contact Parameters on Under-Platform Dampers Coupled with Blade Dynamics. Int. J. Mech. Sci. 2019, 159, 450–458. [Google Scholar] [CrossRef]
- Li, D.; Botto, D.; Xu, C.; Liu, T.; Gola, M. A Micro-Slip Friction Modeling Approach and Its Application in Underplatform Damper Kinematics. Int. J. Mech. Sci. 2019, 161–162, 105029. [Google Scholar] [CrossRef]
- Li, D.; Xu, C.; Botto, D.; Zhang, Z.; Gola, M. A Fretting Test Apparatus for Measuring Friction Hysteresis of Bolted Joints. Tribol. Int. 2020, 151, 106431. [Google Scholar] [CrossRef]
- Li, D.; Botto, D.; Xu, C.; Gola, M. A New Approach for the Determination of the Iwan Density Function in Modeling Friction Contact. Int. J. Mech. Sci. 2020, 180, 105671. [Google Scholar] [CrossRef]
- Feldman, M. Non-Linear System Vibration Analysis Using Hilbert Transform--I. Free Vibration Analysis Method “Freevib”. Mech. Syst. Signal Process. 1994, 8, 119–127. [Google Scholar] [CrossRef]
- Craig, R.R.; Bampton, M.C.C. Coupling of Substructures for Dynamic Analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef] [Green Version]










| 12 | 41,428.6 | 4866.6 | 11.7 | 68,285.7 | 6587.2 | 10.2 |
| 14 | 50,000.0 | 10,042.7 | 20.1 | 61,428.6 | 10,822.9 | 17.6 |
| 16 | 50,000.0 | 5439.4 | 10.9 | 72,857.1 | 6550.7 | 9.0 |
| 18 | 55,714.3 | 9546.3 | 17.1 | 75,714.3 | 11,395.6 | 15.1 |
| 20 | 58,571.4 | 11,672.8 | 19.9 | 84,285.7 | 14,891.4 | 17.7 |
| 22 | 61,428.6 | 16,485.4 | 26.8 | 84,285.7 | 19,768.3 | 23.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dastani, H.; Botto, D.; Glorioso, M. Experimental and Numerical Investigation of Contact Parameters in a Dovetail Type of Blade Root Joints. Appl. Sci. 2021, 11, 12008. https://doi.org/10.3390/app112412008
Dastani H, Botto D, Glorioso M. Experimental and Numerical Investigation of Contact Parameters in a Dovetail Type of Blade Root Joints. Applied Sciences. 2021; 11(24):12008. https://doi.org/10.3390/app112412008
Chicago/Turabian StyleDastani, Hadi, Daniele Botto, and Matteo Glorioso. 2021. "Experimental and Numerical Investigation of Contact Parameters in a Dovetail Type of Blade Root Joints" Applied Sciences 11, no. 24: 12008. https://doi.org/10.3390/app112412008
APA StyleDastani, H., Botto, D., & Glorioso, M. (2021). Experimental and Numerical Investigation of Contact Parameters in a Dovetail Type of Blade Root Joints. Applied Sciences, 11(24), 12008. https://doi.org/10.3390/app112412008







