Estimation of the Tapered Gutenberg-Richter Distribution Parameters for Catalogs with Variable Completeness: An Application to the Atlantic Ridge Seismicity
Abstract
:1. Introduction
2. Methods
2.1. Maximum Likelihood Estimation of the Parameters
2.2. Estimation of the Uncertainties
3. Data
4. Results
5. Discussion
6. Conclusions
- (1)
- We introduce a new method to estimate the parameters of the tapered Gutenberg-Richter distribution and their uncertainties in the case of catalogs with a variable through-time magnitude of completeness;
- (2)
- We apply this method to the Atlantic ridge seismicity, finding a clear distinct behavior both for the parameters and corner magnitude, depending on the faulting mechanism: larger and smaller corner magnitude for normal events, smaller and larger corner magnitude for strike-slip events.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| Mmax | Maximum magnitude |
| MLE | Maximum likelihood estimation |
| Mmin | Magnitude of completeness |
| CMT | Centroid moment tensor catalog |
| CM | Corner magnitude |
References
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Aki, K. Maximum likelihood estimate of b in the formula logN = a − bM and its confidence limits. Bull. Earthq. Res. Inst. 1965, 43, 237–239. [Google Scholar]
- Kagan, Y.Y. Seismic moment distribution revisited: I. Statistical results. Geophys. J. Int. 2002, 148, 520–541. [Google Scholar] [CrossRef] [Green Version]
- Zöller, G.; Holschneider, M. The earthquake history in a fault zone tells us almost nothing about mmax. Seismol. Res. Lett. 2016, 87, 132–137. [Google Scholar] [CrossRef]
- Holschneider, M.; Zöller, G.; Hainzl, S. Estimation of the maximum possible magnitude in the framework of a doubly truncated Gutenberg–Richter model. Bull. Seismol. Soc. Am. 2011, 101, 1649–1659. [Google Scholar] [CrossRef]
- Zöller, G.; Holschneider, M.; Hainzl, S. The maximum earthquake magnitude in a time horizon: Theory and case studies. Bull. Seismol. Soc. Am. 2013, 103, 860–875. [Google Scholar] [CrossRef] [Green Version]
- Geist, E.L.; Parsons, T. Undersampling power-law size distributions: Effect on the assessment of extreme natural hazards. Nat. Hazards 2014, 72, 565–595. [Google Scholar] [CrossRef]
- Kagan, Y.Y.; Schoenberg, F. Estimation of the upper cutoff parameter for the tapered Pareto distribution. J. Appl. Probab. 2001, 38, 168–185. [Google Scholar] [CrossRef] [Green Version]
- Schoenberg, F.P.; Patel, R.D. Comparison of Pareto and tapered Pareto distributions for environmental phenomena. Eur. Phys. J. Spec. Top. 2012, 205, 159–166. [Google Scholar] [CrossRef]
- Kijko, A.; Sellevoll, M.A. Estimation of earthquake hazard parameters from incomplete data files. Part I. Utilization of extreme and complete catalogs with different threshold magnitudes. Bull. Seismol. Soc. Am. 1989, 79, 645–654. [Google Scholar] [CrossRef]
- Weichert, D.H. Estimation of the earthquake recurrence parameters for unequal observation periods for different magnitudes. Bull. Seismol. Soc. Am. 1980, 70, 1337–1346. [Google Scholar] [CrossRef]
- Taroni, M.; Selva, J. GR_EST: An OCTAVE/MATLAB Toolbox to Estimate Gutenberg–Richter Law Parameters and Their Uncertainties. Seismol. Res. Lett. 2021, 92, 508–516. [Google Scholar] [CrossRef]
- Kagan, Y.Y. Earthquake number forecasts testing. Geophys. J. Int. 2017, 211, 335–345. [Google Scholar] [CrossRef] [Green Version]
- Taroni, M.; Akinci, A. Good practices in PSHA: Declustering, b-value estimation, foreshocks and aftershocks inclusion; a case study in Italy. Geophys. J. Int. 2021, 224, 1174–1187. [Google Scholar] [CrossRef]
- Bird, P.; Kagan, Y.Y.; Jackson D., D. Plate tectonics and earthquake potential of spreading ridges and oceanic transform faults. In Plate Boundary Zones; Stein, S., Freymueller, J.T., Eds.; AGU: Washington, DC, USA, 2002; Volume 30, pp. 203–218. [Google Scholar]
- Bird, P.; Kagan, Y.Y. Plate-tectonic analysis of shallow seismicity: Apparent boundary width, beta, corner magnitude, coupled lithosphere thickness, and coupling in seven tectonic settings. Bull. Seismol. Soc. Am. 2004, 94, 2380–2399. [Google Scholar] [CrossRef]
- Kanamori, H. The energy release in great earthquakes. J. Geophys. Res. 1977, 82, 2981–2987. [Google Scholar] [CrossRef] [Green Version]
- Vere-Jones, D.; Robinson, R.; Yang, W. Remarks on the accelerated moment release model: Problems of model formulation, simulation and estimation. Geophys. J. Int. 2001, 144, 517–531. [Google Scholar] [CrossRef] [Green Version]
- Kagan, Y.Y.; Bird, P.; Jackson, D.D. Earthquake patterns in diverse tectonic zones of the globe. Pure Appl. Geophys. 2010, 167, 721–741. [Google Scholar] [CrossRef] [Green Version]
- Wilks, S.S. Mathematical Statistics; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Venzon, D.J.; Moolgavkar, S.H. A method for computing profile-likelihood-based confidence intervals. J. R. Stat. Soc. Ser. C Appl. Stat. 1988, 37, 87–94. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Chou, T.-A.; Woodhouse, J.H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. 1981, 86, 2825–2852. [Google Scholar] [CrossRef]
- Ekström, G.; Nettles, M.; Dziewonski, A.M. The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Inter. 2012, 200–201, 1–9. [Google Scholar] [CrossRef]
- Mizrahi, L.; Nandan, S.; Wiemer, S. The effect of declustering on the size distribution of mainshocks. Seismol. Res. Lett. 2021, 92, 2333–2342. [Google Scholar] [CrossRef]
- Marzocchi, W.; Spassiani, I.; Stallone, A.; Taroni, M. How to be fooled searching for significant variations of the b-value. Geophys. J. Int. 2020, 220, 1845–1856. [Google Scholar] [CrossRef]
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for the exponential distribution with mean unknown. J. Am. Stat. Assoc. 1969, 64, 387–389. [Google Scholar] [CrossRef]
- Taroni, M. Back to the future: Old methods for new estimation and test of the Gutenberg-Richter b-value for catalogs with variable completeness. Geophys. J. Int. 2021, 224, 337–339. [Google Scholar] [CrossRef]
- Zhuang, J.; Ogata, Y.; Wang, T. Data completeness of the Kumamoto earthquake sequence in the JMA catalog and its influence on the estimation of the ETAS parameters. Earth Planets Space 2017, 69, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in earthquake-size distribution across different stress regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Douglas, J.; Edwards, B. Recent and future developments in earthquake ground motion estimation. Earth-Sci. Rev. 2016, 160, 203–219. [Google Scholar] [CrossRef] [Green Version]
- Grezio, A.; Babeyko, A.; Baptista, M.A.; Behrens, J.; Costa, A.; Davies, G.; Geist, E.; Glimsdal, S.; Gonzales, F.I.; Griffin, J.; et al. Probabilistic Tsunami Hazard Analysis: Multiple Sources and Global Applications. Rev. Geophys. 2017, 55. [Google Scholar] [CrossRef]
- Selva, J.; Tonini, R.; Molinari, I.; Tiberti, M.M.; Romano, F.; Grezio, A.; Melini, D.; Piatanesi, A.; Basili, R.; Lorito, S. Quantification of source uncertainties in Seismic Probabilistic Tsunami Hazard Analysis (SPTHA). Geophys. J. Int. 2016, 205, 1780–1803. [Google Scholar] [CrossRef] [Green Version]
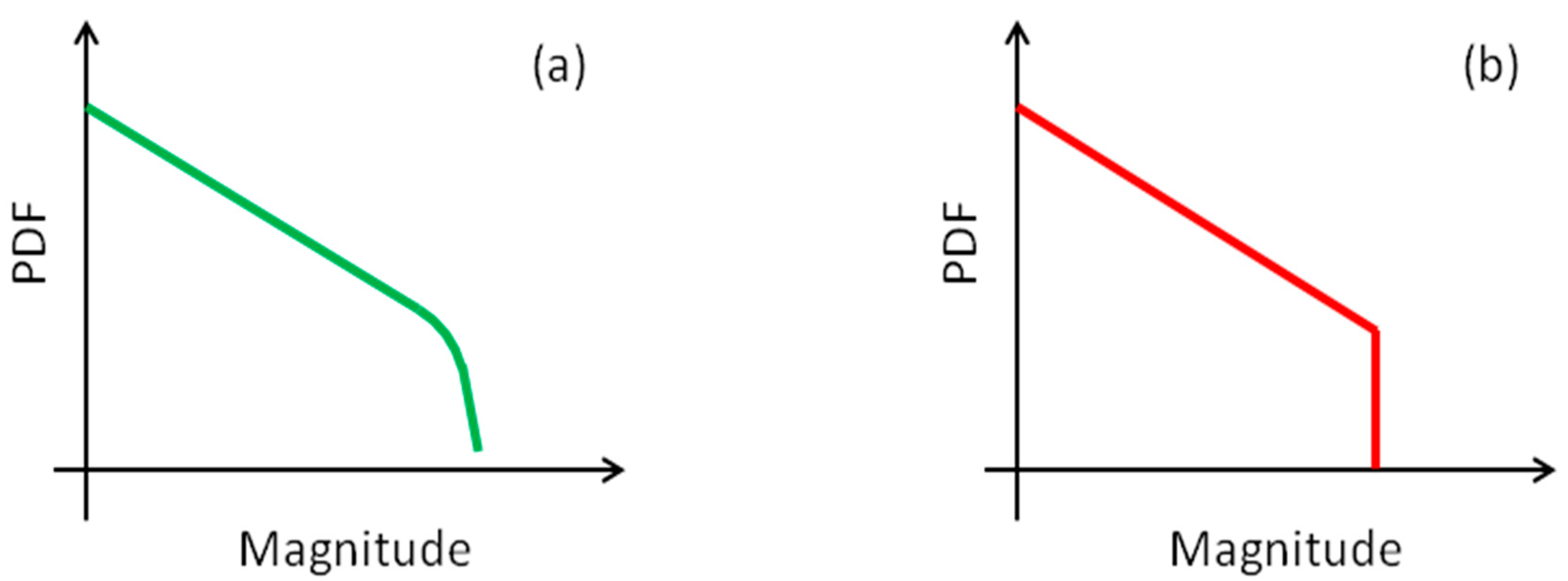


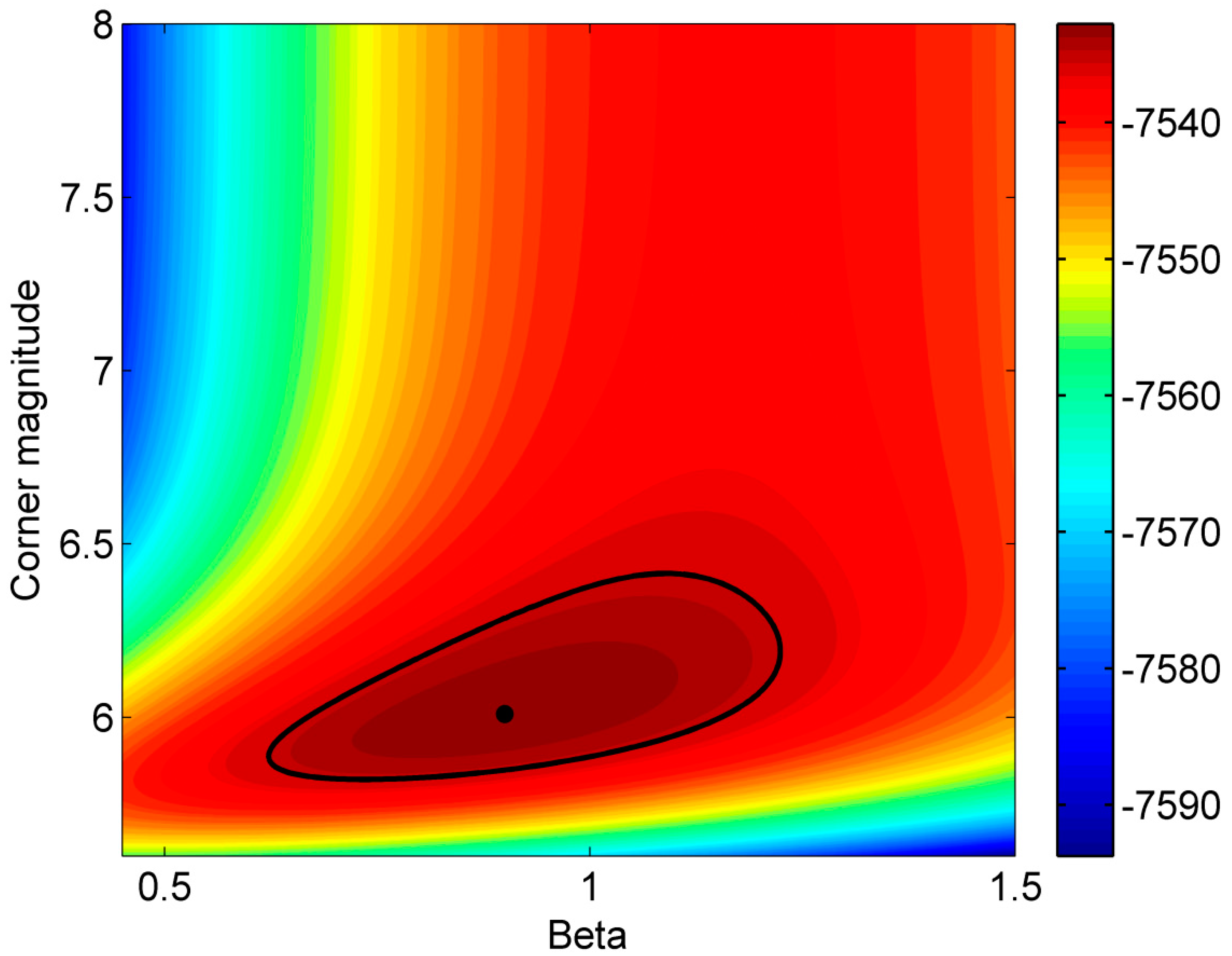




| Number of Simulated Events | Magnitude of Completeness Thresholds | Percentage of Events for Each Completeness | for the Simulations | Percentage of Confidence Regions Containing the Values Used in the Simulations | |||
|---|---|---|---|---|---|---|---|
| 100 | 5.5; 5.0 | 50%; 50% | 0.67 | 0.659 | 6.5 | 6.467 | 94.0% |
| 1000 | 5.5; 5.0 | 50%; 50% | 0.67 | 0.669 | 6.5 | 6.498 | 95.0% |
| 100 | 6.0; 5.0 | 25%; 75% | 0.80 | 0.785 | 7.5 | 7.232 | 93.1% |
| 1000 | 6.0; 5.0 | 25%; 75% | 0.80 | 0.798 | 7.5 | 7.459 | 95.2% |
| 100 | 6.5; 5.3 | 75%; 25% | 0.55 | 0.546 | 7.0 | 6.992 | 94.9% |
| 1000 | 6.5; 5.3 | 75%; 25% | 0.55 | 0.551 | 7.0 | 7.001 | 94.7% |
| Type | Number of Events | Percentage | Maximum Observed Magnitude |
|---|---|---|---|
| Whole catalog | 1168 | 100% | 7.10 |
| Normal events | 595 | 50.9% | 6.14 |
| Strike-slip events | 523 | 44.8% | 7.10 |
| Thrust events | 27 | 2.3% | 6.31 |
| Undefined | 23 | 2.0% | 5.83 |
| Type | Corner Magnitude (MLE) | (MLE) |
|---|---|---|
| Whole catalog | 7.25 | 0.92 |
| Normal events | 5.78 | 1.08 |
| Strike-slip events | 7.01 | 0.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taroni, M.; Selva, J.; Zhuang, J. Estimation of the Tapered Gutenberg-Richter Distribution Parameters for Catalogs with Variable Completeness: An Application to the Atlantic Ridge Seismicity. Appl. Sci. 2021, 11, 12166. https://doi.org/10.3390/app112412166
Taroni M, Selva J, Zhuang J. Estimation of the Tapered Gutenberg-Richter Distribution Parameters for Catalogs with Variable Completeness: An Application to the Atlantic Ridge Seismicity. Applied Sciences. 2021; 11(24):12166. https://doi.org/10.3390/app112412166
Chicago/Turabian StyleTaroni, Matteo, Jacopo Selva, and Jiancang Zhuang. 2021. "Estimation of the Tapered Gutenberg-Richter Distribution Parameters for Catalogs with Variable Completeness: An Application to the Atlantic Ridge Seismicity" Applied Sciences 11, no. 24: 12166. https://doi.org/10.3390/app112412166
APA StyleTaroni, M., Selva, J., & Zhuang, J. (2021). Estimation of the Tapered Gutenberg-Richter Distribution Parameters for Catalogs with Variable Completeness: An Application to the Atlantic Ridge Seismicity. Applied Sciences, 11(24), 12166. https://doi.org/10.3390/app112412166







