Effect of Pitch Parameters on Aerodynamic Forces of a Straight-Bladed Vertical Axis Wind Turbine with Inclined Pitch Axes
Abstract
:1. Introduction
2. Methodology and Computational Model
2.1. Actuator Line Model
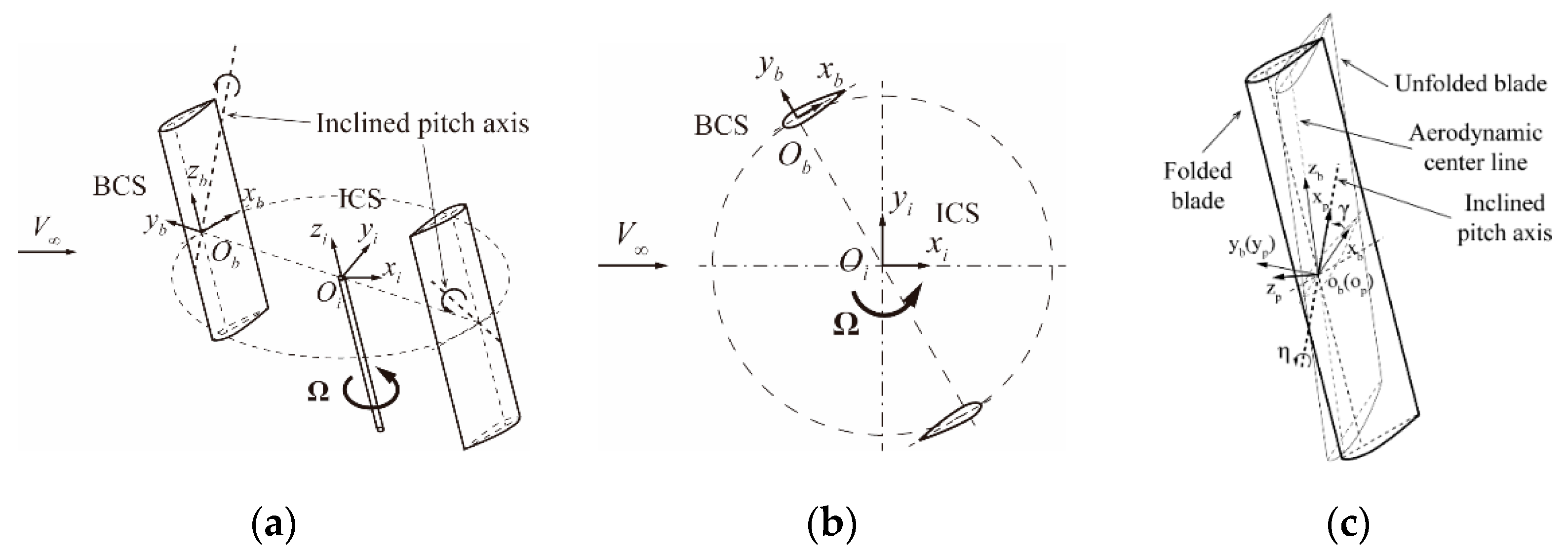
2.2. Wind Turbine Model and Coordinate Systems
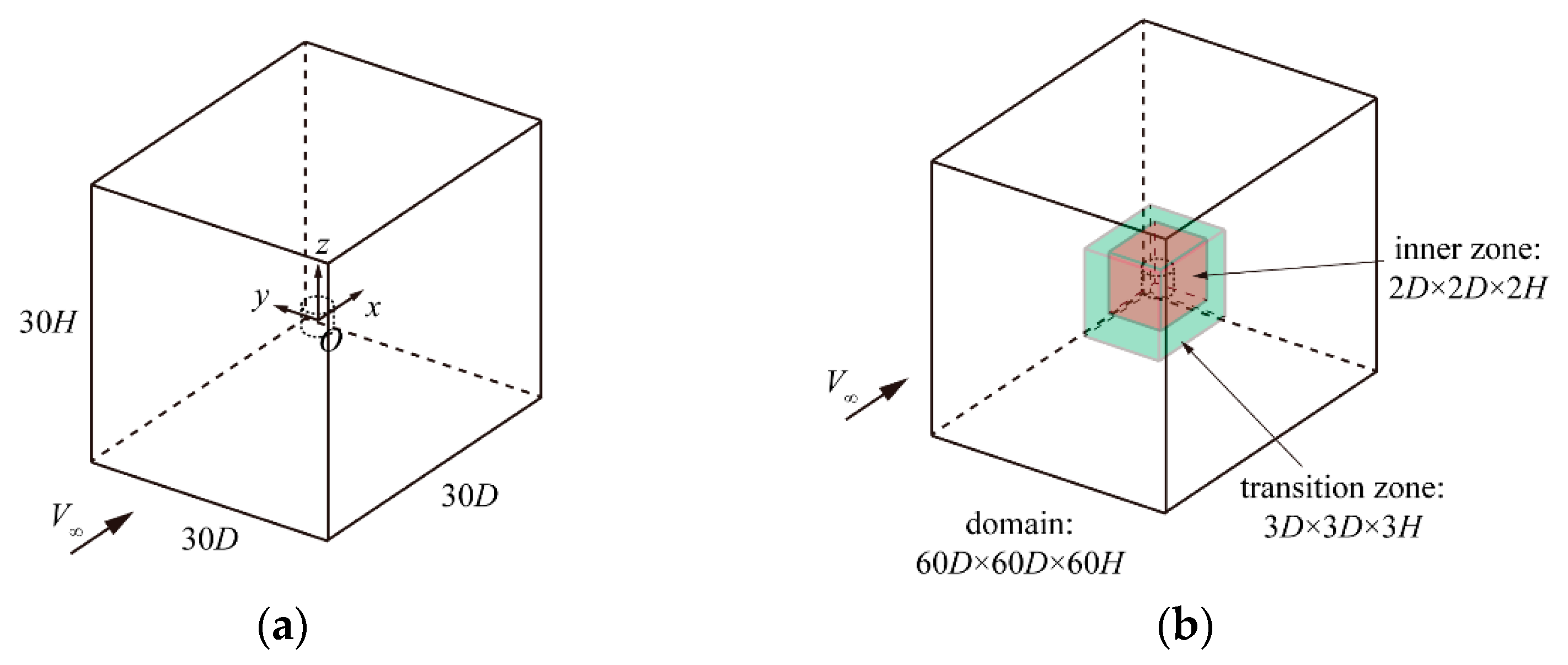
2.3. Computational Setup
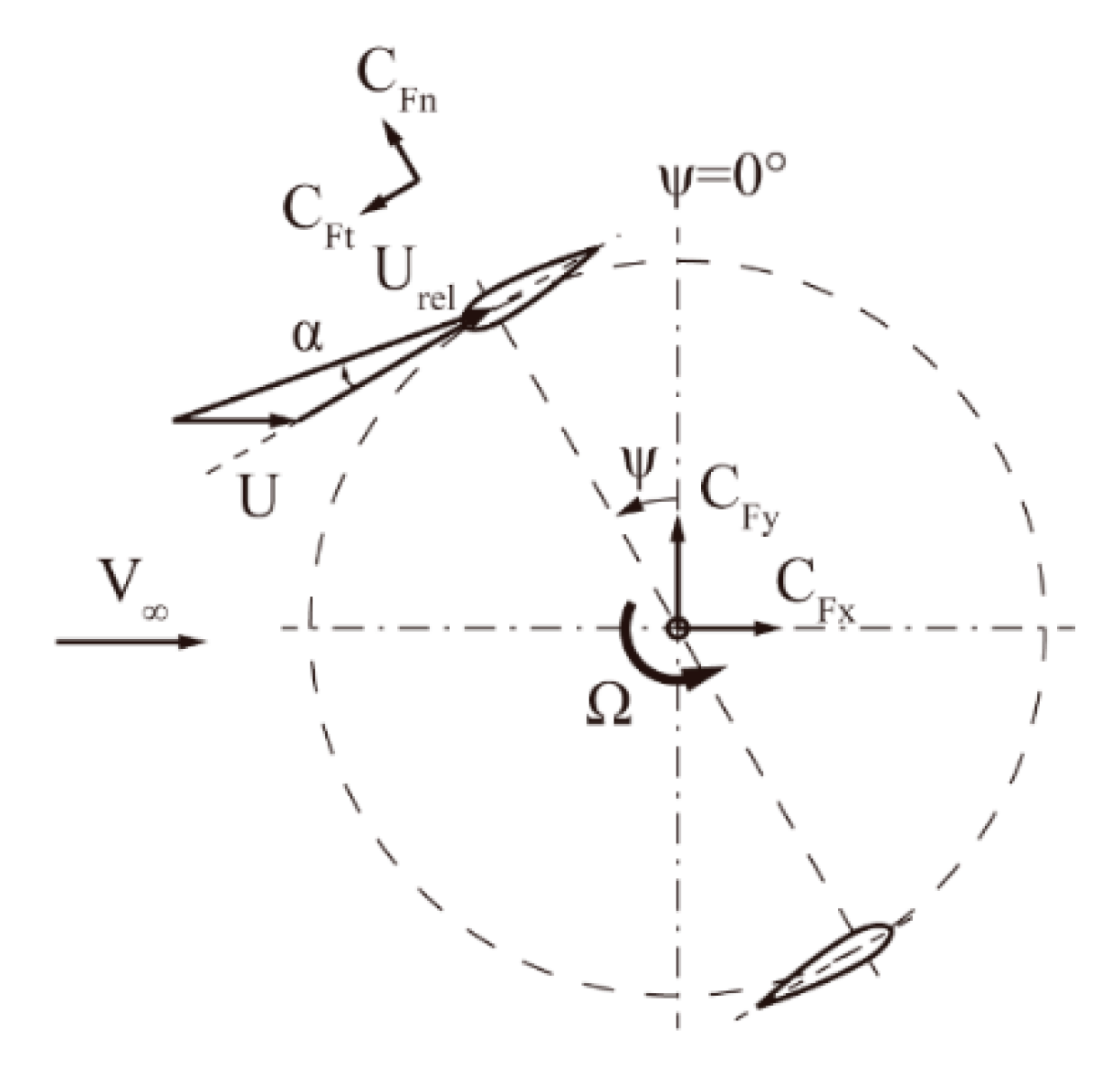
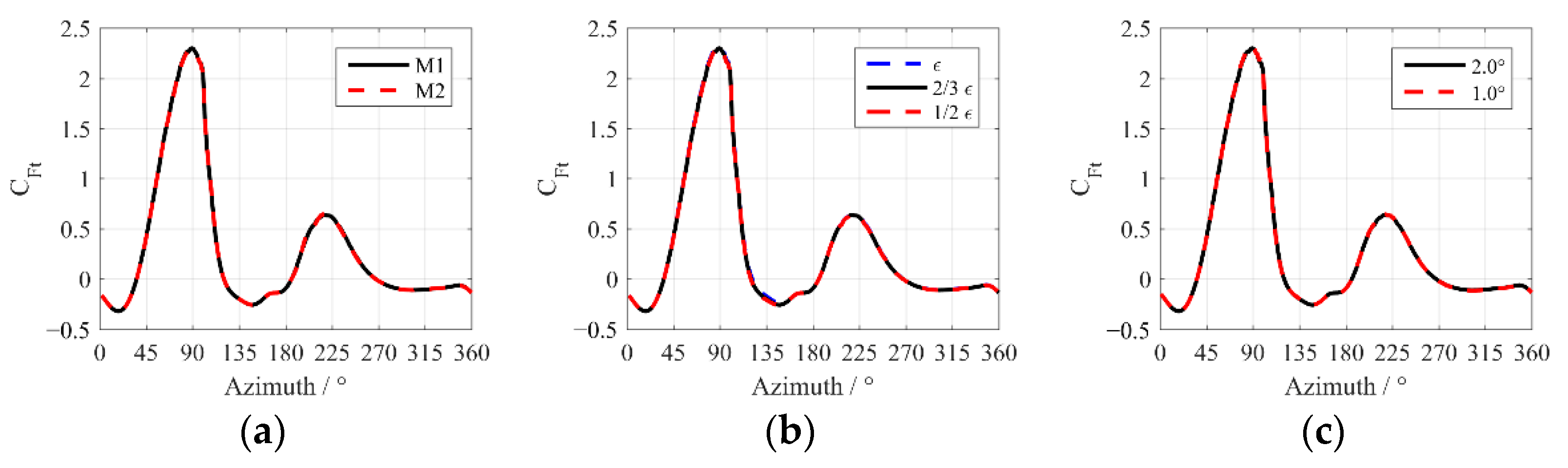
3. Validation
4. Results and Discussion
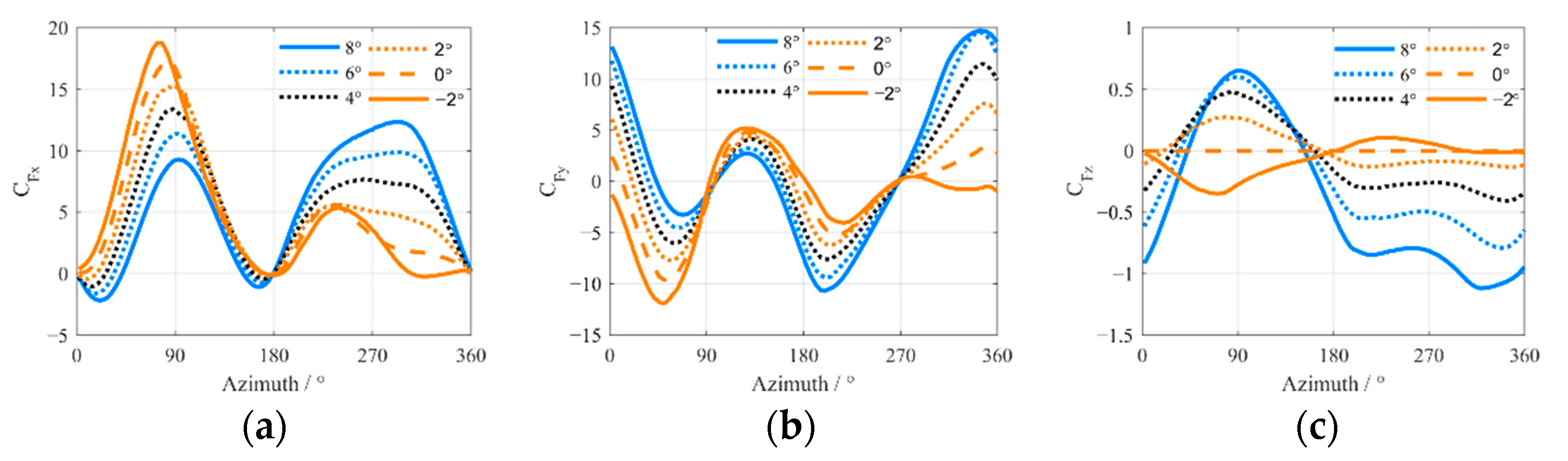
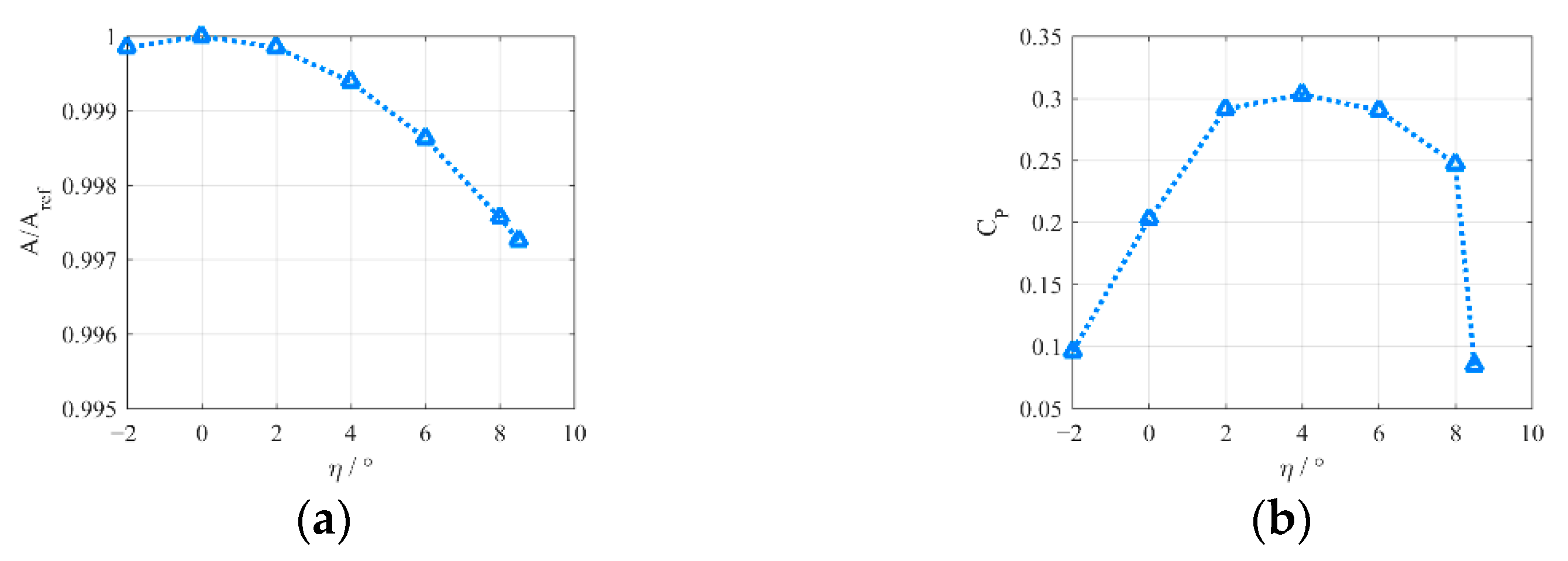
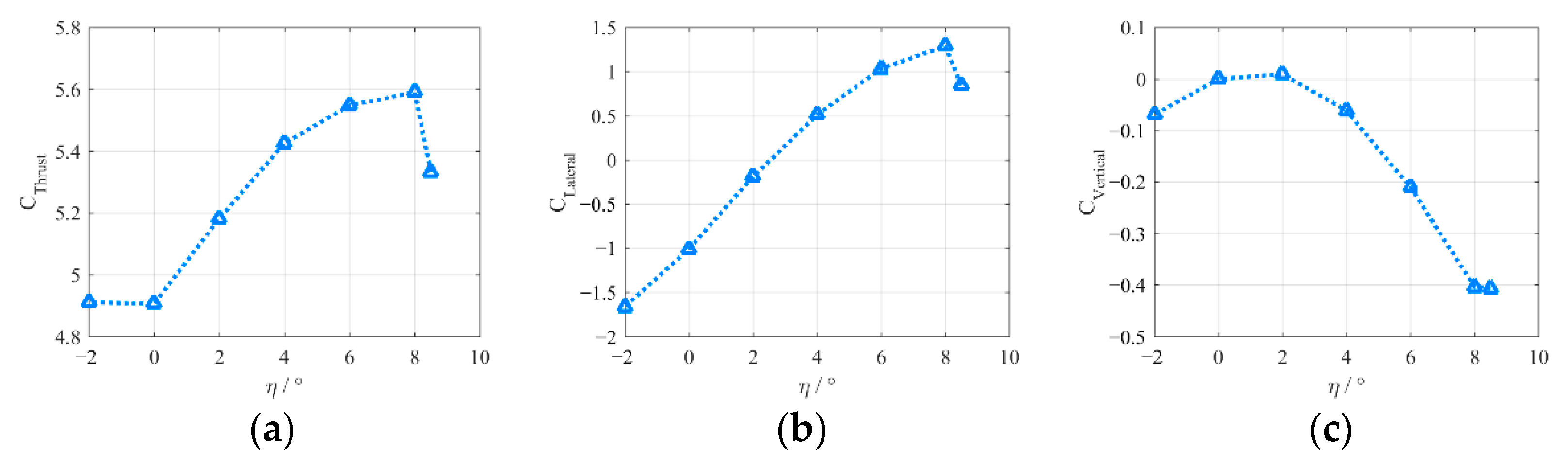
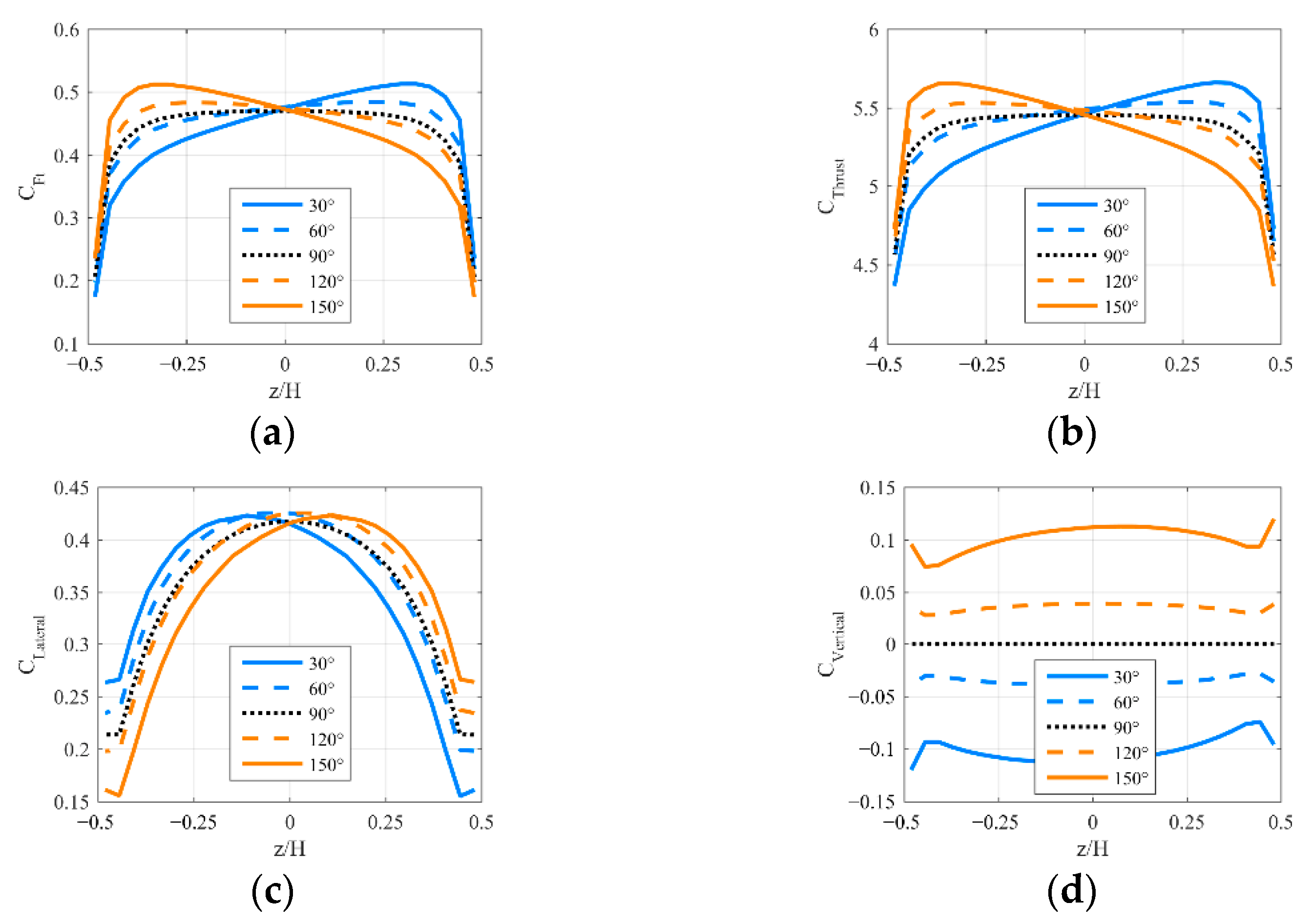
4.1. Fold Angle
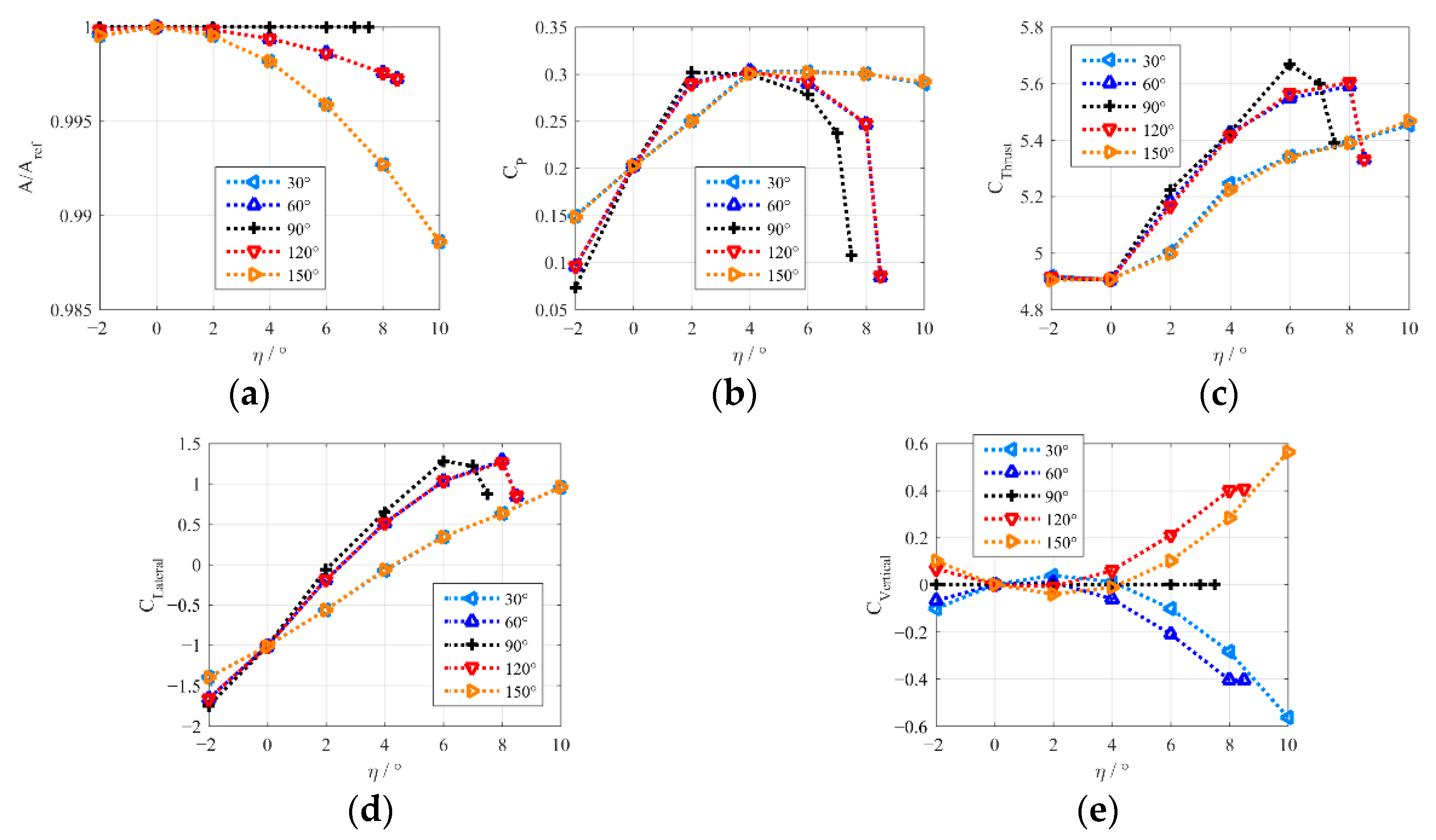
4.2. Incline Angle
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Li, Y.; Yang, C.; Zhang, X.; Wang, Q.; Li, D.; Zhong, W.; Wang, T. Design and Testing of a LUT Airfoil for Straight-Bladed Vertical Axis Wind Turbines. Appl. Sci. 2018, 8, 2266. [Google Scholar] [CrossRef] [Green Version]
- Möllerström, E.; Gipe, P.; Beurskens, J.; Ottermo, F. A historical review of vertical axis wind turbines rated 100 kW and above. Renew. Sustain. Energy Rev. 2019, 105, 1–13. [Google Scholar] [CrossRef]
- Tummala, A.; Velamati, R.K.; Sinha, D.K.; Indraja, V.; Krishna, V.H. A review on small scale wind turbines. Renew. Sustain. Energy Rev. 2016, 56, 1351–1371. [Google Scholar] [CrossRef]
- Guo, J.; Zeng, P.; Lei, L. Performance of a straight-bladed vertical axis wind turbine with inclined pitch axes by wind tunnel experiments. Energy 2019, 174, 553–561. [Google Scholar] [CrossRef]
- Shah, O.R.; Jamal, M.A. Performance Evaluation of a 1 kW Variable Pitch-Straight Blade Vertical Axis Wind Turbine. J. Energy Resour. Technol. 2020, 142. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. Effect of pitch angle on power performance and aerodynamics of a vertical axis wind turbine. Appl. Energy 2017, 197, 132–150. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.-C.; Kuo, C.-H. Effects of pitch angle and blade camber on flow characteristics and performance of small-size Darrieus VAWT. J. Vis. 2012, 16, 65–74. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, R.; Shen, W.; Wang, T.; Xu, B.; Zheng, Y.; Qian, S. Variable Pitch Approach for Performance Improving of Straight-Bladed VAWT at Rated Tip Speed Ratio. Appl. Sci. 2018, 8, 957. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.-B.; Zhang, L.-X.; Li, E.-X.; Zhang, F.-Y. Blade pitch control of straight-bladed vertical axis wind turbine. J. Cent. S. Univ. 2016, 23, 1106–1114. [Google Scholar] [CrossRef]
- Zhang, L.-X.; Liang, Y.-B.; Liu, X.-H.; Guo, J. Effect of blade pitch angle on aerodynamic performance of straight-bladed vertical axis wind turbine. J. Cent. S. Univ. 2014, 21, 1417–1427. [Google Scholar] [CrossRef]
- Zouzou, B.; Dobrev, I.; Massouh, F.; Dizene, R. Experimental and numerical analysis of a novel Darrieus rotor with variable pitch mechanism at low TSR. Energy 2019, 186. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, C.S.; Scheurich, F. Demonstrating that power and instantaneous loads are decoupled in a vertical-axis wind turbine. Wind Energy 2014, 17, 385–396. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Balduzzi, F.; Bianchini, A.; Ferrara, G.; Goude, A. Evaluation of the unsteady aerodynamic forces acting on a vertical-axis turbine by means of numerical simulations and open site experiments. J. Wind Eng. Ind. Aerodyn. 2020, 198. [Google Scholar] [CrossRef]
- Scheurich, F.; Fletcher, T.M.; Brown, R.E. Simulating the aerodynamic performance and wake dynamics of a vertical-axis wind turbine. Wind Energy 2011, 14, 159–177. [Google Scholar] [CrossRef] [Green Version]
- Dyachuk, E.; Rossander, M.; Goude, A.; Bernhoff, H. Measurements of the Aerodynamic Normal Forces on a 12-kW Straight-Bladed Vertical Axis Wind Turbine. Energies 2015, 8, 8482–8496. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.A.; Maeda, T.; Kamada, Y.; Murata, J.; Furukawa, K.; Yamamoto, M. Effect of number of blades on aerodynamic forces on a straight-bladed Vertical Axis Wind Turbine. Energy 2015, 90, 784–795. [Google Scholar] [CrossRef]
- Li, Q.A.; Maeda, T.; Kamada, Y.; Murata, J.; Shimizu, K.; Ogasawara, T.; Nakai, A.; Kasuya, T. Effect of solidity on aerodynamic forces around straight-bladed vertical axis wind turbine by wind tunnel experiments (depending on number of blades). Renew. Energy 2016, 96, 928–939. [Google Scholar] [CrossRef]
- Peng, Y.-X.; Xu, Y.-L.; Zhan, S.; Shum, K.-M. High-solidity straight-bladed vertical axis wind turbine: Aerodynamic force measurements. J. Wind Eng. Ind. Aerodyn. 2019, 184, 34–48. [Google Scholar] [CrossRef]
- Delafin, P.L.; Nishino, T.; Wang, L.; Kolios, A. Effect of the number of blades and solidity on the performance of a vertical axis wind turbine. J. Phys. Conf. Ser. 2016, 753. [Google Scholar] [CrossRef] [Green Version]
- Rogowski, K.; Hansen, M.O.L.; Bangga, G. Performance Analysis of a H-Darrieus Wind Turbine for a Series of 4-Digit NACA Airfoils. Energies 2020, 13, 3196. [Google Scholar] [CrossRef]
- Rogowski, K.; Hansen, M.O.L.; Lichota, P. 2-D CFD Computations of the Two-Bladed Darrieus-Type Wind Turbine. J. Appl. Fluid Mech. 2018, 11, 835–845. [Google Scholar] [CrossRef]
- Song, C.; Wu, G.; Zhu, W.; Zhang, X.; Zhao, J. Numerical Investigation on the Effects of Airfoil Leading Edge Radius on the Aerodynamic Performance of H-Rotor Darrieus Vertical Axis Wind Turbine. Energies 2019, 12, 3794. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Hansen, M.O.L.; Moan, T. Model improvements for evaluating the effect of tower tilting on the aerodynamics of a vertical axis wind turbine. Wind Energy 2015, 18, 91–110. [Google Scholar] [CrossRef]
- Lei, H.; Zhou, D.; Bao, Y.; Chen, C.; Ma, N.; Han, Z. Numerical simulations of the unsteady aerodynamics of a floating vertical axis wind turbine in surge motion. Energy 2017, 127, 1–17. [Google Scholar] [CrossRef]
- Lei, H.; Zhou, D.; Lu, J.; Chen, C.; Han, Z.; Bao, Y. The impact of pitch motion of a platform on the aerodynamic performance of a floating vertical axis wind turbine. Energy 2017, 119, 369–383. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, L.; Gao, X.; Xu, W. Aerodynamics and Motion Performance of the H-Type Floating Vertical Axis Wind Turbine. Appl. Sci. 2018, 8, 262. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.O.L.; Sørensen, N.N.; Sørensen, J.N.; Michelsen, J.A. Extraction of lift, drag and angle of attack from computed 3D viscous flow around a rotating blade. In Proceedings of the European Wind Energy Conference (EWEC 97), Dublin, Ireland, 6–9 October 1997; pp. 499–501. [Google Scholar]
- Rahimi, H.; Schepers, J.G.; Shen, W.Z.; García, N.R.; Schneider, M.S.; Micallef, D.; Ferreira, C.J.S.; Jost, E.; Klein, L.; Herráez, I. Evaluation of different methods for determining the angle of attack on wind turbine blades with CFD results under axial inflow conditions. Renew. Energy 2018, 125, 866–876. [Google Scholar] [CrossRef] [Green Version]
- Jost, E.; Klein, L.; Leipprand, H.; Lutz, T.; Krämer, E. Extracting the angle of attack on rotor blades from CFD simulations. Wind Energy 2018, 21, 807–822. [Google Scholar] [CrossRef]
- Elsakka, M.M.; Ingham, D.B.; Ma, L.; Pourkashanian, M. CFD analysis of the angle of attack for a vertical axis wind turbine blade. Energy Convers. Manag. 2019, 182, 154–165. [Google Scholar] [CrossRef]
- Shen, W.Z.; Hansen, M.O.L.; Sørensen, J.N. Determination of angle of attack (AoA) for rotating blades. In Wind Energy: Proceedings of the Euromech Colloquium; Springer: Berlin/Heidelberg, Germany, 2006; pp. 205–209. [Google Scholar]
- Shen, W.Z.; Hansen, M.O.L.; Sørensen, J.N. Determination of the angle of attack on rotor blades. Wind Energy 2009, 12, 91–98. [Google Scholar] [CrossRef]
- Guo, J.; Lei, L. Flow Characteristics of a Straight-Bladed Vertical Axis Wind Turbine with Inclined Pitch Axes. Energies 2020, 13, 6281. [Google Scholar] [CrossRef]
- Balduzzi, F.; Bianchini, A.; Maleci, R.; Ferrara, G.; Ferrari, L. Critical issues in the CFD simulation of Darrieus wind turbines. Renew. Energy 2016, 85, 419–435. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. CFD simulation of a vertical axis wind turbine operating at a moderate tip speed ratio: Guidelines for minimum domain size and azimuthal increment. Renew. Energy 2017, 107, 373–385. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.A.; Maeda, T.; Kamada, Y.; Murata, J.; Furukawa, K.; Yamamoto, M. The influence of flow field and aerodynamic forces on a straight-bladed vertical axis wind turbine. Energy 2016, 111, 260–271. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Qu, T.; Lei, L. Effect of Pitch Parameters on Aerodynamic Forces of a Straight-Bladed Vertical Axis Wind Turbine with Inclined Pitch Axes. Appl. Sci. 2021, 11, 1033. https://doi.org/10.3390/app11031033
Guo J, Qu T, Lei L. Effect of Pitch Parameters on Aerodynamic Forces of a Straight-Bladed Vertical Axis Wind Turbine with Inclined Pitch Axes. Applied Sciences. 2021; 11(3):1033. https://doi.org/10.3390/app11031033
Chicago/Turabian StyleGuo, Jia, Timing Qu, and Liping Lei. 2021. "Effect of Pitch Parameters on Aerodynamic Forces of a Straight-Bladed Vertical Axis Wind Turbine with Inclined Pitch Axes" Applied Sciences 11, no. 3: 1033. https://doi.org/10.3390/app11031033
APA StyleGuo, J., Qu, T., & Lei, L. (2021). Effect of Pitch Parameters on Aerodynamic Forces of a Straight-Bladed Vertical Axis Wind Turbine with Inclined Pitch Axes. Applied Sciences, 11(3), 1033. https://doi.org/10.3390/app11031033




