Next Article in Journal
Mechanical and Post-Cracking Characteristics of Fiber Reinforced Concrete Containing Copper-Coated Steel and PVA Fibers in 100% Cement and Fly Ash Concrete
Previous Article in Journal
Information Technologies in Complex Socio-Technical Systems Based on Functional Variability: A Case Study on HVAC Maintenance Work Orders
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 11
Issue 3
10.3390/app11031050
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Influence of Biomechanical Parameters on Performance in Elite Triathletes along 29 Weeks of Training

by
Javier Olaya-Cuartero
1,* and
Roberto Cejuela
2
1
Faculty of Health Sciences, Isabel I University, 09003 Burgos, Spain
2
Department-Section of Physical Education and Sport, University of Alicante, 03690 Alicante, Spain
*
Author to whom correspondence should be addressed.
Appl. Sci. 2021, 11(3), 1050; https://doi.org/10.3390/app11031050
Submission received: 10 December 2020 / Revised: 21 January 2021 / Accepted: 21 January 2021 / Published: 25 January 2021
(This article belongs to the Section Applied Biosciences and Bioengineering)
Browse Figures
Versions Notes

Abstract

:
The purpose of the study was to assess how the modification of biomechanical parameters influences the performance of elite triathletes. Four elite international triathletes participated in this study. The anthropometric method ISAK was used to estimate the triathlete’s body composition. For the physiological and biomechanical parameters, a running test (RT) was performed on an outdoor track, with the participants wearing the Stryd Summit Footpod (Stryd, Boulder, CO, USA). The pre-test took place in the last week of an adaptation mesocycle; then, after 29 weeks of training, the triathletes performed the post-test. A within-subject repeated measures design was used to assess changes in the anthropometric, physiological and biomechanical parameters. Pearson correlations (r) were applied to determine the relationship between the performance at different intensities (VT1, VT2 and MAS) and the biomechanical parameters. Concerning the anthropometric characteristics, significant differences were found in the summation (Σ) of skinfold (8.1 cm); as a consequence, the % fat mass was reduced (1.2%). Significant differences were found in the physiological values (VO2 and % VO2max), speed and biomechanical parameters, such as step length normalized, to the specific physiological intensity of the short-distance triathlon, the VT2. Therefore, performance improvement in the running segment could not only be explained by physiological changes, but also by biomechanical parameters changes.

1. Introduction

Triathlon is an endurance sport that comprises a sequential swim, swim-to-cycle transition, cycle, cycle-to-run transition, and run over a variety of long or short distances [1]. Standard races are stipulated by the International Triathlon Union (ITU), including sprint distance (750 m swimming, 20 km cycling and 5 km running) and Olympic distance (1.5 km swimming, 40 km cycling and 10 km running). Although the influence of the segments on the overcome result has been widely studied [2,3,4,5,6], the running segment has been the most studied. In the running segment was found the greatest variation in times for all male world championship triathletes [7]. Previous findings also have shown that running performance is the primary determinant of success in high-level short-distance triathlon races [8]. Other authors concluded that strategies to improve time in the running segment should be the main focus in the preparation of the short-distance triathlon [4]. However, to date, the physiological [9] and biomechanical changes in the performance of the world’s best elite triathletes in short-distance triathlons have not been widely investigated.
Concerning the triathlon performance factors, some authors differentiate between an ergogenic analysis for the determination of the internal load and an analytical analysis for the determination of the technical and tactical physical conditioning factors [10].
Internal load values have been previously studied in elite triathletes [10]—for example, for prescribing the heart rate (HR) zones for training from cycling to running [11]—to determine their significant maximum oxygen uptake (VO2max) [12,13,14]. Nevertheless, performance in triathlon has been associated with the capability of the triathlete to exercise at a lower percentage of VO2max, which is influenced by different factors such as aerobic power, economy of movement and ventilatory threshold 2 (VT2) [15].
The influence of biomechanical factors on performance has also been widely studied. Moore [16] classified them as spatiotemporal, kinematics, kinetics and neuromuscular, although running speed is mainly defined by spatiotemporal parameters, such as step frequency (SF) and step length (SL), which are mutually dependent. Although from a physiological and training point of view running performance has been widely studied, the possible influence of spatiotemporal variables on performance is still an issue of discussion [17]. Even more in elite triathletes due to the lack of analytical analysis of the running segment [10], unlike trained and novice runners [17,18,19]. To understand the influence of biomechanical parameters on performance, anthropometric characteristics must be considered because some of them influence the running success in triathlon [20].
In the last few years, there is a tendency to produce low-cost, portable gait analysis equipment, which has a great advantage over previous methods of analysis that have generally required well-equipped research laboratories [21]. Higginson et al. [22] point out that, from a practical point of view, through accelerometry it is possible to measure the participants in a more natural environment instead of an artificial laboratory. This is important for interpreting the data, taking into account the specificity of the sport because some biomechanical variables, such as leg stiffness, have been shown to influence performance [23,24] while running in specific situations rather than in non-specific situations, such as vertical jumps [18,19]. Currently, Stryd (Stryd Summit Model, Boulder, CO, USA) is a practical portable device that is reliable for measuring running metrics, classified as adequate for running assessment [25]. The concurrent validity of Stryd as compared to OptoGait was low–moderate for contact time (CT) and flying time (FT) and excellent for step length (SL) and step frequency (SF) [25]. This device also has been used in other investigations, showing significant correlations between run mechanics such as contact time, vertical oscillation (VO), step frequency and metabolic demand (VO2/speed) [26]. For this reason, a current systematic review concludes that this device could be a valid tool for measuring temporal parameters [27].
Thus, the main purpose of this study was to analyze the changes in biomechanical parameters in elite triathletes throughout an elite triathlon season. Anthropometric and physiological variables also were analyzed to jointly interpret changes in the running biomechanics. A previous hypothesis reflects that the physiological and anthropometric values will improve and that the spatiotemporal parameters could have a different interpretation than for novice or untrained triathletes measured in a laboratory.

2. Materials and Methods

2.1. Sample

Only 44 triathletes out of 100 participants finished the Spanish Olympic Elite Triathlon Championship in 2019; the remaining 66 participants were lapped or did not finish (DNF) the race. Elite international men triathletes (n = 4), who represent 9% of the elite Spanish triathletes, belonging to the same training group and team, participated in the study (age range: 19–24 years; age: 22.5 ± 1.9 years; height: 1.84 ± 4.1 m (mean ± SD)). All triathletes provided written informed consent to take part in this study, which was previously approved by the Research Ethics Committee of the University of Alicante (UA-2019-05-13). A summary of the training history and racing during the 29 weeks for these subjects is presented in Figure 1.
Besides, the triathletes also carried out a resistance programme throughout the season, with different objectives in each mesocycle, according to the assessment of strength and power in resistance training of Naclerio [28,29]. In the first period of the season (general preparatory period), three weekly sessions were performed during two mesocycles (8 weeks) of endurance strength with low weights (2–4 sets of 8–16 repetitions at 30–40% of 1RM). In the second period of the season (specific preparatory period), two sessions per week were performed during two mesocycles (8 weeks) of explosive strength (2–4 sets of 6–8 repetitions at 50–60% of 1RM). Later, and also during the specific preparatory period, they performed two sessions per week during 1 strength mesocycle (4 weeks) at high execution speeds during the concentric phase (2–4 sets of 2–4 repetitions at 80% of 1RM), including plyometrics exercises. Finally, during the third period of the season (competitive period), they performed two sessions per week of another mesocycle (4 weeks) of explosive strength (2–4 sets of 6–8 repetitions at 50–60% of 1RM), except in competition weeks where no strength session was done. For the rest of the season (last five weeks), they only performed one day of explosive strength.
Concerning the training session, two exercises were done in each workout, one for the upper body (pull-up or bench press) and another for the lower body (squat, deadlift or hip thrust).
Mobility exercises were also included in the warm-up for the swimming and resistance sessions, and also for the running sessions (only when intense sessions were carried out at or above the second ventilatory threshold).

2.2. Procedures

2.2.1. Study Protocol

Before starting the elite national triathlon season, the triathletes rested for two full weeks between the previous and current season. During the first month, all triathletes took part in a mesocycle of adaptation according to the principles of progression and super-compensation training (three weeks of training load and one week of recovery). During this adaptation mesocycle, the triathletes performed four microcycles of 15%, 20%, 25% and 15% of the peak load microcycle of the season along the first, second, third and fourth week, respectively. The running pre-test took place in the last week of this adaptation mesocycle. After 29 weeks of training, the running post-test was performed. Three main training intensities were defined according to the three main training zones defined for this study: ventilatory threshold 1 (VT1) (zone 2), ventilatory threshold 2 (VT2) (zone 4) and maximal aerobic speed (MAS) (zone 6) [30]. These training zones were subdivided into further training zones for daily training. All participants trained with eight individual training zones [31] to be more precise in some workouts and to use the “objective load scale” (ECOs) to control the training load. The ECOs were calculated by multiplying the duration (in minutes) of a training session with a scoring value between 1 and 50, depending on the heart-rate-based training zone (1–8) and by a factor of 1.0, 0.75 or 0.5 for running, swimming or cycling, respectively [31].
Indeed, to quantify the individual training load for each triathlete, a specific test for each discipline was carried out for the swimming and cycling segment. The cycling test was performed in the laboratory; a ramp protocol until exhaustion was used, starting at 50 watts and increasing 5 watts every 12 s [32]. Participants used their own bike; the rear wheel was removed and attached to a Hammer direct drive trainer (CycleOps, Madison, WI, USA). For the cycling test, the same gas-exchange analyzer was used as for the running test (Cosmed® K4b 2, Rome, Italy). The swimming test was carried out in a 25 m pool performing incremental steps in pace every 200 m using the protocol of 7 × 200 each 5 min [33]. The determination of training zones was interpreted using lactate samples of each step. Similar to the running test, VT1, VT2 and VO2max were subdivided into further training zones for daily workouts in swimming and cycling disciplines.

2.2.2. Anthropometry

An anthropometric method was applied to estimate the body composition of the triathletes. All measurements were taken by the same anthropometrist, Level 3 of the International Society for the Advancement of Kinanthropometry (ISAK) and in the same tent (ambient temperature 22 ± 1 °C). The Ross and Marfell-Jones [34] protocol was followed and the measures were taken three times for each subject. The equipment used included a Holtain skinfold calliper (Holtain Ltd., Crymych, UK), a Holtain bone breadth calliper (Holtain Ltd., Crymych, UK), scales, a stadiometer and anthropometric tape (SECA Ltd., Hamburg, Germany). The physical characteristics of age, weight and stature were measured in that order: age, weight and stature. The biepycondilar humerus, bi-styloid and biepicondylar femur breadths; arm relaxed, arm flexed and tense; mid-thigh and calf girths; sub-scapular, biceps, triceps, suprailiac, supraspinal, front thigh and medial calf; and abdominal skinfold measurements were taken.
Muscle mass was calculated using the Lee equation [35]. Fat mass was calculated using the Withers equation [36]. Bone mass was calculated using the Döbeln equation, modified by Rocha [37]. Somatoype was calculated using the Heath–Carter equations [38].

2.2.3. Running Test (RT)

The incremental running test to volitional exhaustion protocol was used to determine the intensities in running. The running test was performed on a 400-m certified track. Participants started at 10 km/h and increased 0.3 km/h every 200 m [39]. The test was conducted using a gas-exchange analyzer (Cosmed® K4b 2, Rome, Italy). All runners performed the maximal test with running shoes between 250 and 300 g weight for each shoe. Participants used the Stryd Summit Footpod (Stryd, Boulder, CO, USA) attached to the runner’s right shoelace equidistant from the participant’s malleolus and the toe of their shoe; the device was connected to a Garmin Fenix 3 hr watch and recorded data each second. The following variables were measured during the tests: oxygen uptake (VO2), ventilation (VE), ventilatory equivalents for oxygen (VE·VO2−1) and carbon dioxide (VE·VCO2−1), as well as the end-tidal partial pressure of oxygen (PETO2) and carbon dioxide (PETCO2).
Maximal oxygen uptake (VO2max) was recorded as the highest VO2 value obtained for any continuous 1-min period. VT1 was determined based on the criteria of an increase in both (VE·VO2−1) and (PETO2) with no increase in (VE·VCO2−1); whereas VT2 was determined using the criteria of an increase in both (VE·VO2−1) and (VE·VCO2−1), and a decrease in (PET CO2). Two independents observers identified VT1 and VT2 and in case of disagreement, the opinion of a third researcher was sought [40]. Heart rate (HR) was continuously monitored during the test using radiotelemetry (Polar Electro®, Kempele, Finland). The maximal aerobic speed (MAS) was determined as the speed associated with the VO2max during the test, as well as the velocity and power linked with the ventilatory thresholds.
The same procedure was used to determine the biomechanical parameters linked to the MAS and ventilatory thresholds. The following spatial variables were analyzed through the Stryd “Power Center” on the Stryd application: stiffness, measured in kilonewtons per meter (kn/m); contact time (CT), measured in milliseconds (ms); vertical oscillation (VO), measured in centimetres (cm); and cadence, measured in steps per minute (spm). The values of the spatiotemporal parameters were averaged over the steps of the same test speed, for at least 30 s. From the recorded contact and flight times was obtained the variable “duty factor”, which is the quotient between the contact time and the total step time [18]. In the same way as in previous investigations, to compare subjects of a different stature, the step amplitude was normalized, dividing it by the height of the trochanter [18].
For flying time (FT), measured in seconds (s), and step length (SL), measured in meters, the same procedure of García Pinillos et al. [25] was used, as follows:
FT (s) = step time (s) − CT (s)
where step time is the time from the beginning of the step cycle (take-off) to the end (previous frame to take-off).
Step time (s) = 60/SF (steps/min).
SL (m) = running velocity (m·min−1)/SF (steps/min)

2.3. Statistical Analyses

Data are presented as the mean and SD. Normality tests were used to study all the dependent variables (Shapiro–Wilk). After the parametricity of the sample was confirmed, a within-subject repeated measures design was used to assess the changes in anthropometric, physiological and biomechanical parameters. Significance was established at p < 0.05. The magnitude of differences or effect sizes (ESs) were calculated according to Cohen’s d [41] and interpreted as small (0.2 < ES < 0.5), moderate (0.5 < ES < 0.8) and large (ES > 0.8). To interpret the magnitude of correlations between the measurement variables, the following criteria were adopted: <0.1 (trivial), 0.1–0.3 (small), 0.3–0.5 (moderate), 0.5–0.7 (large), 0.7–0.9 (very large) and 0.9–1.0 (almost perfect). The coefficient of determination (R2) [42] was used to evaluate the proportion in which the biomechanical parameters explained the performance in each intensity. The concept of the smallest worthwhile change (SWC) to determine the practical significance of interventions was used to assess the changes in biomechanical parameters [43]. All data obtained were analyzed statistically with the software Statistical Package for the Social Sciences (v.25.0 SPSS Inc., Chicago, IL, USA).

3. Results

Table 1 shows the anthropometric characteristics between the pre- and post-test. These values are typical of elite triathletes and lower to elite cyclists [44], and also similar to research [45] in which internationally ranked male triathletes participated. Large ESs were found for all the anthropometric characteristics. Moreover, significant differences were found in Σ 6 skinfolds (8.1 cm) and fat mass kg and %, which was reduced (1.2%), showing lower values than the physical characteristics of elite short- and long-distance triathletes [13].
Table 2 is a comparison of the physiological characteristics of triathletes pre- and post-training. Large ESs were found for the most important performance indicator in the running segment, the speed, in the VT1 and VT2 intensities. Although peak speed remained the same, the VO2max showed large ESs. These values are comparable with values of sub-elite and elite triathletes reported in the literature [15,46,47]. Moreover, significant differences were found in the specific speed (0.97 km h−1) and % VO2max (3.65%) improvement of the short-distance triathlon, the VT2, improving also the VO2 (3.5 mL kg−1 min−1) in this physiological intensity.
Table 3 shows the values of the spatiotemporal parameters of stiffness, contact time (CT), vertical oscillation (VO), cadence (measured in steps per minute (spm)), flying time (FT), step length normalized (SL norm) and “duty factor” between the pre- and post-test. In the same way as with the physiological parameters, the ESs are interpreted due to the small number of the sample. Significant differences were found in SL normalized in VT2 and a tendency is showed in VT1 (p = 0.056), showing large ESs due to the improvement of 10 cm in VT1 and 11 cm in VT2. Small and moderate ESs were found in stiffness, VO, cadence and FT. Controversial changes show the largest ES for CT, which decreased in VT1 and increased in VT2 and MAS.

4. Discussion

As discussed above, due to the small number of the sample, the ESs were analyzed to discuss the results obtained from the pre- and post-test on anthropometric, physiological and biomechanical characteristics. This is the first study that analyzes the biomechanical changes in the running segment in elite triathletes during a season.
Firstly, concerning the anthropometric characteristics, large ESs and significant differences were found in the decrease of Σ6 skinfolds and fat mass. It should be highlighted that although the athletes came from a period of inactivity (two weeks of full rest and four weeks of adaptation mesocycle), these subjects have several years of experience in triathlon training and competition during previous seasons. This, in addition to the use of the ISAK method for estimating body composition, could explain the low body fat mass and fold sum values obtained. Although there would not be enough data to define the impact of the modifications of the anthropometric characteristics on performance, it could be speculated that there was an improvement in performance as a result of this factor since body fat correlates negatively with running success in triathlon because it is essentially a dead weight that must be carried throughout the event [20].
Secondly, regarding the physiological variables, large ESs were found in all parameters, except heart rate and peak speed. The most important predictor of performance [48], the speed, improved 0.45 km h−1 in VT1 and 0.97 km h−1 in VT2, which is the specific physiological intensity of the short-distance triathlon [15], while peak speed did not change. Previous studies [49] partially support the results of the present study, showing an increase in the ventilatory threshold speed but also in peak speed after strength and endurance training in recreational marathon runners. It might be that more concurrent plyometric training could improve the peak speed, VO2max and modify the biomechanical parameters, as previous investigations have shown [19]. The improvements at different speeds could be explained by the changes in the percentages of VO2max at which VT1 and VT2 are determined. For example, VT1 was improved from 66.33% VO2max (pre-test) to 73.56% VO2max (post-test) and VT2 was improved from 84.29% VO2max (pre-test) to 87.94% VO2max (post-test). From a practical point of view, it means that triathletes could run faster at the same physiological intensity [50]. These results are supported by Pallarés and Morán-Navarro [51], who determined the intensity of VT1 as between 65 and 75% of the % VO2max and VT2 as between 75 and 85% of the % VO2max in trained athletes.
Thirdly, focusing attention on the biomechanical parameters, large ESs also could explain the improvement in the performance. The largest ESs were found in SL normalized, increasing 10 cm in VT1 and 11 cm in VT2. These results are supported by previous research [52] in which the maximal and submaximal SL correlated with performance and seems to be fundamental to reach high speeds. The same authors show that the maximal SL recorded in half marathon runners is 1.70 m while in this study it is 1.99 m (in elite triathletes). Therefore, this big difference could explain that, in long-distance events, SL is negatively related to performance [18]. Besides, in previous research [18], it was shown to be worth it to analyze the “duty factor”, which shows a negative relationship with speed, suggesting that future work should be applied in higher level athletes, with the aim to accept or reject some of the results and conclusions. Likewise, in the present study, the “duty factor” also shows a negative relationship with speed (Figure 2). Furthermore, almost perfect and very large correlations were found between this variable and performance in the pre-test, explaining 93% of the performance in VT1 and 72% in VT2; in the post-test, this variable explains 49% in VT1 and 40% in VT2 (Table 4). Small and trivial correlations were found between duty factor and performance in MAS, maybe because it is known that, from a certain level of stress, the step frequency increases markedly, and the amplitude flattens out [53]. Concerning CT, in the same way as in previous investigations [16], controversial results are found, depending on the speed at which the CT is analyzed, but emphasizing the large ESs in all physiological intensities. In VT1, CT is shorter in the post than pre-test. It is suggested that short ground-contact times incur a high metabolic cost because faster force production is required, meaning metabolically expensive fast twitch muscle fibers are recruited [54,55]. In contrast, in VT2 and MAS, the CT is longer. Conversely, long ground-contact times may incur a high metabolic cost because the force is produced slowly, meaning longer braking phases when runners undergo deceleration [56], as in the post-test in comparison to the pre-test in VT2 (3.38 ms) and MAS (4.8 ms). Small and moderate ESs were found in stiffness, VO, cadence and FT. On one hand, it is known that fatiguing runs to volitional exhaustion have led to reductions in leg stiffness [57,58], as in the post-test. Moreover, leg stiffness was higher in all physiological intensities in the pre-test than in the post-test. These non-improvements in leg stiffness are supported by some studies showing that stiffness has not increased and even decreases after 8 weeks of concurrent plyometric and running training in novice runners [19]. On the other hand, it is worth noting the negative correlation between VO and speed in both the pre- and post-test is because a lower VO could make the athlete more efficient [59] and decreases in VO leads to improving the running economy [60]. Hence, increasing VO leads to increases in VO2 [61]. For this reason, a running technique that does not lead to VO2 is important. For example, the running technique characteristic of high-performance triathletes could explain why they can maintain a good technique at high speeds similar to a competition pace. Divert et al. [62] point out that this is what happens when individuals run barefoot, probably due to a smaller vertical displacement during stance. In the investigation of the differences in barefoot–shod [62], it has been shown that the higher oxygen consumption in shod running compared to barefoot running is attributed to the additional mass of the shoe, and that changes in VO2 may be more attributed to the additional mass associated with shoes than to the mechanical alterations in the running pattern. However, in elite triathletes, this decrease in VO as speed increases could be explained by the good running technique at high speeds (competition pace) rather than by the type of shoes. Finally, the distance of the competition or the age matters little to affirm that the optimal cadence is above 170 spm [63]. This is supported by previous research in which trained runners have run at the speed of jogging, during volumetric training and not a competition, and although they decreased their cadences somewhat, they were maintained above 170 spm [64]. Specifically, this cadence is very similar to that of the competition pace (VT2), both in the pre-test (172.2 ± 2.18 spm) and in the post-test (171.2 ± 1.85 spm). It should be kept in mind that runners appear to naturally choose a step frequency or step length that is economically optimal, or at least very near to being economically optimal [16]. As far as the possible limitations of the biomechanical parameters are concerned, it should be noted that all these variables have been measured during incremental ramp tests, where the time of the steps was short. Consequently, the values of the biomechanical parameters were averaged over the steps of the same test speed, at least for 30 s.

5. Conclusions

In brief, improvement in performance in the running segment in triathlon could not only be explained by physiological changes, but also by anthropometric and biomechanical parameters. Anthropometric characteristics, such as a decrement in Σ6 skinfolds and % fat mass, were significantly modified at the end of the season. The performance improvement in the specific intensity of short-distance triathlon (VT2) is not only due to physiological improvements, such as the VO2 and % VO2max at which the thresholds are determined but also to improvements in the biomechanical parameters such as SL normalized. However, it seems difficult to change other factors, such as stiffness, vertical oscillation and cadence, in elite triathletes, while contradictory results continue to be found for contact time. Finally, “duty factor” is a variable to be taken into account in VT1 and VT2, but not in VO2max, maybe because it is known that, from a certain level of stress, the step frequency increases markedly and the amplitude flattens out.

Author Contributions

Conceptualization, J.O.-C. and R.C.; software, J.O.-C.; validation, J.O.-C.; formal analysis, J.O.-C. and R.C.; investigation, J.O.-C. and R.C.; resources, J.O.-C. and R.C.; data curation, J.O.-C.; writing—original draft preparation, J.O.-C.; writing—review and editing, J.O.-C. and R.C.; visualization, R.C.; supervision, R.C.; project administration, R.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

All triathletes provided written informed consent to take part in this study, which was previously approved by the Research Ethics Committee of the University of Alicante (UA-2019-05-13).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

All relevant data are within the manuscript and its Supporting Information files.

Acknowledgments

The authors would like to thank all the triathletes and staff of the University of Alicante professional triathlon team.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bentley, D.; Millet, G.; Vleck, V.; McNaughton, L. Specific aspects of contemporary triathlon: Implications for physiological analysis and performance. Sport. Med. 2002, 32, 345–359. [Google Scholar] [CrossRef] [PubMed]
  2. Piacentini, M.; Bianchini, L.; Minganti, C.; Sias, M.; Di Castro, A.; Vleck, V. Is the Bike Segment of Modern Olympic Triathlon More a Transition towards Running in Males than It Is in Females? Sports 2019, 7, 76. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Horne, M.J. The relationship of race discipline with overall performance in sprint and standard distance triathlon age-group world championships. Int. J. Sport. Sci. Coach. 2017, 12, 814–822. [Google Scholar] [CrossRef]
  4. Figueiredo, P.; Marques, E.A.; Lepers, R. Changes in contributions of swimming, cycling, and running performances on overall triathlon performance over a 26-year period. J. Strength Cond. Res. 2016, 30, 2406–2415. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  5. Vleck, V.; Bürgi, A.; Bentley, D. The consequences of swim, cycle, and run performance on overall result in elite olympic distance triathlon. Int. J. Sports Med. 2006, 27, 43–48. [Google Scholar] [CrossRef]
  6. Landers, G.J.; Blanksby, B.A.; Ackland, T.R.; Monson, R. Swim Positioning and its Influence on Triathlon Outcome. Int. J. Exerc. Sci. 2008, 1, 93–105. [Google Scholar]
  7. Landers, G.J.; Blanksby, B.A.; Ackland, T.R.; Smith, D. Morphology and performance of world championship triathletes. Ann. Hum. Biol. 2000, 27, 387–400. [Google Scholar] [CrossRef]
  8. Van Schuylenbergh, R.; Vanden Eynde, B.; Hespel, P. Prediction of sprint triathlon performance from laboratory tests. Eur. J. Appl. Physiol. 2004, 91, 94–99. [Google Scholar] [CrossRef]
  9. Rüst, C.; Lepers, R.; Stiefel, M.; Rosemann, T.; Knechtle, B. Performance in Olympic triathlon: Changes in performance of elite female and male triathletes in the ITU World Triathlon Series from 2009 to 2012. Springerplus 2013, 2, 685. [Google Scholar] [CrossRef] [Green Version]
  10. Cejuela, R.; Pérez-Turpin, J.; Villa, G.; Cortell, J.; Rodríguez-Marroyo, J. Análisis de los factores de rendimiento en triatlón distancia sprint. J. Hum. Sport Exerc. 2009, 2, 1–25. [Google Scholar] [CrossRef] [Green Version]
  11. Carey, D.G.; Tofte, C.; Pliego, G.J.; Raymond, R.L. Transferability of running and cycling training zones in triathletes: Implications for steady-state exercise. J. Strength Cond. Res. 2009, 23, 251–258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  12. Laursen, P.B.; Shing, C.M.; Tennant, S.C.; Prentice, C.M.; Jenkins, D.G. A comparison of the cycling performance of cyclists and triathletes. J. Sports Sci. 2003, 21, 411–418. [Google Scholar] [CrossRef] [PubMed]
  13. Millet, G.P.; Dréano, P.; Bentley, D.J. Physiological characteristics of elite short- and long-distance triathletes. Eur. J. Appl. Physiol. 2003, 88, 427–430. [Google Scholar] [CrossRef] [PubMed]
  14. Schabort, E.J.; Killian, S.C.; St Clair Gibson, A.; Hawley, J.A.; Noakes, T.D. Prediction of triathlon race time from laboratory testing in national triathletes. Med. Sci. Sports Exerc. 2000, 32, 844–849. [Google Scholar] [CrossRef]
  15. Sleivert, G.G.; Rowlands, D.S. Physical and physiological factors associated with success in the triathlon. Sport. Med. 1996, 22, 8–18. [Google Scholar] [CrossRef]
  16. Moore, I.S. Is there an economical running technique? A review of modifiable biomechanical factors affecting running economy. Sport. Med. 2016, 46, 793–807. [Google Scholar] [CrossRef] [Green Version]
  17. Gómez-Molina, J.; Ogueta-Alday, A.; Stickley, C.; Cámara, J.; Cabrejas-Ugartondo, J.; García-López, J. Differences in spatiotemporal parameters between trained runners and untrained participants. J. Strength Cond. Res. 2017, 31, 2169–2175. [Google Scholar] [CrossRef] [Green Version]
  18. Ogueta-Alday, A.; Morante, J.C.; Rodríguez-Marroyo, J.A.; Villa, J.G.; García-López, J. Influencia de los parámetros biomecánicos en el rendimiento y la economía de corredores de fondo aficionados. Biomecánica 2011, 19, 17–27. [Google Scholar] [CrossRef]
  19. Gómez-Molina, J.; Ogueta-Alday, A.; Camara, J.; Stickley, C.; García-lópez, J. Effect of 8 weeks of concurrent plyometric and running training on spatiotemporal and physiological variables of novice runners. Eur. J. Sport Sci. 2018, 18, 162–169. [Google Scholar] [CrossRef]
  20. Atwater, A.E. Gender differences in running. In Biomechanics of Distance Running; Human Kinetics Publishers: Champaign, IL, USA, 1990; pp. 321–362. [Google Scholar]
  21. Norris, M.; Anderson, R.; Kenny, I.C. Method analysis of accelerometers and gyroscopes in running gait: A systematic review. Proc. Inst. Mech. Eng. Part P J. Sport. Eng. Technol. 2014, 228, 3–15. [Google Scholar] [CrossRef] [Green Version]
  22. Higginson, B.K. Methods of running gait analysis. Curr. Sports Med. Rep. 2009, 8, 136–141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Morgan, D.W.; Bransford, D.R.; Costill, D.L.; Daniels, J.T.; Howley, E.T.; Krahenbuhl, G.S. Variation in the aerobic demand of running among trained and untrained subjects. Med. Sci. Sport. Exerc. 1995, 27, 404–409. [Google Scholar] [CrossRef]
  24. Saunders, P.U.; Pyne, D.B.; Telford, R.D.; Hawley, J.A. Factors affecting running economy in trained distance runners. Sport. Med. 2004, 34, 465–485. [Google Scholar] [CrossRef] [PubMed]
  25. García-Pinillos, F.; Roche-Seruendo, L.E.; Marcén-Cinca, N.; Marco-Contreras, L.A.; Latorre-Román, P.A. Absolute reliability and concurrent validity of the Stryd system for the assessment of running stride kinematics at different velocities. J. Strength Cond. Res. 2018, 35, 78–84. [Google Scholar] [CrossRef] [PubMed]
  26. Aubry, R.L.; Power, G.A.; Burr, J.F. An assessment of running power as a training metric for elite and recreational runners. J. Strength Cond. Res. 2018, 32, 2258–2264. [Google Scholar] [CrossRef]
  27. Olaya-Cuartero, J.; Cejuela, R. Contextualisation of running power: A systematic review. J. Phys. Educ. Sport 2020, 20, 2044–2051. [Google Scholar]
  28. Naclerio Ayllón, F.; Jiménez Gutiérrez, A. Entrenamiento De La Fuerza Contra Resistencias: Cómo Determinar Las Zonas De Entrenamiento. J. Hum. Sport Exerc. 2007, II, 42–52. [Google Scholar] [CrossRef] [Green Version]
  29. Naclerio, F.; Jiménez, A.; Alvar, B.A.; Peterson, M.D. Assessing Strenght and Power in Resistance Training. J. Hum. Sport Exerc. 2009, 4, 100–113. [Google Scholar] [CrossRef] [Green Version]
  30. Skinner, J.; McLellan, T. The transition from aerobic to anaerobic metabolism. Res. Q. Exerc. Sport 1980, 51, 234–248. [Google Scholar] [CrossRef]
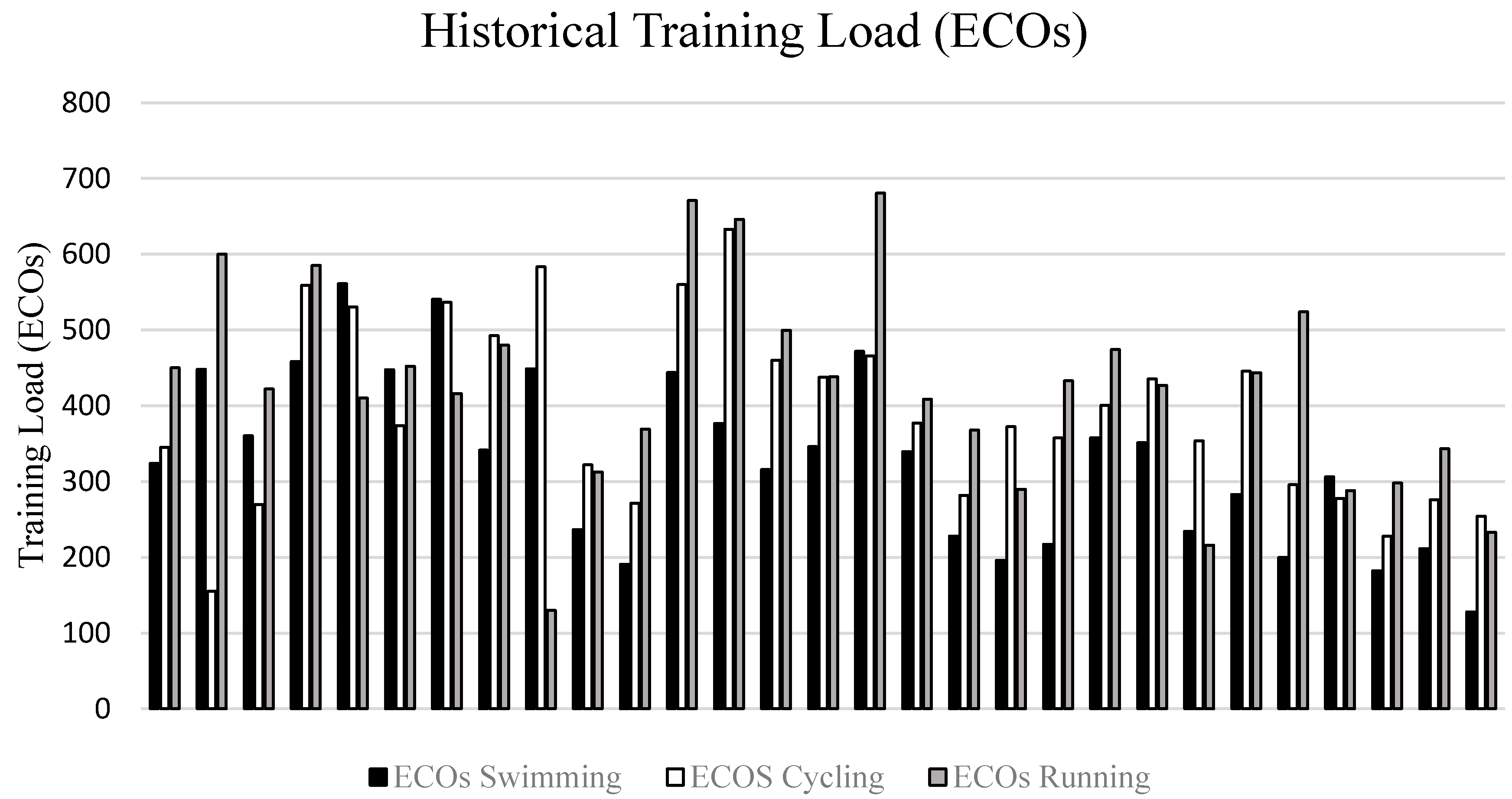
  31. Cejuela, R.; Esteve-Lanao, J. Training load quantification in triathlon. J. Hum. Sport Exerc. 2011, 6, 218–232. [Google Scholar] [CrossRef] [Green Version]
  32. Muñoz, I.; Cejuela, R.; Seiler, S.; Larumbe, E.; Esteve-Lanao, J. Training-intensity distribution during an ironman season: Relationship with competition performance. Int. J. Sports Physiol. Perform. 2014, 9, 332–339. [Google Scholar] [CrossRef] [PubMed]
  33. Sweetenham, B.; Atkinson, J. Championship Swim Training; Kinetics, H., Ed.; Human Kinetics Books: Champaign, IL, USA, 2003; ISBN 9780736045438. [Google Scholar]
  34. Ross, W.D.; Marfell-Jones, M.J. Kinanthropometry. Physiological Testing of the High-Performance Athlete; Human Kinetics Books: Champaign, IL, USA, 1991. [Google Scholar]
  35. Lee, J.B.; Sutter, K.J.; Askew, C.D.; Burkett, B.J. Identifying symmetry in running gait using a single inertial sensor. J. Sci. Med. Sport 2010, 13, 559–563. [Google Scholar] [CrossRef] [PubMed]
  36. Withers, R.T.; Craig, N.P.; Bourdon, P.C.; Norton, K.I. Relative body fat and anthropometric prediction of body density of male athletes. Eur. J. Appl. Physiol. Occup. Physiol. 1987, 56, 191–200. [Google Scholar] [CrossRef] [PubMed]
  37. Rocha, M. Peso osseo do brasileiro de ambos os sexos de 17–25 anos. Arq. Anat. Antropol. 1975, 1, 445. [Google Scholar]
  38. Carter, J.E.L. The Heath-Carter Anthropometric Somatotype; Instruction Manual: San Diego, CA, USA, 2002. [Google Scholar]
  39. Brue, F. Une Variante du test de piste progressif et maximal de Leger et Boucher pour la precise et facile de la vitesse maximale aerobie. French Athl. Fed. 1985, 25–30. [Google Scholar]
  40. Doherty, M.; Nobbs, L.; Noakes, T.D. Low frequency of the “plateau phenomenon” during maximal exercise in elite British athletes. Eur. J. Appl. Physiol. 2003, 89, 619–623. [Google Scholar] [CrossRef]
  41. Cohen, J. Statistical power Analysis for the Behavioral Sciences; Abingdon Press: Abingdon, Virginia, 1988. [Google Scholar]
  42. Motulsky, H.; Christopoulos, A. Fitting Models to Biological Data Using Linear and Nonlinear Regression; A practical Guide to Curve fitting; Oxford Unversity Press: Oxford, UK, 2003. [Google Scholar]
  43. Hopkins, W.G. Measures of reliability in sports medicine and science. Sport. Med. 2000, 30, 1–15. [Google Scholar] [CrossRef] [Green Version]
  44. Brunkhorst, L.; Kielstein, H. Comparison of anthropometric characteristics between professional triathletes and cyclists. Biol. Sport 2013, 30, 269–273. [Google Scholar] [CrossRef] [Green Version]
  45. Chollet, D.; Hue, O.; Auclair, F.; Millet, G.; Chatard, J. The effects of drafting on stroking in elite male triathletes. Eur. J. Appl. Physiol. 2000, 82, 413–417. [Google Scholar] [CrossRef]
  46. Basset, F.A.; Boulay, M.R. Specificity of treadmill and cycle ergometer tests in triathletes, runners and cyclists. Eur. J. Appl. Physiol. Occup. Physiol. 2000, 81, 214–221. [Google Scholar] [CrossRef]
  47. Schneider, D.A.; Lacroix, K.A.; Atkinson, G.R.; Troped, P.J.; Pollack, J. Ventilatory threshold and maximal oxygen uptake during cycling and running in triathletes. Med. Sci. Sports Exerc. 1990, 22, 257–264. [Google Scholar] [CrossRef] [PubMed]
  48. Billat, V. Fisiología y Metodología del Entrenamiento; Paidotribo: Barcelona, Spain, 2002; ISBN 84-8019-627-0. [Google Scholar]
  49. Ferrauti, A.; Bergermann, M.; Fernandez-Fernandez, J. Effects of a concurrent strength and endurance training on running performance and running economy in recreational marathon runners. J. Strength Cond. Res. 2010, 24, 2770–2778. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  50. Cardona, C.; Cejuela, R.; Esteve-Lanao, J. Manual Para Entrenar Deportes de Resistencia; All in Your Mind: Guadalajara, Mexico, 2019; ISBN 9781074568122. [Google Scholar]
  51. Pallarés, J.; Morán-Navarro, R. Propuesta metodológica para el entrenamiento de la resistencia cardiorrespiratoria. J. Spor Heal. Res. 2012, 4, 119–136. [Google Scholar]
  52. Gómez-Molina, J.; Ogueta-Alday, A.; Camara, J.; Stickley, C.; Rodríguez-Marroyo, J.A.; García-López, J. Predictive variables of half-marathon performance for male runners. J. Sport. Sci. Med. 2017, 16, 187–194. [Google Scholar]
  53. Weyand, P.G.; Sternlight, D.B.; Bellizzi, M.J.; Wright, S. Faster top running speeds are achieved with greater ground forces not more rapid leg movements. J. Appl. Physiol. 1991, 89, 1991–1999. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  54. Roberts, T.J.; Kram, R.; Weyand, P.G.; Taylor, C.R. Energetics of bipedal running. I. Metabolic cost of generating force. J. Exp. Biol. 1998, 201, 2745–2751. [Google Scholar]
  55. Kram, R.; Taylor, C. Energetics of running: A new perspective. Nature 1990, 346, 265–267. [Google Scholar] [CrossRef]
  56. Nummela, A.; Keränen, T.; Mikkelsson, L.O. Factors related to top running speed and economy. Int. J. Sports Med. 2007, 28, 655–661. [Google Scholar] [CrossRef]
  57. Fourchet, F.; Girard, O.; Kelly, L.; Horobeanu, C.; Millet, G.P. Changes in leg spring behaviour, plantar loading and foot mobility magnitude induced by an exhaustive treadmill run in adolescent middle-distance runners. J. Sci. Med. Sport 2015, 18, 199–203. [Google Scholar] [CrossRef]
  58. Hayes, P.R.; Caplan, N. Leg stiffness decreases during a run to exhaustion at the speed at VO2max. Eur. J. Sport Sci. 2014, 14, 556–562. [Google Scholar] [CrossRef]
  59. Slawinski, J.S.; Billat, V.L. Difference in mechanical and energy cost between highly, well, and nontrained runners. Med. Sci. Sports Exerc. 2004, 36, 1440–1446. [Google Scholar] [CrossRef] [PubMed]
  60. Moore, I.S.; Jones, A.; Dixon, S. The pursuit of improved running performance: Can changes in cushioning and proprioception influence running economy and injury risk? Footwear Sci. 2013, 5, S61–S62. [Google Scholar] [CrossRef] [Green Version]
  61. Tseh, W.; Caputo, J.L.; Morgan, D.W. Influence of gait manipulation on running economy in female distance runners. J. Sport. Sci. Med. 2008, 7, 91–95. [Google Scholar]
  62. Divert, C.; Mornieux, G.; Freychat, P.; Baly, L.; Mayer, F.; Belli, A. Barefoot-shod running differences: Shoe or mass effect? Int. J. Sports Med. 2008, 29, 512–518. [Google Scholar] [CrossRef]
  63. Conoboy, P.; Dyson, R. Effect of aging on the stride pattern of veteran marathon runners. Br. J. Sports Med. 2006, 40, 601–604. [Google Scholar] [CrossRef] [Green Version]
  64. Tartaruga, M.; Brisswalter, J.; Peyré-Tartaruga, L.A.; Otávio, A.; Ávila, V.; Alberton, C.L.; Coertjens, M.; Cadore, E.L.; Tiggemann, C.L.; Silva, E.M.; et al. The Relationship Between Running Economy and Biomechanical Variables in Distance Runners. Res. Q. Exerc. Sport 2012, 833, 367–375. [Google Scholar] [CrossRef]
Applsci 11 01050 g001 550
Figure 1. Historical objective load scale (ECOs) training load in the disciplines of swimming, cycling and running performed by the triathletes during the season.
Figure 1. Historical objective load scale (ECOs) training load in the disciplines of swimming, cycling and running performed by the triathletes during the season.
Applsci 11 01050 g001
Applsci 11 01050 g002 550
Figure 2. Evolution of the contact time, flight time and duty factor, as the test speed increases in the selected sample (n = 4 elite triathletes) in ventilatory thresholds 1 (VT1) and 2 (VT2) and maximal aerobic speed (MAS).
Figure 2. Evolution of the contact time, flight time and duty factor, as the test speed increases in the selected sample (n = 4 elite triathletes) in ventilatory thresholds 1 (VT1) and 2 (VT2) and maximal aerobic speed (MAS).
Applsci 11 01050 g002
Table
Table 1. Anthropometric characteristics (mean ± SD) of the triathletes pre- and post-training.
Table 1. Anthropometric characteristics (mean ± SD) of the triathletes pre- and post-training.
Pre-TestPost-TestpES
Weight (kg)72.4 ± 5.271.4 ± 4.20.1470.97
Σ 6 skinfolds (cm)42.5 ± 4.534.4 ± 1.80.017 *2.39
Lean mass (kg)33.3 ± 1.733 ± 1.40.1371.01
Fat mass (kg)5.6 ± 0.84.7 ± 0.40.027 *2.03
Fat mass (%)7.7 ± 0.96.5 ± 0.50.019 *2.30
* Significantly different from the pre-training value (p < 0.05).
Table
Table 2. Physiological characteristics (means ± SD) of the triathletes pre- and post-training.
Table 2. Physiological characteristics (means ± SD) of the triathletes pre- and post-training.
Pre-TestPost-TestpES
VT1
Speed (km h−1)14.95 ± 0.3915.4 ± 0.730.1031.16
VO2 (mL kg−1 min−1)47.5 ± 4.853.50 ± 1.290.0811.29
% VO2max (mL kg−1 min−1)66.33 ± 7.7773.56 ± 1.470.1061.15
HR (bpm)151.25 ± 15.48158.5 ± 7.680.3180.6
VT2
Speed (km h−1)16.98 ± 0.6217.95 ± 0.79 *0.0321.9
VO2 (mL kg−1 min−1)60.5 ± 3.1164 ± 2.94 *0.0122.71
% VO2max (mL kg−1 min−1)84.29 ± 1.187.94 ± 1.59 *0.0132.65
HR (bpm)174.5 ± 10.54177.5 ± 10.340.1820.87
MAS
Peak speed (km h−1)20.13 ± 0.7120.13 ± 0.6210
VO2max (mL kg−1 min−1)71.75 ± 2.8772.75 ± 2.220.0921.22
% VO2max (mL kg−1 min−1)100100
HRmax (bpm)189.75 ± 7.04191 ± 9.310.4640.42
* Significantly different from the pre-training value (p < 0.05); VT = ventilatory threshold; MAS = maximal aerobic speed.
Table
Table 3. The pre-test and post-test biomechanical parameters for running after 29 weeks training.
Table 3. The pre-test and post-test biomechanical parameters for running after 29 weeks training.
Pre-TestPost-TestSWCResultpES
VT1
Stiffness (kn/m)10.95 ± 1.6110.73 ± 0.390.3220.2250.7510.17
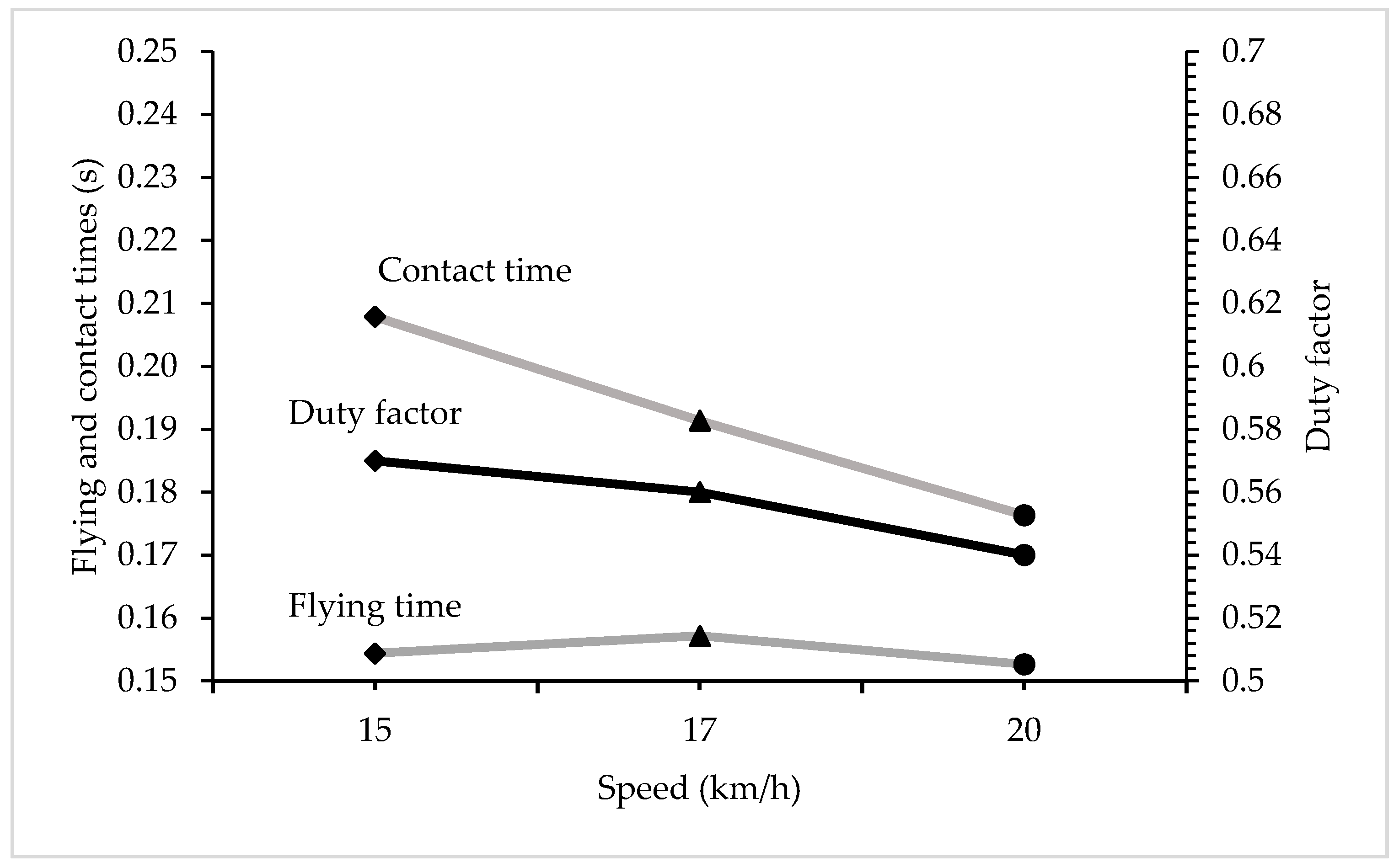
CT (ms)207.88 ± 1.37204.98 ± 1.930.2732.90.0691.39
VO (cm)9.15 ± 0.529.03 ± 0.310.1040.1250.4920.39
Cadence (spm)165.68 ± 3.31167 ± 1.590.663−1.3250.2920.64
FT (s)0.154 ± 0.010.154 ± 0.0050.0010.0000.9750.02
SL norm (m)1.62 ± 0.061.72 ± 0.090.013−0.0990.0561.52
Duty Factor0.57 ± 0.010.57 ± 0.010.0020.0030.2570.7
VT2
Stiffness (kn/m)11.03 ± 1.3210.55 ± 0.410.2640.4750.4880.39
CT (ms)191.35 ± 2.94194.73 ± 4.120.587−3.3750.1870.85
VO (cm)8.75 ± 0.328.75 ± 0.170.0640.00010
Cadence (spm)172.2 ± 2.18171.2 ± 1.850.4361.0000.4140.47
FT (s)0.157 ± 0.0050.156 ± 0.0030.00090.00140.3770.52
SL norm (m)1.79 ± 0.061.90 ± 0.080.012−0.1040.017 *2.41
Duty Factor0.06 ± 0.010.56 ± 0.010.002−0.0060.1690.9
MAS
Stiffness (kn/m)10.93 ± 1.5810 ± 0.340.3170.9250.2870.65
CT (ms)176.33 ± 4.5181.13 ± 1.10.899−4.8000.1650.91
VO (cm)7.93 ± 0.62 8.05 ± 0.310.125−0.1250.6330.27
Cadence (spm)182.5 ± 5.38179.9 ± 2.471.0762.6000.3630.54
FT (s)0.153 ± 0.0010.152 ± 0.0010.0020.0000.9560.3
SL norm (m)1.96 ± 0.051.99 ± 0.090.010−0.0290.2790.66
Duty Factor0.54 ± 0.020.54 ± 0.010.004−0.0070.4060.48
* Significantly different from the pre-training value (p < 0.05); VT = ventilatory threshold; MAS = maximal aerobic speed; CT = contact time; VO = vertical oscillation; FT = flying time; SL norm = step length normalized; SWC = smallest worthwhile change; ES = effect size.
Table
Table 4. Contribution of the biomechanical parameters to the performance at different speeds.
Table 4. Contribution of the biomechanical parameters to the performance at different speeds.
R2Stiffness (kn/m)CT (ms)VO (cm)Cadence (spm)FT (s)SL norm (m)Duty Factor
VT1 speed (km/h)
Pre0.3600.910.870.930.630.93
Post0.990.840.230.130.370.950.49
VT2 speed (km/h)
Pre0.270.260.230.090.580.420.72
Post0.660.590.090.330.100.910.40
MAS (km/h)
Pre0.580.290.450.670.240.290.07
Post0.830.920.150.220.060.90
R2 = coefficient of determination; VT = ventilatory threshold; MAS = maximal aerobic speed; CT = contact time; VO = vertical oscillation; FT = flying time; SL norm = step length normalized; ES = effect size.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Olaya-Cuartero, J.; Cejuela, R. Influence of Biomechanical Parameters on Performance in Elite Triathletes along 29 Weeks of Training. Appl. Sci. 2021, 11, 1050. https://doi.org/10.3390/app11031050

AMA Style

Olaya-Cuartero J, Cejuela R. Influence of Biomechanical Parameters on Performance in Elite Triathletes along 29 Weeks of Training. Applied Sciences. 2021; 11(3):1050. https://doi.org/10.3390/app11031050

Chicago/Turabian Style

Olaya-Cuartero, Javier, and Roberto Cejuela. 2021. "Influence of Biomechanical Parameters on Performance in Elite Triathletes along 29 Weeks of Training" Applied Sciences 11, no. 3: 1050. https://doi.org/10.3390/app11031050

APA Style

Olaya-Cuartero, J., & Cejuela, R. (2021). Influence of Biomechanical Parameters on Performance in Elite Triathletes along 29 Weeks of Training. Applied Sciences, 11(3), 1050. https://doi.org/10.3390/app11031050

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop