The Energy-Aware Multi-UAV Dispatch and Handoff Algorithm for Maximizing the Event Communication Time in Disasters
Abstract
:1. Introduction and Related Work
- 1.
- We first propose the mobile GCS to carry UAVs to the disaster area for recovering broken links. GCS adopts the UAV pool to record information of all UAVs and schedules all events stored in the proposed event queue for efficient multi-UAV dispatching.
- 2.
- Then we propose the energy-aware multi-UAV dispatch algorithm (EAMUD) to dispatch multiple UAVs to the disaster area for building the FANET, by considering the UAV battery charging progress and energy consumption for flying and communication. Further, EAMUD performs the proposed Event-Based Dispatching (EBD) algorithm to check whether communication durations of all dispatched UAVs overlap or not to maximize the event communication time.
- 3.
- For continuing communication of the broken link before the dispatched UAV drains its remaining energy, we propose the UAV handover process of EAMUD such that GCS can dispatch an optimal UAV to hand over the dispatched one. Further, whenever GCS cannot find enough available UAVs in the UAV pool to serve the current sub-event, two exception handling methods, i.e., Drop and Postpone, are proposed in EAMUD to schedule the scarce UAV resources efficiently, which in turn extends the event communication time.
- 4.
- For given events, we propose the linear programming optimization equations to compute the optimal event communication time as the performance benchmark for dispatching UAVs in the ideal scenario.
2. Energy-Aware Multi-UAV Dispatch Algorithm (EAMUD)
2.1. The Two-Layer FANET-VANET Network in Disaster
2.2. The Energy Model of UAV Battery
2.2.1. Recharging of the UAV Battery
2.2.2. Energy Consumption of the UAV Battery
- ■
- Energy consumption for the U2U communication
- ■
- Energy consumption for the U2V communication
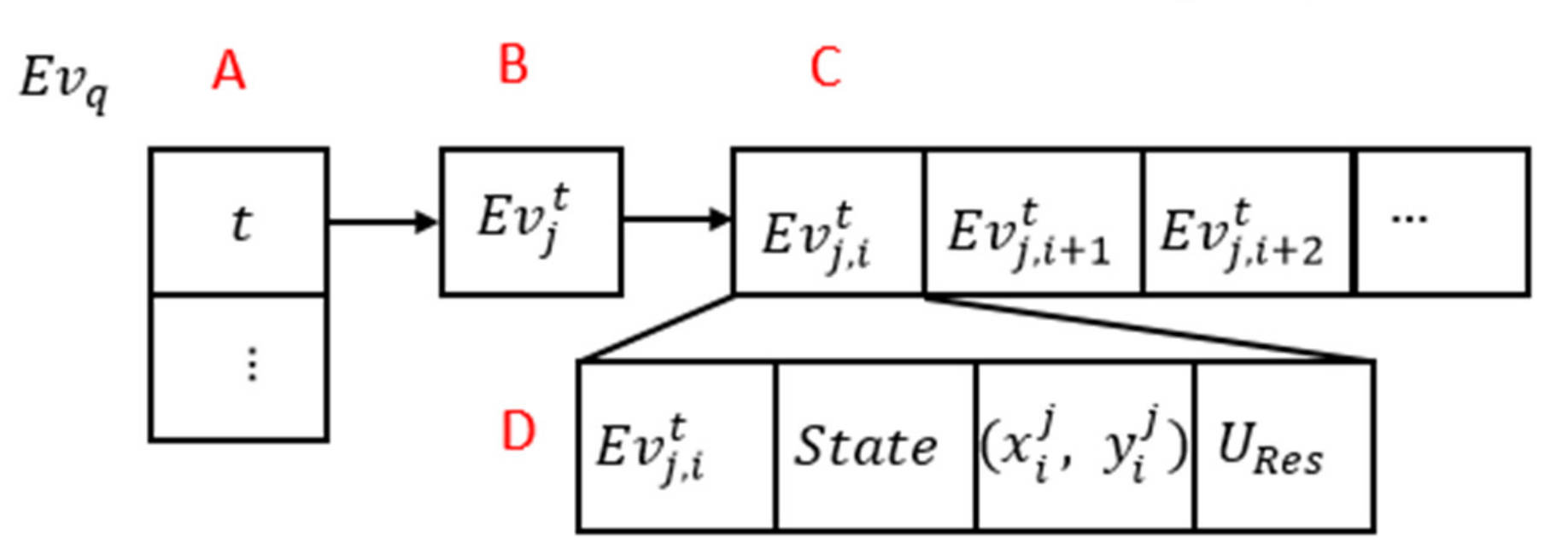
2.3. The Event Queue and UAV Pool of GCS
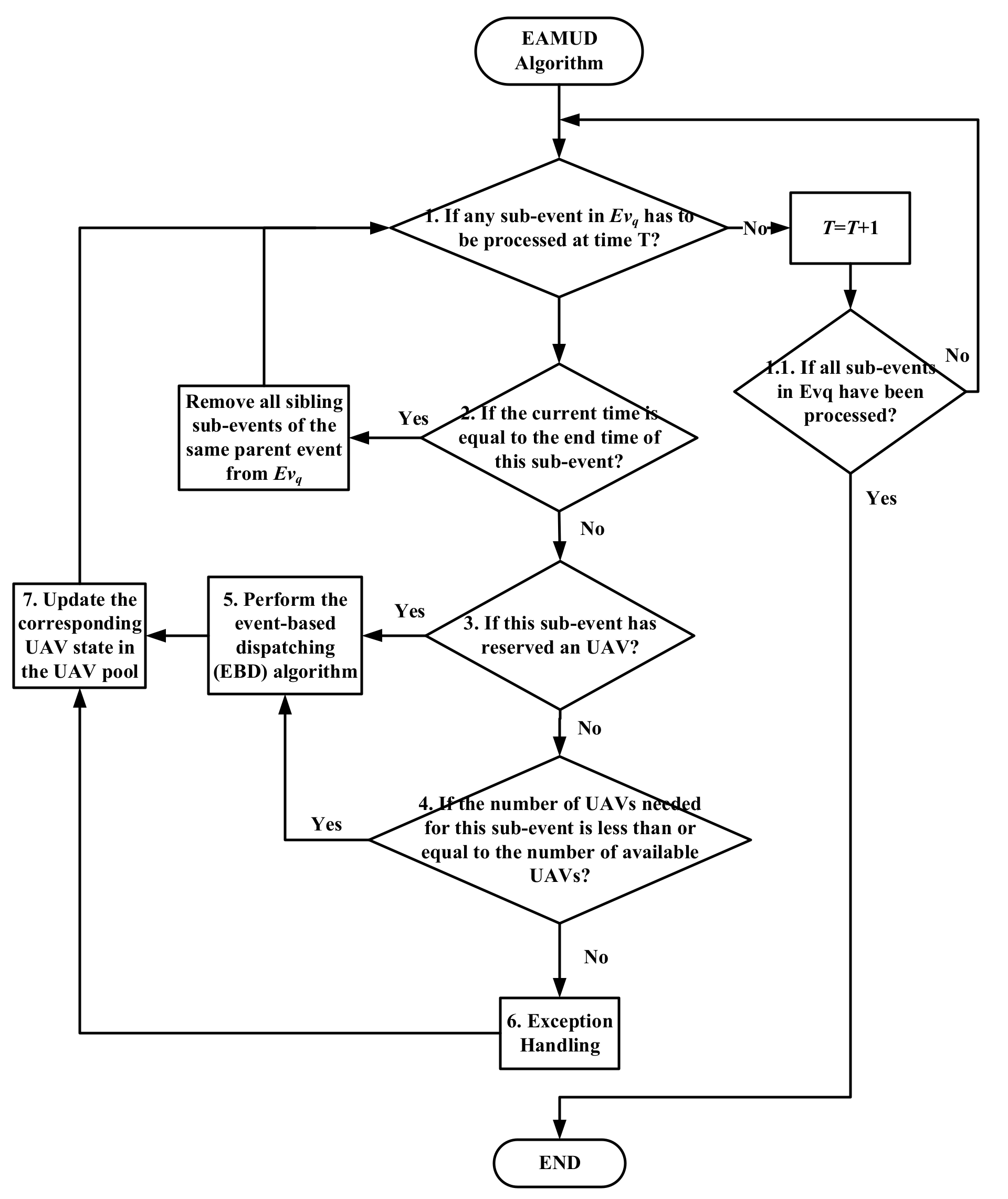
2.4. Details of the EAMUD Algorithm
- 1.
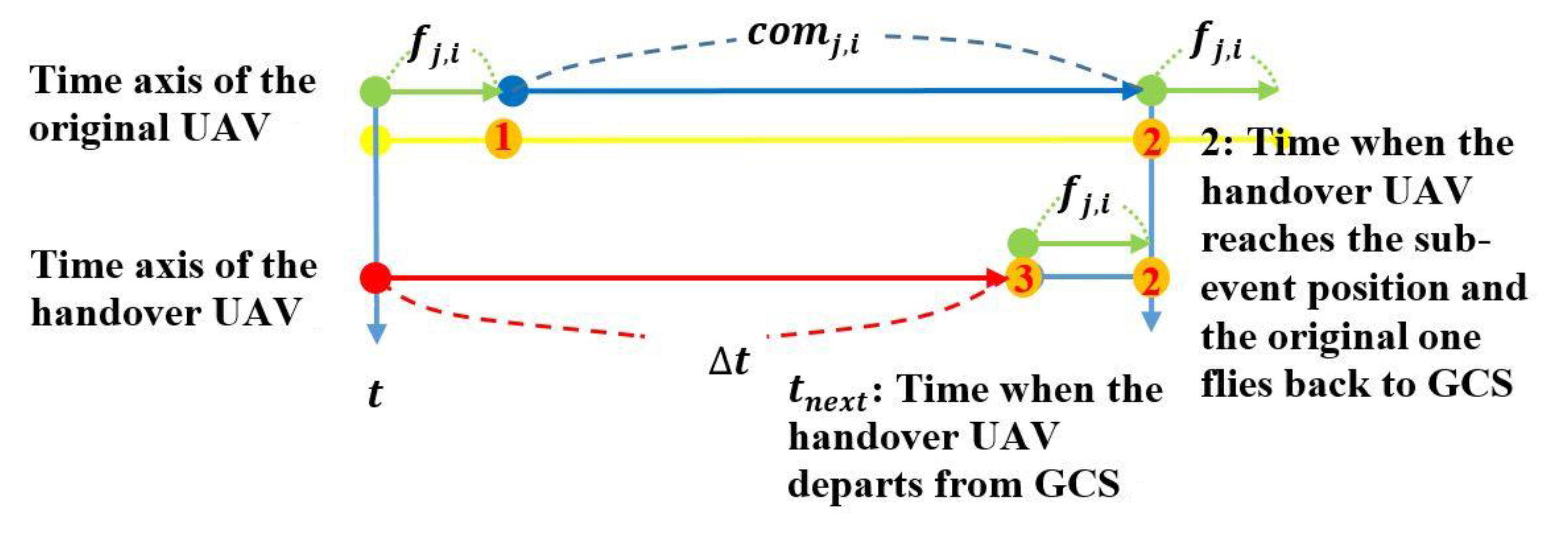
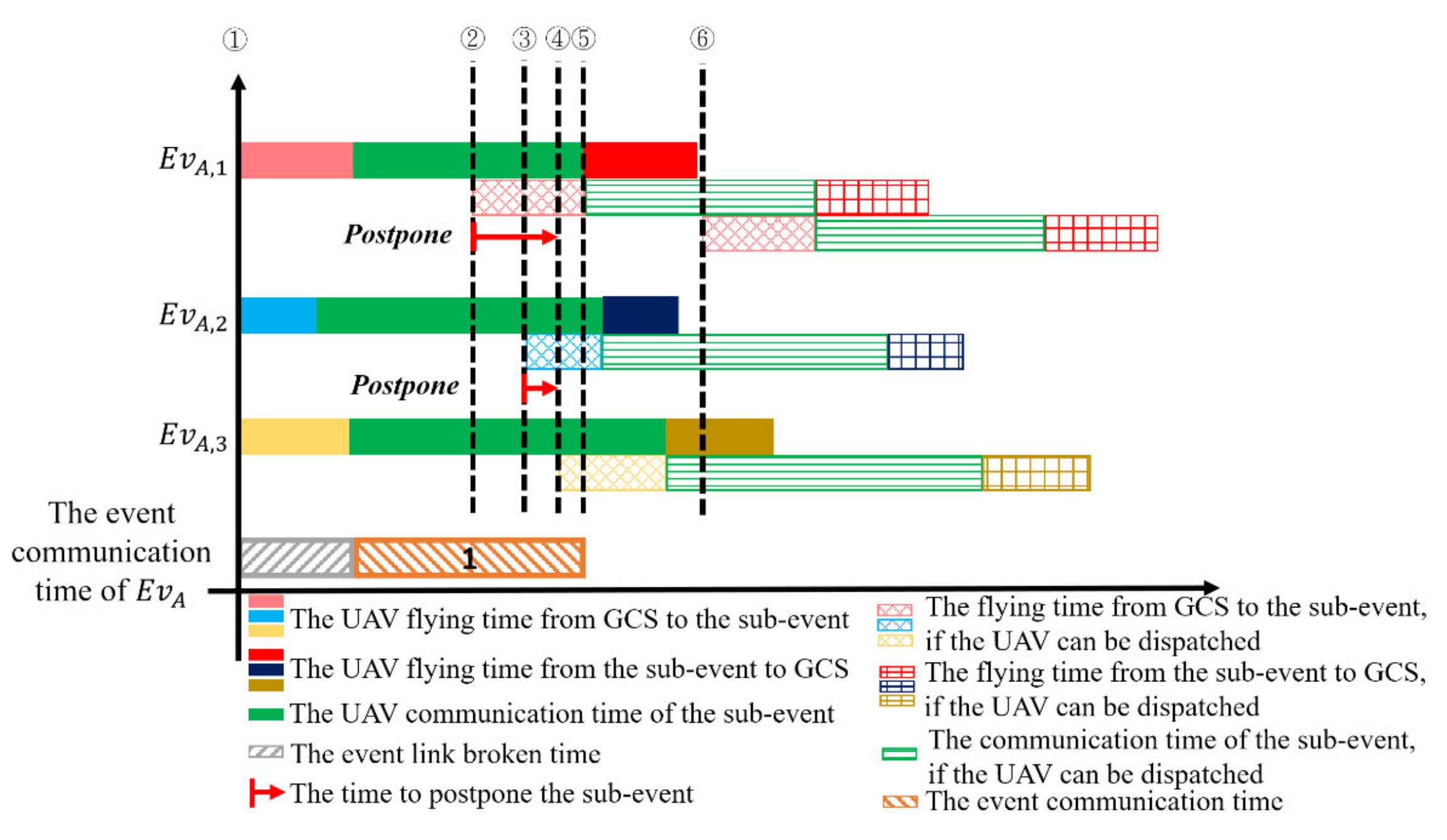
- If this sub-event is not the last sibling one of its parent event, the GCS will postpone it to the processing time of next sub-event, which has not been checked, of the same parent event:As shown in Figure 4, has three sub-events , and . According to Equation (8), the GCS calculates the handover interval, i.e., , of the original dispatched UAV for and knows it has to dispatch a handover UAV to replace the energy-drained one at time 2. For maximizing the event communication time of the whole event, the EAMUD algorithm has to check whether the GCS could dispatch UAVs for all other sub-events, i.e., and , during time 2 to time 6, which indicates the time for the GCS to dispatch the next handover UAV for replacing the preceding dispatched one at time 2. If the GCS is not able to dispatch a handover UAV at the processing time of , i.e., time 3, which will introduce a communication break for this event later and waste the handover UAV dispatched for at time 2. Hence, the EAMUD algorithm postpones these two sub-events, and , to the processing time of next sub-event at time 4 and then performs EAMUD again.
- 2.
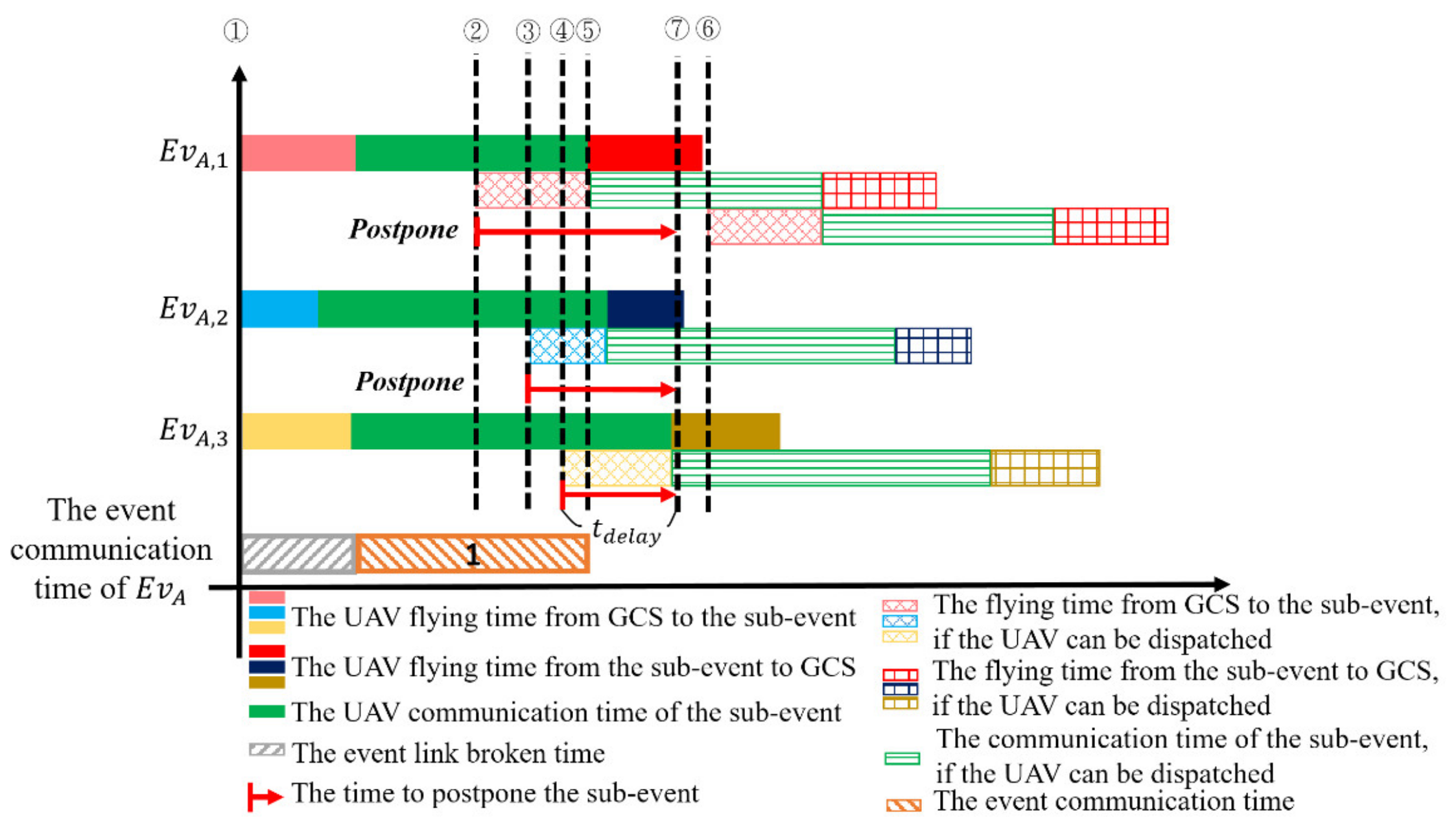
- If this sub-event is the last sibling one of its parent event, the GCS will postpone all sub-events to its processing time plus a delay interval :As the case mentioned above, if the GCS can dispatch a handover UAV at time 3 to but cannot dispatch another handover UAV at time 4 to the last sub-event , this scenario means that both handover UAVs, which are dispatched at time 2 and 3, are wasted. Hence, as shown in Figure 5, the EAMUD algorithm postpones these two sub-events, and , to time 4, i.e., the processing time of the last sub-event , plus . After that, the GCS performs EAMUD again. All sub-events are first sorted according to their Euclidean distance to the GCS. Then by averaging the flying time difference of any two adjacent sub-events of an event as follows:where is the average flying speed of the UAV, is the Euclidean distance between the GCS and the location of the i-th sub-event of event and is the sub-event number of , the value of is calculated accordingly.
- Step 1.
- EAMUD first checks if there is any sub-event in has to be processed at time T. If yes, EAMUD executes Step 2. Otherwise, the current time will advance to to execute Step 1.1.
- Step 1.1
- If there is any sub-event in has to be processed, EAMUD goes to Step 1. Otherwise, EAMUD stops its execution because it has processed all sub-events in .
- Step 2.
- EAMUD checks if the current time is equal to the end time of this sub-event. If yes, which means the parent event of this sub-event has finished, all sibling sub-events of the same parent event have to be removed from . Otherwise, EAMUD goes to Step 3.
- Step 3.
- EAMUD checks whether this sub-event has reserved a UAV. If no, it goes to Step 4. Otherwise, it executes the algorithm in Step 5 to check UAV dispatching, based on of this sub-event.
- Step 4.
- If the number of UAVs needed for this sub-event is less than or equal to the number of UAVs which states are Available in the UAV Pool, EAMUD will dispatch this number of Available UAVs from the UAV pool for this sub-event, with the highest battery powers first criterion. After that, EAMUD goes to Step 5. If the number of UAVs needed for this sub-event is higher than the number of UAVs which states are Available in the UAV Pool, EAMUD must handle this exception by jumping to Step 6.
- Step 5.
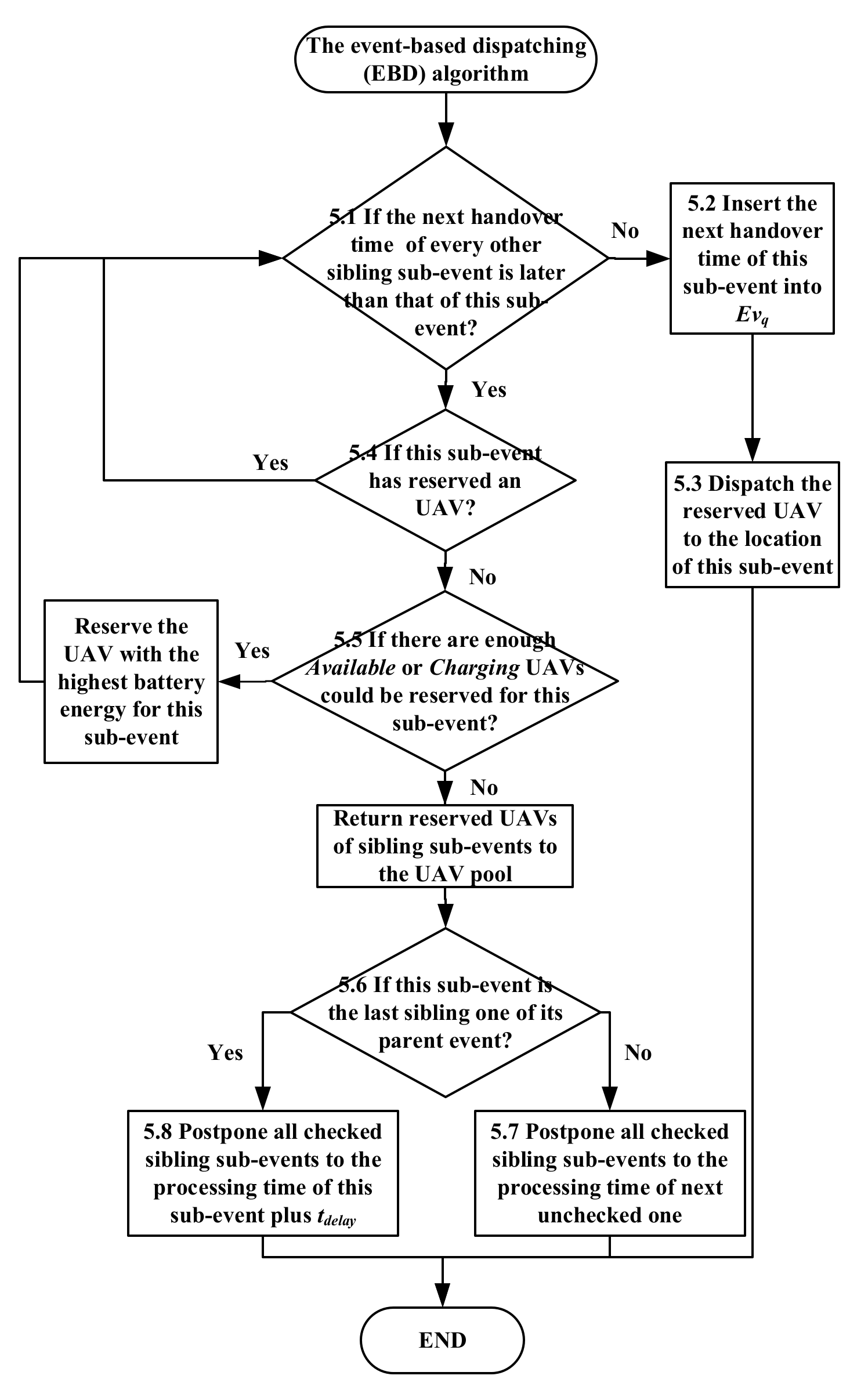
- At this step, EAMUD performs the event-based dispatching (EBD) algorithm to check whether communication durations of UAVs already dispatched for all other sibling sub-events could overlap with the communication duration of the UAV dispatched for this sub-event. If yes, the communication link failure of this event has been recovered during the overlap duration, which raises the event communication time. The flow of the EBD algorithm is shown in Figure 7 and its details are explained as follows:
- Step 5.1
- If the next handover time of every other sibling sub-event is later than that of this sub-event, which means that each sub-event has reserved its handover UAV at its corresponding handover time , EBD goes to Step 5.2. Otherwise, it performs Step 5.4.
- Step 5.2
- Insert the next handover time of this sub-event into and goes to Step 5.3.
- Step 5.3
- Dispatch the reserved UAV to the location of this sub-event for continuing the event communication. At this time, the EBD algorithm has completed its checking process and goes back to Step 7 of EAMUD.
- Step 5.4
- If this sub-event has not reserved a UAV, this EBD algorithm goes to Step 5.5. Otherwise, it goes back to Step 5.1.
- Step 5.5
- According to status of all UAVs in the UAV pool of the GCS, EBD can decide if there are enough Available or Charging UAVs could be reserved for this sub-event. If yes, the GCS will reserve the UAV having the highest battery energy for this sub-event and this algorithm goes back to Step 5.1. If the GCS fails to reserve any UAV for this sub-event, it will cancel UAV reservations of all sub-events which have been checked in Step 5, return these reserved UAVs to the UAV pool and go to Step 5.6.
- Step 5.6
- If this sub-event is the last sibling one of its parent event, EBD goes to Step 5.8. Otherwise, it goes to Step 5.7.
- Step 5.7
- Because this sub-event is not the last sibling one of its parent event, the GCS will postpone all checked sub-events to the processing time of next sibling sub-event, which has not been checked by this algorithm, as mentioned in case 1 above. EBD then goes to Step 7.
- Step 5.8
- Because this sub-event is the last sibling one of its parent event, the GCS will postpone all sibling sub-events to its processing time plus a delay interval . EBD then goes to Step 7.
- Step 6.
- Two exception handling methods are proposed here.
- The Drop method:
- a.
- Remove this sub-event from to stop dispatching the handover UAV for this sub-event.
- b.
- For maintaining the link communication of an event, each sub-event of this event must be served by a dispatched UAV. Since this sub-event has been removed from , all sibling sub-events must be removed from to avoid wasting UAV energy.
- The Postpone method:
- a.
- Assume the processing time of this sub-event i is . This method is to postpone its processing time to and modifies its information in .
- b.
- Each sibling sub-event with its processing time earlier than is postponed to . All corresponding information in are updated accordingly.
- Step 7.
- According to results of Step 5 and Step 6, GCS updates the corresponding UAV state in the UAV pool as Available, Charging, Reserved, or Dispatched, respectively. Then, the current time will advance to and EAMUD continues to check other sub-events in by going back to Step 1.
3. Linear Programming Formulation for Maximizing the Event Communication Time in the Ideal Scenario
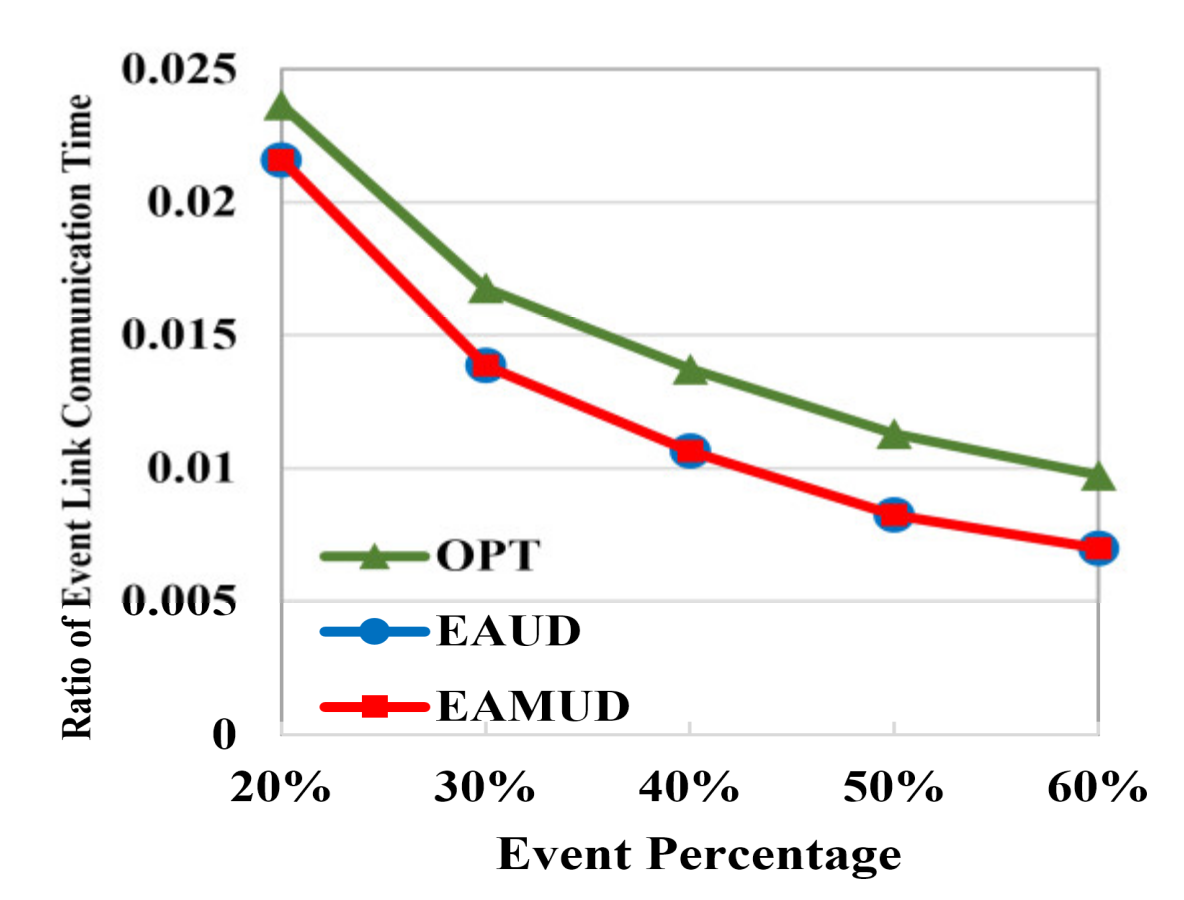
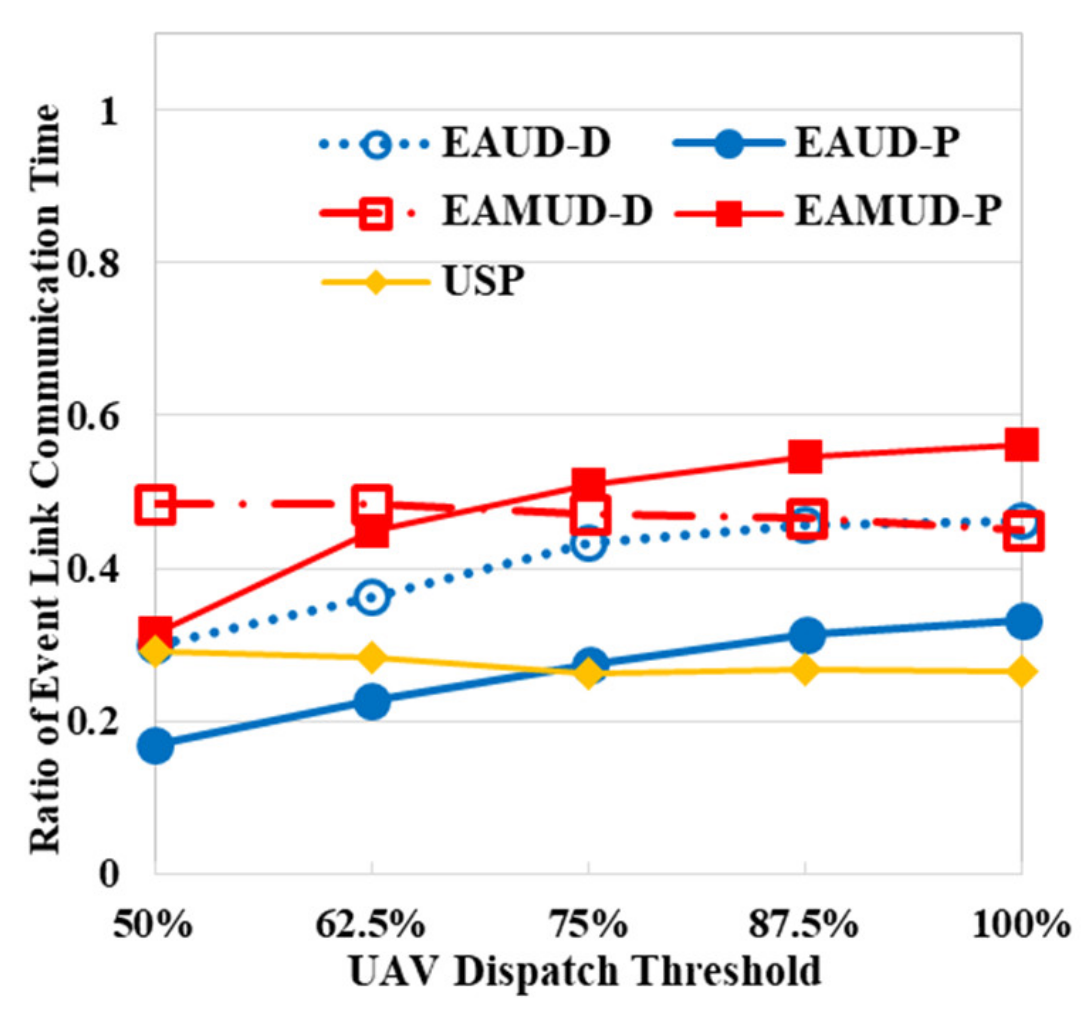
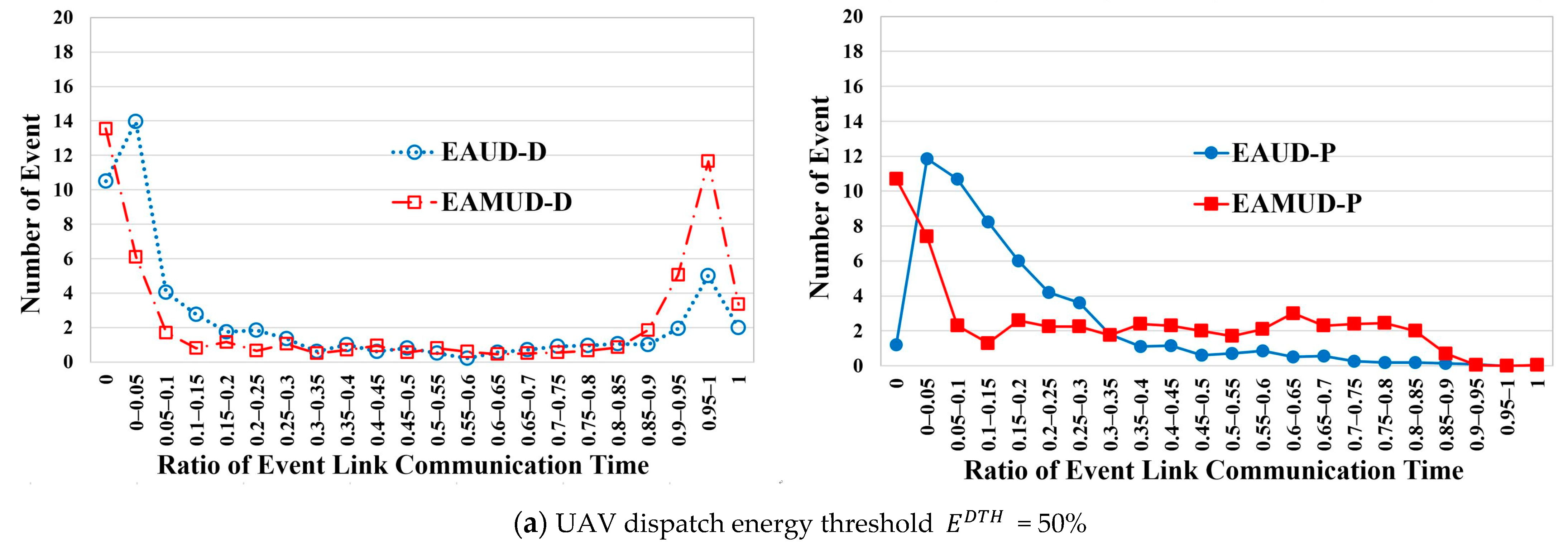
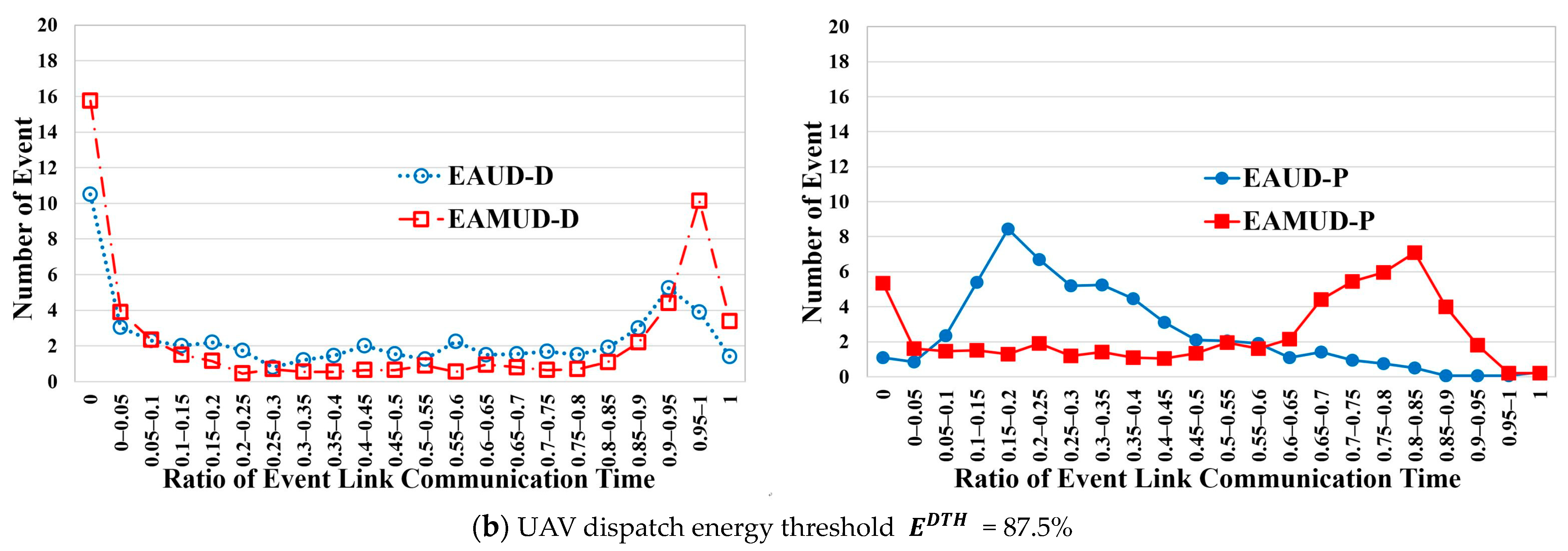
4. Performance Evaluation
4.1. Analytical Results of the Linear Programming Equations in the Ideal Scenario
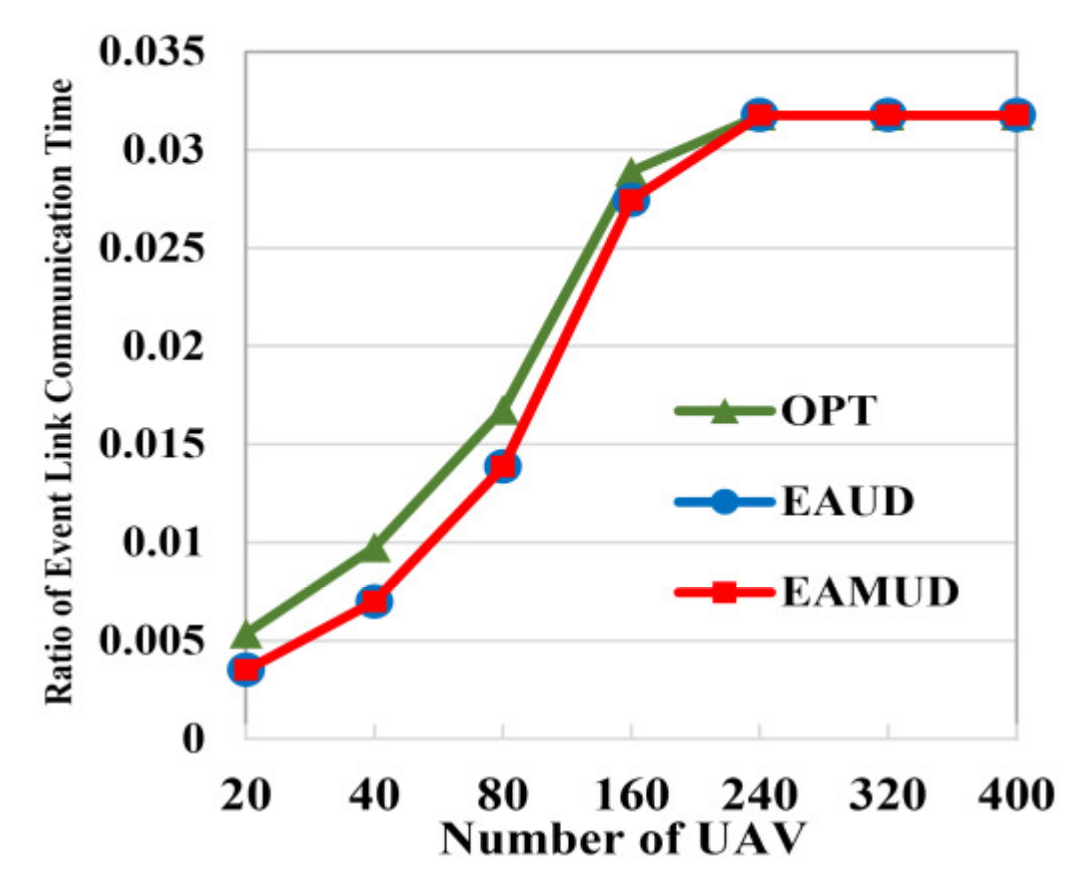
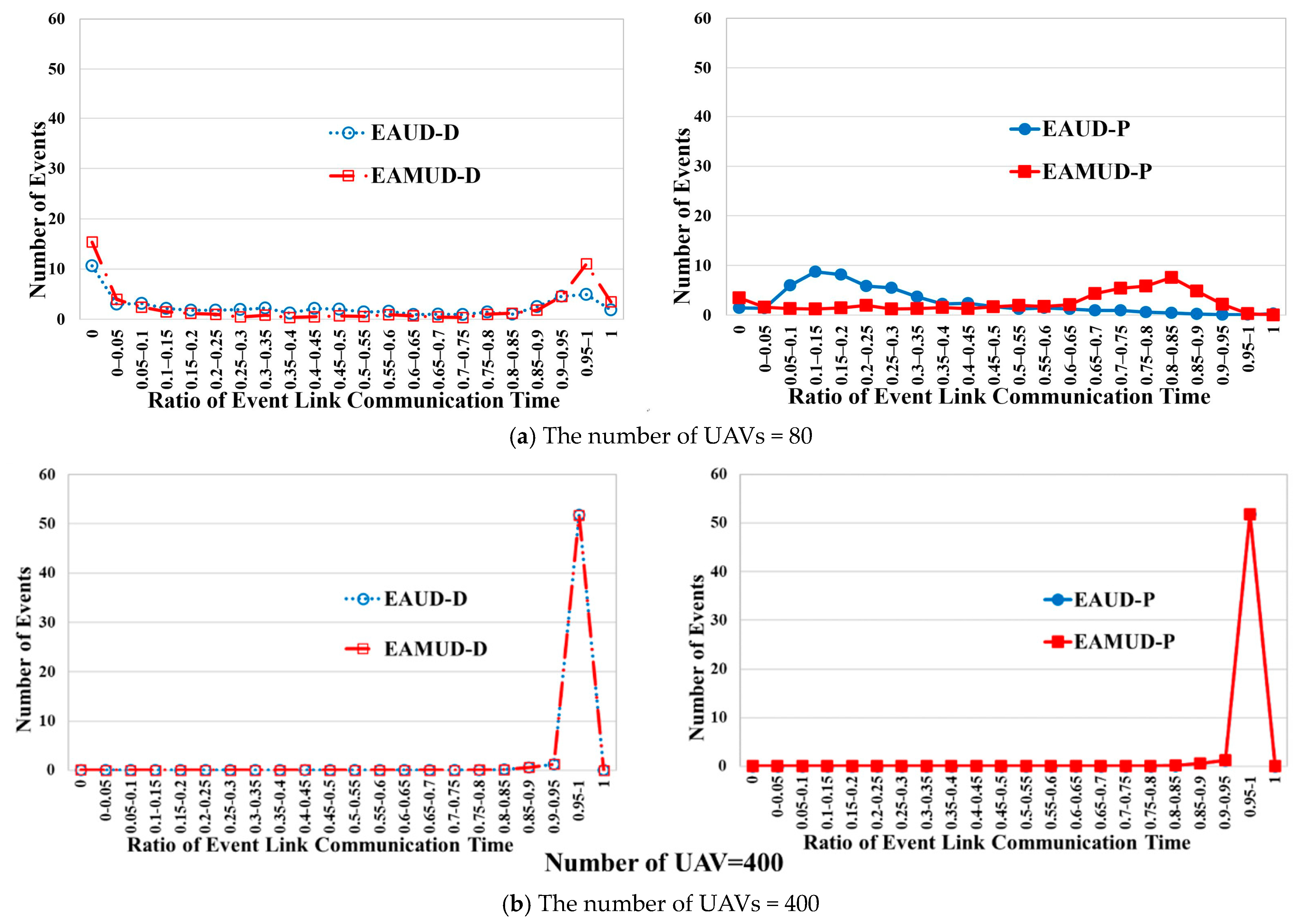
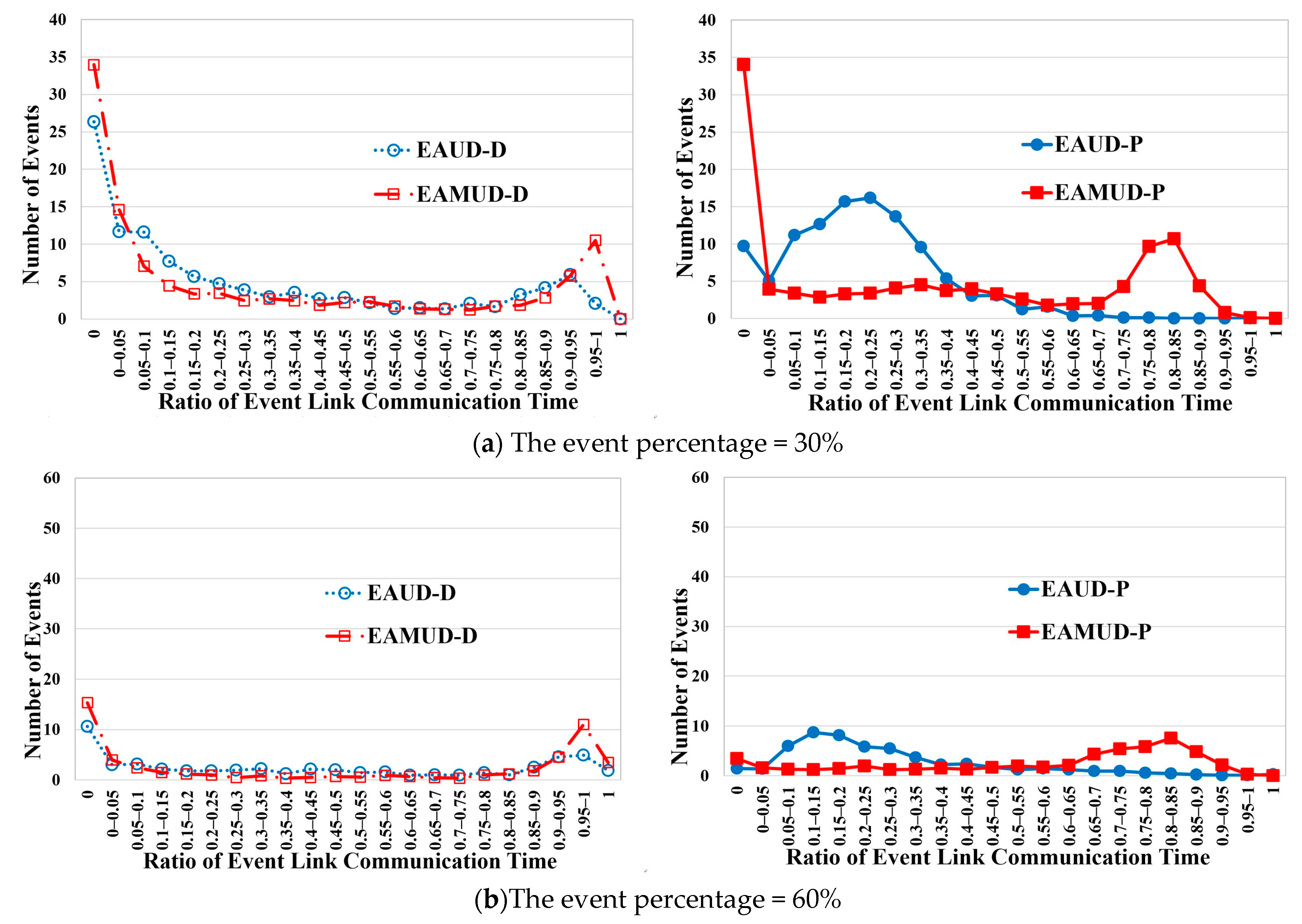
4.2. Performance Results in the Real Scenario
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| A2A | Air-to-air |
| A2G | Air-to-ground |
| EAMUD | energy-aware multi-UAV dispatch algorithm |
| EAMUD-D | EAMUD with the Drop method |
| EAMUD-P | EAMUD with the Postpone method |
| EAUD-D | EAUD with the Drop method |
| EAUD-P | EAUD with the Postpone method |
| EBD | Event-Based Dispatching |
| Event queue | |
| FANET | Flying Ad hoc Network |
| G2A | Ground-to-air |
| G2G | Ground-to-ground |
| GCS | Ground control station |
| LIP | Linear Integer Problem |
| LoS | Line-of-sight |
| MILP | Mixed integer linear programming |
| NLoS | Non-line-of-sight |
| SNR | Signal-to-noise ratio |
| U2U | UAV-to-UAV |
| U2V | UAV-to-Vehicle |
| UAS | Unmanned Aerial System |
| UAV | unmanned aerial vehicle |
| VANET | Vehicular ad hoc network |
References
- Sahingoz, O.K. Networking models in flying ad-hoc networks (FANETs): Concepts and challenges. J. Intell. Robot. Syst. 2014, 74, 513–527. [Google Scholar] [CrossRef]
- Menouar, H.; Guvenc, I.; Akkaya, K.; Uluagac, A.S.; Kadri, A.; Tuncer, A. UAV-enabled intelligent transportation systems for the smart city: Applications and challenges. IEEE Commun. Mag. 2017, 55, 22–28. [Google Scholar] [CrossRef]
- Aasen, H. UAV spectroscopy: Current sensors, processing techniques and theoretical concepts for data interpretation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8809–8812. [Google Scholar]
- Rosner, D.; Trifu, C.; Tranca, C.; Vasilescu, I.; Stancu, F. Magnetic field sensor for UAV power line acquisition and tracking. In Proceedings of the 17th RoEduNet Conference: Networking in Education and Research, Cluj-Napoca, Romania, 6–8 September 2018; pp. 1–5. [Google Scholar]
- Zhao, H.; Wang, H.; Wu, W.; Wei, J. Deployment algorithms for UAV airborne networks toward on-demand coverage. IEEE J. Sel. Areas Commun. 2018, 36, 2015–2031. [Google Scholar] [CrossRef]
- Sharma, V.; Srinivasan, K.; Chao, H.-C.; Hua, K.-L.; Cheng, W.-H. Intelligent deployment of UAVs in 5G heterogeneous communication environment for improved coverage. J. Netw. Comput. Appl. 2017, 85, 94–105. [Google Scholar] [CrossRef]
- Qureshi, K.N.; Abdullah, A.H.; Lloret, J.; Altameem, A. Road-aware routing strategies for vehicular ad hoc networks: Characteristics and comparisons. Int. J. Distrib. Sens. Netw. 2016, 16, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Hajlaoui, R.; Guyennet, H.; Moulahi, T. A survey on heuristic-based routing methods in vehicular ad-hoc network: Technical challenges and future trends. IEEE Sens. J. 2016, 16, 6782–6792. [Google Scholar] [CrossRef]
- Husain, A.; Sharma, S. Performance evaluation of location-based geocast routing using directed flooding rectangular forwarding zone in city VANET. Int. J. Eng. Technol. Innov. 2015, 5, 264–278. [Google Scholar]
- Huang, C.-F.; Jhang, J.-H. Efficient RSU selection approaches for load balancing in vehicular ad hoc networks. Adv. Technol. Innov. 2020, 5, 56–63. [Google Scholar] [CrossRef]
- Zhou, Y.; Cheng, N.; Lu, N. Multi-UAV-aided networks: Aerial-ground cooperative vehicular networking architecture. IEEE Veh. Technol. Mag. 2015, 10, 36–44. [Google Scholar] [CrossRef]
- Wang, X.; Fu, L.; Zhang, Y.; Gan, X.; Wang, X. VDNet: An infrastructure-less UAV-assisted sparse VANET system with vehicle location prediction. Wirel. Commun. Mob. Comput. 2016, 16, 2991–3003. [Google Scholar] [CrossRef]
- Oubbati, O.S. CRUV: Connectivity-based traffic density aware routing using UAV for VANETs. In Proceedings of the International Conference on Connected Vehicles and Expo (ICCVE), Shenzhen, China, 19–23 October 2015; pp. 68–73. [Google Scholar]
- Oubbati, O.S.; Lakas, A.; Lagraa, N. UVAR: An Intersection UAV-assisted VANET Routing Protocol. In Proceedings of the IEEE Wireless Communications and Networking Conference, Doha, Qatar, 3–6 April 2016; pp. 1–6. [Google Scholar]
- Yim, J.; Park, H.; Kwon, E.; Kim, S.; Lee, Y.-T. Low-power image stitching management for reducing power consumption of UAVs for disaster management system. In Proceedings of the IEEE International Conference on Consumer Electronics, Las Vegas, NV, USA, 12–14 January 2018; pp. 1–3. [Google Scholar]
- Ezequiel, C.A.F.; Cua, M.; Libatique, N.C.; Tangonan, G.L.; Alampay, R.; Labuguen, R.T.; Favila, C.M.; Honrado, J.L.E.; Canos, V.; Devaney, C.; et al. UAV aerial imaging applications for post-disaster assessment, environmental management and infrastructure development. In Proceedings of the International Conference on Unmanned Aircraft Systems, Orlando, FL, USA, 27–30 May 2017; pp. 274–283. [Google Scholar]
- Rokhmana, C.A.; Andaru, R. Utilizing UAV-based mapping in post disaster volcano eruption. In Proceedings of the International Annual Engineering Seminar, Yogyakarta, Indonesia, 1–3 August 2016; pp. 202–205. [Google Scholar]
- Erdelj, M.; Natalizio, E. UAV-assisted disaster management: Applications and open issues. In Proceedings of the International Conference on Computing, Networking and Communications, Kauai, HI, USA, 15–18 February 2016; pp. 1–5. [Google Scholar]
- Hayat, S.; Yanmaz, E.; Muzaffar, R. Survey on unmanned aerial vehicle networks for civil applications: A communications viewpoint. IEEE Commun. Surv. Tutor. 2016, 18, 2624–2661. [Google Scholar] [CrossRef]
- Jeong, D.; Park, S.Y.; Lee, H.J. DroneNet: Network reconstruction through sparse connectivity probing using distributed UAVs. In Proceedings of the IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications, Hong Kong, China, 30 August–2 September 2015; pp. 1797–1802. [Google Scholar]
- Erdelj, M.; Natalizio, E.; Chowdhury, K.R. Help from the sky: Leveraging UAVs for disaster management. IEEE Pervasive Comput. 2017, 16, 24–32. [Google Scholar] [CrossRef]
- Ghazzai, H.; Kadri, A.; Ghorbel, M.B.; Menouar, H. Optimal sequential and parallel UAV scheduling for multi-event applications. In Proceedings of the IEEE 87th Vehicular Technology Conference, Porto, Portugal, 3–6 June 2018; pp. 1–6. [Google Scholar]
- Erdelj, M.; Król, M.; Natalizio, E. Wireless sensor networks and multi-UAV systems for natural disaster management. Comput. Netw. 2017, 124, 72–86. [Google Scholar] [CrossRef]
- Palmer, J.; Yuen, N.; Ore, J.-P. On air-to-water radio communication between UAVs and water sensor networks. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5311–5317. [Google Scholar]
- Jia, S.; Zhang, L. Modelling unmanned aerial vehicles base station in ground-to-air cooperative networks. IET Commun. 2017, 11, 1187–1194. [Google Scholar] [CrossRef]
- Erdelj, M.; Saif, O.; Natalizio, E.; Fantoni, I. UAVs that fly forever: Uninterrupted structural inspection through automatic UAV replacement. Ad Hoc Netw. 2017, 94, 101612. [Google Scholar] [CrossRef] [Green Version]
- Dietrich, T.; Andryeyev, O.; Zimmermann, A.; Mitschele-Thiel, A. Towards a unified decentralized swarm management and maintenance coordination based on MAVLink. In Proceedings of the International Conference on Autonomous Robot Systems and Competitions, Bragança, Portugal, 4–6 May 2016; pp. 124–129. [Google Scholar]
- Motlagh, N.H.; Bagaa, M.; Taleb, T. UAV selection for a UAV-based integrative IoT platform. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Eclipse IDE for Java Developers. Available online: https://www.eclipse.org/downloads/packages/release/2020-09/r/eclipse-ide-java-developers (accessed on 31 October 2020).
- Cavalcante, T.R.; Bessa, F.I.V.; Cordeiro, L.C. Planning and evaluation of UAV mission planner for intralogistics problems. In Proceedings of the Brazilian Symposium on Computing Systems Engineering (SBESC), Paraná, Brazil, 7–10 November 2017; pp. 9–16. [Google Scholar]



| Features | Handle Multiple Events and Dispatch Multiple UAVs for an Event | Consider the UAV Charging Progress and Energy Consumption for Flying and Communication | Check whether the Dispatched UAVs Can Maximize the Event Communication Time | Consider the UAV Handover Process and Handle Exceptions | Propose the LP Optimization Equations to Compute the Optimal Event Communication Time | |
|---|---|---|---|---|---|---|
| Research | ||||||
| Ref. [22] | No | Yes | No | No | No | |
| Ref. [26] | No | No | No | No | No | |
| Ref. [27] | No | No | No | No | No | |
| Ref. [28] | No/Yes | No | No | No | No | |
| EAMUD | Yes | Yes | Yes | Yes | Yes | |
| UAV Pool | |||||
|---|---|---|---|---|---|
| UAV_id | State | Sub-ev ID | |||
| Available | 100 | ||||
| Available | 100 | ||||
| Available | 93 | ||||
| Charging | 40 | ||||
| Dispatched | 97 | 3 | |||
| Dispatched | 70.5 | 3 | |||
| Reserved | 45 | ||||
| Item | Value |
|---|---|
| Simulation time | 172,800 s |
| Event duration () | 57,600 s |
| The number of total road segments () | 245 |
| UAV flying speed () | 10 m/s |
| UAV communication range () | 300 m |
| U2U carrier frequency () | 1 GHz |
| U2V carrier frequency () | 5.9 GHz |
| The unit energy consumed on flying () | 115 J/s |
| Charge current () | 3 A |
| Charge current voltage () | 4.2 V |
| SNR threshold () | 2 dB |
| Noise powers of U2V and U2U (, ) | −80 dBm |
| Required transmission powers of U2V and U2U (, ) | 27 dBm |
| UAV dispatch energy threshold () | 50, 62.5, 75, 87.5 (default), 100% |
| Number of UAVs | 20, 40, 80 (default), 160, 240, 320, 400 |
| Event percentage (EP) | 20, 30 (default), 40, 50, 60 % |
| UAV battery capacity () | 251,748 J |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, I.-C.; Liao, C.-S.; Yen, C.-E. The Energy-Aware Multi-UAV Dispatch and Handoff Algorithm for Maximizing the Event Communication Time in Disasters. Appl. Sci. 2021, 11, 1054. https://doi.org/10.3390/app11031054
Chang I-C, Liao C-S, Yen C-E. The Energy-Aware Multi-UAV Dispatch and Handoff Algorithm for Maximizing the Event Communication Time in Disasters. Applied Sciences. 2021; 11(3):1054. https://doi.org/10.3390/app11031054
Chicago/Turabian StyleChang, Ing-Chau, Chi-Sheng Liao, and Chin-En Yen. 2021. "The Energy-Aware Multi-UAV Dispatch and Handoff Algorithm for Maximizing the Event Communication Time in Disasters" Applied Sciences 11, no. 3: 1054. https://doi.org/10.3390/app11031054
APA StyleChang, I.-C., Liao, C.-S., & Yen, C.-E. (2021). The Energy-Aware Multi-UAV Dispatch and Handoff Algorithm for Maximizing the Event Communication Time in Disasters. Applied Sciences, 11(3), 1054. https://doi.org/10.3390/app11031054






