A Closed-Form Solution for the Inverse Kinematics of the 2n-DOF Hyper-Redundant Manipulator Based on General Spherical Joint
Abstract
:1. Introduction
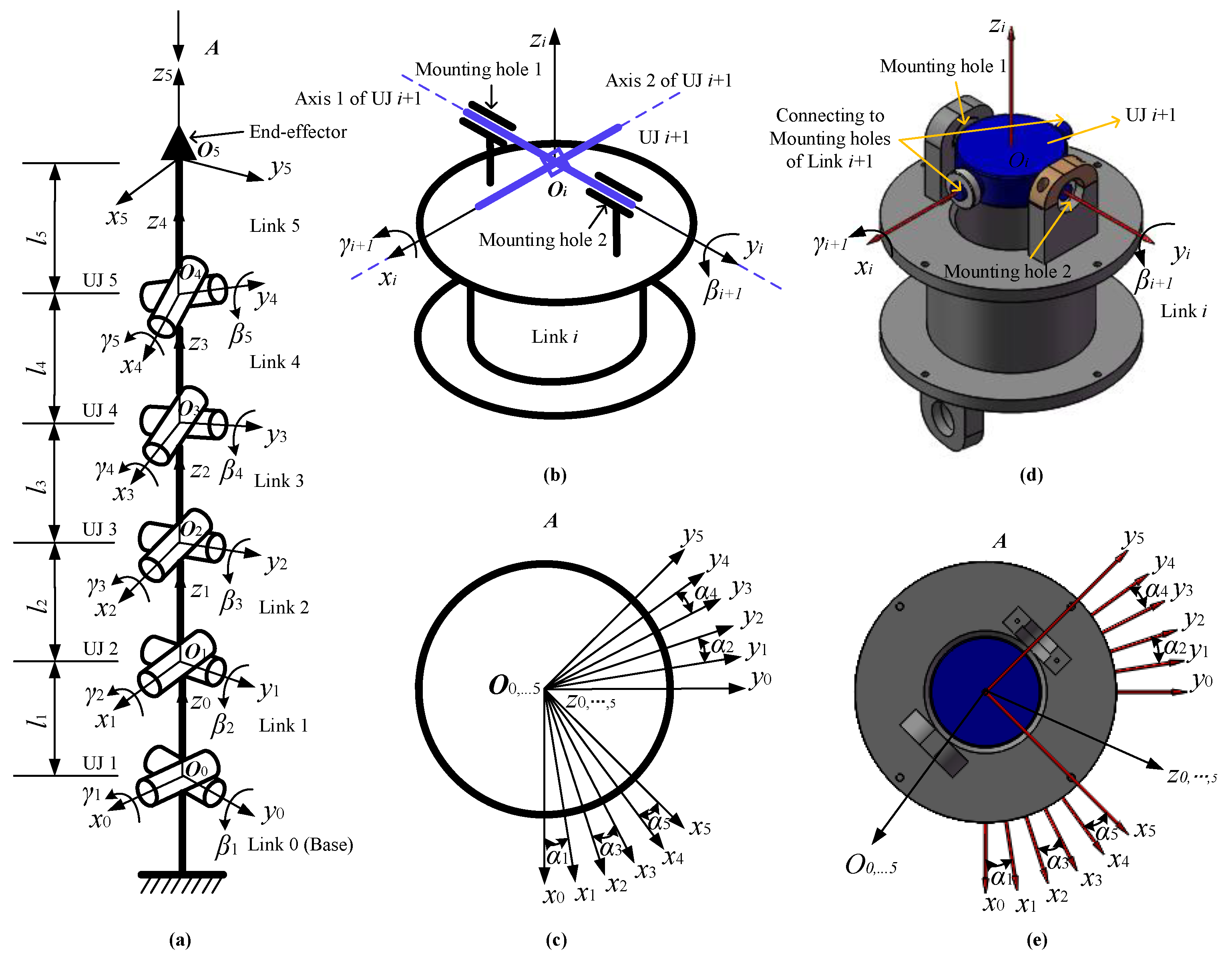
2. Forward Kinematics
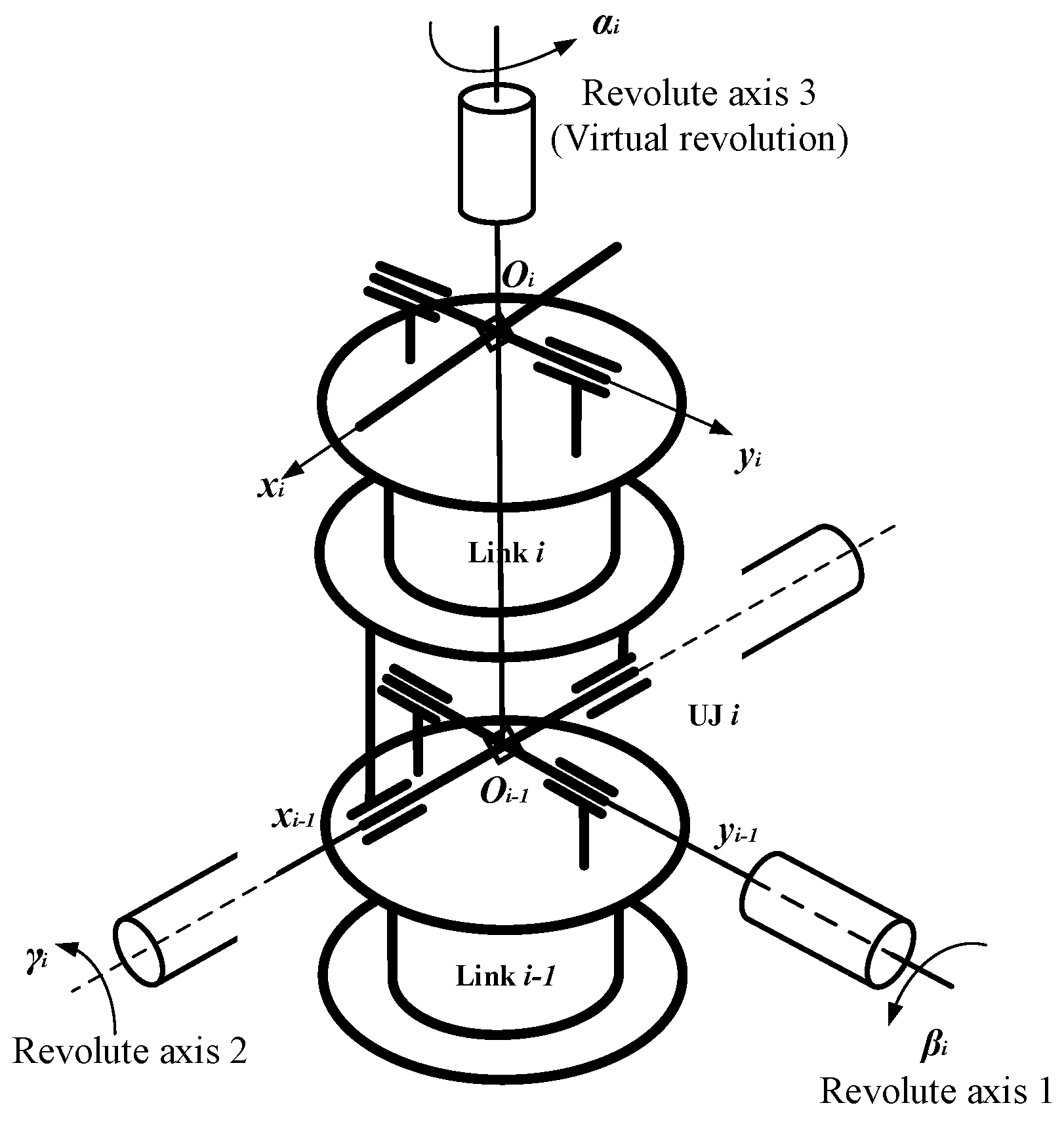
- Locate the origin of Frame at the intersection of the two axes of UJ ;
- Choose axis along the central axis of Link ;
- Choose axis along the common axis (Axis 1 of UJ ) of the two mounting holes (mounting holes 1 and 2) of Link for UJ ;
- Choose axis to complete a right-handed frame. At this time, this axis coincides with the Axis 2 of UJ when the corresponding rotation angle of UJ is equal to zero. When the angle is not equal to zero, the coincidence no longer exists.
- and denote the rotation matrix of the homogeneous transformation matrix and , respectively.
- and denote the position vector of the homogeneous transformation matrix and , respectively.
- and denote the expressions of the rotation matrix and , respectively.
- , , , and , , , denote the expressions of , , , and , , , , respectively.
3. Inverse Kinematics
3.1. General Spherical Joint
3.2. Closed-Form Solution for Single-GSJ Section
3.3. Closed-Form Solution for Multiple-GSJ Section
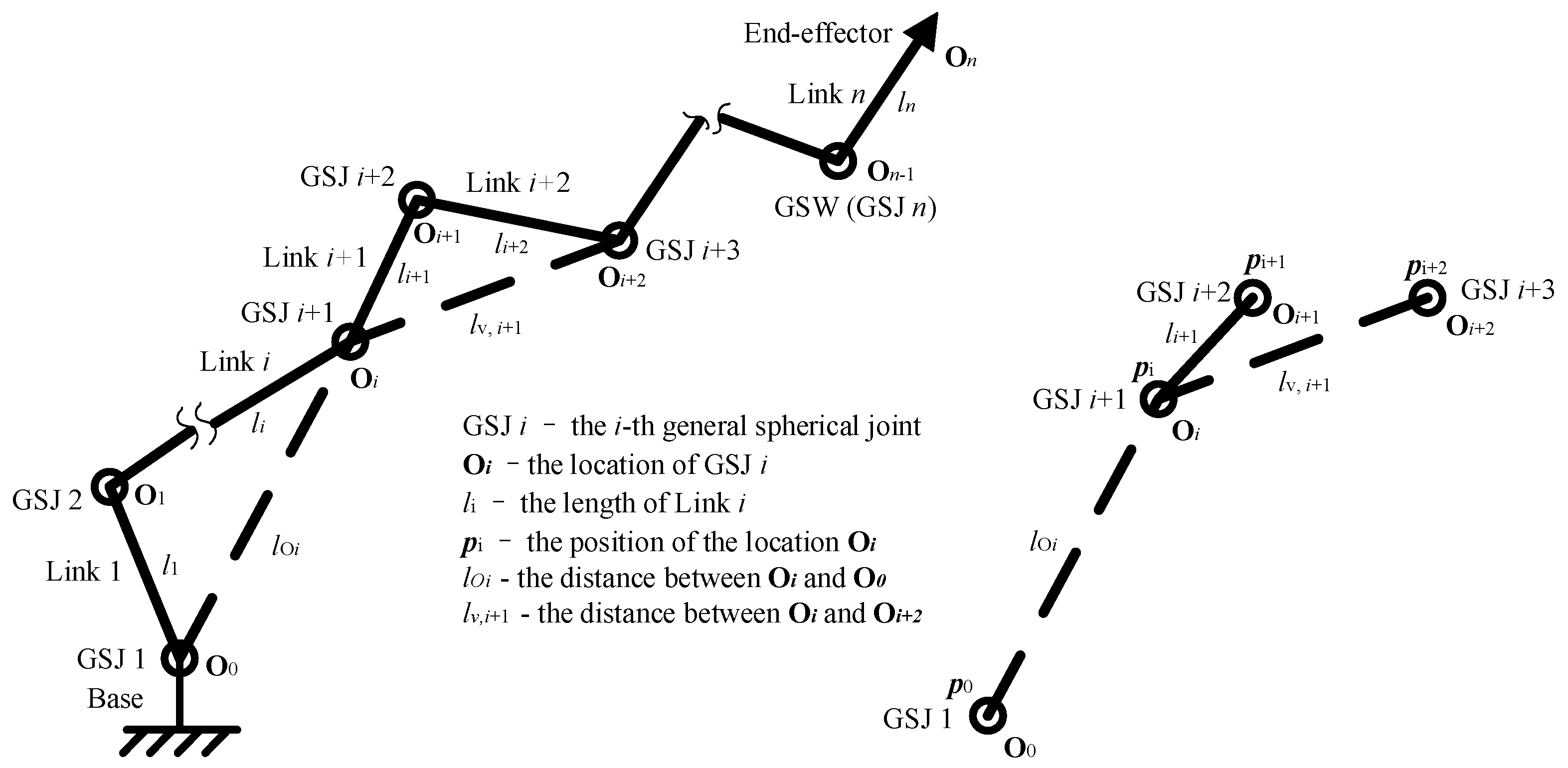
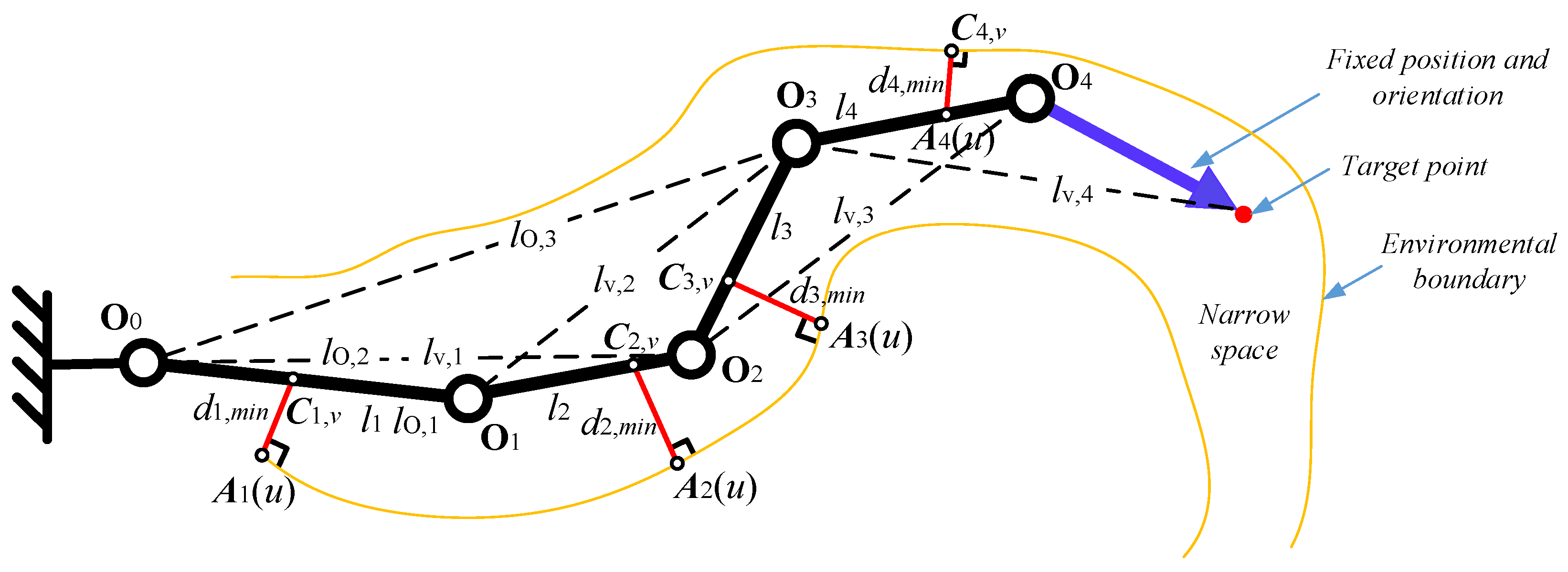
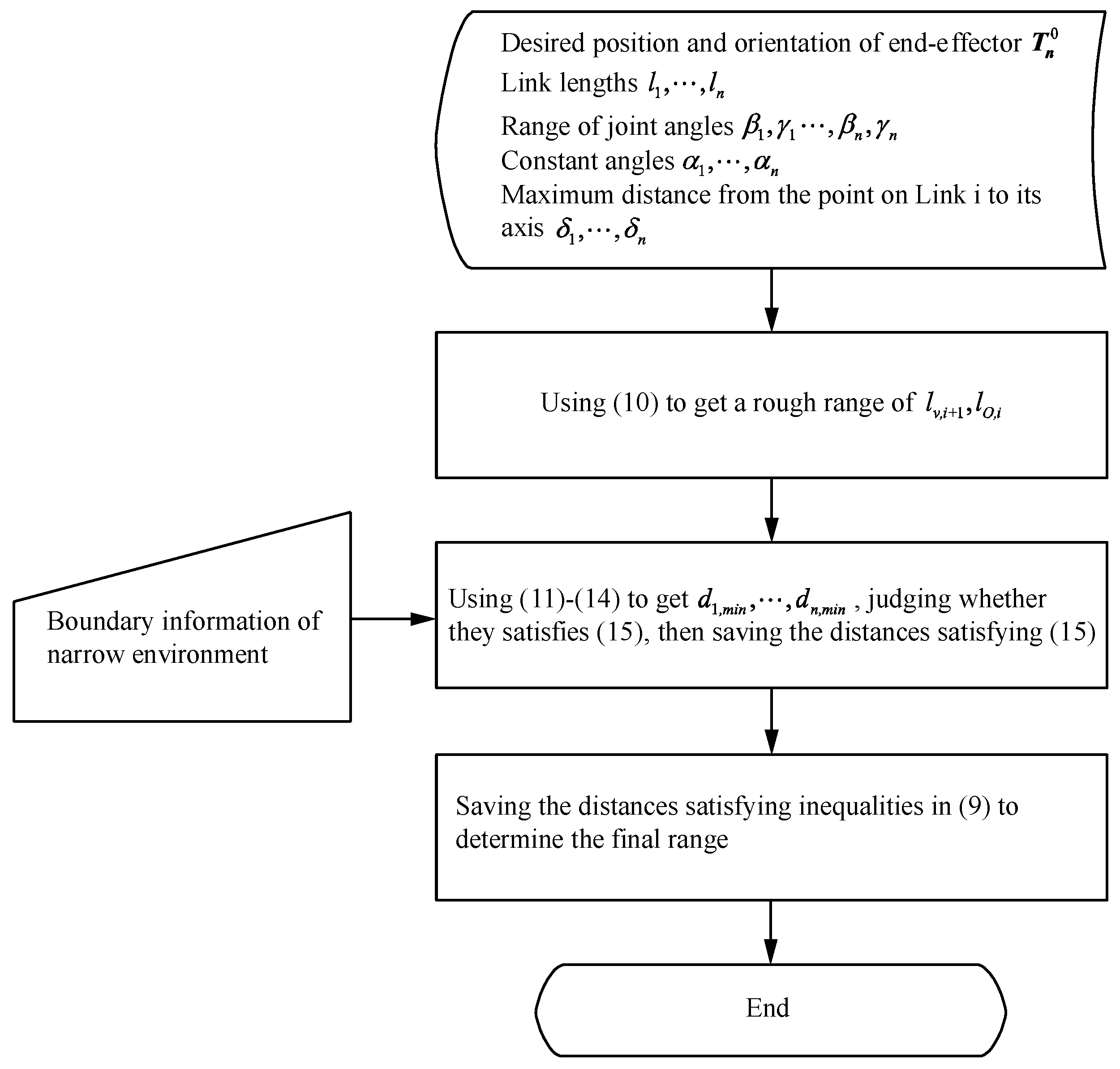
3.3.1. Locations of the GSJs
3.3.2. Determination of and
3.3.3. GSJ Angles for Multiple-GSJ Section
4. Simulation
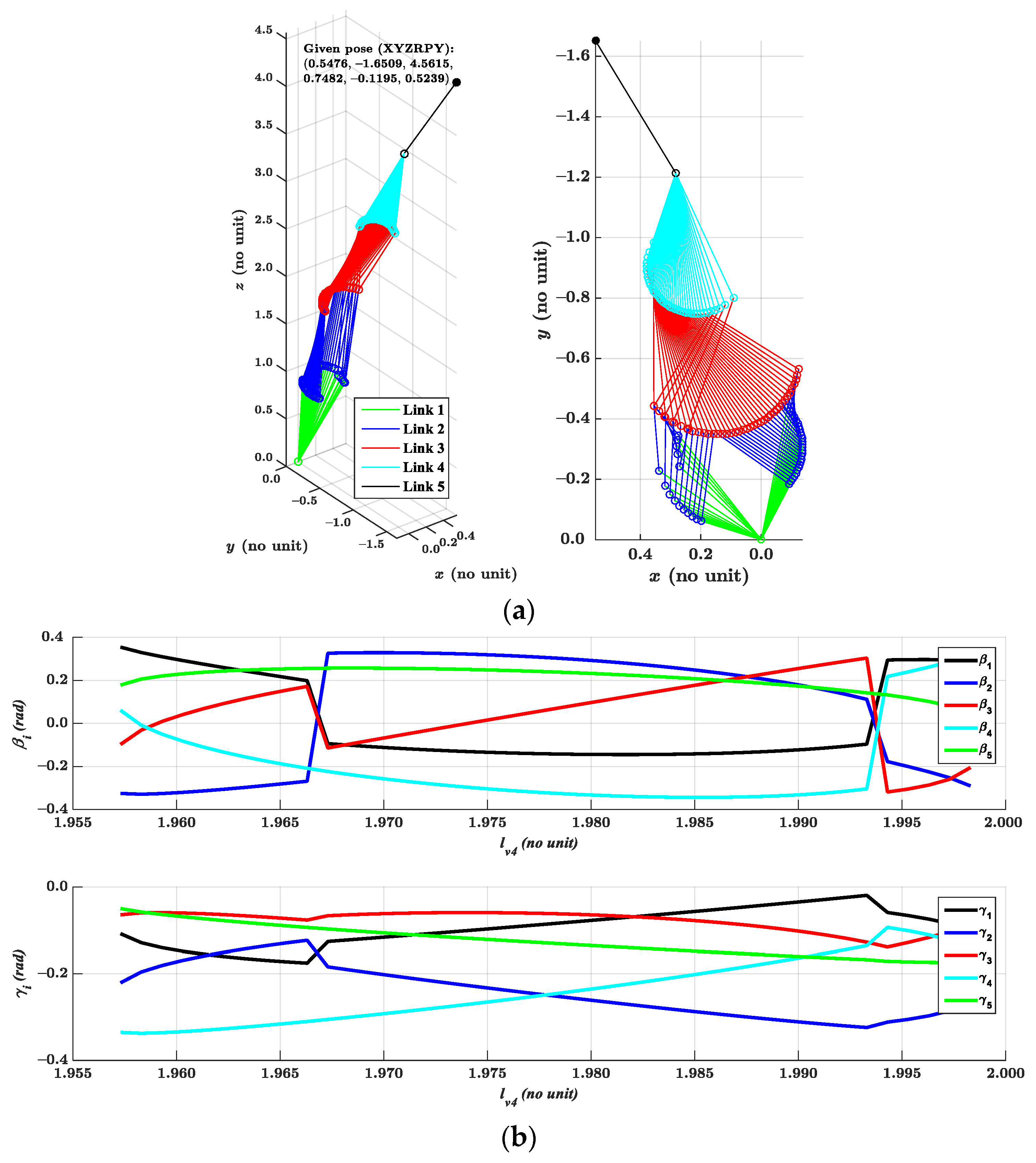
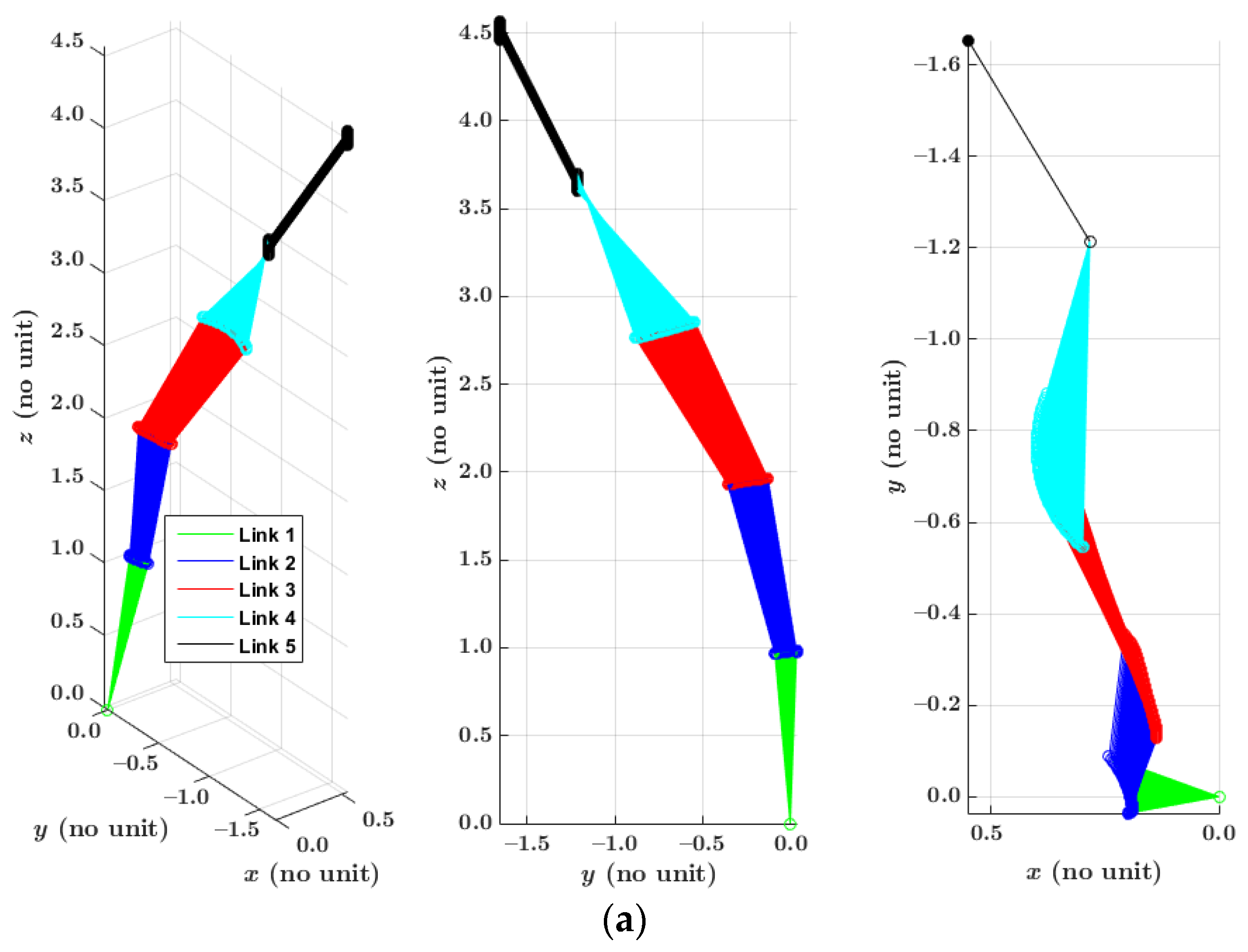
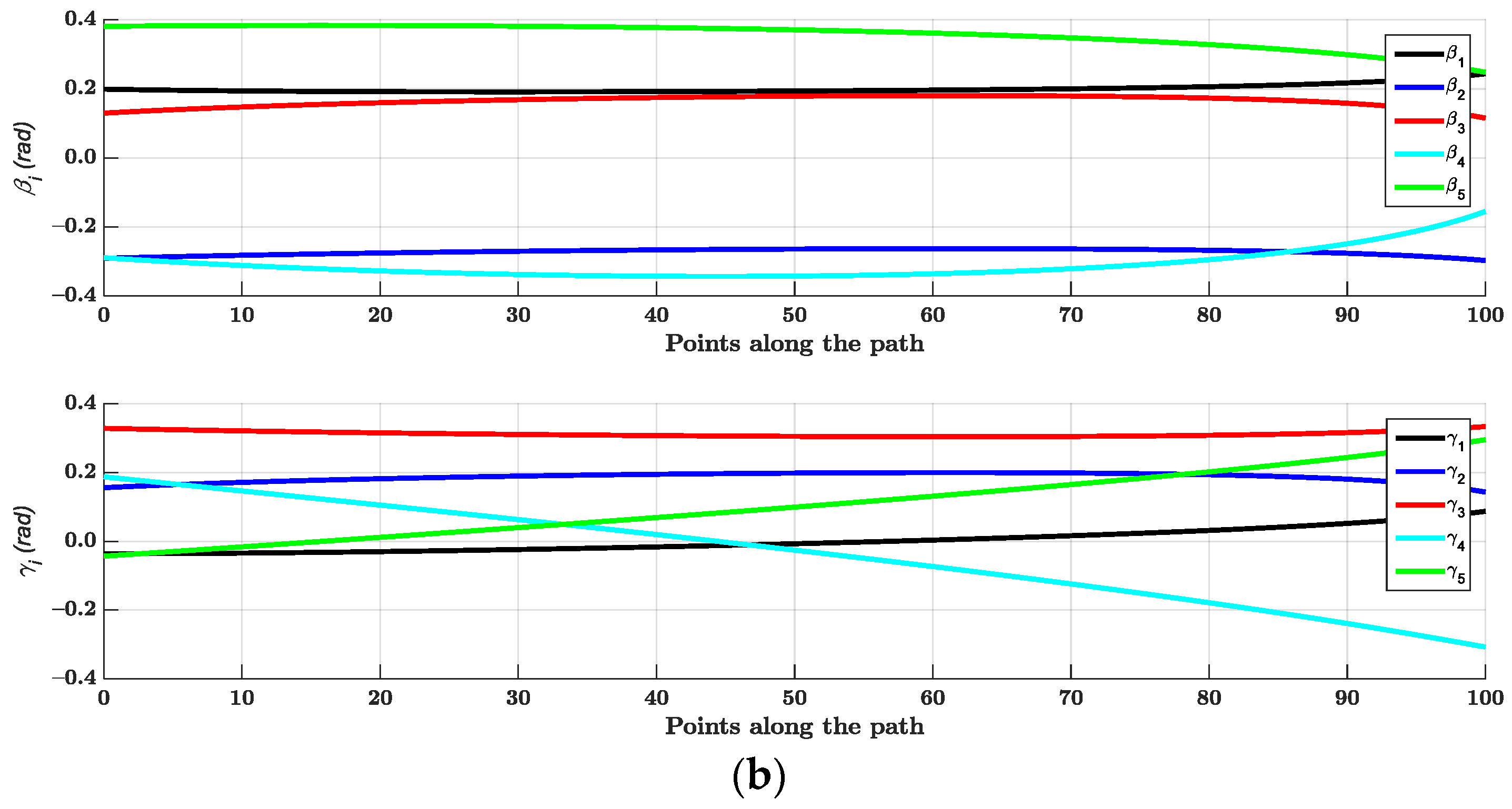
4.1. Solutions for a Random Single Given Pose
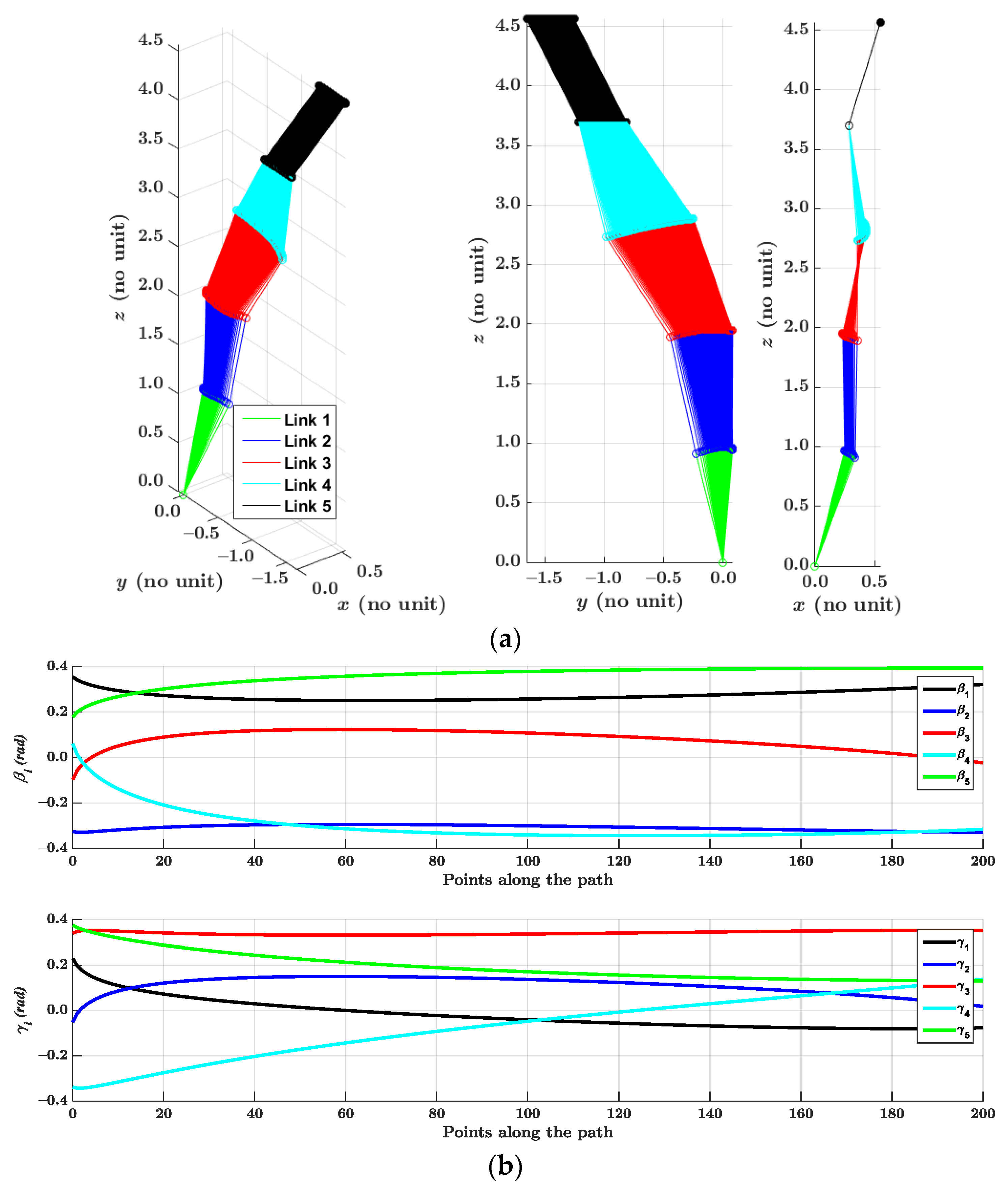
4.2. Solutions for the Straight-Line Paths along the x-axis, y-axis, and z-axis of the Base Frame
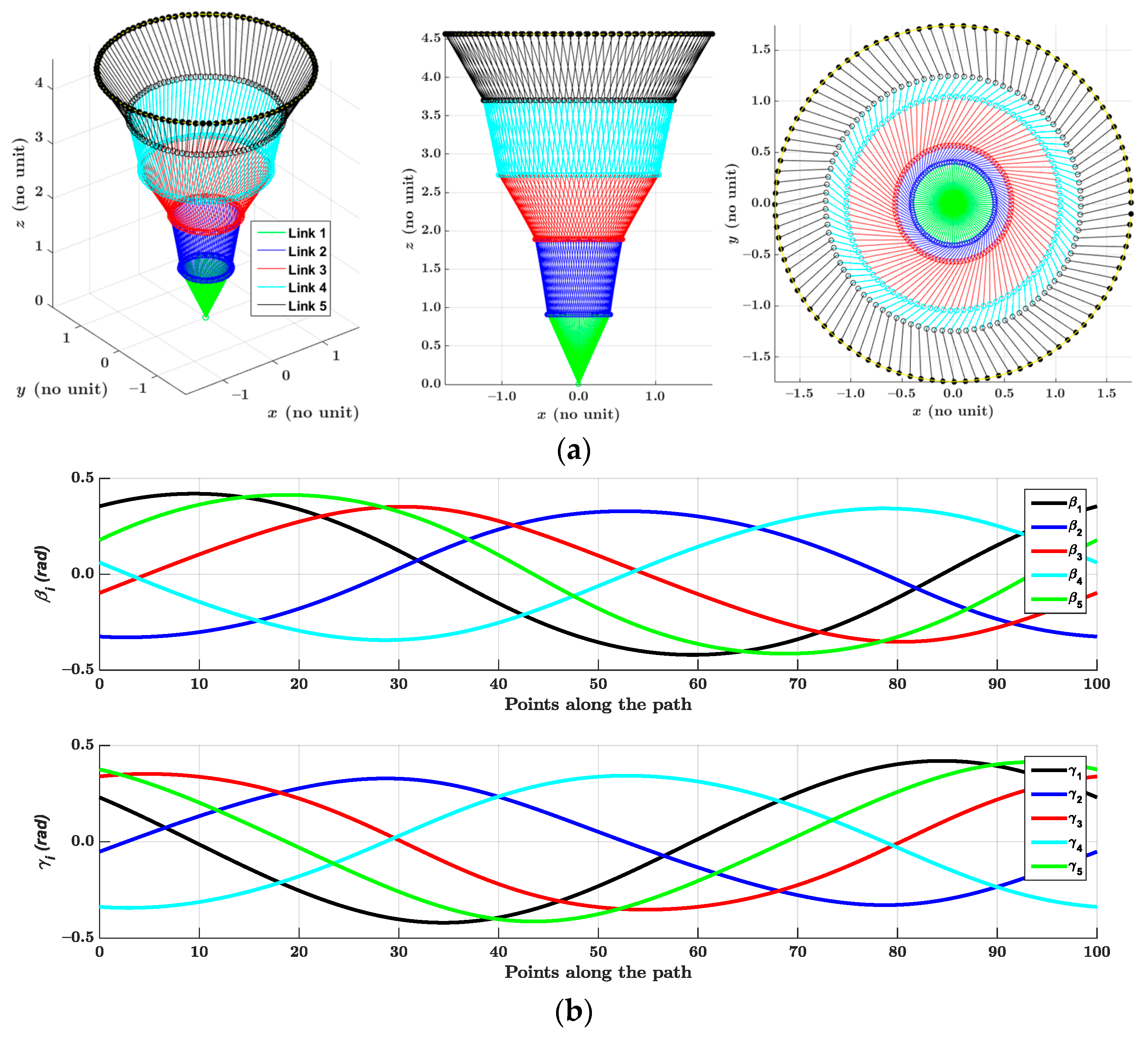
4.3. Solution for a Circle Path
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hussain, R.; Qureshi, A.; Mughal, R.A.; Ijaz, R.; Rashid, N.; Tiwana, M.I.; Iqbal, J. Inverse kinematics control of redundant planar manipulator with joint constraints using numerical method. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems (ICCAS), Busan, Korea, 13–16 October 2015; pp. 806–810. [Google Scholar]
- Du, H.B.; Zhao, Y.W.; Li, X.G.; Han, J.D.; Wang, Z.; Song, G.L. A closed-loop framework for inverse kinematics of the 7-DOF manipulator. In Proceedings of the 2nd International Conference on Control Science and Systems Engineering, Singapore, 27–29 July 2016; pp. 237–241. [Google Scholar]
- Deepak, T.; Ambarish, G.; Norman, B. Real-time inverse kinematics techniques for anthropomorphic limbs. Graph Models 2000, 62, 353–388. [Google Scholar]
- Omisore, M.O.; Han, S.; Ren, L.; Zhang, N.; Wang, L. Noniterative geometric approach for inverse kinematics of redundant leadmodule in a radiosurgical snakelike robot. Biomed. Eng. Online 2017, 16, 93. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Isiah, Z.; Luis, B. A novel closed-form solution for the inverse kinematics of redundant manipulators through workspace analysis. Mech. Mach. Theory 2018, 121, 829–843. [Google Scholar]
- Pieper, D. The Kinematics of Manipulation under Computer Control. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1968. [Google Scholar]
- Srinivas, N.; Matthew, A.C.; Bryan, A.J.; Walker, I.D. Closed-form inverse kinematics for continuum manipulators. Adv. Robot. 2009, 23, 2077–2091. [Google Scholar]
- Pfurner, M. Closed form inverse kinematics solution for a redundant anthropomorphic robot arm. Comput. Aided Geom. D 2016, 47, 163–171. [Google Scholar] [CrossRef]
- Kai, X.; Wukun, M.; Zhixiong, Y.; Han, L.; Zhu, X. Design of a hyper-redundant continuum manipulator for intra-cavity tasks. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics, Bali, Indonesia, 5–10 December 2014; pp. 380–385. [Google Scholar]
- Wenfu, X.; Zonggao, M.; Tianliang, L.; Liang, B. A modified modal method for solving the mission-oriented inverse kinematics of hyper-redundant space manipulators for on-orbit servicing. Acta Astronaut. 2017, 139, 54–66. [Google Scholar]
- Chirikjian, G.; Burdick, J. A modal approach to hyper-redundant manipulator kinematics. IEEE Trans. Robot. Autom. 1994, 10, 343–354. [Google Scholar] [CrossRef] [Green Version]
- Goldenberg, A.A.; Benhabib, B.; Fenton, R.G. A complete generalized solution to the inverse kinematics of robots. IEEE J. Robot. Autom. 1985, 1, 14–20. [Google Scholar] [CrossRef]
- Sugihara, T. Solvability-Unconcerned Inverse Kinematics by the Levenberg–Marquardt Method. IEEE Trans. Robot. 2011, 27, 984–991. [Google Scholar] [CrossRef]
- Wang, L.-C.; Chen, C. A combined optimization method for solving the inverse kinematics problems of mechanical manipulators. IEEE Trans. Robot. Autom. 1991, 7, 489–499. [Google Scholar] [CrossRef]
- Li, Y.; Leong, S.H. Kinematics control of redundant manipulators using a CMAC neural network combined with a genetic algorithm. Robotica 2004, 22, 611–621. [Google Scholar] [CrossRef]
- Yin, F.; Wang, Y.; Yang, Y. Inverse kinematics solution for robot manipulator based on neural network under joint subspace. Int. J. Comput. Commun. 2012, 7, 459–472. [Google Scholar]
- Beheshti, M.T.H.; Tehrani, A.K.; Ghanbari, B. An optimized adaptive fuzzy inverse kinematics solution for redundant manipulators. In Proceedings of the 2003 IEEE International Symposium on Intelligent Control, Houston, TX, USA, 5–8 October 2003; pp. 924–929. [Google Scholar]
- Kesheng, W. Application of genetic algorithms to robot kinematics calibration. Int. J. Syst. Sci. 2009, 40, 147–153. [Google Scholar]
- Ananthanarayanan, H.; Ordóñez, R. Real-time inverse kinematics of (2n+1) DOF hyper-redundant manipulator arm via a combined numerical and analytical approach. Mech. Mach. Theory 2015, 91, 209–226. [Google Scholar] [CrossRef]
- Kim, J.S.; Jeong, J.H.; Park, J.H. Inverse kinematics of a redundant manipulator based on conformal geometry using geometric approach. In Proceedings of the 2015 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO), Colmar, France, 21–23 July 2015; pp. 179–185. [Google Scholar]
- Kireanski, M.V.; Petrovie, T.M. Combined analytical-pseudoinverse inverse kinematic solution for simple redundant manipulators and singularity avoidance. Int. J. Robot. Res. 1993, 12, 188–196. [Google Scholar] [CrossRef]
- Huang, H.; Dong, E.; Xu, M.; Yang, J.; Low, K.H. Mechanism design and kinematic analysis of a robotic manipulator driven by joints with two degrees of freedom (DOF). Ind. Robot. 2018, 45, 34–43. [Google Scholar] [CrossRef] [Green Version]
- Tang, L.; Wang, J.; Zheng, Y.; Gu, G.; Zhu, L.; Zhu, X. Design of a cable-driven hyper-redundant robot with experimental validation. Int. J. Adv. Robot. Syst. 2017, 14, 172988141773445. [Google Scholar] [CrossRef] [Green Version]
- Borwein, J.M.; Crandall, R.E. Closed forms: What they are and why we care. N. Am. Math. Soc. 2013, 60, 50–65. [Google Scholar] [CrossRef] [Green Version]
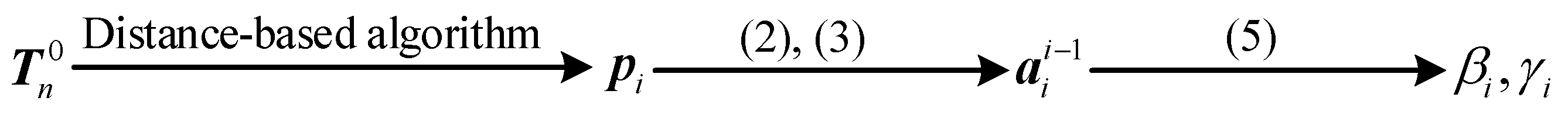



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, Y.; Quan, P.; Lin, H.; Wei, D.; Di, S. A Closed-Form Solution for the Inverse Kinematics of the 2n-DOF Hyper-Redundant Manipulator Based on General Spherical Joint. Appl. Sci. 2021, 11, 1277. https://doi.org/10.3390/app11031277
Lou Y, Quan P, Lin H, Wei D, Di S. A Closed-Form Solution for the Inverse Kinematics of the 2n-DOF Hyper-Redundant Manipulator Based on General Spherical Joint. Applied Sciences. 2021; 11(3):1277. https://doi.org/10.3390/app11031277
Chicago/Turabian StyleLou, Ya’nan, Pengkun Quan, Haoyu Lin, Dongbo Wei, and Shichun Di. 2021. "A Closed-Form Solution for the Inverse Kinematics of the 2n-DOF Hyper-Redundant Manipulator Based on General Spherical Joint" Applied Sciences 11, no. 3: 1277. https://doi.org/10.3390/app11031277




