Passive Control of Base Pressure: A Review
Abstract
:1. Introduction
2. Various Types of Passive Controls
2.1. Passive Control in the Form of Cavity
2.2. Passive Control with Rib
2.3. Passive Control with Dimple
2.4. Passive Control with Static Cylinder
2.5. Passive Control in the Form of Spikes
2.6. Passive Control in the Form of Splitter Plate
2.7. Other Types of Passive Control Technique
3. Findings Discussion
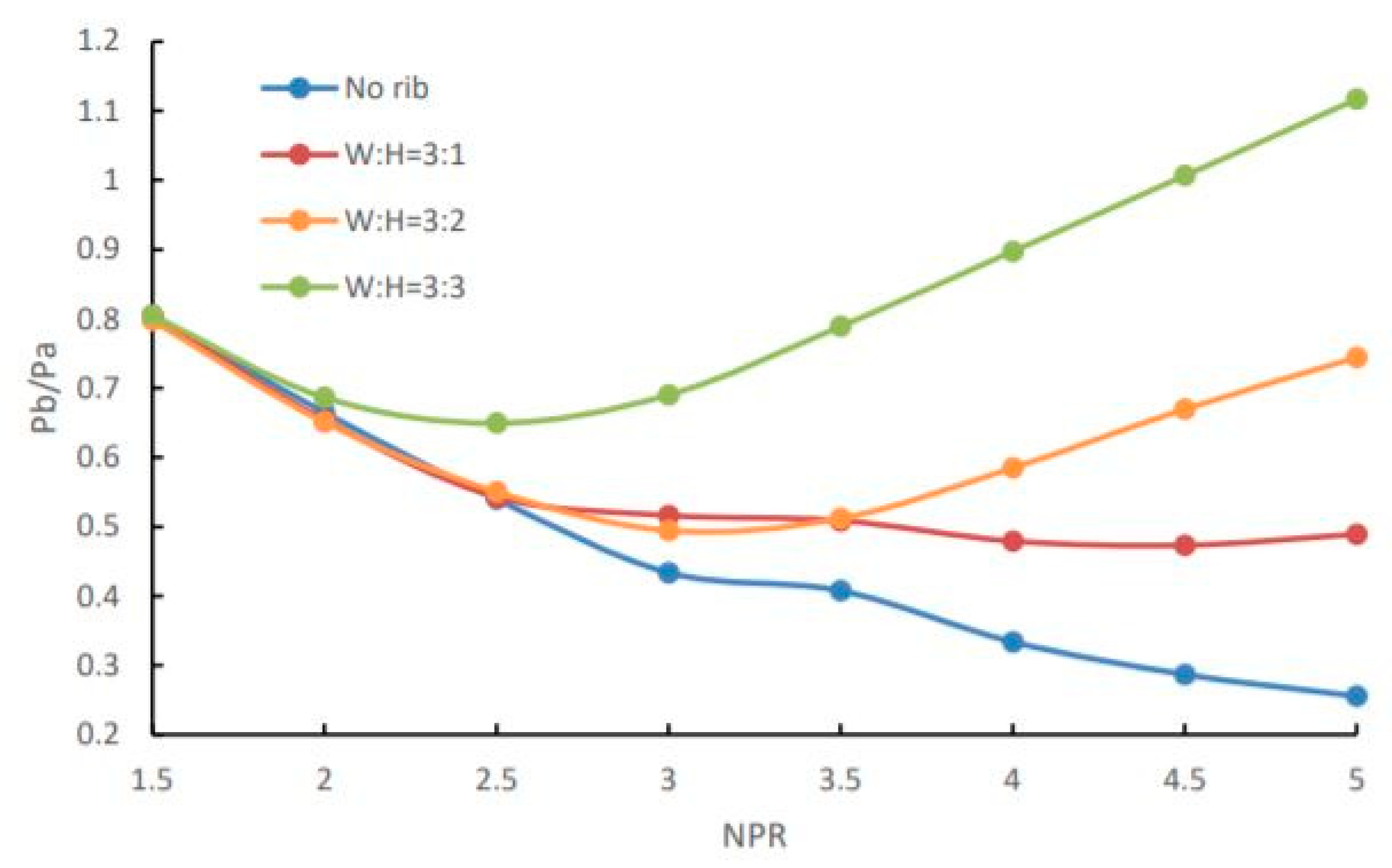
- All the passive control methods to regulate base pressure are useful in creating a favourable pressure gradient. These techniques are also inadequately effective in the presence of an adverse pressure gradient (i.e., when the jets are over-expanded). In passive control, the level of expansion (i.e., Pe/Pa) plays a vital role in fixing the base pressure values. It is seen that whenever the area ratio is five and above, the control effectiveness is minimal/not useful even though the flow from the nozzles is under the influence of a favourable pressure gradient. The physics behind this trend maybe when the relief effect due to an area ratio increase is beyond some limit. The flow from the converging or converging-diverging nozzle discharged into the enlarged duct tends to attach with reattachment length other than the optimum for a strong vortex at the base. This process makes the NPR effect on base pressure become insignificant after a critical area ratio. The review shows that when the jets are under-expanded for a lower area ratio, the passive control is significant, and base pressure is equal to the atmospheric pressure, or is more than the ambient pressure. Results indicate that for certain combinations of the parameters, an under-expansion level of 1.5 (i.e., Pe/Pa = 1.5) is the optimum value resulting in a maximum increase in the base pressure.
- A new passive control device was considered for a form-drag reduction in the flow over a two-dimensional bluff body with a blunt trailing edge. The system consists of small tabs on the top and bottom edges of a bluff trail to effectively interrupt a two-dimensional wake. A wind tunnel experiment and a large-scale simulation were conducted to test its drag reduction efficiency. Extensive parametrical research is conducted experimentally by changing the passive control’s height and width in the form of a tab and the spacing along the span between the adjacent tabs. The Reynolds numbers considered for the study are 20,000, 40,000, and 80,000. The base pressure increases for a wide range of parameters (i.e., drag reduces) at all three Reynolds numbers.
- Similarly, the splitter plate’s effect at various length locations is useful in the base drag reduction at various NPR, Mach numbers, area ratios, and length-to-diameter ratios. The passive control in the form of a splitter plate is significant, resulting in reducing the drag. Drag is reduced from 9% to 57% by attaching the splitter plate to the cylinder. With vertical splitter plates positioned downstream of a straight base, drag reductions of nearly 12% were obtained. Finally, the results presented herein confirm the advantage of splitter plates in reducing aerodynamic drag and demonstrate the need to develop systems capable of adapting their position and angular orientation to external conditions. Triangular splitters that divide the near wake into one-half, one-third, and one-fourth cylinder regions were designed to exploit this flow’s specific stability characteristics. The impact of the immediate wake flow changes the base pressure and eventually affects the base drag. A base drag reduction of as high as 39% is achieved by employing the splitter plate, whereas, with passive control with spike, the base pressure starts to increase right from the beginning and becomes more than atmospheric pressure at L/W = 6 to 10, and acquired base pressure values are 5% more than atmospheric pressure. The effect of spike and grooved spikes play an essential role in fixing the base pressure values. The impact of cavities is to reduce the oscillations in the enlarged duct.
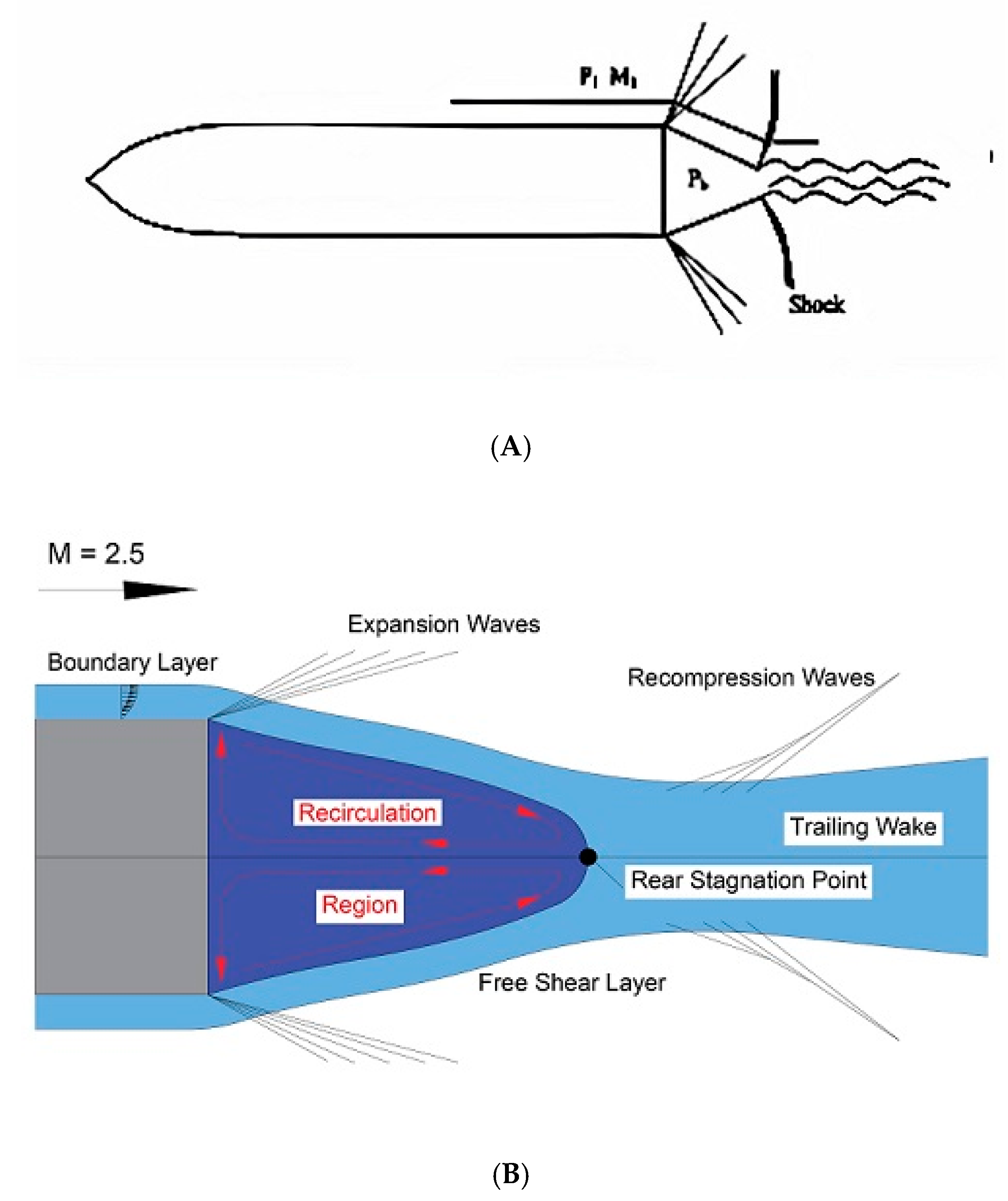
- A computational fluid dynamics simulation over a payload fairing of the satellite launch vehicle with aerospike presence is carried out. The payload fairing significantly modifies its flow field and reduces the aerodynamic drag at transonic and supersonic speeds. The simulations were done by solving time-dependent compressible turbulent axisymmetric Navier-Stokes equations. The closure of the system of equations is achieved using an algebraic turbulence model. The numerical simulation is performed on a single-block structured computational domain. The flow field over the aerospike depends on the freestream Mach number. The effects of the aerospike attached to payload fairing are studied with velocity and density plots. The schlieren pictures, oil flow, and the pressure measurements on an aerospike attached to the payload fairing are analyzed and compared with the present numerical results with the Mach number in the range of 0.8 ≤ M ≤ 3.0 and freestream Reynolds number range 33.35 × 106/m ≤ Re∞ ≤ 46.75 × 106/m. The Mach number range covers the maximum drag and dynamic conditions during the typical satellite launch vehicle’s ascent flight. A distinct flow field is found for M∞ < 1 and M∞ > 1 with and without the aerospike attached to the payload fairing. The Flow separation is found at all the freestream Mach numbers over the aerospike, with the recirculation zone being Mach number dependent. As the freestream Mach number increases, the separation zone becomes steeper. It is found that the aerospike attached to the payload fairing leads to drag decline.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| X | Axial distance along the duct |
| D | Diameter of the duct |
| L | Length of the duct |
| G | Distance between the rear base point of the cylinder and the leading edge of the splitter plates |
| d | Cylinder diameter. |
| NPR | Nozzle Pressure Ratio |
| x | Mean velocity field in the plane |
| c | Adjustable distance to the ground called ground clearance |
| BFS | Backward Facing Step |
| CDnet | Net drag coefficient |
| Cpb | Base pressure coefficient |
| BB | Blunt Base Model |
| SVC | Small Length Ventilated Model |
| SC | Solid Model |
| L/D | Length-to-Diameter Ratio of the enlarged duct (pipe) |
| PIV | Particle Image Velocimetry |
| L/W | Length-to-Width Ratio |
| PCD | Pitch Circle Diameter |
| St | Strouhal Number |
| f | Vortex shedding frequency |
| D | Height of the backward-facing step |
| U | Freestream velocity |
| P | Pressure |
| M | Mach number |
References
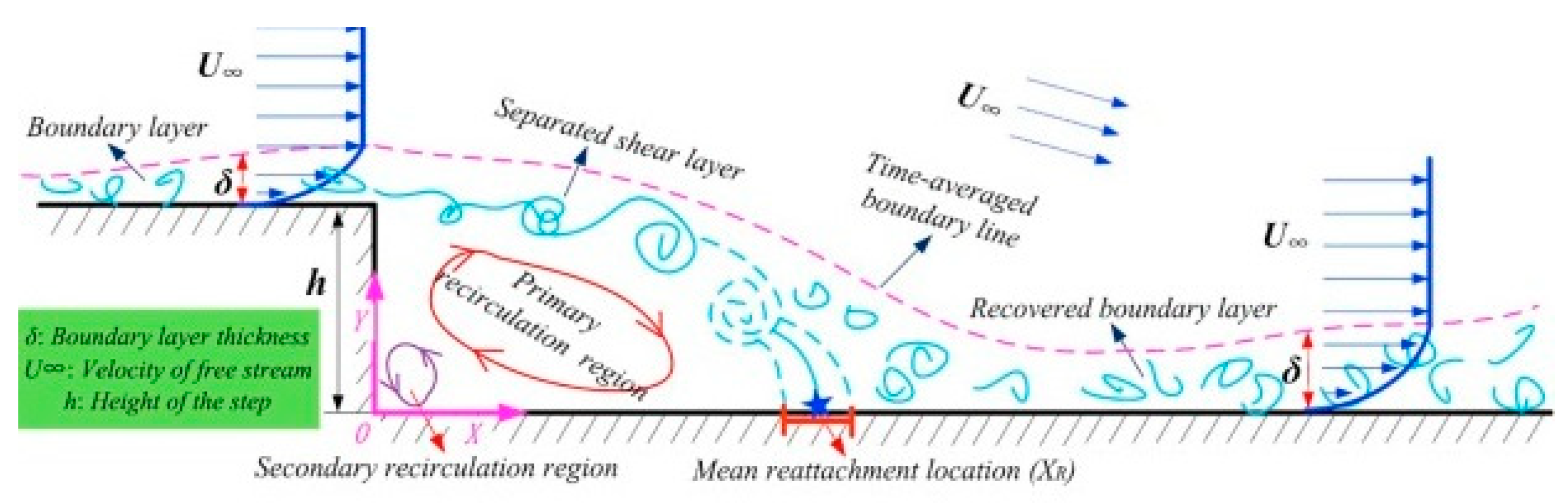
- Hsu, C.-W.; Lin, S.-Y. Investigation of characteristics of shear layer: Application of synthetic jet in backward-facing step flow field. Trans. Can. Soc. Mech. Eng. 2016, 40, 787–797. [Google Scholar] [CrossRef]
- Rajendran, P.; Sethuraman, V.; Khan, S.A. Base and wall pressure control using cavities and ribs in suddenly expanded flows-an overview. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 66, 120–134. [Google Scholar]
- Wang, F.; Gao, A.; Wu, S.; Zhu, S.; Dai, J.; Liao, Q. Experimental Investigation of Coherent Vortex Structures in a Backward-Facing Step Flow. Water 2019, 11, 2629. [Google Scholar] [CrossRef] [Green Version]
- Ashcroft, G.; Zhang, X. Vortical structures over rectangular cavities at low speed. Phys. Fluids 2005, 17, 015104. [Google Scholar] [CrossRef]
- Pandey, K.M.; Rathakrishnan, E. Annular Cavities for Base Flow Control. Int. J. Turbo Jet-Engines 2006, 23, 113–128. [Google Scholar] [CrossRef]
- Khan, S.A.; Mohammed, A.; GM, F.A. Passive control of base drag in compressible subsonic flow using multiple cavity. Int. J. Mech. Prod. Eng. Res. Dev. 2018, 8, 39–44. [Google Scholar]
- Khan, S.A.; Al Robaian, A.A.; Asadullah, M.; Khan, A.M. Grooved cavity as a passive controller behind backward facing step. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 53, 185–193. [Google Scholar]
- Vikramaditya, N.S.; Viji, M.; Verma, S.B.; Ali, N.; Thakur, D.N. Base Pressure Fluctuations on Typical Missile Configuration in Presence of Base Cavity. J. Spacecr. Rocket. 2018, 55, 335–345. [Google Scholar] [CrossRef]
- Mariotti, A.; Buresti, G.; Gaggini, G.; Salvetti, M.V. Separation control and drag reduction for boat-tailed axisymmetric bodies through contoured transverse grooves. J. Fluid Mech. 2017, 832, 514–549. [Google Scholar] [CrossRef]
- Howell, J.; Sims-Williams, D.; Sprot, A.; Hamlin, F.; Dominy, R. Bluff Body Drag Reduction with Ventilated Base Cavities. SAE Int. J. Passeng. Cars Mech. Syst. 2012, 5, 152–160. [Google Scholar] [CrossRef] [Green Version]
- Bonnavion, G.; Cadot, O.; Herbert, V.; Parpais, S.; Vigneron, R.; Delery, J. Effect of a base cavity on the wake modes of the squareback Ahmed body at various ground clearances and application to drag reduction. In Congrès Français de Mécanique; Association Française de Mécanique (AFM): Lille, France, 2017. [Google Scholar]
- Ahmed, S.R.; Ramm, G.; Faltin, G. Some Salient Features of the Time-Averaged Ground Vehicle Wake. SAE Tech. Paper Ser. 1984, 473–503. [Google Scholar] [CrossRef]
- Lucas, J.-M.; Cadot, O.; Herbert, V.; Parpais, S.; Délery, J. A numerical investigation of the asymmetric wake mode of a squareback Ahmed body—Effect of a base cavity. J. Fluid Mech. 2017, 831, 675–697. [Google Scholar] [CrossRef] [Green Version]
- Rathakrishnan, E. Effect of ribs on suddenly expanded flows. AIAA J. 2001, 39, 1402–1404. [Google Scholar] [CrossRef]
- Yedlapalli, S.; Vijayaraja, A.V.K.; Rathakrishnan, E. Base Pressure Control by using Ribs in Subsonic and Sonic Suddenly Expanded Flows. In Proceedings of the 2nd International Conference on Recent Advances in Experimental Fluid Mechanics, Andhra Pradesh, India, 3–6 March 2008. [Google Scholar]
- Nathan, K.R.; Vijayaraja, K.; Elangovan, S.; Rathakrishnan, E. Effect of Annular Rib Position in Suddenly Expanded Supersonic Flow. In Proceedings of the International Conference on Aerospace Science and Technology, Bangalore, India, 26–28 June 2008. [Google Scholar]
- Vijayaraja, K.; Senthilkumar, C.; Elangovan, S.; Rathakrishnan, E. Base Pressure Control with Annular Ribs. Int. J. Turbo Jet-Engines 2014, 31, 111–118. [Google Scholar] [CrossRef]
- Khan, A.; Mazlan, N.M.; Ismail, M.A. Analysis of Flow through a Convergent Nozzle at Sonic Mach Number for Area Ratio 4. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 62, 66–79. [Google Scholar]
- Khan, S.A.; Asadullah, M.; Sadhiq, J. Passive control of base drag employing dimple in subsonic suddenly expanded flow. Int. J. Mech. Mechatron. Eng. IJMME-IJENS 2018, 18, 69–74. [Google Scholar]
- Asadullah, M.; Khan, S.A.; Asrar, W.; Sulaeman, E. Passive control of base pressure with static cylinder at supersonic flow. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 370, p. 012050. [Google Scholar]
- Khan, S.A.; Ullah, M.A.; Ahmed, G.F.; Jalaluddin, A.; Baig, M.A.A. Flow control with aero-spike behind bluff body. Int. J. Mech. Prod. Eng. Res. Dev. 2018, 8, 1001–1008. [Google Scholar]
- Mehta, R. Drag reduction for payload fairing of satellite launch vehicle with aerospike in transonic and low supersonic speeds. Adv. Aircr. Spacecr. Sci. 2020, 7, 371–385. [Google Scholar]
- Khan, S.A.; Alrobaian, A.A.; Asad Ullah, M.; Rao, A. Threaded spikes for bluff body base flow control. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 53, 194–203. [Google Scholar]
- Hwang, J.-Y.; Yang, K.-S.; Sun, S.-H. Reduction of flow-induced forces on a circular cylinder using a detached splitter plate. Phys. Fluids 2003, 15, 2433–2436. [Google Scholar] [CrossRef]
- Soumya, S.; Prakash, K.A. Effect of splitter plate on fluid flow characteristics past a triangular cylinder. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 822, p. 012054. [Google Scholar]
- Jodai, Y.; Takahashi, Y.; Ichimiya, M.; Osaka, H. The Effects of Splitter Plates on Turbulent Boundary Layer on a Long Flat Plate Near the Trailing Edge. J. Fluids Eng. 2008, 130, 051103. [Google Scholar] [CrossRef]
- Bearman, P.W. Investigation of the flow behind a two-dimensional model with a blunt trailing edge and fitted with splitter plates. J. Fluid Mech. 1965, 21, 241. [Google Scholar] [CrossRef]
- Nash, J.; Callinan, J.; Quincey, V. Experiments on Two-Dimensional Base Flow at Subsonic and Transonic Speeds; ARC: London, UK, 1963; Volume 25070. [Google Scholar]
- Gilliéron, P.; Kourta, A. Aerodynamic drag reduction by vertical splitter plates. Exp. Fluids 2009, 48, 1–16. [Google Scholar] [CrossRef]
- Reedy, T.M.; Elliott, G.S.; Dutton, J.C.; Lee, Y. Passive Control of High-Speed Separated Flows Using Splitter Plates. AIAA J. 2012, 50, 1586–1595. [Google Scholar] [CrossRef]
- Falchi, M.; Provenzano, G.; Pietrogiacomi, D.; Romano, G.P. Experimental and numerical investigation of flow control on bluff bodies by passive ventilation. Exp. Fluids 2006, 41, 21–33. [Google Scholar] [CrossRef]
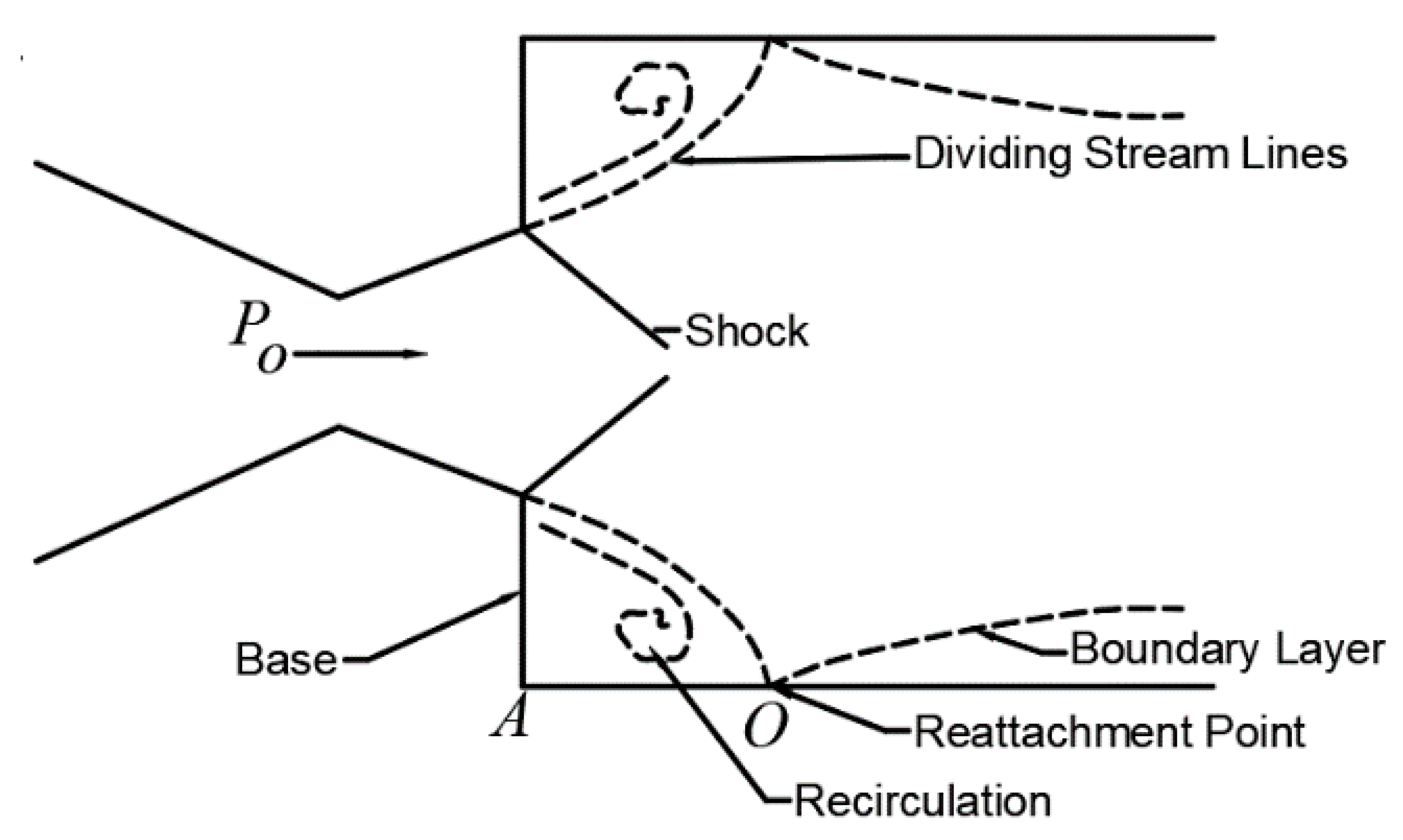
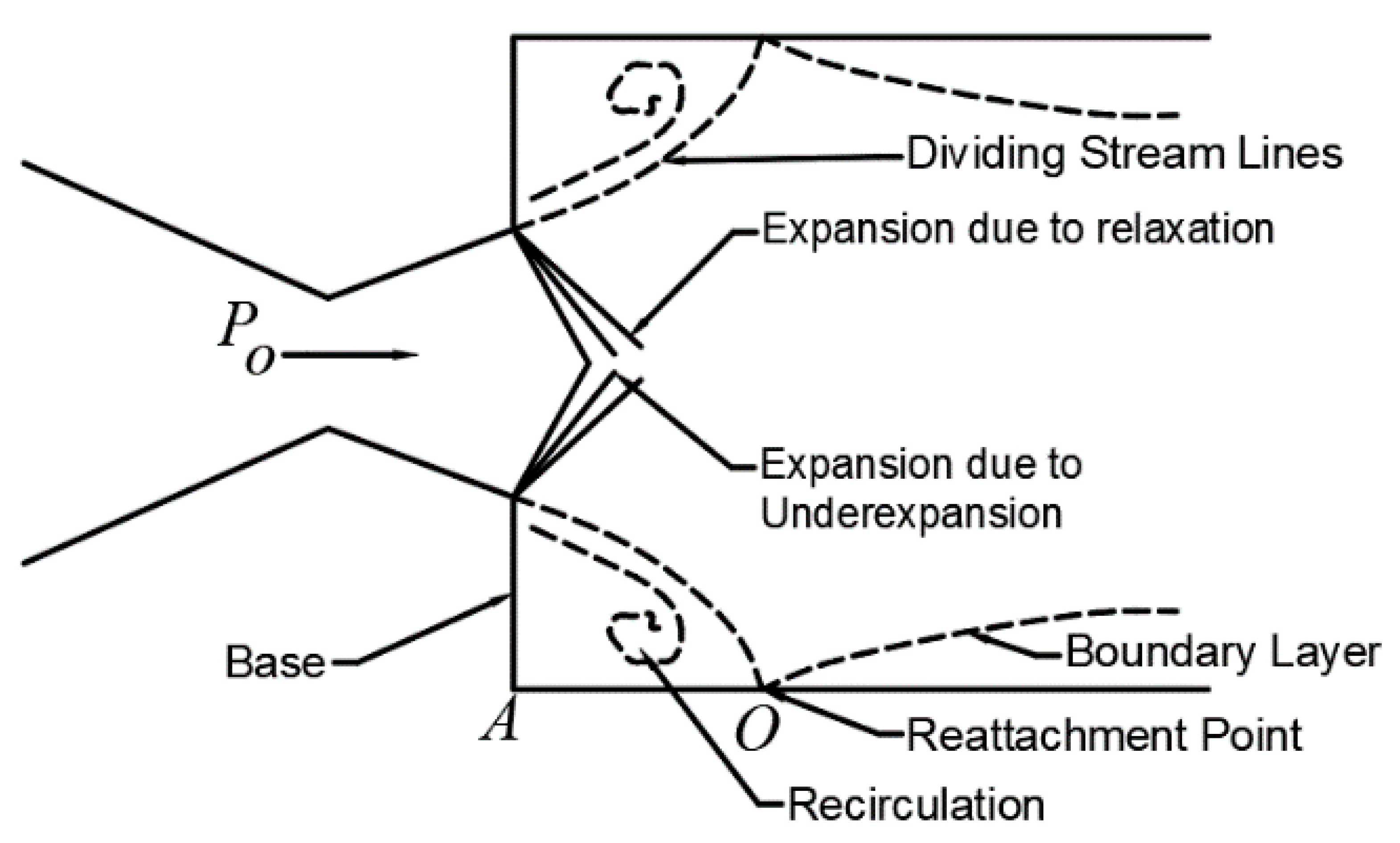
- Boswell, B.A.; Dutton, J.C. Flow visualizations and measurements of a three-dimensional supersonic separated flow. AIAA J. 2001, 39, 113–121. [Google Scholar] [CrossRef]
- Moore, F.G.; Wilcox, F.; Hymer, T. Improved Empirical Model for Base Drag Prediction on Missile Configurations Based on New Wind Tunnel Data; Naval Surface Warfare Center Dahlgren Div Va: Dahlgren, VA, USA, 1992. [Google Scholar]
- De La Cruz, J.M.G.; Oxlade, A.R.; Morrison, J. Passive control of base pressure on an axisymmetric blunt body using a perimetric slit. Phys. Rev. Fluids 2017, 2, 043905. [Google Scholar] [CrossRef]
- Bao, Y.; Tao, J. The passive control of wake flow behind a circular cylinder by parallel dual plates. J. Fluids Struct. 2013, 37, 201–219. [Google Scholar] [CrossRef]
- Loosen, S.; Statnikov, V.; Meinke, M.; Schröder, W. Modal analysis of passive flow control for the turbulent wake of a generic planar space launcher. CEAS Space J. 2017, 10, 189–202. [Google Scholar] [CrossRef]
- Park, H.; Lee, D.; Jeon, W.-P.; Hahn, S.; Kim, J.; Kim, J.; Choi, J.; Choi, H. Drag reduction in flow over a two-dimensional bluff body with a blunt trailing edge using a new passive device. J. Fluid Mech. 2006, 563, 389. [Google Scholar] [CrossRef] [Green Version]
- Bearman, P.W. The Effect of Base Bleed on the Flow behind a Two-Dimensional Model with a Blunt Trailing Edge. Aeronaut. Q. 1967, 18, 207–224. [Google Scholar] [CrossRef]
- Tripathi, A.; Manisankar, C.; Verma, S. Control of base pressure for a boat-tailed axisymmetric afterbody via base geometry modifications. Aerosp. Sci. Technol. 2015, 45, 284–293. [Google Scholar] [CrossRef]
- A Simple Passive Device for the Drag Reduction of an Ahmed Body. J. Appl. Fluid Mech. 2021, 14, 147–164. [CrossRef]
- Mariotti, A.; Buresti, G.; Salvetti, M.V. Separation delay through contoured transverse grooves on a 2D boat-tailed bluff body: Effects on drag reduction and wake flow features. Eur. J. Mech. B/Fluids 2019, 74, 351–362. [Google Scholar] [CrossRef]
- Capone, A.; Romano, G.P. Investigation on the effect of horizontal and vertical deflectors on the near-wake of a square-back car model. J. Wind. Eng. Ind. Aerodyn. 2019, 185, 57–64. [Google Scholar] [CrossRef]
- Pavia, G.; Passmore, M.; Varney, M. Low-frequency wake dynamics for a square-back vehicle with side trailing edge tapers. J. Wind. Eng. Ind. Aerodyn. 2019, 184, 417–435. [Google Scholar] [CrossRef] [Green Version]
- Altaf, A.; Omar, A.A.; Asrar, W. Review of passive drag reduction techniques for bluff road vehicles. IIUM Eng. J. 2014, 15, 15. [Google Scholar] [CrossRef]
- Choi, H.; Jeon, W.-P.; Kim, J. Control of Flow over a Bluff Body. Annu. Rev. Fluid Mech. 2008, 40, 113–139. [Google Scholar] [CrossRef] [Green Version]
- Mukut, A.N.M.M.I.; Abedin, M.Z. Review on Aerodynamic Drag Reduction of Vehicles. Int. J. Eng. Mater. Manuf. 2019, 4, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Zhang, Y.; Zhu, H.; Xiao, H. Aerodynamic drag reduction and flow control of Ahmed body with flaps. Adv. Mech. Eng. 2017, 9, 1687814017711390. [Google Scholar] [CrossRef]
- Kim, D.; Lee, H.; Yi, W.; Choi, H. A bio-inspired device for drag reduction on a three-dimensional model vehicle. Bioinspiration Biomim. 2016, 11, 026004. [Google Scholar] [CrossRef] [PubMed]
- Altaf, A.; Omar, A.A.; Asrar, W. Passive drag reduction of square back road vehicles. J. Wind. Eng. Ind. Aerodyn. 2014, 134, 30–43. [Google Scholar] [CrossRef]
- Mariotti, A.; Buresti, G.; Salvetti, M.V. Connection between base drag, separating boundary layer characteristics and wake mean recirculation length of an axisymmetric blunt-based body. J. Fluids Struct. 2015, 55, 191–203. [Google Scholar] [CrossRef]
- Mariotti, A.; Buresti, G. Experimental investigation on the influence of boundary layer thickness on the base pressure and near-wake flow features of an axisymmetric blunt-based body. Exp. Fluids 2013, 54, 1–16. [Google Scholar] [CrossRef]
- Beaudoin, J.-F.; Aider, J.-L. Drag and lift reduction of a 3D bluff body using flaps. Exp. Fluids 2008, 44, 491–501. [Google Scholar] [CrossRef]


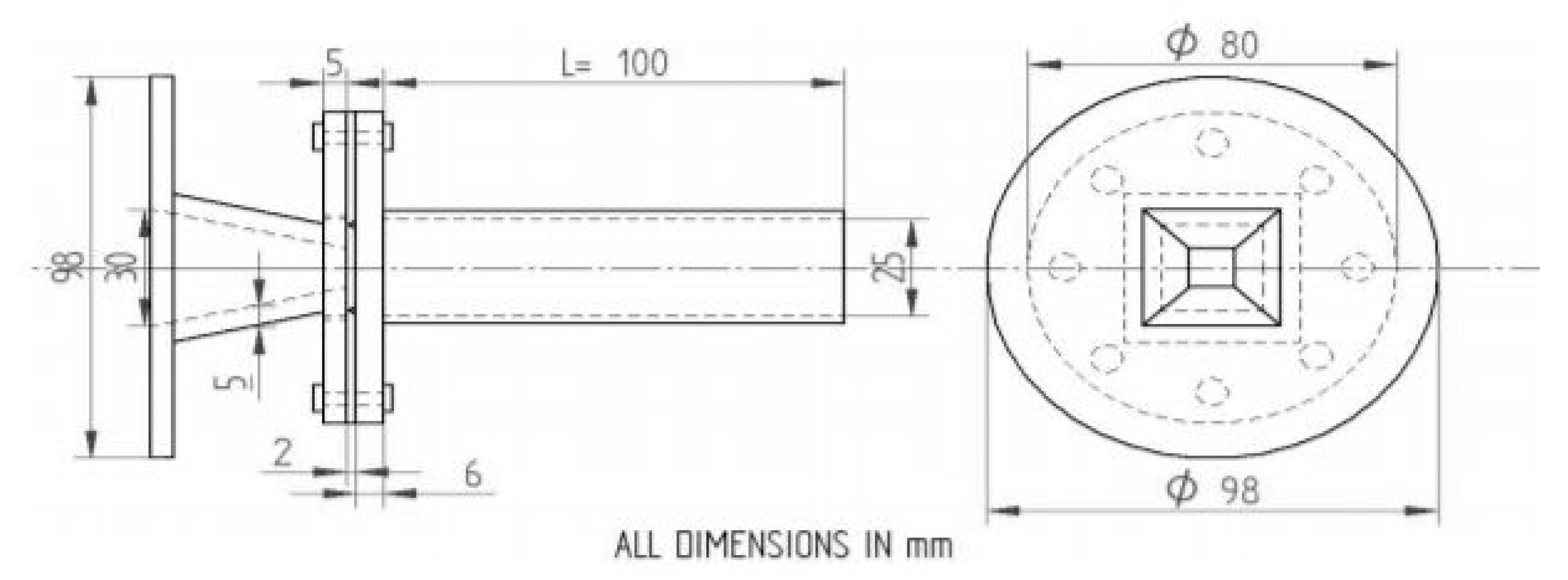
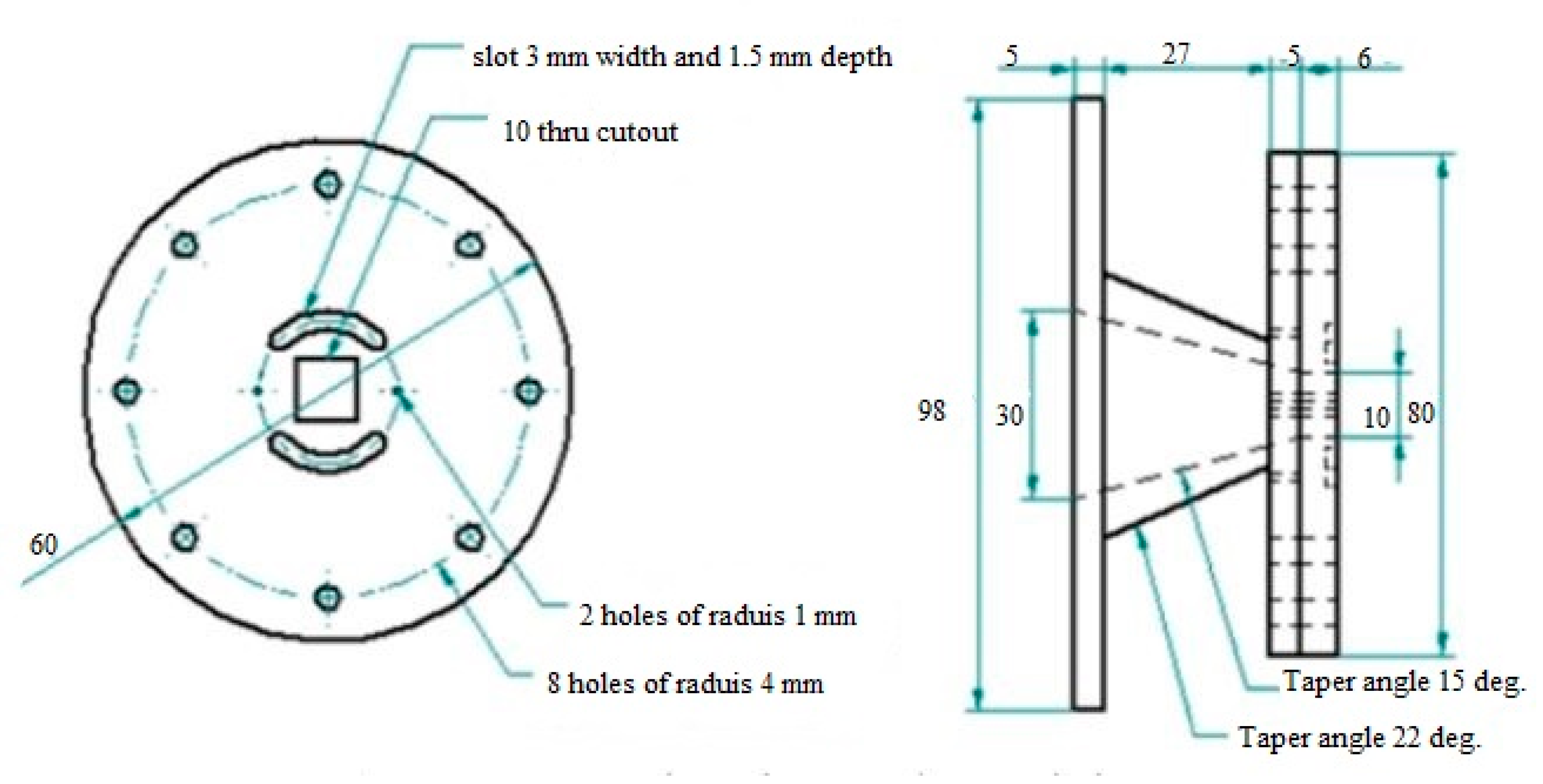

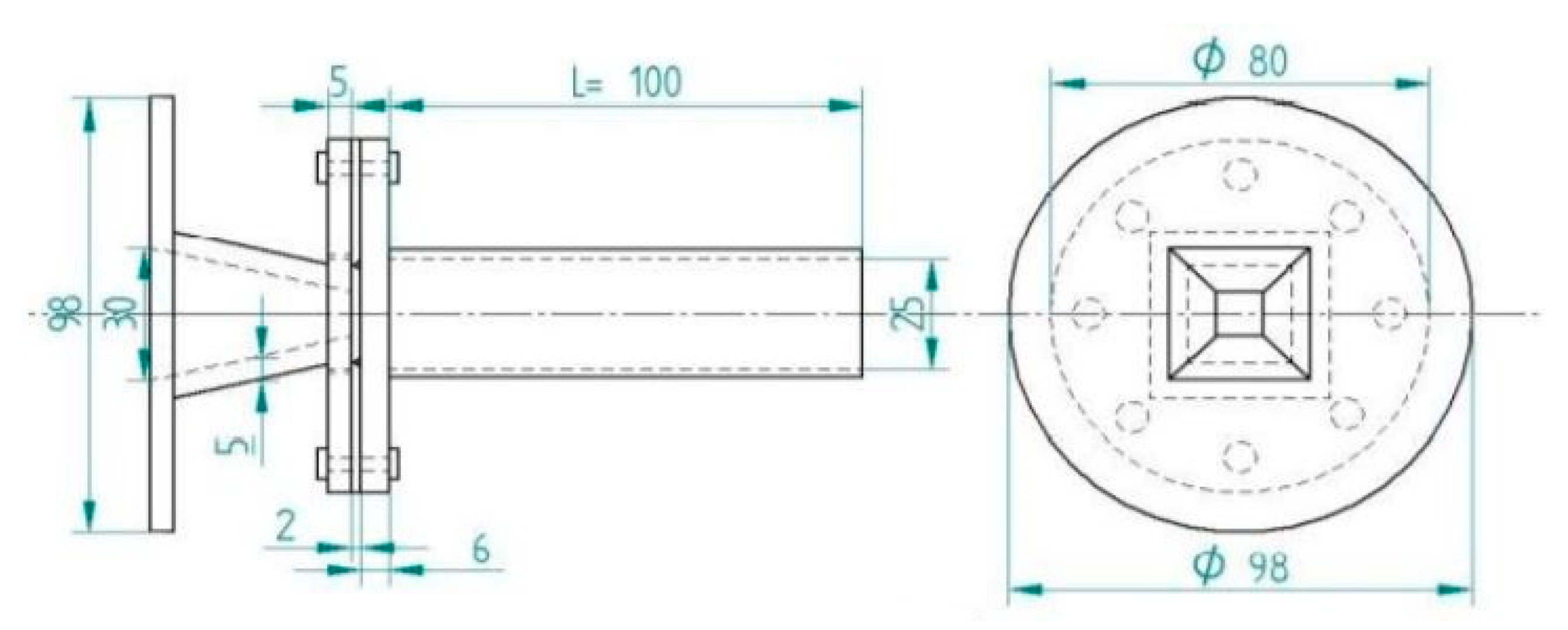
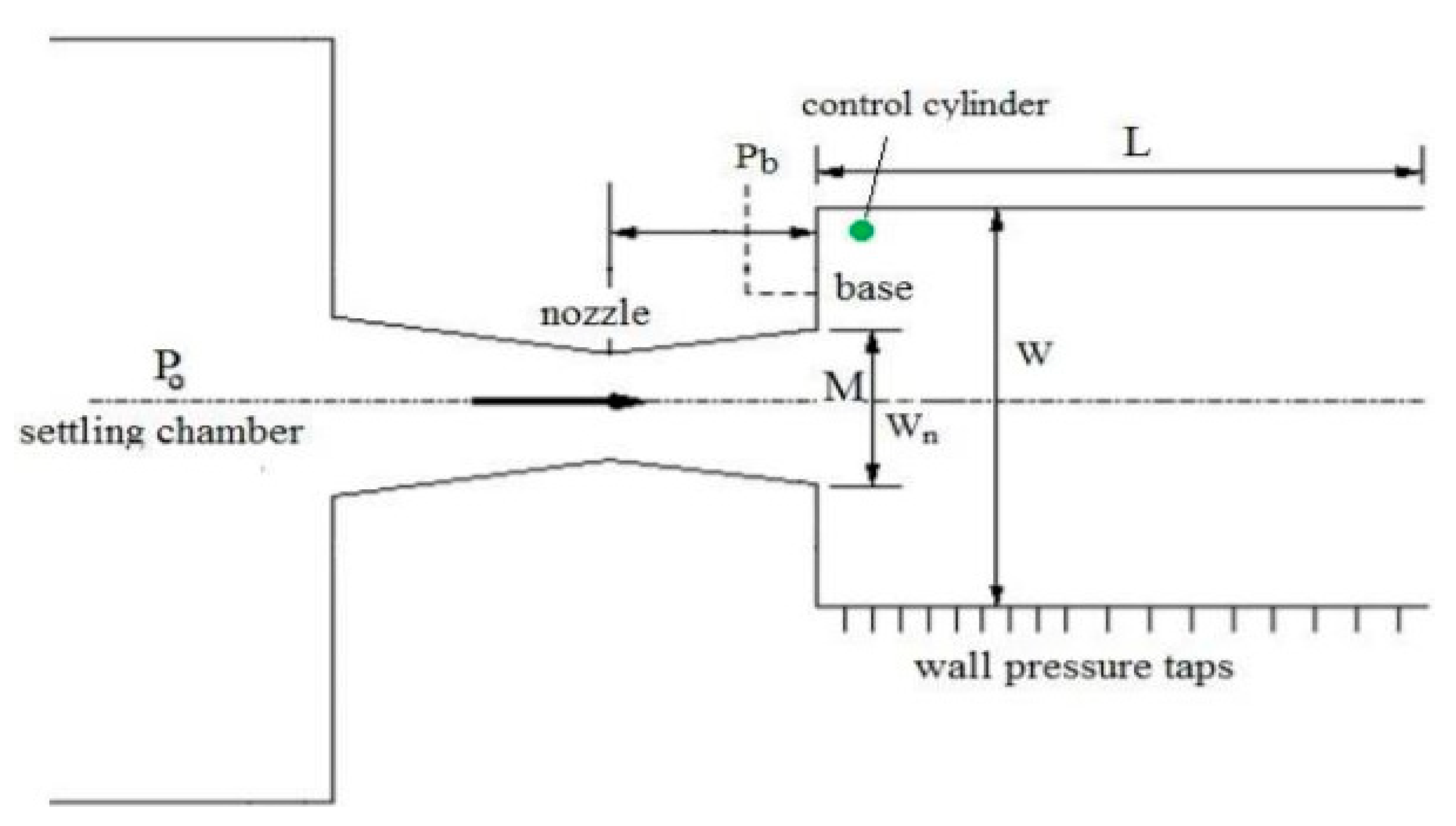

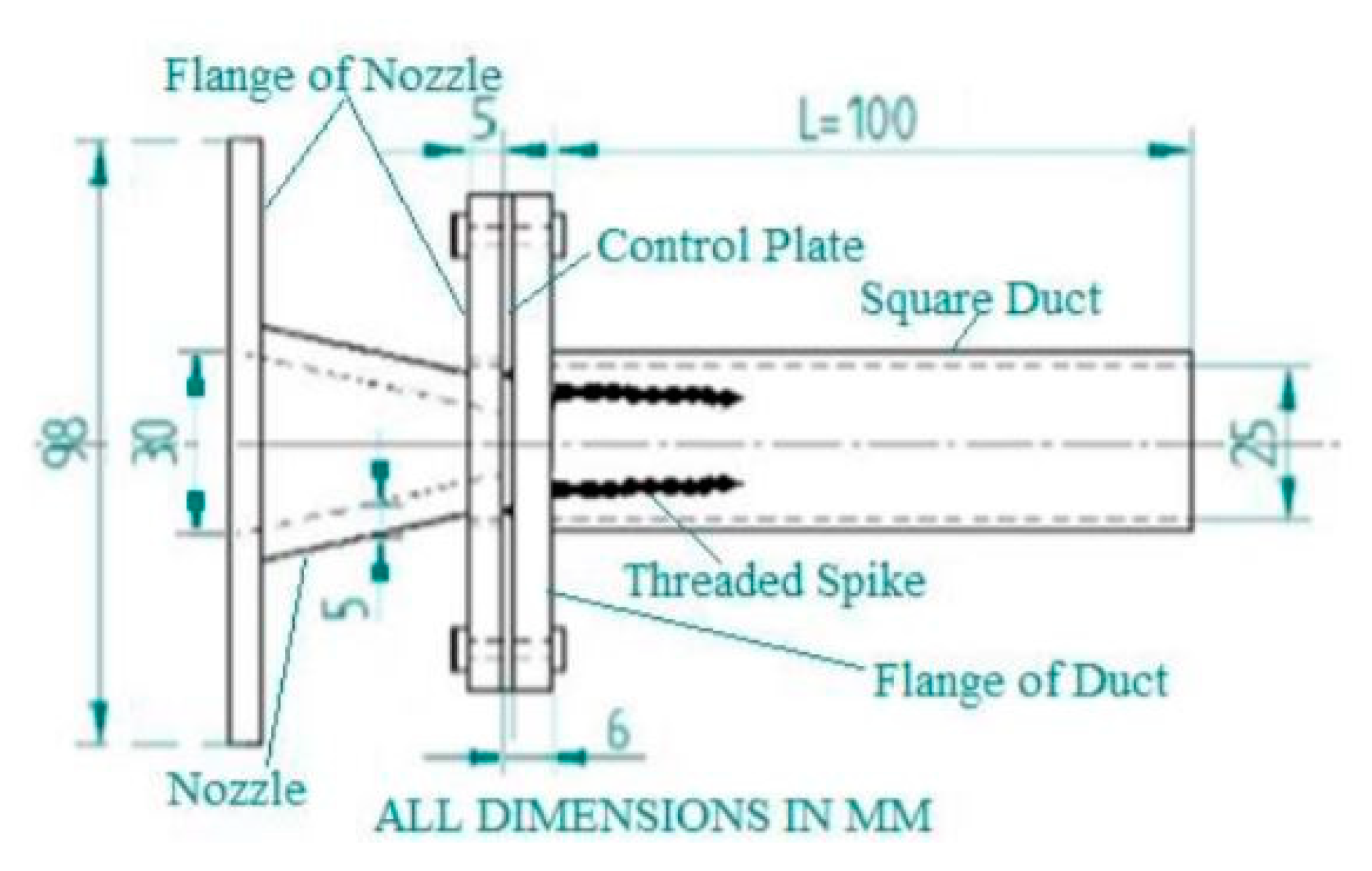
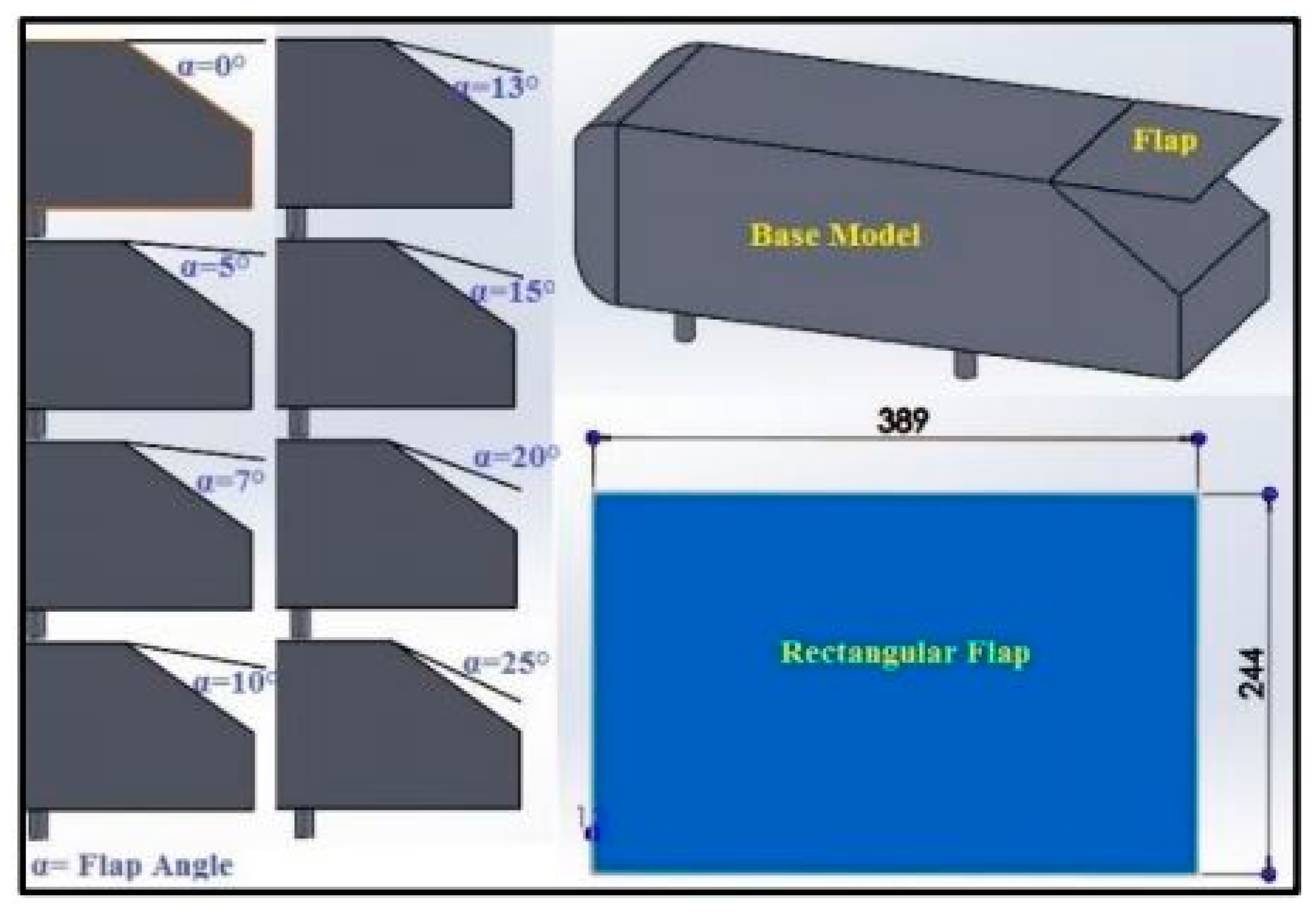
| Type of Passive Control | Effect on Flow Field/Effect on Base Pressure Control |
|---|---|
| For Internal Flow Conditions | |
| Rectangular shaped cavity | Shear layer development & increase in vorticity thickness increases the base pressure. |
| Semi-circular grooves | Reduces the base drag |
| Rectangular Rib | Reverse flow creates a low-pressure zone by the vortex |
| Dimples | Passive control highly effective at higher NPR |
| Static cylinder | Increases base pressure up to 59% |
| Aerospikes | Reduces the suction at the base and increases base pressure up to 5% more than atmospheric pressure.When the aerospikes are located at the nose, they decrease the fore-body drag. |
| Threaded spikes | Due to the threads, it develops vortices and manipulates the flow field & ultimately increases base pressure. |
| For External Flow Conditions | |
| Base Cavity | Increases the recirculation region size |
| Ventilated cavity | Increases base pressure by a natural bleeding process |
| Transverse cavity | Reduces pressure drag |
| Boattailing | Reduces the base drag depends on the ratio of Db/D. Where Db is the boattail base diameter and D is the maximum diameter of the projectile. |
| Baseline and shallow cavity | Creates viscous vortex flow, which is a source of low pressure. |
| Forward-facing Aerospike | Reduces fore-body aerodynamic drag by dividing the stagnation region of the nose area along the length of the projectile and modifying the flow field. |
| Splitter plate | A splitter plate is also used to divide the stagnation region in front of the nose along the width. With an increase in Reynolds number, the drag reduction increases up to 6.7% |
| Triangular splitter plate | Total drag reduction up to 57% |
| Thin slit at the base region | Increases vortex shedding & results in increased wake rotational speed |
| Symmetric plates attached to the rear surface | Maximum drag reduction achieved at attachment angle 40 to 50 degrees |
| Semi-circular lobes | The semi-circular lobes Improve turbulent mixing & the creation of the shear layer. It also reduces the reattachment length significantly by 75%. |
| Tabs | Optimal tab configuration gives 30% increases in base pressure. |
| Rectangular flap | Up to 14% drag reduction is achieved. |
| Horizontal and vertical deflectors | They Reduce drag due to the decline in the wake. |
| Triangular and elliptical flap | 11.1% drag reduction in oval shape whereas 6% drag reduction in other shapes. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.; Rajendran, P.; Sidhu, J.S.S. Passive Control of Base Pressure: A Review. Appl. Sci. 2021, 11, 1334. https://doi.org/10.3390/app11031334
Khan A, Rajendran P, Sidhu JSS. Passive Control of Base Pressure: A Review. Applied Sciences. 2021; 11(3):1334. https://doi.org/10.3390/app11031334
Chicago/Turabian StyleKhan, Ambareen, Parvathy Rajendran, and Junior Sarjit Singh Sidhu. 2021. "Passive Control of Base Pressure: A Review" Applied Sciences 11, no. 3: 1334. https://doi.org/10.3390/app11031334
APA StyleKhan, A., Rajendran, P., & Sidhu, J. S. S. (2021). Passive Control of Base Pressure: A Review. Applied Sciences, 11(3), 1334. https://doi.org/10.3390/app11031334





