1. Introduction
With the rapid development of China’s economy, shallow coal resources are increasingly in short supply. It has become an inevitable trend to mine deep coal resources [
1,
2,
3]. However, the high stress and complicated geological environment often cause serious deformation and damage in the roadway and a huge loss of personnel and equipment. In this case, greater importance is to be attached to bolt support, which serves as the active control over roadway deformation [
4,
5,
6].
1.1. Evolution Process of Bolts
Bolt support has a long history of development. Due to different geological conditions and technological levels, many types of bolts have been developed [
7,
8,
9,
10]. Bolt support is initially applied to the roadway whose surrounding rock is relatively stable and mechanical bolts like the inverted wedge bolt and expansion shell bolt are the mainstream [
11]. Generally speaking, mechanical bolts improve the anchorage force mainly through pressing the drill hole wall, which in turn raises a much higher demand on the borehole diameter. If the surrounding rock is unstable and fractures are common, mechanical bolts will not function as designed. In this case, friction bolts are developed [
12,
13]. Split-set bolts and expanded-tube bolts are typical friction bolts. This type of bolt boasts merits of full-length anchorage, but its loading capacity is relatively low, thus failing to satisfy the demand of long-term support, especially in watery or broken surrounding rocks.
To solve this problem, bonded bolts are employed gradually to bolt support in complex geological conditions for the purpose of permanent support [
14,
15]. The bonding material can tightly bond the bolt body and the borehole wall to achieve permanent anchorage. Cement bonding materials that harden quickly in contact with water were first used as anchoring agents in bolts, and this series of bolts are called “cement bolts” [
16]. However, given that it is difficult to control precisely the setting time, the installation quality often fails to reach the design requirements. This can cause low anchorage force and an unreliable supporting effect. Therefore, cement is gradually replaced by epoxy resin as the binding material. Now, resin bolts have become the most widely used bolts [
17]. The setting rate of epoxy resin is much higher, enabling the bolts to provide bearing capacity in a short period and thus guaranteeing the installation quality. Resin bolts can be divided into two types: resin anchorage bolts and resin anchorage cable [
18,
19,
20]. Resin bolts are generally high-strength finish-rolled threaded steel bars, which are rigid materials and cannot be bent. Restricted by the height of the roadway, the length of the bolt is generally between 1.8 and 2.5 m. The bolts adopt a nut-rotating installation method, which can only provide a pretightening force of about 30 kN to the roadway surface, and the initial anchoring force is small. However, the resin cables are made of steel-stranded wire, which is a flexible material, and the length of the cables is not restricted by the roadway section. The cables are installed with anchor tensioning, which can provide higher pretightening force. The initial anchor force can reach 100–200 kN, which can better control the roadway deformation.
1.2. Control Theory and Technology of Roadway Surrounding Rock
In order to better play the supporting role of bolts, many surrounding rock control theories have been formed at home and abroad. Rabcevicz [
21] proposed the new Austrian method, which is based on engineering experience and rock mechanics theory, emphasizing that the bearing capacity of surrounding rocks should be fully activated to form the bearing circle together with the support body. Dong et al. [
22] put forward the theory of loose circle, which proved that the larger the loose circle, the more violent the roadway bursting and deformation, and the more difficult the support. Hou et al. [
23] put forward the theory of surrounding rock strength strengthening, believing that the essence of bolt support is the interaction between bolt and surrounding rock to form an anchorage carrier, so as to jointly resist tunnel deformation. Lu et al. [
24] proposed the anchoring force mechanism of the bolt, believing that the bolt changes the strength and stress of the surrounding rock by applying the anchoring force to the surrounding rock. Therefore, many bolt control technologies are proposed, among which bolt and cable combined support technology is one of the most commonly used support forms in the current roadway [
25].
Combined support of bolt and cable generally refers to the combination of short bolt and long cable. The length of bolt is generally 1.8–2.5 m, and the length of the cable is usually 6–9 m. The short bolt compacts and strengthens the shallow surrounding rock, and improves the integrity of the shallow surrounding rock. Compared with the short bolt, the long cable can improve the stability of the surrounding rock by mobilizing the bearing capacity of the surrounding rock deeper in the roof. However, due to the short length of the bolt, the surrounding rock fracture exists extensively in and out of the bolt anchorage zone in practical engineering. Under the action of mining-induced pressure, the fracture is easy to expand and penetrate. The bolt anchorage zone has the characteristics of overall subsidence. At the same time, due to the limitation of construction machinery and tools, the pretension of cable is limited, which cannot effectively reinforce the large range of rock mass. The synergistic effect of cable is relatively limited, which is not conducive to resisting strong impact dynamic load [
26]. Therefore, in view of this problem, Zhang et al. [
27] proposed the control theory of continuous beam in coal roadway, which is to timely construct the thick prestressed anchored rock beam with more than the critical anchorage length in the roadway roof. The core idea is to restrain the expansion and connection of fractures in the anchorage zone, control the flexural deformation of the roof, avoid collapse and instability, and realize the safety of the roadway roof. Long bolts provide the supporting material required to construct thick-layer anchored rock beams, and the length of the bolts should generally reach 3.5–4.5 m. However, the rebar bolts cannot be bent and cannot meet the length requirements. Although the length of the anchor cable can meet the requirements, the installation and tightening time of the cable is too long, generally two to three times the installation time of the bolts, resulting in low tunneling efficiency and affecting the safe and efficient production of coal mines.
In this paper, by referring to the bolt nut installation method and the flexible rod material of the anchor cable, a flexible long bolt that is not restricted by the height of the roadway and can be installed quickly is developed. The performance test and analysis of the flexible bolt are carried out to determine the best specification. Finally, the flexible bolt is applied to the roadway with a composite roof, and the bearing law of the bolt and the deformation characteristics of the roadway surface are monitored.
2. Flexible Bolt
2.1. Components
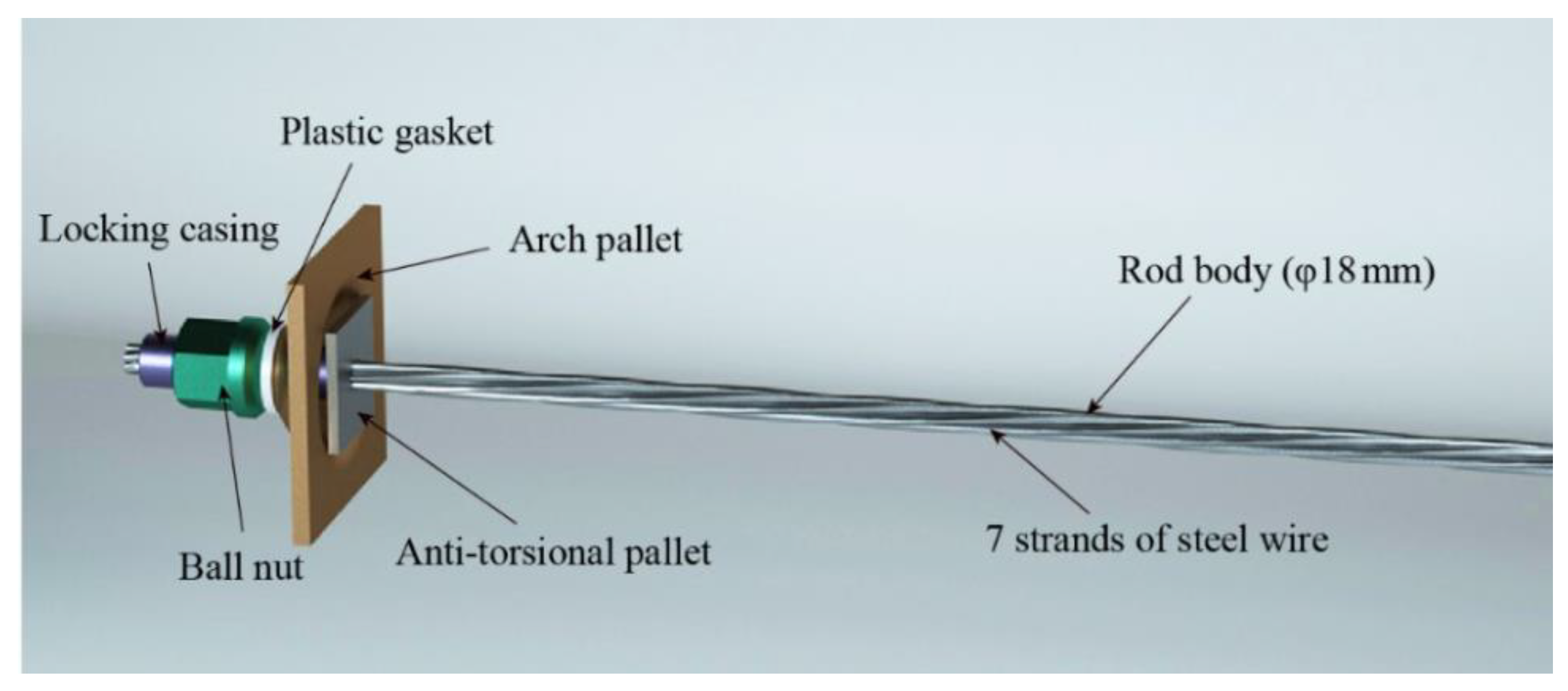
The flexible bolt is composed of rod body that is made of seven strands of steel wire, locking casing, spring, plastic gasket, ball nut, pallet, arch pallet, and anti-torsional pallet (as shown in
Figure 1). The locking casing and springs are extruded at one end of the rod body. After the rolling process, the outside of the locking casing is threaded to allow the installation of ball nut. Between the ball nut and arch pallet is an anti-torsional pallet to ease the friction between the ball nut and pallet, which enables a higher conversion of torque to pretension. The internal hole of the anti-torsional pallet is designed to be plum-shaped to prevent the rod body from rotation when pretension force is exerted on the flexible bolt.
2.2. Processing Course
The processing course is mainly divided into two processes: extrusion process and rolling process.
- (1)
Extrusion process
The equipment used in this process is an extrusion machine, as shown in
Figure 2a. The plastic gasket and locking casing are set at one end of the rod body in turn. The former is set at the inner side of the latter to increase the friction between the locking casing and rod body. Then the locking casing and the rod body are put into the V-shaped internal groove. The pushing gear of the extrusion machine seizes the rod body and pushes the locking casing out of the V-shaped internal groove. The plastic deformation occurring in the locking casing and plastic gasket locks them firmly with the rod body. The whole extrusion process is done.
- (2)
Rolling process
The equipment used in this process is a thread rolling machine, as shown in
Figure 2b. The extruded locking casing is set between two rollers and then the oil pipe and thread rolling machine are switched on. The smooth surface of the locking casing will then be threaded. By then, the flexible bolt is produced as designed, which is shown in
Figure 2c. Compared with the threading techniques by cutting, thread rolling technology can effectively improve the internal and external quality of the samples. The radial compressive stress produced in the processing course can improve remarkably the fatigue strength and torsional strength of the sample.
2.3. Installation Method
It is noteworthy in the installation process of a flexible bolt that the anti-torsional pallet should be set on the rod body first to make it contact the locking casing, and then the rod body is pushed into the bolt hole by the bolt driller. The anti-torsional pallet should be set just between the metal mesh on the roadway roof and the locking casing to produce greater friction between the anti-torsional and arch pallets and the roof metal mesh. In this case, when applying torque to the flexible bolt, its rod body will not rotate due to the restraint of the anti-torsional pallet, thus providing greater pretension force to prevent the early deformation of the roadway roof. Just like the ordinary rigid bolts, the flexible bolts can be preloaded simply with nuts, which save the trouble of tensioning installation of cable, thus improving the installation speed.
2.4. Advantage
- (1)
The flexible bolt is made of steel-stranded wire. The rod body can be bent, which can break through the limit of the excavation height, and then can build a thick anchor structure of roof, which greatly increases the flexural rigidity and strength of the roof, thus realizing the safety control of the roadway.
- (2)
The installation method of the flexible bolt is the same as an ordinary rigid bolt. It only needs to be pretightened with a nut, which avoids the installation of the cable tension type, greatly improving the installation speed of the flexible bolt, which is beneficial to increase the tunneling speed of the roadway.
- (3)
The yield strength of the flexible bolt body is 1860 MPa, which can resist large deformation of the surrounding rock.
3. Sample Preparation and Test Method
3.1. Sample Preparation
The roof anchorage quality of flexible bolts is determined by the friction between the locking casing and the rod body. If the friction is small, the locking casing will disengage the rod body under the action of roof pressure, thus causing the invalidation of flexible bolts. Since the size of rod body is fixed, the main factor that influences the friction between the locking casing and rod body is the size of the locking casing, to be specific, its diameter and length. Therefore, the optimal size of flexible bolts can be obtained through the tests on the diameters and lengths of locking casing.
A seven-strand steel wire whose diameter is 17.8 mm was selected as the rod body, with a length of 600 mm. The length of locking casing was set in three specifications: 100, 120, and 140 mm (as is shown in
Figure 3). The diameter of locking casing was set in three specifications, too: 30, 33, and 42 mm.
Table 1 lists the serial number of samples in accordance with the size of locking casing. As can be seen from the table, there were in total nine groups of specifications. To minimize the error, three samples were taken from each group. For the convenience of static tensile test in the laboratory, two locking casings of the same size were set at a distance of 30 mm away from each end of the rod body. As shown in
Figure 4, the samples of flexible bolt D1L2 were numbered as D1L2-1, D1L2-2, and D1L2-3 from the bottom up.
3.2. Test Equipment and Method
The MTS electrohydraulic servo system was used in this static tensile test. The model of this system is C64.106/1000 kN. As shown in
Figure 5, the MTS system is composed of two units: control unit and loading unit. The computer control unit analyzes and designs the loading program, which is then carried out by the loading unit. This tensile test employs a displacement load pattern, and the loading rate is 0.2 mm/s. As seen in
Figure 5, the steel laggings at the upper and lower end of the sample are clamped by the upper and lower fixtures of the MTS loading unit, respectively. Then the lower fixture moves downward to conduct the tensile test of the flexible bolt sample.
4. Static Tensile Test Results and Mechanical Analysis of Flexible Bolts
4.1. Flexible Bolts with Ø30 mm Locking Casing
Figure 6 and
Figure 7 show the mechanical response and failure mode of flexible bolts with Ø30 mm locking casing. As
Figure 6a shows, when the length of locking casing of the three bolt samples is 100 mm, the resistance change trend of the three samples are approximately the same: firstly, a sharp increase to the peak resistance, then a drastic decline, and then a slight increase for a long time, and finally oscillation fall. Before the bolt displacement reaches 15 mm, all three samples reach their respective peak resistances, but their peak resistances vary remarkably; the peak resistance of D1L1-1, D1L1-2, and D1L1-3 is 170 kN, 96 kN, and 236 kN, respectively. The higher the peak resistance, the greater the resistance decline. Meanwhile, the mechanical response of the three samples during the final failure is different from each other. The resistance change curves also demonstrate that the bolt performance is unstable when the length of locking casing is 100 mm. When the displacement of D1L1-2 sample reaches 55 mm, its resistance remains unchanged; in other words, the bolt is in a constant resistance state. This indicates that the locking casing is being pulled out at a constant speed and the friction between the locking casing and rod body sets off the resistance. However, in the final test phase of D1L1-1and D1L1-3 samples, the resistance experiences an oscillation fall, indicating that the spring in the locking casing is breaking gradually, which in turn causes the constant change of friction between the locking casing and rod body. From
Figure 7a, it can be seen that the steel-wire rod body does not fail; the locking casings of the three samples are pulled out, leaving long and fresh scratches on the rod body. The displacement in the test is mostly the relative displacement between the locking casing and rod body. The length of scratch on the rod body is naturally the length of relative displacement.
From
Figure 6b, it can be known that when the length of the locking casing of the three bolt samples is 120 mm, the trend of the resistance change of the three samples is approximately the same and the peak resistances are quite close to each other. Before the bolt displacement reaches 20 mm, the bolt resistance increases linearly with the displacement and the bolt is in quasi-elastic stage. When the displacement exceeds 20 mm, the bolt is in a yield stage and the increase of bolt resistance slows down remarkably compared with that of the quasi-elastic stage. Finally, the resistance reaches its peak resistance. The peak resistance of D1L1-1, D1L1-2, and D1L1-3 is 332, 338, and 351 kN, and the corresponding displacement is 24.65, 32.12, and 31.24 mm, respectively. After reaching the peak resistance, breakage occurs in the bolts of all three samples. New characteristics appear in the failure mode and mechanical response. To be specific, sequential breakage of steel wire is the main characteristic. Each breakage of the steel wire is followed by a slight rise of bolt resistance, but the resistance is smaller than the peak resistance of the preceding breakage. In other words, after each breakage, the peak resistance reduces by stage. Meanwhile, the number of stage peak resistances also denotes the number of broken steel wires. Take D1L2-3 as an example, there are four stage peak resistances in bolt resistance, indicating that there are four steel wires breaking during the static tensile test. From
Figure 7b, it can be known that the characteristics of bolt failure change when the length of locking casing increases. The failure mode turns from locking casing being pulled out to steel wire breaking by stage. The breakage positions of the steel wires are all located in the area where the locking casing and rod body contact, indicating that the locking casing does certain damage to the steel-wire rod body in the extrusion process.
From
Figure 6c, it can be known that when the length of the locking casing of the three samples further increases to 140 mm, the resistance change trend of the three samples are quite similar to what is shown in
Figure 6b. To be specific, the bolt resistance also has three stages: quasi-elastic, yield, and late breaking stage. Similar to the case of 120 mm-long locking casing, the displacement amount is about 20 mm when the bolt enters yield stage. The peak resistance of D1L1-1, D1L1-2, and D1L1-3 is 356, 358, and 350 kN, with corresponding displacements of 31.16, 36.00, and 31.44 mm, respectively. As the length of locking casing increases, the friction between the locking casing and rod body increases correspondingly, which causes more steel wires breakages in sample D1L3 than in sample D1L2 in the late failure stage. As is shown in
Figure 7c, the number of steel wire breakage all exceeds four. In addition, the impact force of steel wire breakage bends the steel wire remarkably.
4.2. Flexible Bolts with Ø33 mm Locking Casing
Figure 8 and
Figure 9 show the mechanical response and failure mode of flexible bolts with Ø33 mm locking casing. As shown in
Figure 8a, when the length of the locking casing of the three bolt samples is 100 mm, the bolt resistance shows an overall change trend of sharp rise and sharp fall. Before the bolt displacement reaches 22 mm, all three samples reach their peak resistances. The peak resistance of D2L1-1and D2L1-3 is 311 and 303 kN, respectively, but that of D2L1-2 is relatively small, 197 kN. During the late breaking stage, drastic variations appear between D2L1-1 and the other two samples. The resistance of D2L1-1 witnesses a sharp decline from peak resistance to its minimum. By contrast, the resistance of D2L1-2 and D2L1-3 experiences a long and relatively mild decline, the displacement reaching 112 and 78 mm, respectively. As is shown in
Figure 9a, the core steel wire of D2L1-1 breaks, causing the resistance to drop suddenly to below 60 kN. The rate of resistance drop reaches up to 80%, triggering the prewarning of the MTS system and in turn terminating the static tensile test. No damage is done to the locking casing of D2L1-2 and D2L1-3. Instead, the locking casing is just pulled out and leaves long scratches on the rod body.
From
Figure 8b, it can be known that when the length of the locking casing of the three bolt samples is 120 mm, the resistance change trend of the three samples is approximately the same. During the quasi-elastic stage, the gradient of the three samples varies slightly: that of D2L2-1 takes the lead and is followed by that of D2L2-3 while the gradient of D2L2-2 is the smallest. However, during the yield stage, the resistance change curve of the three samples is virtually close. During the breaking stage, the bolt samples show a characteristic of sequential breakage. The peak resistance of D2L2-1, D2L2-2, and D2L2-3 is 372, 373, and 369 kN, respectively. As shown in
Figure 8b, all three sample bolts have a serious deformation, and many steel wires have broken.
From
Figure 8c, it can be known that when the length of the locking casing of the three samples further increases to 140 mm, the resistance change trend of D2L3-2 and D2L3-3 is quite similar. To be specific, the bolt resistance also experiences three stages: quasi-elastic stage, yield stage, and late breaking stage. However, remarkable variation appears between the two samples and D2L3-1, whose peak resistance is 228 kN, being only 62% of the other two samples. After the peak resistance, as the displacement of D2L3-1 increases, the bolt resistance decreases slowly. This is mainly because the friction between the locking casing and rod body declines gradually when the locking casing is pulled out. During the final breaking stage, the resistance shows a characteristic cyclic oscillation rise. This is mainly because the springs in the locking casing break by stage and new friction is produced between the broken springs and rod body, which in turn increases the resistance. As is shown in
Figure 8c, no steel wire breaks in D2L3-1, only leaving scratches on the rod body. Five steel wires break in D2L3-2 and one wire breaks in D2L3-3, which is in line with the change trend shown in
Figure 8c.
4.3. Flexible Bolts with Ø42 mm Locking Casing
Figure 10 and
Figure 11 show the mechanical response and failure mode of flexible bolts with Ø42 mm locking casing. As shown in
Figure 10a, when the length of the locking casing of the three bolt samples is 100 mm, the resistance change trend of the three samples are approximately the same: firstly, a sharp increase to the peak resistance, then a drastic decline, and finally a long constant resistance deformation. Before the bolt displacement reaches 20 mm, all the three samples reach their respective peak resistances: D3L1-1, 333 kN; D3L1-2, 328 kN; and D3L1-3, 339 kN. After the peak resistance, the locking casings of the three samples are all pulled out, causing a sharp decline in bolt resistance, which is finally maintained within 80–120 kN. In the process of the locking casing being pulled out, the displacement of all three sample bolts increases continuously, but the resistance does not change remarkably. The final displacement of the three samples is 100, 63, and 75 mm. As can be seen from
Figure 11a, no failure occurs to the rod body of the three samples, and the steel wires do not loosen, either. However, the locking casings of the three samples are pulled out to different degrees, leaving scratches of different length on the rod body.
From
Figure 10b, it can be known that when the length of the locking casing of the three bolt samples is 120 mm, the resistance change curves of the three samples are approximately the same during the quasi-elastic stage. However, during the yield stage and breaking stage, the resistance change trend varies. The bolts of D3L2-2 and D3L2-3 have a similar change during the yield stage; when reaching the peak resistance, one steel wire breaks, causing the instant drop of resistance. In addition, the locking casing of D3L2-2 shows a slight trace of being pulled out. The resistance of D3L2-1 fluctuates slightly during the yield stage; its locking casing is pulled out during the breaking stage and its final displacement exceeds 90 mm. As can be seen from
Figure 11b, the deformation of all three sample bolts is rather slight: the locking casing of D3L2-1 is pulled out, and the core steel wire of D3L2-2 and D3L2-3 is broken.
From
Figure 8c, it can be known that when the length of the locking casing of the three samples further increases to 140 mm, the resistance change trend of the three samples differs. For D3L3-1, its locking casing is pulled out after the quasi-elastic stage and yield stage, causing the instant drop of bolt resistance and the subsequent long constant resistance state. For D3L3-2, its displacement is rather small during the yield stage until its locking casing is pulled out. When its resistance drops to 160 kN, it has a long constant resistance deformation. Its final displacement reaches 83 mm. For D3L3-3, its steel wires are broken after the quasi-elastic stage and yield stage. The peak resistance of D3L3-1, D3L3-2, and D3L3-3 is 362, 345, and 369 kN. As is shown in
Figure 11c, the locking casings of D3L3-1 and D3L3-2 are pulled out to different degrees. Three steel wires are broken in the rod body of D3L3-3 and the rod body bends remarkably, with the wires loosened. What is shown in
Figure 11c is in line with the resistance change trend shown in
Figure 10c.
The drastic increase in the diameter of locking casing causes the reduction of socketed force between the locking casing and rod body, which in turn leads to the slip of rod body and invalidation of flexible bolts in the end.
4.4. Analysis and Discussion of Test Results
4.4.1. Determination of Locking Casing Specifications
Table 2 lists the mechanical parameters of nine groups of flexible bolts with different specifications. As shown in the table, the diameter and length of locking casing are of great influence on the mechanical property of flexible bolts. When the diameter of locking casing is 30 mm, the average peak resistance of D1L1, D1L2, and D1L3 is 167, 340, and 355 kN, and the corresponding displacement is 11.98, 29.50, and 32.87 mm, respectively. Compared with those of D1L1, the peak resistance and corresponding displacement of D1L2 rise by 104% and 146%, respectively, whereas those of D1L3 are only 4% and 11% higher than D1L2. When the diameter of the locking casing is 33 mm, the average peak resistance of D2L1, D2L2, and D2L3 is 270, 371, and 369 kN, and the corresponding displacement is 19.68, 32.59, and 34.81, respectively. Compared with those of D2L1, the peak resistance and corresponding displacement of D2L2 rise by 37% and 66%, respectively, whereas those of D2L3 are only −1% and 7% higher than D2L2. When the diameter of the locking casing is 42 mm, the average peak resistance of D3L1, D3L2, and D3L3 is 333, 356, and 359 kN, respectively, and the corresponding displacement is 18.25, 25.94, and 26.85 mm, respectively. Compared with those of D3L1, the peak resistance and corresponding displacement of D3L2 rise by 7% and 42%, respectively, whereas those of D3L3 are only 1% and 4% higher than D3L2. As can be deduced from this analysis, when the diameter of locking casing is fixed, the bolt resistance tends to increase as the length of locking casing increases, but the increased amplitude tends to narrow down gradually. When the length of locking casing is 120 mm, the flexible bolt demonstrates a much better and more stable mechanical property than in the case of 100 mm. When the length of locking casing is 140 mm, the mechanical property of the flexible bolt does not show much difference from the case of 120 mm; in other words, its mechanical property does not rise remarkably. Thus, in view of the processing cost of flexible bolts, the length of locking casing is determined to be 120 mm.
As is shown in
Table 2, when the length of locking casing is 120 mm, the average peak resistance of D1L2, D2L2, and D3L2 is 340, 371, and 356 kN, respectively. The peak resistance increases as the diameter of locking casing increases. However, it can be known from
Figure 6,
Figure 8, and
Figure 10 that the locking casing of D3L2 can be pulled out easily after its peak resistance, demonstrating less stability than D1L2 and D2L2. Accordingly, the Ø42 mm locking casing cannot meet the safety demand. Moreover, the thread of the Ø30 mm locking casing is the first-sequence thread while that of Ø33 mm is the second-sequence thread. Therefore, in consideration of the match between flexible bolt and construction equipment like bolt drillers, and the later promotion and application, the diameter of locking casing is determined to be 30 mm.
4.4.2. Mechanism of Action between Locking Casing and Rod Body
Figure 12 illustrates schematically the tail structure of flexible bolt and the situation where the locking casing is pulled out. As shown in
Figure 12a, the tail structure of the flexible bolt is composed of locking casing, spring, and rod body. The locking casing and spring are extruded together onto the rod body by the extrusion machine (as shown in
Figure 2a).
Figure 12b presents a cross-sectional view of the tail structure after extrusion. Under the action of extrusion force, the locking casing would deform plastically, thus producing great holding force on the rod body. Meanwhile, since the cross-section of the spring is triangular, it will embed into the inner side of locking casing and the surface of rod body, increasing the friction between locking casing and rod body, and thus guaranteeing that the locking casing will not slip. Since the rigidity of locking casing is much lower than that of flexible bolt, the spring will not do serious damage to the rod body. The results of static tensile test also illustrate that the damage done by the spring does not influence the bearing capacity of flexible bolts. Kang et al. [
28] conducted static tensile tests through which the peak resistance of cable was obtained to be approximately 341 kN. By contrast, the average peak resistance of D1L1 flexible bolts is 340 kN. Thus, it can be concluded that the damage done by the locking casing to the bolt is very slight.
Figure 12c shows the failure mode when the locking casing is pulled out. As can be known from
Section 4.3, when the diameter of the locking casing is too large or the length is too short, the mechanical property of flexible bolts becomes unstable. When the peak resistance is reached, the locking casing can be pulled out easily. In the course of locking casing being pulled out, the spring breaks into some small segments (as shown in
Figure 12d), indicating that the spring is indeed embedded into the inner side of the locking casing after the extrusion process and produces greater friction. However, when the diameter is 42 mm or the length is 100 mm, the friction between locking casing and rod body is insufficient to resist greater tensile force. With proper specifications (length: 120 mm; diameter: 30 mm), the steel wires break in turn and the locking casing is not pulled out. This failure mode reflects the most stable mechanical property of flexible bolts, thus enabling the flexible bolts to resist the great deformation in the roadway surrounding rock.
5. Cyclic Mechanical Property of Flexible Bolts
The friction between rod body and locking casing has a direct impact on the mechanical property of flexible bolts. Therefore, before the engineering application, it is necessary to study further the mechanical characteristics of flexible bolts under cyclic dynamic loading. An MTS electrohydraulic servo system was used to conduct cyclic loading–unloading tests to two groups of flexible bolts (Group A and Group B). The diameter and length of the locking casing are 30 mm and 120 mm, respectively (same as D1L2). The cyclic loading was divided into two modes: equal-lower-limit-and-equiamplitude loading, and increasing-lower-limit-and-equiamplitude loading. The mechanical responses of the two loading modes are shown in
Figure 13 and
Figure 14, respectively.
As is shown in
Figure 13, a single tensile resistance–displacement curve is added as a reference to the result of the noncyclic static tensile test. The test results indicate that the tensile resistance– displacement curve is divided into three stages: quasi-elastic stage (OD), yield stage (DE), and breaking stage (EF). The yield resistance and peak resistance are 288 and 340 kN, respectively. The equal-lower-limit-and-equiamplitude cyclic loading tests were conducted with flexible bolts (numbered as A1~A4). The loading mode follows: when the tensile force upon the flexible bolts (A1~A4) reaches 280, 300, 320, and 340 kN, respectively, cyclic loading is initiated with an amplitude of 200 kN; the lower limits of tensile force upon the four flexible bolts (A1~A4) are 80, 100, 120, and 140 kN, respectively. Cyclic loading is repeated 50 times; when cyclic loading is finished, tensile force is exerted on the bolts continuously until they break.
As can be seen from
Figure 13, the upper limit of cyclic loading on the A1 bolt is located in the quasi-elastic stage; most of the deformation can be restored and the relative displacement corresponding to the cyclic loading–unloading stroke reaches 1.4 mm. The residual deformation is mainly ascribed to the fact that the steel-strand rod body is tensioned. The upper limits of cyclic loading on A2~A4 bolts are all located in the yield stage; the deformation can still be partially restored and the relative displacements corresponding to the cyclic loading–unloading strokes finally reach 2.2, 3.7, and 6.0 mm, respectively. As the upper limit of cyclic loading increases constantly, the residual deformation rises correspondingly, whereas the resilience declines gradually. The ultimate peak tensile forces of A1~A4 bolts are 350, 348, 335, and 354 kN, respectively, with a mean peak force of 347 kN. Thus it can be seen that in contrast to the flexible bolts without cyclic loading, the peak resistance of the flexible bolts that undergo cyclic loading does not vary much, although it displays a slight rise. This indicates that cyclic loading does not change fundamentally the stress state within the bolt, which in turn makes it possible for the bolt to maintain its mechanical property. The gradual changes in loading–unloading amplitude, upper limit, and lower limit demonstrate that the mechanical property of flexible bolts is determined by the upper limit of cyclic loading, whereas the unloading amplitude and lower limit do not affect the mechanical property significantly. Furthermore, it proves that the support system of flexible bolts is not affected much by the stress adjustment and small impact disturbance caused by the roadway excavation.
Figure 14 displays the tensile resistance–displacement curve of increasing-lower-limit-and-equiamplitude cyclic loading. Its loading–unloading mode follows: 120 kN↘ 80 kN↗ 140 kN↘ 100 kN↗ 160 kN↘ 120 kN↗⋯; the unloading amplitude is 40 kN and the loading amplitude is 60 kN, and the resistance of upper and lower limit increases by 20 kN for every loading–unloading cycle period.
As can be seen from
Figure 14, B1 bolt reaches its peak resistance force after eleven cycle periods and then breaks during the twelfth period; its peak resistance force is 345 kN. In terms of its general evolution characteristics, the tensile resistance–displacement curve of B1 is also divided into three stages, which is similar to the case of bolts without cyclic loading. To be specific, the first nine cycle periods are located in the quasi-elastic stage; the last three cycle periods are located in the yield stage. The tensile resistance–displacement curve appears to be virtually linear when the flexible bolt undergoes cyclic loading–unloading, displaying remarkable characteristics of linear elasticity. No apparent “hysteresis loop” is observed, which often appears in rocks. At the same time, it is found that in the quasi-elastic stage, the displacement of contiguous cycle periods varies slightly. To be specific, the displacement between the sixth and seventh cycle periods is highly close to that between the seventh and eighth periods. However, in the yield stage, the displacement of contiguous cycle periods varies significantly; in addition, the displacement within one cycle period is also relatively large. This indicates that plastic deformation occurred to the flexible bolt in the yield stage. Moreover, this further reveals that during the initial period of roadway support, when deformation is to occur to the surrounding rock, the prestressed flexible bolts can bear the load immediately. The bolts can bear the stress fluctuation caused by stress adjustment in the mine even when the axial load of the bolts increases.
6. Engineering Application
As shown by the static tensile test and cyclic dynamic load test conducted, the mechanical property of flexible bolts remains stable under the conditions of static and dynamic load. Due to the relatively large friction between the locking casing and steel-strand bolt, no slipping and damage occurs. Accordingly, it can be concluded that flexible bolts can adapt to the stress fluctuation and the impact of dynamic load in the process of driftage.
Currently, the flexible bolts have been popularized and applied in the Yaoqiao Coal Mine in Jiangsu Province. Through the feedback of engineering practice in the coal mines, the control effect of roadway surrounding rock is very good, and the roadway efficiency is greatly improved. Next, this paper introduces the geological situation and monitoring condition of the coal mine in detail.
6.1. Geological Background
Flexible bolts were applied in Yaoqiao Coal Mine, Xuzhou city, Jiangsu province, China. As a relatively large coal mine in the east of China, the mine has an annual raw coal output of 4.45 million tons. The mining area extends 13.70 km from east to west, and 4.65 km from south to north, covering an area of approximately 63.8 km2. The mining depth stretches from −135 to −1300 m. The complex geological environment of this coal mine makes roadway deformation a prominent problem in the actual mining process. Therefore, it is highly appropriate to apply flexible bolts in this coal mine. This test lays a solid foundation for the future application and promotion of flexible bolts.
The material roadway of the 7704 working face is selected as the testing zone. The coal seam where this roadway is located is the 7# coal seam whose burial depth is 170–1335 m and whose thickness is 1.38–9.86 m. The average thickness of coal seam is 4.8 m and the average dip angle of the coal seam is 13°.
6.2. Supporting Design
The section of this roadway is rectangular, 4800 mm in width, and 3200 mm in height. With an area of 15.36 m
2, this roadway can be classified as roadway with large openings. In view of the geological environment and stress conditions of the roadway, a new bolt support design is put forward, as shown in
Figure 15.
The roof is supported solely by flexible bolts whose diameter and length are 17.8 mm and 4080 mm, respectively. Four bolts are arranged in a row with a bolt spacing of 1400 mm and row spacing of 1000 mm. All bolts are installed vertical to the roof. For each flexible bolt, two epoxy resin anchoring agents (23 mm diameter and 60 mm length) and one arch-pallet (size: 300 × 300 × 10 mm) are provided. The steel mesh on the roof is 4800 × 1100 mm in size and 4.5 mm in diameter. The overlapping length of steel meshes is 100 mm. The preload of bolts is no lower than 80 kN.
The rib is supported by screw steel bolts whose diameter is 20 mm and length is 2000 mm. In total, eight bolts are arranged on both ribs, four at one rib with the bolt spacing 900 mm and row spacing 1000 mm. For each bolt, two epoxy resin anchoring agents (23 mm diameter and 60 mm length) and one arch-pallet (size: 150 × 150 × 10 mm) are provided. Diamond metal mesh is used in the coal pillar rib and plastic mesh is used in the mining rib. The preload of bolts is no lower than 30 kN.
6.3. Monitoring Scheme and Results
To master the bearing law of flexible bolts and the corresponding control over the roadway surrounding rock, it is of necessity to monitor the axial load of the bolts, the surface displacement of roadway, and the development law of surrounding rock fractures. Two monitoring stations for bolt axial load (a1 and a2), one monitoring station for surface displacement (b), and one monitoring station for borehole camera images (c), are set in the testing zone.
Figure 16 shows the monitoring results.
Figure 16a shows the results of axial load of flexible bolts. As shown in the dynamometers a1 and a2, the preload is 80.5 and 84.5 kN, respectively. Within the distance of 10 m to the excavation face, the axial load increases sharply by 20%. Since the bolts are in high-stress quasi-elastic stage, the bolts come to function rapidly in response to any deformation in the surrounding rock of the roof, thus bringing the early roadway deformation under control [
27]. Within the distance of 80 m to the excavation face, the axial load increases slightly. During this period, the roof deformation develops at a quite limited rate. The dynamometers a1 and a2 show that the axial load is fixed finally at 109 and 104 kN, respectively. The development law of axial load demonstrates that flexible bolts can adjust to the surrounding rock deformation and thus achieve the final goal of bringing it under control.
Figure 16b shows the monitoring results of surface displacement in the roadway. Similar to the axial load, the surface displacement also rises sharply at first, then experiences a mild increase, and tends to be stable in the end. The sharp rise in roadway displacement occurs within the distance of 20 m to the excavation face; the mild increase appears within the distance of 90 m to the excavation face. From this analysis, it can be known that compared with bolt stress, roadway deformation possesses some degree of delay. The final subsidence of the roof is 15 mm and the rib convergence is 23 mm.
Figure 16c presents the monitoring results of borehole camera on the roof. This borehole is set in the middle of the testing zone. Through observing the situation of borehole wall, the fracture development in the roof surrounding rock can be deduced indirectly. As shown in the figure, there exist one case of serious damage and two annular fractures within the depth of 1.0 m in the roof. Within this area (top-coal), deformation and damage occur easily under the action of stress. Within the depth of 1.0–2.5 m, there exist two tiny fractures, and beyond the depth of 2.5 m, no fracture or separation layer is observed.
With the support of flexible bolts, the control effect on the roadway surrounding rock is improved remarkably, as can be seen in
Figure 17 (the photos taken on the scene). The even transmission of roof stress improves the roof pressure on the ribs, which in turn lessens the damage on the ribs and realizes a virtuous cycle.
6.4. Analysis and Discussion
The surrounding rock damage after excavation shows a characteristic of circular distribution [
26]. Macro damage would occur in the shallow surrounding rock and the fractures have certain openings. Accordingly, the shallow surrounding rock belongs to a strong fracture circle. Rock body damage would occur in the deep surrounding rock, but no noticeable fractures can be observed. Thus, the deep surrounding rock still possesses a strong bearing capacity, belonging to a weak fracture circle. There is no damage in the deeper surrounding rock. The rock body only deforms elastically and can transmit the stress continuously, thus belonging to an elastic circle. In this case, the bolt support should penetrate the fracture circles to locate the anchorage point within the elastic circle, thus realizing transboundary support. The large-scale displacement in the shallow surrounding rock can be restrained through the small-scale displacement in the deep surrounding rock, hence controlling the rock body damage and inhibiting fracture development in the surrounding rock [
29,
30].
Limited by the excavation height and construction equipment, the bolts are usually installed within the range of fracture circles in the actual construction practices. Accordingly, the surrounding rock damage would deteriorate to some degree. The innovative flexible bolt structure can solve this difficult problem. The flexibility of steel-wire rod body can guarantee the sufficient length of the bolts. Meanwhile, the bolt end can be preloaded with ball nut, which makes it unnecessary to prestress the steel-wire rod body with locksets. In this way, fast installation can be realized, saving up to 50% installation time.
The fracture circles extend to 2.5 m deep in the roadway roof in this test and the roadway is 3200 mm high. In view of the existence of float coal on the roadway floor, the maximum length of rigid bolts can be no longer than 2.5 m, thus failing to meet the demand of transboundary support. By contrast, the length of flexible bolts reaches 4080 mm and the anchored segment is located in the elastic circle of the surrounding rock. In this case, the roof can become a thick anchored rock beam, improving the flexural rigidity of the roof to a noticeable degree. Meanwhile, the increase of anchorage depth makes it possible to reduce the number of flexible bolts needed, thus increasing the rate of bolt support. The preload of flexible bolts is set at 80 kN and the flexible bolts are in the quasi-elastic stage (
Figure 6b). When minor deformation occurs in the roof surrounding rock, the flexible bolts can function rapidly to inhibit further development of fractures, which guarantees the integrity of roof as well as the excavation safety.
7. Conclusions
Through innovation to the tail structure of flexible bolts, the installation of flexible bolts is free from the limitation of excavation height. The locking casing and the spring are extruded onto the rod body of flexible bolts at first. The extruded locking casing is then processed by a thread rolling machine. In this way, the flexible bolts can be installed in the same way as the rigid bolts, thus realizing the fast installation and improving the bolt support speed.
The static tensile test results show that the diameter and length of locking casing exerts great impact on the mechanical property of flexible bolts. When the diameter of locking casing is fixed, the peak resistance and its corresponding displacement increase as the length of locking casing increases, but the increased amplitude tends to reduce gradually. When the length of locking casing is fixed, too large a diameter would make the mechanical property unstable. Through laboratory tests, the locking casing specifications to be applied in the field test are determined as follows: length: 120 mm; diameter: 30 mm; peak resistance: over 330 kN; corresponding displacement: over 25 mm. The flexible bolt can control the roof deformation in time by increasing the resistance rapidly, but at the same time it leaves some margin for minor deformation. The mechanical property of the flexible bolts is rather stable: no locking casing is pulled out to invalidate the bolt support. The failure mode is that the steel wires break in turn.
As shown in the cyclic dynamic loading test compared with that of static tensile test, the peak resistance force of flexible bolts witnesses a slight rise to 347 kN on average after cyclic loading. This indicates that the mechanical property of flexible bolts remains stable after cyclic loading. In other words, flexible bolts can adapt to the stress fluctuation caused by the roadway excavation.
The field test results show that the 4080 mm-long flexible bolts can penetrate the fracture circles of the roadway roof and anchor directly on the elastic circle. In this case, the thickness of the anchoring layer increases noticeably, which in turn strengthens the flexural rigidity of the roof and guarantees the roadway safety. The ball nut can be screwed up to the rod body by bolt driller directly, saving the installation time by up to 50% and achieving timely support.
In addition, the single support by flexible bolts can avoid the construction mess, which used to be a common occurrence when bolts of various specifications are used. Meanwhile, the number of flexible bolts in each row is reduced to four. This can increase the speed of bolt support, which in turn improves driving efficiency.
Author Contributions
Data curation, Z.X.; formal analysis, Z.X., J.W., and M.S.; funding acquisition, N.Z.; investigation, Z.X., N.Z., and Q.W.; writing—original draft, Z.X.; writing—review and editing, Z.X., N.Z., Q.W., and J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study is financially supported by the Fundamental Research Funds for the Central Universities (2020ZDPYZD02).
Conflicts of Interest
The authors declare no conflict of interest.
References
- He, M.C. Latest progress of soft rock mechanics and engineering in China. J. Rock Mech. Geotech. Eng. 2014, 4, 165–179. [Google Scholar] [CrossRef]
- Ju, Y.; Zhu, Y.; Xie, H.P.; Nie, X.D.; Zhang, Y.; Lu, C.; Gao, F. Fluidized mining and in-situ transformation of deep underground coal resources: A novel approach to ensuring safe, environmentally friendly, low-carbon, and clean utilisation. Int. J. Coal Sci. Technol. 2019, 6, 184–196. [Google Scholar] [CrossRef]
- Vervoort, A. Various phases in surface movements linked to deep coal longwall mining: From start-up till the period after closure. Int. J. Coal Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Ortlepp, W.D.; Stacey, T.R. Performance of tunnel support under large deformation static and dynamic loading. Tunn. Undergr. Space Tech. 1998, 13, 15–21. [Google Scholar] [CrossRef]
- Smith, J.A.; Ramandi, H.L.; Zhang, C.G.; Timms, W. Analysis of the influence of groundwater and the stress regime on bolt behaviour in underground coal mines. Int. J. Coal Sci. Technol. 2019, 6, 286–300. [Google Scholar] [CrossRef]
- Liang, M.F.; Fang, X.Q. Application of fiber bragg grating sensing technology for bolt force status monitoring in roadways. Appl. Sci. 2018, 8, 107. [Google Scholar] [CrossRef]
- Hoek, E.; Kaiser, P.K.; Bawden, W.F. Support of Underground Excavations in Hard Rock; A.A. Balkema: Rotterdam, The Netherlands; Brookfield, VT, USA, 1995. [Google Scholar]
- Li, D.Q.; Masoumi, H.; Hagan, P.C.; Saydam, S. Experimental and analytical study on the mechanical behaviour of cable bolts subjected to axial loading and constant normal stiffness. Int. J. Rock Mech. Min. Sci. 2019, 113, 83–91. [Google Scholar] [CrossRef]
- Li, D.Q.; Masoumi, H.; Saydam, S.; Hagan, P.C. Mechanical characterisation of modified cable bolts under axial loading: An extensive parametric study. Rock Mech. Rock Eng. 2018, 51, 2895–2910. [Google Scholar] [CrossRef]
- Wu, Y.; Hao, Y.; Tao, J.; Teng, Y.; Dong, X. Non-destructive testing on anchorage quality of hollow grouted rock bolt for application in tunneling, lessons learned from their uses in coal mines. Tunn. Undergr. Space Tech. 2019, 93, 103094. [Google Scholar] [CrossRef]
- Cai, M.; Champaigne, D. Infuence of bolt-grout bonding on MCB conebolt performance. Int. J. Rock Mech. Min. Sci. 2012, 49, 165–175. [Google Scholar] [CrossRef]
- Scott, J. Friction rock stabilizers and their application to ground control problems. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1974, 26, 51. [Google Scholar]
- Wang, X.Y.; Bai, J.B.; Guo, G.L.; Yu, Y. Test and application of hydraulic expansion bolts in a roadway under goaf with ultrarclose separation. Int. J. Min. Sci. Technol. 2014, 24, 839–846. [Google Scholar] [CrossRef]
- Pells, P.; Bertuzzi, R. Permanent rockbolts-the problems are in the detail. In Proceedings of the Tenth Australian Tunneling Conference Melbourne Australia, Melbourne, Australia, 21–24 March 1999. [Google Scholar]
- Yan, S.; Song, Y.B.; Bai, J.B.; Elmo, D. A study on the failure of resin end-anchored rockbolts subjected to tensile load. Rock Mech. Rock Eng. 2018, 52, 1917–1930. [Google Scholar] [CrossRef]
- Feng, X.W.; Zhang, N.; Yang, S.; He, F.Z. Mechanical response of fully bonded bolts under cyclic load. Int. J. Rock Mech. Min. Sci. 2018, 109, 138–154. [Google Scholar] [CrossRef]
- Li, C.C.; Doucet, C. Performance of D-bolts under dynamic loading. Rock Mech. Rock Eng. 2012, 45, 193–204. [Google Scholar] [CrossRef]
- Hyett, A.J.; Bawden, W.F.; Reichert, R.D. The effect of rock mass confinement on the bond strength of fully grouted cable bolts. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1992, 29, 503–524. [Google Scholar] [CrossRef]
- Wu, C.; Yuan, C.X.; Wen, G.J.; Han, L.; Liu, H.J. A dynamic evaluation technique for assessing gas output from coal seams during commingling production within a coalbed methane well: A case study from the Qinshui Basin. Int. J. Coal Sci. Technol. 2020, 7, 122–132. [Google Scholar] [CrossRef]
- Zuo, J.P.; Wang, J.T.; Jiang, Y.Q. Macro/meso failure behavior of surrounding rock in deep roadway and its control technology. Int. J. Coal Sci. Technol. 2019, 6, 301–319. [Google Scholar] [CrossRef]
- Wilhelm, G. Roadway support development and planning. Glueckauf 1984, 120, 395–396. [Google Scholar]
- Dong, F.T.; Song, H.W.; Guo, Z.H.; Lu, S.M.; Liang, S.J. Support theory of loose surrounding rock zone of roadway. J. China Coal Soc. 1994, 19, 21–32. [Google Scholar]
- Hou, C.J.; Gou, P.F. Mechanism study on strength enhancement for the rocks surrounding roadway supported by bolt. Chin. J. Rock Mech. Eng. 2000, 19, 342–345. [Google Scholar]
- Lu, S.L.; Fu, G.B.; Tang, L. Regularity of deformation of rocks around roadway under mining influence and change of rockbolt resistance. J. China Univ. Min. Technol. 1999, 28, 1–3. [Google Scholar]
- Kang, H.P. Sixty years development and prospects of rock bolting technology for underground coal mine roadways in China. J. China Univ. Min. Technol. 2016, 45, 1071–1081. [Google Scholar]
- Xie, Z.Z.; Zhang, N.; Feng, X.W.; Liang, D.X.; Wei, Q.; Weng, M.Y. Investigation on the evolution and control of surrounding rock fracture under different supporting conditions in deep roadway during excavation period. Int. J. Rock Mech. Min. Sci. 2019, 123, 104122. [Google Scholar] [CrossRef]
- Zhang, N.; Han, C.L.; Xie, Z.Z. Theory of continuous beam control and high efficiency supporting technology in coal roadway. J. Min. Strata Control. Eng. 2019, 1, 48–55. [Google Scholar]
- Kang, H.P.; Yang, J.H.; Jiang, P.F. Tests and analysis on mechanical properties for cable bolts. Coal Sci. Technol. 2015, 6, 29–33. [Google Scholar]
- Wang, B.; Dang, F.; Chao, W.; Miao, Y.P.; Li, J.; Chen, F. Surrounding rock deformation and stress evolution in pre-driven longwall recovery rooms at the end of mining stage. Int. J. Coal Sci. Technol. 2019, 6, 536–546. [Google Scholar] [CrossRef]
- Wang, H.W.; Xue, S.; Jiang, Y.D.; Deng, D.X.; Shi, S.Z.; Zhang, D.Q. Field investigation of a roof fall accident and large roadway deformation under geologically complex Conditions in an underground coal mine. Rock Mech. Rock Eng. 2018, 51, 1863–1883. [Google Scholar] [CrossRef]
Figure 1.
Schematic diagram of a flexible bolt.
Figure 1.
Schematic diagram of a flexible bolt.
Figure 2.
Processing course of flexible bolt: (a) extrusion process, (b) rolling process, (c) flexible bolt.
Figure 2.
Processing course of flexible bolt: (a) extrusion process, (b) rolling process, (c) flexible bolt.
Figure 3.
Length measurement of locking casing.
Figure 3.
Length measurement of locking casing.
Figure 4.
Sample of flexible bolt.
Figure 4.
Sample of flexible bolt.
Figure 5.
Test equipment: (A) denotes the rod body, (B) refers to the locking casing, (C) indicates the steel lagging, and (D) shows the nut.
Figure 5.
Test equipment: (A) denotes the rod body, (B) refers to the locking casing, (C) indicates the steel lagging, and (D) shows the nut.
Figure 6.
Mechanical response of flexible bolts with different Ø30 mm locking casing lengths: (a) 100 mm, (b) 120 mm, and (c) 140 mm.
Figure 6.
Mechanical response of flexible bolts with different Ø30 mm locking casing lengths: (a) 100 mm, (b) 120 mm, and (c) 140 mm.
Figure 7.
Failure mode of flexible bolt with Ø30 mm locking casing: (a) D1L1, (b) D1L2, (c) D1L3.
Figure 7.
Failure mode of flexible bolt with Ø30 mm locking casing: (a) D1L1, (b) D1L2, (c) D1L3.
Figure 8.
Mechanical response of flexible bolts with different Ø33 mm locking casing lengths: (a) 100 mm, (b) 120 mm, and (c) 140 mm.
Figure 8.
Mechanical response of flexible bolts with different Ø33 mm locking casing lengths: (a) 100 mm, (b) 120 mm, and (c) 140 mm.
Figure 9.
Failure mode of flexible bolts with Ø33 mm locking casing: (a) D2L1, (b) D2L2, and (c) D2L3.
Figure 9.
Failure mode of flexible bolts with Ø33 mm locking casing: (a) D2L1, (b) D2L2, and (c) D2L3.
Figure 10.
Mechanical response of flexible bolts with different Ø42 mm locking casing lengths: (a) 100 mm, (b) 120 mm, and (c) 140 mm.
Figure 10.
Mechanical response of flexible bolts with different Ø42 mm locking casing lengths: (a) 100 mm, (b) 120 mm, and (c) 140 mm.
Figure 11.
Failure mode of flexible bolt with Ø42 mm locking casing: (a) D3L1, (b) D3L2, and (c) D3L3.
Figure 11.
Failure mode of flexible bolt with Ø42 mm locking casing: (a) D3L1, (b) D3L2, and (c) D3L3.
Figure 12.
Tail structure of the flexible bolt and the situation where the locking casing is pulled out: (a) the components of the tail structure of flexible bolts, (b) a cross-sectional view of the tail structure after extrusion, (c) the failure mode when locking casing is pulled out, and (d) spring segments.
Figure 12.
Tail structure of the flexible bolt and the situation where the locking casing is pulled out: (a) the components of the tail structure of flexible bolts, (b) a cross-sectional view of the tail structure after extrusion, (c) the failure mode when locking casing is pulled out, and (d) spring segments.
Figure 13.
Tensile resistance–displacement curve of equal-lower-limit-and-equiamplitude cyclic loading.
Figure 13.
Tensile resistance–displacement curve of equal-lower-limit-and-equiamplitude cyclic loading.
Figure 14.
Tensile resistance–displacement curve of increasing-lower-limit-and-equiamplitude cyclic loading.
Figure 14.
Tensile resistance–displacement curve of increasing-lower-limit-and-equiamplitude cyclic loading.
Figure 15.
Support design of the testing roadway.
Figure 15.
Support design of the testing roadway.
Figure 16.
Results of the roadway monitoring: (a) axial load of flexible bolts, (b) surface displacement in the roadway, and (c) borehole camera images and corresponding analysis.
Figure 16.
Results of the roadway monitoring: (a) axial load of flexible bolts, (b) surface displacement in the roadway, and (c) borehole camera images and corresponding analysis.
Figure 17.
Field photos of testing roadway: (a) roof and (b) rib.
Figure 17.
Field photos of testing roadway: (a) roof and (b) rib.
Table 1.
Serial number of flexible bolts.
Table 1.
Serial number of flexible bolts.
| | Length | 100 mm | 120 mm | 140 mm |
|---|
| Diameter | |
|---|
| 30 mm | D1L1 | D1L2 | D1L3 |
| 33 mm | D2L1 | D2L2 | D2L3 |
| 42 mm | D3L1 | D3L2 | D3L3 |
Table 2.
Mechanical parameters of flexible bolts with different specifications.
Table 2.
Mechanical parameters of flexible bolts with different specifications.
| | Maximum Resistant Force (kN) | Average Resistant Force (kN) | Displacement Corresponding to Maximum Resistance (mm) | Average Displacement (mm) | Elongation of Flexible Bolt (%) |
|---|
| D1L1 | 170 | 96 | 236 | 167 | 12.63 | 8.44 | 14.88 | 11.98 | 2.0 |
| D1L2 | 332 | 338 | 351 | 340 | 25.15 | 32.12 | 31.24 | 29.50 | 4.9 |
| D1L3 | 356 | 358 | 350 | 355 | 31.16 | 36.00 | 31.44 | 32.87 | 5.5 |
| D2L1 | 311 | 197 | 303 | 270 | 20.01 | 17.28 | 21.76 | 19.68 | 3.3 |
| D2L2 | 372 | 373 | 369 | 371 | 35.93 | 35.56 | 26.29 | 32.59 | 5.4 |
| D2L3 | / | 370 | 367 | 369 | / | 37.85 | 31.77 | 34.81 | 5.8 |
| D3L1 | 333 | 328 | 339 | 333 | 19.05 | 15.93 | 19.77 | 18.25 | 3.0 |
| D3L2 | 340 | 362 | 365 | 356 | 21.92 | 27.84 | 28.05 | 25.94 | 4.3 |
| D3L3 | 362 | 345 | 369 | 359 | 28.32 | 19.84 | 32.40 | 26.85 | 4.5 |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).