A Multiobjective Decision-Making Model for Risk-Based Maintenance Scheduling of Railway Earthworks
Abstract
:1. Introduction
2. Stability Assessment of Earthworks
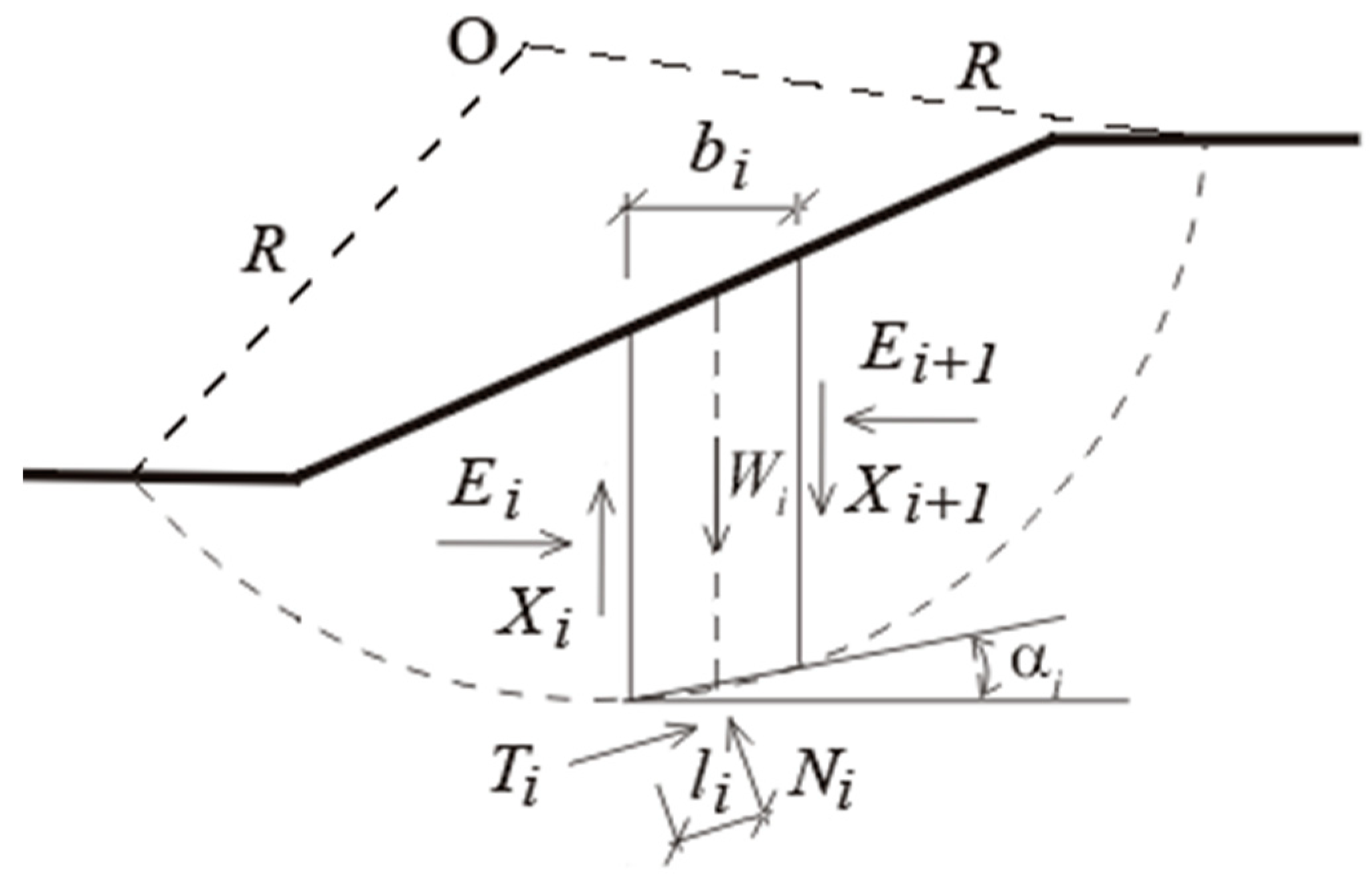
2.1. Slope Stability
2.2. Reliability of Slopes
3. Multiobjective Decision-Making Model for Maintenance Planning
3.1. Model Description
- 2.
- The next step is to perform tradeoffs among the attributes in order to find a solution that either maximizes or minimizes the stated performance goals or objectives. These tradeoffs characterize the relative importance of attributes for their defined objectives/performance goals. A direct rating method is applied to determine the weighting factors of the attributes, which is represented in Equation (10).
- 3.
- The next step of the MAUT application is the computation of the aggregated utility of each alternative based on both the computed SUF and the relative weighting factors. For the final aggregation, the multiplicative or addictive form can be used. The additive form requires the attributes to be mutually and preferentially independent. Preferentially independent means that the preferences of one attribute are not dependent on the preferences of another. When attributes are not mutually and preferentially independent, the multiplicative form is used [44]. Here, as the attributes (presented in Section 4.1.2) are found to be mutually and preferentially independent, the additive form is used to compute the total aggregated score of each alternative, see Equation (11):
- 4.
- Finally, maintenance alternatives are ranked based on the magnitude of their aggregated score. The maintenance alternative that contributes most to the realization of the defined objectives is ranked the highest.
3.2. Attributes
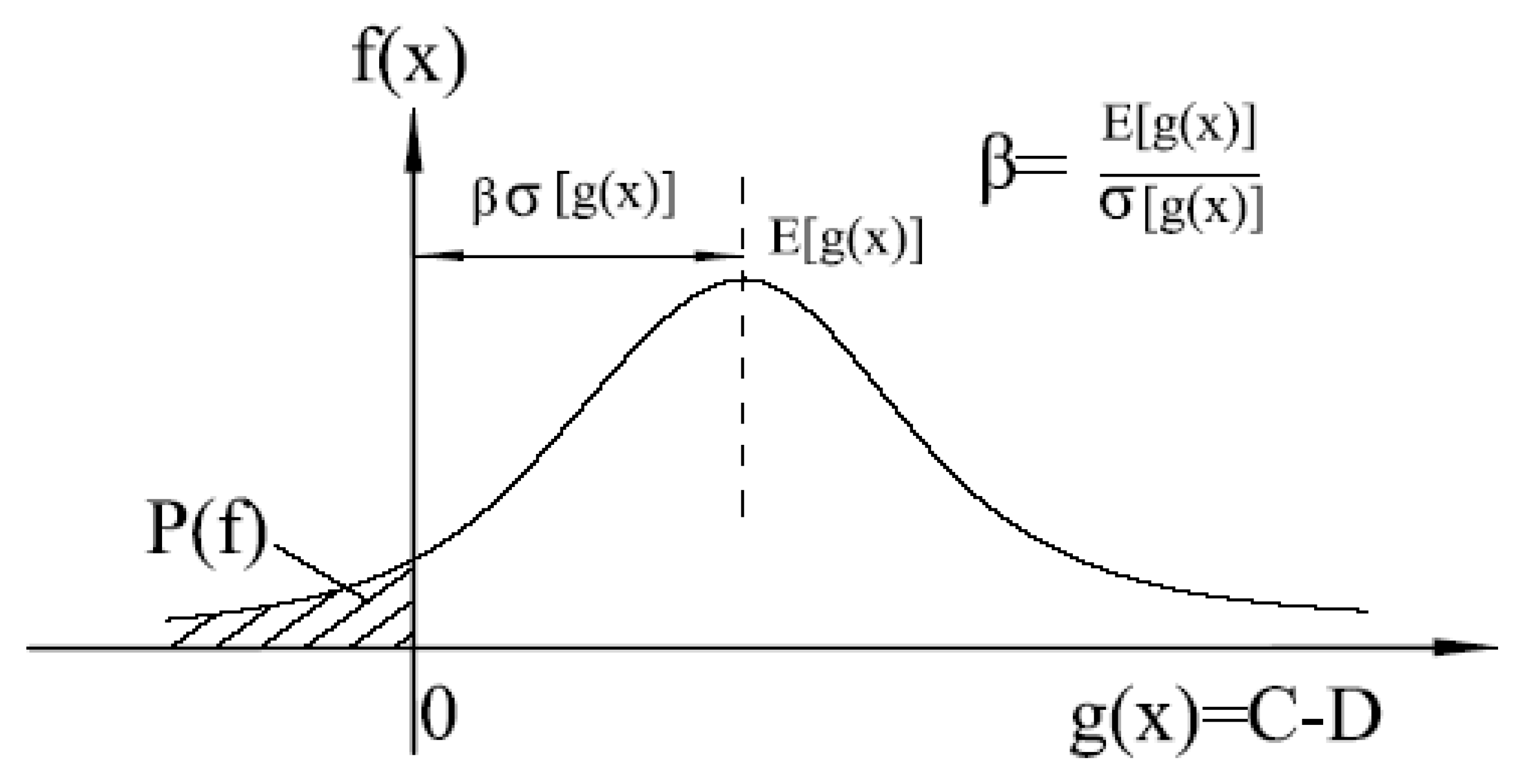
3.2.1. Safety–Change in Reliability Index Due to an Intervention
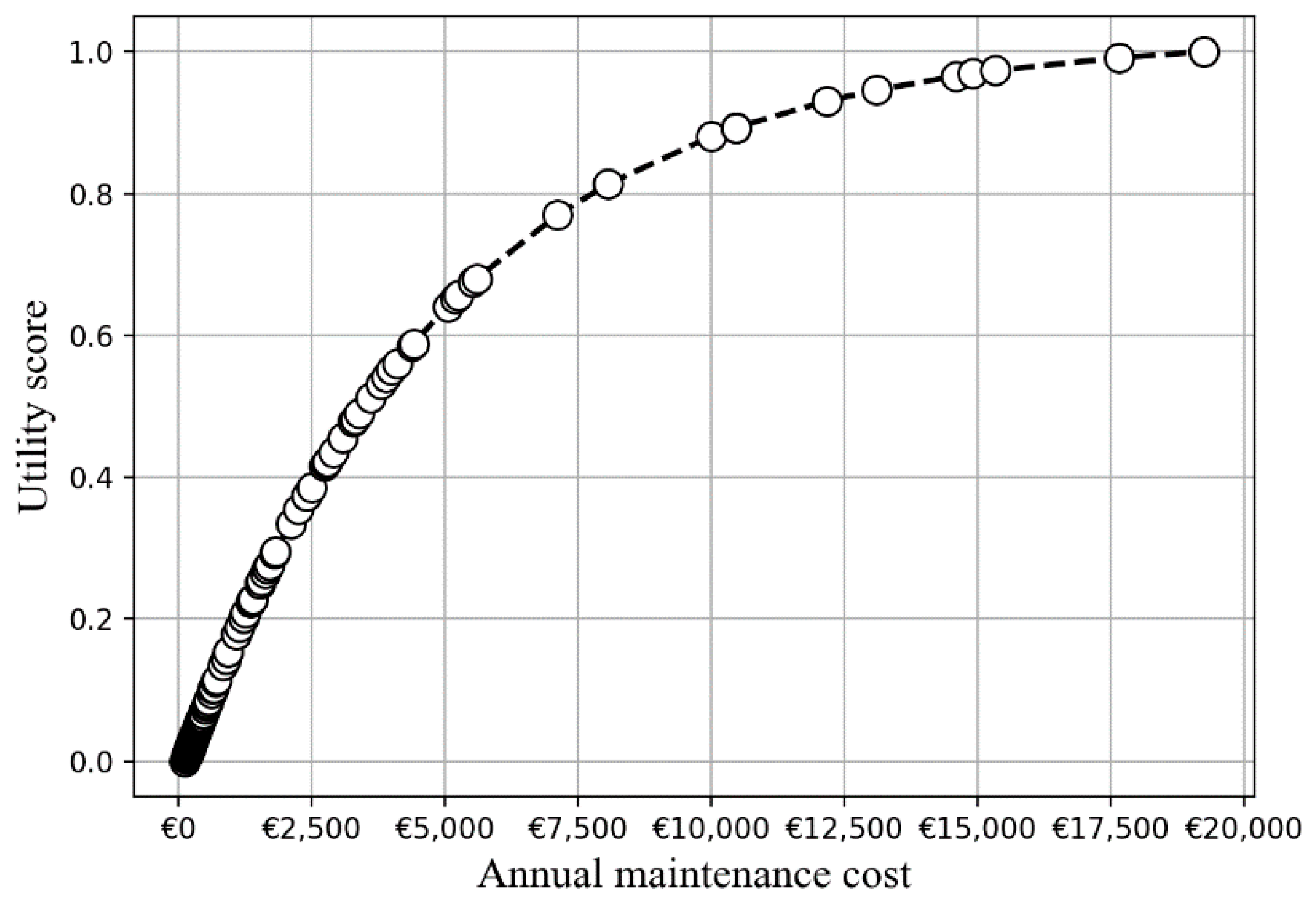
3.2.2. Economy–Annual Maintenance Cost
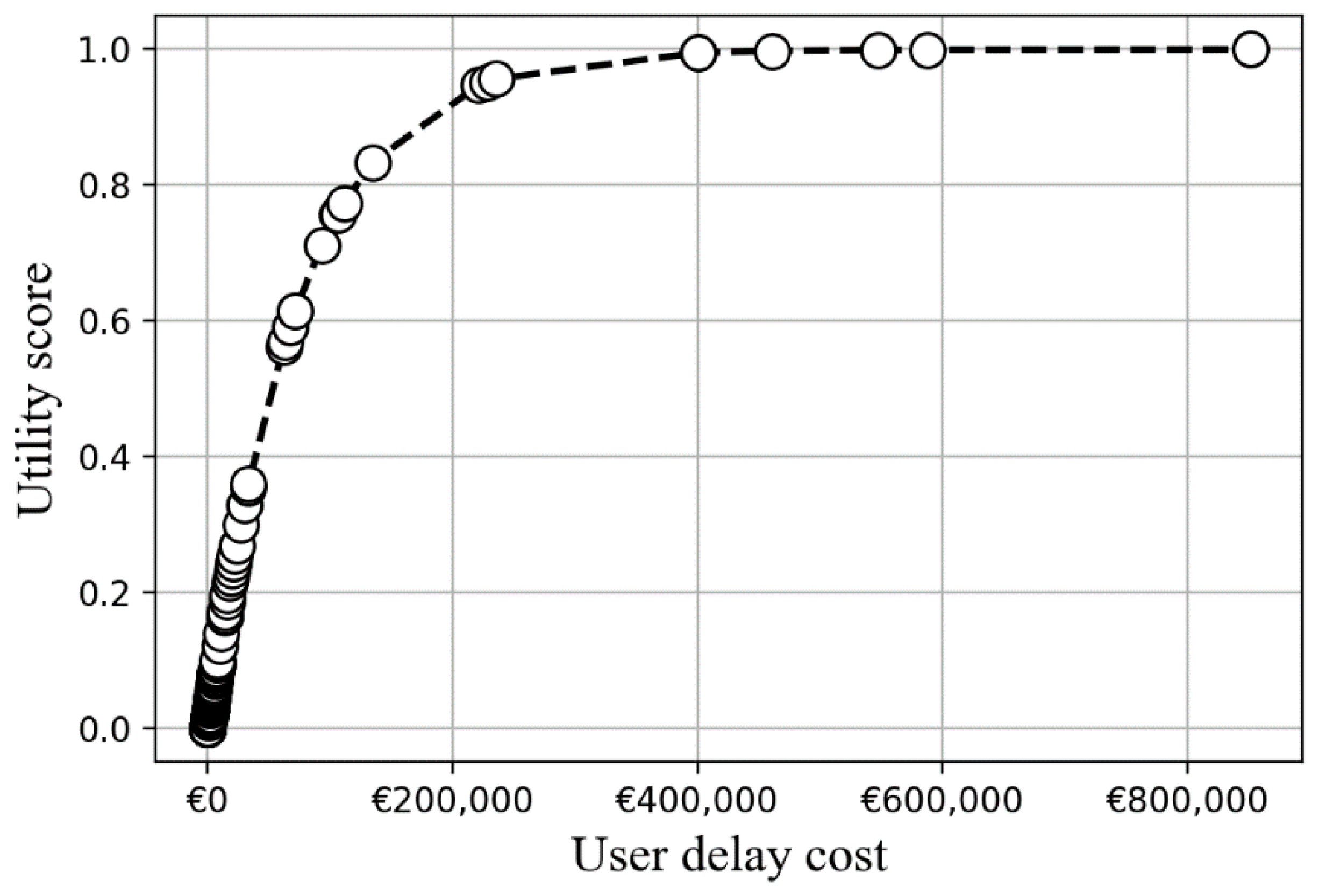
3.2.3. Availability–User Delay Cost
4. Case Study
4.1. Application of Multi-Attribute Utility Theory (MAUT)
4.1.1. Assessment of Single Utility Function
4.1.2. Attribute Tradeoff
4.1.3. Aggregated Utility and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stenström, C.; Norrbin, P.; Parida, A.; Kumar, U. Preventive and corrective maintenance—Cost comparison and cost–benefit analysis. Struct. Infrastruct. Eng. 2016, 12, 603–617. [Google Scholar] [CrossRef]
- Tao, Z.; Zophy, F.; Wiegmann, J. Asset management model and systems integration approach. Transp. Res. Rec. J. Transp. Res. Board 2000, 1719, 191–199. [Google Scholar] [CrossRef]
- Network Rail. Earthworks: Cutting Slopes and Embankments. 2018. Available online: https://www.networkrail.co.uk/running-the-railway/looking-after-the-railway/earthworks-cutting-slopes-and-embankments (accessed on 20 May 2020).
- Allah Bukhsh, Z.; Stipanovic, I.; Klanker, G.; O’Connor, A.; Doree, A.G. Network level bridges maintenance planning using Multi-Attribute Utility Theory. Struct. Infrastruct. Eng. 2019, 15, 872–885. [Google Scholar] [CrossRef] [Green Version]
- Arif, F.; Bayraktar, M.E.; Chowdhury, A.G. Decision Support Framework for Infrastructure Maintenance Investment Decision Making. J. Manag. Eng. 2016, 32, 04015030. [Google Scholar] [CrossRef] [Green Version]
- Al-Douri, Y.K.; Tretten, P.; Karim, R. Improvement of railway performance: A study of Swedish railway infrastructure. J. Mod. Transp. 2016, 24, 22–37. [Google Scholar] [CrossRef] [Green Version]
- European Commission. Statistics|Eurostat. 2019. Available online: https://ec.europa.eu/eurostat/databrowser/view/ttr00003/default/table?lang=en (accessed on 20 May 2020).
- Martinović, K.; Gavin, K.; Reale, C.; Mangan, C. Rainfall thresholds as a landslide indicator for engineered slopes on the Irish Rail network. Geomorphology 2018, 306, 40–50. [Google Scholar] [CrossRef] [Green Version]
- Briggs, K.M.; Loveridge, F.A.; Glendinning, S. Failures in transport infrastructure embankments. Eng. Geol. 2017, 219, 107–117. [Google Scholar] [CrossRef] [Green Version]
- Kite, D.; Siino, G.; Audley, M. Detecting Embankment Instability Using Measurable Track Geometry Data. Infrastructures 2020, 5, 29. [Google Scholar] [CrossRef] [Green Version]
- Gavin, K.; Xue, J. A simple method to analyze infiltration into unsaturated slopes. Comput. Geotech. 2008, 35, 223–230. [Google Scholar] [CrossRef]
- Zhang, L.L.; Zhang, J.; Zhang, L.M.; Tang, W.H. Stability analysis of rainfall-induced slope failure: A review. Proc. Inst. Civil Eng. Geotech. Eng. 2011, 164, 299–316. [Google Scholar] [CrossRef] [Green Version]
- Martinović, K.; Gavin, K.; Reale, C. Development of a landslide susceptibility assessment for a rail network. Eng. Geol. 2016, 215, 1–9. [Google Scholar]
- Loveridge, F.A.; Spink, T.W.; O’Brien, A.S.; Briggs, K.M.; Butcher, D. The impact of climate and climate change on infrastructure slopes, with particular reference to southern England. Q. J. Eng. Geol. Hydrogeol. 2010, 43, 461–472. [Google Scholar] [CrossRef]
- Pradel, D.; Raad, G. Effect of permeability on surficial stability of homogeneous slopes. J. Geotech. Eng. 1993, 119, 315–332. [Google Scholar] [CrossRef]
- Ridley, A. Role of pore water pressures in embankment stability. Proc. Inst. Civil Eng. Geotech. Eng. 2004, 157, 193–198. [Google Scholar] [CrossRef]
- Vardon, P.J. Climatic influence on geotechnical infrastructure: A review. Environ. Geotech. 2015, 2, 166–174. [Google Scholar] [CrossRef]
- Stirling, R.A.; Toll, D.G.; Glendinning, S.; Helm, P.; Yildiz, A.; Hughes, P.N.; Asquith, J.D. Weather-driven deterioration processes affecting the performance of embankment slopes. Géotechnique 2020. [Google Scholar] [CrossRef]
- Jennings, P.J.; Muldoon, P. Assessment of Stability of Man-Made Slopes in Glacial Till: Case Study of Railway Slopes, Southwest Ireland. In Proceedings of the Seminar “Earthworks in Transportation”, Dublin, Ireland, 12 December 2001. [Google Scholar]
- Noakes, A.J.P.; Mason-Jarvis, L.F.; Taylor, G.R.; Evans, E. Geospatial assessment methods for geotechnical asset management of legacy railway embankments. Q. J. Eng. Geol. Hydrogeol. 2020, 53, 339–348. [Google Scholar] [CrossRef]
- Spink, T. Strategic geotechnical asset management. Q. J. Eng. Geol. Hydrogeol. 2019, 53, 304–320. [Google Scholar] [CrossRef]
- Allah Bukhsh, Z.; Stipanovic, I. Predictive Maintenance for Infrastructure Asset Management. IT Prof. 2020, 22, 40–45. [Google Scholar] [CrossRef]
- Su, Z.; Jamshidi, A.; Núñez, A.; Baldi, S.; De Schutter, B. Multi-level condition-based maintenance planning for railway infrastructures—A scenario-based chance-constrained approach. Transp. Res. Part C Emerg. Technol. 2017, 84, 92–123. [Google Scholar] [CrossRef]
- Kabir, G.; Sadiq, R.; Tesfamariam, S. A review of multi-criteria decision-making methods for infrastructure management. Struct. Infrastruct. Eng. 2014, 10, 1176–1210. [Google Scholar] [CrossRef]
- Stipanovic, I.; Klanker, G. Performance goals for roadway bridges. In Proceedings of the 8th International Conference on Bridge Maintenance, Safety and Management, Foz do Iguaçu, Brazil, 26–30 June 2016; pp. 960–964. [Google Scholar]
- Kovačević, M.S.; Bačić, M.; Stipanović, I.; Gavin, K. Categorization of the Condition of Railway Embankments Using a Multi-Attribute Utility Theory. Appl. Sci. 2019, 9, 5089. [Google Scholar] [CrossRef] [Green Version]
- Allah Bukhsh, Z.; Saeed, A.; Stipanovic, I.; Doree, A.G. Predictive maintenance using tree-based classification techniques: A case of railway switches. Transp. Res. Part C Emerg. Technol. 2019, 101, 35–54. [Google Scholar] [CrossRef]
- Allah Bukhsh, Z.; Stipanovic, I.; Doree, A.G. Multi-year maintenance planning framework using multi-attribute utility theory and genetic algorithms. Eur. Transp. Res. Rev. 2020, 12, 3. [Google Scholar] [CrossRef]
- Gavin, K.; Xue, J. Use of a genetic algorithm to perform reliability analysis of unsaturated soil slopes. Géotechnique 2009, 59, 545–549. [Google Scholar] [CrossRef]
- Xue, J.F.; Gavin, K. Simultaneous determination of critical slip surface and reliability index for slopes. J. Geotech. Geoenviron. Eng. 2007, 133, 878–886. [Google Scholar] [CrossRef]
- Martinović, K.; Reale, C.; Gavin, K. Fragility curves for rainfall-induced shallow landslides on transport networks. Can. Geotech. J. 2018, 55, 852–861. [Google Scholar] [CrossRef] [Green Version]
- Reale, C.; Xue, J.; Gavin, K. Using Reliability Theory to Assess the Stability and Prolong the Design Life of Existing Engineered Slopes. In Geotechnical Safety and Reliability; American Society of Civil Engineers: Reston, VA, USA, 2017; pp. 61–81. Available online: https://ascelibrary.org/doi/abs/10.1061/9780784480731.006 (accessed on 20 May 2020).
- Low, B.; Zhang, J.; Tang, W.H. Efficient system reliability analysis illustrated for a retaining wall and a soil slope. Comput. Geotech. 2011, 38, 196–204. [Google Scholar] [CrossRef]
- Zhao, Y.; Ono, T. A general procedure for first/second-order reliabilitymethod (form/sorm). Struct. Saf. 1999, 21, 95–112. [Google Scholar] [CrossRef]
- Reale, C.; Xue, J.F.; Pan, Z.; Gavin, K. Deterministic and probabilistic multi-modal analysis of slope stability. Comput. Geotech. 2015, 66, 172–179. [Google Scholar] [CrossRef]
- Reale, C.; Xue, J.; Gavin, K. System reliability of slopes using multimodal optimisation. Géotechnique 2016, 66, 413–423. [Google Scholar] [CrossRef]
- Keeney, R.L.; von Winterfeldt, D. M13 Practical Value Models. In Advances in Decision Analysis: From Foundations to Applications; Cambridge University Press: Cambridge, UK, 2007; pp. 232–252. [Google Scholar]
- Meyer, J. Representing risk preferences in expected utility based decision models. Ann. Oper. Res. 2010, 176, 179–190. [Google Scholar] [CrossRef]
- Keeney, R.L.; Raiffa, H.; Meyer, R.F. Decisions with Multiple Objectives: Preferences and Value Trade-Offs; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Kirkwood, C.W. Strategic decision making multiobjective decision analysis with spreadsheets. J. Oper. Res. Soc. 1998, 49, 96–97. [Google Scholar] [CrossRef]
- Thevenot, H.J.; Steva, E.D.; Okudan, G.E.; Simpson, T.W. A multi-attribute utility theory-based approach to product line consolidation and selection. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Philadelphia, PA, USA, 10–13 September 2006. [Google Scholar]
- Middleton, M. Data Analysis Using Microsoft Excel: Updated for Windows 95; Wadsworth Publishing: Belmont, CA, USA, 1996. [Google Scholar]
- Caballero, R.J.; Krishnamurthy, A. Collective risk management in a flight to quality episode. J. Financ. 2008, 63, 2195–2230. [Google Scholar] [CrossRef] [Green Version]
- Krishnamurty, S. Normative decision analysis in engineering design. Decis. Mak. Eng. Des. 2006, 4, 21–33. [Google Scholar]
- Zavadskas, E.K.; Liias, R.; Turskis, Z. Multi-attribute decision -making methods for assessment of quality in bridges and road construction: State-of-the-art surveys. Balt. J. Road Bridge Eng. 2008, 3, 152–160. [Google Scholar] [CrossRef]
- Dabous, S.A.; Alkass, S. A multi-attribute ranking method for bridge management. Eng. Constr. Archit. Manag. 2010, 17, 282–291. [Google Scholar] [CrossRef]
- Chowdhury, R.; Flentje, P. Role of slope reliability analysis in landslide risk management. Bull. Eng. Geol. Environ. 2003, 62, 41–46. [Google Scholar] [CrossRef]
- US Army Corps of Engineers. Risk-Based Analysis in Geotechnical Engineering for Support of Planning Studies; Publications on Engineering and Design; No. 1110-2-556; Army Corps of Engineers: Washington, DC, USA, 1999. [Google Scholar]
- Whitman, R.V. Evaluating calculated risk in geotechnical engineering. J. Geotech. Eng. 1984, 110, 143–188. [Google Scholar] [CrossRef]
- Irish Rail. Network Statement. 2018. Available online: https://www.irishrail.ie/IrishRail/media/Imported/ie_2018_network_statement_(final_version).pdf (accessed on 20 May 2020).
- Barrett, A.; Ramdas, V. Report on Whole Life Cycle Analysis Tool D4.3. DESTination RAIL. 2018. Available online: https://ec.europa.eu/research/participants/documents/downloadPublic?documentIds=080166e5b8f56880&appId=PPGMS (accessed on 20 May 2020).
- Claudio, D.; Okudan, G.E. Utility function-based patient prioritisation in the emergency department. Eur. J. Ind. Eng. 2010, 4, 59–77. [Google Scholar] [CrossRef]


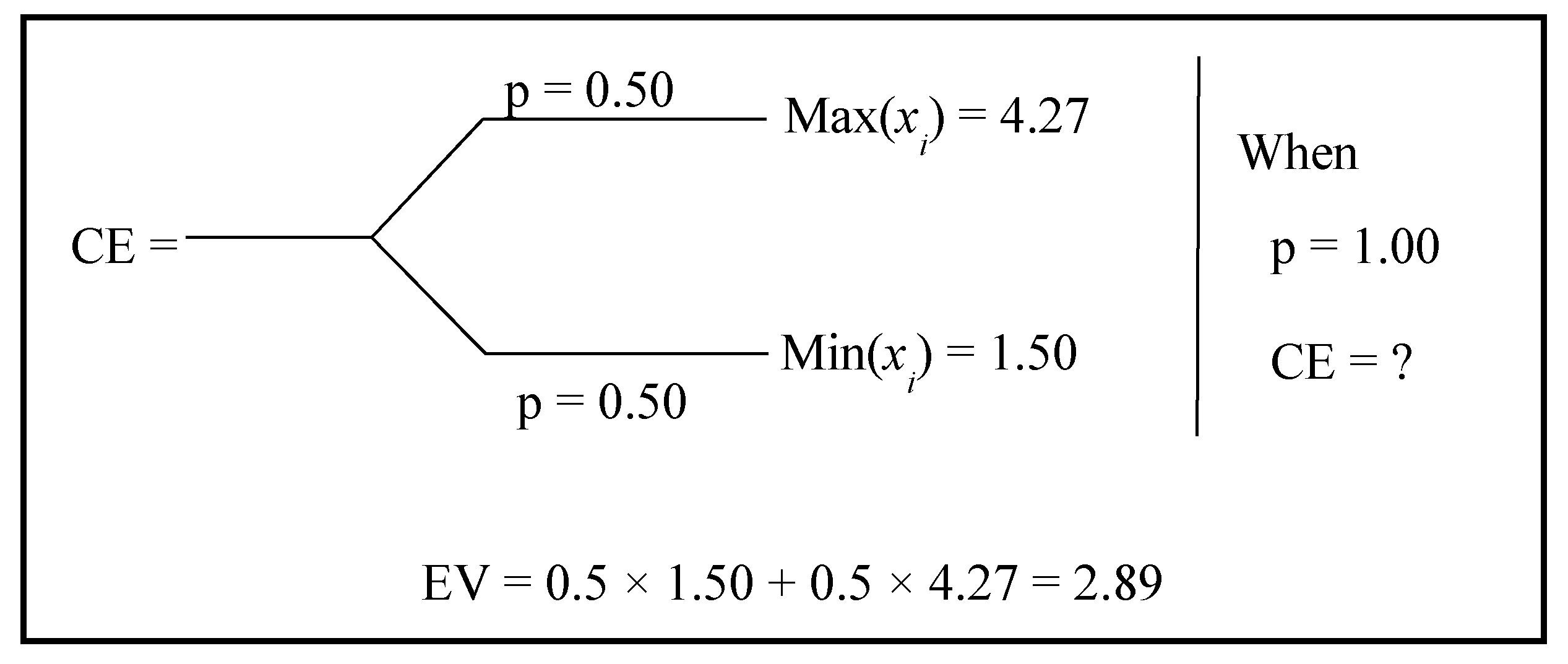

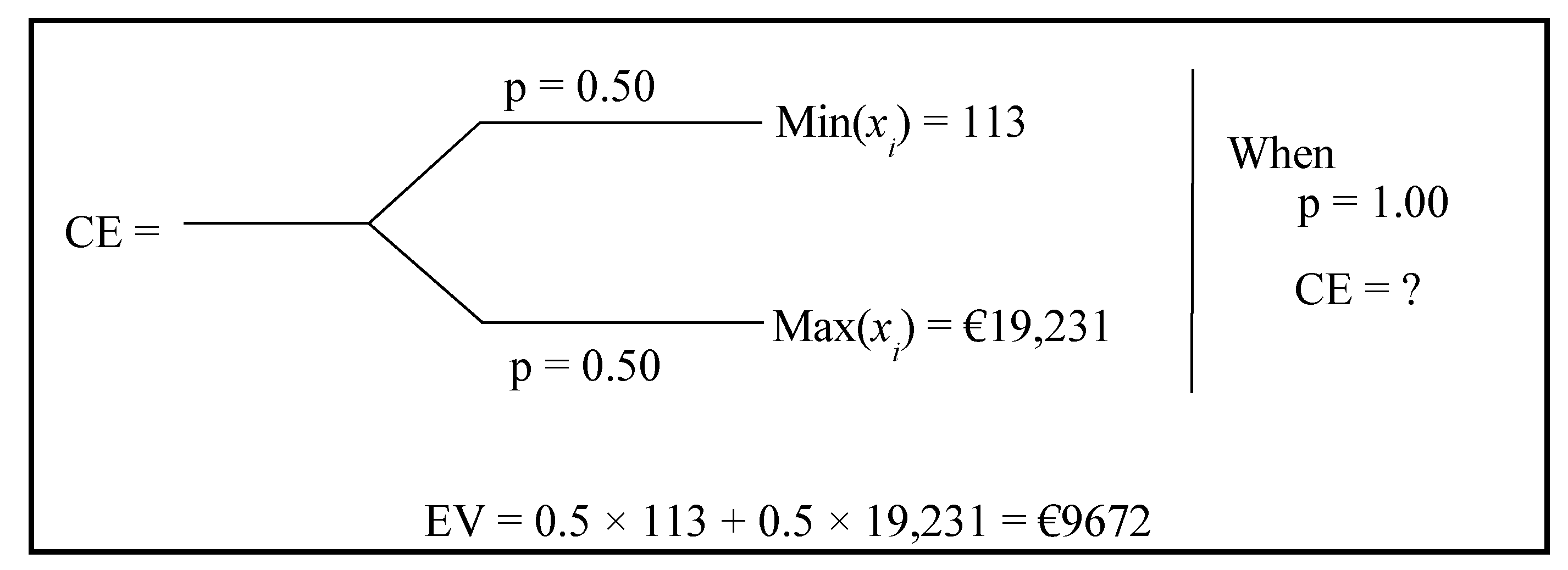
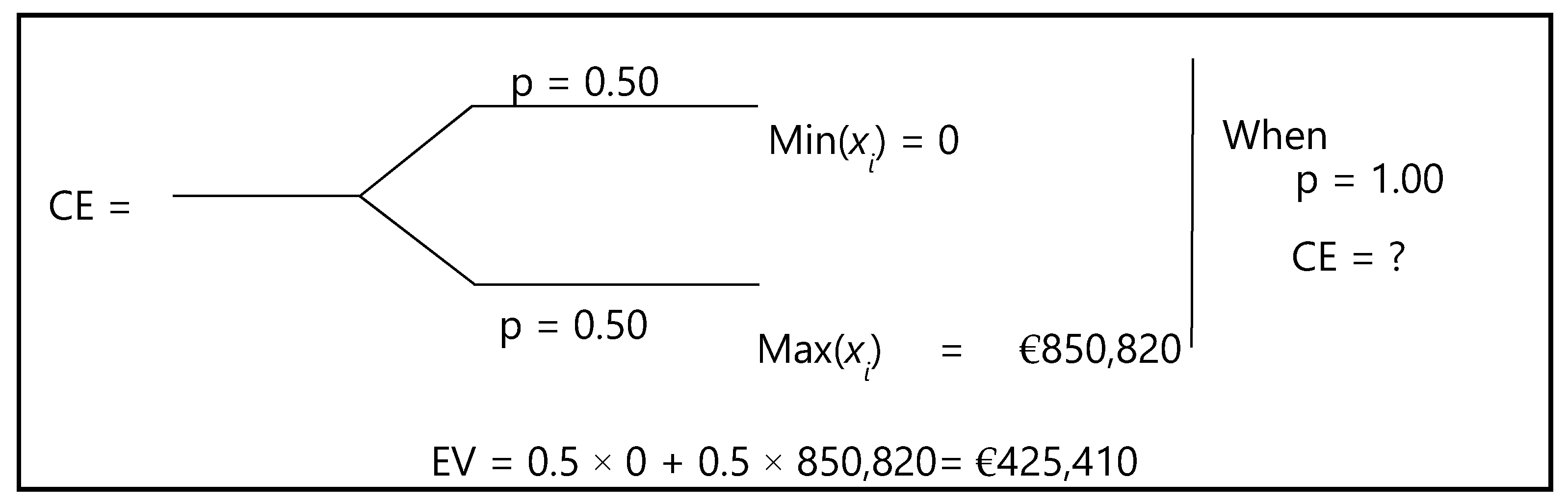
| Maintenance Levels | Description of Damage | Maintenance Option | Maintenance Cost (Unit Cost) * | Downtime/Duration [days] | Reduced Speed (km/h) | Failure Mechanism | Reliability Index after | Expected Lifespan [years] |
|---|---|---|---|---|---|---|---|---|
| Minimum | Blocked drains | Vegetation clearance-drainage | Mobilization €1000, + €1/m′ | 1 | 0 | Planar | 4 | 5 |
| Insufficient or overgrown vegetation | Vegetation clearance-management | Mobilization €1000, + €5/m′ | 0 | 25 | Planar | 4 | 10 | |
| Medium | Tension cracks | Passive debris barrier | Mobilization €1000, + €300/m′ | 1 | 0 | Planar | 3 | 20 |
| Major water seepage | Passive debris barrier | Mobilization €1000, + €300/m′ | 1 | 0 | Rotational | 3 | 20 | |
| Maximum | Redesign requirements (clearance widening) | Retaining wall (various types) | Mobilization €2500, + €700/m′ | 4 | 0 | Rotational | 5 | 30 |
| Landslide | Benching; berms | Mobilization €2500, + €400/m′ | 3 | 0 | Rotational | 3 | 40 | |
| Oversteep asset | Regrading | Mobilization €2500, + €400/m′ | 3 | 0 | Both | 3.5 | 50 |
| Maintenance Levels | Description of Damage | Maintenance Option | Maintenance Cost (Unit Cost) * | Downtime/Duration [days] | Reduced Speed (km/h) | Failure Mechanism | Reliability Index after | Expected Lifespan [years] |
|---|---|---|---|---|---|---|---|---|
| Medium | Oversteep asset | Installation of a rock face mesh | Mobilization €1000, + €400/m′ | 2 | 0 | Wedge | 4 | 20 |
| Tension cracks | Passive debris barrier | Mobilization €1000, + €300/m′ | 1 | 0 | Wedge | 3.5 | 20 | |
| Maximum | Landslide/rockfall | Regrading | Mobilization €1000 + €1000/m′ | 10 | 0 | Wedge or rotational | 4.5 | 50 |
| Over-steep/fractured | Shotcrete and anchors | Mobilization €20,000 + €1600 m′ | 20 | 0 | Wedge | 4 | 50 | |
| Loose debris | Shotcrete | Mobilization €10,000 + €500 m′ | 4 | 0 | - | 2.5 | 10 |
| Performance Aspect | Attribute | Weights | Rating |
|---|---|---|---|
| Economy | Annual maintenance cost | 25 | 25/100 = 0.25 |
| Reliability | Improved reliability | 50 | 50/100 = 0.50 |
| Availability | User delay cost | 25 | 25/100 = 0.25 |
| Slope ID | Type | Failure Mechanism | Maintenance Level | Damage Description | Maintenance Option | Annual Maintenance Cost (AMC) | User Delay Cost (UDC) | Reliability Improvement (RI) | Utility of AMC | Utility of UDC | Utility RI | MAUT Score | Rank |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 731 | Soil Cutting | Planar | Do minimum | Insufficient or overgrown vegetation | Vegetation clearance-drainage | 351.50 | 0.00 | 3.50 | 0.05 | 0.00 | 0.13 | 0.08 | 1 |
| 659 | Soil Cutting | Rotational | Do maximum | Oversteep asset | Regrading | 930.00 | 3365.03 | 3.50 | 0.15 | 0.04 | 0.13 | 0.11 | 2 |
| 884 | Embankment | Planar | Do minimum | Insufficient or overgrown vegetation | Vegetation clearance-drainage | 144.50 | 0.00 | 2.97 | 0.01 | 0.00 | 0.26 | 0.13 | 3 |
| 355 | Embankment | Planar | Do minimum | Insufficient or overgrown vegetation | Vegetation clearance-drainage | 155.00 | 0.00 | 2.96 | 0.01 | 0.00 | 0.26 | 0.13 | 4 |
| 147 | Embankment | Planar | Do minimum | Insufficient or overgrown vegetation | Vegetation clearance-drainage | 214.50 | 0.00 | 2.96 | 0.02 | 0.00 | 0.26 | 0.14 | 5 |
| 334 | Embankment | Planar | Do minimum | Insufficient or overgrown vegetation | Vegetation clearance-drainage | 237.00 | 0.00 | 2.97 | 0.03 | 0.00 | 0.26 | 0.14 | 6 |
| 512 | Embankment | Planar | Do minimum | Insufficient or overgrown vegetation | Vegetation clearance-drainage | 132.00 | 0.00 | 2.92 | 0.00 | 0.00 | 0.28 | 0.14 | 7 |
| 511 | Embankment | Planar | Do minimum | Insufficient or overgrown vegetation | Vegetation clearance-drainage | 244.00 | 0.00 | 2.95 | 0.03 | 0.00 | 0.27 | 0.14 | 8 |
| 152 | Embankment | Planar | Do minimum | Insufficient or overgrown vegetation | Vegetation clearance-drainage | 209.50 | 0.00 | 2.92 | 0.02 | 0.00 | 0.28 | 0.14 | 9 |
| 345 | Embankment | Planar | Do minimum | Insufficient or overgrown vegetation | Vegetation clearance-drainage | 356.50 | 0.00 | 2.92 | 0.05 | 0.00 | 0.28 | 0.15 | 10 |
| Slope ID | Type | Failure Mechanism | Maintenance Level | Damage Description | Maintenance Option | Annual Maintenance Cost (AMC) | User Delay Cost (UDC) | Reliability Improvement (RI) | Utility of AMC | Utility of UDC | Utility RI | MAUT Score | Rank |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 049 | Soil Cutting | Rotational | Do maximum | Oversteep asset | Regrading | 2098.00 | 1370.99 | 1.53 | 0.33 | 0.02 | 0.98 | 0.33 | 179 |
| 030 | Embankment | Rotational | Do maximum | Oversteep asset | Regrading | 1514.00 | 7413.78 | 1.50 | 0.25 | 0.09 | 1.00 | 0.25 | 180 |
| 531 | Embankment | Rotational | Do maximum | Oversteep asset | Regrading | 2890.00 | 0.00 | 1.56 | 0.44 | 0.00 | 0.96 | 0.44 | 181 |
| 116 | Soil Cutting | Rotational | Do maximum | Oversteep asset | Regrading | 2482.00 | 18,813.26 | 1.60 | 0.39 | 0.22 | 0.92 | 0.39 | 182 |
| 472 | Embankment | Rotational | Do maximum | Oversteep asset | Regrading | 5250.00 | 19,884.27 | 1.78 | 0.66 | 0.23 | 0.80 | 0.66 | 183 |
| 271 | Soil Cutting | Rotational | Do maximum | Oversteep asset | Regrading | 5042.00 | 0.00 | 1.59 | 0.64 | 0.00 | 0.94 | 0.64 | 184 |
| 378 | Soil Cutting | Rotational | Do maximum | Oversteep asset | Regrading | 4090.00 | 61,982.55 | 1.82 | 0.56 | 0.56 | 0.78 | 0.56 | 185 |
| 527 | Soil Cutting | Planar | Do minimum | Insufficient or overgrown vegetation | Vegetation clearance-drainage | 278.50 | 850,820.52 | 1.74 | 0.03 | 1.00 | 0.83 | 0.03 | 186 |
| 664 | Embankment | Rotational | Do maximum | Oversteep asset | Regrading | 17,642.00 | 111,343.65 | 2.37 | 0.99 | 0.77 | 0.48 | 0.99 | 187 |
| 390 | Soil Cutting | Rotational | Do maximum | Oversteep asset | Regrading | 13,090.00 | 0.00 | 1.65 | 0.95 | 0.00 | 0.89 | 0.95 | 188 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stipanovic, I.; Bukhsh, Z.A.; Reale, C.; Gavin, K. A Multiobjective Decision-Making Model for Risk-Based Maintenance Scheduling of Railway Earthworks. Appl. Sci. 2021, 11, 965. https://doi.org/10.3390/app11030965
Stipanovic I, Bukhsh ZA, Reale C, Gavin K. A Multiobjective Decision-Making Model for Risk-Based Maintenance Scheduling of Railway Earthworks. Applied Sciences. 2021; 11(3):965. https://doi.org/10.3390/app11030965
Chicago/Turabian StyleStipanovic, Irina, Zaharah Allah Bukhsh, Cormac Reale, and Kenneth Gavin. 2021. "A Multiobjective Decision-Making Model for Risk-Based Maintenance Scheduling of Railway Earthworks" Applied Sciences 11, no. 3: 965. https://doi.org/10.3390/app11030965
APA StyleStipanovic, I., Bukhsh, Z. A., Reale, C., & Gavin, K. (2021). A Multiobjective Decision-Making Model for Risk-Based Maintenance Scheduling of Railway Earthworks. Applied Sciences, 11(3), 965. https://doi.org/10.3390/app11030965







