Intrinsically Motivated Open-Ended Multi-Task Learning Using Transfer Learning to Discover Task Hierarchy
Abstract
1. Introduction
2. State of the Art
2.1. Intrinsic Motivation for Cross-Task Interpolation
2.2. Hierarchically Organised Tasks
2.3. Active Imitation Learning (Social Guidance)
- the transfer of knowledge needs only one type of information. However, for multi-task learning, the demonstrations set should provide different types of information depending on the task and the knowledge of the learning. Indeed, in imitation learning works, different kinds of information for transfer of knowledge have been examined separately, depending on the setup at hand: external reinforcement signals [33], demonstrations of actions [34], demonstrations of procedures [35], advice operators [36] or disambiguation among actions [37]. The combination of different types of demonstrations has been studied in [38] for multi-task learning, where the proposed algorithm Socially Guided Intrinsic Motivation with Active Choice of Teacher and Strategy (SGIM-ACTS) showed that imitating a demonstrated action and outcome has different effects depending on the task, and that the combination of different types of demonstrations with autonomous exploration bootstraps the learning of multiple tasks. For hierarchical RL, algorithm Socially Guided Intrinsic Motivation with Procedure Babbling (SGIM-PB) in [35] could also take advantage of demonstrations of actions and task decomposition. We propose in this study to examine the role of each kind of demonstrations with respect to the control tasks in order to learn task hierarchy.
- the timing of these demonstrations has no influence. However, in curriculum learning the timing of knowledge transfer should be essential. Furthermore, the agent best knows when and what information it needs from the teachers, and active requests for knowledge transfer should be more efficient. For instance, a reinforcement learner choosing when to request social guidance was shown in [39] making more progress. Such techniques are called active imitation learning or interactive learning, and echo the psychological descriptions of infants’ selectivity in social partners and its link to their motivation to learn [40,41]. Active imitation learning has been implemented [42] where the agent learns when to imitate using intrinsic motivation for a hierarchical RL problem in a discrete setting. For continuous action, state and goal spaces, the SGIM-ACTS algorithm [38] uses intrinsic motivation to choose not only the kind of demonstrations, but also when to request for demonstrations and who to ask among several teachers. SGIM-ACTS was extended for hierarchical reinforcement learning with the algorithm Socially Guided Intrinsic Motivation with Procedure Babbling (SGIM-PB) in [35]. In this article, we will study whether a transfer of a batch of data or an active learner is more efficient to learn task hierarchy.
2.4. Summary: Our Contribution
- Discovering and exploiting the task hierarchy using a dual representation of complex actions in action and outcome spaces;
- Combining autonomous exploration of the task decompositions with imitation of the available teachers, using demonstrations as task dependencies;
- Using intrinsic motivation, and more precisely its empirical measures of progress, as its guidance mechanism to decide which information to transfer across tasks; and for imitation, when how and from which source of information to transfer.
3. Our Approach
3.1. Problem Formalization
3.2. Procedures
3.3. Algorithm
- Dimensionality and boundaries of the action primitive space ;
- Dimensionality and boundaries of each of the outcome subspaces ;
- Dimensionality and boundaries of the procedural spaces , defined as all possible pairs of two outcome subspaces.
| Algorithm 1 SGIM-PB and its SGIM-TL variant |
|
3.3.1. Exploration Strategies
3.3.2. Interest Mapping
4. Experiment
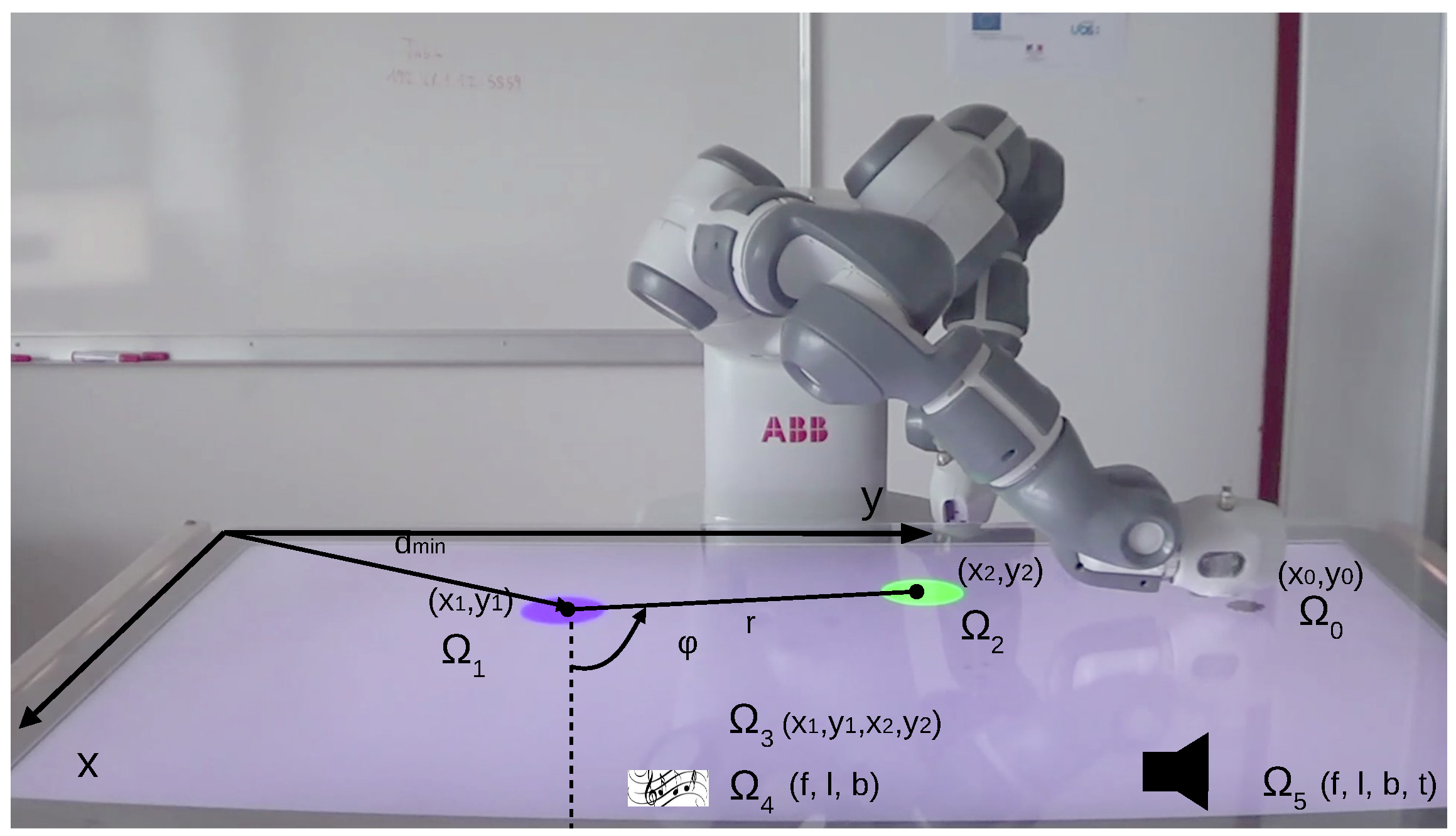
4.1. Experimental Setup
4.2. Experiment Variables
4.2.1. Action Spaces
4.2.2. Outcome Spaces
- : positions touched on the table;
- : positions of the first object;
- : positions of the second object;
- : positions of both objects;
- : burst sounds produced;
- : maintained sounds produced.
4.3. Teachers
- ProceduralTeacher1: ;
- ProceduralTeacher2: ;
- ProceduralTeacher3: ;
- ProceduralTeacher4: .
- ActionTeacher0 (): 11 demos of action primitives;
- ActionTeacher1 (): 10 demos of size 2 actions;
- ActionTeacher2 (): 8 demos of size 2 actions;
- ActionTeacher34 ( and ): 73 demos of size 4 actions.
- ActionTeacher0 (): 9 demos of action primitives;
- ActionTeacher1 (): 7 demos of size 2 actions;
- ActionTeacher2 (): 7 demos of size 2 actions;
- ActionTeacher3 (): 32 demos of size 4 actions;
- ActionTeacher4 (): 7 demos of size 4 actions.
4.4. Evaluation Method
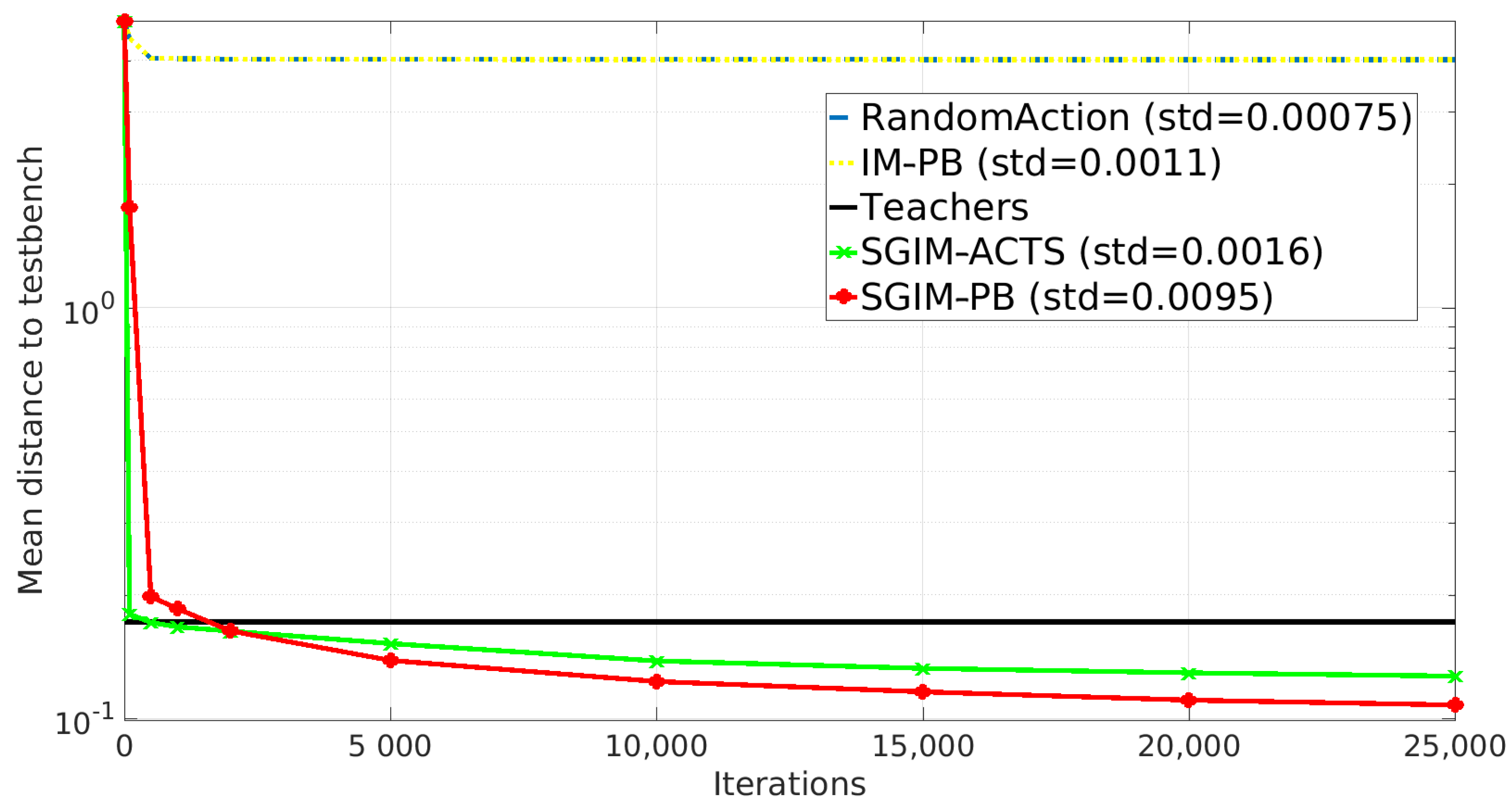
- RandomAction: random exploration of the action space ;
- IM-PB: autonomous exploration of the action and procedural space driven by intrinsic motivation;
- SGIM-ACTS: interactive learner driven by intrinsic motivation. Choosing between autonomous exploration of the action space and mimicry of any action teacher;
- SGIM-PB: interactive learner driven by intrinsic motivation. Has autonomous exploration strategies (of the action or procedural space) and mimicry ones for any procedural teacher and ActionTeacher0;
- Teachers: non-incremental learner only provided with the combined knowledge of all the action teachers.
5. Results
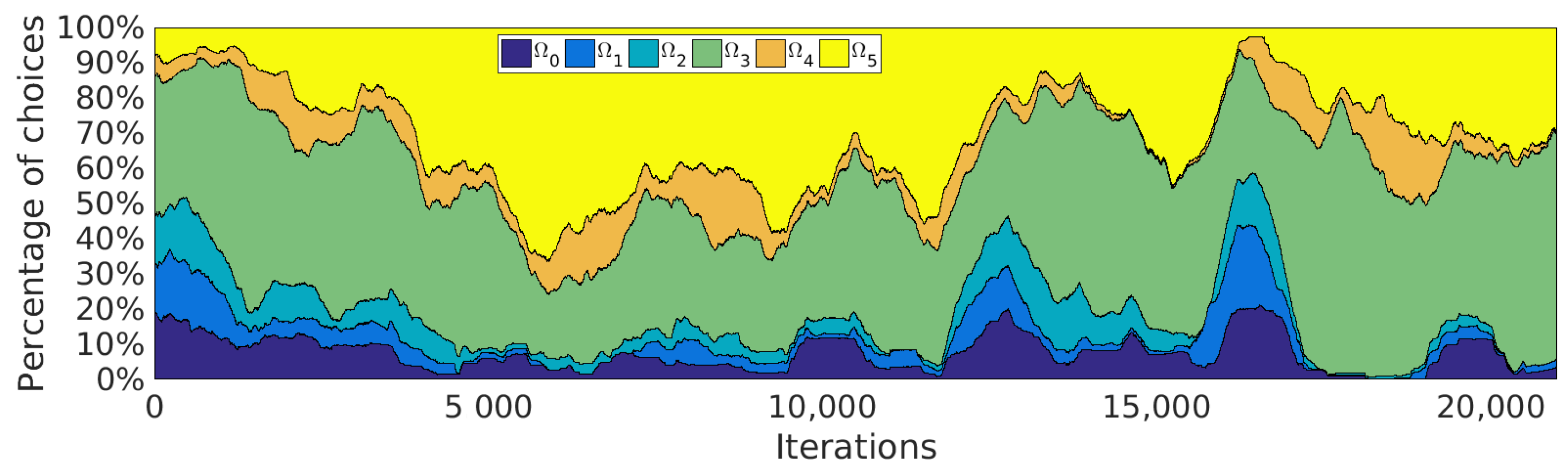
5.1. Task Decomposition and Complexity of Actions
5.1.1. Task Hierarchy Discovered
5.1.2. Length of the Chosen Actions
5.2. Imitation Learning Bootstraps the Learning of Procedures: Role of Imitation
5.3. Procedures Are Essential for Higher Level of Hierarchy Tasks: Role of Procedures
5.3.1. Demonstrations of Procedures
5.3.2. Autonomous Exploration of Procedures
5.4. Curriculum Learning by SGIM-PB
5.5. Data Efficiency of Active Learning: Active Imitation Learning vs. Batch Transfer
- Left-Yumi-SGIM-PB: the classical SGIM-PB learner using its left arm, using from the exact same strategies as on the simulated setup, without any procedure transferred;
- Left-Yumi-SGIM-TL: a modified SGIM-PB learner, benefiting from the strategies used on the simulated setup, and which benefits from the dataset as a Transferred Lump at the initialisation phase: at the beginning their learning process. No actions are transferred, and the transferred data are only used for computing local exploration of the procedural space, so they don’t impact the interest model nor the test evaluations reported in the next section.
5.5.1. Evaluation Performance
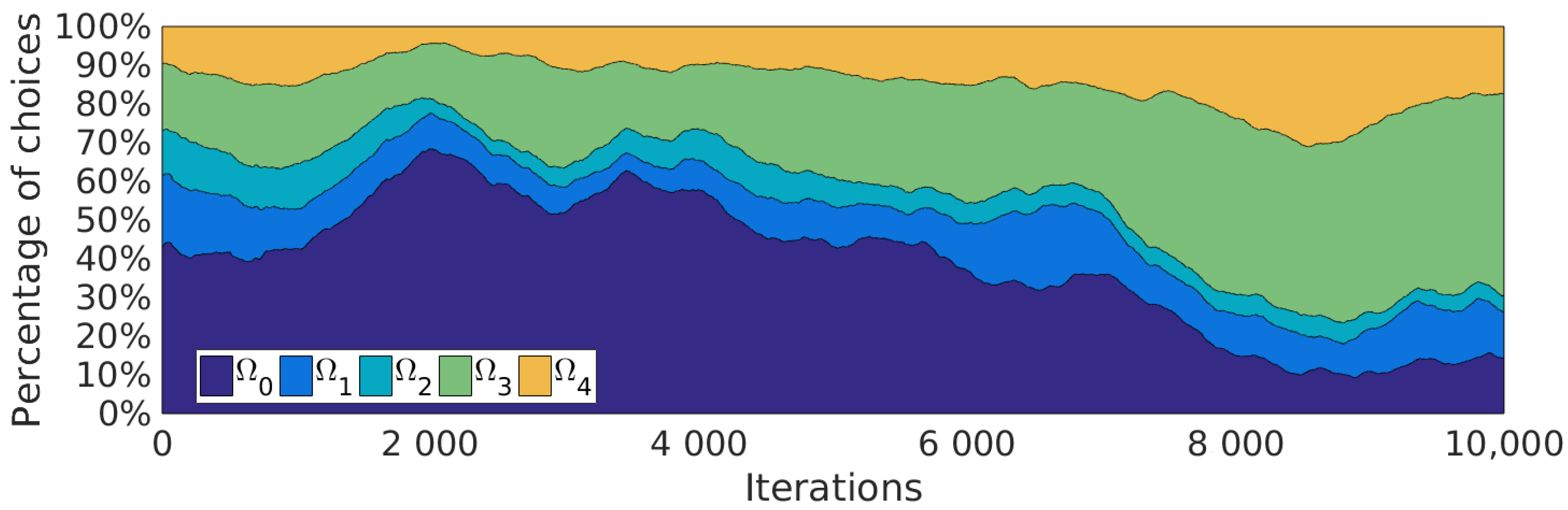
5.5.2. Procedures Learned
5.5.3. Procedures Used during Learning
5.5.4. Strategical Choices
6. Discussion
- procedures representation and task composition become necessary to reach tasks of higher hierarchy. It is not a simple bootstrapping effect.
- transfer of knowledge of procedures is efficient for cross-learner transfer of knowledge even when they have different embodiments.
- active imitation learning of procedures is more advantageous than imitation from a dataset provided from the initialization phase.
6.1. A Goal-Oriented Representation of Actions
6.2. Transfers of Knowledge
- What information to transfer? For compositional tasks, a demonstration of task decomposition is more useful than a demonstration of an action, as it helps bootstrap cross-task transfer of knowledge. Our case study shows a clear advantage of procedure demonstrations and procedure exploration. On the contrary, for simple tasks, action demonstrations and action space exploration show more advantages. Furthermore, for cross-learner transfer, especially when the learners have different embodiments, this case study indicates that demonstrations of procedures are still helpful, whereas demonstrations of actions are no longer relevant.
- How to transfer? We showed that decomposition of a hierarchical task, through procedure exploration and imitation, is more efficient than learning directly action parameters, i.e., interpolation of action parameters. This confirms the results found in a more simple setup in [35].
- When to transfer? Our last setup shows that an active imitation learner asking adapted demonstrations, as its competence increases, performs almost better than when it is given a significantly larger batch of data at initialisation time. More generally for a less data-hungry transfer learning algorithm, the transferred dataset should be given to the learner in a timely manner so that the information is adapted to the current level of the learner, i.e., its zone of proximal development [52]. This advantage has already been shown by an active and strategic learner—SGIM-IM [53], a simpler versions of SGIM-PB—which had better performance than passive learners for multi-task learning using action primitives.
- Which source of information? Our strategical learner chooses for each task the most efficient strategy between self-exploration and imitation. Most of all, it could understand the domain of expertise of the different teachers and choose the most appropriate expert to imitate. The results of this case study confirms the results found in [35] in a simpler setup and in [38] for learning action primitives.
7. Conclusions
- Hierarchical RL: it learns online task decomposition on 4 levels of hierarchy using the procedural framework; and it exploits the task decomposition to match the complexity of the sequences of action primitives to the task;
- Curriculum learning: it autonomously switches from simple to complex tasks, and from exploration of actions for simple tasks to exploration of procedures for the most complex tasks;
- Imitation learning: it empirically infers which kind of information is useful for each kind of task and requests just a small amount of demonstrations with the right type of information by choosing between procedural and action teachers;
- Transfer of knowledge: it automatically decides what information, how, when to transfer and which source of information for cross-task and cross-learner transfer learning.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Zech, P.; Renaudo, E.; Haller, S.; Zhang, X.; Piater, J. Action representations in robotics: A taxonomy and systematic classification. Int. J. Robot. Res. 2019, 38, 518–562. [Google Scholar] [CrossRef]
- Elman, J. Learning and development in neural networks: The importance of starting small. Cognition 1993, 48, 71–99. [Google Scholar] [CrossRef]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum Learning. In Proceedings of the 26th Annual International Conference on Machine Learning; ACM: New York, NY, USA, 2009; pp. 41–48. [Google Scholar]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Taylor, M.E.; Stone, P. Transfer learning for reinforcement learning domains: A survey. J. Mach. Learn. Res. 2009, 10, 1633–1685. [Google Scholar]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Whiten, A. Primate culture and social learning. Cogn. Sci. 2000, 24, 477–508. [Google Scholar] [CrossRef]
- Call, J.; Carpenter, M. Imitation in Animals and Artifacts; Chapter Three Sources of Information in Social Learning; MIT Press: Cambridge, MA, USA, 2002; pp. 211–228. [Google Scholar]
- Tomasello, M.; Carpenter, M. Shared intentionality. Dev. Sci. 2007, 10, 121–125. [Google Scholar] [CrossRef]
- Piaget, J. The Origins of Intelligence in Children (M. Cook, Trans.); WW Norton & Co: New York, NY, USA, 1952. [Google Scholar]
- Deci, E.; Ryan, R.M. Intrinsic Motivation and Self-Determination in Human Behavior; Plenum Press: New York, NY, USA, 1985. [Google Scholar]
- Oudeyer, P.Y.; Kaplan, F.; Hafner, V. Intrinsic Motivation Systems for Autonomous Mental Development. IEEE Trans. Evol. Comput. 2007, 11, 265–286. [Google Scholar] [CrossRef]
- Schmidhuber, J. Formal Theory of Creativity, Fun, and Intrinsic Motivation (1990–2010). IEEE Trans. Auton. Ment. Dev. 2010, 2, 230–247. [Google Scholar] [CrossRef]
- Baranes, A.; Oudeyer, P.Y. Intrinsically motivated goal exploration for active motor learning in robots: A case study. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 1766–1773. [Google Scholar]
- Rolf, M.; Steil, J.; Gienger, M. Goal Babbling permits Direct Learning of Inverse Kinematics. IEEE Trans. Auton. Ment. Dev. 2010, 2, 216–229. [Google Scholar] [CrossRef]
- Forestier, S.; Mollard, Y.; Oudeyer, P. Intrinsically Motivated Goal Exploration Processes with Automatic Curriculum Learning. arXiv 2017, arXiv:1708.02190. [Google Scholar]
- Colas, C.; Fournier, P.; Chetouani, M.; Sigaud, O.; Oudeyer, P.Y. CURIOUS: Intrinsically Motivated Modular Multi-Goal Reinforcement Learning. In International Conference on Machine Learning; Chaudhuri, K., Salakhutdinov, R., Eds.; PMLR: Cambridge, MA, USA, 2019; Volume 97, pp. 1331–1340. [Google Scholar]
- Giszter, S.F. Motor primitives—new data and future questions. Curr. Opin. Neurobiol. 2015, 33, 156–165. [Google Scholar] [CrossRef] [PubMed]
- Arie, H.; Arakaki, T.; Sugano, S.; Tani, J. Imitating others by composition of primitive actions: A neuro-dynamic model. Robot. Auton. Syst. 2012, 60, 729–741. [Google Scholar] [CrossRef]
- Riedmiller, M.; Hafner, R.; Lampe, T.; Neunert, M.; Degrave, J.; van de Wiele, T.; Mnih, V.; Heess, N.; Springenberg, J.T. Learning by Playing Solving Sparse Reward Tasks from Scratch. arXiv 2018, arXiv:1802.10567. [Google Scholar]
- Barto, A.G.; Konidaris, G.; Vigorito, C. Behavioral hierarchy: Exploration and representation. In Computational and Robotic Models of the Hierarchical Organization of Behavior; Springer: Berlin/Heidelberg, Germany, 2013; pp. 13–46. [Google Scholar]
- Konidaris, G.; Barto, A.G. Skill Discovery in Continuous Reinforcement Learning Domains using Skill Chaining. Adv. Neural Inf. Process. Syst. (NIPS) 2009, 22, 1015–1023. [Google Scholar]
- Barto, A.G.; Mahadevan, S. Recent advances in hierarchical reinforcement learning. Discret. Event Dyn. Syst. 2003, 13, 41–77. [Google Scholar] [CrossRef]
- Manoury, A.; Nguyen, S.M.; Buche, C. Hierarchical affordance discovery using intrinsic motivation. In Proceedings of the 7th International Conference on Human-Agent Interaction; ACM: New York, NY, USA, 2019; pp. 193–196. [Google Scholar]
- Kulkarni, T.D.; Narasimhan, K.; Saeedi, A.; Tenenbaum, J. Hierarchical deep reinforcement learning: Integrating temporal abstraction and intrinsic motivation. Adv. Neural Inf. Process. Syst. 2016, 29, 3675–3683. [Google Scholar]
- Duminy, N.; Nguyen, S.M.; Duhaut, D. Learning a set of interrelated tasks by using sequences of motor policies for a strategic intrinsically motivated learner. In Proceedings of the 2018 Second IEEE International Conference on Robotic Computing (IRC), Laguna Hills, CA, USA, 31 January–2 February 2018. [Google Scholar]
- Schaal, S. Learning from demonstration. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1997; pp. 1040–1046. [Google Scholar]
- Billard, A.; Calinon, S.; Dillmann, R.; Schaal, S. Handbook of Robotics; Number 59; Chapter Robot Programming by Demonstration; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Muelling, K.; Kober, J.; Peters, J. Learning table tennis with a mixture of motor primitives. In Proceedings of the 2010 10th IEEE-RAS International Conference on Humanoid Robots, Nashville, TN, USA, 6–8 December 2010; pp. 411–416. [Google Scholar]
- Reinhart, R.F. Autonomous exploration of motor skills by skill babbling. Auton. Robot. 2017, 41, 1521–1537. [Google Scholar] [CrossRef]
- Taylor, M.E.; Suay, H.B.; Chernova, S. Integrating reinforcement learning with human demonstrations of varying ability. In The 10th International Conference on Autonomous Agents and Multiagent Systems-Volume 2; International Foundation for Autonomous Agents and Multiagent Systems: Richland, SC, USA, 2011; pp. 617–624. [Google Scholar]
- Thomaz, A.L.; Breazeal, C. Experiments in Socially Guided Exploration: Lessons learned in building robots that learn with and without human teachers. Connect. Sci. 2008, 20, 91–110. [Google Scholar] [CrossRef]
- Grollman, D.H.; Jenkins, O.C. Incremental learning of subtasks from unsegmented demonstration. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 261–266. [Google Scholar]
- Duminy, N.; Nguyen, S.M.; Duhaut, D. Learning a Set of Interrelated Tasks by Using a Succession of Motor Policies for a Socially Guided Intrinsically Motivated Learner. Front. Neurorobot. 2019, 12, 87. [Google Scholar] [CrossRef]
- Argall, B.D.; Browning, B.; Veloso, M. Learning robot motion control with demonstration and advice-operators. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 399–404. [Google Scholar]
- Chernova, S.; Veloso, M. Interactive Policy Learning through Confidence-Based Autonomy. J. Artif. Intell. Res. 2009, 34, 1. [Google Scholar] [CrossRef]
- Nguyen, S.M.; Oudeyer, P.Y. Active choice of teachers, learning strategies and goals for a socially guided intrinsic motivation learner. Paladyn J. Behav. Robot. 2012, 3, 136–146. [Google Scholar] [CrossRef]
- Cakmak, M.; Chao, C.; Thomaz, A.L. Designing interactions for robot active learners. IEEE Trans. Auton. Ment. Dev. 2010, 2, 108–118. [Google Scholar] [CrossRef]
- Begus, K.; Southgate, V. Active Learning from Infancy to Childhood; Chapter Curious Learners: How Infants’ Motivation to Learn Shapes and Is Shaped by Infants’ Interactions with the Social World; Springer: Berlin/Heidelberg, Germany, 2018; pp. 13–37. [Google Scholar]
- Poulin-Dubois, D.; Brooker, I.; Polonia, A. Infants prefer to imitate a reliable person. Infant Behav. Dev. 2011, 34, 303–309. [Google Scholar] [CrossRef]
- Fournier, P.; Colas, C.; Sigaud, O.; Chetouani, M. CLIC: Curriculum Learning and Imitation for object Control in non-rewarding environments. IEEE Trans. Cogn. Dev. Syst. 2019, 1. [Google Scholar] [CrossRef]
- Duminy, N.; Nguyen, S.M.; Duhaut, D. Effects of social guidance on a robot learning sequences of policies in hierarchical learning. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018. [Google Scholar]
- Asada, M.; Hosoda, K.; Kuniyoshi, Y.; Ishiguro, H.; Inui, T.; Yoshikawa, Y.; Ogino, M.; Yoshida, C. Cognitive developmental robotics: A survey. IEEE Trans. Auton. Ment. Dev. 2009, 1, 12–34. [Google Scholar] [CrossRef]
- Cangelosi, A.; Schlesinger, M. Developmental Robotics: From Babies to Robots; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Nguyen, S.M.; Oudeyer, P.Y. Socially Guided Intrinsic Motivation for Robot Learning of Motor Skills. Auton. Robot. 2014, 36, 273–294. [Google Scholar] [CrossRef]
- Kubicki, S.; Pasco, D.; Hoareau, C.; Arnaud, I. Using a tangible interactive tabletop to learn at school: Empirical studies in the wild. In Actes de la 28ième Conférence Francophone sur l’Interaction Homme-Machine; ACM: New York, NY, USA, 2016; pp. 155–166. [Google Scholar]
- Pastor, P.; Hoffmann, H.; Asfour, T.; Schaal, S. Learning and generalization of motor skills by learning from demonstration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 763–768. [Google Scholar]
- Stulp, F.; Schaal, S. Hierarchical reinforcement learning with movement primitives. In Proceedings of the 2011 11th IEEE-RAS International Conference on Humanoid Robots, Bled, Slovenia, 26–28 October 2011; pp. 231–238. [Google Scholar]
- Da Silva, B.; Konidaris, G.; Barto, A.G. Learning Parameterized Skills. arXiv 2012, arXiv:1206.6398. [Google Scholar]
- Sutton, R.S.; Precup, D.; Singh, S. Between MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning. Artif. Intell. 1999, 112, 181–211. [Google Scholar] [CrossRef]
- Vygotsky, L.S. Mind in Society: The Development of Higher Psychological Processes; Cole, M., John-Steiner, V., Scribner, S., Souberman, E., Eds.; Harvard University Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Nguyen, S.M.; Oudeyer, P.Y. Interactive Learning Gives the Tempo to an Intrinsically Motivated Robot Learner. In Proceedings of the 2012 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012), Osaka, Japan, 29 November–1 December 2012. [Google Scholar]






















| Algorithm | Action Representation | Strategies | Transferred Dataset | Timing of the Transfer | Transfer of Knowledge |
|---|---|---|---|---|---|
| IM-PB [27] | parametrised actions, procedures | auton. action space explo., auton. procedural space explo. | None | NA | cross-task transfer |
| SGIM-ACTS [38] | parametrised actions | auton. action space explo., mimicry of an action teacher | Teacher demo. of actions | Active request by the learner to the teacher | imitation |
| SGIM-TL | parametrised actions, procedures | auton. action space explo., auton. procedural space explo., mimicry of an action teacher, mimicry of a procedure teacher | Another robot’s procedures, Teacher demo. of actions and procedures | Procedures transf. at initalization time, Active request by the learner to the teacher | cross-task transfer, imitation |
| SGIM-PB | parametrised actions, procedures | auton. action space explo., auton. procedural space explo., mimicry of an action teacher, mimicry of a procedure teacher | Teacher demo. of actions and procedures | Active request by the learner to the teacher | cross-task transfer, imitation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duminy, N.; Nguyen, S.M.; Zhu, J.; Duhaut, D.; Kerdreux, J. Intrinsically Motivated Open-Ended Multi-Task Learning Using Transfer Learning to Discover Task Hierarchy. Appl. Sci. 2021, 11, 975. https://doi.org/10.3390/app11030975
Duminy N, Nguyen SM, Zhu J, Duhaut D, Kerdreux J. Intrinsically Motivated Open-Ended Multi-Task Learning Using Transfer Learning to Discover Task Hierarchy. Applied Sciences. 2021; 11(3):975. https://doi.org/10.3390/app11030975
Chicago/Turabian StyleDuminy, Nicolas, Sao Mai Nguyen, Junshuai Zhu, Dominique Duhaut, and Jerome Kerdreux. 2021. "Intrinsically Motivated Open-Ended Multi-Task Learning Using Transfer Learning to Discover Task Hierarchy" Applied Sciences 11, no. 3: 975. https://doi.org/10.3390/app11030975
APA StyleDuminy, N., Nguyen, S. M., Zhu, J., Duhaut, D., & Kerdreux, J. (2021). Intrinsically Motivated Open-Ended Multi-Task Learning Using Transfer Learning to Discover Task Hierarchy. Applied Sciences, 11(3), 975. https://doi.org/10.3390/app11030975







