Recent Progress on Novel DSP Techniques for Mode Division Multiplexing Systems: A Review
Abstract
:1. Introduction
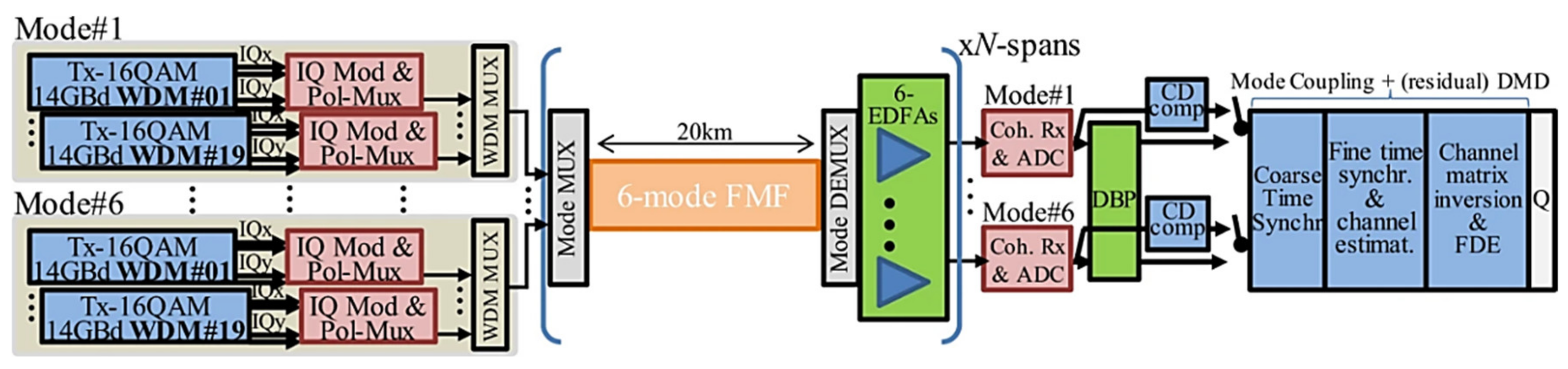
2. Linear DSP MIMO Technique for MDM Systems
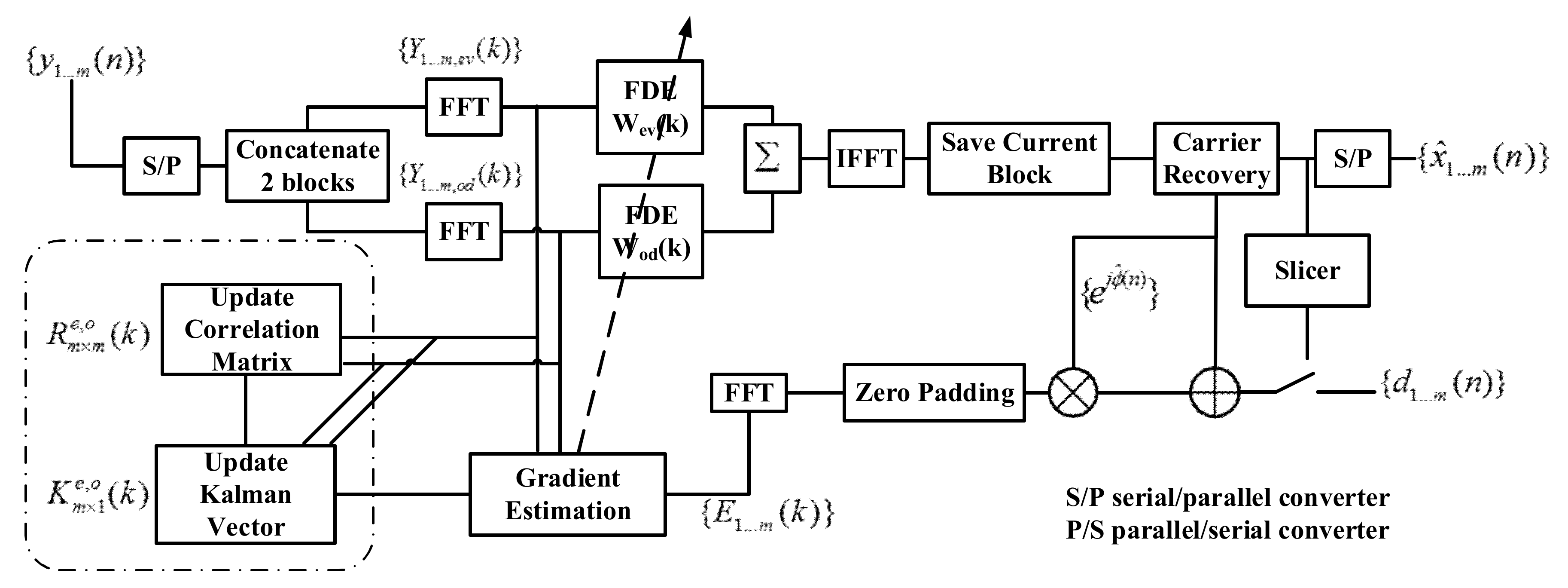
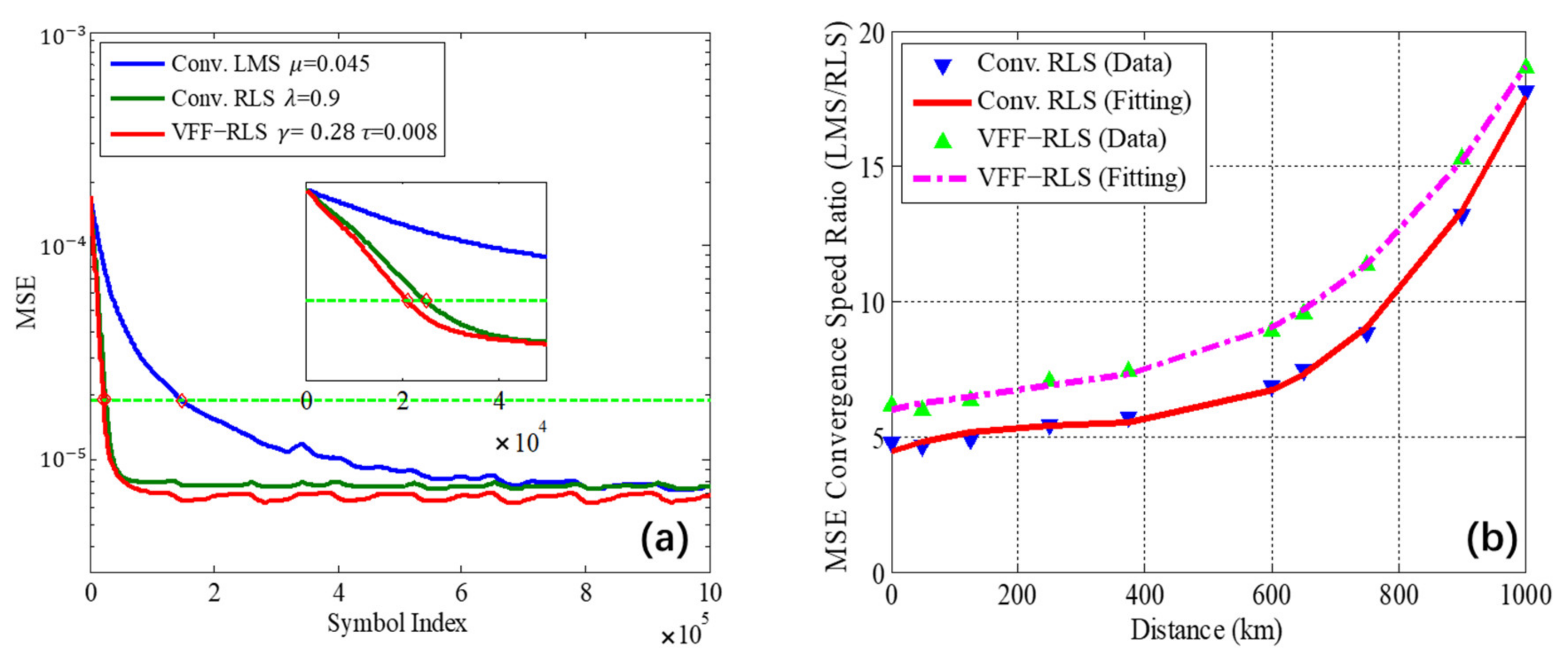
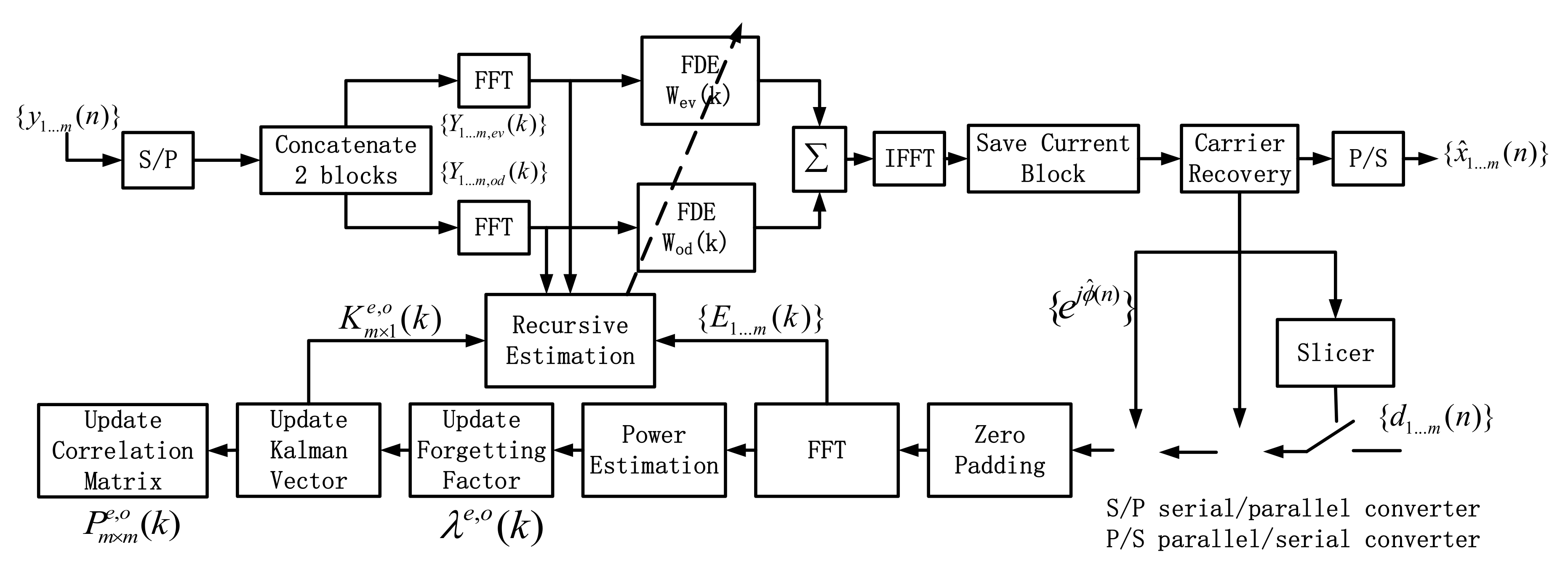
3. RLS MIMO Algorithms and Its Application on Equalization of TV Effects
4. DSP Techniques on Compensation of MDL Effects in FMF Links
4.1. Maximum-Likelihood (ML) Detector
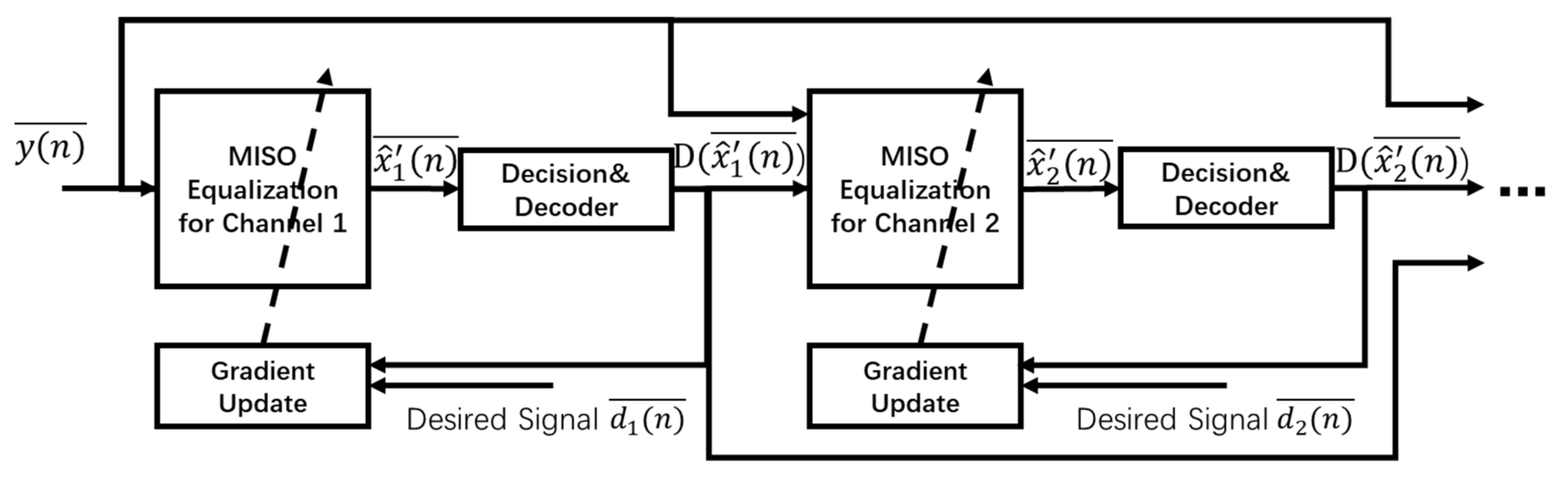
4.2. Interference Cancellation (IC)
4.3. Space-Time Coding Technique (STC)
5. Novel DSP Techniques for MIMO Systems
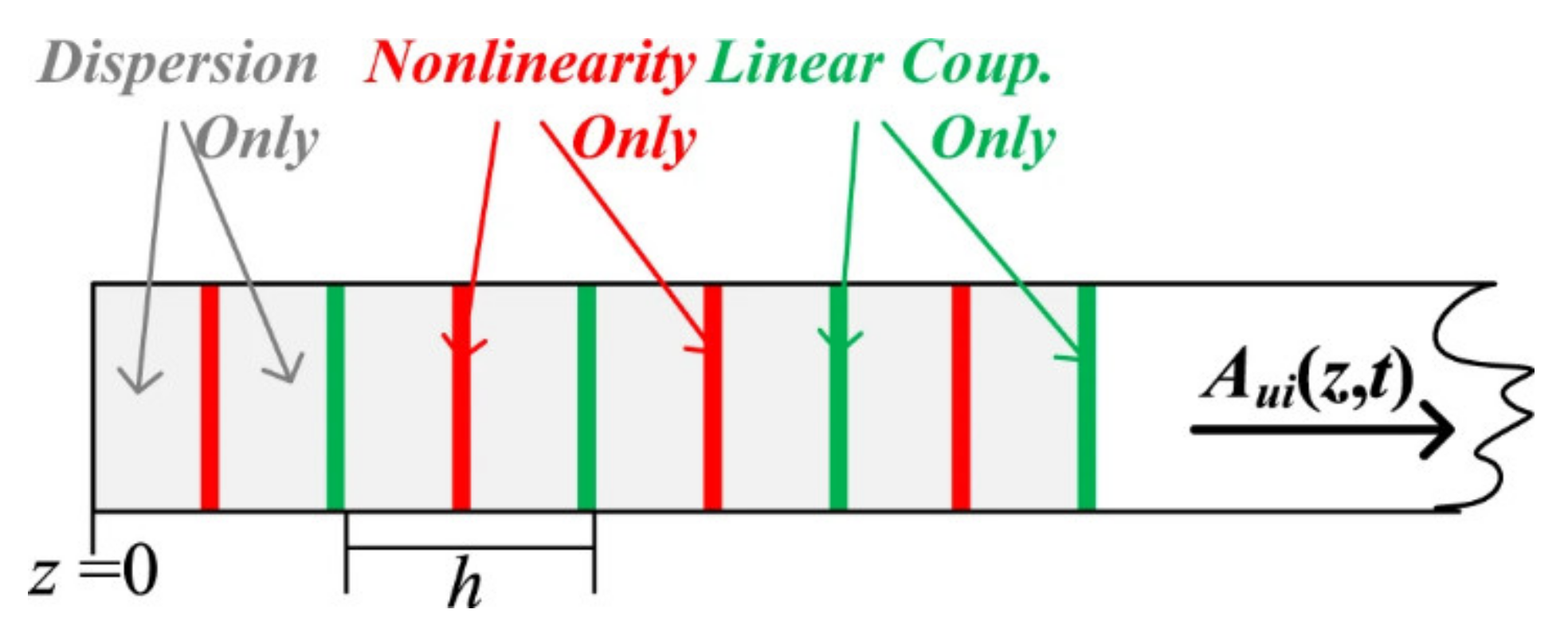
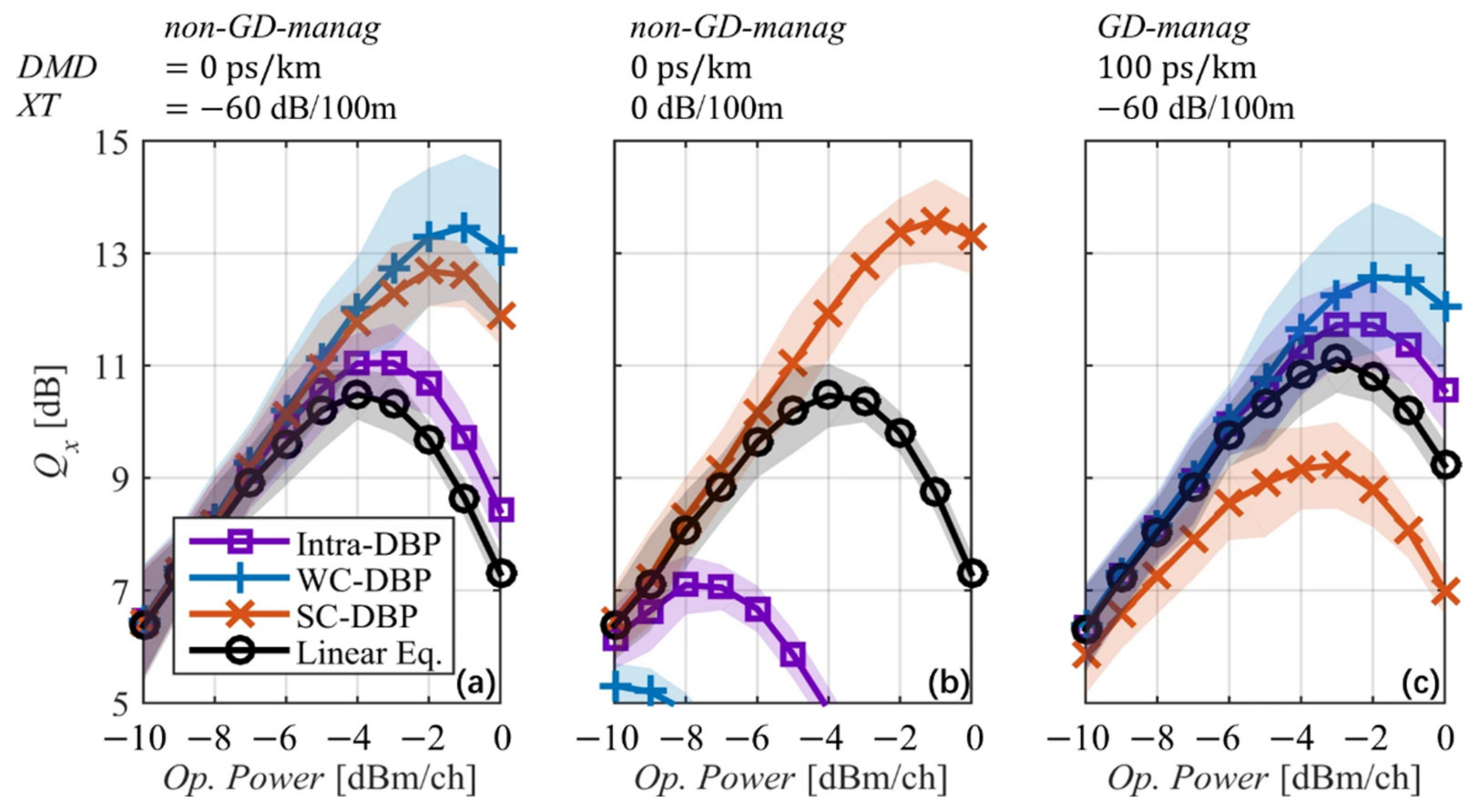
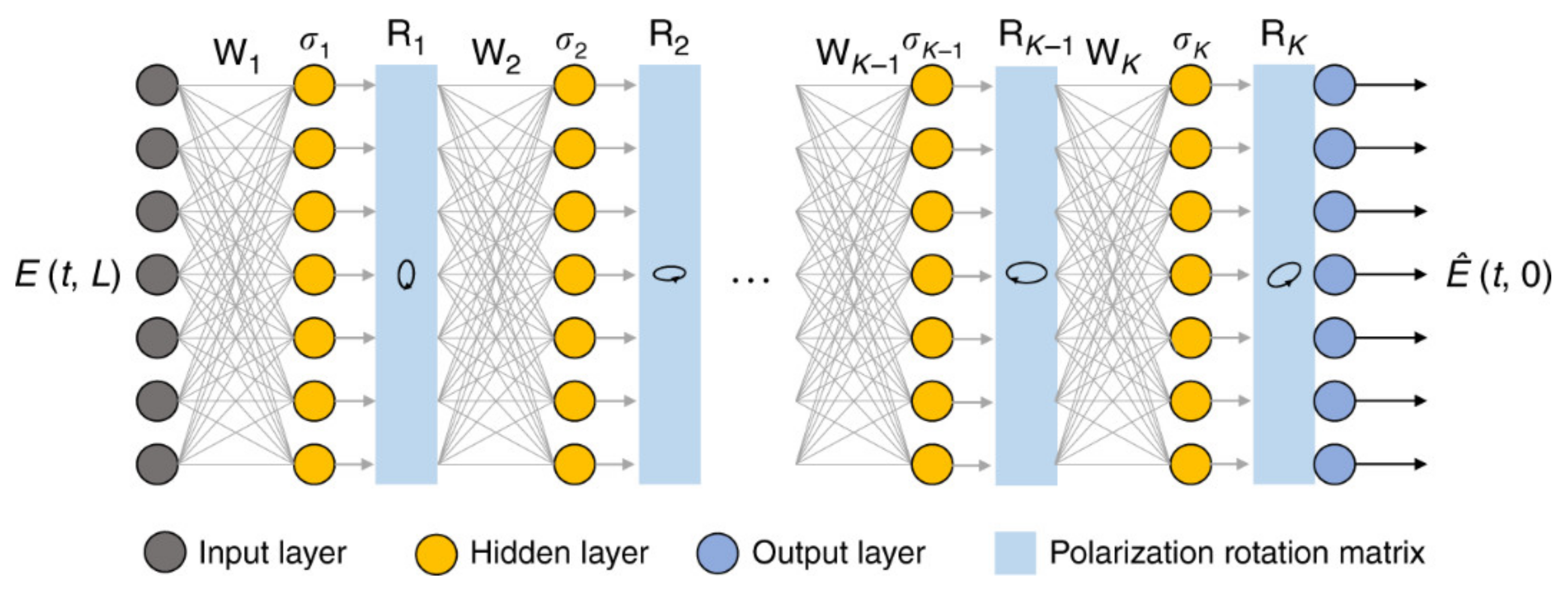
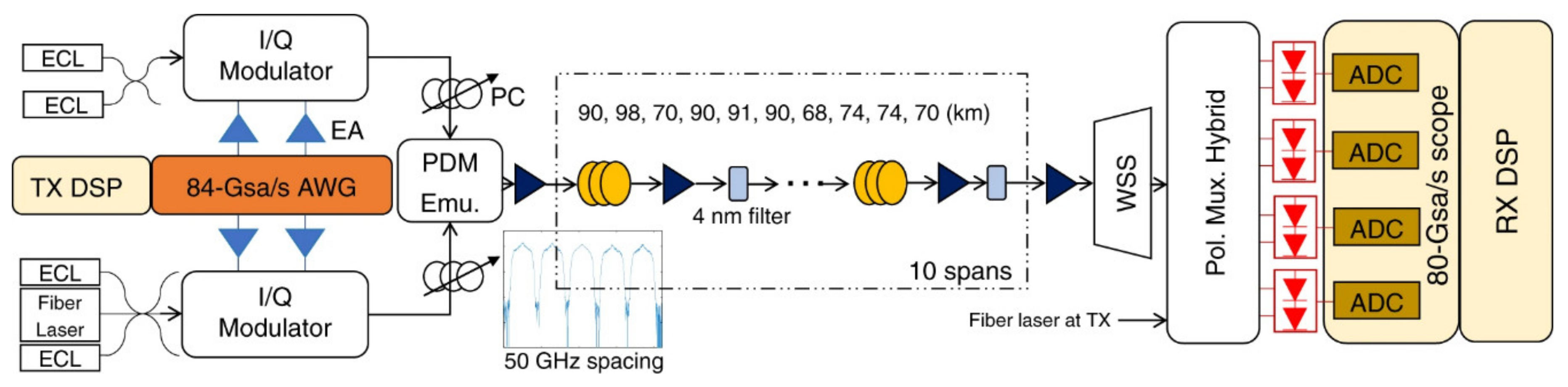
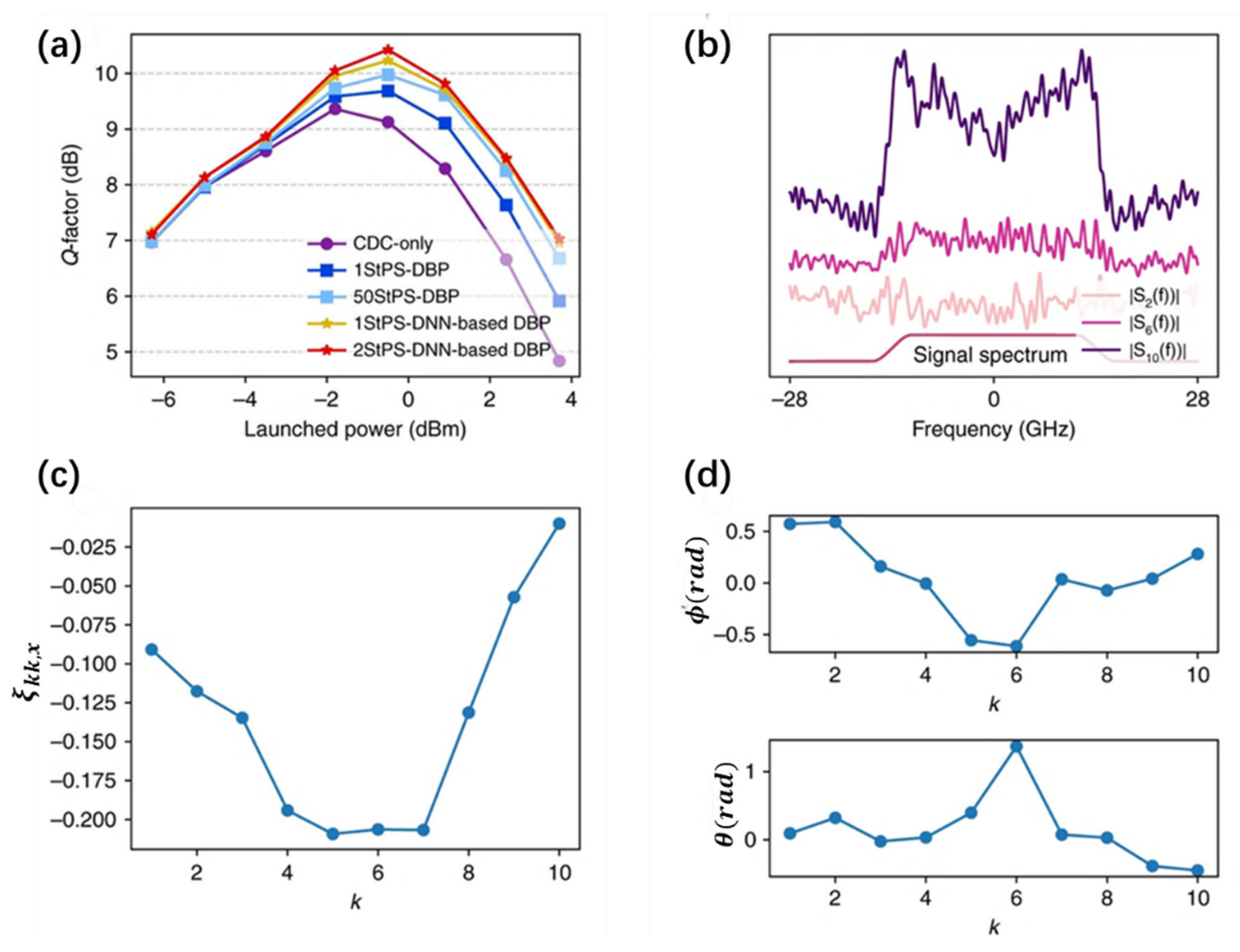
5.1. Digital Back-Propagation Algorithm (DBP)
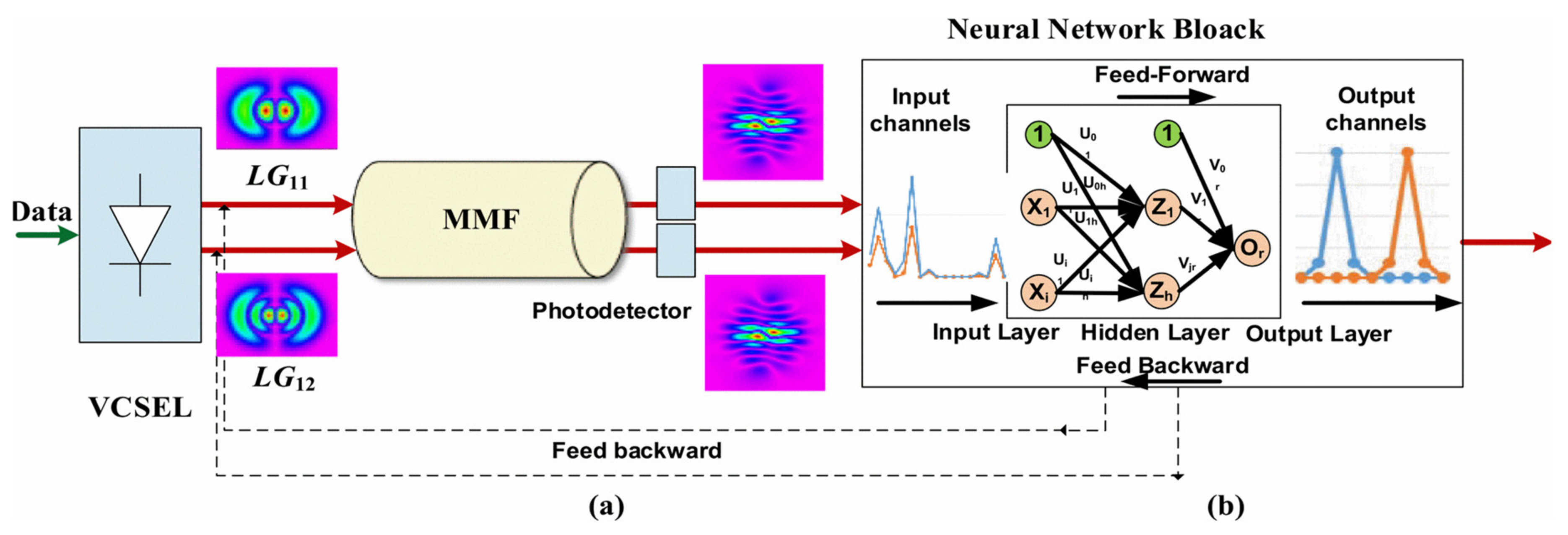
5.2. Artificial Intelligence (AI) Technology for MIMO Equalization
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef] [Green Version]
- Essiambre, R.; Tkach, R.W. Capacity trends and limits of optical communication networks. Proc. IEEE 2012, 100, 1035–1055. [Google Scholar] [CrossRef]
- Kitayama, K.-I.; Diamantopoulos, N.-P. Few-Mode Optical Fibers: Original Motivation and Recent Progress. IEEE Commun. Mag. 2017, 55, 163–169. [Google Scholar] [CrossRef]
- Puttnam, B.J.; Luis, R.S.; Klaus, W.; Sakaguchi, J.; Delgado Mendinueta, J.M.; Awaji, Y.; Wada, N.; Tamura, Y.; Hayashi, T.; Hirano, M.; et al. 2.15 Pb/s Transmission Using a 22 Core Homogeneous Single-mode Multi-core Fiber and Wideband Optical Comb. In Proceedings of the European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015. [Google Scholar]
- Rademacher, G.; Luis, R.S.; Puttnam, B.J.; Awaji, Y.; Wada, N. Crosstalk dynamics in multi-core fibers. Opt. Express 2017, 25, 12020–12028. [Google Scholar] [CrossRef] [PubMed]
- Ryf, R.; Fontaine, N.K.; Chang, S.H.; Alvarado, J.C.; Huang, B.; Antonio-Lopez, J.; Chen, H.; Essiambre, R.-J.; Burrows, E.; Tkach, R.W.; et al. Long-Haul Transmission over Multi-Core Fibers with Coupled Cores. In Proceedings of the European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017. [Google Scholar]
- Inan, B.; Spinnler, B.; Ferreira, F.; van den Borne, D.; Lobato, A.; Adhikari, S.; Sleiffer, V.A.J.M.; Kuschnerov, M.; Hanik, N.; Jansen, S.L. DSP complexity of mode-division multiplexed receivers. Opt. Express 2012, 20, 10859–10869. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pan, Z.; Weng, Y.; He, X.; Wang, J. Adaptive Frequency-domain Equalization and MIMO Signal Processing in Mode Division Multiplexing Systems Using Few-mode Fibers. In Proceedings of the Signal Processing in Photonic Communications (SPPCom), Vancouver, BC, Canada, 18–20 July 2016. [Google Scholar]
- Arik, S.O.; Askarov, D.; Kahn, J.M. Adaptive frequency-domain equalization in mode-division multiplexing systems. J. Lightwave Technol. 2014, 32, 1841–1852. [Google Scholar] [CrossRef]
- Faruk, M.S.; Kikuchi, K. Adaptive frequency-domain equalization in digital coherent optical receivers. Opt. Express 2011, 19, 12789–12798. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yi, W.; Xuan, H.; Zhongqi, P. Performance Analysis of Low-complexity Adaptive Frequency-domain Equalization and MIMO Signal Processing for Compensation of Differential Mode Group Delay in Mode-division Multiplexing Communication Systems Using Few-mode Fibers. In Proceedings of the Next-Generation Optical Communication: Components, Sub-Systems and Systems V, San Francisco, CA, USA, 16–18 February 2016. [Google Scholar]
- Chen, Z.; Tran, A.V.; Do, C.C.; Simin, C.; Anderson, T.; Skafidas, E. Digital Signal Processing for Training-Aided Coherent Optical Single-Carrier Frequency-Domain Equalization Systems. J. Lightwave Technol. 2014, 32, 4110–4120. [Google Scholar] [CrossRef]
- Pittala, F.; Slim, I.; Mezghani, A.; Nossek, J.A. Training-aided frequency-domain channel estimation and equalization for single-carrier coherent optical transmission systems. J. Lightwave Technol. 2014, 32, 4247–4261. [Google Scholar] [CrossRef]
- Xuan, H.; Yi, W.; Junyi, W.; Pan, Z. Noise Power Directed Adaptive Frequency Domain Least Mean Square Algorithm with Fast Convergence for DMGD Compensation in Few-mode Fiber Transmission Systems. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Francisco, CA, USA, 9–13 March 2014. [Google Scholar]
- Puttnam, B.J.; Sakaguchi, J.; Mendinueta, J.M.D.; Klaus, W.; Awaji, Y.; Wada, N.; Kanno, A.; Kawanishi, T. Investigating self-homodyne coherent detection in a 19 channel space-division-multiplexed transmission link. Opt. Express 2013, 21, 1561–1566. [Google Scholar] [CrossRef]
- Yi, W.; Ting, W.; Zhongqi, P. Fast-convergent Adaptive Frequency-domain Recursive Least-squares Algorithm with Reduced Complexity for MDM Transmission Systems Using Optical Few-mode Fibers. In Proceedings of theConference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 June 2016. [Google Scholar]
- Xi, C.; Jiayuan, H.; An, L.; Jia, Y.; Shieh, W. Characterization of Dynamic Evolution of Channel Matrix in Two-mode Fibers. In Proceedings of the OFC Collocated National Fiber-Optic Engineers’ Conference (OFC/NFOEC), Anaheim, CA, USA, 17–21 March 2013. [Google Scholar]
- Chen, X.; He, J.; Li, A.; Ye, J.; Shieh, W. Characterization and analysis of few-mode fiber channel dynamics. IEEE Photonics Technol. Lett. 2013, 25, 1819–1822. [Google Scholar] [CrossRef]
- Hu, Q.; Chen, X.; Shieh, W. Comparison of Channel Fluctuation Between Single-mode Fibers and Few-mode Fibers Using Stokes-space Analysis. In Proceedings of the OptoElectronics and Communications Conference (OECC) and Australian Conference on Optical Fibre Technology (ACOFT), Melbourne, VIC, Australia, 6–10 July 2014. [Google Scholar]
- Warm, S.; Petermann, K. Splice loss requirements in multi-mode fiber mode-division-multiplex transmission links. Opt. Express 2013, 21, 519–532. [Google Scholar] [CrossRef] [PubMed]
- Krummrich, P.M. Optical amplification and optical filter based signal processing for cost and energy efficient spatial multiplexing. Opt. Express 2011, 19, 16636–16652. [Google Scholar] [CrossRef] [PubMed]
- Cocq, G.L.; Quiquempois, Y.; Rouge, A.L.; Bouwmans, G.; El Hamzaoui, H.; Delplace, K.; Bouazaoui, M.; Bigot, L. Few mode Er3+-doped fiber with micro-structured core for mode division multiplexing in the C-band. Opt. Express 2013, 21, 31646–31659. [Google Scholar] [CrossRef]
- Ryf, R.; Fontaine, N.K.; Dunayevsky, J.; Sinefeld, D.; Blau, M.; Montoliu, M.; Randel, S.; Liu, C.; Ercan, B.; Esmaeelpour, M.; et al. Wavelength-selective Switch for Few-mode Fiber Transmission. In Proceedings of the European Conference and Exhibition on Optical Communication (ECOC), London, UK, 22–26 September 2013. [Google Scholar]
- Winzer, P.J.; Foschini, G.J. MIMO capacities and outage probabilities in spatially multiplexed optical transport systems. Opt. Express 2011, 19, 16680–16696. [Google Scholar] [CrossRef]
- Ip, E.; Milione, G.; Huang, Y.-K.; Wang, T. Impact of Mode-dependent Loss on Long-haul Transmission Systems Using Few-mode Fibers. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–24 March 2016. [Google Scholar]
- Xuan, H.; Yi, W.; Zhongqi, P. A Step-Size Controlled Method for Fast Convergent Adaptive FD-LMS Algorithm in Few-Mode Fiber Communication Systems. J. Lightwave Technol. 2014, 32, 3820–3826. [Google Scholar] [CrossRef]
- Rademacher, G.; Petermann, K. Nonlinear Gaussian Noise Model for Multimode Fibers with Space-Division Multiplexing. J. Lightwave Technol. 2016, 34, 2280–2287. [Google Scholar] [CrossRef]
- Essiambre, R.-J.; Mestre, M.A.; Ryf, R.; Gnauck, A.H.; Tkach, R.W.; Chraplyvy, A.R.; Sun, Y.; Jiang, X.; Lingle, R. Experimental investigation of inter-modal four-wave mixing in few-mode fibers. IEEE Photonics Technol. Lett. 2013, 25, 539–542. [Google Scholar] [CrossRef]
- Antonelli, C.; Shtaif, M.; Mecozzi, A. Modeling of nonlinear propagation in space-division multiplexed fiber-optic transmission. J. Lightwave Technol. 2016, 34, 36–54. [Google Scholar] [CrossRef]
- Ferreira, F.M.; Costa, C.S.; Sygletos, S.; Ellis, A.D. Nonlinear Compensation Using Digital Back-Propagation in Few-Mode Fibre Spans with Intermediate Coupling. In Proceedings of the European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017. [Google Scholar]
- Ferreira, F.M.; Costa, C.S.; Sygletos, S.; Ellis, A.D. Overcoming degradation in spatial multiplexing systems with stochastic nonlinear impairments. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef]
- Fan, Q.; Zhou, G.; Gui, T.; Lu, C.; Lau, A.P.T. Advancing theoretical understanding and practical performance of signal processing for nonlinear optical communications through machine learning. Nat. Commun. 2020, 11, 1–11. [Google Scholar] [CrossRef]
- Lobato, A.; Ferreira, F.; Inan, B.; Adhikari, S.; Kuschnerov, M.; Napoli, A.; Spinnler, B.; Lankl, B. Maximum-Likelihood Detection in Few-Mode Fiber Transmission With Mode-Dependent Loss. IEEE Photonics Technol. Lett. 2013, 25, 1095–1098. [Google Scholar] [CrossRef]
- Xi, C.; Jia, Y.; Yue, X.; An, L.; Jiayuan, H.; Qian, H.; Shieh, W. Equalization of Two-mode Fiber Based MIMO Signals with Larger Receiver Sets. In Proceedings of the European Conference and Exhibition on Optical Communications (ECOC), Amsterdam, Netherlands, 16–20 September 2012. [Google Scholar]
- Randel, S.; Ryf, R.; Sierra, A.; Winzer, P.J.; Gnauck, A.H.; Bolle, C.A.; Essiambre, R.-J.; Peckham, D.W.; McCurdy, A.; Lingle, R. 6 × 56-Gb/s mode-division multiplexed transmission over 33-km few-mode fiber enabled by 6×6 MIMO equalization. Optics Express 2011, 19, 16697–16707. [Google Scholar] [CrossRef] [PubMed]
- Randel, S.; Winzer, P.J.; Montoliu, M.; Ryf, R. Complexity Analysis of Adaptive Frequency-Domain Equalization for MIMO-SDM Transmission. In Proceedings of the European Conference and Exhibition on Optical Communication (ECOC), Stevenage, UK, 22–26 September 2013. [Google Scholar]
- Neng, B.; Guifang, L. Adaptive Frequency-domain Equalization for Mode-division Multiplexed Transmission. IEEE Photonics Technol. Lett. 2012, 24, 1918–1921. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, J.; Weng, Y.; Pan, Z. A Fast Convergence Frequency Domain Least Mean Square Algorithm for Compensation of Differential Mode Group Delay in Few Mode Fibers. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 17–21 March 2013. [Google Scholar]
- Kudo, R.; Kobayashi, T.; Ishihara, K.; Takatori, Y.; Sano, A.; Miyamoto, Y. Coherent optical single carrier transmission using overlap frequency domain equalization for long-haul optical systems. J. Lightwave Technol. 2009, 27, 3721–3728. [Google Scholar] [CrossRef]
- Li, G.; Bai, N.; Zhao, N.; Xia, C. Space-division multiplexing: The next frontier in optical communication. Adv. Opt. Photonics 2014, 6, 413–487. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Zhao, J.; Bai, N.; Ip, E.; Wang, T.; Li, G. Experimental Demonstration of Adaptive Recursive Least Square Frequency-domain Equalization for Long-distance Mode-division Multiplexed Transmission. In Proceedings of the European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015. [Google Scholar]
- Fontaine, N.K.; Ryf, R.; Chen, H.; Benitez, A.V.; Amezcua-Correa, R. 30 × 30 MIMO Transmission over 15 Spatial Modes. In Proceedings of the Optical Fiber Communicaiton Conference (OFC), Los Angeles, CA, USA, 24–26 March 2015. [Google Scholar]
- Benvenuto, N.; Cherubini, G.; Tomasin, S. Algorithms for Communications Systems and Their Applications; Wiley Online Library: Hoboken, NJ, USA, 2002; pp. 197–203. [Google Scholar]
- Paleologu, C.; Benesty, J.; Ciochina, S. A robust variable forgetting factor recursive least-squares algorithm for system identification. IEEE Signal Process. Lett. 2008, 15, 597–600. [Google Scholar] [CrossRef]
- Wang, J. A Variable Forgetting Factor RLS Adaptive Filtering Algorithm. In Proceedings of the IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications (MAPE), Beijing, China, 27–29 October 2009. [Google Scholar]
- Park, D.J.; Jun, B.E.; Kim, J.H. Fast tracking RLS algorithm using novel variable forgetting factor with unity zone. Electron. Lett. 1991, 27, 2150–2151. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, J.; Bai, N.; Ip, E.; Wang, T.; Li, Z.; Li, G. Experimental demonstration of adaptive vff-rls-fde for long-distance mode-division multiplexed transmission. Opt. Express 2018, 26, 18362–18367. [Google Scholar] [CrossRef]
- Choutagunta, K.; Ryf, R.; Fontaine, N.; Wittek, S.; Alvarado-Zacarias, J.C.; Mazur, M.; Haoshuo, C.; Essiambre, R.J.; Amezcua-Correa, R.; Hayashi, T.; et al. Modal Dynamics in Spatially Multiplexed Links. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019. [Google Scholar]
- Wenbo, Y.; Zhiqun, Y.; Xutao, W.; Lin, Z.; Guifang, L. Frequency-Domain VFF-RLS Equalization for the Time-Varying Mode-Division Multiplexed Channels. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 10–15 May 2020. [Google Scholar]
- Leung, S.-H.; So, C.F. Gradient-based variable forgetting factor RLS algorithm in time-varying environments. IEEE Trans. Signal Process. 2005, 53, 3141–3150. [Google Scholar] [CrossRef]
- Jankiraman, M. Space-Time Codes and MIMO Systems; Artech House: Fitchburg, MA, USA, 2004; pp. 22–23. [Google Scholar]
- Shibahara, K.; Mizuno, T.; Lee, D.; Miyamoto, Y. Advanced MIMO Signal Processing Techniques Enabling Long-Haul Dense SDM Transmissions. J. Lightwave Technol. 2018, 36, 336–348. [Google Scholar] [CrossRef]
- Lobato, A.; Ferreira, F.; Rabe, J.; Inan, B.; Adhikari, S.; Kuschnerov, M.; Napoli, A.; Spinnler, B.; Lankl, B. On the Mode-dependent Loss Compensation for Mode-division Multiplexed Systems. In Proceedings of the 15th International Conference on Transparent Optical Networks (ICTON), Cartagena, Spain, 23–27 June 2013. [Google Scholar]
- Biglieri, E.; Calderbank, R.; Constantinides, A.; Goldsmith, A.; Paulraj, A.; Poor, H.V. MIMO Wireless Communications; Cambridge University Press: Cambridge, UK, 2007; pp. 186–190. [Google Scholar]
- Lobato, A.; Chen, Y.; Jung, Y.; Chen, H.; Inan, B.; Kuschnerov, M.; Fontaine, N.K.; Ryf, R.; Spinnler, B.; Lankl, B. 12-mode OFDM transmission using reduced-complexity maximum likelihood detection. Opt. Lett. 2015, 40, 328–331. [Google Scholar] [CrossRef] [PubMed]
- Lobato, A.; Rabe, J.; Ferreira, F.; Kuschnerov, M.; Spinnler, B.; Lankl, B. Near-ML detection for MDL-impaired few-mode fiber transmission. Opt. Express 2015, 23, 9589–9601. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Tian, Z.; Guijun, H. Complex lattice reduction aided detection for mode-division multiplexing systems with mode dependent loss and differential mode group delay. Opt. Commun. 2019, 442, 65–70. [Google Scholar] [CrossRef]
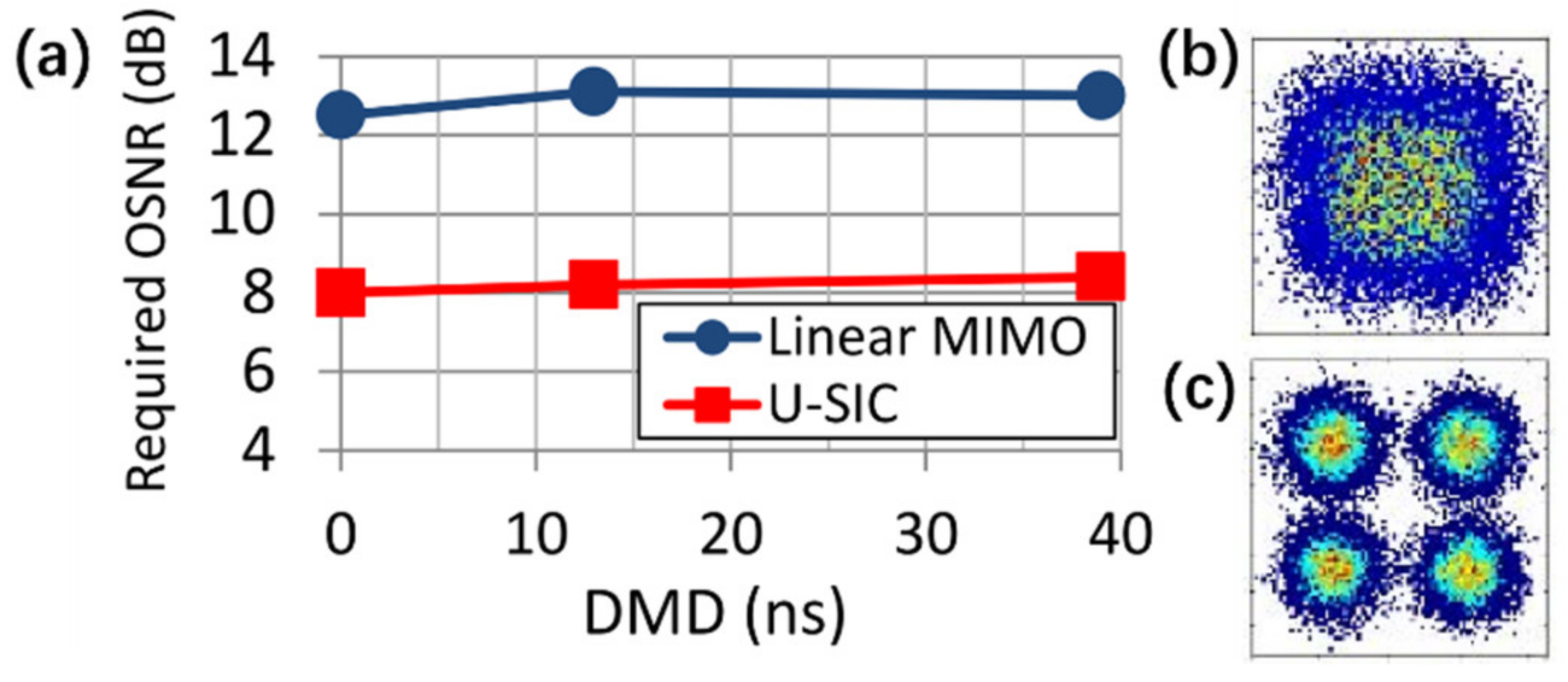
- Shibahara, K.; Mizuno, T.; Miyamoto, Y. LDPC-coded FMF Transmission Employing Unreplicated Successive Interference Cancellation for MDL-Impact Mitigation. In Proceedings of the European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017. [Google Scholar]
- Shibahara, K.; Mizuno, T.; Miyamoto, Y. Interference Cancelling Techniques for Long-haul MIMO-SDM Transmission. In Proceedings of the Signal Processing in Photonic Communications (SPPCom), Zurich, Switzerland, 2–5 July 2018. [Google Scholar]
- Shibahara, K.; Mizuno, T.; Doohwan, L.; Miyamoto, Y.; Ono, H.; Nakajima, K.; Amma, Y.; Takenaga, K.; Saitoh, K. DMD-Unmanaged Long-Haul SDM Transmission Over 2500-km 12-Core 3-Mode MC-FMF and 6300-km 3-Mode FMF Employing Intermodal Interference Canceling Technique. J. Lightwave Technol. 2019, 37, 138–147. [Google Scholar] [CrossRef]
- Shibahara, K.; Mizuno, T.; Doohwan, L.; Miyamoto, Y.; Ono, H.; Nakajima, K.; Amma, Y.; Takenaga, K.; Saitoh, K. Iterative unreplicated parallel interference canceler for MDL-tolerant dense SDM (12-Core 3-Mode) transmission over 3000 km. J. Lightwave Technol. 2019, 37, 1560–1569. [Google Scholar] [CrossRef]
- Tarokh, V.; Seshadri, N.; Calderbank, A.R. Space-time codes for high data rate wireless communication: Performance criterion and code construction. IEEE Trans. Inf. Theory 2002, 44, 744–765. [Google Scholar] [CrossRef] [Green Version]
- Awwad, E.; Othman, G.R.B.; Jaouen, Y. Space-time Coding and Optimal Scrambling for Mode Multiplexed Optical Fiber Systems. In Proceedings of the IEEE International Conference on Signal Processing for Communications (ICC), London, UK, 8–12 June 2015. [Google Scholar]
- Awwad, E.; Othman, G.R.B.; Jaouen, Y. Space-Time Coding Schemes for MDL-Impaired Mode-Multiplexed Fiber Transmission Systems. J. Lightwave Technol. 2015, 33, 5084–5094. [Google Scholar] [CrossRef]
- Shibahara, K.; Mizuno, T.; Takara, H.; Kawakami, H.; Lee, D.; Miyamoto, Y.; Matsuo, S.; Saitoh, K.; Yamada, M. Space-time Coding-assisted Transmission for Mitigation of MDL Impact on Mode-division Multiplexed Signals. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–24 March 2016. [Google Scholar]
- Yingchao, X.; Yu, T.; Bo, H.; Han, Y.; Juhao, L.; Paikun, Z.; Yongqi, H.; Zhangyuan, C. Mode-Interleaving Method with Improved Transmission Reach for MDL-Impaired MDM Systems. In Proceedings of the Asia Communications and Photonics Conference (ACP), Wuhan, China, 2–5 November 2016. [Google Scholar]
- Amhoud, E.M.; Othman, G.R.B.; Bigot, L.; Mengdi, S.; Andresen, E.R.; Labroille, G.; Bigot-Astruc, M.; Jaouen, Y. Experimental Demonstration of Space-Time Coding for MDL Mitigation in Few-Mode Fiber Transmission Systems. In Proceedings of the European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017. [Google Scholar]
- Amhoud, E.M.; Othman, G.R.B.; Jaouen, Y. Design Criterion of Space-time Codes for SDM Optical Fiber Systems. In Proceedings of the International Conference on Telecommunications (ICT), Thessaloniki, Greece, 16–18 May 2016. [Google Scholar]
- Amhoud, E.M.; Jaouen, Y.; Ben-Othman, G.R. Joint Space-time Coding and FEC for MDL Mitigation in Few-mode Fiber Systems. In Proceedings of the Novel Optical Materials and Applications (NOMA), Vancouver, BC, Canada, 18–20 July 2016. [Google Scholar]
- Amhoud, E.M.; Othman, G.R.B.; Jaouen, Y. Concatenation of Space-Time Coding and FEC for Few-Mode Fiber Systems. IEEE Photonics Technol. Lett. 2017, 29, 603–606. [Google Scholar] [CrossRef]
- Yi, W.; Xuan, H.; Junyi, W.; Zhongqi, P. Rigorous Study of Low-complexity Adaptive Space-time Block-coded MIMO Receivers in High-speed Mode Multiplexed Fiber-optic Transmission Links Using Few-mode Fibers. In Proceedings of the Next-Generation Optical Communication: Components, Sub-Systems and Systems VI, San Francisco, CA, USA, 31 January–2 February 2017. [Google Scholar]
- Yi, W.; Xuan, H.; Wang, Y.; Pacheco, M.C.; Junyi, W.; Pan, Z. Mode-dependent Loss Mitigation Scheme for PDM-64QAM Few-Mode Fiber Space-division-multiplexing Systems via STBC-MIMO Equalizer. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 14–19 May 2017. [Google Scholar]
- Yong Qiang, H.; Wen Tao, L.; Xiao Chuan, X.; Chen, R.T. Orthogonal STBC for MDL mitigation in mode division multiplexing system with MMSE channel estimation. J. Lightwave Technol. 2017, 35, 1858–1867. [Google Scholar]
- Yongqiang, H.; Li, L.; Weiting, S.; Guangming, S.; Huaxi, G. Hybrid IRS and DFE Detection Scheme for MDL-impaired Transmission with TAST Coding. J. Lightwave Technol. 2019, 37, 4251–4259. [Google Scholar]
- Mumtaz, S.; Essiambre, R.-J.; Agrawal, G.P. Nonlinear Propagation in Multimode and Multicore Fibers: Generalization of the Manakov Equations. J. Lightwave Technol. 2013, 31, 398–406. [Google Scholar] [CrossRef] [Green Version]
- Giacoumidis, E.; Le, S.T.; Ghanbarisabagh, M.; McCarthy, M.; Aldaya, I.; Mhatli, S.; Jarajreh, M.A.; Haigh, P.A.; Doran, N.J.; Ellis, A.D.; et al. Fiber nonlinearity-induced penalty reduction in CO-OFDM by ANN-based nonlinear equalization. Opt. Lett. 2015, 40, 5113–5116. [Google Scholar] [CrossRef] [PubMed]
- Siming, L.; Alfadhli, Y.M.; Shuyi, S.; Mu, X.; Huiping, T.; Gee-Kung, C. A Novel ANN Equalizer to Mitigate Nonlinear Interference in Analog-RoF Mobile Fronthaul. IEEE Photonics Technol. Lett. 2018, 30, 1675–1678. [Google Scholar]
- Caballero, F.J.V.; Ives, D.J.; Laperle, C.; Charlton, D.; Zhuge, Q.; O’Sullivan, M.; Savory, S.J. Machine learning based linear and nonlinear noise estimation. J. Opt. Commun. Netw. 2018, 10, D42–D51. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Y.X.; Yu, J. Optical Performance Monitoring of 56Gbps Optical PAM4 Signal Using Artificial Neural Networks. In Proceedings of the Asia Communications and Photonics Conference (ACPC), Guangzhou, Guangdong, China, 10–13 November 2017. [Google Scholar]
- Yu, Z.; Wan, Z.; Shu, L.; Hu, S.; Zhao, Y.; Zhang, J.; Xu, K. Loss weight adaptive multi-task learning based optical performance monitor for multiple parameters estimation. Opt. Express 2019, 27, 37041–37055. [Google Scholar] [CrossRef]
- Rahmani, B.; Loterie, D.; Konstantinou, G.; Psaltis, D.; Moser, C. Multimode optical fiber transmission with a deep learning network. Light-Sci. Appl. 2018, 7, 69. [Google Scholar] [CrossRef]
- Fan, P.; Ruddlesden, M.; Wang, Y.; Zhao, L.; Lu, C.; Su, L. Learning Enabled Dense Space-division Multiplexing through a Single Multimode Fibre. arXiv 2020, arXiv:2002.01788, preprint. [Google Scholar]
- Karanov, B.; Chagnon, M.; Thouin, F.; Eriksson, T.A.; Bulow, H.; Lavery, D.; Bayvel, P.; Schmalen, L. End-to-End Deep Learning of Optical Fiber Communications. J. Lightwave Technol. 2018, 36, 4843–4855. [Google Scholar] [CrossRef]
- Fazea, Y.; Sajat, M.S.; Ahmad, A.; Alobaedy, M.M. Channel Optimization in Mode Division Multiplexing Using Neural Networks. In Proceedings of the IEEE International Colloquium on Signal Processing and Its Applications (CSPA), Batu Feringghi, Malaysia, 9–10 March 2018. [Google Scholar]
- Poudel, B.; Oshima, J.; Kobayashi, H.; Iwashita, K. MIMO detection using a deep learning neural network in a mode division multiplexing optical transmission system. Opt. Commun. 2019, 440, 41–48. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Wei, J.; Aldaya, I.; Barry, L.P. Exceeding the Nonlinear Shannon-Limit in Coherent Optical Communications by MIMO Machine Learning. arXiv 2018, arXiv:1802.09120. [Google Scholar]








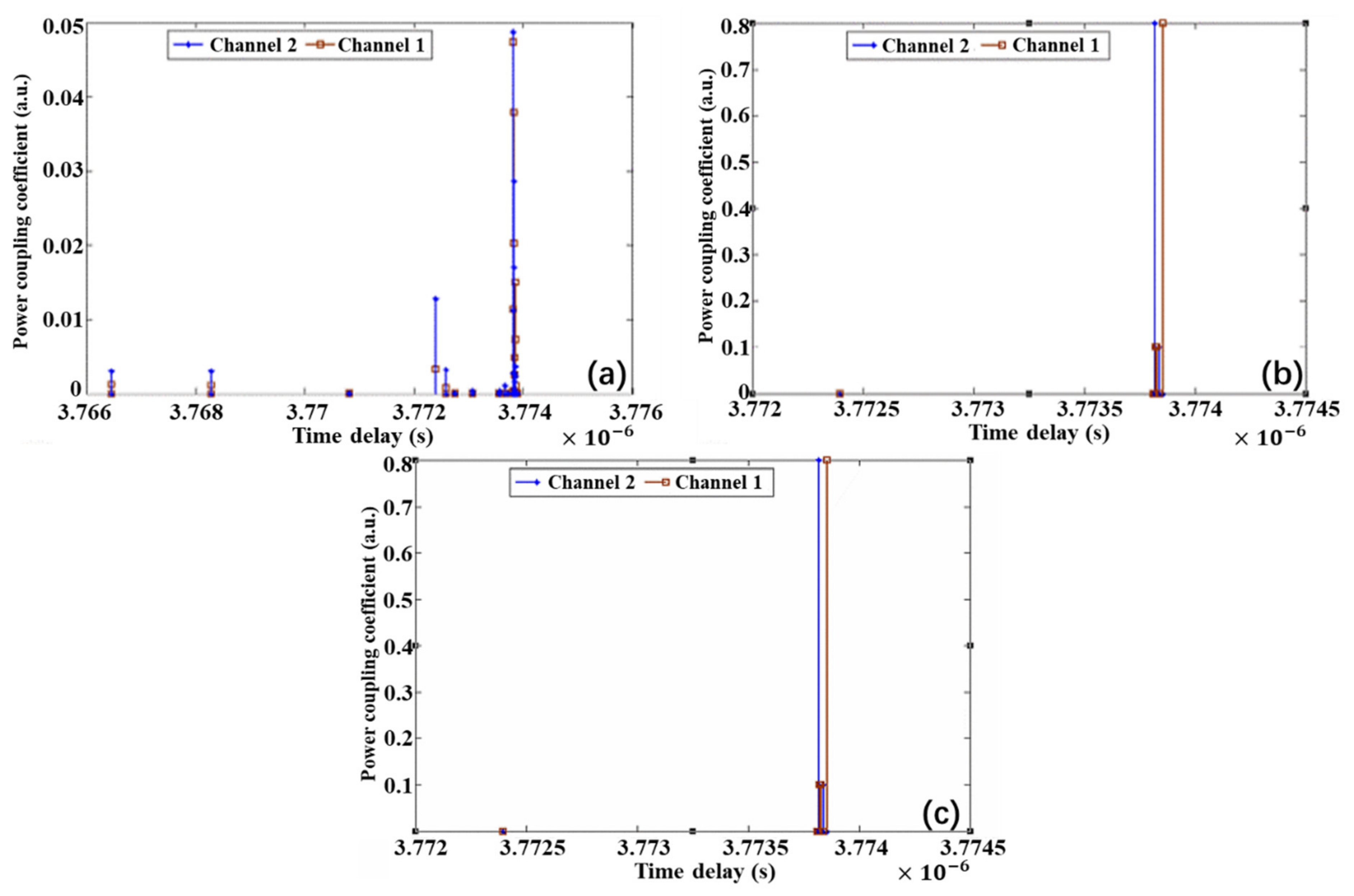
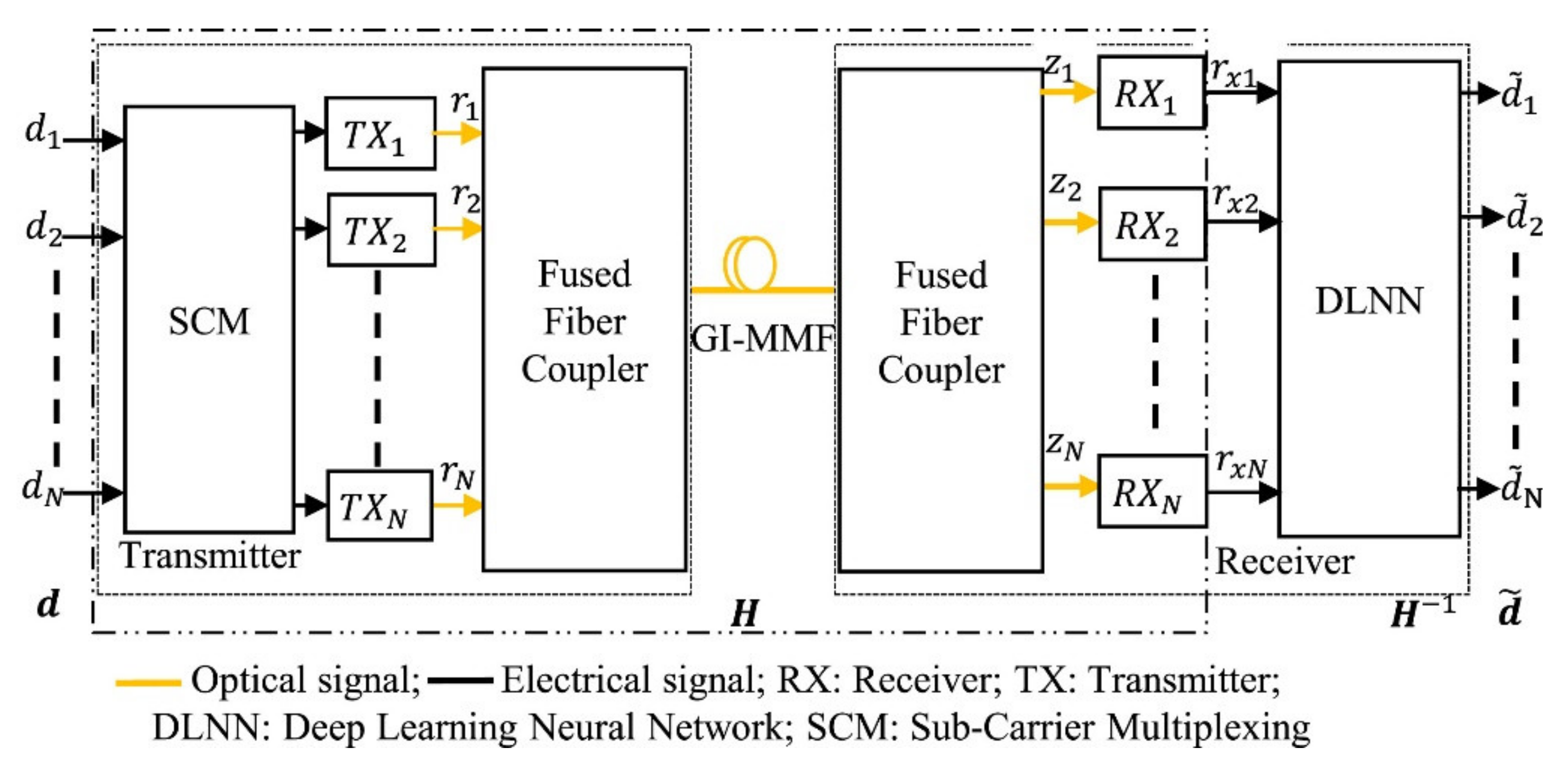
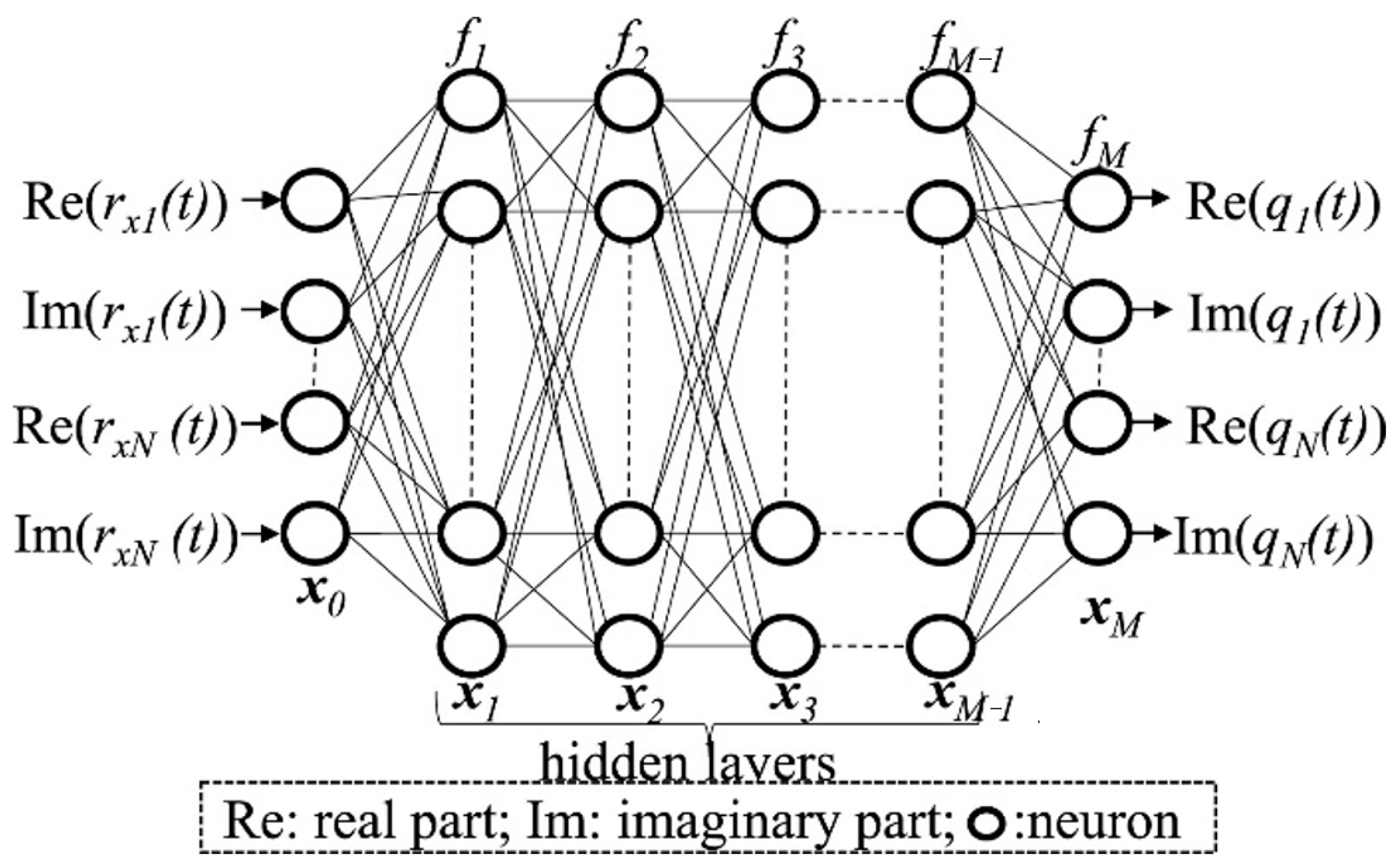


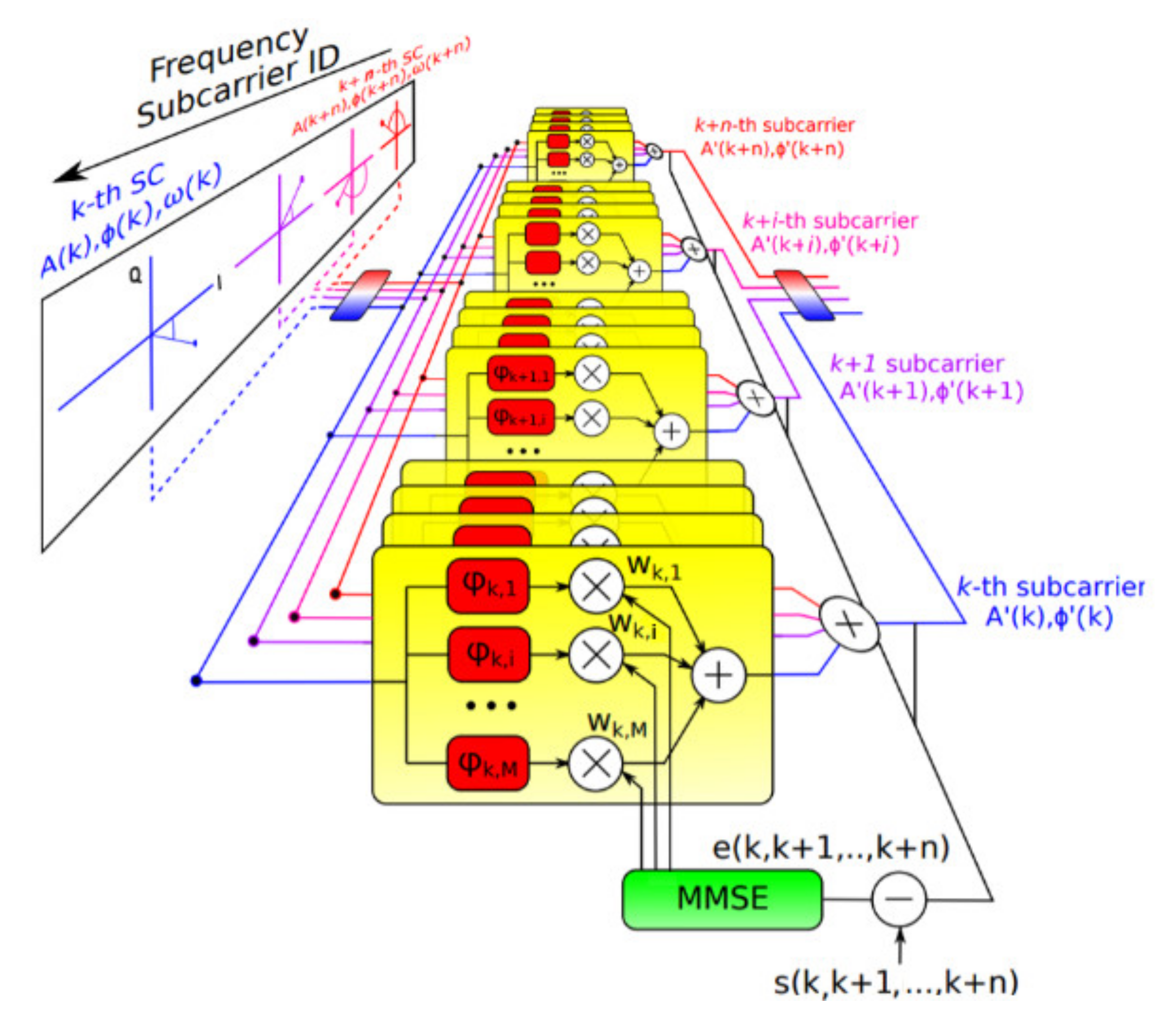
| Operation | Number of Complex Multiplications | |
|---|---|---|
| LMS | RLS | |
| Compute output | ||
| Update filter coef. | ||
| FFT/IFFT | ||
| Update Kalman vector | - | |
| Update correlation matrix | - | |
| Classification | Receiver-Side | Transmitter-Side | |
|---|---|---|---|
| Name | ML | IC | STC |
| Complexity | High | Low | Moderate (excluding equalizer) |
| Advantages | Optimal equalizer | Suboptimal equalizer | Easily compatible with other solutions; Coder technique |
| Disadvantages | High complexity | Worse performance | Loss of multiplexing gain; Required for extra coder and equalizer |
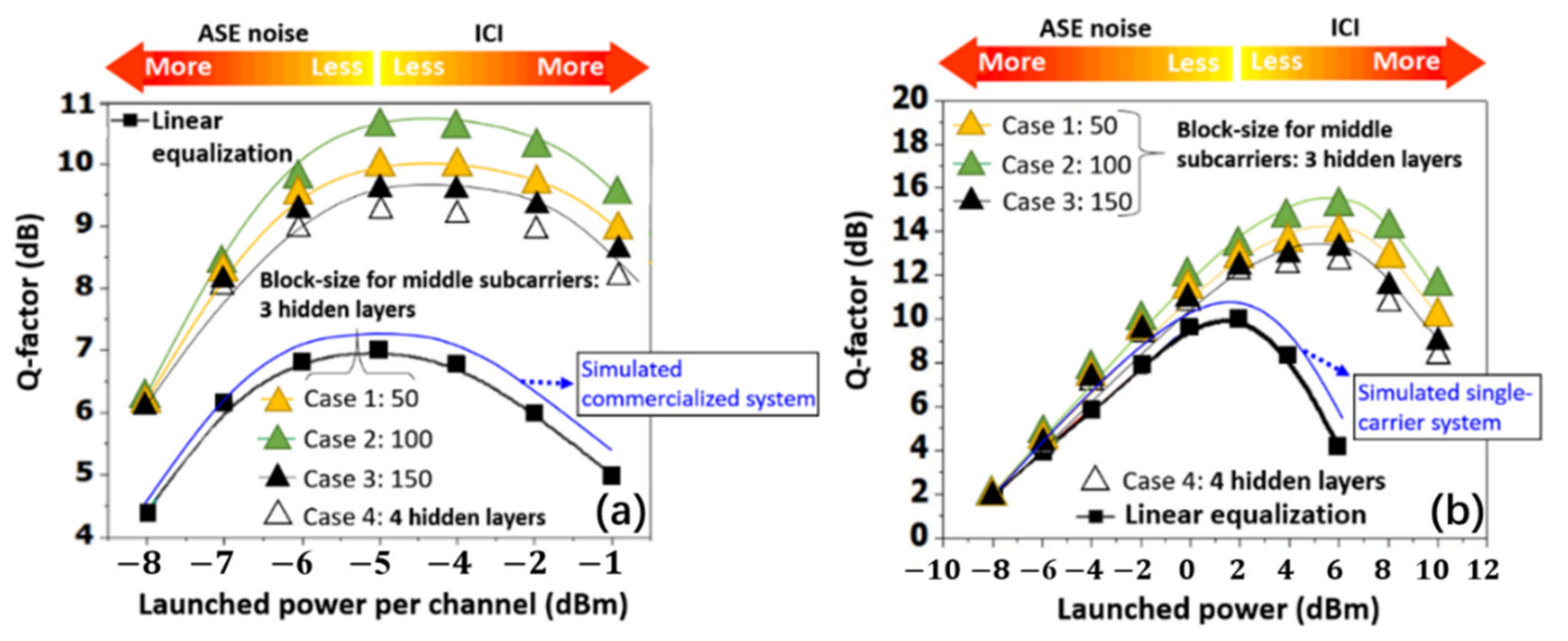
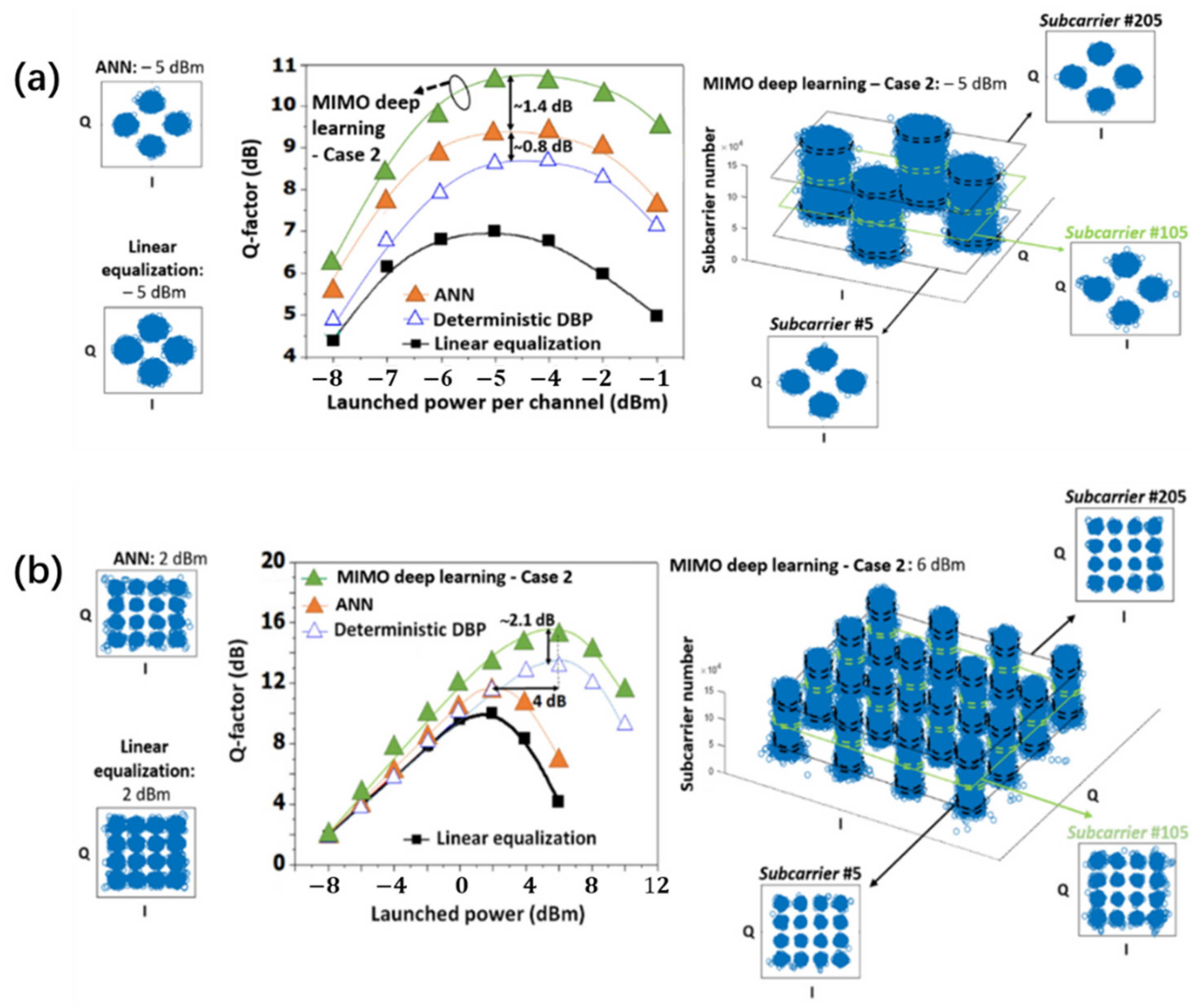
| Cases | Block-Size for Middle Subcarriers | Hidden Layers |
|---|---|---|
| 1 | 50 | 3 |
| 2 | 100 | 3 |
| 3 | 150 | 3 |
| 4 | 2 × 54 (middle groups), 2 × 51 (edge groups) | 4 |
| Structures of NN | Applications |
|---|---|
| ANN | Compensating mode coupling and DMD |
| DLNN | MIMO detection |
| 3D-ANN | MIMO equalization in the presence of FWM |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Yu, W.; Peng, G.; Liu, Y.; Zhang, L. Recent Progress on Novel DSP Techniques for Mode Division Multiplexing Systems: A Review. Appl. Sci. 2021, 11, 1363. https://doi.org/10.3390/app11041363
Yang Z, Yu W, Peng G, Liu Y, Zhang L. Recent Progress on Novel DSP Techniques for Mode Division Multiplexing Systems: A Review. Applied Sciences. 2021; 11(4):1363. https://doi.org/10.3390/app11041363
Chicago/Turabian StyleYang, Zhiqun, Wenbo Yu, Guanju Peng, Yaping Liu, and Lin Zhang. 2021. "Recent Progress on Novel DSP Techniques for Mode Division Multiplexing Systems: A Review" Applied Sciences 11, no. 4: 1363. https://doi.org/10.3390/app11041363






