Prediction of Model Distortion by FEM in 3D Printing via the Selective Laser Melting of Stainless Steel AISI 316L
Abstract
:1. Introduction
- What are the roles of simulation in preparation for the fabricating process with SLM technology? How accurate are they in predicting the dimensional deviation of the printed parts?
- How dimensionally accurate is the SLM-fabricated part in comparison with the Computer Aided Design (CAD) design?
- What are the controllable factors that need to be considered in the whole process to obtain dimensionally, functionally, and economically optimal SLM-fabricated parts?
2. Materials and Methods
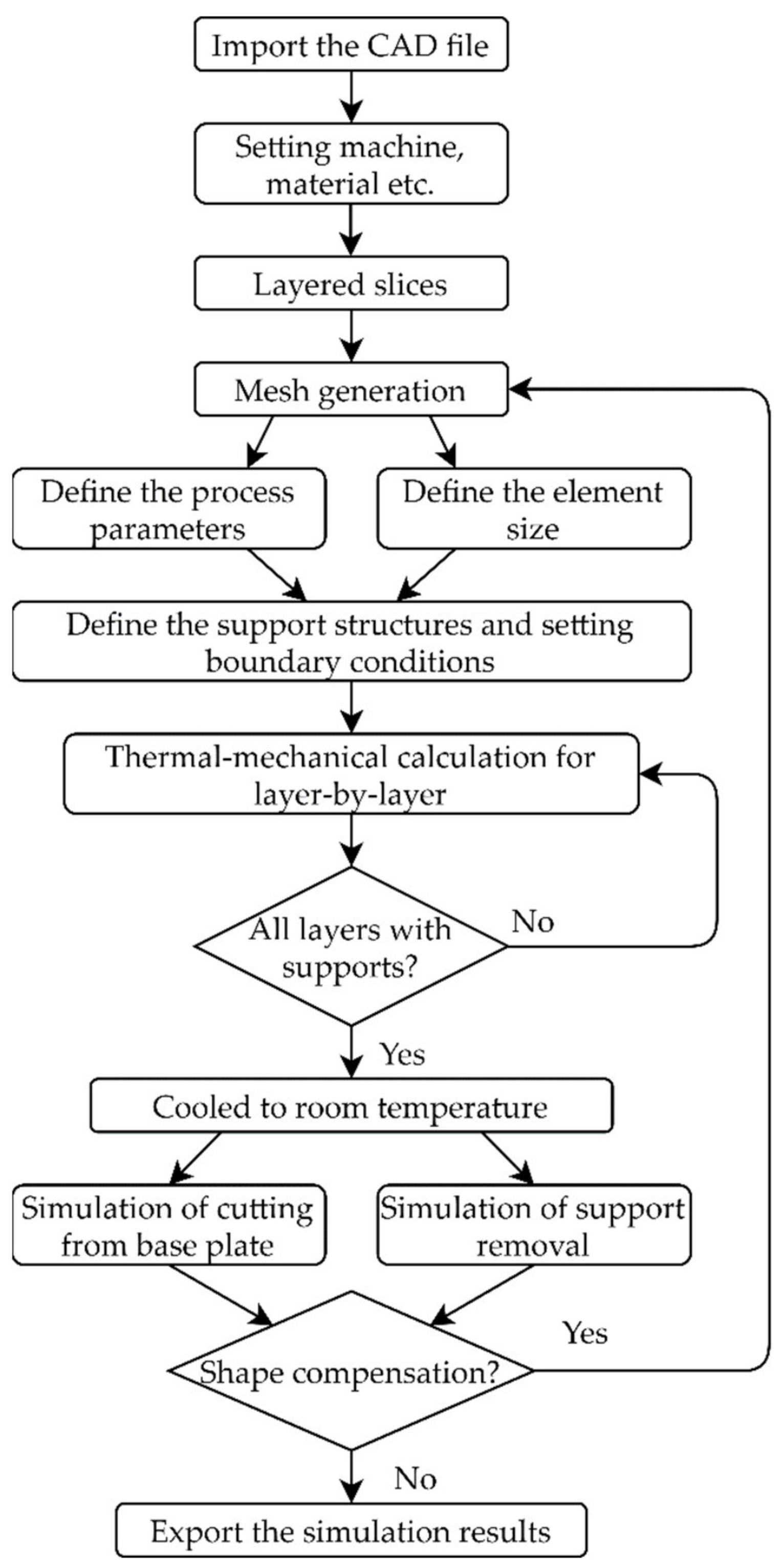
2.1. ANSYS Additive Suite
2.2. MSC Simufact
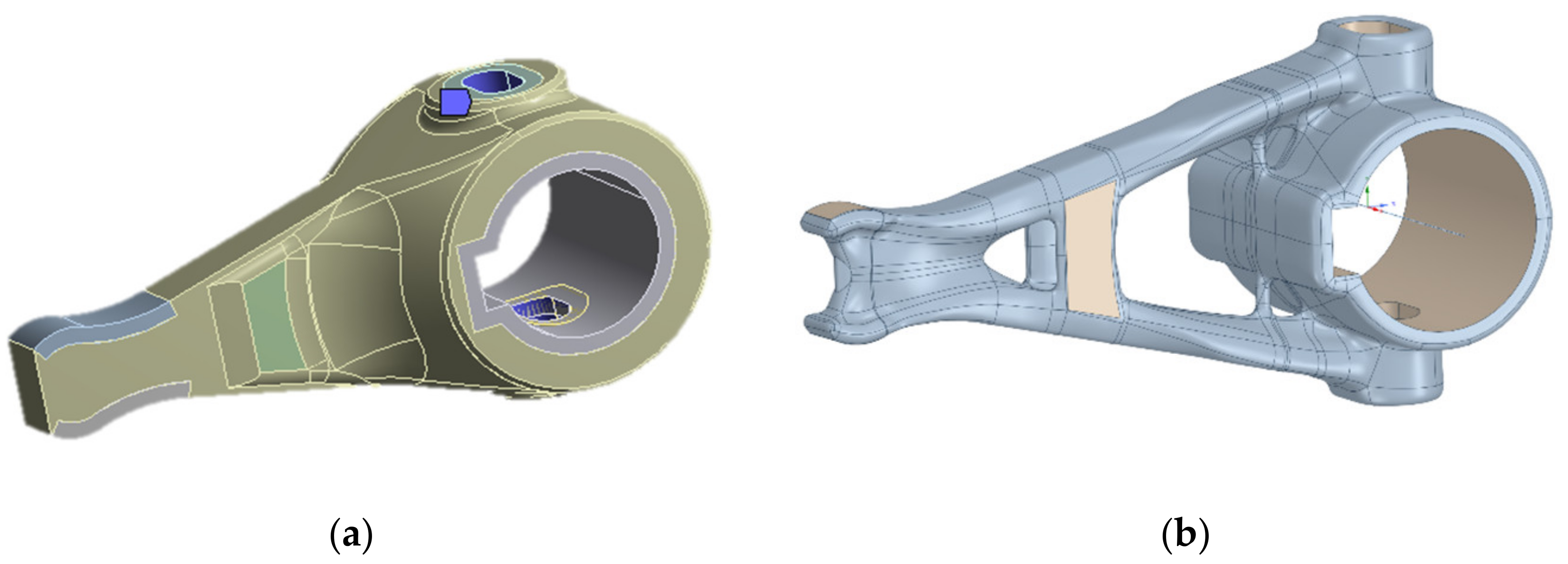
2.3. Topology Optimization
2.4. Orientation of Parts in the Build Chamber
2.5. SLM Printer RenAM400
2.6. Digital Image Correlation
2.7. 3D Scanner HandyScan Black
3. Results and Discussion
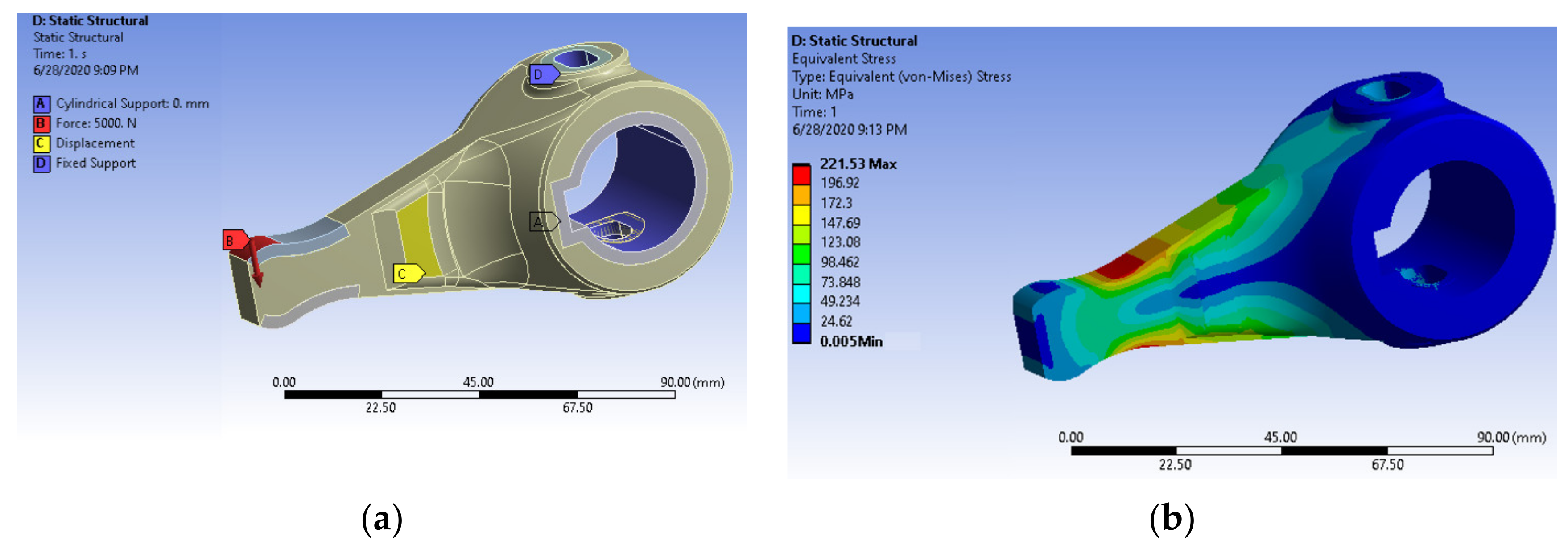
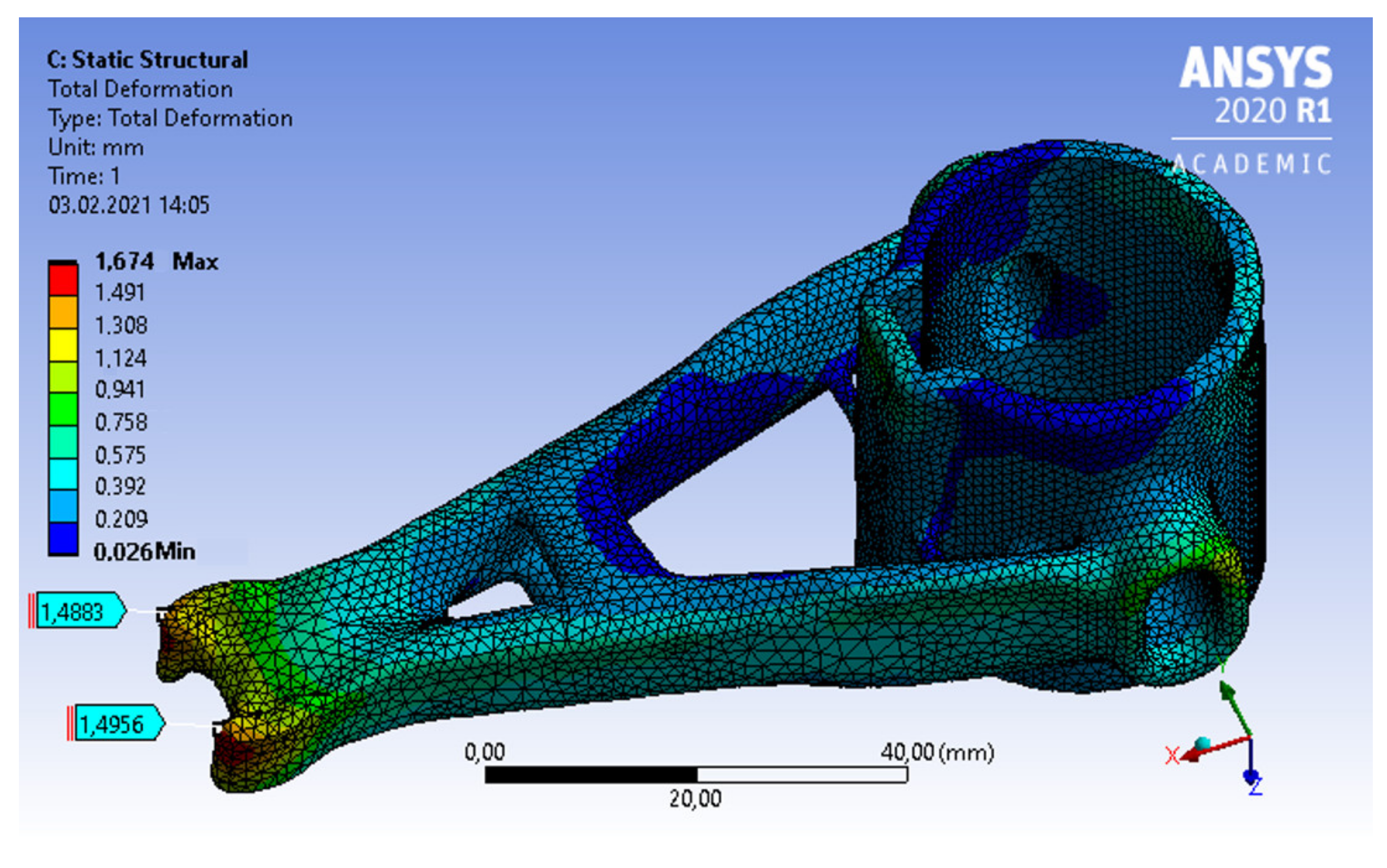
3.1. Simulation for Total Displacement in the AAS
3.2. Simulation for Total Displacement in MSC Simufact
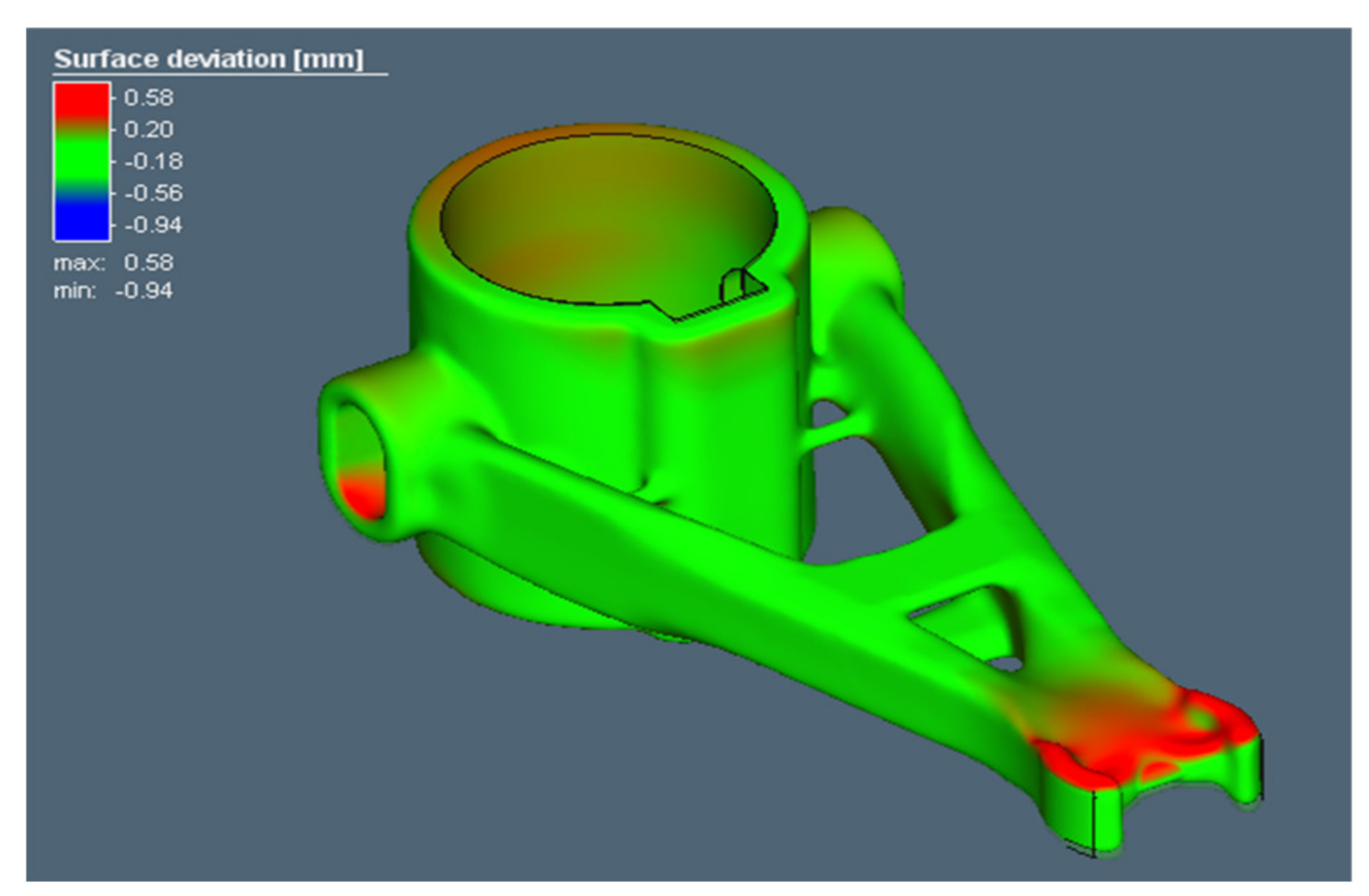
3.3. Validation of the Results
4. Conclusions
- From a part designed for the traditional manufacturing method, utilization of topology optimization can reduce the volume of the part by up to 63%, while ensuring the equivalent strength. The 3D printing technology, subsequently, can be utilized to fabricate the complex optimized shape.
- Cost efficiency can be improved by minimizing the support structures when orienting the part on the base plate. However, as previously discussed, ac ompromise has to be made between the mechanical properties and the manufacturability of the printed parts. This factor, indeed, is most important for industrial and serial production.
- ANSYS simulation brings closer results to experiments considering deviation values.
- The two measurements realized by the different methods (DIC and 3D scanning) provided equivalent results for deflections, which contrasted with the numerical results. For more sufficient QC process, 3D scanning is recommended.
- When comparing the simulations with real measurements, a deviation of 0.17 mm was achieved. The nature of this difference was expected in the linear structural analysis. Significant residual stresses can lead to the yielding of the material. The stainless steel showed slight viscoplastic behavior, even at room temperature.
- To achieve higher precision in surface finishing or dimensioning below the deviation level presented in this study, extra surface treatment and machining must be carried out on the printed parts.
- The support elements generated in both pieces of software can be successfully utilized in place of supports generated in the slicer software.
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Q.; Liang, X.; Hayduke, D.; Liu, J.; Cheng, L.; Oskin, J.; Whitmore, R.; To, A.C. An inherent strain based multiscale modeling framework for simulating part-scale residual deformation for direct metal laser sintering. Addit. Manuf. 2019, 28, 406–418. [Google Scholar] [CrossRef]
- Ansari, J.; Nguyen, D.-S.; Park, H.S. Investigation of SLM Process in Terms of Temperature Distribution and Melting Pool Size: Modeling and Experimental Approaches. Materials 2019, 12, 1272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hajnys, J.; Pagáč, M.; Měsíček, J.; Petru, J.; Król, M. Influence of scanning strategy parameters on residual stress in the SLM process according to the bridge curvature method for AISI 316L stainless steel. Materials 2020, 13, 1659. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lindgren, L. Computational Welding Mechanics; Woodhead: Cambridge, UK, 2007. [Google Scholar]
- Chiumenti, M.; Cervera, M.; Salmi, A.; de Saracibar, C.A.; Dialami, N.; Matsui, K. Finite element modeling of multi-pass welding and shaped metal deposition processes. Comput. Methods Appl. Mech. Eng. 2010, 199, 2343–2359. [Google Scholar] [CrossRef]
- Lundbäck, A.; Lindgren, L.-E. Modelling of metal deposition. Finite Elements Anal. Des. 2011, 47, 1169–1177. [Google Scholar] [CrossRef]
- Hussein, A.; Hao, L.; Yan, C.; Everson, R.M. Finite element simulation of the temperature and stress fields in single layers built without-support in selective laser melting. Mater. Des. 2013, 52, 638–647. [Google Scholar] [CrossRef]
- Zhang, D.; Cai, Q.; Liu, J.; Zhang, L.; Li, R. Select laser melting of W-Ni–Fe powders: Simulation and experimental study. Int. J. Adv. Manuf. Technol. 2010, 51, 649–658. [Google Scholar] [CrossRef]
- Keller, N.; Ploshikhim, V. New method for fast predictions of residual stress and distortion of AM parts. In Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference; The University of Texas: Austin, TX, USA, 2016; pp. 1229–1237. [Google Scholar]
- Afazov, S.; Denmark, W.A.; Toralles, B.L.; Holloway, A.; Yaghi, A. Distortion prediction and compensation in selective laser melting. Addit. Manuf. 2017, 17, 15–22. [Google Scholar] [CrossRef]
- Song, X.; Feih, S.; Zhai, W.; Sun, C.-N.; Li, F.; Maiti, R.; Wei, J.; Yang, Y.; Oancea, V.; Brandt, L.R.; et al. Advances in additive manufacturing process simulation: Residual stresses and distortion predictions in complex metallic components. Mater. Des. 2020, 193, 108779. [Google Scholar] [CrossRef]
- Pástor, M.; Hagara, M.; Čarák, P. Residual stresses measurement around welds by optical methods. In Proceedings of the 58th International Scientific conference on Experimental Stress Analysis 2020, Luhacovice, Czech Republic, 3–6 June 2019; VSB-Technical University of Ostrava: Ostrava, Czech Republic, 2020; pp. 371–381, ISBN 978-80-248-4451-0. [Google Scholar]
- Borralleras, P.; Segura, I.; Aranda, M.A.; Aguado, A. Influence of experimental procedure on d-spacing measurement by XRD of montmorillonite clay pastes containing PCE-based superplasticizer. Cem. Concr. Res. 2019, 116, 266–272. [Google Scholar] [CrossRef]
- Mayer, T.; Brändle, G.; Schönenberger, A.; Eberlein, R. Simulation and validation of residual deformations in additive manu-facturing of metal parts. Heliyon 2020, 6, 1–13. [Google Scholar] [CrossRef]
- Çelebi, A.; Appavuravther, E.Z. Analyzing the Effect of Voxel Mesh and Surface Mesh Application on Residual Stress by Simufact Additive Software. Düzce Üniversitesi Bilim ve Teknoloji Dergisi 2018, 6, 930–940. [Google Scholar] [CrossRef] [Green Version]
- Bian, P.; Shi, J.; Liu, Y.; Xie, Y. Influence of laser power and scanning strategy on residual stress distribution in additively manufactured 316L steel. Opt. Laser Technol. 2020, 132, 106477. [Google Scholar] [CrossRef]
- Training Manual 14TS210N; Kopřivnice: Kopřivnice, Czech Republic, 2011.
- Sotola, M.; Stareczek, D.; Rybansky, D.; Prokop, J.; Marsalek, P. New Design Procedure of Transtibial ProsthesisBed Stump Using Topological Optimization Method. Symmetry 2020, 12, 1837. [Google Scholar] [CrossRef]
- Jancar, L.; Pagac, M.; Mesicek, J.; Stefek, P. Design Procedure of a Topologically Optimized Scooter Frame Part. Symmetry 2020, 12, 755. [Google Scholar] [CrossRef]
- Mesicek, J.; Pagac, M.; Petru, J.; Novak, P.; Hajnys, J.; Kutiova, K. Topological Optimization of the Formula Student Bell Crank. MM Sci. J. 2019, 2019, 2964–2968. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, T.; Yang, S.; Ren, Z. A methodology for topology optimization based on level set method and its application to piezoelectric energy harvester design. Int. J. Appl. Electromagn. Mech. 2019, 59, 79–85. [Google Scholar] [CrossRef]
- Sigmund, O. Morphology-based black and white filters for topology optimization. Struct. Multidiscip. Optim. 2007, 33, 401–424. [Google Scholar] [CrossRef] [Green Version]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization: Theory, Method and Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Sigmund, O.; Peterson, J. Numerical instabilities in topology optimization: A survey on procedures dealing with checker-boards, mesh-dependencies and local minima. Struct. Optim. 1998, 16, 68–75. [Google Scholar] [CrossRef]
- Bruns, T.E.; Tortorelli, D.A. Topology optimization of non-linear elastic structures and compliant mechanisms. Comput. Methods Appl. Mech. Eng. 2001, 190, 3443–3459. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Workbench—ANSYS Help. 2020. Available online: https://ansyshelp.ansys.com/Account/Login?ReturnUrl=%2FViews%2FSecured%2Fcorp%2Fv195%2Fwb_sim%2Fds_topo_opt_level_set (accessed on 10 November 2020).
- Hitzler, L.; Hirsch, J.; Heine, B.; Merkel, M.; Hall, W.; Öchsner, A. On the Anisotropic Mechanical Properties of Selective Laser-Melted Stainless Steel. Materials 2017, 10, 1136. [Google Scholar] [CrossRef] [PubMed] [Green Version]







| Parameter | Value |
|---|---|
| Element size | 1 mm |
| Method | Cartesian |
| Hatch spacing | 0.11 mm |
| Scan speed | 650 mm/s |
| Laser power | 200 W |
| Preheat temperature | 22 °C |
| Layer thickness | 50 µm |
| Scan strategy | Meander |
| Parameter | Value |
|---|---|
| Element size | 1 mm |
| Method | Inherent Strains |
| Hatch spacing | 0.11 mm |
| Scan speed | 650 mm/s |
| Laser power | 200 W |
| Preheat temperature | Ambient |
| Layer thickness | 50 µm |
| Scan strategy | Meander |
| Rank | Supported Area (cm2) | Support Volume (cm3) | Outbox Volume (cm3) | Height (mm) | Centre of Gravity (mm) |
|---|---|---|---|---|---|
| 1 | 19.771 | 28.888 | 250.340 | 46.1 | 24.5 |
| 2 | 19.830 | 29.109 | 250.340 | 46.1 | 24.5 |
| 3 | 28.269 | 40.362 | 250.340 | 115.6 | 24.5 |
| 4 | 38.284 | 61.889 | 250.340 | 60.1 | 40.0 |
| 5 | 19.462 | 22.309 | 298.763 | 53.0 | 31.6 |
| 6 | 17.050 | 21.325 | 311.980 | 58.5 | 24.5 |
| 7 | 25.250 | 87.678 | 250.340 | 115.6 | 78.6 |
| 8 | 9.974 | 25.466 | 506.948 | 100.3 | 43.0 |
| 9 | 12.244 | 36.140 | 505.806 | 99.2 | 43.4 |
| Parameter | Value |
|---|---|
| Laser power | 200 W |
| Hatch spacing | 0.11 mm |
| Scan speed | 650 mm/s |
| Preheat temperature | Ambient |
| Layer thickness | 50 µm |
| Scan strategy | Meander |
| Numerical Method | Max. Value of Deflection |
|---|---|
| ANSYS Additive Suite | 1.496 mm |
| MSC Simufact | 0.580 mm |
| Experimental Method | Max. Value of Deflection |
| Digital image correlation | 1.137 mm |
| 3D scanner HandyScan | 1.327 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pagac, M.; Hajnys, J.; Halama, R.; Aldabash, T.; Mesicek, J.; Jancar, L.; Jansa, J. Prediction of Model Distortion by FEM in 3D Printing via the Selective Laser Melting of Stainless Steel AISI 316L. Appl. Sci. 2021, 11, 1656. https://doi.org/10.3390/app11041656
Pagac M, Hajnys J, Halama R, Aldabash T, Mesicek J, Jancar L, Jansa J. Prediction of Model Distortion by FEM in 3D Printing via the Selective Laser Melting of Stainless Steel AISI 316L. Applied Sciences. 2021; 11(4):1656. https://doi.org/10.3390/app11041656
Chicago/Turabian StylePagac, Marek, Jiri Hajnys, Radim Halama, Tariq Aldabash, Jakub Mesicek, Lukas Jancar, and Jan Jansa. 2021. "Prediction of Model Distortion by FEM in 3D Printing via the Selective Laser Melting of Stainless Steel AISI 316L" Applied Sciences 11, no. 4: 1656. https://doi.org/10.3390/app11041656
APA StylePagac, M., Hajnys, J., Halama, R., Aldabash, T., Mesicek, J., Jancar, L., & Jansa, J. (2021). Prediction of Model Distortion by FEM in 3D Printing via the Selective Laser Melting of Stainless Steel AISI 316L. Applied Sciences, 11(4), 1656. https://doi.org/10.3390/app11041656










